1 Introduction

Vortex is a common phenomenon in turbulent flow, which is closely related to drag, lift, vibration, noise, etc. Accurate capture of vortices is the basis for the simulation of the flow field. In the last 30 years, various fluid dynamics governing equations is expressed in eddies perspective, and they explain many problems in the flow field from another angle [8].

The earliest definition of vortex was defined by the vorticity tube, which is considered to be equivalent to a vortex. The method is categorized as the first generation of vortex identification. In the past 30 years, scholars proposed the Q-criterion, \(\Delta \), \({\uplambda }_{2}\) and so on. These parameters are usually based on the Cauthy-Stokes decomposition of the velocity gradient tensor. They are regarded as the second-generation vortex identifications [8]. However, there are some problems with these methods. In 2014, the Vortex and Turbulence Research Team at the University of Texas at Arlington (UTA Team) focused on developing a new generation of vortex identification method, omega, which defines a vortex as a connected region where the vorticity exceeds the deformation [9]. Meanwhile, Liutex is proposed to represent the local rigid rotation of fluids. Such the third-generation vortex identification technology can describe the absolute strength, the relative strength, the rotational axis, the vortex core position and size, and the vortex boundary. Other vortex identification methods fail to answer these problems, except for the vortex boundary [3, 10].

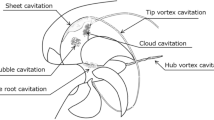
The simulation of the wake of an open-water propeller is a complex problem in the field of hydrodynamics, not only for the complex geometry of the propeller, but also for the existence of complex vortex systems in the propeller wake, such as hub and tip vortex [6]. For high-speed operating conditions, cavitation may occur. The interaction between cavitation and wake vortices enhances the pulsation of turbulent flow and increases turbulent kinetic energy. The accurate prediction of propeller thrust and torque is dependent on the accuracy of the flow field, and the precise capture of vortex is the basis of all this [14]. The first and second generation vortex identification methods cause shear tensor and false vorticity near the boundary, and the omega identification method helps overcome these problems.

In recent years, the prediction of propeller noise has become a research hotspot. Due to the underwater incompressibility, it is not feasible to use direct numerical simulation (DNS) to predict the noise. Therefore, acoustic analogy becomes the main method [1, 4, 6]. In the acoustic analogy, the area near the propeller is regarded as the near field, and all nonlinear effects are within this range. With the assumption of compact sound sources, the sound pressure can be obtained by radiating the sound source obtained by CFD calculation to the far field. This method was first proposed by Lighthill [7] and developed by Curle [2] and Ffowcs Williams et al. [5] They classified sound sources into three types: monopoles, dipoles, and quadrupoles. Among them, the quadrupole is considered to be related to the vortex, so the accurate capture of the vorticity is the basis of noise prediction.

In this paper, the wake of the DTMB4119 propeller are studied, and the third-generation vortex identification method is used to analyze the noise in cavitation and non-cavitation conditions. The sound pressure distribution law is explained from the perspective of vortex. The structure of this paper is arranged as follows: Chap. 2 is the mathematical foundation, including omega expression, DDES turbulence model, Schnerr-Sauer cavitation model and FW-H acoustic equation. The Chap. 3 introduces the settings of numerical examples. Chapter 4 presents the hydrodynamic results, including the verification of hydrodynamic results and the analysis of vortex structure. Chapter 5 presents the sound field results, which are divided into near-field and far-field results. Finally, Chap. 6 gives the conclusion.

2 Mathematical Formulations

2.1 Omega Vortex Identification Method

Vorticity does not represent fluid rotation because the effects of deformation should also be considered. The relationship between the two is like a mixture of salt and water. The salinity does not depend on the mass of salt. It depends on the ratio of salt and water. Larger vorticity does not necessarily cause strong rotations, and small vorticity may also cause strong rotations. The Blasius boundary layer is a typical example. The third generation of vortex identification technology uses the ratio of vorticity and deformation to define the vortex boundary. \(\Omega \) is defined as a ratio of the vorticity tensor norm squared over the sum of the vorticity tensor norm squared and deformation tensor norm squared.

$$\boldsymbol{\varOmega }\text{=}\frac{{\Vert {\varvec{B}}\Vert }_{\text{F}}^{2}}{{\Vert {\varvec{A}}\Vert }_{\text{F}}^{2} +{\Vert {\varvec{B}}\Vert }_{\text{F}}^{2}}=\frac{b}{a+b}$$

where, \(a={\Vert {\varvec{A}}\Vert }_{\text{F}}^{2}\), \(b={\Vert {\varvec{B}}\Vert }_{\text{F}}^{2}\). To prevent the appearance of unphysical vortices, a small value \(\upepsilon \) is added to the denominator, as shown below.

$$\boldsymbol{\varOmega }=\frac{b}{a+b+\epsilon }$$

Many scholars examined the robustness of \(\boldsymbol{\varOmega }\) and found that the range of vortices hardly changes between the thresholds of 0.52–0.6. This is one of the advantages of the third-generation vortex identification technology over the previous methods, which are often sensitive to threshold values. For \(\boldsymbol{\varOmega }\), increasing or decreasing the threshold values only make the vortex structure thinner or fatter. But a higher threshold value is needed if the position of the vortex core is desired, such as 0.8, 0.9, etc.

2.2 Turbulence Model

The problem of propeller wake is still an open issue, and the interaction between turbulence and cavitation is particularly complex. Previous studies proved that the RANS model cannot obtain the small-scale vortices for the underwater propeller, which has a great impact on the acoustic prediction [13].

For this reason, this paper uses the improved Spalart–Allmaras DES as the turbulence model, namely SA-DDES [12]. Its governing equation is,

$$\frac{\partial \stackrel{\sim }{\nu }}{\partial t}+div(\stackrel{\sim }{\nu }u)=\frac{1}{{C}_{\sigma }}\{div[(\nu +\stackrel{\sim }{\nu })grad\stackrel{\sim }{\nu }]+{C}_{b2}\frac{\partial \stackrel{\sim }{\nu }}{\partial {x}_{i}}\frac{\partial \stackrel{\sim }{\nu }}{\partial {x}_{j}}\}+{C}_{b1}\tilde{S }\stackrel{\sim }{\nu }-{C}_{w1}{f}_{w}{\left(\frac{\stackrel{\sim }{\nu }}{\tilde{d }}\right)}^{2}$$

The first term on the left side is the transient term, and the second term is the convection term; the first term on the right side is the diffusion term, the second term is the source term, and the third term is the dissipation term. The DDES equation modifies \(\tilde{d }\) in the formula to

$$\tilde{d }={d}_{w}-{f}_{d}\cdot \mathrm{max}({d}_{w}-{C}_{DES}\Delta ,0)$$
$${f}_{d}=1-\mathrm{tanh}[{(8{r}_{d})}^{3}]$$
$${r}_{d}=\frac{{\nu }_{t}+\nu }{\sqrt{{U}_{ij}{U}_{ij}}{(\kappa {d}_{w})}^{2}}$$

2.3 Cavitation Model

The cavitation model, or mass transport model, is derived from the commonly-used Rayleigh-Plesset cavity dynamics equation. The process of condensation and evaporation in cavitation describes the changes in each phase by adding source terms. This paper adopts the Schnerr-Sauer cavitation model [11]. The mass conversion equation of the model is as follows:

$$\frac{\partial ({\rho }_{v}{\alpha }_{v})}{\partial t}+\frac{\partial ({\rho }_{v}{\alpha }_{v}{u}_{j})}{\partial {x}_{j}}={\dot{m}}^{+}-{\dot{m}}^{-}$$

where \({\mathrm{\alpha }}_{\mathrm{v}}\) is the vapor volume fraction, and the source terms \({\dot{m}}^{+}\) and \({\dot{m}}^{-}\) represent the evaporation and condensation processes, respectively. When the phase change occurs, there is

$${\dot{m}}^{+}=\frac{{\uprho }_{\mathrm{v}}{\rho }_{l}}{\rho }{\alpha }_{v}(1-{\alpha }_{v})\frac{3}{{R}_{b}}\sqrt{\frac{2}{3}\frac{\mathrm{max}({p}_{v}-p,0)}{{\rho }_{l}}}$$
$${\dot{m}}^{-}=\frac{{\uprho }_{\mathrm{v}}{\rho }_{l}}{\rho }{\alpha }_{v}(1-{\alpha }_{v})\frac{3}{{R}_{b}}\sqrt{\frac{2}{3}\frac{\mathrm{max}(p-{p}_{v},0)}{{\rho }_{l}}}$$

Among them, \({\dot{m}}^{+}\) represents the evaporation process, and \({\dot{m}}^{-}\) represents the condensation process. \({R}_{b}\) is the radius of the cavity, and \({p}_{v}\) is the saturation vapor pressure at the local temperature. The calculation formula of the cavity radius is:

$${\mathrm{R}}_{\mathrm{b}}={\left(\frac{{\alpha }_{v}}{(1-{\alpha }_{v})}\frac{3}{4\pi }\frac{1}{{N}_{b}}\right)}^\frac{1}{3}$$

Among them, \({N}_{b}={10}^{13}{m}^{-3}\) is the cavity number density.

2.4 FW-H Formulation

Here, we use the most widely used and universally significant FW-H equation, as is shown below.

$$\left(\frac{1}{{c}^{2}}\frac{{\partial }^{2}}{\partial {t}^{2}}-{\nabla }^{2}\right){p}^{^{\prime}}=\frac{\partial }{\partial t}\left[{\rho }_{0}{\nu }_{n}\delta \left(f\right)\right]-\frac{\partial }{\partial {x}_{i}}\left[p{n}_{i}\delta \left(f\right)\right]++\frac{{\partial }^{2}}{\partial {x}_{i}\partial {x}_{j}}[H(f){T}_{ij}]$$

The surface of an object can be represented by \(f(x,t)=0\), where \(\nabla f=\overrightarrow{n}\) points to the normal direction outside the object surface. According to the linear assumption, \(p^{\prime}={c}^{2}\rho ^{\prime}={c}^{2}(\rho -{\rho }_{0})\), where \(c\) and \({\rho }_{0}\) respectively represent the fluid sound velocity and density under the undisturbed fluid medium. \(\delta (f)\) represents the Dirac function. The National Aeronautics and Space Administration (NASA) summarized the different integral solutions of the FW-H equation and systematically named these solutions, such as Farassat Formulations 1 and Farassat Formulations 1A. The derivation process of Farassat Formulation 1A is omitted here, and the integral result expression is directly given as follows:

$$\begin{aligned}4\pi p{^{\prime}}_{T}\left(x,t\right) & ={\int }_{f=0}{\left[\frac{{\rho }_{0}{\dot{\nu }}_{n}}{r{\left(1-{M}_{r}\right)}^{2}}+\frac{{\rho }_{0}{\nu }_{n}{\widehat{r}}_{i}{\dot{M}}_{i}}{r{\left(1-{M}_{r}\right)}^{3}}\right]}_{ret}dS+\\ & \quad +{\int }_{f=0}{[\frac{{\rho }_{0}c{\nu }_{n}({M}_{r}-{M}^{2})}{{r}^{2}{(1-{M}_{r})}^{3}}]}_{ret}dS\end{aligned}$$
$$ \begin{aligned} 4\pi p^{\prime}_L \left( {x,t} \right) & = \int \limits_{f = 0} \left[ {\frac{{\dot{p}{\text{cos}}\theta }}{{cr\left( {1 - M_r } \right)^2 }} + \frac{{\hat{r}_i \dot{M}_i p{\text{cos}}\theta }}{{cr\left( {1 - M_r } \right)^3 }}} \right]_{ret} dS \\ & \;\;\;\; + \int \limits_{f = 0} \left[ {\frac{{p\left( {{\text{cos}}\theta - M_i n_i } \right)}}{{r^2 \left( {1 - M_r } \right)^2 }} + \frac{{\left( {M_r - M^2 } \right)p{\text{cos}}\theta }}{{r^2 \left( {1 - M_r } \right)^3 }}} \right]_{ret} dS \\ \end{aligned} $$

Here, \(p{^{\prime}}_{T}\) stands for thickness noise. \(p{^{\prime}}_{L}\) stands for load noise, \(\left(x,t\right) (y,t)\) are the space–time variables of the observation point and the sound source respectively; \(r=\left|x-y\right|\) is the norm of the vector radius from the observation point to the sound source; \(\widehat{{r}_{i}}=\frac{(x-y)}{r}\) represents the normalization of the vector radius; \({\mathrm{M}}_{\mathrm{r}}=\frac{\widehat{{r}_{i}}{v}_{i}}{c}\) is the sound source Mach number in the satellite coordinate system; \(1-{M}_{r}\) is called the Doppler factor; \(\dot{{v}_{n}}=\frac{\partial }{\partial \tau }(v\cdot n)\) represents the derivative of the speed to the sound source time; \(\mathrm{cos}\theta ={n}_{i}\widehat{{r}_{i}}\) is the vector path from the observation point to the sound source; \({\left[\right]}_{\mathrm{ret}}\) is retarded time, which represents the satellite coordinates after considering the Doppler effect.

3 Numerical Setup

The DTMB 4119 propeller (three-blade) is selected as the research object. As a well-known model widely used both in hydrodynamic and hydroacoustic fields, this propeller has a simple geometric structure and relatively detailed hydrodynamics experimental data [4]. The basic parameters of the propeller are shown in Table 17.1.

Table 17.1 DTMB 4119 propeller geometry model parameters
Full size table

The numerical domain is cylindrical, as shown in the Fig. 17.1. The propeller is arranged 2D downstream of the inflow patch, and the outflow patch is 4D away from the disk, so that the wake can be fully developed before reaching the outlet. The diameter of the outer cylinder is set as 3D to avoid interference with the flow of the propeller.

Fig. 17.1
A set of 2 illustrations. 1, a horizontal cylinder with measurements of total L = 6 D, D subscript c = 3 D, and propeller measurements of D subscript A = 1.2 D, and the L 2=4 D. 2, a propeller mesh with 3 blades and trailing and leading edges.

The left panel: Diagram of the calculation domain; The right panel: The propeller mesh

Full size image

The calculation example uses unstructured grids, and the total number of grids is 3.45 million. The y + value at the boundary layer is less than 10, which meets the requirements of the DDES turbulence model. Figure 17.1 shows the mesh distribution on the propeller surface.

4 Hydrodynamic Results

4.1 Hydrodynamic Verification

Figure 17.2 shows the comparison between the hydrodynamic coefficient obtained by the computation and the experiment under different advance coefficients. It can be seen that the error is very small. The thrust coefficient, the torque coefficient and the efficiency are defined as below:

Fig. 17.2
A line graph of K subscript T 10 K subscript q, eta versus J. 6 curves represents K subscript T EXP and D D E S, 10 K subscript Q EXP and D D E S, eta EXP and D D E S in a downward trend. Eta EXP and D D E S peak at 0.7 in 0.9 J.

The calculated \({\mathrm{K}}_{\mathrm{T}}\), \({\mathrm{K}}_{\mathrm{Q}}\) and \(\upeta \) under different advance coefficients compared with the experiment results [4]

Full size image
$${K}_{T}=\frac{T}{\rho {n}^{2}{D}^{4}}, {K}_{Q}=\frac{Q}{\rho {n}^{2}{D}^{5}}, \upeta =\frac{{K}_{T}\cdot D}{{K}_{Q}}$$

Three sections y/D = -–0.25,0.5,1 are plotted in the time-averaged contours of axial velocity, turbulent kinetic energy (TKE), and Q amplitudes, as Fig. 17.3 shows. The suction force is dominant in the upstream region, which can be seen from the axial velocity and the TKE cloud diagram. Besides, there is almost no vortex upstream of the propeller except near the hub, which is related to the small upstream TKE. The axial velocity downstream is mainly distributed in the range of the disk surface, and this area produces the most of the thrust force. The tip vortex becomes weak rapidly with the increase of the distance, but the hub vortex can continue for a long way. The TKE of the tip part gradually decreases in the downstream region, but the TKE of the hub part is increasing.

Fig. 17.3
An illustration of 9 time-averaged contours with 3 horizontal 3 D cylinders arranged in 3 columns presents the axial velocity, turbulent kinetic energy, and Q amplitudes. 3 Cylinder labels y = negative 0.25 D, 0.5 D, and 1 D.

The time-averaged contours of axial velocity, turbulent kinetic energy (TKE), and Q amplitudes plotted in three sections y/D = –0.25,0.5,1

Full size image

In the Fig. 17.4, the pressure, the epsilon of DDES and the turbulent viscosity are plotted on the three cross-sections. The low-pressure core inside the tip vortex can still be seen until y/D = 1. In the hub vortex, the epsilon is large, which can be considered as the area where the sound source is concentrated. Satisfactory values are also obtained for the viscosity in the tip and hub vortex regions.

Fig. 17.4
An illustration of 9 analysis images demonstrates the pressure, the epsilon of D D E S, and the turbulent viscosity on the three cross-sections in 3 columns. 3 Cylinder labels y = negative 0.25 D, 0.5 D, and 1 D.

The pressure, the epsilon of DDES and the turbulent viscosity on the three cross-sections y/D = –0.25,0.5,1

Full size image

4.2 Vortex Comparison

\({{\varvec{\Omega}}}_{\mathbf{R}}\) Are compared with vorticity in this subsection. The second-generation vortex ‘vorticity’ has an obvious drawback, that is, there is false vortex near the AMI surface. The third-generation vortex ‘\({{\varvec{\Omega}}}_{\mathbf{R}}\)’ solves the problem of false signal on the AMI surface in the vorticity, but the false signal at the boundary still exists (Fig. 17.5).

Fig. 17.5
A set of 2 contour diagrams compare the vorticity cloud chart and the omega cloud chart. The vorticity and omega gradient scales are at the bottom.

The comparison between vorticity cloud chart (left panel) and omega cloud chart (right panel)

Full size image

For comparison, a cavitation condition is set here, and the relevant parameters of the operating condition are shown in Table 17.2. Here we compare the Q criterion and \({{\varvec{\Omega}}}_{\mathbf{R}}\) in the cavitation state, and find that \({{\varvec{\Omega}}}_{\mathbf{R}}\) can not only capture the vortex structure further downstream, but also eliminate the false vortex on the wall (Fig. 17.6).

Table 17.2 The cavitation condition parameters
Full size table
Fig. 17.6
A set of 2 illustrations of cavitation conditions of Q = 300 and omega subscript R = 0.52. Both exhibits a propeller with spiral waves. At the bottom U magnitude scale ranges from 1.00 + 01 to 1.80 + 01.

The comparison for cavitation conditions between Q-criterion and \({\Omega }_{\mathrm{R}}\): The left panel shows the Q = 300 iso surface; The right panel shows \({\Omega }_{\mathrm{R}}=0.52\) iso surface

Full size image

5 Hydroacoustic Results

5.1 Near-Field Sound Pressure

The near-field sound pressure is analyzed in this section. In the near field of the propeller, six near-field probes are set up in sequence from upstream to downstream, as Fig. 17.7 shows. Taking the object surface as the integral surface, the dipole contribution, monopole contribution and CFD measurement values of 6 test points are plotted respectively, see Fig. 17.8. It is easy to see that the sound pressure at point A2 is the largest, no matter which sound pressure point, the contribution of the dipole is much greater than that of the monopole. And the total sound pressure is relatively consistent with the CFD measurements.

Fig. 17.7
A 3-dimensional illustration of a propeller's side view with 3 blades and 6 near field probes A subscript 1 to 6.

The six near-field microphones positions: All of these probes are in the \(\mathrm{x}=0\) plane and \(\mathrm{x}=0.8\mathrm{D}\) plane. \({\mathrm{A}}_{2}\) probe is located at \(\mathrm{y}=0\). The spacing of two adjacent microphones is 0.2D

Full size image
Fig. 17.8
A set of 4 line graphs of P of p a versus time in seconds. 6 curves represent A subscript 1 to 6 in fluctuation trends.

The near-field sound pressure predicted by FW-H equation: The upper row is non-cavitation condition. The lower row is cavitation condition. The left column shows the monopole results. The right column shows the dipole results (Fig. 17.9).

Full size image

At the same near-field test point, for cavitation, the results of acoustic analogy and CFD measurement are quite different, as Fig. 17.8 shows. This is mainly because the influence of nonlinear sound sources is not considered, and the existence of two-phase flow also has an influence on sound pressure propagation [14].

Fig. 17.9
Two contour plots of the nonlinear sound distribution for non-cavitation and cavitation conditions. On the right, the nonlinear source scale ranges from 1.0 e + 04 to 1.0 e + 04.

The nonlinear sound source distribution: The left is the non-cavitation condition; The right is the cavitation condition

Full size image

The difference between the two cases can be explained from the perspective of nonlinear sound sources. The sound source of the cavitation is longer than that of the non-cavitation, and it is more complicated near the object surface. The reason is the vortex distribution.

5.2 Far-Field Directivity

As for the far field, 4 planes are selected, and 36 test points are set for each plane, as Fig. 17.10 shows. The penetrable integral surface is used to calculate the acoustic directivity. In this way, nonlinear terms can be considered. Therefore, it can be seen that there are quadrupole characteristics on the two X planes, see Fig. 17.11. This is because the quadrupole is dominant in the far field. On the Y plane, it shows a uniform distribution.

Fig. 17.10
An illustration of 2 horizontal dotted ellipses, X 0 and X 1, and 2 vertical dotted ellipses, Y 0 and Y 1, with a propeller at the center.

The sketch of far-field microphones distributed on 4 planes: X0 = 0, X1 = –3D, Y0 = 0, Y1 = 3D. The radius of the probes is 10D

Full size image
Fig. 17.11
A set of 4 radar charts of O A S P L distribution on 4 planes. Plots 2 sets of 2 lines of X 0 and 1, and Y 0 and 1 for non-cavitation and cavitation conditions.

The OASPL distribution on 4 planes for far field: The upper row shows the non-cavitation condition; The lower row shows the cavitation condition

Full size image

As for the cavitation, the decay speed of cavitation is less than that of non-cavitation, which is caused by different vorticity distribution laws. This can also be explained by the distribution of \({{\varvec{\Omega}}}_{\mathbf{R}}\). As shown in the Fig. 17.12, the vorticity of Y1 is already small for non-cavitation conditions, while for cavitation, the vortex is still considerable. Therefore, the decay of the cavitation state is slower.

Fig. 17.12
Two cloud map diagrams illustrate the non-cavitation and cavitation conditions with vertical line labels Y 1. Cavitation exceeds the Y 1 line.

The cloud map for \({\Omega }_{\mathrm{R}}\): The top panel is for non-cavitation condition; The bottom panel is for cavitation condition. The plane Y1 is marked by the black line

Full size image

6 Conclusion

The wake characteristics of the DTMB4119 propeller is analysed using the third-generation vortex identification technology. With the DDES turbulence model and the Schnerr Sauer cavitation model, both non-cavitating and cavitating conditions are simulated. The force coefficients are calculated and compared with the experimental results to verify the accuracy of the simulation. Changes in turbulent kinetic energy and turbulent viscosity et al. are analysed at different sections. The distribution of sound pressure is analyzed from the near-field and far-field perspectives, and an explanation is attempted from the distribution of \({{\varvec{\Omega}}}_{\mathbf{R}}\). Three conclusions are gotten:

  • The third-generation vortex recognition technology can capture more detailed vortex structures and eliminate false vortex signals on the AMI surface.

  • For the distribution of Lighthill sound sources, the vortex distribution given by Liutex is more consistent with the sound source distribution.

  • Nonlinear terms dominate far-field noise. \({{\varvec{\Omega}}}_{\mathbf{R}}\), which predicts the vortex structure more accurately, can explain the far-field decay law better.