Keywords

1 Introduction

Tele-operation systems are widely applied to many hard-to-reach environments, such as aerospace [1], medical surgery [2], deep-sea exploration [3] and so on. Especially, in the medical surgery tele-operation system, at the console, the surgeon commands the master surgical manipulator to perform surgery on the patient. In teleoperation systems, the human operates the master manipulator, and the slave manipulator may follow the trajectory of the master side. Normally, there is a communication channel between the master side and the slave side since they are located in different sites.

In the bilateral teleoperation system, the time delay may be occurred owing to the communication channel between the master and the remote slave side. Many researchers devote themselves to various control methods in order to realize trajectory tracking as well as to enhance the accurate force feedback of the slave side. Some researchers studied the stability of the force feedback bilateral teleoperation system are analyzed from the direction of Lyapunov-Krasovskii theory and hybrid system theory [4,5,6,7]. Others use the four-channel structure to carry out bilateral coordinated control of the teleoperation system [8, 9]. However, in most exist work, the integral network of teleoperation systems are assumed to be passive. The part active power may be produced due to the development and the introduce of more soft master manipulators and devices.

Ensuring the stability of bilateral teleoperation systems with part active power, we design a control structure based on the four-channel wave variables under the condition under constant time delay. The advantage of the four-channel is the clear structure and the parameters are relatively transparent. At the same time, the wave variable algorithm may ensure the stability of the system under different time delays. In the view of the network energy, the stability condition is discussed and a PD bilateral controller is applied, so as to achieve high tracking performances. The rest of paper is organized as follows. The bilateral teleoperation system with part active power is introduced in Sect. 2. The stability is detailed analyzed and the stability condition is discussed in Sect. 3. The PD bilateral controller and numerical simulations are explained in Sect. 4. Conclusions are drawn in the conclusion part.

2 Bilateral Teleoperation System with Part Active Power

The passive theory is similar to Lyapunov theory, both of which analyzes the stability of the system from the perspective of the energy. Many physical systems in reality, such as electromechanical systems, have the nature of passive theory. The basic idea of the passive theory is that if a physical system consumes energy, then this system is passive. Thus, it can be obtained that the system is stable.

For a certain physical system, as shown in Fig. 1, the input vector and output vector are defined as x and y respectively, then the input power Pin of the system is:

$$ P_{in} = x^T y $$
(1)
Fig. 1.
figure 1

Single port physical system.

Full size image

For the physical system shown in Fig. 1, the input power is equal to the sum of the system power consumption \({P}_{diss}\) and the change of the system energy storage \({E}_{store}\),

$$ P_{in} = \frac{{dE_{store} }}{dt} + P_{diss} $$
(2)

(2) indicates that the power input to the system may be consumed or stored by the system. Integrating (2) from any initial time t0 to a certain time t, the energy change relationship can be obtained as follows:

$$ \int_{t0}^t {P_{in} } d\tau = \int_{t0}^t {x^T y} d\tau = E_{store} (t_0 ) - E_{store} (t_0 ) + \int_{t0}^t {P_{diss} } d\tau $$
(3)

If (3) always satisfies following relation,

$$ \int_{t0}^t {P_{in} } d\tau \ge - E_{store} (t_0 ) $$
(4)

Then the system can be determined to be passive, which can further conclude that the system is stable.

Figure 1 displays a single-port network, while our current teleoperation system is generally simplified into a two-port network analysis as shown in Fig. 2.

Fig. 2.
figure 2

Two-port physical system

Full size image

The input power \({P}_{in}\) of the two-port physical system shown in Fig. 2 can be expressed as follows,

$$ P_{\rm{in}} = x_1^T y_1 - x_2^T y_2 $$
(5)

Assuming that the initial energy storage of the two-port network is 0, from any time t0 to the current time t, if (6) is satisfied, the two-port network is considered passive.

$$ \int_{t0}^t {(x_1^T y_1 - x_2^T y_2 )\,} d\tau \ge 0 $$
(6)

Currently, the majority of bilateral teleoperation systems addressed in existed litteratures are recommended for the passive input of master terminal. However, we discover through theoretical derivation that adds certain part active components to the input of main terminal which may still achieve system stability control and position tracking. The integral network may be regarded as the combination of an active part and passive part. Our work is focused on arrange the limitation of the active part so that the overall system can be still stable and energy dissipative. In this case, the stability of the integral system, and the relationship between input and output power may be examined from an energy standpoint to determine and discussed.

3 Stability Analysis of Part Active Four Channel Network

3.1 Network Power

The entire working network can be simplified into a two-port network, as illustrated in Fig. 3.

Fig. 3.
figure 3

Network power

Full size image

Figure 3 shows the power flow into the part active network and the power flow is given as follow,

$$ P = f_1 V_1 - f_2 V_2 = \frac{dE}{{dt}} + P_{diss} $$
(7)

In formula (7), \({f}_{1}\), \( {V}_{1}\) represents the force input and speed input information of the left port, and \({f}_{2}\), \({V}_{2}\) represents the force input and speed input information of the right port. \({P}_{diss}^{L}\) and \({P}_{diss}^{R}\) represents the power dissipation of the left and right ports. From Eq. (7), we can extend it appropriately, because the framework of the entire system is based on the four-channel structure and wave variable algorithm, so b represents the wave impedance, and the following equation can also be obtained:

$$ P_1 = \frac{1}{2b}f_1^2 + \frac{b}{2}V_1^2 - \frac{1}{2b}(f_1 - bV_1 )^2 = f_1 V_1 $$
(8)
$$ P_2 = \frac{1}{2b}f_2^2 + \frac{b}{2}V_2^2 - \frac{1}{2b}(f_2 + bV_2 )^2 = f_2 V_2 $$
(9)

Making the difference between (8) and (9) to get the power consumed by the entire network \(\mathrm{\Delta P}\), we may get

$$ \Delta P = f_1 V_1 - f_2 V_2 = \frac{1}{2b}f_1^2 + \frac{b}{2}V_1^2 - \frac{1}{2b}(f_1 - bV_1 )^2 - [\frac{1}{2b}f_2^2 + b/2V_2^2 - \frac{1}{2b}(f_2 + bV_2 )^2 ] $$
(10)

3.2 The Asymmetric Delay of Vm, Fs

Since the entire communication channel has time delay, considering following asymmetric delay characteristics of \({V}_{m}\) and \({F}_{s}\), we can get:

$$ \begin{array}{*{20}l} {P = \frac{1}{b}f_1^2 - \frac{b}{2}T_f^2 V_2^2 - \frac{1}{2b}(f_1 - bV_1 )^2 } \hfill \\ { + \,bV_2^2 - \frac{1}{2b}T_b f_1^2 - \frac{1}{2b}(f_2 + bV_2 )^2 } \hfill \\ { + \,\frac{d}{dt}(\int_{t - Tb}^t {\frac{1}{2b}f_2^2 (\tau )d\tau } ) + \frac{d}{dt}(\int_{t - Tf}^t {\frac{b}{2}V_1^2 (\tau )} d\tau ) + D.} \hfill \\ \end{array} $$
(11)

\({T}_{b}\) and \({T}_{f}\) in (11) are respectively the time delays of the communication channel, \(\uptau \) is input torque, and D is a function about time t. From (11), it can be seen that the system energy E(t) and the dissipation power \({P}_{diss}\) have following relations,

$$ E\left( t \right) = \mathop \smallint \limits_{t - Tb}^t \frac{1}{2b}f_2^2 \left( \tau \right)d\tau + \mathop \smallint \limits_{t - Tf}^t \frac{b}{2}V_1^2 \left( \tau \right)d\tau $$
(12)
$$ P_{diss} = \frac{1}{b}f_1^2 - \frac{1}{2b}(f_1 - bV_1 )^2 + bV_2^2 - \frac{1}{2b}(f_2 + bV_2 )^2 - \frac{b}{2}T_f V_2^2 - \frac{1}{2b}T_b f_1^2 $$
(13)

3.3 Analysis of the Stability Condition of Part Active Network

The energy of the entire system can be derived from the following (14):

$$ \begin{array}{*{20}l} {E_{flow} (t) = \int_0^t {P(\tau )} d\tau } \hfill \\ { = \int_0^t {(\frac{dE}{{dt}} + P_{diss} + D)} (\tau )d\tau } \hfill \\ { = E(t) - E(0) + \int_0^t {P_{diss} (\tau )} d\tau + \int_0^t {D(\tau )} d\tau } \hfill \\ \end{array} $$
(14)

It can be easily seen that if E(t) in (12) contains a square term, then E(t) ≥ 0. To make the entire system satisfy the passive condition, the following relation must be established \({E}_{flow}(t)\)≥0. Therefore, we deduced following conditions that \(D(\tau )\) and \({\int }_{0}^{t}D(\tau )d\tau \) must be satisfied,

  1. (1)

    D(t) = f(t).

  2. (2)

    D(t) can be differential, and \(\exists \frac{\mathrm{dD}(\mathrm{t})}{\mathrm{dt}},\left|\frac{\mathrm{dD}(\mathrm{t})}{\mathrm{dt}}\right|\le \mathrm{D},\frac{{\mathrm{d}}^{2}\mathrm{D}(\mathrm{t})}{{\mathrm{dt}}^{2}}\ge 0\).

  3. (3)

    \({\int }_{0}^{\mathrm{t}}\mathrm{D}(\uptau )\mathrm{d\tau }=\frac{\mathrm{D}}{2}{\mathrm{t}}^{2}\ge 0\).

According to above three conditions (1) (2) (3), we can use the way of squeeze for the \({\int }_{0}^{t}D(\tau )d\tau \):

$$ E_{flow} \left( t \right) \ge - E\left( 0 \right) + \mathop \smallint \limits_0^t P_{diss} \left( \tau \right) $$
(15)

Assuming that E(0) = D, the quantitative relationship between the initial energy and the extreme value identity at the adjacent active energy can be derived. Therefore, we can obviously get the inequality of \({E}_{flow}(t)\ge {\int }_{0}^{t}{P}_{diss}(\tau )d\tau \). In this way, the passivity of the entire system can be proven.

4 Numerical Simulations and Results

In the numerical simulation, both master and slave manipulators are used same two-degree-of-freedom manipulators as shown in Fig. 4. The dynamics model, inertia, Coriolis and Centrifugal, Jacobian matrices in the dynamic function are written as follows. Both of the master and the slave side take PID motion controls.

Fig. 4.
figure 4

Model of two-degree-of-freedom manipulators of both master and slave side.

Full size image

The parameters are applied the same as in [3]. The two links lengths of the manipulators are l1 and l2, and the masses of manipulators are m1 and m2 respectively. Let the rotation angle of the connecting joint at a certain time be \({\theta }_{1}, {\theta }_{2}\). The angular velocity of its rotations are the differential of the rotation angle, which is \(\dot{\theta }_1 ,\dot{\theta }_2\). q is the joint angle, which can be represented by a matrix containing the angle parameter of \({\theta }_{1}, {\theta }_{2}\), which is expressed as \(q={\left(\begin{array}{cc}{\theta }_{1}& {\theta }_{2}\end{array}\right)}^{T}\).\(\tau \) is the torque on each joint, and it can express as \(\tau ={\left(\begin{array}{cc}{\tau }_{1}& {\tau }_{2}\end{array}\right)}^{T}\). \({F}_{h}\) is the force exerted by the operator on the main manipulator, while \({F}_{e}\) is the force of the salve manipulator and the operating environment.

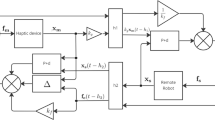
The four channel network diagram of the entire system is showed in Fig. 5. First, we input a step wave and pulse wave in the x and y directions of the master and the slave sides. The position tracking is displayed in Fig. 6. The first joint's torque of the master side is represented by a yellow solid line, and the second joint torque is represented by a purple solid line. From the results, it can be seen that the control effect of the entire system has high efficiency. Meanwhile, the tracking performance is relatively excellent. The force signal tracking is illustrated in Fig. 7. The force of the master terminal is represented by blue and red curves, and the force of the slave terminal is marked with yellow and purple curves. From the results, it can be seen that the transparency and feedback of the force control effect in the entire system are all pretty superior.

Fig. 5.
figure 5

The diagram of part active teleoperation system.

Full size image
Fig. 6.
figure 6

Position tracking of joints of master and slave manipulators.

Full size image
Fig. 7.
figure 7

Force tracking of joints of master and slave manipulators.

Full size image

5 Conclusion

This paper firstly introduces a new four-channel double-wave variable control structure based on part active network. The purpose is to ensure the synchronous tracking of the force of the manipulator without losing the stability of the motion. From the theoretical point of view, we analyze and discuss the stability of the network from the perspective of network energy. Then, a PD bilateral controller is designed. Numerical simulation results show that the proposed method under the constant time delay condition has comparatively brilliant position tracking and force tracking performances between the master and slave manipulators.