Keywords

1 Introduction

At present, our neighboring countries and regions have already equipped or are developing a large number of third and fourth-generation fighter with maneuverability more than 9 g. The escape strategy is also becoming more and more intelligent, which poses a serious challenge to the precise strike of the air-to-air missile on the target [1, 2].

The missile guidance law design problem can be transformed into a control problem that satisfies certain constraints. Generally, these constraints are control energy, terminal miss distance, attack time, attack angle and so on. In fact, these constraints are the guidance errors chosen when the guidance law is designed, which is very important. The purpose of guidance is achieved by controlling the guidance error to zero. The control methods used are all tools to reduce the guidance error, and different control methods require different guidance information.

For the guidance law of attacking maneuvering targets, the control energy and terminal miss distance (or its equivalent) are generally used as guidance errors. Specifically, the guidance error based on optimal control theory and game theory is generally zero effort miss (ZEM), and the guidance error based on nonlinear control theories, such as, sliding mode control, backstepping control, and dynamic surface control is the line-of-sight (LOS) angular rate. These guidance laws have been extensively studied in recent years.

Based on modern control theory, DV Stallard, P. Zarchan and others have studied the APNGL to compensate the target acceleration. It is not only necessary to assume the target maneuvering model beforehand, but also to accurately estimate the target maneuvering acceleration [3,4,5,6]. The guidance performance is poor when the actual target maneuvering style is mismatched with the model. Based on the differential game theory, the differential game guidance law is studied, but the two-point boundary value problem is encountered when solving the equation, and it is difficult to obtain an analytical solution [7,8,9,10,11,12]. Guidance law based on differential games need to know target maneuver information and accurate missile model, therefor, this method has certain limitations.

The study of guidance laws based on fuzzy control, sliding mode control, feedback linearization control, backstepping control are particularly attractive [13, 14]. Feedback linearization methods require an accurate known system control model, which is difficult for complex nonlinear missile systems [15,16,17]. The sliding mode and backstepping guidance law are robust to system uncertainty, and a large number of research results have been achieved [18,19,20,21,22,23]. In the design process, only the upper bound of the target acceleration is required, but the switching item needs to be handled well to avoid control command chatter. The advantage of fuzzy control is that it does not rely on an accurate system model, but the design of fuzzy rules relies on rich experience [24,25,26]. Using artificial intelligence method to design guidance law only trains and learns one of the parameters, the design cycle is long, and the interpretability is low [27,28,29]. Fuzzy control and artificial intelligence method are only auxiliary means to optimize certain parameters, but cannot fundamentally solve the problem of sensitivity to target maneuvering.

In the above studies, the reasons for the poor guidance performance are that the actual maneuvering of the target does not match the model, the target maneuvering acceleration information is difficult to accurately estimate, and the missile is not sensitive to the target maneuvering, etc.

In this paper, an adaptive guidance law that is robust to arbitrary maneuvering of the target based on the sliding mode control theory was studied. By defining a new guidance error, the missile can be made to respond quickly to the maneuver of the target, and the overload demand is reasonably distributed during the flight. In addition, MDI which can evaluate the magnitude of the guidance error is defined, and the guidance parameters are adaptively adjusted according to MDI, which not only ensures a small guidance error but also can well suppress the chatter caused by sliding mode control.

2 Guidance Process Description

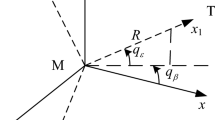
The geometry of vertical planar interception is depicted in Fig. 1, respectively.

Fig. 1.
figure 1

Planar interception geometry

Full size image

In the figure, \(R\) and \(q\) denote the relative distance and the LOS angle, respectively; \(V_{m}\) and \(V_{t}\) denote the velocities of the missile and the target, respectively; \(\theta_{m}\) and \(\theta_{t}\) denote the velocity inclination angles of the missile and the target, respectively.

The planar interception equations satisfy the following relation

$$ R\dot{q} = V_{m} \sin (q - \theta_{m} ) - V_{t} \sin (q - \theta_{t} ) $$
(1)
$$ - \dot{R} = V_{m} \cos (q - \theta_{m} ) - V_{t} \cos (q - \theta_{t} ) $$
(2)

Define \(\eta_{m} = q - \theta_{m}\), \(\eta_{t} = q - \theta_{t}\), \(\eta_{m}\) and \(\eta_{t}\) denote the lead angles of the missile and the target, respectively. Differentiating Eqs. (1) and (2) with respect to time, and there is

$$ R\ddot{q} + 2\dot{R}\dot{q} = - a_{m} \cos \eta_{m} + a_{t} \cos \eta_{t} + \dot{V}_{m} \sin \eta_{m} - \dot{V}_{t} \sin \eta_{t} $$
(3)
$$ \ddot{R} = R\dot{q}^{2} - a_{m} \sin \eta_{m} + a_{t} \sin \eta_{t} - \dot{V}_{m} \cos \eta_{m} + \dot{V}_{t} \cos \eta_{t} $$
(4)

where \(a_{m} = V_{m} \dot{\theta }_{m}\) and \(a_{t} = V_{t} \dot{\theta }_{t}\) denote the normal accelerations of the missile and the target, respectively.

According to the principle of parallel approach guidance method, the ultimate goal of guidance control is

$$ \dot{q} = 0 $$
(5)

Substituting Eq. (5) into Eq. (1) yields

$$ V_{m} \sin (q - \theta_{m} ) = V_{t} \sin (q - \theta_{t} ) $$
(6)

or equivalently

$$ \theta_{m} = q - a\sin \left[ {\tau \sin (q - \theta_{t} )} \right] $$
(7)

where \(\tau = \frac{{V_{t} }}{{V_{m} }}\). If Eq. (7) holds, the LOS angular rate is zero, and the ideal velocity inclination angle \(\theta_{m}^{p}\) is defined as follows

$$ \theta_{m}^{p} = q - a\sin \left( {\tau \sin \eta_{t} } \right) $$
(8)

The optimal interception can be achieved as long as is gradually satisfied during the flight. Thus, the guidance angle error \(\varepsilon\) can be defined as

$$ \varepsilon = \theta_{m}^{p} - \theta_{m} $$
(9)

The guidance law should ensure \(\varepsilon\) as small as possible.

3 Design of Robust Guidance Law

3.1 Guidance Law Design

It can be seen from Eqs. (1) and (2) that the planar interception equations are nonlinear. Due to the maneuvering of the target, the attack situation changes drastically at the terminal trajectory, and linearizing the nonlinear equations will bring large error, and can not achieve the expected purpose. Therefore, using the sliding mode control method to derive a guidance law with strong robustness to target maneuvering. The sliding mode control has strong robustness to a class of bounded disturbances, and is suitable for nonlinear interception systems. The design index is related to the selection of the sliding surface function, which can theoretically ensure the trajectory convergence.

Firstly, choosing a sliding surface function as given by

$$ s = \dot{q} + \lambda \left( {\theta_{m}^{p} - \theta_{m} } \right) $$
(10)

where \(\lambda\) is a positive number. The purpose of this design is to meet the requirements of \(\dot{q} = 0\) and \(\theta_{m} = \theta_{m}^{p}\) on the sliding surface. It should be noted that, unlike the APNGL, which takes the ZEM as the guidance error, it will use \(\dot{q} + \lambda \left( {\theta_{m}^{p} - \theta_{m} } \right)\) as a new guidance error here, and the goal of the control is to make the guidance error tends to zero.

Secondly, designing the control law to ensure the attraction characteristics of the sliding mode hyperplane \(s = 0\), so that the system can enter the sliding mode as soon as possible. Constructing a Lyapunov function \(V = \frac{{s^{2} }}{2}\), then the missile acceleration command should satisfy \(V\left( t \right) \ge 0\) and \(\dot{V}\left( t \right) < 0\) for any \(t \in \left[ {t_{0}, t_{f} } \right]\). Then the LOS angular rate reach to the sliding surface in finite time and converge to zero. That is, there exists \(t_{1} \in \left[ {t_{0}, t_{f} } \right]\), \(\dot{q} = 0\) and \(\theta_{m} \left( t \right) = \theta_{m}^{p}\) is available when \(t \ge t_{1}\).

For ease of derivation, let \(\phi = a\sin \left( {\tau \sin \eta_{t} } \right)\), deffierentiating \(\phi\) with respect to time yields

$$ \dot{\phi } = \frac{{d\left( {\tau \sin \eta_{t} } \right)}}{{\sqrt {1 - \left( {\tau \sin \eta_{t} } \right)^{2} } }} = \frac{{\dot{\tau }\sin \eta_{t} + \tau \cos \eta_{t} \dot{\eta }_{t} }}{\cos \phi } = \frac{{\dot{\tau }\sin \eta_{t} + \tau \dot{q}\cos \eta_{t} - \frac{{a_{t} }}{{V_{m} }}\cos \eta_{t} }}{\cos \phi } $$
(11)

where \(\dot{\tau } = \frac{{\dot{V}_{t} V_{m} - \dot{V}_{m} V_{t} }}{{V_{m}^{2} }}\), \(\dot{\eta }_{t} = \dot{q} - \dot{\theta }_{t}\).

Due to \(\dot{\theta }_{m}^{p} = \dot{q} - \dot{\phi }\), \(\dot{\theta }_{m} = \frac{{a_{m} }}{{V_{m} }}\), there is

$$ \begin{gathered} \dot{\theta }_{m}^{p} - \dot{\theta }_{m} = \dot{q} - \frac{1}{\cos \phi }\left( \begin{gathered} \dot{\tau }\sin \eta_{t} + \tau \dot{q}\cos \eta_{t} - \hfill \\ \frac{{a_{t} }}{{V_{m} }}\cos \eta_{t} \hfill \\ \end{gathered} \right) - \frac{{a_{m} }}{{V_{m} }} \hfill \\ = \left( {1 - \frac{{\tau \cos \eta_{t} }}{\cos \phi }} \right)\dot{q} - \frac{1}{\cos \phi }\left( \begin{gathered} \dot{\tau }\sin \eta_{t} - \hfill \\ \frac{{a_{t} }}{{V_{m} }}\cos \eta_{t} \hfill \\ \end{gathered} \right) - \frac{{a_{m} }}{{V_{m} }} \hfill \\ \end{gathered} $$
(12)

According to Eq. (3), there is

$$ \ddot{q} = \frac{1}{R}\left( { - 2\dot{R}\dot{q} - a_{m} \cos \eta_{m} + a_{t} \cos \eta_{t} + \dot{V}_{m} \sin L - \dot{V}_{t} \sin A} \right) $$
(13)
$$ \begin{gathered} \dot{s} = \ddot{q} + \lambda \left( {\dot{\theta }_{m}^{p} - \dot{\theta }_{m} } \right) = \frac{1}{R}\left( \begin{gathered} - 2\dot{R}\dot{q} - a_{m} \cos \eta_{m} + a_{t} \cos \eta_{t} + \hfill \\ \dot{V}_{m} \sin L - \dot{V}_{t} \sin A \hfill \\ \end{gathered} \right) - \frac{{\lambda a_{m} }}{{V_{m} }} + \hfill \\ \lambda \left( {1 - \frac{{\tau \cos \eta_{t} }}{\cos \phi }} \right)\dot{q} - \frac{\lambda }{\cos \phi }\left( {\dot{\tau }\sin \eta_{t} - \frac{{a_{t} }}{{V_{m} }}\cos \eta_{t} } \right) \hfill \\ \end{gathered} $$
(14)

Adding the term \(Ks + L{\text{sgn}} \left( s \right) - Ks - L{\text{sgn}} \left( s \right)\) to the right-hand side of Eq. (14), where \(K\) and \(L\) are both positive numbers, and \({\text{sgn}} \left( s \right)\) is the sign function of \(s\), and there is

$$ \begin{gathered} \dot{s} = \frac{1}{R}\left\{ {\left[ {K - 2\dot{R} + \lambda R\left( {1 - \frac{{\tau \cos \eta_{t} }}{\cos \phi }} \right)} \right]\dot{q} + K\lambda \left( {\theta_{m}^{p} - \theta_{m} } \right) - \left( {\cos \eta_{m} + \frac{\lambda R}{{V_{m} }}} \right)a_{m} } \right\} + \hfill \\ \frac{1}{R}\left[ {\left( {1 + \frac{\lambda R}{{V_{m} \cos \phi }}} \right)a_{t} \cos \eta_{t} + \dot{V}_{m} \sin \eta_{m} - \dot{V}_{t} \sin \eta_{t} - \frac{{\lambda R\dot{\tau }\sin \eta_{t} }}{\cos \phi } + L{\text{sgn}} \left( s \right)} \right] + \hfill \\ \frac{1}{R}\left[ { - Ks - L{\text{sgn}} \left( s \right)} \right] \hfill \\ \end{gathered} $$
(15)

If the missile acceleration command in Eq. (15) satisfies

$$ \begin{gathered} \left( {\cos L + \frac{\lambda R}{{V_{m} }}} \right)a_{m} = \left[ {K - 2\dot{R} + \lambda R\left( {1 - \frac{{\tau \cos \eta_{t} }}{\cos \phi }} \right)} \right]\dot{q} + K\lambda \left( {\theta_{m}^{p} - \theta_{m} } \right) + \hfill \\ \left( {1 + \frac{\lambda R}{{V_{m} \cos \phi }}} \right)a_{t} \cos \eta_{t} + \dot{V}_{m} \sin \eta_{m} - \dot{V}_{t} \sin \eta_{t} - \frac{{\lambda R\dot{\tau }\sin \eta_{t} }}{\cos \phi } + L{\text{sgn}} \left( s \right) \hfill \\ \end{gathered} $$
(16)

then

$$ \dot{s} = \frac{1}{R}[Ks + L{\text{sgn}} (s)] $$
(17)
$$ \dot{V} = s\dot{s} = - \frac{1}{R}\left[ {Ks^{2} + L{\text{sgn}} \left( s \right)s} \right] = - \frac{1}{R}\left[ {Ks^{2} + L\left| s \right|} \right] $$
(18)

Because \(K\) and \(L\) are positive numbers, \(\dot{V} \le 0\) is true for all \(s\) except \(s{ = }0\).

That is, Eq. (16) can ensure that the derivative of the Lyapunov function is a value not greater than zero and not constant to zero, which meets the design requirements. Then the designed guidance law is given by

$$ a_{m} = \frac{1}{Ka}\left\{ \begin{gathered} \left[ {K - 2\dot{R} + \lambda R\left( {1 - \frac{{\tau \cos \eta_{t} }}{\cos \phi }} \right)} \right]\dot{q} + K\lambda \left( {\theta_{m}^{p} - \theta_{m} } \right) + L{\text{sgn}} \left( s \right) \hfill \\ \left( {1 + \frac{\lambda R}{{V_{m} \cos \phi }}} \right)a_{t} \cos \eta_{t} + \dot{V}_{m} \sin \eta_{m} - \dot{V}_{t} \sin \eta_{t} - \frac{{\lambda R\dot{\tau }\sin \eta_{t} }}{\cos \phi } \hfill \\ \end{gathered} \right\} $$
(19)

where \(Ka = \cos L + \frac{\lambda R}{{V_{m} }}\).

3.2 Guidance Law Stability Analysis

The stability of the guidance law is analyzed by using the Lyapunov stability theory. We obtain the results presented in the following Throerm 1.

Theorem 1.

For the guidance equations described by Eqs. (3) and (4), when the parameter \(K\) and \(L\) in Eq. (19) is greater than zero, the guidance law ensures that the state of the guidance system converges to the sliding mode surface before the terminal time of the guidance process, and optimal interception can be achieved.

Proof.

Firstly, it is proved that the sliding mode surface function can converge to zero.

According to the designed sliding mode guidance law, the derivative of the Lyapunov function is \(\dot{V} = - \frac{K}{R}\left[ {s^{2} + \rho \left| s \right|} \right] \le 0\), which is true for any \(R > 0\), where \(\rho = \frac{L}{K}\), that is \(\frac{1}{2}\frac{{ds^{2} }}{dt} = - \frac{K}{R}\left( {s^{2} + \rho \left| s \right|} \right) \le 0\).

If \(s\left( t \right) = 0\), the initial state of the system is on the sliding surface, and it holds for any \(t \ge 0\).

If \(s\left( t \right) \ne 0\), suppose \(s\left( t \right) > 0\), then \(\dot{s} = - \frac{K}{R}\left( {s + \rho } \right)\), let \(\sigma = s + \rho\), there is

$$ \frac{{\dot{\sigma }}}{\sigma } = - \frac{K}{R} $$
(20)

Let \(K = - k\dot{R} > 0\), then \(\frac{{\dot{\sigma }}}{\sigma } = k\frac{{\dot{R}}}{R}\). Integrate Eq. (20) yields.

\(\ln (\sigma (t))\left| {_{0}^{t} = k\ln (R(t))\left| {_{0}^{t} } \right.} \right.\), then

$$ \sigma \left( t \right) = \sigma \left( 0 \right)\left( {\frac{R\left( t \right)}{{R\left( 0 \right)}}} \right)^{k} $$
(21)

Due to \(s = \sigma - \rho\), and consider the situation of \(s(t) < 0\), we can get

$$ \left| {s\left( t \right)} \right| = - \rho + \left[ {\left| {s\left( 0 \right)} \right| + \rho } \right] \cdot \left| {\frac{R\left( t \right)}{{R\left( 0 \right)}}} \right|^{k} $$
(22)

It can be seen that the convergence of \(s\left( t \right)\) is exponential, the convergence speed is fast when \(k > 1\), and the convergence speed is slow when \(k < 1\), but it will eventually converge to zero.

Secondly, it is proved that \(s\left( t \right)\) will converge to zero before the interception point, not at the interception point.

For any non-zero relative distance \(\overline{R}\) satisfy

$$ \overline{R} \ge R\left( 0 \right)\left( {\frac{\rho }{{\left| {s\left( 0 \right)} \right| + \rho }}} \right)^{1/k} $$
(23)

Substituting Eq. (23) into Eq. (22) to have, it is shown that before the interception occurs(), the sliding mode guidance law has already controlled the system states to the sliding surface, and then will move on the hyperplane. That is, exists, there is when.

Finally, it is proved that when, there must be and, that is, the optimal interception can be achieved.

When \(s(t) = 0\), there is \(\dot{q} + \lambda (\theta_{m}^{p} - \theta_{m} ) = 0\), obviously the special solution is and . Below we have to show that this particular solution is also a general solution according to the given sliding mode guidance law.

By using counterevidence, assuming that on the sliding mode \(s(t) = 0\) there are \(\dot{q} \ne 0\) and \(\theta_{m} \ne \theta_{m}^{p}\), from the interception Eq. (1), \(\frac{{R\dot{q}}}{{V_{m} }} = \sin \eta_{m} - \tau \sin \eta_{t}\), and substitute it into \(s(t)\) gives \(\sin \eta_{m} - \tau \sin \eta_{t} + \frac{\lambda R}{{V_{m} }}(\theta_{m}^{p} - \theta_{m} ) = 0\), due to \(\theta_{m}^{p} = q - a\sin (\tau \sin \eta_{t} )\), let \(\eta_{m}^{p} = q - \theta_{m}^{p}\), then \(\tau \sin \eta_{t} = \sin \eta_{m}^{p}\), there is \(\sin \eta_{m} - \sin \eta_{m}^{p} + \frac{\lambda R}{{V_{m} }}(\theta_{m}^{p} - \theta_{m} ) = 0\), or equivalently

$$ \frac{\lambda R}{{V_{m} }} = \frac{{\sin \eta_{m}^{p} - \sin \eta_{m} }}{{\eta_{m}^{p} - \eta_{m} }} $$
(24)

The left side of Eq. (24) is a number that is always greater than zero, while the right side may be less than zero depending on the value of \(\eta_{m}\), which contradict each other. So when \(s\left( t \right) = 0\), there must be \(\dot{q} = 0\) and \(\theta_{m} = \theta_{m}^{p}\).

In addition, the acceleration command of the missile on the sliding surface is

$$ a_{m} = \frac{1}{Ka}\left\{ {\left( {1 + \frac{\lambda R}{{V_{m} \cos \phi }}} \right)a_{t} \cos \eta_{t} + \dot{V}_{m} \sin \eta_{m} - \dot{V}_{t} \sin \eta_{t} - \frac{{\lambda R\dot{\tau }\sin \eta_{t} }}{\cos \phi }} \right\} $$
(25)

Which is bounded obviously, means that the required control energy is limited.

In the above proof process, the assumptions used are \(K = - k\dot{R} > 0\) and \(L = \rho K\). Substituting \(V_{c} = - \dot{R}\) into Eq. (19) gives

$$ a_{m} = \frac{1}{Ka}\left\{ \begin{gathered} \left[ {\left( {k + 2} \right) + \lambda R\left( {1 - \frac{{\tau \cos \eta_{t} }}{\cos \phi }} \right)} \right]V_{c} \dot{q} + kV_{c} \lambda \left( {\theta_{m}^{p} - \theta_{m} } \right) + \rho kV_{c} {\text{sgn}} \left( s \right) + \hfill \\ \left( {1 + \frac{\lambda R}{{V_{m} \cos \phi }}} \right)a_{t} \cos \eta_{t} + \dot{V}_{m} \sin \eta_{m} - \dot{V}_{t} \sin \eta_{t} - \frac{{\lambda R\dot{\tau }\sin \eta_{t} }}{\cos \phi } \hfill \\ \end{gathered} \right\} $$
(26)

Let \(a_{m1} = \left[ {\left( {k + 2} \right) + \lambda R\left( {1 - \frac{{\tau \cos \eta_{t} }}{\cos \phi }} \right)} \right]V_{c} \dot{q}\), \(a_{m2} = kV_{c} \lambda \left( {\theta_{m}^{p} - \theta_{m} } \right)\), \(a_{m3} = \rho kV_{c} {\text{sgn}} \left( s \right)\), \(a_{m4} = \left( {1 + \frac{\lambda R}{{V_{m} \cos \phi }}} \right)a_{t} \cos \eta_{t}\), \(a_{m5} = \dot{V}_{m} \sin \eta_{m} - \dot{V}_{t} \sin \eta_{t} - \frac{{\lambda R\dot{\tau }\sin \eta_{t} }}{\cos \phi }\), then

$$ a_{m} = \frac{{a_{m1} + a_{m2} + a_{m3} + a_{m4} + a_{m5} }}{{K_{a} }} $$
(27)

Based on the analysis above, the derived sliding mode guidance law with robustness to target maneuvering is mainly composed of five parts, namely proportional guidance term (\(a_{m1}\)), guidance angle error compensation term (\(a_{m2}\)), sliding mode control term (\(a_{m3}\)), target maneuver acceleration compensation item (\(a_{m4}\)) and velocity change rate compensation item (\(a_{m5}\)).

Remark 1.

  1. 1.

    Compared with APNGL, Eq. (26) contains \(a_{m2}\), \(a_{m3}\) and \(a_{m5}\), the guidance information is more abundant;

  2. 2.

    The guidance error is the LOS angular rate and the guidance angle error. The guidance error is more sensitive to the target maneuver, and only when both \(\varepsilon\) and \(\dot{q}\) are relatively small, the miss distance is small;

  3. 3.

    The guidance law has a large overload command in the early stage to eliminate the guidance angle error as soon as possible, and a small overload command after that to save missile energy, and the overload demand distribution is more reasonable.

4 Implementation of Guidance Law

4.1 Chatter Adaptive Suppression

From Eq. (27), it can be seen that the sign function appears in \(a_{m3}\), which is easy to cause chatter and affect guidance accuracy. In this paper, the sign function is first replaced by the hyperbolic tangent function, namely

$$ a_{m3} = \rho kV_{c} \tanh \left( {{s \mathord{\left/ {\vphantom {s d}} \right. \kern-\nulldelimiterspace} d}} \right) $$
(28)

where \(\tanh \left( {s/d} \right) = \frac{{e^{{s/d}} - e^{{ - s/d}} }}{{e^{{s/d}} + e^{{ - s/d}} }} \), \(d\) is a positive number, the slope of the hyperbolic tangent curve at the origin can be changed by adjusting the size of \(d\). Figure 2 shows a comparison of the hyperbolic tangent curves at different \(d\).

Fig. 2.
figure 2

Hyperbolic tangent curve with different \(d\)

Full size image

Furthermore, in order to adaptively suppress system chatter, the MDI is given by

$$ \upsilon = \left| {\mu \dot{q} \cdot t_{go} + \left( {1 - \mu } \right)\varepsilon } \right| $$
(29)

where \(\mu\) is a positive number less than 1, \(t_{go} = - \frac{R}{{V_{c} }}\) is the time-to-go, and \(\upsilon\) can be used to evaluate the magnitude of the guidance error, \(d\) is adaptively adjusted according to \(\upsilon\)

$$ d = 1 - 10\upsilon $$
(30)

Limit the range of d between 0.1 and 0.8. In this way, when \(\upsilon\) is large, reduce d to speed up the command response and quickly eliminate the guidance error; Otherwise, increase d to reduce the system chatter, so as to achieve the purpose of adaptively suppressing the chatter.

4.2 Simplification of Guidance Law

The guidance law described by Eq. (26) is the complete form, but it requires a lot of guidance information, some of which are not easy to obtain, which will bring many difficulties to practical application, and reasonable simplification must be made.

In the terminal guidance stage of intercepting, the velocity change rate and the lead angle of missile and target is not large, so the term \(a_{m5}\) is ignored. As an external disturbance with an upper bound, the term \(a_{m4}\) suppressed by the term \(a_{m3}\) does not need to know the specific value.

Both \(a_{m3}\) and \(a_{m2}\) need to calculate the guidance angle error \(\varepsilon = \theta_{m}^{p} - \theta_{m}\), in which the velocity inclination angle of the target is used, and this information is also difficult to obtain accurately, so it’s necessary to simplify it.

It can be seen from Eqs. (8) and (9):

$$ \varepsilon = \theta_{m}^{p} - \theta_{m} = q - \theta_{m} - a\sin \left( {\frac{{V_{t} \sin \left( {q - \theta_{t} } \right)}}{{V_{m} }}} \right) $$
(31)

According to Eq. (1),

$$ \frac{{V_{t} \sin (q - \theta_{t} )}}{{V_{m} }} = \sin (q - \theta_{m} ) - \frac{{R\dot{q}}}{{V_{m} }} $$
(32)

Substituting Eq. (32) into Eq. (31) gives

$$ \varepsilon = \theta_{m}^{p} - \theta_{m} = q - \theta_{m} - a\sin \left( {\sin (q - \theta_{m} ) - \frac{{R\dot{q}}}{{V_{m} }}} \right) $$
(33)

It can be approximately obtained

$$ a\sin \left( {\sin (q - \theta_{m} ) - \frac{{R\dot{q}}}{{V_{m} }}} \right) \approx q - \theta_{m} + a\sin \left( { - \frac{{R\dot{q}}}{{V_{m} }}} \right) $$
(34)

Substituting Eq. (34) into Eq. (33) gives

$$ \varepsilon \approx a\sin \left( {\frac{{R\dot{q}}}{{V_{m} }}} \right) $$
(35)

Then the sliding surface function is

$$ s = \dot{q} + \lambda \varepsilon \approx \dot{q} + \lambda a\sin \left( {\frac{{R\dot{q}}}{{V_{m} }}} \right) $$
(36)

Let \(K_{N} = \frac{{\left( {k + 2} \right) + \lambda R\left( {1 - \frac{{\tau \cos \eta_{t} }}{\cos \phi }} \right)}}{{K_{a} }}\) and \(K_{M} = \frac{k}{{K_{a} }}\), the simplified form of the guidance law is given by

$$ a_{m} = K_{N} V_{c} \dot{q} + K_{M} V_{c} \lambda \varepsilon + \rho K_{M} V_{c} \tanh \left( {s/d} \right) $$
(37)

5 Simulation Results

In order to verify the guidance performance of the robust guidance law derived in this paper, a lot of simulation work was done in planar and three-dimensional space under different simulation conditions.

5.1 Planar Simulation

Simulation Description. Assuming that both the missile and the target move in the vertical planar, the target maneuvering acceleration is 12 g, the maneuvering form is S-type, and the period of S-type maneuvering is 10 s. The maneuvering moment of target is 8s～0.5 s before encountering it, with an interval of 0.5 s. The time constant of missile is 0.15 s, the missile overload command limit is 36 g.

The initial parameters and the values of the relevant guidance parameters during the simulation are shown in Table 1.

Table 1. Initial simulation parameter
Full size table

The guidance laws used in the simulation are as follows.

  1. 1.

    APNGL, \(a_{m} = NV_{c} \dot{q} + \frac{N}{2}a_{t}\)

  2. 2.

    Robust adaptive guidance law(RAGL), Eq. (26)

  3. 3.

    Simplified robust adaptive guidance law(SRAGL), Eq. (39)

Analysis of Simulation Results. The miss distance and flight time corresponding to the three guidance laws are given, as shown in Fig. 3, the x-axis represents the target maneuver moment befor the interception point, and the y-axis represents the miss distance or flight time.

Fig. 3.
figure 3

Miss distance and time of flight under different guidance laws

Full size image

It can be seen from Fig. 3 that the robust adaptive guidance law can significantly reduce the amount of miss distance caused by the large overload of maneuvering. And more importantly, the performance of the SRAGL is comparable to RAGL, making it more valuable for engineering applications.

The reason for the large amount of miss distance when maneuver moment is 5.5 s before the interception point is that, the direction of the maneuvering acceleration of the target suddenly changes about 0.5 s before encountering, the missile is too late to respond, which is the “optimal maneuver” it can do for the target.

The following takes target maneuver moment is 4 s before the interception point as an example to compare the simulation curves in detail. It can be seen from Fig. 4 that under the action of the RAGL or SRAGL, the missile flight trajectory is more flat.

Fig. 4.
figure 4

Relative motion trajectory of missile and target

Full size image

It can be seen from Fig. 5 that RAGL responds faster to the target maneuver, and the overload requirement at the end of the trajectory is small. Under the action of the RAGL, the LOS angular rate is basically maintained near 0°/s.

Fig. 5.
figure 5

Missile and target acceleration and LOS angular rate

Full size image

It can be seen from Fig. 6 that, the guidance angle error can converges to within 2° quickly under the action of RAGL1, the variation of the MDI of RAGL is relatively small, and it basically remains within 0.02 before encountering the target. The simulation shows that if the MDI is less than 0.05 when encountering the target, the miss distance will not be large.

Fig. 6.
figure 6

Guidance angle error and MDI

Full size image

5.2 Simulation in 6-DOF

The designed RAGL is verified in a 6-DOF simulation environment. The simulation conditions are shown in Table 2, where \(H_{m}\) denotes missile height, \(V_{m}\) denotes missile velocity, \(H_{t}\) denotes target height, \(V_{t}\) denotes target velocity, \(D\) denotes distance, \(A_{t}\) denotes target maneuvering acceleration.

The guidance laws used are APNGL and SRAGL. The target maneuvering style include U-type maneuvers and S-type maneuvers, and the maneuvering planar includes horizontal and vertical planars, which are the typical maneuvering styles of the target, and the rest are various combinations of these maneuvering styles. The S maneuver requires a 50° change in the direction of the target velocity. In the simulation, the maneuvering time is 15 s ~ 0.5s before encountering the target, and the interval is 0.5 s.

Table 2. Simulation condition
Full size table

Comparing the missile terminal velocity and miss distance obtained by simulation, the simulation results of condition 1 is shown in Fig. 7.

In the figure, H-U denotes U-style maneuver in the horizontal planar, V-U denotes U-style maneuver in the vertical planar, H-S denotes S-style maneuver in the horizontal planar, V-S denotes S-style maneuver in the vertical planar. The blue line is the result of APNGL, and the red line is the result of SRAGL.

Fig. 7.
figure 7

Miss distance and terminal velocity comparison of condition1

Full size image

The results of condition 2 is shown in Fig. 8.

Fig. 8.
figure 8

Miss distance and terminal velocity comparison of condition2

Full size image

The results of condition 3 is shown in Fig. 9.

Fig. 9.
figure 9

Miss distance and terminal velocity comparison of condition3

Full size image

It can be seen from the figures that the SRAGL can significantly reduce the miss distance caused by the target's large overload maneuver at the end of the trajectory, and is insensitive to target maneuvering style and maneuvering planar. The missile terminal velocity is also higher than APNGL, indicating that less control energy is required for the new guidance law.

In order to further illustrate the problem, a statistical analysis was carried out on the average miss distance in the above simulation results, as shown in Table 3.

It can be seen from Table 3 that the SRAGL can greatly reduce the average miss distance by up to 60% or more. It fully shows that in most cases, the SRAGL has higher guidance accuracy.

Table 3. Average miss distance(m) comparison
Full size table

6 Conclusion

In this paper, an adaptive guidance law that is robust to arbitrary maneuver of the target is studied by using the sliding mode control theory and the principle of “parallel approach guidance”. By defining a new guidance error, the robust adaptive guidance law is derived from the Lyapunov stability, and the convergence proof are carried out. The guidance parameters are adaptively adjusted according to MDI, and the guidance law is more suitable for engineering applications after being appropriately simplified.

The simulation results show that the RAGL or SRAGL has better performance than APNGL. However, in a complex battlefield environment, especially when the guidance information is inaccurate, the performance of the new guidance law is more critical for practical engineering applications, which is a topic that needs to be studied further in the next step.