Keywords

1 Introduction

During the recent decades, containment control has received considerable attention for multi-agent systems (MASs) [1,2,3,4]. In [1], a containment control protocol of semi-markovian MASs was proposed. The works in [2] and [3] studied the distributed containment control issues of nonlinear MASs with full state constraints and input quantization, respectively. Li \(et\ al.\) in [4] proposed an adaptive finite-time containment control protocol for a class of MASs with input delay.

However, in practical applications, it is noting that the sensors of agents may undergo faults during operation, which will lead to the loss of information and may bring severe destruction to the performance of systems. Thus, how to solve the adaptive containment control issue of uncertain MASs subject to sensor faults is a nontrivial problem. Fortunately, Wu \(et\ al.\) in [5] designed a bipartite containment control protocol for stochastic MASs with sensor faults and dead zone. In [6], Cao \(et\ al.\) designed an adaptive neural networks compensation controller to settle the problem of sensor faults. In addition, since the prescribed performance control method can improve the transient performance of the system, Li \(et\ al.\) [7] studied the nontriangular structure nonlinear system with prescribed performance and obtained a better simulation result. Thus, how to extend the prescribed performance control approach to the MASs subject to sensor faults is a significant topic.

On the other hand, event-triggered control method has huge advantages in decreasing signal transmission and computational resources. For instance, Ni \(et\ al.\) in [8] studied the event-triggered consensus tracking problem on directed graphs for high-order MASs. In [9], the containment control issue was researched for strict-feedback MASs with event-triggered mechanism.

Motivated by the aforementioned observations, this paper develops an event-based adaptive fuzzy containment control scheme for MASs subject to sensor faults and prescribed performance. The advantages of our work are listed as follows: (i) By combining the adaptive compensation control scheme with prescribed performance control scheme, an adaptive fuzzy containment control approach for nonlinear MASs with sensor faults is developed, which can achieve the better transient performance. (ii) By applying the technique of command-filter with backstepping control strategy, the problem of “complexity explosion” result from the derivatives of virtual controllers are settled.

2 Preliminaries and Problem Formulation

2.1 Graph Theory

The information interchange between followers and leaders is expressed by a graph \(\tilde{\mathcal {G}}=(\tilde{\mathcal {H}},\tilde{\mathcal {X}})\) with a node set \(\tilde{\mathcal {H}}=\{n_{1},\) \(n_{2},\ldots , n_{N+M}\}\) and an edge set \(\tilde{\mathcal {X}}=\{(n_{i},\) \(n_{j})\in \tilde{\mathcal {H}}\times \tilde{\mathcal {H}}\}.\) Nodes numbered \(1, \ldots , N\) donate the followers, and nodes numbered \(N+1, \ldots , N+M\) donate the leaders. The adjacency matrix \(\tilde{\varLambda } = [a_{ij}]\in R^{(N+M)\times (N+M)}\), where \(a_{ij}=1\), if \((n_{i},n_{j})\in \tilde{\mathcal {X}}\), otherwise, \(a_{ij}=0\). \((n_{i},\) \(n_{j})\in \tilde{\mathcal {X}}\) expresses that agent i can get message from agent j. \(\tilde{\mathcal {L}} =[l_{ij}]\) donates the Laplacian matrix with \( \tilde{\mathcal {L}}=\tilde{\mathcal {D}}-\tilde{\varLambda }\). The degree matrix \(\tilde{\mathcal {D}}\) = diag\(\left\{ { {{d_{1,}\ldots d_{N}}}}\right\} \) with \(d_{i}=\sum _{j\in N_{i}}a_{ij}\).

2.2 Problem Formulation

Consider nonlinear MASs with sensor faults consisting of N followers, which can be described as

$$\begin{aligned} \left\{ \begin{aligned} \dot{x}_{i,m}&=x_{i,m+1}+f_{i,m}(\underline{x}_{i,m}),&\\ \dot{x}_{i,n}&=b_{i}u_{i}+f_{i,n}(\underline{x}_{i,n}),&\\ y_{i}&=g_{i}(x_{i,1}),&\end{aligned} \right. \end{aligned}$$
(1)

where \(\underline{x}_{i,m}=[x_{i,1}, ...,x_{i,m}]^{T}\in R^{m}\) \((i=1, ...,N, \text { }m=1,...,n)\) , \(u_{i}\in R\), \(y_{i}\in R\) are the systems states, the control inputs and the system outputs, respectively. \( f_{i,m}(\cdot )\) are unknown smooth nonlinear functions, and \(b_{i}\) is an unknown constant.

Similar to [10], the sensor fault model is described as \(g_{i}(x_{i,1})=\upsilon _{i}(t)x_{i,1}+\iota _{i}(t)\), where the unknown parameters \(\bar{\upsilon } _{i,\min }\) denotes the minimum sensor effectiveness and satisfies \(\upsilon _{i}(t)\in \left[ \bar{\upsilon }_{i,\min },1\right] \), and \(\iota _{i}\) denotes its accuracy coefficient which satisfies \(\iota _{i}(t)\in \left[ -\bar{\iota } _{i},\bar{\iota }_{i}\right] \), where \(\bar{\iota }_{i}>0\). In addition, the different cases of sensor faults are also same as [10].

Let \(h_{i,s}=(\upsilon _{i}(t)-1)x_{i,1}+\iota _{i}(t)\). We have \(y_{i}=x_{i,1}+h_{i,s}\). The derivative of \(y_{i}\) is presented as

$$\begin{aligned} \dot{y}_{i}=\dot{x}_{i,1}+h_{i,ps} , \end{aligned}$$
(2)

with \(h_{i,ps}=\dot{h}_{i,s}\).

Prescribed Performance. Prescribed performance and the containment error \(\ell _{i,1}\left( t\right) \) are described in [11], and the containment error can be constrained as

$$\begin{aligned} -\sigma _{1i}\zeta _{i}(t)<\ell _{i,1}\left( t\right) <\sigma _{2i}\zeta _{i}(t), \text { }\forall t\geqslant 0, \end{aligned}$$
(3)

where \(\sigma _{1i}>0\) and \(\sigma _{2i}\leqslant 1\) are constants. \(\zeta _{i}(t)\) is strictly decreasing continuous function with boundary when time function limits to infinity \({\underset{t\longrightarrow \infty }{\lim }} \zeta _{i}(t)=\zeta _{i\infty }(t)\) \(\left( \zeta _{i\infty }(t)>0\right) \). For a given performance function \(\zeta _{i}(t)\), there is an initial value \( \zeta _{i}\left( 0\right) \) which satisfies \(-\sigma _{1i}\zeta _{i}(0)<\ell _{i,1}\left( 0\right) <\sigma _{2i}\zeta _{i}(0)\), and \(\zeta _{i}(t)\) is chosen as \(\zeta _{i}(t)=(\zeta _{i0}-\zeta _{i\infty })e^{-b_{i}t}+\zeta _{i\infty }, \text { }\forall t\geqslant 0\), where \(b_{i}>0\) is the convergence rate of \(\ell _{i,1}.\) Under steady states condition, the maximum allowable values of \(\ell _{i,1}\) are \(\zeta _{i\infty }>0\) and \(\zeta _{i0}(t)>\zeta _{i\infty }(t)>0\).

The transformed error is expressed as \(\chi _{i,1}=\varOmega _{i}^{-1}\left( \frac{\ell _{i,1}\left( t\right) }{\zeta _{i}(t)}\right) \), then, by differentiating \(\chi _{i,1}\), one obtains

$$\begin{aligned} \dot{\chi }_{i,1}=r_{i}\left( \dot{\ell }_{i,1}-{\dot{\zeta }_{i}(t)\ell _{i,1}}/{ \zeta _{i}(t)}\right) , \end{aligned}$$
(4)

where \(r_{i}=1/2\zeta _{i}(t)\left( 1/(\varOmega _{i}^{-1}(\cdot )+\sigma _{1i})-1/(\varOmega _{i}^{-1}-\sigma _{2i})\right) .\)

Proposition 1

The coordinate transformation for the prescribed performance \(\chi _{i,1}\) is bounded for all \(t\ge 0\).

Lemma 1

[12]. If the transformed error \(\chi _{i,1}\) is bounded, then all \(t\geqslant 0\) satisfies the prescribed performance of the error surface \(\ell _{i,1}\), that is, (3) is satisfied.

Event-Triggered Control Strategy. The event-based control scheme is proposed to decrease the waste of unnecessary interactive information resources. The designed event-triggered strategy [6] is described by

$$\begin{aligned} u_{i}(t)&=\omega _{i}(t_{i,k}),\forall t\in [t_{i,k},t_{i,k+1}),\end{aligned}$$
(5)
$$\begin{aligned} t_{i,k+1}&=\inf \{t>t_{i,k}||\kappa _{i}(t)|\ge \nu _{i}|\omega _{i}(t)|+\epsilon _{i}\}, \end{aligned}$$
(6)

where \(\omega _{i}(t)\) represents the transition continuous control law. \( \kappa _{i}(t)=\omega _{i}(t)-u_{i}(t)\), \(0<\nu _{i}<1\) and \(\epsilon _{i}>0\) are design parameters. \(t_{i,k},k\in Z^{+}\) represents the input update time. The control signal \(\omega _{i}(t_{i,k+1})\) transmits to the actuator when the condition (6) is triggered.

\(u_{i}\) is written as

$$\begin{aligned} u_{i}(t)=\frac{\omega _{i}(t)-\mu _{i}^{2}(t)\epsilon _{i}}{1+\mu _{i}^{1}(t)\nu _{i}}, \end{aligned}$$
(7)

where \(|\mu _{i}^{1}(t)|\le 1\) and \(|\mu _{i}^{2}(t)|\le 1\).

In order to solve the issue of unknown control direction, we use the Nussbaum-type function similar to [12].

Lemma 2

[13]. Suppose that \(V(t)>0\) and \(N(\eta _{i})\) are smooth functions designed on \( [0,t_{f})\). If \(V(t)\le S+\int _{0}^{t}\Big (\beta _{i}N(\eta _{i})\dot{\eta _{i}} +\dot{\eta _{i}}\Big )e^{\varpi \tau }d\tau \) holds, then V(t), \(\eta _{i}\) and \(\int _{0}^{t}\Big (\beta _{i}N(\eta _{i})\dot{\eta _{i}} +\dot{\eta _{i}}\Big )e^{\varpi \tau }d\tau \) are bounded on \([0,t_{f})\), where S and \(\varpi \) are nonnegative constants, \(\beta _{i}\ne 0\) is a constant.

Lemma 3

[14]. Let the continuous function \(f(\cdot )\) be designed as a compact set \(\varOmega \), and there exists a constant \(\varepsilon >0\). The fuzzy-logic systems (FLSs) are designed as \( \underset{x\in \varOmega }{\sup }\left| f(x)-W^{T}\varphi (x)\right| \le \varepsilon , \) where W is the ideal constant weight vector, \(\varphi (x)>0\) is the basis function vector.

Furthermore, the constant \(\theta _{i,m}\) and \(\varTheta _{i,1}\) can be defined as \(\theta _{i,m} = \ \parallel W_{i,m}\parallel ^2\), \(\varTheta _{i,1} = \ \parallel W_{i,ps}\parallel ^2\), \((\text { } i=1,\ldots ,N, \text { } m=1,\ldots ,n)\), where \(\theta _{i,m}\) and \(\varTheta _{i,1}\) are unknown positive constants since \(W_{i,m}\) and \(W_{i,ps}\) are unknown. \(\tilde{\theta }_{i,m}=\theta _{i,m}-\hat{\theta }_{i,m}\) and \(\tilde{\varTheta } _{i,1}=\varTheta _{i,1}-\hat{\varTheta }_{i,1}\) are the estimation errors, where \(\hat{ \theta }_{i,m}\) and \(\hat{ \varTheta }_{i,1}\) are the estimations of \(\theta _{i,m}\) and \(\varTheta _{i,1}\), respectively.

2.3 Adaptive Fuzzy Event-Triggered Containment Control

Select the coordinate transformation as

$$\begin{aligned} \ell _{i,1}&=\sum _{j=1}^{N}a_{ij}\left( y_{i}-y_{j}\right) +\sum _{l=N+1}^{N+M}a_{il}(y_{i}-y_{ld}) , \end{aligned}$$
(8)
$$\begin{aligned} \ell _{i,m}&=x_{i,m}-o_{i,m}, \end{aligned}$$
(9)
$$\begin{aligned} z_{i,m}&= o_{i,m}-\alpha _{i,m-1},\text { }m=2,...,n, \end{aligned}$$
(10)

where \(\ell _{i,m}\), \(o_{i,m}\), \(z_{i,m}\) and \(\alpha _{i,m-1}\) are virtual error surface, first-order filter output signal, filtering error and virtual control signal, respectively.

The first-order filter is defined to cope with the problem of “explosion of complexity”, which can be defined as

$$\begin{aligned} \varsigma _{i,m}\dot{o}_{i,m}+o_{i,m}=\alpha _{i,m-1},\ o_{i,m}(0)=\alpha _{i,m-1}(0), \end{aligned}$$
(11)

where \(\varsigma _{i,m}\) is a positive design parameter. According to (10) and (11), it can be summarized as \(\dot{o}_{i,m}=-\frac{z_{i,m}}{\varsigma _{i,m}}\), then

$$\begin{aligned} \dot{z}_{i,m}=-\frac{z_{i,m}}{\varsigma _{i,m}}+M_{i,m}(\cdot ), \end{aligned}$$
(12)

where \(M_{i,m}(\cdot )=-\dot{\alpha }_{i,m-1}\) is a continuous function.

Step \(\boldsymbol{1}\). Construct Lyapunov function as

$$\begin{aligned} V_{i,1}=\frac{\chi _{i,1}^{2}}{2}+\frac{\tilde{\theta }_{i,1}^{2}}{2\gamma _{1i,1}}+\frac{\tilde{\varTheta }_{i,1}^{2}}{2\gamma _{2i,1}}, \end{aligned}$$
(13)

where \(\gamma _{1i,1}\) and \(\gamma _{2i,1}\) are positive design parameters.

By combining (1), (2), (4), (8) and (13), we get

$$\begin{aligned} \dot{V}_{i,1} \le \&\chi _{i,1}r_{i}(d_{i}(\ell _{i,2}+z_{i,2}+\alpha _{i,1})-\sum _{j=1}^{N}a_{ij}x_{j,2}+F_{i,1}+F_{i,ps}-\sum _{l=N+1}^{N+M}a_{ij}\dot{y}_{ld} \nonumber \\&-\frac{\dot{\zeta }_{i}(t)\ell _{i,1}}{ \zeta _{i}(t)})-\frac{\tilde{\theta }_{i,1}\dot{\hat{\theta }}_{i,1}}{\gamma _{1i,1}} -\frac{ \tilde{\varTheta }_{i,1}\dot{\hat{\varTheta }}_{i,1}}{\gamma _{2i,1}}. \end{aligned}$$
(14)

where \(F_{i,1}=d_{i}f_{i,1}(\underline{x}_{i,1})-\sum _{j=1}^{N}a_{ij}f_{j,1}( \underline{x}_{j,1})\), and \(F_{i,ps}=d_{i}h_{i,ps}-\sum _{j=1}^{N}a_{ij}h_{j,ps}\).

By combining Young’s inequality and FLSs, we get

$$\begin{aligned} \chi _{i,1}r_{i}d_{i}(\ell _{i,2}+z_{i,2})&\le \chi _{i,1}^{2}r_{i}^{2}d_{i}^{2}+ \frac{\ell _{i,2}^{2}+z_{i,2}^{2}}{2}, \\ \chi _{i,1}r_{i}F_{i,1}&\le \frac{\chi _{i,1}^{2}r_{i}^{2}\theta _{i,1}\varphi _{i,1}^{T}(X_{i,1})\varphi _{i,1}(X_{i,1})}{2p_{i,1}^{2}}+\frac{\chi _{i,1}^{2}r_{i}^{2}}{2} +\frac{p_{i,1}^{2}}{2}+\frac{ \varepsilon _{i,1}^{2}}{2},\\ \chi _{i,1}r_{i}F_{psi}&\le \frac{\chi _{i,1}^{2}r_{i}^{2}\varTheta _{i,1}\varphi _{i,ps}^{T}(X_{i,ps})\varphi _{i,ps}(X_{i,ps})}{2p_{i,ps}^{2}} +\frac{\chi _{i,1}^{2}r_{i}^{2}}{2}+\frac{p_{i,ps}^{2}}{2}+\frac{ \varepsilon _{i,ps}^{2}}{2}, \end{aligned}$$

where \(p_{i,1}\), \(p_{i,ps}\), \(\varepsilon _{i,1}\) and \(\varepsilon _{i,ps}\) are nonnegative constants, \(\varphi _{i,1}(X_{i,1})\) and \(\varphi _{i,ps}(X_{i,ps})\) are fuzzy basis function vectors with \(X_{i,1}=[x_{i,1}^{T},x_{j,1}^{T}]^{T}\) and \( X_{i,ps}=[x_{i,ps}^{T},x_{j,ps}^{T}]^{T}\).

Design the virtual control law and adaptive laws as

$$\begin{aligned} \alpha _{i,1} =&-\frac{1}{d_{i}}(\frac{c_{i,1}\chi _{i,1}}{r_{i}}+\chi _{i,1}r_{i}d_{i}^{2}-\sum _{j=1}^{N}a_{ij}x_{j,2}+\chi _{i,1}r_{i}-\sum _{l=N+1}^{N+M}a_{ij}\dot{y}_{ld}-\frac{\dot{\zeta }_{i}(t)\ell _{i,1}}{\zeta _{i}(t)} \nonumber \\&+\frac{\chi _{i,1}r_{i}\hat{\theta }_{i,1}\varphi _{i,1}^{T}(X_{i,1})\varphi _{i,1}(X_{i,1})}{ 2p_{i,1}^{2}}{2p_{i,1}^{2}}+\frac{\chi _{i,1}r_{i}\hat{\varTheta }_{i,1}\varphi _{i,1}^{T}(X_{i,1})\varphi _{i,1}(X_{i,1})}{2p_{i,ps}^{2}}), \end{aligned}$$
(15)
$$\begin{aligned} \dot{\hat{\theta }}_{i,1}=\,&\gamma _{1i,1}(\frac{\chi _{i,1}^{2}r_{i}^{2}\varphi _{i,1}^{T}(X_{i,1})\varphi _{i,1}(X_{i,1})}{ 2p_{i,1}^{2}}-\delta _{1i,1}\hat{\theta }_{i,1}), \nonumber \\ \dot{\hat{\varTheta }}_{i,1}=\,&\gamma _{2i,1}(\frac{\chi _{i,1}^{2}r_{i}^{2}\varphi _{i,ps}^{T}(X_{i,ps})\varphi _{i,ps}(X_{i,ps})}{ 2p_{i,ps}^{2}}-\delta _{2i,1}\hat{\varTheta }_{i,1}), \end{aligned}$$
(16)

where \(c_{i,1},\) \(\delta _{1i,1}\) and \(\delta _{2i,1}\) are positive constants to be designed.

From (15) and (16), \(\dot{V}_{i,1}\) becomes

$$\begin{aligned} \dot{V}_{i,1} \le&\,\frac{\ell _{i,2}^{2}+z_{i,2}^{2}}{2}-c_{i,1}\chi _{i,1}^{2}+\delta _{1i,1}\tilde{\theta }_{i,1}\hat{\theta }_{i,1}+\delta _{2i,1}\tilde{\varTheta }_{i,1}\hat{\varTheta }_{i,1}\nonumber \\&+\frac{p_{i,1}^{2}}{2} +\frac{\varepsilon _{i,1}^{2}}{2}+\frac{p_{i,ps}^{2}}{2}+\frac{\varepsilon _{i,ps}^{2}}{2}. \end{aligned}$$
(17)

Step \(\boldsymbol{m}\). The Lyapunov function is chosen as

$$\begin{aligned} V_{i,m}=V_{i,m-1}+\frac{\ell _{i,m}^{2}}{2}+\frac{\tilde{\theta }_{i,m}^{2}}{ 2\gamma _{1i,m}}+\frac{z_{i,m}^{2}}{2}, \end{aligned}$$
(18)

where \(\gamma _{1i,m}\) is a positive design constant.

By differentiating \(V_{i,m}\), it yields that

$$\begin{aligned} \dot{V}_{i,m} \le \,&\dot{V}_{i,m-1}+\ell _{i,m}(\ell _{i,m+1}+z_{i,m+1}+\alpha _{i,m+1}+f_{i,m}(\underline{x}_{i,m})-\dot{o}_{i,m})-\frac{\tilde{ \theta }_{i,m}\dot{\hat{\theta }}_{i,m}}{\gamma _{1i,m}} \nonumber \\&+z_{i,m}\Big (-\frac{z_{i,m}}{\varsigma _{i,m}}+M_{i,m}(\cdot )\Big ). \end{aligned}$$
(19)

Design the virtual control law and adaptive law as

$$\begin{aligned} \alpha _{i,m} =\,&-c_{i,m}\ell _{i,m}-\frac{3\ell _{i,m}}{2}+\dot{o} _{i,m}-\frac{\ell _{i,m}\hat{\theta }_{i,m}\varphi _{i,m}^{T}(\underline{x} _{i,m})\varphi _{i,m}(\underline{x}_{i,m})}{2p_{i,m}^{2}}, \end{aligned}$$
(20)
$$\begin{aligned} \dot{\hat{\theta }}_{i,m}=\,&\gamma _{1i,m}(\frac{\ell _{i,m}^{2}\varphi _{i,m}^{T}(\underline{x}_{i,m})\varphi _{i,m}(\underline{x}_{i,m})}{ 2p_{i,m}^{2}}-\delta _{i,m}\hat{\theta }_{i,m}), \end{aligned}$$
(21)

then, one has

$$\begin{aligned} \dot{V}_{i,m} \le \,&\overset{m+1}{\underset{q=2}{\sum }}\frac{z_{i,q}^{2}}{2}+\overset{m+1}{\underset{q=2}{\sum }}\frac{ \ell _{i,q}^{2}}{2}-c_{i,1}\chi _{i,1}^{2}-\overset{m}{\underset{q=2}{\sum }}c_{i,q}\ell _{i,q}^{2}+\overset{m}{\underset{q=1}{\sum }}\delta _{1i,q}\tilde{\theta }_{i,q}\hat{ \theta }_{i,q}+\delta _{2i,1}\tilde{\varTheta }_{i,1}\hat{\varTheta }_{i,1}\nonumber \\&+\overset{m}{\underset{q=2}{\sum }}z_{i,q}\Big (-\frac{z_{i,q}}{\varsigma _{i,q}} +M_{i,q}(\cdot )\Big )+\overset{m}{\underset{q=1}{\sum }}\frac{p_{i,q}^{2}}{2}+\overset{m}{ \underset{q=1}{\sum }}\frac{\varepsilon _{i,q}^{2}}{2}+\frac{p_{i,ps}^{2}}{2}+ \frac{\varepsilon _{i,ps}^{2}}{2}, \end{aligned}$$
(22)

where \(c_{i,m}\), \(\delta _{i,m}\), \(p _{i,m}\) and \(\varepsilon _{i,m}\) are nonnegative design parameters.

Step \(\boldsymbol{n}\). Construct the following Lyapunov function as

$$\begin{aligned} V_{i,n}=V_{i,n-1}+\frac{\ell _{i,n}^{2}}{2}+\frac{\tilde{\theta }_{i,n}^{2}}{ 2\gamma _{1i,n}}+\frac{z_{i,n}^{2}}{2}, \end{aligned}$$
(23)

where \(\gamma _{1i,n}>0\) is a design parameter.

From (12) and (23), the derivative of \(V_{i,n}\) becomes

$$\begin{aligned} \dot{V}_{i,n} \le \,&\dot{V}_{i,n-1}+\ell _{i,n}\Big (b_{i}u_{i}+f_{i,n}( \underline{x}_{i,n})-\dot{o}_{i,n}\Big )-\frac{\tilde{\theta }_{i,n}\dot{\hat{\theta }}_{i,n}}{\gamma _{1i,n}}+z_{i,n}\Big (-\frac{z_{i,n}}{\varsigma _{i,n}}+M_{i,n}(\cdot )\Big ). \end{aligned}$$
(24)

Design the transition continuous control law and adaptive law as

$$\begin{aligned} \omega _{i} =\,&N(\eta _{i})(1+\mu _{i}^{1}\nu _{i})\Big (c_{i,n}\ell _{i,n}+ \frac{\ell _{i,n}}{2}-\dot{o}_{i,n}+\frac{\ell _{i,n}\hat{\theta }_{i,n}}{2p_{i,n}^{2}}-\frac{\mu _{i}^{2}\epsilon _{i}}{1+\mu _{i}^{1}\nu _{i}}\Big ), \end{aligned}$$
(25)
$$\begin{aligned} \dot{\eta }_{i} =\,&c_{i,n}\ell _{i,n}^{2}+\frac{\ell _{i,n}^{2}}{2}+\frac{\ell _{i,n}^{2} \hat{\theta }_{i,n}\varphi _{i,n}^{T}(\underline{x}_{i,n})\varphi _{i,n}( \underline{x}_{i,n})}{2p_{i,n}^{2}}-\ell _{i,n}\dot{o}_{i,n}-\frac{\ell _{i,n}\mu _{i}^{2}\epsilon _{i}}{ 1+\mu _{i}^{1}\nu _{i}}, \end{aligned}$$
(26)
$$\begin{aligned} \dot{\hat{\theta }}_{i,n}=\,&\gamma _{1i,n}\Big (\frac{\ell _{i,n}^{2}\varphi _{i,n}^{T}(\underline{x}_{i,n})\varphi _{i,n}(\underline{x}_{i,n})}{ 2p_{i,n}^{2}}-\delta _{1i,n}\hat{\theta }_{i,n}\Big ), \end{aligned}$$
(27)

where \(c_{i,n}\), \(\delta _{i,n}\), \(p _{i,n}\) and \(\varepsilon _{i,n}\) are nonnegative constants.

Based on (7) and (24)–(27), one can obtain

$$\begin{aligned} \dot{V}_{i,n} \le \,&\overset{n}{\underset{q=2}{\sum }}\frac{z_{i,q}^{2}}{2}+b_{i}N(\eta _{i})\dot{\eta }_{i}+\dot{\eta } _{i}-c_{i,1}\chi _{i,1}^{2}-\overset{n}{\underset{q=2}{\sum }}c_{i,q}\ell _{i,q}^{2} +\overset{n}{\underset{q=1}{\sum }}\delta _{1i,q}\tilde{\theta }_{i,q}\hat{\theta }_{i,q}+\overset{n}{\underset{q=1}{\sum }}\frac{p_{i,q}^{2}}{2} \nonumber \\&+\overset{n}{ \underset{q=1}{\sum }}\frac{\varepsilon _{i,q}^{2}}{2}+\delta _{2i,1}\tilde{\varTheta }_{i,1}\hat{\varTheta }_{i,1}+\frac{p_{i,ps}^{2}}{2}+ \frac{\varepsilon _{i,ps}^{2}}{2} +\overset{n}{\underset{q=2}{\sum }}z_{i,q}\Big (-\frac{z_{i,q}}{\varsigma _{i,q}}+M_{i,q}(\cdot )\Big ). \end{aligned}$$
(28)

3 Stability Analysis

Theorem 1

Considering the controlled MASs subject to sensor faults and unknown nonlinearities (1), all signals in the system are semi-globally uniformly ultimately bounded (SGUUB), and all followers can converge to the convex hull constituted by multiple leaders.

Proof

Based on Young’s inequality, it yields that \( \tilde{\theta }_{i,q}\hat{\theta }_{i,q}\ \le \ \frac{\theta _{i,q}^{2}}{2}-\frac{ \tilde{\theta }_{i,q}^{2}}{2},\text { } \tilde{\varTheta }_{i,1}\hat{\varTheta }_{i,1}\ \le \ \frac{\varTheta _{i,1}^{2}}{2}-\frac{ \tilde{\varTheta }_{i,1}^{2}}{2},\text { } -z_{i,q}M_{i,q}(\cdot )\ \le \ \frac{z_{i,q}^{2}\bar{M}_{i,q}^{2}(\cdot )}{2}+ \frac{1}{2}, \) and there is a scalar \(\bar{M}_{i,q}(\cdot )\) \(>0\) that satisfies \(\left| M_{i,q}(\cdot )\right| <\bar{M}_{i,q}(\cdot )\).

Then, construct the Lyapunov function as

$$\begin{aligned} V=\sum _{i=1}^{N}\sum _{q=1}^{n}V_{i,q}. \end{aligned}$$

From (24) and Youngs inequality, the derivative of V is computed as

$$\begin{aligned} \dot{V} \le \,&\overset{N}{\underset{i=1}{\sum }}\Big (b_{i}N(\eta _{i})\dot{ \eta }_{i}+\dot{\eta } _{i}-c_{i,1}\chi _{i,1}^{2}-\overset{n}{\underset{q=2}{\sum }} c_{i,q}\ell _{i,q}^{2}-\overset{n}{\underset{q=1}{\sum }}\delta _{1i,q}\frac{\tilde{\theta } _{i,q}^{2}}{2}-\delta _{2i,1}\frac{\tilde{\varTheta }_{i,1}^{2}}{2} \nonumber \\&+\overset{n}{\underset{q=2}{\sum }}z_{i,q}^{2}\Big (-\frac{1}{\varsigma _{i,q}}+ \frac{\bar{M}_{i,q}^{2}(\cdot )}{2}+\frac{1}{2}\Big )+\varPsi _{i}\Big ), \end{aligned}$$
(29)

where \(\varPsi _{i}=\overset{n}{\underset{q=1}{\sum }}\delta _{1i,q}\frac{\theta _{i,q}^{2}}{2}+\delta _{2i,1}\frac{\varTheta _{i,1}^{2}}{2}+\overset{n}{ \underset{q=1}{\sum }}\frac{p_{i,q}^{2}}{2}+\overset{n}{\underset{q=1}{\sum } }\frac{\varepsilon _{i,q}^{2}}{2}+\frac{p_{i,ps}^{2}}{2}+\frac{\varepsilon _{i,ps}^{2}}{2}.\)

The design parameter is chosen as \(\frac{1}{\varsigma _{i,q}}-\frac{\bar{M} _{i,q}^{2}(\cdot )}{2}-\frac{1}{2}>0\). Let \(\varpi =2\min \left\{ c_{i,q}, \frac{1}{\varsigma _{i,q}}-\frac{\bar{M} _{i,q}^{2}(\cdot )}{-}\frac{1}{2},\delta _{1i,q},\delta _{2i,1}\right\} \), then,

$$\begin{aligned} \dot{V}\ \le \ \overset{N}{\underset{i=1}{\sum }}\Big (b_{i}N(\eta _{i})\dot{ \eta }_{i}+\dot{\eta } _{i}\Big )-\varpi V+\varPsi , \end{aligned}$$
(30)

where \(\varPsi =\overset{N}{\underset{i=1}{\sum }}\varPsi _{i}\).

Multiplying (30) by \(e^{\varpi t}\) and integrating on the interval [0, t), it yields

$$\begin{aligned} V(t)\le \frac{\varPsi }{\varpi }+V(0)+e^{-\varpi t}\sum _{i=1}^{N}\int _{0}^{t} \Big (b_{i}N(\eta _{i})\dot{\eta }_{i}+\dot{\eta } _{i}\Big )e^{\varpi \tau }d\tau . \end{aligned}$$
(31)

According to Lemma 2, we obtain V(t), \(\eta _{i} \) and \(\int _{0}^{t}\Big ( b_{i}N(\eta _{i})\dot{\eta }_{i}+\dot{\eta } _{i}\Big )e^{\varpi \tau }d\tau \) are bounded on \([0,t_{f})\), and \(\chi _{i,1},\) \(\ell _{i,m}\text { }(m=2,\cdots , n),\) \(\hat{\theta }_{i,m}\) and \(\hat{\varTheta }_{i,1}\) are bounded. Therefore, all signals of the closed-loop system are SGUUB. According to \(\kappa _{i}(t)=\omega _{i}(t)-u_{i}(t)\) for \(\forall t\in [t^{*},t_{\pi +1})\), we obtain \(\frac{d}{dt}|\kappa _{i}|=\frac{d}{dt}(\kappa _{i}*\kappa _{i})^{\frac{1}{2}}=\text {sign}(\kappa _{i}) \dot{\kappa }_{i}\le |\dot{\omega }_{i}|.\) Since all signals in the system are bounded, there exist a constant \(\varrho _{i}>0\) satisfying \(|\dot{\omega }_{i}|\le \varrho _{i}\). For \(\kappa _{i}(t_{\pi })=0\) and \(lim_{t\rightarrow t_{\pi +1}}\kappa _{i}(t)=\epsilon _{i}\), the lower bound \(t^{*}\ge \frac{\epsilon _{i}}{\varrho _{i}}\) of the time intervals events can be obtained, thus, the Zeno behavior can be avoided.

4 Simulation Results

Example 1

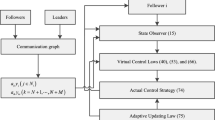
Choose MASs (Fig. 1) with sensor fault as

$$\begin{aligned} \left\{ \begin{array}{rl} \dot{x}_{i,1}&{}=x_{i,2}+x_{i,1}^{2}\sin (x_{i,1}), \\ \dot{x}_{i,2}&{}=b_{i}u_{i}+x_{i,2}\sin (x_{i,1}), \\ y_{i}&{}=x_{i,1}+h_{i,s}. \end{array} \right. \end{aligned}$$
(32)
Fig. 1.
figure 1

Communication topology.

Full size image

The leaders’ trajectories are defined as

$$\begin{aligned} \left\{ \begin{array}{l} y_{5d}=0.1-\exp \left( -t\right) , \\ y_{6d}=0.1\sin (t+1.5)-0.1. \end{array} \right. \end{aligned}$$
(33)
Fig. 2.
figure 2

(a) The outputs of leaders and followers (b) Containment errors limited in the prescribed performance bounds.

Full size image

Select design parameters as \([c_{1,1}\),  \(c_{2,1}\),  \(c_{3,1}\),  \( c_{4,1}\) \(]^{T}\)\(=[0.07,\) 0.11,  0.04,  \(0.1]^{T},\) \([c_{2,1},\) \(c_{2,2},\) \(c_{32,},\) \(c_{4,2}]^{T}=[0.06,\) 0.5,  0.08,  \(0.1]^{T},\) \( p_{i,1}=p_{i,2}=50,\) \(p_{i,ps}=52,\) \([\nu _{1},\) \(\nu _{2},\) \(\nu _{3},\) \(\nu _{4}]^{T}=[0.5,\) 0.65,  0.1,  \(0.09]^{T}\),\(\ \mu _{i}^{1}=0.01,\) \(\mu _{i}^{2}=1,\) \(\delta _{1i,1}=\delta _{2i,1}=40,\) \( \delta _{1i,2}=35,\) \(\varepsilon _{i}=0.15,\) \(\gamma _{1i,1}=\gamma _{1i,2}=20,\) \(\gamma _{2i,1}=50,\) \(\varsigma _{i,2}=0.3,\) \(b_{i}=2\), and the initial parameters are define as 0. Design the performance function as \( \zeta _{i}(t)=(9.5-1.7)e^{-0.46t}+1.7,\) where \(\sigma _{1i}=0.08\) and \(\sigma _{2i}=0.09\). Figure 2(a) represents that the trajectories of all followers can reach the convex formed by leaders, and (b) presents the containment errors limited in the prescribed performance bounds. The trajectories and release instants of control signals are shown in Fig. 3. In addition, the sampling time is chosen as 0.01s, compared with the time-triggered method, the proposed event-triggered method can save communication resources effectively.

Fig. 3.
figure 3

(a) Curves of control signals \(u_{i}\) (b) Release instants of \(u_{i}\).

Full size image

5 Conclusion

This paper has investigated an adaptive event-triggered containment control method for MASs subject to sensor faults. The adaptive faults compensation control technology has been used to handle the sensor faults. FLSs and Nussbaum-type function have been employed to cope with unknown nonlinearities and unknown control directions, respectively. Finally, some simulation results have been presented to verify the availability of the devised control strategy.