Keywords

1 Introduction

Researchers have paid close attention to the huge unlicensed bandwidth available in free space optical (FSO) communication systems. The atmospheric turbulence and pointing error limit the capabilities of FSO systems, such as high security, quick deployment, and flexibility [1, 2]. In addition, mixed RF/FSO relay systems have arisen as a result of the use of FSO systems as an complementary form of radio frequency (RF) equivalents [3,4,5,6]. Because of its simplicity, the amplify-and-forward (AF) relaying approach has gained a lot of traction.

Multiuser diversity (MUD) techniques have been developed in [7] to boost the data rate supplied by wireless networks across RF fading channels. RF systems can employ the diversity gain provided by MUD systems from several users transmitting at the same time to boost throughput. MUD can take advantage of fluctuating RF channels by assigning common resources to the user with the best channel. The user with the highest signal-to-noise ratio (SNR) is chosen for transmission in this approach. Furthermore, interference from other modes of transmission in the immediate neighborhood limits the performance of any realistic wireless communication system. Importantly, relay networks with various co-channel interferences (CCIs) at the receiving nodes impair the desired signal quality.

In the literature, there has been a lot of work on mixed RF/FSO relaying systems [3, 5, 7,8,9]. The dual hop mixed RF/FSO asymmetric relaying was proposed in [3], where the authors developed an estimate of the entire system’s outage probability (OP). The Rayleigh distribution was used to represent the RF link, whereas Gamma-Gamma atmospheric turbulence was used to model the FSO link. Using pointing faults on the FSO link subject to intensity modulation with direct detection (IM/DD) and heterodyne detection, the authors of [5] completed a unified study of mixed RF/FSO relaying system. Research works [7,8,9] examined the performance of a dual hop RF/FSO connection using recently proposed generalized \(\mathcal {M}\)-distribution and Double Generalized Gamma (D-GG) fading models.

While the majority of the published results for FSO relay-assisted communications have depended on the absence of CCI, it becomes crucial to emphasize that because RF links are involved, asymmetric RF/FSO relay systems can be intrinsically subject to the impact of CCI. In RF systems, frequency re-use also creates a source of interference, according to [10]. The authors of [11] were inspired by the interference-limited performance of mixed RF/FSO systems to construct the expression of OP and bit error rate (BER) for an AF relaying system. To illustrate accurate and asymptotic performance of the whole system in [11], the channel of interfering signals was modeled as the Nakagami-\(m\) distribution fading, while the FSO systems was studied using the D-GG turbulence model. The authors in [12] have derived the closed form formulation of OP by observing the effect of interference at the relay node. In addition, [13] describes an examination of a dual-hop FSO/RF cooperative system in which the FSO and RF links undergo Malaga and generalized-K distributed fadings, respectively.

The majority of past research has focused on mixed RF/FSO relay systems with the premise of interference-free transmission. Furthermore, works that address the issue of interference in FSO systems have not addressed the benefits that the MUD scheme can provide. We intend to study asymmetric relaying with generalized fading models in the presence of MUD, which is missing in the literature. To increase the performance of the RF link, we consider an asymmetric mixed RF/FSO fixed gain relay method with sub-carrier intensity modulation (SIM) and MUD at the source in this study. In addition, we evaluate the influence of several CCIs on the communication to make the system model more feasible. Therefore, the system model presented in this paper is different from that given in [3, 5, 7,8,9, 11,12,13,14,15,16]. In addition to this, we model the RF link with Nakagami-\(m\) fading model [17]. With interference at relay and destination nodes, we study the system subjected highly adverse conditions. Unequal interferers with non-identical statistical characteristics have been considered on both the links to observe the effect of simultaneous transmission from different kinds communication systems. D-GG fading distribution is used to model atmospheric turbulence on the FSO link.

2 System and Channel Models

In this section, the system and channel models of the considered relaying strategy is discussed.

Table 1. List of symbols.
Full size table

2.1 System Model

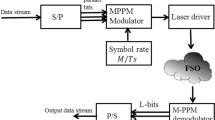
Consider an asymmetric RF/FSO dual hop cooperative relaying system with \(K\) RF mobile users intend to send data to the destination node \(D\) through the relay node \(R\). The randomness offered by the RF channel increases as the number of users on the RF link increases, which is utilized by the node \(R\) for increasing system throughput. Moreover, the \(K\) users communicate with the relay node in the vicinity of \(L\) CCIs at the relay node. On source-to-relay (SR) link, the signal received \(y_{ {SR, j}}\) from \(j^{th}\)-user at node \(R\) is given by

$$\begin{aligned} y_{SR, j} = \sqrt{P_{SR, j}} h_{SR, j} d_{RF} + \sqrt{P_{I1}} \sum _{i=1}^{L} h_{SR, i} x_{r,i} + N_{RF} \end{aligned}$$
(1)

where suffix \(j\) corresponds to the \(j^{th}\)-user and all the symbols are defined in Table 1. In the second phase, the relay node amplifies the signal \(y_{SR, j}\) and transmits the same towards the destination node \(D\). In the presence of \(M\) CCIs at the destination node, the received signal is expressed as

$$\begin{aligned} y_{j,RD} =&(\eta I )^{\frac{\rho }{2}} G\sqrt{P_{SR, j}} h_{SR, j} d_{RF} + (\eta I )^{\frac{\rho }{2}} G\sqrt{P_{I_1}}\sum _{i=1}^{L}h_{R, i} x_{r,i} \nonumber \\ {}&+ (\eta I)^{\frac{\rho }{2}}\sqrt{P_{I_2}} \sum _{i=1}^{M}h_{D,i} x_{d,i} + N_o \end{aligned}$$
(2)

The various symbols in (2) have been defined in Table 1. As mentioned in [10], the gain \(G\) can be formulated as

$$\begin{aligned} G^2= \frac{1}{{P_{SR, j}}{|h_{SR, j}|}^2 + P_{I_1}\sum _{i=1}^{L} {|h_{R,i}|}^2 + {\sigma _n}^2} \end{aligned}$$
(3)

For the cooperative relay strategy, the signal-to-interference-plus-noise (SINR) can be written using (2) as [10]

$$\begin{aligned} \gamma _{ {e2e}{}} = \frac{\gamma _{ {SR}{},j}^{eff}\gamma _{ {RD}{}}^{eff}}{\gamma _{ {SR}{},j}^{eff}+\gamma _{ {RD}{}}^{eff}+ 1} \end{aligned}$$
(4)

where the effective instantaneous SINR on the RF link corresponding to the \(j^{th}\) user considering both RF fading as well as the interference statistics is denoted by \(\gamma _{ {SR}{},j}^{eff}\) and is given by the relation \(\gamma _{ {SR}{},j}^{eff}=\frac{\gamma _{ {k}{}}}{1+ \sum _{i=1}^{L} \gamma _{ {I_{r}}{},i}}\). On the other hand, \(\gamma _{ {RD}{}}^{eff}\) denotes the effective SINR on the wireless optical link considering atmospheric scintillation, pointing errors, path loss and interference defined as \(\gamma _{ {RD}{}}^{eff} = \frac{\gamma _{ {RD}{}}}{1+ \sum _{i}^{M} \gamma _{ {I_{d}}{},i}}\). The variables \(\gamma _{ {I_{r}}{}}\) and \(\gamma _{ {I_{d}}{}}\) denote interfering signal at relay and destination nodes, respectively. For mathematical tractability, consider an upper bound, \(\gamma _{ {{e2e}}{}} < \gamma _{ {up}{}} \), such that

$$\begin{aligned} \gamma _{ {{e2e}}{}} = \min \left( {\gamma _{ {SR}{},j}^{eff}, \gamma _{ {RD}{}}^{eff}}\right) \end{aligned}$$
(5)

2.2 Channel Model

2.2.1 RF Link

The \(k^{th}\) user on the RF link follows the probability density function (PDF) of Nakagami-\(m\) distribution as given below [17]

$$\begin{aligned} f_{\gamma _k} (\gamma ) = \frac{\beta ^{m_{SR}}}{\varGamma (m_{SR})} \gamma ^{m_{SR}-1}\exp (-\beta \gamma ) \end{aligned}$$
(6)

where \(m_{SR}\) is the shape parameter and \(\beta =\frac{m_{SR}}{\bar{\gamma }_{k}} \). Furthermore, using the notion of ordered statistics as follows, the PDF with \(K\) users may be produced as

$$\begin{aligned} f_{\gamma _{SR},j}(\gamma ) = K [F_{\gamma _{k}}(\gamma )]^{K-1}f_{\gamma _k} (\gamma ) \end{aligned}$$
(7)

Hence, considering (6) and (7), for integer values of fading parameter \(m_{ {SR}{}}\), the closed-form expression for the PDF of RF link experiencing Nakagami-\(m\) fading can be obtained as [6]

$$\begin{aligned}&f_{\gamma _{SR},j}(\gamma ) = \frac{K\beta ^{m_{SR}}}{\varGamma (m_{SR})} \sum _{n_1=0}^{K-1} (-1)^{n_1} \left( {\begin{array}{c}K-1\\ n_1\end{array}}\right) \nonumber \\&\times \sum _{n_2=0}^{n_1(m_{SR}-1)} \zeta _{n_{1}n_{2}}(m_{SR}) \gamma ^{m_{SR}+n_2-1} \beta ^{n_2} \exp (-\beta (n_1+1)\gamma ) \end{aligned}$$
(8)

where \(\zeta _{n_{1}n_{2}}(m_{ {SR}{}})\) is the multinomial expansion’s coefficient involved in the derivation of (8) which can be recursively obtained using the relation \(\zeta _{n_{1}n_{2}}=\sum _{b=n_1 -x+1}^{n_1}\frac{\lambda _{bn_{2}-1}}{n_1-b} \text{ I}_{ {[0,(n_2-1)(x-1)]}{ }} \) where \(I_{ {[a,b]}{ }}\) is defined in [17, Eq. (9.120)]. Moreover, the PDF of the total interference-to-noise ratio (INR) \(\sum _{i=1}^{L} \gamma _{ {I_{r}}{ },i}\) can be expressed as [6] \(f_{_{{ {I_{r}}{ }}}}(\gamma ) = \bigg [\frac{m_{1}}{\varOmega _I{_1}}\bigg ]^{m_{1}L} \frac{\gamma ^{m_{1}L-1}}{\varGamma (m_{1}L)}\exp \bigg (-\frac{m_{1}L}{\varOmega _I{_1}}\gamma \bigg )\) where \(m_1\) is Nakagami-\(m\) fading parameter and \(\varOmega _I{_1}\) is the interference to noise ratio (INR) on the RF link. The effective PDF can be simplified as [6]

$$\begin{aligned} f^{eff}_{\gamma _{SR},j}(\gamma )&= \sum _{n_1=0}^{K-1} \sum _{n_2=0}^{n_1(m_{SR}-1)} A_2 \gamma ^{m_{SR}+n_2-1} e^{[-\beta (n_1+1)\gamma ]}\nonumber \\&\times U\big (m_{1}L, m_{1}L+1+m_{SR}+n_2 , \mathcal {B}_0(\gamma )\big ) \end{aligned}$$
(9)

where \(U(a,b,z) \) is the confluent hypergeometric function of second kind as defined in [18, Eq. (9.211.4)], \(\mathcal {B}_0(\gamma ) = \beta (n_1+1)\gamma +\frac{m_{1}}{\varOmega _I{_1}} \), the constant \(A_1 = \frac{K\beta ^{m_{SR}}}{\varGamma (m_1L)\varGamma (m_{SR})} \left( \frac{m_1}{\varOmega _{I_1}} \right) ^{m_1L} \), \(A_2 = A_1 (-1)^{n_1} \left( {\begin{array}{c}K-1\\ n_1\end{array}}\right) \varGamma (m_1L)\zeta _{n_{1}n_{2}}(m_{SR}) \beta ^{n_2} \). The cumulative distribution function (CDF) on the RF link can be derived as \(F^{eff}_{\gamma _{SR}}(\gamma ) = \int _{0}^{\infty } f^{eff}_{\gamma _{SR}}(\gamma ) d\gamma \). After some mathematical manipulations, the CDF of \(\gamma _{ {SR}{ },j}^{eff} \) can be expressed as follows [6]

$$\begin{aligned}&F^{eff}_{\gamma _{SR},j}(\gamma ) =\frac{K}{\varGamma m_{ {SR}{ }}} \sum _{n_1=0}^{K-1} \sum _{n_2=0}^{n_1(m_{SR}-1)} A_3 \bigg [1 - \sum _{m=0}^{n_2+m_{SR}-1} e^{(-\beta (n_1+1)\gamma )} \nonumber \\ {}&\times \frac{\{(n_1+1)\beta \gamma \}^{m}}{m!} U\bigg (m_{1}L, m_{1}L+1+m , \mathcal {B}_0(\gamma ) \bigg )\bigg ] \end{aligned}$$
(10)

where \(A_3\) is given by

$$\begin{aligned} A_3&= (-1)^{n_1} \left( {\begin{array}{c}K-1\\ n_1\end{array}}\right) (m_{SR}+n_2-1)!\zeta _{n_{1}n_{2}}(m_{SR}) \nonumber \\&\times (n_1+1)^{-n_2-m_{SR}} \end{aligned}$$
(11)

On the other hand, it is assumed that \(R\) \(\rightarrow \) \(D\) link undergoes the turbulence-induced fading \(I_a\) and the pointing errors \(I_p\) such that \(I=I_aI_p\). The pointing error parameters are obtained from the reference [1]. The atmospheric turbulence fading \(I_a\) on the FSO link is modeled as double generalized gamma (GG) fading model [9] and the PDF of \(I_a\) can be expressed as [9]

(12)

where \(\tau _0 = \left[ \varDelta (\sigma :\beta _1), \varDelta (\lambda :\beta _2)\right] \) with \(\varDelta (z:x)\) representing \([\frac{x}{z}, \frac{x+1}{z}, \dots , \frac{x+z-1}{z}]\), where is the Meijer-G function defined in [18, Eq. (9.301)] and \(y=\alpha _2\lambda \). Moreover, the SNR PDF on FSO link experiencing a double GG fading model with the effect of pointing errors is given by [9]

(13)

with

$$\begin{aligned} \mathcal {D}_1 = \frac{\xi ^2 \sigma ^{\beta _1-\frac{1}{2}} \sigma ^{\beta _2-\frac{1}{2}} (2\pi )^{1-\frac{\sigma +\lambda }{2}} }{\varGamma (\beta _1) \varGamma (\beta _2)} \end{aligned}$$
(14)
$$\begin{aligned} \mathcal {D}_2 = \frac{\beta _1^\sigma \beta _2^\lambda }{\lambda ^\lambda \sigma ^\sigma \varOmega _1^{\sigma } \varOmega _2^{\lambda }} \end{aligned}$$
(15)

where \(\tau _1 = \left[ \frac{\xi ^2}{y}, \varDelta (\sigma :\beta _1), \varDelta (\lambda :\beta _2) \right] \), \(\tau _2=\left[ 1+\frac{\xi ^2}{y}\right] \), \(\mu _r= \frac{\left( \eta \mathbb {E} (I)\right) ^r}{N_0} \) and \(r\) denotes the kind of demodulation scheme [9]. Considering \(\mathcal {D}_3= \prod _{g=1}^{\sigma +\lambda } \varGamma \left( \frac{1}{y} + \tau _{ {0,g}{3.5 pt}} \right) \), \(z\) can be given as \(z=\frac{\mathcal {D}_1(\mathcal {D}_2)^{1/y}\mathcal {D}_3}{(1+\xi ^2)} \).

Furthermore, the following is the unified CDF of the FSO channel over double GG air turbulence with pointing errors [9]

(16)

where \(n=r(\lambda +\sigma +1) \), \(\mathcal {D}_4= \frac{\xi ^2 \sigma ^{\beta _1-\frac{1}{2}} \sigma ^{\beta _2-\frac{1}{2}} (2\pi )^{1-\frac{r(\sigma +\lambda )}{2}} r^{(\beta _1+\beta _2-2)} }{y\varGamma (\beta _1) \varGamma (\beta _2)} \), \(\mathcal {D}_5= \left( \frac{\mathcal {D}_2 z^y }{r^{\sigma +\lambda }} \right) ^r \), \(\tau _3= \left[ \varDelta (r: \tau _2) \right] \) and \(\tau _4= \left[ \varDelta (r: \tau _1) \right] \) comprising of \(r(\lambda +\sigma +1) \) terms. Moreover, the interference on the destination is assumed to follow the PDF [19]

$$\begin{aligned} f_{_{{ {I_{d}}{ }}}}(\gamma )&= \frac{\gamma ^{M-1}}{\varOmega _I{_2}(M-1)!} \exp \left( -\frac{\gamma }{\varOmega _I{_2}} \right) \end{aligned}$$
(17)

where \(\varOmega _I{_2}\) is the INR on the FSO link. Given that \(I_{d}\) and \(\gamma _{ {RD}{ }}\) are independent, the CDF of \(\gamma _{ {RD}{ }}^{eff}\) can be derived using

$$\begin{aligned}&F^{eff}_{\gamma _{RD}}(\gamma ) = \int _{0}^{\infty } F_{ {RD}{ }}(\gamma (1+x)) f_{_{{ {I_{d}}{ }}}}(x) dx \end{aligned}$$
(18)

Substituting (16) and (17) in (18), and assuming \(1+y=z\), above integral may be formulated as

$$\begin{aligned}&F^{eff}_{\gamma _{RD}}(\gamma ) = \mathcal {D}_6 \left( \mathcal {J}_1-\mathcal {J}_2 \right) \end{aligned}$$
(19)

where \(\mathcal {D}_6 = \frac{\mathcal {D}_4}{{\varOmega _I{_2}}^{M} (M-1)! } \exp ({1}/{\varOmega _I{_2}} ) \) and

(20)

Resorting to binomial expansion \((z-1)^{M-1} = \sum _{i=0}^{M-1} \left( {\begin{array}{c}M-1\\ i\end{array}}\right) (-1)^{M-1-i} z^i \) as per [18, Eq. (1.11)] for integer values of \(M\) and with the aid of [20, Eq. (07.34.21.0013.01)], integral \(\mathcal {J}_1\) can be given as

(21)

where \(\mathcal {D}_7 = \mathcal {D}_5 (y \varOmega _I{_2} /\mu _r)^{y} \), \(\mathcal {D}_{10} = \frac{y^{i+\frac{1}{2}} (\varOmega _I{_2})^{i+1}}{(2\pi )^{\frac{y-1}{2}}} \) and \(\tau _5 = \left[ \frac{(-i)}{y},\dots , \frac{(v-1-i)}{y} \right] \). On the other hand, assuming \(x_i =\left( {\begin{array}{c}M-1\\ i\end{array}}\right) (-1)^{M-1-i}\), the integral \(\mathcal {J}_2\) can be given as

(22)

The integral \(\mathcal {J}_2\) can be expressed in complex integral form on using [20, Eq. (07.34.02.0001.01)]. By virtue of [18, Eq. (8.380)] and [21, Eq. (28-30)] and with some mathematical manipulations, the integral \(\mathcal {J}_2\) shown in (23) where

figure b

\([1]_{x}\) represents sequence of \(1^{'s} \) of length \(x\) and \(\text {H}_{\text{ p}_1, \text{ q}_1:\text{ p}_2,\text{ q}_2:\text{ p}_3,\text{ q}_3}^{\text{0 },\text{ m}_1:\text{ m}_2,\text{ n}_2:\text{ m}_3,\text{ n}_3}\left[ \mathcal {A}_1 , \mathcal {A}_2 \right] =\mathcal {H}\left[ \mathcal {A}_1, \mathcal {A}_2 \right] \) is the bivariate Fox-H function given in [22, Eq. (28)]. Substituting (21) and (23) into (19), we obtain the closed form equation of CDF on FSO link in the presence of multiple interferers as given below

(24)

Moreover, the PDF of end-to-end SNR can be derived by utilizing the relationship (18). Using the identity [20, Eq. (07.34.21.0013.01)] and [22], the closed form expression for the overall PDF can be written as shown below

(25)

In (25), the parameters involved in Meijer-G function has been derived as \(\tau _6=\left[ \frac{\tau _2}{r},\dots , \frac{\tau _2+r-1}{r}, \frac{1-(i+2)}{y}, \dots , \frac{y-(i+2)}{y} \right] \) and \(\tau _7=\Big [\frac{\tau _1}{r},\dots ,\) \( \frac{\tau _1+r-1}{r}, \dots , \frac{\tau _1(\lambda +\sigma +1)+r-1}{r} \Big ] \). The argument of the Meijer-G equals \(\mathcal {D}_8 = \mathcal {D}_2 z^y \{r\}^{(-r(\lambda +\sigma ))} \left( \frac{\varOmega _I2}{y \mu _r} \right) ^{y}\), \(\mathcal {D}_{11} = \frac{\mathcal {D}_1 \exp (\frac{1}{{\varOmega _I{_2}}})}{r\lambda {\varOmega _I{_2}}^{M}(M-1)!}\) and \(\mathcal {D}_{12} = \frac{y^{i+\frac{3}{2}} (\varOmega _I{_2})^{i+2} (r)^{c*}}{(2\pi )^{\left\{ {y-1}+\left( \frac{(r-1)(\lambda +\sigma )}{2}\right) \right\} }} \). The bivariate Fox’s H-function is defined in (26).

figure c

3 Performance Analysis

In this section, we investigate various performance metrics of relay system based on the aforementioned SNR bound.

3.1 Exact Outage Probability

The outage probability (OP) of a wireless communication system is an important performance measure. The likelihood that the instantaneous SNR goes below a pre-specified threshold \(\gamma _{ {{th}}{ }}\) is defined as OP. The end-to-end CDF \(F_{e_{2} e} (\gamma )\) of the overall system can be written as

$$\begin{aligned} F_{e_{2} e} (\gamma ) = F^{eff}_{\gamma _{SR},j}(\gamma ) + F^{eff}_{\gamma _{RD}}(\gamma ) - F^{eff}_{\gamma _{SR},j}(\gamma ) F^{eff}_{\gamma _{RD}}(\gamma ) \end{aligned}$$
(27)

Hence, substituting (10) and (24) into (27), and by putting \(\gamma = \gamma _{ {{th}}}\) we can obtain the overall CDF of the considered system.

Fig. 1.
figure 1

Outage Probability of dual hop mixed RF/FSO relaying system with varying number of CCIs.

Full size image
Fig. 2.
figure 2

Outage Probability of dual hop mixed RF/FSO relaying system for varying FSO link parameters.

Full size image

4 Results

The results of the research study have been discussed in this section. The outage performance of the mixed RF/FSO relaying system is shown in Fig. 1. The outage probability has been plotted against the average SNR per hop in this graph. The comparison was made for a variety of RF users, as well as the number of interferers at the relay and destination nodes. The graphic has actually showed the fluctuating strength of air turbulence. It can be shown that as the number of CCIs grows, so does the outage. The asymptotic representation of the outage probability is also shown in the plot. Monte-Carlo simulations were used to verify the results. The effect of pointing inaccuracy and optical demodulation type is displayed in Fig. 2. It can be seen that the outage probability rises as the pointing inaccuracy rises (lower value of \(xi\)). The chance of an outage is also influenced by optical demodulation. The plot shows that when coherent detection is used \(r=1\), the system’s outage probability is much higher than when coherent detection is used \(r=2\). Also shown are the asymptotic and Monte-Carlo results.

5 Conclusion

The analysis of a mixed RF/FSO relaying system in the presence of interferers on the relay and destination nodes is presented in this paper. The fading of the RF link was modeled using the Nakagami-\(m\) distribution, whereas the turbulence of the FSO link was studied using the D-GG distribution. We offer the analysis for the OP of the overall system for the considered system model.