Keywords

1 Introduction

Major changes have been introduced in the structure of electric power utilities around the world to improve the efficiency and reliability of power systems [1]. Power system deregulation and increased renewable energy (RE) integration are the major factors in the restructured power system environment. In this environment, control is greatly decentralized and Independent System Operators (ISOs) are responsible for maintaining the system frequency and tie-line power flow amongst other ancillary services [2]. Generation utilities may or may not take part in automatic generation control (AGC) or load frequency control (LFC); these make the task of frequency control more complicated to achieve. Several works have reported various approaches for LFC design when considering power system deregulation to improve the frequency response of the system [3,4,5].

In a similar way to power system deregulation, the structure of the emerging power system that incorporates RE systems, such as wind and solar plants and other distributed energy resources, is different from the conventional power system. The key technical concern that affects the increasing penetration level of RE systems is associated with their capability in performing as efficiently and consistently as conventional generation systems. This is because they affect the dynamic behavior and response of large power systems differently from their conventional counterparts [6]. Despite the rapid technological advancements in the RE industry, the task of frequency regulation remains a challenge, and this constitutes the limitation of increasing RE share in modern power systems. The study conducted in [7] predicted that with the current growth rate of RE penetration, the total system inertia would reduce significantly to values that threaten system frequency recovery and stability during power imbalance and other power system contingencies [8]. Therefore, technical methods for providing or emulating inertia need to be developed.

The virtual inertia control strategy is a promising solution in emulating the inertia characteristics of a prime mover by deploying an appropriate control algorithm in the power electronics converter of a dedicated energy storage system (ESS) [9]. Several control strategies have been adopted in the design of a virtual inertia control: the authors in [10] proposed a coefficient diagram method; a dynamic equation and adaptive fuzzy technique were proposed in [11], a derivative-controlled solar and ESS was proposed in [12], and a model predictive control (MPC) approach was designed in [13] to improve the frequency regulation capability of low-inertia microgrid systems. The artificial bee colony (ABC) algorithm was used to tune the derivative-virtual inertia control for wind energy systems in [14]. Reference [15] adopted the chicken swarm optimization algorithm in tuning the parameters of an adaptive virtual inertia controller, and the particle swarm optimization (PSO) was used in [16]. Some artificial intelligence techniques have found application in the design of virtual inertia systems; a reinforcement learning-based approach was used in [17] and [18] to design a virtual inertia controller for low-inertia power systems. In [19], a radial basis function neural network was trained to implement a virtual synchronous generator. Author of [20] implemented a virtual inertia controller using the wavelet fuzzy neural network. These control methods that apply artificial neural networks are largely dependent on the availability of data to sufficiently train the model, therefore, such control methods might result in over-fitting if the training data is insufficient, thereby compromising the performance of the control system. The fuzzy logic control is an intelligent control technique that can been used to improve performance in terms of virtual inertia control because of its high computational efficiency in handling nonlinear complexities that are characterized with modern power systems [21]. In [22], the type-I fuzzy logic was proposed for virtual inertia control of an interconnected microgrid with high RE penetration. Reference [23] augmented a low-inertia wind farm with a type-I fuzzy-based ESS to improve the primary frequency response of the system. While the type-I fuzzy system has been successfully implemented, it is less efficient in handling different power quality threshold requirements and uncertainties. Based on this limitation, the type-II fuzzy offers an extra degree of freedom to model the uncertainties that cannot be quantified by two-dimensional MFs of the type-I fuzzy system [24]. References [25, 26] proposed the type-II fuzzy logic system to mitigate LFC problems in RE-integrated power systems.

Based on the literature, no previous work has reported the development of advanced control strategies for virtual inertia emulation in large power systems with high penetration of RE systems in the deregulated environment. Therefore, the contributions of this paper are: the design of a new type-II fuzzy-based virtual inertia control strategy to improve the frequency response and stability of power systems; the performance of the proposed type-II fuzzy-based virtual inertia controller is improved by tuning its weights with the ABC optimization algorithm, the cost function used in the optimization process is formulated to be model-dependent such that the proposed virtual inertia system does not behave as a continuous infinite energy source; the proposed optimal type-II fuzzy-based virtual inertia control strategy is implemented in the emerging power system environment which considers high RE penetration and deregulation.

The remainder of this paper is structured as follows: Section 2 presents the small-signal modelling of power system for frequency response analysis in the restructured environment, Sect. 3 presents the concept of inertia and the proposed optimized type-II fuzzy logic for inertia emulation, Sect. 4 discusses the simulation results of the proposed control strategy and Sect. 5 presents the conclusion.

2 System Modeling

2.1 Dynamics of Power System Deregulation

In the formulation of the frequency response model of the interconnected power system in the restructured environment, it is important to include the dynamics of the open-energy market scenarios that occur between power vendors–generating companies (GENCOs) and vendees–distribution companies (DISCOs). For an interconnected power system with N control areas, the contract participation matrix (CPM) between GENCOs and DISCOs can be defined as

$$\begin{aligned} \text {CPM}= \left[ \begin{array}{cccc} cpf_{11} &{} cpf_{12} &{} \cdots &{} cpf_{1N} \\ cpf_{21} &{} cpf_{22} &{} \cdots &{} cpf_{2N} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ cpf_{n1} &{} cpf_{n2} &{} \cdots &{} cpf_{nN} \end{array} \right] \end{aligned}$$
(1)

where \(cpf_{nN}\) is the contract participation factor of the nth GENCO of the Nth area. The sum of the elements in each column of the CPM must be equal to 1. Furthermore, there could exist a scenario where there is exchange of power between interconnected areas via tie lines at scheduled values during steady-state operation. In this scenario, the GENCOs in Area i are in a power purchase contract with the DISCOs is Area j; therefore, the non-diagonal elements of the CPM are non-zero. The scheduled tie line power flow to Area i for N interconnected control areas can be written as

$$\begin{aligned} \varDelta P^{sch}_{tie,i} = \sum _{j=1 \atop j \ne i}^{N}\left( \sum _{k=1}^{n} cpf_{kj}\right) \varDelta P_{D_{c,j}} -\sum _{k=1}^{n}\left( \sum _{j=1 \atop j \ne i}^{N} cpf_{jk}\right) \varDelta P_{D_{c,i}} \end{aligned}$$
(2)

where \(\varDelta P_{D_{c,i}}\) and \(\varDelta P_{D_{c,j}}\) are the total power demand (contracted) of DISCOs in Areas \(i \text { and } j\) respectively, given that \(\{ i,\, j\, \in \, N\}\).

2.2 Small-Signal Modelling of Modern Power System

In this subsection, the frequency response model of a modern power system is presented using small-signal derivations. The system model takes into account the deductions from the previous subsection. The frequency response model shown in Fig. 1 represents the small signal derivation of the ith control area of an interconnected power system in the restructured power system environment. The frequency response of Area i resulting from the net active power generation and demand is

$$\begin{aligned} \varDelta {f}_{i} = \frac{1}{2H_{i}s + D_{i}} (\varDelta P_{m_{i}} + \varDelta P_{res_{i}} - \varDelta P_{tie,i} - \varDelta P_{D_{i}}) \end{aligned}$$
(3)

where H is the total inertia constant of the synchronized rotating masses, D is the damping parameter, \(\varDelta P_{m}\) is the total change in mechanical power of the GENCOs, \(\varDelta P_{res}\) is the total change in power of the RE systems, \(\varDelta P_{tie}\) is the change in tie line power flow, and \(\varDelta P_{D}\) is the total load change in Area i.

The change in output mechanical power of the GENCOs in the ith area is given by

$$\begin{aligned} \varDelta P_{m_{i}} = \sum _{j=1}^{n} \varDelta P_{m_{j}} = \sum _{j=1}^{n} \quad \frac{1}{s T_{t_{j}}+1} \varDelta P_{g_{j}} \end{aligned}$$
(4)

where \(T_t\) is the time constant of the turbine and \(\varDelta P_g\) is the change in input setpoint to the turbine, i.e., adjustment of speed governor set point. It is important to note that unlike the traditional power system environment, the dynamics of the speed governor must include a setpoint resulting from power system deregulation (contracted power) [27]. Therefore, the response of the speed governor of the GENCO in the restructured system can be obtained from

$$\begin{aligned} \varDelta P_g = \frac{1}{sT_g + 1} \left( \frac{-1}{R} \varDelta f + \sigma \varDelta P_{lfc} + \varDelta P_c\right) \end{aligned}$$
(5)
Fig. 1.
figure 1

Frequency response model of a power system in the restructured environment.

Full size image

where \(T_g\) is the time constant of the governor, R is droop parameter for primary frequency control, \(\sigma \) is the generator participation index (\(\sigma \in \{0,1\}\) and \(\sum \sigma = 1\)) for the GENCOs in Area i participating in LFC while \(\varDelta P_{lfc}\) is the change in control signal from the secondary frequency controller and \(\varDelta P_c\) is the change in the set point due to deregulation. The \(\varDelta P_{c}\) for the nth GENCO in the Area i can be expressed as

$$\begin{aligned} \varDelta P_{c_{i,n}} = \sum _{i=1}^{N} cpf_{n,i} \varDelta P_{D_{i}} \end{aligned}$$
(6)

The LFC action for the restructured power system is different from the conventional power system because it takes into formulation the scheduled inter-area power flow, \(\varDelta P_{tie}^{sch}\). The LFC action for Area i can be deduced from

$$\begin{aligned} \varDelta P_{lfc,i} = \frac{-K_i}{s} \left( \beta _i \varDelta f_i + \varDelta P_{tie,i}\right) \end{aligned}$$
(7)

where \(K_i\) and \(\beta _i\) are the integral gain of the LFC and frequency bias of Area i respectively, and

$$\begin{aligned} \varDelta P_{tie,i}^{err} = \varDelta P_{tie,i}^{sch} + \varDelta P_{tie,i} \end{aligned}$$
(8)

For the hybrid tie line interconnection considered in this study, inter area power flow to Area i from Area j is given

$$\begin{aligned} \varDelta P_{tie,i} = \left( \frac{2 \pi T_{ij}}{s} + \frac{K_{dc}}{1+s T_{dc}} \right) (\varDelta f_i - \varDelta f_j) \end{aligned}$$
(9)

where \(T_{ij}\) is the synchronizing coefficient of the ac tie line between Areas \(i \text { and } j\), and \(K_{dc}\) and \(T_{dc}\) are the gain and time constant of the dc line between Areas i and j respectively.

With the growing share of RE systems in the modern energy mix, they are to contribute to frequency control according to the grid code specifications. For the ith area in N interconnected control areas, the change in total output power of the RE system resulting from droop control and fluctuation can be derived using

$$\begin{aligned} \varDelta P_{res,i} = \sum _{j=1}^{n} \varDelta P_{res_{j}} = \frac{1}{1+sT_{res_{j}}} \left( \frac{1}{K_{res_{j}}} \varDelta f_i + \varDelta P_{res}^{var} \right) \end{aligned}$$
(10)

where \(T_{res_j}\) is the time constant, \(K_{res_j}\) is the droop parameter and \(\varDelta P_{res}^{var}\) is the variation in output of the RE system. Finally, the change in demand in Area i that impacts the frequency response of the system is the summation of contracted and non-contracted demand can be mathematically expressed as

$$\begin{aligned} \varDelta P_{D_{i}} = \varDelta P_{D_{c,i}} + \varDelta P_{D_{uc,i}} \end{aligned}$$
(11)

The equations derived in (3) to (11) can be used to obtain the state space model for small signal stability analysis. For the ith control area, we can write the state-space model as

(12)

where \(A, \, B, \text { and } C\) are the system, input, and output matrices respectively with appropriate dimensions while X, U are state and input vectors respectively that are given as

(13)

3 Proposed Virtual Inertia Control Strategy

3.1 Virtual Inertia

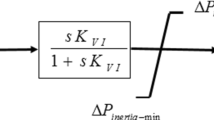
The virtual inertia concept is proposed to emulate the damping and inertia characteristics of conventional synchronous generators, therefore maintaining or increasing the overall inertia of the system. This facilitates the increased penetration of RE systems into the energy mix without compromising the frequency stability of the system. In this work, virtual inertia control as a new ancillary service in which inertia emulation is achieved using the combination of an ESS, power electronic converter, and an appropriate control strategy is proposed. The ESS acts as an inertia unit that injects instantaneous active power into the system to reduce the rate of change of frequency (RoCoF) and frequency deviation. The derivative control strategy is the kernel of the virtual inertia control, it can modify the output of the ESS depending on the RoCoF during a frequency event or disturbance. The block diagram of the derivative-based virtual inertia control is presented in Fig. 2. The output of the ESS is constricted between the minimum and maximum active power rating of the ESS which gives the practical operating condition of the ESS and ensure it does not behave as an infinite energy source. The equation for the dynamic inertia emulation using the derivative control strategy can be derived as:

Fig. 2.
figure 2

Small-signal model of virtual inertia strategy.

Full size image
$$\begin{aligned} \varDelta P_{vi} = H_{vi} \left( \frac{1}{1+ sT_{ess}} \right) \cdot \frac{d(\varDelta f)}{dt} \end{aligned}$$
(14)

where \(\varDelta P_{vi}\) is the virtual power that contributes to the inertia response of the system, \(T_{ess}\) is the time constant of the low pass filter acting as ESS converter, and \(H_{vi}\) is the virtual inertia gain. The choice of \(H_{vi}\) is very important because it significantly affects the response of the virtual inertia controller. Large values of \(H_{vi}\) will repress the frequency deviation with smaller overshoot and undershoot but increase the settling time of the frequency while smaller values of \(H_{vi}\) will quickly restore the frequency of the system but with high oscillation and amplitude of deviation. This makes the conventional virtual inertia control strategy with fixed inertia gain perform poorly under dynamic frequency events. Therefore, this work proposes the application of the type-II fuzzy logic system to calculate the appropriate inertia gain, thus developing an adaptive virtual inertia controller that can perform efficiently and optimally under various operating conditions.

3.2 Type-II Fuzzy Logic System

The control structure has three basic stages: input processing (fuzzification) that converts the crisp input to fuzzy input; an inference engine that determines the fuzzy output based on some complex calculations and rule base; and output processing (type-reduction and defuzzification) that reduces and converts the type-II fuzzy output to crisp output [28]. The type-II fuzzy set (FS) \(\tilde{F}\) where \(l \in L\) and can be characterised as

$$\begin{aligned} \tilde{F}=\left\{ \left( (l, m),\mu _{\tilde{F}}(l,m)\right) |\, \forall \, l \in L, \forall \, m \in J_{l} \subseteq [0,1]\right\} \end{aligned}$$
(15)

where \(\mu _{\tilde{F}}(l,m)\) is a type-II membership function (MF), l is a primary variable, m is the secondary variable in which \(0 \le \mu _{\tilde{F}}(l,m) \le 1\) and \(J_{l}\) is the primary membership of l.

\(\tilde{F}\) can also be expressed as

$$\begin{aligned} \tilde{F}=\int _{l \in L} \int _{m \in J_{l}} \mu _{\tilde{F}}(l, m) /(l, m) \quad J_{l} \subseteq [0,1] \end{aligned}$$
(16)

where \(\int \int \) denotes union over all possible l and m. When there are no uncertainties, the type-II FS reduces to a type-I FS such that the secondary variable becomes \(\mu _{F}(l)\) and \(0\le \mu _{F}(l) \le 1\).

When all \(\mu _{\tilde{F}}(l,m) = 1\), \(\tilde{F}\) is said to be an interval type-II FS [29]. The interval type-II FS reduces (16) to

$$\begin{aligned} \tilde{F}=\int _{l \in L} \int _{m \in J_{l}} 1 /(l, m) \quad J_{l} \subseteq [0,1] \end{aligned}$$
(17)

Due to the uncertainty associated with the interval type-II FS, the boundary of uncertainty in the type-II MF is defined as the footprint of uncertainty (FOU). The outer boundary (\(\overline{\mu }\)) of the FOU is the upper membership function (UMF) and the inner boundary (\(\underline{\mu }\)) is the lower membership function (LMF) so that

$$\begin{aligned} {\text {FOU}}(\tilde{F})=\bigcup _{l \in L} J_{l} \end{aligned}$$
(18)
$$\begin{aligned} \overline{\mu }_{\tilde{F}}(l) \equiv \overline{{\text {FOU}}}(\tilde{F}) \quad \forall \, l \in L \end{aligned}$$
(19)
$$\begin{aligned} \underline{\mu }_{\tilde{F}}(l) \equiv \underline{{\text {FOU}}}(\tilde{F}) \quad \forall \, l \in L \end{aligned}$$
(20)

The rule structure for the type-II fuzzy logic is similar to the type-I fuzzy, for a fuzzy logic structure with a K number of rules, the nth rule can be expressed in the form:

$$\begin{aligned} \begin{aligned} R_{n}:&\text { If } l_{1} \text { is } \tilde{F}_{1,n} \text { and } \ldots l_{i} \text { is } \tilde{F}_{i,n} \ldots \text { and } l_{I} \text { is } \tilde{F}_{I,n} \\&\text { Then }y\text { is } \tilde{Y}_{n} \end{aligned} \end{aligned}$$
(21)

where n = (1, 2, ..., K). This type reduction block maps the type-II FLC into a type-I FLC by computing the centroid of the interval type-II FLC associated with each fired by using

$$\begin{aligned} Y_{\tilde{F}}=1 /\left\{ y_{p}, \ldots , y_{q}\right\} \end{aligned}$$
(22)

where \(y_p \text { and } y_q\) can be calculated using

$$\begin{aligned} y_{p}=\frac{\sum _{i=1}^{Q} y_{i} \bar{\mu }_{\tilde{F}}\left( y_{i}\right) +\sum _{i=P+1}^{N} y_{i} \underline{\mu }_{\tilde{F}}\left( y_{i}\right) }{\sum _{i=1}^{P} \bar{\mu }_{\tilde{F}}\left( y_{i}\right) +\sum _{i=P+1}^{N} \underline{\mu }_{\tilde{F}}\left( y_{i}\right) } \end{aligned}$$
(23)
$$\begin{aligned} y_{q}=\frac{\sum _{i=1}^{Q} y_{i} \underline{\mu }_{\bar{F}}\left( y_{i}\right) +\sum _{i=Q+1}^{N} y_{i} \bar{\mu }_{\tilde{F}}\left( y_{i}\right) }{\sum _{i=1}^{Q} \underline{\mu }_{\bar{F}}\left( y_{i}\right) +\sum _{i=Q+1}^{N} \bar{\mu }_{\bar{F}}\left( y_{i}\right) } \end{aligned}$$
(24)

The switching point P and Q in (23) and (24) are iteratively determined using the Karnik-Mendel (KM) algorithm [30]. The crisp output y is computed by the defuzzifier using

$$\begin{aligned} y(\mathbf {x})=\frac{1}{2}\left[ y_{p}(l)+y_{q}(l)\right] \end{aligned}$$
(25)
Fig. 3.
figure 3

Proposed virtual inertia control strategy.

Full size image

3.3 Adaptive Virtual Inertia Based on Type-II Fuzzy Logic Control

In this subsection, the proposed virtual inertia control method based on the type-II fuzzy system is developed as shown in Fig. 3. The inputs to the type-II fuzzy logic system are the frequency deviation, \(\varDelta f\) and its derivative, . These inputs are firstly normalized with the weights \(W_1\) and \(W_2\) respectively so that the final inputs to the type-II fuzzy logic system are

$$\begin{aligned} \text {Input } 1 = W_1 \cdot \varDelta f \end{aligned}$$
(26)
(27)
Table 1. Fuzzy rule table
Full size table

The normalized inputs are then fuzzified using the membership functions. In this work, the triangular membership function is used because of its ease of computation, few design parameters, and less complexity in practical realization when compared to other types of membership functions. Due to these reasons, seven triangular membership functions are chosen to define the universe of discourse of the type-II fuzzy system. They are defined using the linguistic variables: Negative Big (NB), Negative Medium (NM), Negative Small (NS), Zero (Z), Positive Small (PS), Positive Medium (PM), and Positive Big (PB). The corresponding membership parameters of the seven linguistic variables are determined from (23) and (24). The fuzzified inputs which are the embedded fuzzy sets within the FOU are processed in the inference engine to generate appropriate fuzzy outputs with the aid of the fuzzy rules given in Table 1. The inference engine uses the min and max methods for the Meet and Join operations respectively. The Meet and Join operations map the fuzzified inputs into fuzzy outputs with the strength of the fired rule(s). The output of the inference engine is a type-II fuzzy set that cannot be directly converted to the crisp output, that is, virtual inertia gain. The type-reducer is used to convert the type-II fuzzy set to type-I fuzzy set using the KM algorithm, the smallest and largest centroids are computed using (23) and (24). The type-I fuzzy output is then converted to the normalized virtual inertia gain using (25). The normalized virtual inertia gain is scaled with weight \(W_3\) to generate the actual inertia gain, \(H_{vi}\). The values of the input and output weights (\(W_1,\, W_2,\, W_3\)) are critical in the design and performance of the fuzzy logic system for the proposed application; therefore, the ABC optimization algorithm is employed to determine their values. Due to space limitation, detail of the ABC can be accessed in [14]. The cost function used in the optimization process is a two-fold objective function that computes the derivative of the frequency deviation and absolute frequency deviation. For the ith control area with virtual inertia capability, the cost function can be formulated as

$$\begin{aligned} C_{f_{i}} = \sum ^{T}_{n=1}\left( |\varDelta f_i(n)|^2 +\frac{|\varDelta f_i(n)- \varDelta f_i(n-1)|}{t} \right) \end{aligned}$$
(28)

where t is the time between the actual present and previous frequency measurement. It is specified as the sample time of the controller. The values of the weights for the type-II fuzzy controller are presented in Table ??. The proposed optimized type-II fuzzy-based virtual inertia control system can recalculate the inertia gain to track the frequency to a zero steady-state value. Therefore, frequency deviation in Area i given in (3) can be written as

$$\begin{aligned} \varDelta {f}_{i} = \frac{1}{2H_{i}s + D_{i}} \times (\varDelta P_{m_{i}} + \varDelta P_{res_{i}} - \varDelta P_{tie,i} - \varDelta P_{D_{i}} + \varDelta P_{vi}) \end{aligned}$$
(29)

4 Simulation and Discussion

In this section, the efficiency of the proposed type-II fuzzy-based virtual inertia controller is validated through extensive simulation in MATLAB. The test system for the simulation is the conventional two-area power system model that is used for frequency stability studies [31]. The model is updated to include the dynamics of modern power systems such as hybrid tie line transmission, power system deregulation, and unequal area capacities. In Area 2 of the test system, one of the conventional plants has been replaced with a RE system to simulate high penetration of RE and reduced equivalent inertia; therefore, the proposed virtual inertia strategy is implemented in Area 2 and its robustness is evaluated against the conventional and type-I fuzzy-based virtual inertia methods proposed in [32] and [22] respectively, it is important to mention that the two methods in the literature were redeveloped to satisfactorily fit the system used in this work.

4.1 Eigenvalue Analysis

In this section, the stability of the test system is analyzed by inspecting the properties of its eigenvalues. For a system to be stable, all the real parts of its eigenvalues have to be negative (on the left half of the complex s-plane).

Table 2. Eigenvalues of system model
Full size table

In Table 2, the eigenvalues of the test system are presented, it can be observed that all the eigenvalues have a negative real part, therefore, indicating an asymptotically stable system. It can be seen that the modes \(\lambda _1\) and \(\lambda _2\) which corresponds to \(\varDelta f_1\) and \(\varDelta f_2\) respectively are in a better region of stability with high magnitudes in the real parts of their eigenvalues. The complex modes of the eigenvalues (\(\lambda _{4-7} \text { and } \lambda _{10,11}\)) indicate that the system will oscillate before reaching steady-state during small perturbations.

4.2 Load Variation

In this scenario, the effectiveness of the proposed virtual inertia control strategy is demonstrated. A step load change of \(\varDelta P_{D_{uc}}\,= \, 0.1\)p.u in Area 2 at 10 s is simulated to illustrate the frequency response of the system during load variation. Figure 4(a) and (b) show the frequency deviation and derivative of frequency deviation in Area 2 under this contingency.

Fig. 4.
figure 4

(a) Frequency deviation in Area 2 (b) rate of change of frequency deviation in Area 2 under step load variation.

Full size image
Fig. 5.
figure 5

Frequency deviation in Area 1 under step load variation in Area 2.

Full size image

Generally, it can be observed that the frequency response of Area 2 is improved when the virtual inertia control is incorporated into the system compared to the absence of virtual inertia in the system. More specifically, the proposed type-II fuzzy-based virtual inertia control method outperforms the type-I fuzzy-based and conventional virtual inertia control methods with the least amplitude of frequency deviation, transient excursions, and fastest recovery of the derivative of frequency deviation with damped oscillations and minimal overshoots. The performance of the proposed type-II fuzzy virtual inertia control strategy can be demonstrated by observing the change in active power of the ESS \(\varDelta P_{vi}\), as shown in Fig. 6. It can be seen that with the proposed virtual inertia strategy, the ESS is capable of injecting high instantaneous active power needed to suppress the frequency deviation when compared to other virtual inertia control methods. It is important to mention that virtual inertia elements are zero net energy devices during steady-state operation, this criteria must the considered in the design of the intelligent control systems to implement virtual inertia devices such that they do not become an infinite energy source. Due to the interconnection that exists between Areas 1 and 2, it is consequential that the perturbations in Area 2 affect Area 1 and vice versa. Therefore, it is important to observe the frequency response of Area 1 due to the contingency in Area 2 for this scenario as shown in Fig. 5. It can be observed while the presence of virtual inertia in Area 2 helps to reduce the frequency deviation amplitudes and oscillations, the proposed type-II fuzzy-based virtual inertia achieved the least amplitude of frequency deviation with a smooth transition to zero steady-state deviation.

Fig. 6.
figure 6

Output power of ESS under step load variation.

Full size image

4.3 High Renewable Energy Fluctuation

In this scenario, a more severe contingency is considered to show the robustness of the proposed virtual inertia control strategy. With the high penetration of RE systems, it is practical that the overall systems inertia and damping characteristics are affected, and with the high fluctuation of the RE sources, the frequency response of the system can be significantly affected.

Fig. 7.
figure 7

Net fluctuation of RE power in Area 2.

Full size image

The high RE fluctuation in Area 2 as shown in Fig. 7 is used to replicate this contingency, and Figs. 8 and 9 show the behaviour under this contingency. From Fig. 8(a), it is shown that the frequency deviation in Area 2 fluctuates above and below zero steady-state due to the nature of the disturbance. It shows that the proposed type-II fuzzy-based virtual inertia control strategy has the least amplitude of frequency deviation when compared to the type-I fuzzy-based and conventional virtual inertia control strategies. The derivative of the frequency deviation shown in Fig. 8(b) shows the effectiveness of the proposed type-II fuzzy-based virtual inertia strategy in achieving faster response to keep the rate of change of frequency deviation within zero with the lowest transient excursion. This good frequency response is a result of the rapid absorption/charging (negative \(\varDelta P_{vi}\)) and injection/discharging (positive \(\varDelta P_{vi}\)) by the ESS as shown in Fig. 9(a). It shows that the proposed type-II fuzzy-based virtual inertia control strategy can efficiently adjust the virtual inertia gain, \(H_{vi}\), to varying values as a function of the system contingency. The adjustment of the virtual inertia gain can be seen in Fig. 9(b). While the conventional virtual inertia control strategy has a fixed gain and the type-I fuzzy-based virtual inertia control strategy adjusts the virtual inertia gain around the fixed inertia gain, the proposed type-II fuzzy-based virtual inertia strategy can adjust the virtual inertia gain to values that improve the frequency response and stability of the system.

Fig. 8.
figure 8

(a) Frequency deviation in Area 2 (b) rate of change of frequency deviation in Area 2 under RE fluctuation.

Full size image

4.4 Parameter Variation

In system design, inaccurate parameter estimations, the variation of system parameters with time, and the removal of some systems components can reduce the efficient performance of the system practically. Therefore, it is important to test the robustness of the control systems during design with parameter variations. In this scenario, the robustness of the proposed type-II fuzzy-based virtual inertia control strategy is tested by simulating the contingencies in Sect. 4.2 and 4.3 under these parameter variations in Area 2: \(R_3 = -30\%\), \(D_2 = -50\%\), \(H_2 = -50\%\), \(T_t = +25\%\), \(T_g = + 20\%\), \(K_2 = -30\%\), and \(\beta _2 = +25\%\). It can be observed from Fig. 10(a) that with the absence of virtual inertia, there is serious frequency deviation with high oscillations. With the conventional and type-I fuzzy-based virtual inertia control strategies, the frequency dip is improved by 32% and 30% respectively with noticeable oscillations. However, the application of the proposed type-II fuzzy-based virtual inertia control strategy significantly improves the frequency dip by approximately 70% with damped oscillations. Furthermore, the rate of change of frequency deviation rapidly settles to zero with the proposed virtual inertia strategy when compared to other virtual inertia control strategies as seen in Fig. 10(b). The improved performance in the frequency response is due to the adaptive property of the type-II fuzzy controller in selecting the virtual inertia gains as shown in Fig. 11(b) which helps to dynamically adjust the output active power of the ESS as shown in Fig. 11(a) when compared to the conventional and type-I fuzzy-based virtual inertia control strategies. It is shown that the proposed type-II fuzzy-based virtual inertia control strategy is robust so that it efficiently performs during parameter variations and maintains the frequency stability of the system in severe scenarios.

Fig. 9.
figure 9

(a) Output power of ESS (b) Virtual inertia gain under RE fluctuation.

Full size image
Fig. 10.
figure 10

(a) Frequency deviation in Area 2 (b) rate of change of frequency deviation in Area 2 under parametric variation.

Full size image
Fig. 11.
figure 11

(a) Output power of ESS (b) Virtual inertia gain under parametric variation.

Full size image

From the results presented in the section, it can be appreciated that a properly designed conventional virtual inertia control strategy can perform as relatively efficiently as the type-I fuzzy-based virtual inertia control strategy; however, the proposed type-II fuzzy-based virtual inertia control strategy significantly outperforms both control strategies.

5 Conclusion

This paper presents a new virtual inertia control system using a type-II fuzzy logic control strategy. The proposed virtual inertia control strategy is used in the control loop of a dedicated ESS to improve the frequency response of a system with a high penetration of renewable energy sources in a restructured power system environment. The ABC optimization algorithm is utilized to tune the weights of the proposed controller to improve its performance. The robustness of the proposed controller is assessed under several operating scenarios and compared with the type-I fuzzy and conventional virtual inertia control strategies. The simulation results show the effectiveness of the proposed strategy to improve the frequency response of the system, thereby enhancing its stability and resilience.