Keywords

1 Introduction

The index rainfall (IR) is a variable defined as a central tendency (mean or median of series of values of rainfall), which poses a real problem as to its estimation in ungauged regions, using growth curves resulting from a regional frequency analysis such as L-moments for example in [1].

Also, This IR is useful when it comes to evaluating the probable maximum precipitation by methods derived from the general formulation of Chow [2,3,4,5], which are providing a valuable tool for the hydrologic design of hydraulic structures. The procedure developed by Hershfield [3, 4] and later modified by Hershfield [5] is based on the general frequency equation of Chow [2]. This technique requires a series of maximum annual daily rainfall measurements at a particular observation point as the input data [6].

The IR is still considered a basic means in the rainfall-runoff transfer process [7]. Several models (Crupedix, Sogreah, and Socose) should be listed since they are applied in Algeria; for more details refer to [8]. All these methods are a useful tool used in the hydraulic design of flood protection infrastructures and flood risk management [9, 10].

The present contribution aims to model the index rainfall (IR) in Cheliff watershed (Algeria) using: (i) exclusively the mean annual precipitation as predictor in the simple linear model of Body [11]. (ii) the combination of the geographical coordinates with the mean annual precipitation as the predictors and (iii) exclusively the geographical coordinates of the measurement stations as predictors. So, we will explore in the two later models, the predictive capabilities of the rule-based technique named Cubist model (which is an improvement of the M5Trees model).

In Algeria, this aspect of the study has not been supported by published studies excepted for the document of Body [11]. In this document, the author uses the isohyets of the mean annual rainfall provided by the maps of Chaumont and Paquin [12], which explain the spatial distribution of the IR through three regional formulations of simple linear regression. These three relationships applicable in (Algeria: east, west, and Sahara) were based on series of rainfall measurements for the period (1913–1963).

2 Material and Methods

2.1 Study Area

The hydrographic basin named Cheliff is located in the northwest of Algeria country. It is limited between geographic coordinates 0.36° and 3.36° of longitude East and 34.49° and 36.38° of latitude North (Fig. 76.1, Table 76.1). It is coded (01) among (17) other watersheds, and it covers the area of 43,750 km2. It is considered the largest basins in the country. The climate type is the semi-arid Mediterranean with warm summers and cold winters. The precipitations have a large variability with a trend of decrease from north to south and from east to west. The mean annual precipitation ranges from 153.80 to 599.50 mm (Table 76.1).

Fig. 76.1
A location map highlights the rain gauge stations Cheliff watershed. It also depicts the areas of watershed limit.

Location of rain gauge stations

Full size image
Table 76.1 Summary of 5 attributes in the 75 rain gauge stations in Cheliff watershed
Full size table

2.2 Data Description

The first analysis of the dataset revealed that there are 92 rain gauge stations, with maximum daily rainfall records in the Cheliff watershed. However, some stations only have short records. To satisfy statistical requirements, we selected the stations with at least 20 years of records. Finally, according to this principle, 75 rain gauge stations were chosen with an average length of 48 years. All the stations, numbered from 1 to 75, are located at various places throughout the study area (Cheliff basin), as shown in Fig. 76.1. All data set used in the present study are provided by National Agency for Water Resources. (NAWR); in French: Agence Nationale des Ressources Hydrauliques [7].

The relationship between the index rainfall (IR) and the predictors is shown by the correlation matrix plot (Fig. 76.2), which is the pairwise relationship between two variables with corresponding correlation coefficients for each indicator. The correlations and histograms for a data matrix are given in Fig. 76.2.

Fig. 76.2
A correlation matrix plot illustrates, the relationship between Index rainfall and the predictors. It depicts the corresponding correlation coefficients for each indicator.

Correlations and histograms for a data matrix (all data: 75 cases)

Full size image

2.3 Methodology

2.3.1 Simple Linear Regression

The simple linear regression (SLR) estimates the index rainfall IR as a linear function of one predictor (X) and written: \( IR = a_{0} + bX\); where a0 and b are the linear coefficients for the SLR. The coefficients are estimated using the well-known least square method.

In Algeria, this aspect of the study has been maintained in the document of Body [11], in which the author uses the isohyets of the mean annual precipitation (MAP) from the maps of Chaumont and Paquin [12] to explain the spatial distribution of the index rainfall (IR) through three regional relations of simple linear regression. These three relationships applicable in (Algeria: East, West, and Sahara) were based on series of rainfall measurements for the period (1913–1963) [11]. The Cheliff watershed is concerned by the first relation written as:

$$ IR = 0.0525*MAP + 18.6 $$
(76.1)

2.3.2 Cubist Model

Rule-based models consist of one or more crossed if/then conditions for the predictors that divider the data [13]. Within these dividers, a model is used to forecast the response [13].

Cubist is a rule-based model that is an extension of Quinlan’s M5 model tree [14]. These models are based on the predictors used in previous splits. Also, there are intermediate linear models at each step of the tree. The modern version of model rules was called Cubist. There were small technical differences between Cubist and M5 rules enumerated in Kuhn and Johnson [13], “but the main improvements were: (i) an ensemble method for predictions called committees, and (ii) a nearest-neighbor adjustment that occurs after the model predictions” [13].

2.3.3 Cross Validation

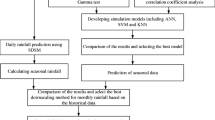
Performances of both models with best parameters, were evaluated through a leave-one-out cross-validation approach (LOOCV). We used the covariates of 70% of all data to perform cross-validation and determine the best parameters. Then, the final models were built using the best parameters. Finally, the covariates of 30% of the remaining data were applied to the models to predict index rainfall.

The LOOCV is a particular case of K-fold cross-validation (K = n = length of the sample equal to 75 cases), which is one of the most commonly used methods of evaluating the predictive performances [15].

2.3.4 Accuracy Assessment

There is no single statistic that captures all aspects of interest [16, 17]. For this reason, it is useful to consider important performance statistics. In the following definitions, Oi represents the ith observed value and Mi represents the ith modelled value for a total of n observations. Om and Mm are the average values of Oi and Mi. The accuracy of the predictions was assessed using some evaluation indices such as Correlation Coefficient (R), Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE). The expressions and the brief explanations for these metrics are given below.

2.3.4.1 Correlation Coefficient (R)

The (Pearson) correlation coefficient (R) measures the strength of the linear and the agreement between observed and predicted (modelled) samples, i.e., how close the model predictions fall along a 45-degree line from the origin to the observed data.

$$ R = \frac{{\frac{1}{n}\mathop \sum \nolimits_{i}^{n} (O_{i} - O_{m} )(M_{i} - M_{m} )}}{{\sqrt {\frac{1}{n}\mathop \sum \nolimits_{i = 1}^{n} (O_{i} - O_{m} )^{2} } \sqrt {\frac{1}{n}\mathop \sum \nolimits_{i = 1}^{n} (M_{i} - M_{m} )^{2} } }}. $$
(76.2)
2.3.4.2 Root Mean Squared Error (RMSE)

The RMSE is a commonly statistic used that provides a good overall measure of how close modelled (predicted) values are to observed values.

$$ RMSE = \left( {\frac{{\mathop \sum \nolimits_{i = 1}^{n} (M_{i} - O_{i} )^{2} }}{n}} \right)^{1/2} $$
(76.3)

2.3.5 Mean Absolute Error (MAE)

The MAE is the average absolute difference of the estimated (predicted) value from the reference (observed).

$$ MAE = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left| {M_{i} - O_{i} } \right|}}{n} $$
(76.4)

3 Material and Methods

In the presented study, the proposed models were: (i) SLR, (ii) Cubist. All data processing in this study was performed using R software and Excel of Microsoft.

3.1 Results and Hyperparameters Tuning

In the process of the rule-based regression of the Cubist models and of the simple linear regression, an approximate function is determined to predict the value of the output. First, the datasets are randomly separated to a training set and a test set. In this contribution, approximately 70% (54 cases) of the available data (75 cases) were randomly chosen to establish the training phase. While, 30% (21 cases) of the available data were used for testing purpose. The test set was used to evaluate the accuracy of the function and estimate the performance of the adopted models. The input parameters (longitude (Lon), latitude (Lat), altitude (Alt), and mean annual precipitation (MAP)) in the Cubist models are the variables that affect the prediction target (index rainfall (IR)). For the Simple Linear Regression, the relation (76.1) of Body [11] is evaluated to predict the same target (IR), using Excel software.

In the application of Cubist experiments, the caret package in R [18] was utilized to build a rule-based regression model. The Cubist regression model, which has two tweaking parameters that can be fine-tuned; neighbors and committees, the tuning parameters are established as follows: the optimum hyper-parameter committees is selected in the range of [1:100] incrementing one at a time and the optimum hyper-parameter neighbors are selected in the range of [0:9] incrementing one at a time. To tune the Cubist model over different values of neighbors and committees, the train function in the caret package [18] can be employed to optimize the previously mentioned parameters. A smaller value of RMSE indicates better optimization results of the Cubist models. The relationship between committees and neighbors is shown in Figs. 76.3 and 76.4. The finally determined values for the Cubist models (Figs. 76.3 and 76.4) are: committees = 1 and 89; neighbors = 5 and 9 in the models with and without introducing MAP as predictor, respectively.

Fig. 76.3
A graph illustrates the RMSE leave-out cross-validation, for committees from 0 to 100. It determines the optimal turning parameters of the cubist model with the MAP predictor.

Leave one out cross-validated RMSE profiles for determining the optimal tuning parameters of Cubist model with MAP predictor

Full size image
Fig. 76.4
A graph illustrates the RMSE leave-out cross-validation, for committees from 0 to 100. It determines the optimal turning parameters of the cubist model without the MAP predictor.

Leave one out cross-validated RMSE profiles for determining the optimal tuning parameters of Cubist model without MAP predictor

Full size image

The tuned hyperparameters, the R packages, the functions and the ranges of parameters for both models are summarized in the Table 76.2.

Table 76.2 Hyperparameters tuned in the cubist models with and without MAP as predictor
Full size table

3.2 Results of the Test Set

To confirm the predictive models based on the predicted and observed values, 21 testing cases were validated by the Simple Linear Regression (SLR) and two Cubist models. Figures 76.5, 76.6 and 76.7 and Table 76.3 illustrate the results. Figures 76.5, 76.6 and 76.7 show the observed versus predicted index rainfall by SLR and the Cubist models using test data. In Table 76.3, The R, RMSE and MAE of the SLR for 21 sets of testing data are 0.820, 6.045 mm and 4.582 mm, respectively. The R, RMSE and MAE of the first Cubist model (with introducing MAP variable as predictor) for 21 sets of testing data are 0.842, 4.860 mm and 3.934 mm, respectively.

Fig. 76.5
A graph illustrates, the predicted Index rainfall, with, observed Index rainfall by the linear regression model in the testing phase

Observed versus predicted index rainfall by linear regression model of body [11]; in the testing phase (perfect line in green color)

Full size image
Fig. 76.6
A graph illustrates the predicted Index rainfall, with observed Index rainfall, for the cubist model in the testing phase with MAP as a predictor.

Observed versus predicted index rainfall by cubist model (with introducing MAP as predictor) in the testing phase (perfect line in green color)

Full size image
Fig. 76.7
A graph illustrates the predicted Index rainfall, with observed Index rainfall, for the cubist model in the testing phase without MAP as a predictor.

Observed versus predicted index rainfall by Cubist model (without introducing MAP as predictor) in the testing phase (perfect line in green color)

Full size image
Table 76.3 The performance of different prediction models for test data
Full size table

While, the R, RMSE and MAE of the second Cubist model (without introducing MAP variable as predictor) for 21 sets of testing data are 0.760, 5.643 mm and 3.709 mm, respectively.

The performance has been assessed by the SLR model and the two of Cubist modeling approaches. In case of the gauged regions and the availability of precipitation data like annual values, the SLR and the first Cubist model are required to predict the index rainfall. Nevertheless, the second Cubist model is recommended in case of the ungauged regions, without losing much performance.

4 Conclusion

This work surveys the ability of the simple linear regression and the Cubist rule-based regression techniques for estimating the index rainfall. It demonstrates the relevance of the idea, which investigates the use of geographical information of rain gauge stations as the predictors. The study concluded that the SLR approach is more suitable for predicting the index rainfall in gauged regions. However, the Cubist model can be an acceptable alternative way using only the geographic predictors to predict the index rainfall in ungauged regions.