Keywords

1 Introduction

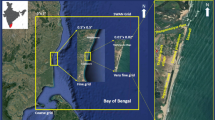
Cat Hai is a small island with one side is adjacent to the sea and the other 3 sides are bordered by estuaries and canals (Fig. 1). The area from Ben Got to Hoang Chau is directly influenced by waves from sea side, which is one of the factors that directly affect the accretion, erosion and inundation of the area [1]. There were some studies on wave fields in Cat Hai island area few year ago [2, 3]. However, from 2018 up to now, there are two container ports has been built and operating in Cat Hai island. In addition, there is a 10 km long dike under construction in the island and the Vinfast car factory encroached the sea, the furthest place nearly 1 km which is obviously changing the coastline in the island (see Fig. 2). Currently, there is no study on the effects of this new construction on the local wave field from Ben Got to Hoang Chau. Meanwhile, the population density is very dense behind this dike area.

Nowadays, with the development of science and technology, numerical models have become an indispensable tool for forecasting the coastal wave field. The models mentioned here: Bouss-2D model in the SMS model set [4, 5], MIKE 21 model in MIKE model set [6, 7], D-WAVE model (SWAN) in the model set DELFT 3D model [8, 9], model EFDC [10], model STWAVE in CEDAS model set [11, 12]. Bouss-2D model is a modern and powerful model in calculating the wave field in the coastal area and has not been applied in Vietnam. This study is going to use the Bouss-2D model to calculate the wave field in the Cat Hai island area for the cases with and without the new constructions/dikes to assess the impact of constructions/dikes on the wave field from Ben Got to Hoang Chau.

Fig. 1.
figure 1

Image of Cat Hai island location taken in August 2014.

Full size image
Fig. 2.
figure 2

Construction image of Cat Hai island taken in May 2019.

Full size image

2 Methodology

2.1 Theoretical Description

BOUSS-2D is based on Boussinesq-type equations derived by Nwogu [13, 14]. The equations are depth-integrated equations for the conservation of mass and momentum for nonlinear waves propagating in shallow and intermediate water depths. For short-period waves, the horizontal velocities are no longer uniform over depth and the pressure is non-hydrostatic. The vertical profile of the flow field is obtained by expanding the velocity potential, Φ, as a Taylor series about an arbitrary elevation; \({z}_{\alpha }\), in the water column. For waves with length, L, much longer than the water depth, h, the series is truncated at second order resulting in a quadratic variation of the velocity potential over depth (See Eq. 1).

$$\Phi (x,z,t)={\phi }_{\alpha }+{\mu }^{2}({z}_{\alpha }-z)[\nabla {\phi }_{\alpha }.\nabla h]+\frac{{\mu }^{2}}{2}\left[({z}_{\alpha }+h{)}^{2}-(z+h{)}^{2}\right]{\nabla }^{2}{\phi }_{\alpha }+{\rm O}({\mu }^{4})$$
(1)

Where \({\phi }_{a}=\Phi (x,{z}_{\alpha },t),\nabla =(\partial /{\partial }_{x},\partial /{\partial }_{y}),\mu =h/L\) is a measure of frequency dispersion. The horizontal and vertical velocities are obtained from the velocity potential as.

$$\begin{aligned} u(x,z,t)&=\nabla \Phi ={u}_{\alpha }+({z}_{\alpha }-z)[\nabla ({u}_{\alpha }.\nabla h)+(\nabla .{u}_{\alpha })\nabla h]\\&\quad +\frac{1}{2}\left[({z}_{\alpha }+h{)}^{2}-(z+h{)}^{2}\right]\nabla (\nabla .{u}_{\alpha })\end{aligned}$$
(2)
$$w(x,z,t)=\frac{\partial \Phi }{\partial z}=-[{u}_{\alpha }.\nabla h+(z+h)\nabla .{u}_{\alpha }]$$
(3)

Where \({u}_{a}=\nabla \Phi {|}_{{z}_{\alpha }}\) is the horizontal velocity at \(z={z}_{\alpha }\). Given a vertical profile for the flow field, the continuity and Euler (momentum) equations can be integrated over depth, reducing the three-dimensional problem to two dimensions. For weakly nonlinear waves with height, H, much smaller than the water depth, h, the vertically integrated equations are written in terms of the water-surface elevation \(\eta (x,t)\) and velocity \({u}_{\alpha }(x,t)\) as;

$${\eta }_{t}+\nabla .{u}_{f}=0$$
(4)
$$\begin{aligned} &{u}_{\alpha ,t}+g\nabla \eta +({u}_{\alpha }.\nabla ){u}_{\alpha }+{z}_{\alpha }\left[\nabla ({u}_{\alpha ,t}.\nabla h)+(\nabla .{u}_{\alpha ,t})\nabla h\right]\\ &\quad +\frac{1}{2}\left[({z}_{\alpha }+h{)}^{2}-{h}^{2}\right]\nabla (\nabla .{u}_{\alpha ,t})=0 \end{aligned}$$
(5)

where \({u}_{f}\) is the volume flux density given by:

$$\begin{aligned} {u}_{f}&={\int }_{-h}^{\eta }udz=(h+\eta ){u}_{\alpha }+h\left({z}_{\alpha }+\frac{h}{2}\right)[\nabla ({u}_{\alpha }.\nabla h)+(\nabla .{u}_{\alpha })\nabla h]\\ & \quad +h\left[\frac{({z}_{\alpha }+h{)}^{2}}{2}-\frac{{h}^{2}}{6}\right]\nabla (\nabla .{u}_{\alpha })\end{aligned}$$
(6)

The depth-integrated equations are able to describe the propagation and transformation of irregular multidirectional waves over water of variable depth. The elevation of the velocity variable \({z}_{\alpha }\) is a free parameter and is chosen to minimize the differences between the linear dispersion characteristics of the model and the exact dispersion relation for small amplitude waves. The optimal value, \({z}_{\alpha }=-0.535h\), is close to middepth.

For near-rupture waves in shallow water, the small nonlinear wave hypotheses are no longer correct. Nwogu [14] further developed these systems of nonlinear equations by presenting nonlinear components as a function of velocity on the free surface. These systems of nonlinear equations are written as follows;

$${\eta }_{t}+\nabla .{u}_{f}=0$$
(7)
$$\begin{aligned}& {u}_{\alpha ,t}+g\nabla \eta +({u}_{\eta }.\nabla ){u}_{\eta }+{w}_{\eta }\nabla {w}_{\eta }+({z}_{\alpha }-\eta )\left[\nabla ({u}_{\alpha ,t}.\nabla h)+(\nabla .{u}_{\alpha ,t})\nabla h\right]\\ & \quad +\frac{1}{2}\left[({z}_{\alpha }+h{)}^{2}-(h+\eta {)}^{2}\right]\nabla (\nabla .{u}_{\alpha ,t})-\left[({u}_{\alpha ,t}.\nabla h)+(h+\eta )\nabla .{u}_{\alpha ,t}\right]\nabla \eta\\&\quad +\left[\nabla ({u}_{\alpha ,t}.\nabla h)+(\nabla .{u}_{\alpha ,t})\nabla h+({z}_{\alpha }+h)\nabla (\nabla .{u}_{\alpha })\right]{z}_{\alpha ,t}=0 \end{aligned}$$
(8)

where, \({z}_{\alpha }\) is now a function of time and is given by \({z}_{\alpha }+h=0.465(h+\eta )\). The volume flux density is given by;

$$\begin{aligned} {u}_{f}&=(h+\eta )\left\{{u}_{\alpha }+\left[({z}_{\alpha }+h)-\frac{(h+\eta )}{2}\right][\nabla ({u}_{\alpha }.\nabla h)+(\nabla .{u}_{\alpha })\nabla h]\right.\\ &\quad \left. +\left[\frac{({z}_{\alpha }+h{)}^{2}}{2}-\frac{(h+\eta {)}^{2}}{6}\right]\nabla (\nabla .{u}_{\alpha })\right\}\end{aligned}$$
(9)

The fully nonlinear equations are able to implicitly model the effects of wave-current interaction. Currents can either be introduced through the boundaries or by explicitly specifying a current field, U.

Fig. 3.
figure 3

Computational grid for finite difference scheme.

Full size image

The weakly and fully nonlinear Boussinesq equations are solved in the time-domain using a finite-difference method. The computational domain is discretized as a rectangular grid with grid sizes Δx and Δy, in the x and y directions, respectively. The equation variables \(\eta ,{u}_{\alpha },{\nu }_{\alpha }\) are defined at the grid points in a staggered manner as shown in Fig. 3. The water depth and surface elevation are defined at grid points (i, j), while the velocities are defined half a grid point on either side of the elevation grid points (Fig. 3).

The numerical solution scheme is an implicit Crank-Nicolson scheme with a predictor-corrector method used to provide the initial estimate. The first step in the solution scheme is the predictor step in which values of the variables at an intermediate time-step \(t=(n+1/2)\Delta t\) are determined using known values at \(t=n\Delta t\) (Δt is the time-step size). The second step is the corrector step in which predicted values \(t=(n+1/2)\Delta t\) are used to provide an initial estimate of the values at \(t=(n+1)\Delta t\). The last step is an iterative Crank-Nicolson scheme, which is repeated until convergence.

The resulting Crank-Nicolson formulation for the weakly nonlinear form of the mass and momentum equations can be written as:

$${\delta }_{t}\eta =-{\delta }_{x}^{(1)}{u}_{f}^{n+1/2}-{\delta }_{y}^{(1)}{\nu }_{f}^{n+1/2}$$
(10)
$$\begin{aligned} &{\delta }_{t}({u}_{\alpha }+{f}_{4}{\delta }_{x}^{(2)}{u}_{\alpha }+{f}_{2}{\delta }_{xx}{u}_{\alpha })=-g{\delta }_{x}^{(1)}{\eta }^{n+1/2}-\frac{1}{2}{\delta }_{x}^{(1)}\left[{\left({\overline{{u}_{\alpha }^{n+1/2}}}^{x}\right)}^{2}\right]\\& \quad -{\delta }_{y}^{(1)}\left({\overline{{\nu }_{\alpha }^{n+1/2}}}^{x}{\overline{{u}_{\alpha }^{n+1/2}}}^{y}\right)-{f}_{4}\left[{\delta }_{y}^{(1)}(h){\delta }_{t}{\delta }_{x}^{(1)}\left({\overline{{\nu }_{\alpha }^{n+1/2}}}^{y}\right)+{\delta }_{x}^{(1)}(h){\delta }_{t}{\delta }_{y}^{(1)}\left({\overline{{\nu }_{\alpha }^{n+1/2}}}^{x}\right)\right]-{f}_{2}{\delta }_{t}{\delta }_{xy}{\nu }_{\alpha }^{n+1/2}\end{aligned}$$
(11)
$$\begin{aligned} &{\delta }_{t}({\nu }_{\alpha }+{f}_{4}{\delta }_{y}^{(2)}{\nu }_{\alpha }+{f}_{2}{\delta }_{yy}{\nu }_{\alpha })=-g{\delta }_{y}^{(1)}{\eta }^{n+1/2}-\frac{1}{2}{\delta }_{y}^{(1)}\left[{\left({\overline{{\nu }_{\alpha }^{n+1/2}}}^{y}\right)}^{2}\right]\\ &\quad -{\delta }_{x}^{(1)}\left({\overline{{\nu }_{\alpha }^{n+1/2}}}^{x}{\overline{{u}_{\alpha }^{n+1/2}}}^{y}\right)-{f}_{4}\left[{\delta }_{y}^{(1)}(h){\delta }_{t}{\delta }_{x}^{(1)}\left({\overline{{u}_{\alpha }^{n+1/2}}}^{y}\right)+{\delta }_{x}^{(1)}(h){\delta }_{t}{\delta }_{y}^{(1)}\left({\overline{{u}_{\alpha }^{n+1/2}}}^{x}\right)\right]-{f}_{2}{\delta }_{t}{\delta }_{xy}{u}_{\alpha }^{n+1/2}\end{aligned}$$
(12)

To solve the governing equations, appropriate boundary conditions have to be imposed at the boundaries of the computational domain. The types of boundaries considered in BOUSS-2D include:

Fully reflecting or solid wall boundaries: Along solid wall or fully reflecting boundaries, the horizontal velocity normal to the boundary must be zero over the entire water depth, i.e.,

$$u.n=0-h<z<\eta$$
(13)

External wave generation boundaries: Along external wave generation boundaries, time-histories of velocities \({u}_{\alpha }\) or \({\nu }_{\alpha }\), and flux densities \({u}_{f}\) or \({\nu }_{f}\) corresponding to an incident storm condition are specified. The time-histories may correspond to regular or irregular, unidirectional or multidirectional waves.

Internal wave generation boundaries: in BOUSS-2D with the governing equations modified to allow for the generation of waves inside the computational domain and absorb reflected waves in a damping layer placed behind the generation boundary to prevent a buildup of wave energy inside the domain.

Wave absorption or damping regions: Expressed through coefficients μ(x) is the damping strength with units of \({s}^{-1}\).

Porous structures: The equations for the porous area were obtained by substitution u with u/n, where n is the porosity.

2.2 Numerical Model Setup

The seabed topography is a very important parameter for running the model, the author has collected from the Central Hydrometeorological Forecast Center (Fig. 4). These are the depth data of the coastal and estuarine areas of Hai Phong city, supplemented and updated from the depth measurement data of a number of other project projects that have been done in this area such as the field visits. Surveying the Port and Waterway Consulting Center (TEDI) in 2006, the survey of the Institute of Geography in 2007 and 2008. Then the author used software such as DTM, Google Earth Pro to recalibrate the topography to the real variety. The coastline of Cat Hai in 2015 has been encroached upon compared to 2008 and describes the shoreline of newly constructed works.

Fig. 4.
figure 4

Seabed topography of the Cat Hai island. Units in m.

Full size image

The author establishes the offshore boundary at a depth of nearly 40 m, more than 50 km from the shore, corresponding to the size of the calculated grid area 7600 × 54000 m, the calculated grid cell is 10 × 10 m. Deep water wave parameters: for storm level 10, design tidal water level frequency of 5%, storm surge frequency of 20%. Therefore, the deep water wave parameters include: the design water level of +3.25 m, the average wave height of 5.03 m and the average wave period is 9.88 s [2]. The JONSWAP spectrum wave conditions are used in this simulation study. Boundary conditions applied in this study includes the damping width of 20 m, the damping coefficient of 0.2, the constant chezy roughness type with coefficient of 80 and the porosity friction factors: 2.4 for turbulent, 800 for lamia and the added mass coefficient of 0.8.

3 Results and Discussions

The wave field from Ben Got to Hoang Chau have been simulated without and with the newly constructions in the Cat Hai island and the simulated results have been presented in Fig. 5 and Fig. 6, respectively. It can be seen from Fig. 5 that the wave height varies from 1.2 m to 2.1 m along the coastal area from Ben Got to Hoang Chau for the case without newly constructions. For the case with new constructions (ports, Vinfast dikes), the wave height has been significant increased up to 1.8 m to 3.2 m (see Fig. 6).

Several points, P1–P5, along the coastal line have been chosen to investigate the change of the significant wave heights without and with the new constructions (See Fig. 7 & Fig. 8). It is shown that at point P1 (at the Hoang Chau dike toe) the significant wave height is about from 1.2 m to 1.63 m with no construction in place (Point P1 in Fig. 7). When the new constructions are built, the significant wave height at P1 have been increased to about from 1.6 m to 1.98 m (Point P1 in Fig. 8) and that wave field have significant effects on the activities of the vessels in the area.

Table 1 present the simulated significant wave heights at point P1–P5 along the coastal area from Ben Got to Hoang Chau (Fig. 7 & Fig. 8). As we can see from Table 1 that in general the significant wave heights at points P1–P3 have been increased with the present of the Vinfast dike and other new constructions. On the other hand, the significant wave heights at points P4–P5 are decreased from 1.4 m to 0.82 m with the new constructions in place and this shows that the new constructions play a role as a protection measure for the coastal area from P4 to P5 (Ben Got to Lach Huyen port).

Fig. 5.
figure 5

Results of the local wave field without new construction. Units in m.

Full size image
Fig. 6.
figure 6

Results of the local wave field with new construction. Units in m.

Full size image
Fig. 7.
figure 7

Wave heights along the coastal area without new constructions. Units in m.

Full size image
Fig. 8.
figure 8

Wave heights along the coastal area with new constructions. Units in m.

Full size image
Table 1. Summary of the significant wave heights at points P1-P5.
Full size table

4 Conclusions

This paper have applied the modern numerical model BOUSS-2D in the SMS model set to investigate the effects of the newly construtions on the wave field of the coastal area in Cat Hai island in Hai Phong province in Vietnam. The simulation has been carried out for the coastal area from Ben Got to Hoang Chau for the cases without and with the new constructions along the island. The results showed that for the case with the new constructions the significant wave height at the toe of the dikes from Ben Got to Hoang Chau is higher than that without new constructions about from 0.3 m to 0.4 m. In constrast, in the Lach Huyen port area, the significant wave height is reduced from 0.4 to 0.6 m for the case with the new constructions. The finding of this study may help the community to propose measures to reinforce dikes and to protect the living area behind the dikes in Hoang Chau, Van Chan- Gia Loc, Gia Loc- Ben Got during storms because the effects of the new buildings.

Bouss2D software is open software for free research in a short time of two weeks. The software is easy to install, easy to use interface and with enthusiastic software support team. It is recommended for the students and researchers to use the Bouss2D for their study and research.