Keywords

1 Introduction

FG porous materials are known as recently advanced materials, in which the properties of the materials are characterized by the distribution of porosity in the microstructure. FG porous materials offer a light-weight design with advanced performances for engineers. Thus, structures using FG porous materials have attracted several research works (e.g., [1,2,3,4]).

On the other hand, sandwich structures are used widely in various engineering fields, such as structural engineering, mechanical engineering, marine engineering, and aerospace engineering, due to their light-weight and high strength performance. The major drawback of these structures is the discontinuity of material properties between the layers, which may cause de-bonding when the structure is subjected to impact loadings [5]. FG materials, therefore, have been introduced to sandwich structures to form a new kind of structure named Functionally Graded Sandwich (FGS) structure [6]. With their continuous and smooth variation of the properties, FG materials help to reduce the de-bonding in sandwich structures. Commonly, there exist two main types of FGS structures: the first one has an FG core and two homogeneous face sheets; the second one has a homogeneous core and two FG face sheets [5]. Recently, a new type of FGS structures, where an FG porous core is sandwiched between two FG face layers, has been studied [7, 8].

It is well known that the performance of an FGS structure is dependent on the properties of the constituent materials as well as the material distribution. To obtain optimal performance, the structure should be designed through an optimization procedure. Several works have been carried out for the optimization of FGS structures, which are reviewed in Ref. [5]. However, there is no work done for the optimal design of the FGS structures with FG porous core and two FG face sheets.

In this paper, the optimal design of a functionally graded sandwich porous (FG-SWP) beam is freshly addressed. The studied beam has an FG porous core sandwiched between two FG face sheets. The material distribution of the face sheets, the porosity distribution, and the layer thickness of the FG-SWP beam are tailored to maximize the fundamental natural frequency. Different beam theories are adopted to analyze the free vibration behavior of the beam. For this purpose, the frequency of the beam is obtained by a general analytical solution developed by Hung and Truong [7]. Due to the complexity of this highly non-linear optimization problem that is not easy to solve using conventional gradient-based optimization techniques, various meta-heuristics are implemented to derive the optimal design. The efficiency of the considered meta-heuristics, as well as the influence of the beam theories on the obtained beam design, is studied through numerical examples of slender and thick beams.

2 Frequency Maximization for FG-SWP Beams

2.1 Design Problem

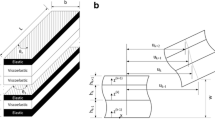
Consider an FG-SWP beam with three layers as shown in Fig. 1 [7]. The beam has two FG layer faces and an FG porous core. The beam is numbered by the thickness ratio of the layers from the bottom \(\left( {z = h_{1} = - h/2} \right)\) to the top \(\left( {z = h_{4} = + h/2} \right)\). For example, the 1-1-1 beam presents a beam that has an equal layer thickness.

Fig. 1.
figure 1

Layout of FG-SWP beam [7]

Full size image

The Young’s modulus and the mass density of the layers are assumed to vary in thickness direction as per the following laws:

$$ \begin{aligned} E^{{(3)}} (z) & = (E_{c} - E_{m} )\left( {\frac{{z - h_{4} }}{{h_{3} - h_{4} }}} \right)^{p} + E_{m} \,\,;\,\,\,\rho ^{{(3)}} (z) = (\rho _{c} - \rho _{m} )\left( {\frac{{z - h_{4} }}{{h_{3} - h_{4} }}} \right)^{p} + \rho _{m} \,\,\,{\text{with}}\,\,\,\,z \in \left[ {h_{3} ,h_{4} } \right] \\ E^{{(2)}} (z) & = E_{m} \left[ {1 - e_{0} \cos \left( {\frac{{\pi z}}{{h_{3} - h_{2} }}} \right)} \right]{\text{ ;}}\,\,\rho ^{{(2)}} (z) = \rho _{m} \left[ {1 - e_{m} \cos \left( {\frac{{\pi z}}{{h_{3} - h_{2} }}} \right)} \right]{\text{ }}\,\,{\text{with}}\,\,\,\,z \in \left[ {h_{2} ,h_{3} } \right] \\ E^{{(1)}} (z) & = (E_{c} - E_{m} )\left( {\frac{{z - h_{1} }}{{h_{2} - h_{1} }}} \right)^{p} + E_{m} \,\,;\,\,\,\rho ^{{(1)}} (z) = (\rho _{c} - \rho _{m} )\left( {\frac{{z - h_{1} }}{{h_{2} - h_{1} }}} \right)^{p} + \rho _{m} \,\,\,\,\,{\text{with}}\,\,\,z \in \left[ {h_{1} ,h_{2} } \right] \\ \end{aligned} $$
(1)

where \(E(z),_{{}}^{{}} \rho (z)\) are, respectively, the effective Young’s modulus and mass density; \(E_{m} ,_{{}}^{{}} \rho _{m}\) and \(E_{c} ,_{{}}^{{}} \rho _{c}\) are, respectively, Young’s modulus and mass density of metal and ceramic; \(e_{0} ,_{{}}^{{}} e_{m}\) represent the coefficients of porosity for Young’s modulus and mass density, respectively. The relationship between \(e_{0} ,_{{}}^{{}} e_{m}\) is given by Chen et al. [9]:

$$ e_{m} = 1 - \sqrt {1 - e_{0} } $$
(2)

The beam is to be designed so that the fundamental frequency is maximized. For this purpose, the material distribution and the thickness of each layer are tailored by an optimization procedure. The optimal design problem is defined as:

$$ \begin{gathered} {\text{Maximize}}\;\bar{\omega }(p,e_{0} ,t_{1} ,t_{2} ,t_{3} ) = \omega \frac{{L^{2} }}{h}\sqrt {\frac{{\rho _{m} }}{{E_{m} }}} \hfill \\ {\text{s}}.{\text{t}}. \hfill \\ p_{{\min }} \le p \le p_{{\max }} , \hfill \\ e_{{0\min }} \le e_{0} \le e_{{0\max }} , \hfill \\ 0 \le t_{1} ,t_{2} ,t_{3} \hfill \\ \end{gathered} $$
(3)

where \(\bar{\omega }\) is the normalized fundamental frequency; \(t_{1} ,t_{2} ,t_{3}\) are, respectively, the thickness ratios of the bottom, the core, and the top layers; \(p_{{\min }} ,p_{{\max }}\) are the lower and upper limits of the distribution exponent p; \(e_{{0\min }} ,e_{{0\max }}\) are the lower and upper limits of the porosity coefficient. In this study, the design variables \(p\) and \(e_{0}\) are continuous, while the thickness ratios are integers. Thus, the design problem is a mixed integer optimization problem.

The objective function of the optimization problem requires the free vibration solution of the FG-SWP beam. In this study, a general analytical solution based on various beam theories is established to analyze the beam, which is presented in the following.

2.2 Analytical Solution for Natural Frequency

For analyzing the fundamental frequency of the FG-SWP beam, the analytical solution developed by Hung and Truong [7] is adopted in this study, and briefly presented as follows.

First, the displacement field is described as:

$$ u(x,z,t) = u_{0} (x,t) - z\frac{{\partial w_{0} }}{{\partial x}} + f(z)\theta _{x} \;\;\;\;\;\;\;\;\;\;\;\;\,w(x,z,t) = w_{0} (x,t); $$
(4)

where \(u_{0} ,w_{0}\) are the mid-surface displacements in the \(x\) and \(z\) directions, respectively; \(\theta _{x}\) is the rotation of the mid-surface transverse normal; \(f(z)\) is the shape function depending on the beam theories as given in Table 1.

Table 1. The shape functions of different beam theories
Full size table

The strains are determined from the following relations:

$$ \varepsilon _{{xx}} = \frac{{\partial u}}{{\partial x}} = \frac{{\partial u_{0} }}{{\partial x}} - z\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} + f(z)\frac{{\partial \theta _{x} }}{{\partial x}}\;\;\;\;{\text{ }}\gamma _{{xz}} = \frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}} = f^{'} (z)\theta _{x} $$
(5)

The stresses in each i-th layer are computed by the Hooke’s law as follows; with a constant poisson’s ratio \(\nu\)

$$ \left\{ \begin{gathered} \sigma _{{xx}} \hfill \\ \sigma _{{xz}} \hfill \\ \end{gathered} \right\}^{i} = \left( {\begin{array}{*{20}c} {E(z)} & 0 \\ 0 & {\frac{{k_{s} E(z)}}{{2(1 + \nu )}}} \\ \end{array} } \right)^{i} \left\{ \begin{gathered} \varepsilon _{{xx}} \hfill \\ \gamma _{{xz}} \hfill \\ \end{gathered} \right\}^{i} $$
(6)

where \(k_{s}\) is the shear correction factor, and \(k_{s} = {\text{5}}/{\text{6}}\) for Timoshenko beam theory, otherwise \(k_{s} = 1\).

Applying Hamilton’s principle, the equations of free vibration motion become

$$ \left\{ \begin{aligned} & \frac{{\partial N_{{xx}} }}{{\partial x}} = I_{0} \ddot{u}_{0} - I_{1} \frac{{\partial \ddot{w}_{0} }}{{\partial x}} + I_{3} \ddot{\theta }_{x} \\ & \frac{{\partial ^{2} M_{{xx}} }}{{\partial ^{2} x}} = - I_{1} \frac{{\partial \ddot{u}_{0} }}{{\partial x}} + I_{2} \frac{{\partial ^{2} {{\ddot{w}}}_{0} }}{{\partial ^{2} x}} - I_{4} \frac{{\partial \ddot{\theta }_{x} }}{{\partial x}} - I_{0} \ddot{w}_{0} \\ & \frac{{\partial F_{{xx}} }}{{\partial x}} - H_{{xz}} = I_{3} \ddot{u}_{0} - I_{4} \left( {\frac{{\partial \ddot{w}_{0} }}{{\partial x}}} \right) + I_{5} \ddot{\theta }_{x} \\ \end{aligned} \right. $$
(7)

where the terms in Eq. (7) are defined by:

$$ \begin{aligned} N_{{xx}} & = \int\limits_{A} {\sigma _{{xx}} dA} \,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,M_{{xx}} = - \int\limits_{A} {z\sigma _{{xx}} dA} \,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,F_{{xx}} = \int\limits_{A} {\sigma _{{xx}} f(z)dA} ; \\ \,H_{{xz}} & = \int\limits_{A} {\sigma _{{xz}} \frac{{\partial f(z)}}{{\partial z}}dA} \, \\ I_{0} & = \int\limits_{A} {\rho (z)dA} \,\,\,\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,I_{1} = \int\limits_{A} {z\rho (z)dA} \,\,\,\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,I_{2} = \int\limits_{A} {z^{2} \rho (z)dA} \\ I_{3} & = \int\limits_{A} {f(z)\rho (z)dA} ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,I_{4} = \int\limits_{A} {zf(z)\rho (z)dA} \,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,I_{5} = \int\limits_{A} {f(z)^{2} \rho (z)dA} \\ \end{aligned} $$
(8)

Considering the simply supported condition for the beam, the Navier’s solution has the following form with \(\alpha = m\pi /L\)

$$ u_{0} = \sum\limits_{{m = 1}}^{\infty } {u_{m} \cos (\alpha x)\cos (\omega t)} ;\;w_{0} = \sum\limits_{{m = 1}}^{\infty } {w_{m} \sin (\alpha x)\cos (\omega t)} ;\;\theta _{x} = \sum\limits_{{m = 1}}^{\infty } {u_{m} \cos (\alpha x)\cos (\omega t)} $$
(9)

Taking into account each term of Eq. (9) as a free vibration mode shape, and introducing it into Eqs. (4–7) yield the eigenvalue equations as

$$ \begin{aligned} & \left[ {\left( {A\alpha ^{2} } \right)u_{m} - \left( {B\alpha ^{3} } \right)w_{m} + \left( {C\alpha ^{2} } \right)\theta _{m} } \right] - \omega ^{2} \left[ {I_{0} u_{m} - I_{1} \alpha w_{m} + I_{3} \theta _{m} } \right] = 0 \\ & \left[ { - \left( {B\alpha ^{3} } \right)u_{m} + \left( {D\alpha ^{4} } \right)w_{m} - \left( {F\alpha ^{3} } \right)\theta _{m} } \right] - \omega ^{2} \left[ { - I_{1} \alpha u_{m} + \left( {I_{0} + I_{2} \alpha ^{2} } \right)w_{m} - I_{5} \alpha \theta _{m} } \right] = 0 \\ & \left[ {\left( {C\alpha ^{2} } \right)u_{m} - \left( {F\alpha ^{3} } \right)w_{m} + \left( {H_{1} + G_{1} \alpha } \right)\theta _{m} } \right] - \omega ^{2} \left[ {I_{3} u_{m} - I_{4} \alpha w_{m} + I_{5} \theta _{m} } \right] = 0 \\ \end{aligned} $$
(10)

where \(\omega\) is the natural frequency, and

$$ \begin{aligned} & (A,B,C,D,F,G_{1} ) = \int_{{ - h/2}}^{{h/2}} {E(z)(1,z,f,z^{2} ,zf,f^{2} )dz} ; \\ & H_{1} = \int_{{ - h/2}}^{{h/2}} {\frac{{k_{s} E(z)}}{{2(1 + \nu )}}\left( {f'} \right)^{2} dz} \\ \end{aligned} $$
(11)

3 Implemented Metaheuristics

3.1 Parameter Setting

In this study, different meta-heuristics are implemented to solve the optimal design problem of FG-SWP beam, including differential evolution (DE) [14], genetic algorithm (GA), particle swarm optimization (PSO) [15], teaching-learning-based optimization (TLBO) [16], Jaya [17], and adaptive differential evolution (ANDE) [18]. Details of these optimization techniques can be found in the respective literature. The codes of DE, PSO, TLBO, Jaya, and ANDE are implemented by the first author in MATLAB, whereas the built-in function for GA in MATLAB is utilized. All methods use the same population size of 30. The other control parameters for each method are chosen for good performance of the respective method, and they are given as follows:

  • DE and ANDE: The scaling factor and crossover rate are 0.7 and 0.9, respectively.

  • GA: Multi-point crossover is adopted. The crossover probability is 0.8, and the mutation probability is 0.2.

  • PSO: The inertia weight of 0.6, cognitive learning rate of 1.0, and social learning rate of 1.0 are used.

  • TLBO and Jaya: No parameter setting.

The stopping criterion is \(\left| {f_{{mean}} /f_{{best}} - 1} \right| \le 10^{{ - 6}}\), with \(f_{{mean}} ,f_{{best}}\) are the mean value and the best value of the objective function in the population. This stopping criterion, suggested by Ho et al. [19], appears to be reasonable for the investigated numerical example in this study to obtain stable optimal results. The initial population is randomly generated from the search space. To obtain statistical results for comparison, each method is conducted 20 times with a maximum of 100 generations.

3.2 Constraint Handling

3.2.1 Bound Constraints

The bound constraints are handled by a simple method given in Ref. [20] as follows. During the evolution of a meta-heuristic, if a newly generated variable \(x_{{kj}}^{{new}}\) violates the bound \(b_{j}\), its value will be recalculated by:

$$ x_{{kj}}^{{new}} = \frac{{x_{{kj}}^{{old}} + b_{j} }}{2} $$
(12)

where \(x_{{kj}}^{{new}}\) is the value of the j-th design variable of the k-th solution in the new population; \(x_{{kj}}^{{old}}\) is the value of the j-th design variable of the k-th solution in the old population; \(b_{j}\) is the violated bound.

3.2.2 Integer Variable

In the numerical example, the rounding technique is used to transform a decimal value of the thickness ratio into an integer value.

4 Numerical Results

The FG-SWP beam examined is composed of two materials, aluminum and ceramic, with the properties given in Table 2. Two beam configurations are considered, a slender beam with a height of 5 cm (L/h = 20) and a thick beam with a height of 20 cm (L/h = 5). The thickness ratio limits are: \(0 \le t_{1} ,t_{2} ,t_{3} \le 10\).

Table 2. Material properties of the FG-SWP beam
Full size table

4.1 Comparison Among Meta-heuristics

Table 3 lists the optimization results obtained for the TBT slender beam by the implemented meta-heuristics. The results include the optimal design, the best value, the mean value, the worst value, and the standard deviation of the optimized fundamental frequency. The average number of objective function evaluations (FE) and the number of successful runs (NoS) by each algorithm are also given in Table 3. It is noted that the table presents the normalized thickness ratios for comparison purpose. It is seen that all meta-heuristics derive the same optimal solution. Furthermore, except PSO, all meta-heuristics can produce stable results over 20 runs. PSO has 3 runs that fail to obtain the optimal solution. In terms of the required FE, ANDE is the best optimizer, and TLBO is the worst one. The optimization results for the TBT thick beam are given in Table 4. ANDE, again, requires the smallest FE, and TLBO needs the largest FE. PSO is the most unstable algorithm with only 15 successful runs for the thick beam.

Figure 2 depicts the average convergence history of the objective function for the considered meta-heuristics. It can be seen that PSO has the highest convergence speed in early iterations; however, it is greedy and also causes premature convergence, i.e., obtaining local optimum. ANDE, on the other hand, is faster than DE, GA, TLBO, and as fast as Jaya.

Table 3. Optimization results of the TBT slender beam by different meta-heuristics
Full size table
Table 4. Optimization results of the TBT thick beam by different meta-heuristics
Full size table
Fig. 2.
figure 2

Optimization history of the FG-SWP beam by different meta-heuristics

Full size image

To further explore the effectiveness of ANDE, different settings of control parameters are examined, where the scaling factor F is 0.4 and 0.7, and the crossover rate CR is 0.7 and 0.9. Figure 3 compares the convergences of DE and ANDE corresponding to different parameter combinations to optimize the TBT slender beam. It is seen from Fig. 3 that the parameter combination with F = 0.7 and CR = 0.9 gives the best performance of both DE and ANDE in terms of convergence and stability. These parameter values are therefore applied for DE and ANDE in all the numerical investigations.

Fig. 3.
figure 3

Convergence of DE (a) and ANDE (b) for different parameter settings

Full size image

4.2 Comparison Among Beam Theories

Since ANDE requires the smallest number of function evaluations, it is further utilized to optimize the FG-SWP beam with different beam theories. The optimization results for the slender and thick beams corresponding to different beam theories are shown in Tables 5 and 6, respectively. For the slender beam in Table 5, the results by high-order shear deformation theories (TBT, SBT, HBT, EBT) are the same. However, the thickness ratio of the beam layers obtained by high-order shear deformation theories differs from that obtained by classical beam theory (CBT) and the Timoshenko beam theory (TMT). This can be explained by the effect of the shear deformation on the fundamental frequency of the FG-SWP beam. For the thick beam, the effect of shear deformation is so significant that the optimal thickness ratio of the beam layers obtained by the different beam theories is not identical, as seen from Table 6 i.e., the optimal result depends on the theory used.

Table 5. Optimization results of the TBT slender beam by different beam theories
Full size table
Table 6. Optimization results of the TBT thick beam by different beam theories
Full size table

5 Conclusion

The optimal design of the functionally graded sandwich porous (FG-SWP) beam is addressed for the first time in this paper. The study investigates the effectiveness of different meta-heuristics in tailoring the material distribution, as well as the layer thickness for maximizing the fundamental frequency of the beam. It is shown that the implemented meta-heuristics, including GA, DE, PSO, TLBO, Jaya, and ANDE, can derive the optimal design for different configurations of the FG-SWP beam effectively. Among the considered meta-heuristics, ANDE appears to be the best algorithm in terms of computational cost. In terms of convergence rate, PSO is the fastest algorithm but easily trapped in local minima, while both ANDE and Jaya outperform the remaining algorithms. Moreover, different beam theories are considered for the optimal design of the FG-SWP beam. It is revealed that the optimal design of the FG-SWP beam is influenced by the shear deformation theory applied in calculating the frequency, particularly for the thick beam.