Keywords

1 Introduction

Train integrity is one of the important factors affecting the safe operation of trains. The traditional train integrity monitoring function is mainly realized by checking the occupation of track circuit. To reduce the installation and maintenance costs of equipment, improve the availability of train operation control systems, the next generation train control system (NGTC) requires that the train integrity monitoring function should be completed by on-board equipment [1]. At present, train integrity monitoring methods include the following three methods: the train brake pressure tube, the movement state of the train head and end, and the change of the train length [2]. The last method is simple in principle, which only needs to locate the position of the head and end of the train and calculate the train length in real time to reflect the integrity of the train.

At present, with the further development of satellite positioning technology, its positioning accuracy and reliability have been continuously improved, which has gradually become an important support of train control system [3]. Some scholars have shown that in single constellation system, the result error can reach within 1.5 m through moving-baseline solution [4]. Due to the increase of the number of visible satellites, the multi-constellation positioning can further improve positioning accuracy compared with single constellation system in theory. In February 2020, European Global Navigation Satellite System Administration (GSA) released the third edition of global navigation satellite system (GNSS) User Technical Report, which emphasized that the new situation of GNSS is multi-constellation, multi-frequency and multi-signal development [5]. At the same time, supporting multi-constellation has become the standard of receivers, which shows that multi-constellation positioning has become a trend of satellite navigation system development in future. With successful construction of Beidou Navigation Satellite System (BDS) and its enhancement system [6], GPS and BDS combined positioning can make full use of the global satellite resources, increase the number of visible satellites, and optimize the geometric distribution of satellites, which can effectively improve the reliability and stability [7].

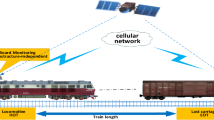
Therefore, this paper proposes a train integrity monitoring method based on multi-constellation moving-baseline solution. The moving-baseline refers to the baseline vector installed between the head and end antennas of the train. After unifying the time system and space system of different constellations, the error in the propagation process and the satellite clock error are eliminated by double difference carrier phase. The double difference carrier phase of different constellations is combined with equal weight. Then the moving-baseline length is solved by Kalman filter algorithm, and the train integrity monitoring is realized by comparing with the actual train length.

2 Multi-constellation System Combination Method

For different satellite positioning systems, the time system and space system are different. Therefore, it is significantly important to unify the time and space system.

2.1 Multi-constellation Time and Space System Combination

In BDS/GPS positioning, it is necessary to change the time system. GPS uses Global Positioning Time (GPST) and BDS uses Beidou Time (BDST). Although both of them belong to atomic time (AT) [8], their starting times are different. The former starts at 0:00:00 on January 6, 1980, but the latter starts at 0:00:00 on January 1, 2006. Because of leap second, the time relationship between BDS and GPS can be expressed as:

$$ GPS_{week} = BDS_{week} + 1356 $$
(1)
$$ GPS_{sec} = BDS_{sec} + 14 $$
(2)

Where \(GPS_{week}\) and \(BDS_{week}\) is the integer weeks of GPST and BDT, \(GPS_{{{\text{sec}}}}\) and \(BDS_{{{\text{sec}}}}\) is the seconds of GPST and BDT.

BDS adopts 2000 Chinese Geodetic Coordinate System (CGCS2000), and GPS adopts American Geodetic Coordinate System (WGS84), which are consistent with the definition of International Earth Reference System (ITRS) and the parameter deviation is small [9]. Table 1 is the parameter comparison between GPS and BDS coordinate system.

Table 1. Fundamental earth parameters of GPS and BDS coordinate system
Full size table

The coordinate origin and major axis of the two coordinate systems are same, and from the current measurement accuracy, the difference between the two coordinate systems due to the parameter difference can be ignored [10].

2.2 Double Difference Carrier Phase Model

The key to calculate the length of moving-baseline is to calculate the relative position of two antennas. At present, there are two basic positioning models, pseudo-range positioning and carrier phase positioning. Carrier phase positioning is realized by measuring the phase change. The error of this method is smaller than pseudo-range positioning. Thus, it is more suitable for high-precision positioning scenes. The carrier phase observation equation can be written as:

$$ \phi = \lambda_{{}}^{ - 1} (\rho_{{\text{b}}}^{{}} - I_{{\text{b}}}^{{}} + T_{{\text{b}}}^{{}} ) + f(\delta t_{R} - \delta t_{S} ) + N_{{\text{b}}}^{{}} + \varepsilon_{{\text{b}}}^{{}} $$
(3)

Where \(\phi\) represents the carrier phase measurement; \(\lambda\) represents the wavelength of the carrier signal; \(\rho\) represents the geometric distance between the satellite and the receiver; \(N\) represents the integer ambiguity; \(\delta t_{R}\) represents the clock difference of the receiver; \(\delta t_{S}\) represents the clock difference of the satellite; \(\varepsilon\) represents the residual error[11].

According to the carrier phase equation, when two antennas receive the \(i^{th}\) satellite at the same time, the observation equation of inter-station difference can be written as:

$$ \phi_{EH}^{i} = \phi_{E}^{i} - \;\phi_{H}^{i} { = }\lambda^{ - 1} \rho_{EH}^{i} + f(\delta t_{{R_{E} }} - \delta t_{{R_{H} }} ) + N_{EH}^{i} { + }\varepsilon_{EH}^{i} $$
(4)

Where \(\phi_{EH}^{i}\) represents the carrier phase difference between two receivers; \(\rho_{EH}^{i}\) is the distance difference between two receiver antennas and satellites; \(N_{EH}^{i}\) is the ambiguity result of single difference and \(\varepsilon_{EH}^{i}\) is the single difference of error.

Similarly, if the \(j^{th}\) satellite is selected as the reference satellite, the inter-satellite carrier phase difference is based on inter-station difference. The double-difference carrier phase observation equation is as follows:

$$ \phi_{EH}^{ij} = \phi_{EH}^{i} - \;\phi_{EH}^{j} { = }\lambda^{ - 1} \rho_{EH}^{ij} + N_{EH}^{ij} + \varepsilon_{EH}^{ij} $$
(5)

Where \(r_{EH}^{ij}\) represents the double difference result of the real distance between \(i^{th}\) and \(j^{th}\), head and end antennas; \(N_{EH}^{ij}\) is the double difference result of the ambiguity, \(\varepsilon_{EH}^{ij}\) is the double difference of the error, and superscript \(ij\) indicates the difference between the \(i^{th}\) satellite and the \(j^{th}\) satellite.

It is necessary to fuse carrier phase of different constellations for multi-constellation systems. When the time system and coordinate system are unified, each constellation system performs inter-satellite difference and inter-station difference independently, and then combines the double-difference carrier phases of different constellations with equal weight to form the carrier phase difference result of multi-constellation system.

3 Solution of Multi-constellation Moving-Baseline Based on Kalman Filter

According to the double-difference carrier phase observation equation, the double-difference ambiguity and relative position coordinates are unknown, which need to be estimated by Kalman filter. Combined with the calculation results of the previous epoch and the measurement results of the current epoch, the state estimation is updated by recursive operation, and through iterative correction to obtain more accurate solution results. Kalman filter predicts the current state through the system model and corrects the predicted state through the measurement model. The system model is:

$$ X_{k} = AX_{k - 1} {\text{ + W}}_{k} $$
(6)

Where \(X_{k}\) is the state vector of the system; \(A\) is the state transition matrix; \(W_{k} \sim N(0,Q)\) is the process noise of the system.

The multi-constellation system needs a more accurate motion model to describe the moving-baseline motion state. Thus, the motion state of the moving-baseline is made as first-order Markov acceleration model. The estimated state includes nine parameters (three-dimensional relative position, three-dimensional relative velocity and three-dimensional relative acceleration) and double-difference integer ambiguity of different constellations. The state matrix of the system can be expressed as:

$$ \begin{aligned} & {\mathbf{X}}_{k}^{{\text{T}}} = \left[ {\Delta x\;\;\Delta y\;\;\Delta z\;\;\Delta v_{x} \;\;\Delta v_{y} \;\;\Delta v_{z} \;\;\dot{\Delta }v_{x} \;\;\dot{\Delta }v_{y} \;\;\;\dot{\Delta }v_{z} } \right. \\ & \;\;\;\;\;\;\;\;\;\;\left. {N_{HE}^{G1Gj} \;\;N_{HE}^{G2Gj} \;\; \cdots \;\;N_{HE}^{{G(n_{G} - 1)Gj}} \;\;N_{HE}^{B1Bj} \;\;N_{HE}^{B2Bj} \;\; \cdots \;\;N_{HE}^{{B(n_{B} - 1)Bj}} } \right] \\ \end{aligned} $$
(7)

Where \(\left( {\Delta v_{x} ,\;\Delta v_{y} ,\;\Delta v_{z} } \right)\) represents the relative velocity in three directions and \(\left( {\dot{\Delta }v_{x} ,\;\dot{\Delta }v_{y} ,\;\dot{\Delta }v_{z} } \right)\) represents the relative acceleration in three directions,\(G\) and \(B\) correspond to GPS system and BDS system respectively; \(n_{G}\) and \(n_{B}\) represent the number of satellites of GPS and BDS respectively; Assume that GPS selects \(j^{th}\) satellite as reference satellite and BDS selects \(k^{th}\) satellite as reference satellite,\(\left( {N_{HE}^{G1Gj} \,\,N_{HE}^{G2Gj} \, \cdots \,N_{HE}^{{G\left( {n_{G} - 1} \right)Gj}} } \right)\) is the matrix composed of double difference integer ambiguity corresponding to GPS system; \(\left( {N_{HE}^{B1Bk} \,\,N_{HE}^{B2Bk} \, \cdots \,N_{HE}^{{B\left( {n_{B} - 1} \right)Bk}} } \right)\) is the matrix composed of double difference integer ambiguity corresponding to BDS system; \(N_{HE}^{G1Gj}\) indicates the whole cycle ambiguity after GPS double difference.

State transition matrix can be written as:

$$ {\mathbf{A}} = \left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{3 \times 3} } & {\Delta T \bullet {\mathbf{I}}_{3 \times 3} } & {{\mathbf{0}}_{3 \times 3} } & {{\mathbf{0}}_{{3 \times [({\text{n}}_{G} { - 1) + }({\text{n}}_{B} { - 1)}]}} } \\ {{\mathbf{0}}_{3 \times 3} } & {{\mathbf{I}}_{3 \times 3} } & {\Delta T \bullet {\mathbf{I}}_{3 \times 3} } & {{\mathbf{0}}_{{3 \times [({\text{n}}_{G} { - 1) + }({\text{n}}_{B} { - 1)}]}} } \\ {{\mathbf{0}}_{3 \times 3} } & {{\mathbf{0}}_{3 \times 3} } & {{\mathbf{I}}_{3 \times 3} } & {{\mathbf{0}}_{{3 \times [({\text{n}}_{G} { - 1) + }({\text{n}}_{B} { - 1)}]}} } \\ {{\mathbf{0}}_{{[({\text{n}}_{G} { - 1) + }({\text{n}}_{B} { - 1)}] \times 3}} } & {{\mathbf{0}}_{{[({\text{n}}_{G} { - 1) + }({\text{n}}_{B} { - 1)}] \times 3}} } & {{\mathbf{0}}_{{[({\text{n}}_{G} { - 1) + }({\text{n}}_{B} { - 1)}] \times 3}} } & {{\mathbf{I}}_{{[({\text{n}}_{G} { - 1) + }({\text{n}}_{B} { - 1)}] \times [({\text{n}}_{G} { - 1) + }({\text{n}}_{B} { - 1)}]}} } \\ \end{array} } \right] $$
(8)

Where \(\Delta T\) is the time interval, \({\mathbf{I}}\) is unit matrix.

The noise matrix of the system can be written as:

$$ {\mathbf{Q}}_{k} = diag\left( {\begin{array}{*{20}c} {{\mathbf{0}}_{1 \times 3} \;\;{\mathbf{0}}_{1 \times 3} } & {\frac{{2 * \Delta T^{2} }}{\tau }} & {\frac{{2 * \Delta T^{2} }}{\tau }} & {\frac{{2 * \Delta T^{2} }}{\tau }} & {w_{{1 \times (n_{G} - 1)}} \;\;w_{{1 \times (n_{B} - 1)}} } \\ \end{array} } \right) $$
(9)

Where \(\tau\) is the correlation time, and \(w\) is the random walk process corresponding to the double difference ambiguity.

The measurement model of Kalman filter system is:

$$ Z_{k} = H_{k} X_{k} + V_{k} $$
(10)

Where \({\mathbf{Z}}_{k}\) is the observation vector of the system; \({\mathbf{H}}_{k}\) is the measurement matrix; \({\mathbf{V}}_{k} \sim N\left( {0,\,{\mathbf{R}}} \right)\) is white noise with Gaussian distribution, and the corresponding covariance matrix is \(R\).

The observation matrix of the system composed of carrier phase double difference results of different constellation systems is as follows:

$$ {\mathbf{Z}}_{k} = - \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\phi_{EH}^{G1Gj} } & {\phi_{EH}^{G2Gj} } & {...} \\ \end{array} } & {\phi_{EH}^{{G(n_{G} - 1)Cj}} \;\;\begin{array}{*{20}c} {\begin{array}{*{20}c} {\phi_{EH}^{B1Bk} } & {\phi_{EH}^{B2Bk} } & {...} \\ \end{array} } & {\phi_{EH}^{{B(n_{B} - 1)Bk}} } \\ \end{array} } \\ \end{array} } \right]^{T} $$
(11)

Measurement matrix of the system is as follows:

$$ {\mathbf{H}}_{k} = \left[ {\begin{array}{*{20}c} {a^{G1Gj} } & {b^{G1Gj} } & {c^{G1Gj} } & {} & {} \\ {a^{G2Gj} } & {b^{G2Gj} } & {c^{G2Gj} } & {} & {} \\ \vdots & \vdots & \vdots & {{\mathbf{0}}_{{(n_{G} - 1) \times 9}} } & { - \lambda_{G} \cdot {\mathbf{I}}_{{(n_{G} - 1) \times (n_{G} - 1)}} } \\ {a^{{G(n_{G} - 1)Gj}} } & {b^{{G(n_{G} - 1)Gj}} } & {c^{{G(n_{G} - 1)Gj}} } & {} & {} \\ {a^{B1Bk} } & {b^{B1Bk} } & {c^{B1Bk} } & {} & {} \\ {a^{B2Bk} } & {b^{B2Bk} } & {b^{B2Bk} } & {} & {} \\ \vdots & \vdots & \vdots & {{\mathbf{0}}_{{(n_{B} - 1) \times 9}} } & { - \lambda_{B} \cdot {\mathbf{I}}_{{(n_{B} - 1) \times (n_{B} - 1)}} } \\ {a^{{B(n_{B} - 1)Bk}} } & {b^{{B(n_{B} - 1)Bk}} } & {c^{{B(n_{B} - 1)Bk}} } & {} & {} \\ \end{array} } \right] $$
(12)

If the head antenna is selected as the main antenna, \(a,\,b,\,c\) in the measurement matrix are the coefficient parameters of Taylor expansion when Kalman filter is linearized:

$$ a^{s} = \frac{{x^{s} - x_{H} }}{{r_{H}^{s} }},\;b^{s} = \frac{{y^{s} - y_{H} }}{{r_{H}^{s} }},\;c^{s} = \frac{{z^{s} - z_{H} }}{{r_{H}^{s} }} $$
(13)

In which \(x^{S} ,y^{S} ,z^{S}\) is the three-dimensional coordinate of satellite, \(x_{H} ,y_{H} ,z_{H}\) is the three-dimensional coordinate of train head antenna, \(r_{H}^{s}\) is the distance between satellite and the approximate position of train head antenna.

After the system model and measurement model are determined, recursive operation needs to be realized through time update and measurement update. The relative position between two antennas in each epoch can be calculated in real time, so the moving-baseline length can be expressed as:

$$ L{ = }\sqrt {\Delta x^{2} + \Delta y^{2} + \Delta z^{2} } $$
(14)

The calculated moving-baseline length L is compared with the real distance between the two antennas, and the current train integrity status can be judged.

4 Results Analysis

In order to verify the performance of the proposed train integrity resolution method, a real experiment was carried out on the Beijing-Shenyang high-speed railway in June 2018. The data not only includes the train running process, but also includes the train inbound and outbound scenes. In this scene, the number of visible satellites and vehicle speed change greatly, which can verify the accuracy and stability of the algorithm.

The train absolute length is 186.9 m between the head and the end antennas centers. Therefore, the absolute distance between the two antennas in the static state is used as a reference to compare with the calculation results.

Fig. 1.
figure 1

Changes in the number of visible satellites

Full size image

Figure 1 shows the change of the visible satellites number of different constellation system. Because the train enter Xinminbei Station and Shenyangxi Railway Station for a short stop between epoch 6738–8459 and epoch 15670–17650. Due to the shelter ceiling in the station, the number of visible satellites decreases a lot.

Fig. 2.
figure 2

Satellite DOP value of GPS

Full size image

Figure 2 shows the GNSS geometry change during the experimental period, where the position dilution of precision (PDOP), the horizontal dilution of precision (HDOP), and the vertical dilution of precision (VDOP) are plotted. PDOP directly reflects the geometric distribution of satellites. Before epoch 6000, the PDOP value is less than 5, between epoch 6738–8459 and epoch 15670–17650, the PDOP value obviously increases and some PDOP values reach 15 because the train enters the station.

Fig. 3.
figure 3

Moving-baseline calculation result of single constellation

Full size image

The result of moving-baseline solution in single GPS system is shown in Fig. 3. After the train enters Xinminbei Railway Station, the number of satellites decreases because the signal in the station is blocked, and the number of visible satellites in some epochs is less than four, so the error of moving-baseline solution results increases, and the maximum error reaches more than 1 m.

Fig. 4.
figure 4

Moving-baseline calculation results of multi-constellation

Full size image

Figure 4 is the calculation result of moving-baseline based on multi-constellation. Compared with the single GPS moving-baseline results, the solution accuracy is obviously higher than single constellation system, and the error is kept within 0.3 m. After 6000 epochs, the multi-constellation moving-baseline solution results are obviously better than the single constellation system. Especially when the satellite observation conditions deteriorate between 6738–8459 and 15670–17650 epochs, the multi-constellation system moving-baseline solution results are more stable and the overall availability of the system is improved.

Fig. 5.
figure 5

Comparison of error cumulative distribution functions

Full size image

The error cumulative distribution function diagram(CDF) of the moving-baseline solution results is shown in Fig. 5. The single GPS solution error is all less than 1.2 m, while the multi-constellation positioning solution error is all less than 0.43 m.

Table 2. Error comparison of single constellation and multi-constellation moving-baseline solution results
Full size table

Table 2 shows the comparison of the maximum error, mean error, root mean square error and standard deviation error between single constellation system and multi-constellation system. The multi-constellation system solution result is obviously better than single constellation system.

5 Conclusions

This paper proposes a train integrity monitoring method based on multi-constellation moving-baseline solution. GPS and BDS are combined and carrier phase double difference model is used to eliminate the errors and satellite clock errors in the propagation path. The moving-baseline length is solved in real time by Kalman filtering algorithm and compared with the actual train length to get the train integrity status.

The mean error of multi constellation moving-baseline is only 0.18 m, which improves the positioning accuracy compared with single constellation. The root mean square error is reduced from 0.65 meters to 0.2 m. The multi constellation combined measurement solution increases the number of satellites in the limited scene, improves the accuracy of train integrity monitoring.