Keywords

1 Introduction

Construction methods of discrete dynamic models for different systems are sufficiently developed and widely used. The parametric identification of discrete models was described in articles by L. Ljung [1], L. Zadeh [2] and Ch. Desoer, V. Strejc [3], V. Kuntsevych [4]. In terms of computer simulations, the modeling method, which is based on discrete state equations, is the most promising [5, 6]. In terms of mathematics, this approach is the most formalized and has practical applications in different areas.

The construction of dynamic models of electrical and electronic circuits was made using optimization approach. This approach was used by P. Stakhiv and Y. Kozak [7,8,9]. This approach makes it possible to build universal models. However, such universalization leads to the appearance of complex optimization problems that are difficult to resolve in a reasonable time, even using modern computer technologies.

There is an actual problem to develop such construction methods of models that would be subjected to the implementation on available computer technologies and provide the necessary performance.

Therefore, there is a need to develop sufficiently universal algorithms for construction of discrete dynamical models using parallelization by which you can effectively build the models for ecological, electricity and other complex systems.

Recently, increasingly researchers use GPUs for accelerating results of mathematical modeling. For examples, A. Kłusek, P. Topa, J. Wąs, R. Lubaś [10] use GPU for social distances model, B. Hamilton, C. Webb. [11] for room acoustics modelling, J. Schalkwijk, H. Jonker, A. Siebesma, E. Meijgaard [12] for weather forecast model.

2 Parallelization Method of Optimization Procedures for Constructing of Discrete Dynamical Models

Let’s consider the generalized mathematical model in the form of state Eqs. (1):

$$ \left\{ {\begin{array}{*{20}c} {\vec{x}^{{\left( {k + 1} \right)}} = F\vec{x}^{\left( k \right)} + G\vec{v}^{\left( k \right)} + \overrightarrow {\Phi } \left( {\vec{x}^{\left( k \right)} ,\vec{v}^{\left( k \right)} } \right)} \\ {\vec{y}^{{\left( {k + 1} \right)}} = C\vec{x}^{{\left( {k + 1} \right)}} + D\vec{v}^{{\left( {k + 1} \right)}} } \\ \end{array} ,} \right. $$
(1)

where \(\vec{x}^{\left( k \right)}\) – the vector of state variables; \(\vec{v}^{\left( k \right)}\) – the input vector; \(\vec{y}^{{\left( {k + 1} \right)}}\) – the output vector; \(F,G,C,D\) – matrixes with unknown coefficients; \(\overrightarrow {\Phi }\) – the nonlinear vector-function with many variables.

This form of model (1) is characterized by some vector of unknown parameters \(\vec{\lambda }\). This vector for this model consists of the elements of matrixes \(F,G,C,D\) and coefficients of the vector-function \(\overrightarrow {\Phi } \left( {\vec{x}^{\left( k \right)} ,\vec{v}^{\left( k \right)} } \right)\).

\(Q\left( {\vec{\lambda }} \right) > 0\) is the criterion for the precision measuring of the model, which determines the deviation of the behavior of the model from the behavior of the simulated object for the known periods of time. The function \(Q\left( {\vec{\lambda }} \right)\) is called the objective function. This function is calculated as a root-mean-square error of model’s values:

$$ Q\left( {\vec{\lambda }} \right) = \sum \left( {\vec{y} - \vec{y}^{*} \left( {\vec{\lambda }} \right)} \right)^{2} , $$
(2)

where \(\vec{y}\) – known characteristics of modeled object, \(\vec{y}^{*} \left( {\vec{\lambda }} \right)\) – transient response that are calculated using the model.

Therefore, the construction of the model can be reduced to calculation values of the vector \(\vec{\lambda }\), when the objective function will be minimal. This problem is solved using the optimization algorithm [13].

The task of finding the minimum point of the nonlinear function \(Q\left( {\vec{\lambda }} \right)\) with many variables is difficult. In discrete dynamic models’ construction, the objective function is a “ravine” with many local minima. For the solution of such problems the Rastrigin’s method of a director cone has the best characteristics [14]. Purposeful scan of local minima can be done using this approach. It accelerates finding of the global minimum of the objective function. But the computational complexity of this problem is quite huge. Also, the significant number of input data is used for the construction of the qualitative model. Consequently, the execution time of the implementation of optimization procedures is also significant [15].

The time complexity of Rastrigin’s optimization algorithm [14] depends linearly on the number of known discrete values from in known function. Accordingly, the computational complexity of the problem will be proportional to the amount of input, not the order of created model. For building a quality model it’s necessary to use a large amount of data for calculating the value of the objective function. Therefore, the time spent of calculation the values of functions will also be significant.

The parallelization of this task using SIMD-architecture was proposed in the article [16]. This architecture allows performing the same thread of instructions for many threads of data. Taking into this approach, the objective function for different values of vector \(\vec{\lambda }\) is calculate independently. Each objective function will be calculated on a separate core of GPU.

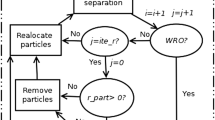
The flowchart diagram of the parallelization algorithm is presented on Fig. 1.

Today the available devices with SIMD-architecture and with better ratio performance/price are the GPUs (Graphics Processing Unit) [17, 18]. Therefore, the proposed algorithm was adapted for these computing accelerators.

In terms of software implementation, the parallelization does not require large expenditures through programming architecture of GPU [19, 20].

According to this proposed algorithm, the selection of each point will be made in a separate thread, which will be executed parallelly. Also, the calculation of the value of the objective function \(Q_{i + 1}^{\left( 1 \right)} , \ldots , Q_{i + 1}^{\left( m \right)}\) in \(m\) points will also be executing out on separate threads.

Same program code is sent to all threads. The input data for each thread are parameters of the next hypercone, they are the same for all threads. The value of objective function is received in each entrance of thread. This value is calculated in random point of hypercone. This value will be different for each thread. All output data is stored in the shared-memory of threads for further calculation of the minimum [21, 22].

The CUDA (Compute Unified Device Architecture) technology was used for programming implementation of parallelization algorithm [20, 23]. Currently the computing using GPUs and CUDA is an innovative combination of features of new generation of graphics processors NVIDIA, that process thousands of threads with high information loading. These features are available through programming language C [17, 24].

3 Discrete Dynamical Model for Sulfur Dioxide Emission Prediction

Today the problem of environmental protection is becoming one of the most important tasks of science, the development of which is accelerated rapidly by technological progress in all countries of the world. The rapid development of industry and the significant growth of traffic flows contribute to the emergence of an acute problem - the protection of ecological systems. In recent decades, ecological systems have been influenced significantly by anthropogenic factors. Therefore, prediction of characteristics changes in such systems is an actual task.

Fig. 1.
figure 1

Flowchart of the parallel algorithm of Rastrigin’s director cone [16]

Full size image

A dangerous environmental situation has already emerged today due to the negative impact of industry in many regions. In particular, pollution of rivers, the air pool, pollution of the landscape, the destruction of forests, vegetation, wildlife, the fertile layer, pollution of groundwater, acoustic, electromagnetic and electrostatic pollution.

For example, the air pool is polluted with gas and aerosol emissions (CO2, polycyclic aromatic hydrocarbons, CO, NOx, SOx, ash, soot and others). Emissions are occurred during the combustion of liquid and solid fuels, which form aerosols when released into the atmosphere. Aerosols can be non-toxic (ash) and toxic (C20H12 is a potent carcinogenic compound). Also, gas emissions can be toxic (NO2, SO2, NO, CO and others) and non-toxic (CO2, H2O). All triatomic gases (H2O, NO2, SO2, and especially CO2) belong to “greenhouse gases”. When gas emissions are released into the atmosphere, they have a complex physicochemical and biological effect on living organisms and humans, the level and character of which depend on their concentration in the air.

The combined effects of gas and aerosol emissions from energy objects can lead to various adverse environmental effects, including crises in the biosphere, such as deterioration of atmospheric transparency, rainfall and acid rain, greenhouse effect.

Therefore, it is important to predict the concentrations of harmful emissions into the atmosphere to prevent environmental problems and respond promptly.

Let’s build a model for prediction of emissions into the atmosphere. Model inputs are weekly averages values of emissions of SO2 (sulfur dioxide) into the air in Żywiec (Poland) in 2018 [25]. It is necessary to create a mathematical model that based on this data. This model should be able to predict the emission of SO2 into the air in 2019.

Let’s building the autonomous discrete dynamic model of the third order for testing of the efficiency of the parallel program of calculation of the objective function. This model has the following form:

$$ \left\{ {\begin{array}{*{20}l} {\left( {\begin{array}{*{20}c} {x_{1}^{{\left( {k + 1} \right)}} } \\ {x_{2}^{{\left( {k + 1} \right)}} } \\ {x_{3}^{{\left( {k + 1} \right)}} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {F_{11} } & {F_{12} } & {F_{13} } \\ {F_{21} } & {F_{22} } & {F_{22} } \\ {F_{31} } & {F_{32} } & {F_{33} } \\ \end{array} } \right) \cdot \left( {\begin{array}{*{20}c} {x_{1}^{\left( k \right)} } \\ {x_{2}^{\left( k \right)} } \\ {x_{3}^{\left( k \right)} } \\ \end{array} } \right)} \hfill \\ {\left( {\begin{array}{*{20}c} {y_{1}^{{\left( {k + 1} \right)}} } \\ {y_{2}^{{\left( {k + 1} \right)}} } \\ {y_{3}^{{\left( {k + 1} \right)}} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {C_{1} } & {C_{2} } & {C_{3} } \\ \end{array} } \right) \cdot \left( {\begin{array}{*{20}c} {x_{1}^{{\left( {k + 1} \right)}} } \\ {x_{2}^{{\left( {k + 1} \right)}} } \\ {x_{3}^{{\left( {k + 1} \right)}} } \\ \end{array} } \right)} \hfill \\ \end{array} } \right., $$
(3)

where \(k = 1, \ldots ,52\).

The objective function is:

$$ Q\left( {\vec{\lambda }_{i} } \right) = \sum\nolimits_{i} {\left| {\left( {\begin{array}{*{20}c} {y_{1} } \\ {y_{2} } \\ {y_{3} } \\ \end{array} } \right) - \left( {\begin{array}{*{20}c} {y_{1}^{*} } \\ {y_{2}^{*} } \\ {y_{3}^{*} } \\ \end{array} } \right)} \right|^{2} .} $$
(4)

4 Research of Efficiency of Parallel Model

Let’s test the program for calculation of the objective function. The following hardware and system software were used for these tests:

  • GPU NVIDIA GeForce GTS250 (16 multiprocessors with 8 cores each);

  • RAM 1024 MB;

  • CPU Core2Duo E8400, 3 GHz;

  • motherboard ASRock G41M-S3.

Let’s considering the performance time of the parallel program for calculation of the objective function on 128 GPU cores. The average time (with 100 launches) of parallel computing of the objective function is 2.74 ms.

Then let’s research the change of the execution time of the program respecting the change of the model order (see on Fig. 2). Obviously, the execution time of parallel calculation of the objective functions will gradually increase with increase of the order of the constructed model.

Fig. 2.
figure 2

Dependence of the execution time of the parallel program on the model order

Full size image

When the number of discrete values will increase, then the execution time of parallel calculation of the objective function will gradually increase (see on Fig. 3).

Fig. 3.
figure 3

Dependence of the execution time of the parallel program on the number of discrete values of model

Full size image

It is also interesting to compare the dependence of the execution time of all the calculations of objective functions on the number of calculations of the objective function. Namely, with different number of threads on GPU. Obviously, such dependence is linear for sequential calculations. This dependence is shown on Fig. 4.

Fig. 4.
figure 4

Dependence of the execution time of the parallel program from the of threads

Full size image

As it is shown on Fig. 4, this dependence is periodic. Since the execution time was calculated along with the data transfer, then there are constant delays in each cycle of optimization algorithm. If we reject these delays then we will see that the periodicity is repeated every 128 threads. Therefore, it is expedient to use the parallelization when the number of threads is a multiple number of GPU cores. In this case it is 128 cores. Then the parallelization will be the most effective.

Build 3D-graph of the dependence of the execution time of the parallel program on the number of threads and the number of GPU blocks (see on Fig. 5).

Fig. 5.
figure 5

Dependence of the execution time of the parallel program on the number of threads and the number of blocks

Full size image

The proposed approach of parallel computing can be used with different optimization algorithms. Therefore, the execution time of the algorithm is not taken into account. In practice, the execution time of the algorithm is less than the required time of calculations of the objective function.

The CPU performance is much higher than the performance of one GPU core. However, the parallel realization will be more effective while calculating the objective function for many sets of the coefficients [20]. Thus, the more calculations of the objective function we conduct, the more efficient will be the parallelization process of construction of discrete dynamical models.

The execution time of the parallel program in one core of GPU is shown on Fig. 6.

Fig. 6.
figure 6

Execution time of the parallel program in one core of GPU

Full size image

As it is shown on Fig. 6, parallelization will be effective when there are a large number of calculations of objective function. Results on Fig. 6 show, that we were able to reduce a computational time from 2 ms to 0.02 ms on 1 and 128 GPU cores respectively, which gives us a speedup  =  100 and parallelization efficiency  =  78.1%.

The construction of such model was performed on central and graphic processing units. Let’s compare the execution time of sequential program and parallel program for constructing a discrete dynamic model. To do this, let's determine the dependence of the model identification time on the number of points that generated on the hypercone (Fig. 7).

Figure 7 shows that the time of sequential program with increasing generated points is increasing gradually, and the time of the parallel program remains constant relatively.

Also, Fig. 7 confirms that the more calculations of the objective function are performed then the more efficient will be the parallelization of discrete dynamic models construction process.

Figure 7 shows the runtime values for one iteration. And for building an accurate model it is necessary to perform thousands, tens of thousands of iterations of calculation of objective function \(Q_{i + 1}^{\left( 1 \right)} , \ldots , Q_{i + 1}^{\left( m \right)}\) in \(m\) points.

The parallelization coefficient of this algorithm can be estimated from the fact that the cost of calculation of the value of the objective function significantly exceeds the computational cost of making decisions according to the optimization algorithm. Since in the parallel implementation of calculation the value of the objective function in different points is performed independently, then the parallelization coefficient is close to the number of processors (provided that the number of calculations of the objective function is multiplied by one step of the optimization procedure).

Fig. 7.
figure 7

Execution time on CPU and on GPU

Full size image

5 Conclusions

A parallel model for the prediction of sulfur dioxide emissions into the air of Żywiec city (Poland) based on historical observations is built and researched in this paper. The construction of this model using traditional sequential algorithm without its parallelization is failed. Because the construction of such model requires tens of thousands of iterations of calculations and computer’s RAM is not enough for it. We have obtained a parallelization efficiency of 78.1% while executing the constructed parallel model on GPU Nvidia GTS250. We also conducted the comparison of the execution time of parallel model respecting the model order, the number of discrete values, the number of GPU threads and the number of GPU blocks. The obtained research results suggest that the constructing discrete dynamic models must include the efficient use of parallel computing resources nowadays.