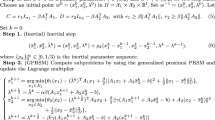Keywords

1 Introduction

Many recent works in three dimensional (3D) reconstruction using Structure-from-Motion (SfM) algorithms has focused on building systems [1, 9, 19] that are capable of handling millions of images from unstructured internet photo collections. Given the feature matches between images, bundle adjustment (BA) [21] is a key component in most SfM systems. It is typically used as the last step in a 3D reconstruction pipeline. For large scale problems however, BA becomes very expensive computationally and thus, creates a bottleneck in the SfM systems. As a result, there has been a lot of interest in developing scalable large scale bundle adjustment algorithms [2, 5, 7, 11, 22].

The BA problem is typically formulated as the minimization of a nonlinear least squares problem, which can be done by using a classical algorithm such as the Levenberg-Marquardt (LM) algorithm. In each iteration of the LM algorithm, a solution to a linear system is required, which is the most computationally expensive step. A lot of research has been focused on making this step cheaper.

In [16], a direct method using Dense Cholesky factorization has been proposed. However, these methods do not scale well as the problem size increases. This has led to the application of iterative methods, specifically the Conjugate Gradient (CG) [18] method, for solving these systems. The convergence of these methods depend upon the condition number of the coefficient matrix. However, it has been observed that BA problems are very ill-conditioned. To solve this problem, preconditioning matrices or preconditioners [18] are applied to the system. They lower the condition number of the systems, which in turn speeds up the convergence of the iterative methods.

In this paper, we propose a new preconditioner which is based on the domain decomposition of the coefficient matrix. As it has been pointed out in [2]: “each point in the SfM problem is a domain, and the cameras form the interface between these domains”. Using the domain decomposition method, we present a technique that can be used for approximating the global Schur complement of the matrix. We name this preconditioner as Mini Schur Complement (MSC) preconditioner. One of the advantages of using this preconditioner is that it is sparse, highly parallelizable and can be scaled up for very large problems. However, the preconditioned operator is unsymmetric. Thus, we use another iterative method known as restarted generalized minimal residual (GMRES). As the results show, solving the normal equations using GMRES preconditioned with MSC gives state-of-the-art performance on the BAL dataset.

The remaining part of the paper is organized as follows. Section 2 introduces the BA problem and also gives a review of the recent work on the use of preconditioned iterative methods. Section 3 gives a brief overview of domain decomposition methods and describes the design and implementation of the MSC preconditioner. Section 4 compares the results of our technique with direct solver and block Jacobi preconditioned GMRES solver. In Sect. 5, we conclude with a discussion.

2 Bundle Adjustment

Bundle adjustment tries to minimize the sum of reprojection errors between the 2D observations and the reprojected 2D points which are determined by the point and camera parameters. More information about this process can be found in [21].

Suppose that the scene to be reconstructed consists of p 3D points (or features), individually denoted as \(y_i, i = 1, \ldots , p,\) and these points are imaged in q cameras, whose individual parameters are denoted as \(z_k, k = 1, \ldots , q.\) Assume that the structure (point) and camera parameters to be estimated are taken in a large state vector \(x \in \mathbb {R}^{(p + q)}\) which has the block structure \(x = [y_1, \ldots , y_p, z_1, \ldots , z_q]^T.\) Then, the reprojection error is defined as \(f_k(x) = r_k(x) - m_{xk} , \text { for k = 1,} \dots , {\text{ q }.}\) Given the mean reprojection error for each camera, the unknown 3D point and camera parameters can be estimated by minimizing the total reprojection error. Define \(F(x) = [f_1(x), \ldots , f_q(x)]^T\) to be a q-dimensional function of the given parameter vector x. Then, the bundle adjustment problem can be stated as

$$\begin{aligned} x^* = \underset{x}{argmin} \frac{1}{2} ||F(x)||_{2}^{2}. \end{aligned}$$
(1)

In (1), the objective function is non-linear. For solving non-linear least squares problems of this form, the Levenberg-Marquardt (LM) algorithm [3, 15, 17] is applied. It is an iterative method where, in each iteration, an affine approximation of the cost function F(x) in a neighbourhood of the current iterate \(x_{t},\) is minimized. It is shown in [3] that the next iterate \(x_{t+1}\) can be computed as

$$\begin{aligned} x_{t+1} = x_t - (J^T J + \lambda ^t\mathtt{diag}(J^T J))^{-1}J^T F(x_t). \end{aligned}$$
(2)

Let \(H_{LM} = J^T J + \lambda ^t \mathtt{diag}(J^T J)\) and \(g = J^T F(x_t).\) Here, J is the Jacobian of F(x) at \(x_t\) and \(\lambda ^t > 0\) is a damping parameter which ensures that \(x_{t+1}\) lies in a neighbourhood of \(x_t.\) It should be noted that the definition of \(H_{LM}\) results in an approximation of the Hessian. Then, rearranging the terms in (2) gives

$$\begin{aligned} H_{LM}\varDelta x = -g, \text { where }\varDelta x = x_{t+1} - x_t. \end{aligned}$$
(3)

The Hessian \(H_{LM}\) is symmetric and positive definite (SPD). Thus, (3) can be solved as \(\varDelta x = -H_{LM}^{-1}g\) to get the exact solution. However, when the problem size becomes large, computing the inverse of \(H_{LM}\) becomes expensive. In these cases, an inexact solution of the system (3) can be computed by using an iterative method, such as GMRES. The convergence of the iterative methods depend on the condition number of the coefficient matrix, the Hessian in this case. For badly conditioned problems, such as bundle adjustment, the condition number can be improved with the help of a preconditioner [18]. This paper proposes the design and implementation of such a preconditioner, which exploits the special structure of the Hessian \(H_{LM}.\)

2.1 Structure of the Hessian

In the state vector x defined in Sect. 2, let s be the size of each point block and c be the size of each camera block. For the BAL dataset used in this paper, \(c = 9\) and \(s = 3.\) Given these block sizes, the Jacobian J can be partitioned into a point part \(J_{s}\) and camera part \(J_{c}\) as \(J = [J_{s};J_{c}],\) which gives

$$\begin{aligned} H_{LM} = \begin{bmatrix} \begin{matrix} J^{T}_{s}J_{s} &{} J^{T}_{s}J_{c} \\ J^{T}_{c}J_{s} &{} J^{T}_{c}J_{c} \end{matrix} \end{bmatrix} = \begin{bmatrix} \begin{matrix} D &{} L^{T} \\ L &{} G \end{matrix} \end{bmatrix}. \end{aligned}$$
(4)

Here, \(D \in \mathbb {R}^{ps\times ps}\) is a block diagonal matrix with p blocks such that each block is of size \(s \times s\) and \(G \in \mathbb {R}^{qc \times qc}\) is a block diagonal matrix with q blocks such that each block is of size \(c \times c\). The matrix \(L \in \mathbb {R}^{qc \times ps}\) is a general block sparse matrix. Thus, we can rewrite (3) as a block structured linear system as follows

$$\begin{aligned} \begin{bmatrix} \begin{matrix} D &{} L^T \\ L &{} G \end{matrix} \end{bmatrix} \begin{bmatrix} \begin{matrix} \varDelta x_s \\ \varDelta x_c \end{matrix} \end{bmatrix} = \begin{bmatrix} \begin{matrix} g_s \\ g_c \end{matrix} \end{bmatrix}, \end{aligned}$$
(5)

where \(\varDelta x = [\varDelta x_s; \varDelta x_c], \varDelta x_{s}\, \text {and}\, \varDelta x_c\) correspond to point parameter blocks and camera parameter blocks of \(\varDelta x\), respectively, and \(g = [g_s ; g_c],\) \(g_{s} \text { and } g_c\) correspond to point and camera parameter blocks of g, respectively. Different approaches have been proposed for solving (5), which exploits the special structure of the Hessian.

2.2 Previous Work

For solving (5), direct methods have been well studied in literature [16, 21]. In [4], the special structure of the Hessian is exploited to solve the system using a reduced camera system and a reduced structure system. A survey of various direct and iterative methods as well the use of various preconditioners can be found in [21]. Cholesky factorization is used for solving the reduced camera system in [16]. However, for large scale problems, this method does not scale satisfactorily.

An advantage of using iterative methods, such as CG, is that these methods require less memory compared to direct methods. This is because these methods require only matrix-vector products. However, since BA problems are very badly conditioned, recent research has focused on obtaining efficient preconditioners to speed up the convergence of these methods. In [2], several classical preconditioners have been implemented and their impact on large scale problems is shown. In [6], Preconditioned Conjugate Gradients (PCG) is used for solving (5) with an incomplete QR factorization based preconditioner. In [22], PCG is used for solving the reduced camera system with the bandwidth limited block diagonal of the Schur complement as the preconditioner. [7] exploits hardware parallelism on multicore CPUs as well as multicore GPUs to solve the BA problem by a new inexact Newton type method. Avanish et al. [14] utilizes the camera-point visibility structure in the scene to form block diagonal and block tridiagonal preconditioners. [11] explores a generalized subgraph preconditioning (GSP) technique which is based on the combinatorial structure of the BA problem. In [12], a preconditioner based on a deflated two grid methods is used with GMRES as the iterative method.

Usually for small to medium sized problems, direct methods converge faster than iterative methods. In this paper, we show that our method is more memory efficient than direct methods and faster than iterative methods preconditioned with block Jacobi, for small to medium problems, to converge to a comparable mean reprojection error. Also, it has been observed that the construction of the MSC preconditioner does not take much time.

3 Domain Decomposition Method

Domain decomposition (DD) methods refer to a class of divide-and-conquer techniques, that have been primarily developed for solving Partial Differential Equations over regions in two or three dimensions. However, the principles used in this techniques have also been exploited in other fields of scientific and engineering computational problems. The DD methods attempt to solve the problem on the entire domain from problem solutions to the subdomains. For more details, see [18, 20]. One of the most widely used non-overlapping DD methods is the Schur complement method, which is described below.

Consider the following block triangular factorization of \(H_{LM}\):

$$\begin{aligned} H_{LM} = \begin{bmatrix} \begin{matrix} D &{} L^{T} \\ L &{} G \end{matrix} \end{bmatrix} = \begin{bmatrix} \begin{matrix} I_{D} &{} 0 \\ LD^{-1} &{} I_{G} \end{matrix} \end{bmatrix} \begin{bmatrix} \begin{matrix} D &{} L^{T} \\ 0 &{} S \end{matrix} \end{bmatrix} \end{aligned}$$

where \(I_{D} \in \mathbb {R}^{ps \times ps}\) and \(I_{G} \in \mathbb {R}^{qc \times qc}\), are identity matrices. Here, \(S = G - LD^{-1}L^{T}\) is the Schur complement of D in \(H_{LM}.\) It has been observed that the construction of S for large problems becomes computationally expensive. Also, the Cholesky decomposition of S leads to dense factors, even though S remains sparse. Here, we present a technique for approximating the Schur complement and design a preconditioner using this approximation.

3.1 The Mini Schur Complement Preconditioner

In [13], several methods for approximation of the global Schur complement S have been mentioned. Here, we construct the Mini Schur Complements (MSC) using the MSC based on Numbering (MSCN) scheme, which is described below.

We consider the block \(2 \times 2\) partitioned system in (4). The matrix \(H_{LM}\) is further partitioned as follows.

(6)

Now, a further approximation of the matrix in (6) is constructed by dropping the blocks \(D_{ij}, L^{T}_{ij},L_{ij}\) and \(G_{ij}\) for which \(i \ne j\). Thus the following approximation \(\hat{H}_{2}\) is obtained.

(7)

Here, the subscript 2 in \(\hat{H}_{2}\) denotes the number of principal sub-matrices of the matrix G, namely, \(G_{11}\) and \(G_{22}.\) The matrix in (7) is further partitioned to get the following matrix

(8)

Again, a sparse approximation of (8) is done by dropping the blocks \(\hat{D}_{ij}, \hat{L}_{ij}^T, \hat{L}_{ij}\) and \(\hat{G}_{ij}\) for which \(i \ne j,\) to obtain the following matrix

Here the subscript 4 in \(\hat{H}_{4}\) denotes the number of principal sub-matrices of matrix G. Eliminating the blocks \(\hat{L}_{ii}\) by using \(\hat{D}_{ii}\) as a pivot, we obtain an approximation to the global Schur complement S by \(\hat{S_{4}} = \mathtt{blkDiag}(S_{ii})\) where \(S_{ii} = \hat{G}_{ii} - \hat{L}_{ii}\hat{D}_{ii}^{-1}\hat{L}_{ii}^{T}\).

The matrix \(S_{ii}\) is called a Mini Schur Complement (MSC). Here, for simplicity, we have partitioned the matrix recursively into a block \(2\, \times \, 2\) matrix. During implementation, by taking advantage of the sparsity structure of the Hessian \(H_{LM}\) and the information about the size of the blocks, we could directly identify the blocks \(\hat{G}_{ii},\hat{D}_{ii}, \hat{L}_{ii}^T\) and \(\hat{L}_{ii},\) such that \(S_{ii}\) is computed as \(S_{ii} = G_{ii} - L_{ii}D_{ii}^{-1}L_{ii}^{T}, \, \text {where } i = 1: m \) and m is the number of MSCs desired.

Fig. 1.
figure 1

The first two plots show the Schur complement of ladybug-372 and ladybug-885 respectively. The third and fourth plots show their respective MSC approximations (\(m=30\) blocks).

Full size image

MSC Preconditioner: Let \(\hat{S}_{m}\) denote the Schur complement approximation computed from m MSCs. Then we construct the MSC preconditioner as

Here D and \(\hat{S}_{m}\) have a block diagonal structure and also, D and L blocks are already available from the coefficient matrix \(H_{LM}.\) Thus, storing the required blocks of the MSC preconditioner does not require much extra memory. In Fig. 1, the Schur complement and the Mini Schur Complement approximation of two problems are shown. It can be seen that the MSC approximation has a lot more sparsity than the global Schur complement.

4 Experimental Evaluation

4.1 Implementation Details

For performing the experiments, we select block D such that the number of rows (and columns) of D is given by 3 \(\times \) (number of points) and block G such that the number of rows (and columns) is given by 9 \(\times \) (number of cameras). The information about the number of points and the number of cameras are available in the dataset. We construct the block Jacobi preconditioner as \(P_{jac} = \mathtt{blkdiag}(D,G)\) (as shown in [2]), where blkdiag forms a block diagonal matrix using the given blocks. For constructing the MSC preconditioner, the number of MSC blocks is taken as 30 blocks.

For the Levenberg-Marquardt algorithm, we use a freely available sparse C++ implementation (SSBA)Footnote 1, which has several cost functions that are used by the LM algorithm for the BA step. Out of these, we choose the bundle_large_lifted_schur cost function implemented in the SSBA package, which is discussed in detail in [23]. The LM algorithm runs for 100 iterations, or till the difference in norms of two consecutive residuals is not less than \(10^{-12}\) in magnitude, whichever criterion is met first. For solving the normal equations in (3) using direct method, SSBA uses LDL factorization [10], which is a Cholesky like factorization method for sparse symmetric positive definite matrices. COLAMD is applied for appropriate column reordering. Both LDL and COLAMD have been adopted from the SuiteSparse package [8].

We experimented with Preconditioned Conjugate Gradient(PCG) as the iterative solver but the results we got using \(P_{jac}\) as a preconditioner were not encouraging. Hence, we implement an MSC preconditioned GMRES with restarts and warm starts [3, p. 393] as an iterative solver in the SSBA package, for solving (3). The restart parameter is taken as 40, thus forming a Krylov subspace of 40 vectors. The GMRES algorithm runs as long as the number of iterations is less than 100 or the norm of the relative residual is not less than \(10^{-2}\) (as taken in [2]), whichever comes first. The GMRES method is implemented using the dfgmres routine available in the INTEL MKL library, version 2019.4.243. All of the experiments are performed on a subset of problems from the BAL dataset [2]. We run all of the experiments on a machine with Intel Pentium(R) processor and 8 GB of RAM. As all the problems from the BAL dataset cannot fit into memory, we select 8 problems for which the number of points varies from 7K to 226K.

4.2 Results

We compare the direct solve, specifically, the LDL factorization method and the restarted GMRES preconditioned with two preconditioners: (1) block Jacobi preconditioner and (2) MSC preconditioner. The problems have been selected from the BAL dataset. We experimented with different number of MSC blocks and found that taking 30 blocks gave optimal results.

Table 1. Average time (in seconds) per iteration for the LM solver using the three methods on 8 problems from the BAL datasets using the bundle_large_lifted_schur cost function routine in SSBA. The time in bold represents the faster of the two preconditioners for iterative solve. The problems are prefixed as: L for LadyBug, TS for Trafalgar Square and D for Dubrovnik.
Full size table

In Table 1, the time per LM iteration and the mean reprojection error for various methods are shown. As we have tested mostly on small to medium sized problems, we observe that direct solve is faster than iterative solve for these problems. However, as can be seen from Fig. 3, the memory requirement for direct solver increases with increase in problem size. Thus, iterative solvers are essential for very large problems. In Table 1, it can be seen that using MSC as a preconditioner results in faster computation time than using block Jacobi as a preconditioner.

Also, from Fig. 3 it can be seen that the MSC preconditioned GMRES is the most memory efficient of the three methods. In Fig. 3, as the number of cameras increases, the size of the L, D factors of block G also increases. Thus, doing an LDL factorization of block G during block Jacobi preconditioner solve requires more time compared to that of MSC, as seen in Fig. 4. Thus, for larger problems, using MSC as a preconditioner is a much better option for a memory constrained system (Fig. 3).

Fig. 2.
figure 2

Plot showing the total time taken for 100 iterations of the Levenberg Marquardt algorithm, using direct solve, block Jacobi preconditioned GMRES and MSC preconditioned GMRES.

Full size image
Fig. 3.
figure 3

Plot showing the memory requirement for the three methods for the 4 largest problems in our paper, as the number of cameras increases. We have plotted the memory for the three methods: L, D factors for direct solve, L, D factors of block G alongwith the Krylov subspace and the memory for storing the MSC block, its L, D factors as well as the Krylov subspace.

Full size image
Fig. 4.
figure 4

Plot showing the time taken for LDL factorization of the G block and the MSC block.

Full size image

5 Conclusions and Future Work

We proposed a technique for the approximation of the global Schur complement and used this approximation to design a preconditioner. We showed some preliminary results which were obtained by implementing our technique as a sequential code. As seen in Fig. 3, this solver has much less memory requirement than the other methods mentioned in the paper, and is also faster than using block Jacobi as a preconditioner. This makes using MSC as a preconditioner a much better choice. Also, since the MSC blocks are non-overlapping, they are independent of each other. Thus, one possible direction of future work is a parallel implementation of the proposed solver. Another direction would be to assess the robustness of the solver for very large scale problems.