Material Study and Fabrication of the Next-Generation Urban Unmanned Aerial Vehicle: Aarush X2

Abstract

Composite designing and airframe fabrication to develop a lightweight, robust, and high-endurance unmanned aerial vehicle (UAV) Aarush X2, next-generation urban unmanned aerial vehicle, are presented in this paper. The composite study investigated the structural feasibility of various lay-ups and fibre orientations using analytical model. The research is performed on the sandwich composite configuration of Divinycell, core, and carbon fibre-reinforced plastic (CFRP), facesheet, bonded with the epoxy matrix of AY-105 (resin) and HY-951 (hardener). The study presented five plies, [0/90/Divinycell/0/90], lay-up to sustain structural loads with the least gross take-off weight (GTOW) for manufacturing the UAV. The fabrication of the UAV was carried out using vacuum-assisted wet lay-up method (VAWLM) and demonstrated a total weight of the airframe 12.1 kg. The flight tests of around 30 h validated the structural capability of the designed sandwich composite along with the fabrication technique selected. The averaged flight time of 2.8 h on a two-stroke gasoline engine, DLE-61, with fuel tank capacity of 1.8 litres was recorded.

1 Introduction

In the aerospace industry, composite materials are widely used because of the high strength and lightweight characteristics offered. As follows, the mechanical prediction of the composite materials has become an active topic of research and has been studied at many diverse scales to tailor the properties. The micromechanical models such as laminate plate theory present a practical approach while designing the composite structures to investigate various fibre orientations, ply thicknesses, volume fractions, and material plies. However, designing the composite alone will not generate a strong and lightweight structure. The composite fabrication process plays a critical role in the manufacturing of a robust structure without defects.

In general, the plate deformation studies are based on the stress and displacement theories, where the broadly accepted displacement plate theory is divided into the laminate plate theory (classical laminate plate theory, CLPT) and shear deformation plate theories (first-order shear deformation theory, FOSDT, and further higher-order shear deformation theory; HOSDT) [1]. In the late nineteenth century, Kirchhoff [2] introduced the CLPT which was later improved by Love [3] in the early twentieth century. The CLPT is a quick and simple approach to predict the mechanical properties of the composite laminates [4]. However, it fits merely for the thin laminate; therefore, thick plate theories such as FOSDT and other HOSDT were formed to predict the solution [5].

The FOSDT developed by Reissner [6] and Mindlin [7] considered the effect due to the transverse shear deformation which was earlier not included in the CLPT. This addition helps FOSDT to study both thin and thick composite laminates. In these studies [6, 7], the displacement w persists to be constant along the thickness; however, the displacements u and v fluctuate linearly along the thickness of each individual layer. FOSDT is more practical than CLPT as the shear strain field is irregular at the linear interface and the displacement results allow composite collapsing. The shear correction factors ascertain the zero transverse shear conditions at the upper and lower plate surfaces. The correction factors are accountable for the accuracy between the numerical solution and the actual data [8]. Most of the structures developed using composites introduce advantages in the physical properties through fibre orientations and thicknesses. Sandhu et al. [9] demonstrated the mechanical effects on a unidirectional composite when the fibre orientations were changed for the plies. This study determined the orientation of the fibre plies for the maximum strength under a biaxial state of stress. The ability to maximise the in-plane stresses of the unidirectional composite was revealed by Brandmaier [10].

The fabrication of the composite is a critical step to construct a strong and lightweight aircraft structure. Dagur et al. [11] presented the utilisation of the vacuum-assisted wet lay-up method (VAWLM) for the sandwich composite fabrication. VAWLM eliminates the excess epoxy from the wetted lay-ups, which supports in reducing the physical weight by developing epoxy consistency in the fabricated composite. The study further claimed that the elevated temperature of the epoxy matrix impregnated in the composite thrusts the air pockets upward and simultaneously eliminated through the vacuum pump connected.

In this research, micromechanical designing and fabrication of the composite unmanned aerial vehicle were investigated. The specific objectives were: (i) to formulate FOSDT model for a sandwich composite, (ii) to optimise ply layers and orientation of the sandwich composite, (iii) to apply formulated FOSDT on fuselage and wing of Aarush X2, (iv) to fabricate Aarush X2 with the designed sandwich composite, (v) to perform flight testing of the Aarush X2.

2 Mathematical Formulation

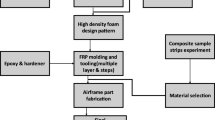
The mathematical modelling of the Divinycell CFRP sandwich laminate was performed to calculate the optimum number of layers and fibre orientations. The entire mathematical designing of the composite is illustrated in Fig. 1. The sandwich composite is an arranged combination of three-section, two facesheets (here CFRP as top/bottom layers) and a core (here Divinycell; centre), as shown in Fig. 2. Each layer of the sandwich composite was modelled with the FOSDT and based upon the following assumptions

Fig. 1

FOSDT approach followed in the present study

Fig. 2

Dimensions and geometry of the sandwich composite

• 1. The thickness of the facesheets, $h_{t,b}$, is relatively lower than the core thickness, $h_{c}$.

• 2. Insignificant in-plane stresses in the core.

• 3. The in-plane displacements remain consistent along with the thickness of the facesheet.

• 4. The out-of-plane displacement is free from the $z$-coordinate.

• 5. Linear in-plane displacements of the core along $z$-coordinate.

2.1 Displacement Field

The displacement field expressed for the core and the facesheet in the FOSDT were as follows

Core:

$${\text{Bottom}}:u = u_{0} - \frac{{(h_{c} + h_{1} )}}{2}\psi_{x} ,u = v_{0} - \frac{{(h_{c} + h_{1} )}}{2}\psi_{y}$$

$${\text{Top}}:u = u_{0} + \frac{{(h_{c} + h_{2} )}}{2}\psi_{x} ,u = v_{0} + \frac{{(h_{c} + h_{2} )}}{2}\psi_{y}$$

$$w = w_{0}$$

where $u,v,$ and $w$ are in-plane displacements in the $x$,$y$, and $z$ directions, respectively; $u_{0}$, $v_{0}$, and $w_{0}$ are mid-plane displacements in the $x$,$y$, and $z$ directions, respectively; $\psi_{x}$, $\psi_{y}$ are rotations of the cross sections.

The displacement field continuity at the top and bottom facesheet interface generates the displacement as shown in Fig. 2. The top and bottom here were refereed as the upper and bottom layer of the sandwich composite.

The subscript and superscript $t,b,$ and $c$ represent the top facesheet, bottom facesheet, and the core.

Top Facesheet

The displacement field adopted for the facesheet from Fig. 2 was defined as

$$\begin{aligned} u_{t} & = u_{c} \left( {\frac{{h_{c} }}{2}} \right) + \left( {Z - \frac{{h_{c} }}{2}} \right)\psi_{x}^{t} ,v_{t} = v_{c} \left( {\frac{{h_{c} }}{2}} \right) + \left( {Z - \frac{{h_{c} }}{2}} \right)\psi_{y}^{t} \\ w_{t} & = w_{0} \\ u_{c} \left( {\frac{{h_{c} }}{2}} \right) & = u_{0} + \left( {\frac{{h_{c} }}{2}} \right)\psi_{x}^{c} + \left( {\frac{{h_{c}^{2} }}{4}} \right)\eta_{x}^{c} + \left( {\frac{{h_{c}^{3} }}{8}} \right)\zeta_{x}^{c} \\ v_{c} \left( {\frac{{h_{c} }}{2}} \right) & = v_{0} + \left( {\frac{{h_{c} }}{2}} \right)\psi_{y}^{c} + \left( {\frac{{h_{c}^{2} }}{4}} \right)\eta_{y}^{c} + \left( {\frac{{h_{c}^{3} }}{8}} \right)\zeta_{y}^{c} \\ u_{t} & = u_{0} + \left( {\frac{{h_{c} }}{2}} \right)\psi_{x}^{c} + \left( {\frac{{h_{c}^{2} }}{4}} \right)\eta_{x}^{c} + \left( {\frac{{h_{c}^{3} }}{8}} \right)\zeta_{x}^{c} + \left( {Z - \frac{{h_{c} }}{2}} \right)\psi_{x}^{t} \\ v_{t} & = v_{0} + \left( {\frac{{h_{c} }}{2}} \right)\psi_{y}^{c} + \left( {\frac{{h_{c}^{2} }}{4}} \right)\eta_{y}^{c} + \left( {\frac{{h_{c}^{3} }}{8}} \right)\zeta_{y}^{c} + \left( {Z - \frac{{h_{c} }}{2}} \right)\psi_{y}^{t} \\ w_{t} & = w_{0} \\ \end{aligned}$$

where $\psi_{y}^{t} ,\psi_{x}^{t}$ are top facesheet rotations in $x$ and $y$ directions; $\eta_{x}^{c} ,\eta_{y}^{c} ,\zeta_{x}^{c} \zeta_{y}^{c}$ are the higher-order relationships.

Bottom Facesheet

From Fig. 2, the displacement field for the bottom facesheet was described as

$$\begin{aligned} u_{b} & = u_{c} \left( { - \frac{{h_{c} }}{2}} \right) + \left( {Z + \frac{{h_{c} }}{2}} \right)\psi_{x}^{b} ,v_{b} = v_{c} \left( { - \frac{{h_{c} }}{2}} \right) + \left( {Z + \frac{{h_{c} }}{2}} \right)\psi_{y}^{b} \\ w_{b} & = w_{0} \\ u_{c} \left( { - \frac{{h_{c} }}{2}} \right) & = u_{0} - \left( {\frac{{h_{c} }}{2}} \right)\psi_{x}^{c} + \left( {\frac{{h_{c}^{2} }}{4}} \right)\eta_{x}^{c} - \left( {\frac{{h_{c}^{3} }}{8}} \right)\zeta_{x}^{c} \\ v_{c} \left( { - \frac{{h_{c} }}{2}} \right) & = v_{0} - \left( {\frac{{h_{c} }}{2}} \right)\psi_{y}^{c} + \left( {\frac{{h_{c}^{2} }}{4}} \right)\eta_{y}^{c} - \left( {\frac{{h_{c}^{3} }}{8}} \right)\zeta_{y}^{c} \\ u_{b} & = u_{0} - \left( {\frac{{h_{c} }}{2}} \right)\psi_{x}^{c} + \left( {\frac{{h_{c}^{2} }}{4}} \right)\eta_{x}^{c} - \left( {\frac{{h_{c}^{3} }}{8}} \right)\zeta_{x}^{c} + \left( {Z + \frac{{h_{c} }}{2}} \right)\psi_{x}^{b} \\ v_{b} & = v_{0} - \left( {\frac{{h_{c} }}{2}} \right)\psi_{y}^{c} + \left( {\frac{{h_{c}^{2} }}{4}} \right)\eta_{y}^{c} - \left( {\frac{{h_{c}^{3} }}{8}} \right)\zeta_{y}^{c} + \left( {Z + \frac{{h_{c} }}{2}} \right)\psi_{y}^{b} \\ w_{b} & = w_{0} \\ \end{aligned}$$

2.2 Strain–Displacement

The strain and displacement associated with the sandwich composite are expressed as

Core

$$\begin{aligned} \varepsilon_{x} & = \varepsilon_{x}^{0} + z\kappa_{x} ,\varepsilon_{y} = \varepsilon_{y}^{0} + z\kappa_{x} ,\gamma_{xy} = \gamma_{xy}^{0} + z\kappa_{xy} \\ \varepsilon_{x}^{0} & = \frac{{\partial u_{0} }}{\partial x},\varepsilon_{y}^{0} = \frac{{\partial v_{0} }}{\partial y},\gamma_{xy}^{0} = \frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x} \\ \kappa_{x} & = \frac{{\partial \psi_{x} }}{\partial x},\kappa_{y} = \frac{{\partial \psi_{y} }}{\partial y},\kappa_{xy} = \frac{{\partial \psi_{x} }}{\partial y} + \frac{{\partial \psi_{y} }}{\partial x}, \\ \gamma_{xz} & = \psi_{x} + \frac{\partial w}{\partial x},\gamma_{yz} = \psi_{y} + \frac{\partial w}{\partial y} \\ \end{aligned}$$

where $\varepsilon_{x} ,\varepsilon_{y} ,\gamma_{xy}$ are the normal strains, $\varepsilon_{x}^{0} ,\varepsilon_{y}^{0} ,\gamma_{xy}^{0}$ are the mid-core strains; $\gamma_{xz} ,\gamma_{yz}$ are the out-plane shear strains;$\kappa_{x} ,\kappa_{y} ,\kappa_{xy}$ are the mid-core curvatures.

Top Facesheet

$$\begin{aligned} \varepsilon_{xx}^{t} & = \frac{{\partial u_{t} }}{\partial x} = \frac{{\partial u_{0} }}{\partial x} + \left( {\frac{{h_{c} }}{2}} \right)\frac{{\partial \psi_{x}^{c} }}{\partial x} + \left( {\frac{{h_{c}^{2} }}{4}} \right)\frac{{\partial \eta_{x}^{c} }}{\partial x} + \left( {\frac{{h_{c}^{3} }}{8}} \right)\frac{{\partial \zeta_{x}^{c} }}{\partial x} + \left( {Z - \frac{{h_{c} }}{2}} \right)\frac{{\partial \psi_{x}^{t} }}{\partial x} \\ \varepsilon_{yy}^{t} & = \frac{{\partial v_{t} }}{\partial y} = \frac{{\partial v_{0} }}{\partial y} + \left( {\frac{{h_{c} }}{2}} \right)\frac{{\partial \psi_{y}^{c} }}{\partial x} + \left( {\frac{{h_{c}^{2} }}{4}} \right)\frac{{\partial \eta_{y}^{c} }}{\partial x} + \left( {\frac{{h_{c}^{3} }}{8}} \right)\frac{{\partial \zeta_{y}^{c} }}{\partial x} + \left( {Z - \frac{{h_{c} }}{2}} \right)\frac{{\partial \psi_{y}^{t} }}{\partial y} \\ \gamma_{xy}^{t} & = \frac{{\partial u_{t} }}{\partial y} + \frac{{\partial v_{t} }}{\partial x} = \left( {\frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x}} \right) + \frac{{h_{c} }}{2}\left( {\frac{{\partial \psi_{x}^{c} }}{\partial y} + \frac{{\partial \psi_{y}^{c} }}{\partial x}} \right) \\ & + \frac{{h_{c}^{2} }}{4}\left( {\frac{{\partial \eta_{x}^{c} }}{\partial y} + \frac{{\partial \eta_{y}^{c} }}{\partial x}} \right) + \frac{{h_{c}^{3} }}{8}\left( {\frac{{\partial \zeta_{x}^{c} }}{\partial y} + \frac{{\partial \zeta_{y}^{c} }}{\partial x}} \right) + \left( {Z - \frac{{h_{c} }}{2}} \right)\left( {\frac{{\partial \psi_{x}^{t} }}{\partial y} + \frac{{\partial \psi_{y}^{t} }}{\partial x}} \right) \\ \gamma_{yz}^{t} & = \frac{{\partial w_{0} }}{\partial y} + \psi_{y}^{t} ,\gamma_{xz}^{t} = \frac{{\partial w_{0} }}{\partial y} + \psi_{y}^{t} \\ \end{aligned}$$

Bottom Facesheet

$$\begin{aligned} \varepsilon_{xx}^{b} & = \frac{{\partial u_{b} }}{\partial x} = \frac{{\partial u_{0} }}{\partial x} - \left( {\frac{{h_{c} }}{2}} \right)\frac{{\partial \psi_{x}^{c} }}{\partial x} + \left( {\frac{{h_{c}^{2} }}{4}} \right)\frac{{\partial \eta_{x}^{c} }}{\partial x} - \left( {\frac{{h_{c}^{3} }}{8}} \right)\frac{{\partial \zeta_{x}^{c} }}{\partial x} + \left( {Z + \frac{{h_{c} }}{2}} \right)\frac{{\partial \psi_{x}^{b} }}{\partial x} \\ \varepsilon_{yy}^{b} & = \frac{{\partial v_{b} }}{\partial y} = \frac{{\partial v_{0} }}{\partial y} - \left( {\frac{{h_{c} }}{2}} \right)\frac{{\partial \psi_{y}^{c} }}{\partial x} + \left( {\frac{{h_{c}^{2} }}{4}} \right)\frac{{\partial \eta_{y}^{c} }}{\partial x} - \left( {\frac{{h_{c}^{3} }}{8}} \right)\frac{{\partial \zeta_{y}^{c} }}{\partial x} + \left( {Z + \frac{{h_{c} }}{2}} \right)\frac{{\partial \psi_{y}^{b} }}{\partial y} \\ \gamma_{xy}^{b} & = \frac{{\partial u_{b} }}{\partial y} + \frac{{\partial v_{b} }}{\partial x} = \left( {\frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x}} \right) - \frac{{h_{c} }}{2}\left( {\frac{{\partial \psi_{x}^{c} }}{\partial y} + \frac{{\partial \psi_{y}^{c} }}{\partial x}} \right) + \frac{{h_{c}^{2} }}{4}\left( {\frac{{\partial \eta_{x}^{c} }}{\partial y} + \frac{{\partial \eta_{y}^{c} }}{\partial x}} \right) \\ &- \frac{{h_{c}^{3} }}{8}\left( {\frac{{\partial \zeta_{x}^{c} }}{\partial y} + \frac{{\partial \zeta_{y}^{c} }}{\partial x}} \right) + \left( {Z + \frac{{h_{c} }}{2}} \right)\left( {\frac{{\partial \psi_{x}^{b} }}{\partial y} + \frac{{\partial \psi_{y}^{b} }}{\partial x}} \right) \\ \gamma_{yz}^{b} & = \frac{{\partial w_{0} }}{\partial y} + \psi_{y}^{b} ,\gamma_{xz}^{b} = \frac{{\partial w_{0} }}{\partial y} + \psi_{y}^{b} \\ \end{aligned}$$

2.3 Constitutive Relations for the Core and Facesheet

For the laminated sandwich composite, the stress–strain relation for the core and facesheet was defined as below

Core

By integrating the stresses over the element thickness, the resultant forces and moments for the sandwich composite core were obtained. The core was supposed as an isotropic and homogenous material with the stress–strain relation as

$$\sigma_{c} = \left\{ {\begin{array}{*{20}c} {\sigma_{zc} } \\ {\sigma_{yzc} } \\ {\sigma_{xzc} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {E_{c} } & 0 & 0 \\ 0 & {G_{c} } & 0 \\ 0 & 0 & {G_{c} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{zc} } \\ {\gamma_{yzc} } \\ {\gamma_{xzc} } \\ \end{array} } \right\}$$

The constitutive equation for the core was defined as

$$\left[ {\begin{array}{*{20}c} N \\ M \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left[ A \right]} & {\left[ B \right]} & {\left[ D \right]} & {\left[ E \right]} \\ {\left[ B \right]} & {\left[ D \right]} & {\left[ E \right]} & {\left[ F \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon^{(0)} } \\ {\chi^{(1)} } \\ \end{array} } \right\}$$

where $\sigma$ is stress; $E$ and $G$ are the principal modulus and shear modulus; $N$, $Q$, and $M$ are the force, stiffness, and moment, respectively; matrices $\left[ A \right],\left[ B \right],$ and $\left[ D \right]$ are defined as extensional stiffness, coupling stiffness, and bending stiffness, respectively.

Facesheet

Both top and bottom facesheets were considered as a laminate, and the stress–strain relation of the kth layer was defined as below (i = 1, 2; lower face, upper face).

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {\sigma_{x} (i)} \\ {\sigma_{y} (i)} \\ {\sigma_{z} (i)} \\ \end{array} } \right]_{k} & = \left[ {\begin{array}{*{20}c} {\overline{Q}_{11} } & {\overline{Q}_{12} } & {\overline{Q}_{16} } \\ {\overline{Q}_{12} } & {\overline{Q}_{22} } & {\overline{Q}_{26} } \\ {\overline{Q}_{16} } & {\overline{Q}_{26} } & {\overline{Q}_{66} } \\ \end{array} } \right]_{k} \left[ {\begin{array}{*{20}c} {\varepsilon_{x} (i)} \\ {\varepsilon_{y} (i)} \\ {\gamma_{xy} (i)} \\ \end{array} } \right] \\ \left\{ {\begin{array}{*{20}l} {\sigma_{xx}^{f} } \hfill \\ {\sigma_{yy}^{f} } \hfill \\ {\tau_{yz}^{f} } \hfill \\ {\tau_{xz}^{f} } \hfill \\ {\sigma_{xy}^{f} } \hfill \\ \end{array} } \right\} & = \left[ {\begin{array}{*{20}l} {\bar{Q}_{11} } \hfill & {\bar{Q}_{12} } \hfill & 0 \hfill & 0 \hfill & {\bar{Q}_{16} } \hfill \\ {\bar{Q}_{21} } \hfill & {\bar{Q}_{22} } \hfill & 0 \hfill & 0 \hfill & {\bar{Q}_{26} } \hfill \\ 0 \hfill & 0 \hfill & {\bar{Q}_{44} } \hfill & {\bar{Q}_{45} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\bar{Q}_{54} } \hfill & {\bar{Q}_{55} } \hfill & 0 \hfill \\ {\bar{Q}_{61} } \hfill & {\bar{Q}_{62} } \hfill & 0 \hfill & 0 \hfill & {\bar{Q}_{66} } \hfill \\ \end{array} } \right]^{(k)} \left\{ {\begin{array}{*{20}l} {\varepsilon_{xx}^{f} } \hfill \\ {\varepsilon_{yy}^{f} } \hfill \\ {\gamma_{yz}^{f} } \hfill \\ {\gamma_{xz}^{f} } \hfill \\ {\gamma_{xy}^{f} } \hfill \\ \end{array} } \right\} \\ f & = {\text{top/bottom}} \\ \end{aligned}$$

Thus, the consecutive equations for the facesheets were expressed as

$$\left[ {\begin{array}{*{20}c} {N_{x} } \\ {N_{y} } \\ {N_{xy} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & {A_{16} } \\ {A_{12} } & {A_{22} } & {A_{26} } \\ {A_{16} } & {A_{26} } & {A_{66} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{y}^{0} } \\ {\gamma_{xy}^{0} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {B_{11} } & {B_{12} } & {B_{16} } \\ {B_{12} } & {B_{22} } & {B_{26} } \\ {B_{16} } & {B_{26} } & {B_{66} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\kappa_{x} } \\ {\kappa_{y} } \\ {\kappa_{xy} } \\ \end{array} } \right]$$

$$\left[ {\begin{array}{*{20}c} {M_{x} } \\ {M_{y} } \\ {M_{xy} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{16} } \\ {C_{12} } & {C_{22} } & {C_{26} } \\ {C_{16} } & {C_{26} } & {C_{66} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{y}^{0} } \\ {\gamma_{xy}^{0} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {D_{11} } & {D_{12} } & {D_{16} } \\ {D_{12} } & {D_{22} } & {D_{26} } \\ {D_{16} } & {D_{26} } & {D_{66} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\kappa_{x} } \\ {\kappa_{y} } \\ {\kappa_{xy} } \\ \end{array} } \right]$$

where

$$\begin{aligned} A_{ij} & = A_{ij} (1) + A_{ij} (2) \\ B_{ij} & = \left( {\frac{{h_{c} + h_{2} }}{2}} \right)A_{ij} (2) - \left( {\frac{{h_{c} + h_{1} }}{2}} \right)A_{ij} (1) \\ C_{ij} & = C_{ij} (1) + C_{ij} (2) \\ D_{ij} & = \left( {\frac{{h_{c} + h_{2} }}{2}} \right)C_{ij} (2) - \left( {\frac{{h_{c} + h_{1} }}{2}} \right)C_{ij} (1) \\ \end{aligned}$$

3 Load Prediction of Aarush X2

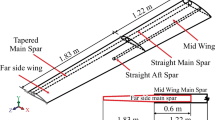
Figure 3 illustrates the subsections of the Aarush X2 which were mechanically critical and studied using the mathematical formulation developed in the present study. Both section A and section B were constructed by the facesheet of unidirectional CFRP and the core of Divinycell. Iterative calculations were performed to obtain the optimised number of layers and the fibre orientation of the facesheet required for the wing and fuselage.

Fig. 3

Top-view of the Aarush X2, with marked zones studied using FOSDT

3.1 Fuselage Belly

The fuselage belly was assumed as a rectangular sandwich composite. The laminate was considered to be clamped at both the ends, and a unidirectional load was induced at x = 1350 mm from one extreme of the plate. The variation in the amount of facesheet layers and the fibre orientations were studied for the fuselage. The material property used to construct the fuselage is shown in Table 1. The boundary conditions of the laminate in the clamped arrangement were ensured by the following constraints

Table 1 Material properties of the CFRP and Divinycell

$$w(0,y) = \psi_{x} (0,y) = \psi_{y} (0,y) = u_{0} (0,y) = v_{0} (0,y) = 0$$

The study for the sandwich composite was performed for three, five, and seven layers, including the core ply. The different configurations, Table 2, were analysed to design the sandwich composite for the fuselage of the Aarush X2. From Table 2, the mid-plane strains and mid-plane curvatures of the five-layer and seven-layer sandwich composite present the possibility applicable to the fuselage; however, the seven-layer lay-up was unessentially strong and heavier than the requisite. Various fibre orientations were further studied, Table 2, and the facesheet [0°/45°] orientation presented the least mid-plane strains and curvatures, hence selected. The optimised sandwich composite, [0°/45°/Divinycell/0°/45°], stress performance is presented in Fig. 4, which denotes $\sigma_{xx}$ to be around 1905 MPa.

Table 2 Sandwich composite configuration studied

Fig. 4

Various stresses calculated for the fuselage and wing using FOSDT

3.2 Wing Skin

The Aarush X2 wing is shown in Fig. 3, where the wing length is 2700 mm. In order to reduce the modelling complexities, (i) the study was performed on a rectangular wing with a 500-mm width, mean of root, and tip chord, (ii) the influence due to spar and ribs was not incorporated, and (iii) single side of the wing is accounted (half of the wingspan, 1350 mm). The mechanical properties of the materials used to construct the sandwich composite are presented in Table 1. The boundary condition of the wing was ensured for the simply supported at one end, which represented mathematically as

$$w(0,y) = M_{x} (0,y) = N_{x} (0,y) = N_{xy} (0,y) = \psi_{y} (0,y) = 0$$

The sandwich composite investigation was performed for various layers and further optimised for the facesheet’s ply fibre orientations. Table 2 demonstrates the sandwich composite with plies 0°/45°/Divinycell/0°/45° suitable for fabricating the wing structure. The stress report of the designed sandwich composite, [0°/90°/Core/0°/90°], in the Aarush X2 wing is represented in Fig. 4, $\sigma_{xx}$ approximately 1342 MPa.

4 Fabrication

VAWLM was implemented to fabricate the designed sandwich composite for the Aarush X2. The different sections of the Aarush X2, fuselage, and wing were fabricated individually initially and hereafter combined to produce the overall system. In order to maintain a clean and defect-free composite, the fabrication of the Divinycell CFRP composite was performed in a closed room chamber. The curing time of the fabrication noted was 6 h, and the resin to hardener combination, AY 105 and HY 991, was used in 10 to 1 part. To maintain a steady fabrication platform, the assemblies were fixed using jigs and fixtures. The temperature of the room was also maintained constant to avoid any sudden escalation or degradation in the curing process, which can cause inter-layer distortions and unevenness. The temperature of the room was maintained at 25 °C.

4.1 Fuselage

The fabrication of the fuselage was a two-step process, as depicted in Fig. 5, where the upper and lower part of the fuselage was fabricated alone at first. The fabrication of each part was performed on the separate moulds for the upper and lower fuselage layers, which was initiated by the surface treatment process. The cleaner and release agent was applied on the mould surface to obtain a clear surface and easy removal of the fuselage composite, respectively. The carbon fabric and Divinycell were cut in accordance with the mould; however, the additional surface area for both was trimmed to avoid shrinkage during the process. The carbon fabric layer was placed at the bottom of the mould, followed by the Divinycell and carbon fibre layer again, which were wetted with epoxy matrix before placing inside the mould. The wetted layers were followed by a separator, breather cloth, and vacuum sheet which were sealed using butyl tape. The entire assembly was attached to a 2.5 HP vacuum pump, which drops the pressure inside the sealed vacuum bag under 1 atm during the fabrication process. VAWLM maintains uniform pressure distribution across the material plies and further acts as a pseudo-forced clamp until the epoxy matrix sets the composite in the required position. The lap pressure exerted during the fabrication process further helped to remove inter-layer air pockets and manufactures a defect-free composite. Subsequently, the fabricated upper and lower layers were linked to each using VAWLM again. In the end, essential mechanical process like drilling was performed to integrate avionics, landing gear, and engine.

Fig. 5

Fabrication of the Aarush X2 fuselage

4.2 Wing

The wings were fabricated in a similar manner as performed for the fuselage, which contains the upper and lower skin fabrication at first. The entire process is depicted in Fig. 6. The surface treatment on the upper and lower skin moulds was executed. The stacking of carbon fabric, Divinycell, separator, breather, and vacuum sheet was implemented in the same way as for the fuselage. The wetted layers on the wing mould were connected to the vacuum pump. The upper and lower skins were joined to each other by employing VAWLM in the end. The process repeated analogously for the left side of the wing, since right-side wing was fabricated before.

Fig. 6

Fabrication of the wing and assembly in the Aarush X2

5 Flight Testing

The flight testing of the Aarush X2, Fig. 7, was performed in the Indian flying conditions for more than 30 h with rigorous take-offs and landings. The final inspection after each flight demonstrated UAV in healthy condition and with further prospects of flight missions. The flight time of 2.8 h was recorded on the DLE-61 engine with the fuel tank capacity of 1.8 litres. The final project flight testing was completed in Bhiwani, Haryana, and the system was inspected by Lockheed Martin officials. The UAV was found fit to be functional for the urban aerial flying conditions with the strong and shock resilient structural body.

Fig. 7

Final flight demonstration and inspection of the Aarush X2 by Lockheed Martin

6 Conclusion

This study investigated mechanical properties of the sandwich composite using FOSDT. The research demonstrated carbon fibre Divinycell sandwich composite structurally suitable and hence is used to manufacture Aarush X2. The work displayed the fabrication methodology employed to fabricate fuselage and wing of the UAV using VAWLM. The study highlights the following observations

• 1. The designed composite with the ply stacking of two upper carbon fibre facesheet layers, core Divinycell layer, and two bottom carbon fibre facesheet layers demonstrated stress of 1905 MPa and 1342 MPa for the fuselage and wing laminate, respectively. The orientation for each facesheet layer was 0° initially.

• 2. The different orientations, [0°/0°]; [0°/90°]; [0°/45°]; [45°/90°], were investigated, and the results presented [0°/45°] orientation to obtain maximum strength when compared to the rest.

• 3. The VAWLM produced sandwich composite free from the manufacturing defects with the smooth surface finish.

• 4. The 30-h Aarush X2 flight indicated no signs of structural failure.

• 5. The research displayed the selected composite designing strategy through FOSDT appropriate, complying with the structural loads estimated.