Keywords

1 Introduction

The increase in urban population in India has led to the unbearable congestion and chaos to already degrading road traffic. To address the issue, underground trains have emerged as one of the most effective means to reduce road traffic as visible from other cities of the world. But transmission of vibration from metro trains to the structures lying nearby [1] experiences low-frequency vibration in the form of rattling of window panels and doors. To study this vibration propagation mechanism many modeling techniques are used by different authors in the past [2] which includes experimental data collection, numerical calculation using finite element method and theoretical method using classical equations of mechanics. Vibration propagation study can be done using either 2D or 3D models. Zhou et al. [3] used 2D theoretical model for simulating the steady response of a floating slab track–tunnel–soil system, Singh et al. [4] simulated the Delhi metro underground tunnel using PLAXIS 2D model, Hung et al. [5] considered 2D profile of the soil perpendicular to the railway track and used finite and infinite element for near- and far-field modeling and many other authors like [6,7,8] have used 2D model. The results obtained by the 2D models are approximate and qualitative in nature [9]. Since the train-track–tunnel–soil interaction system involves complex mechanism of vibration propagation, it becomes necessary to use 3D models as implemented by various authors like Auersch [10] who used 3D slab track models. Forest and Hunt [11] described an analytical 3D model for dynamics of the deep underground railway tunnel and Ma et al. [12] developed the 3D dynamic finite element model to study the impact of metro train-induced vibration on historic buildings.

In this paper the response of track system is studied under the influence of moving metro train inside the tunnel. A dynamic computational model similar to Lei and Noda [13] has been adopted for the vehicle and track coupling system. A vehicle is modeled as quarter-car in which primary and secondary suspension systems are considered and the track system is modeled using finite element model. It was studied by many authors like [14,15,16,17,18] that track profile irregularity is one of the major sources of vibration which further depends on train speed, axle load and volume of traffic. To study the wheel–rail dynamic forces, nonlinear Hertzian contact theory as used by Kacimi et al. [19] is adopted and random irregularity of the track profile is considered as Gaussian random process. The responses are generated at the rail and slab structure and the results are compared with the existing literature. Paper ends with the conclusions of the study.

2 Finite Element Formulation

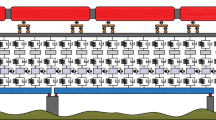
A slab track considered in our study is similar to the CRTS II slab track which is a three-layer slab track system consisting of rail, precast slab and concrete support base as shown in Fig. 1. A discrete support of rail pads/fasteners lies between rail and precast slab, and a layer of cement mortar is provided between precast slab and concrete support layer/tunnel invert which have certain stiffness and damping properties. In the present study, a layer of hydraulically bonded layer (HBL) is considered between tunnel invert and tunnel lining and is represented as the continuous spring and damper elements. The hydraulic bonded layer is a family of cement bounded layer [20] and it consists of cement, lime, gypsum and coal fly ash, which set and harden in the presence of water. Below HBL, the model is considered rigid to confine the study area till the tunnel lining only.

Fig. 1
figure 1

Slab track element (not to scale)

Full size image

The modeling of the track system is done using finite element in which rail, precast slab and concrete support layer is discretized as the 2D beam element having two nodes and each having two degrees of freedom. To cover the mid-frequency ranges of vibration, track length of 120 m is taken which is divided in the element size of 0.6 m, that is, distances between two continuous sleepers.

A typical beam element having two nodes and two degrees of freedoms can be represented as shown in Fig. 2.

Fig. 2
figure 2

Beam element

Full size image

Here \(v_{i}\), \(v_{j}\), \(\theta_{i}\) and \(\theta_{j}\) are the nodal displacements, and displacement at any point along the beam is expressed by the following expression:

$$v = N_{1} v_{i} + N_{2} \theta_{i} + N_{3} v_{j} + N_{4} \theta_{j}$$
(1)

where N1–N4 represent the displacement interpolation functions which are also a function of local coordinate x taken along the beam element. As per the sign convention shown in Fig. 2, the interpolation functions can be written as

$$N_{1} = 1 - \frac{{3x^{2} }}{{l^{2} }} + \frac{{2x^{3} }}{{l^{3} }}$$
(2)
$$N_{2} = - x + \frac{{2x^{2} }}{l} - \frac{{x^{3} }}{{l^{2} }}$$
(3)
$$N_{3} = \frac{{3x^{2} }}{{l^{2} }} - \frac{{2x^{3} }}{{l^{3} }}$$
(4)
$$N_{4} = \frac{{x^{2} }}{l} - \frac{{x^{3} }}{{l^{2} }}$$
(5)

Defining the element nodal displacement vector as

$$a = \left[ {\begin{array}{*{20}c} {v_{i} } & {\theta_{i} } & {v_{j} } & {\theta_{j} } \\ \end{array} } \right]^{T}$$
(6)

Thus, Eq. 1 can be written as

$$f = {\text{Na}}$$
(7)

where

$$N = \left[ {\begin{array}{*{20}c} {N_{1} } & {N_{2} } & {N_{3} } & {N_{4} } \\ \end{array} } \right]$$
(8)

The mass matrix of the beam element is

$$\left[ m \right]^{e} = \int_{v} {\rho \left[ N \right]}^{T} \left[ N \right]{\text{d}}v = \frac{\rho Al}{420}\left[ {\begin{array}{*{20}c} {156} & {22l} & {54} & { - 13l} \\ {22l} & {4l^{2} } & {13l} & { - 3l^{2} } \\ {54} & {13l} & {156} & { - 22l} \\ { - 13l} & { - 3l^{2} } & { - 22l} & {4l^{2} } \\ \end{array} } \right]$$
(9)

The damping matrix of the beam element is

$$\left[ c \right]^{e} = \int_{v} {\rho \left[ N \right]}^{T} \left[ N \right]{\text{d}}v = \frac{cl}{420}\left[ {\begin{array}{*{20}c} {156} & {22l} & {54} & { - 13l} \\ {22l} & {4l^{2} } & {13l} & { - 3l^{2} } \\ {54} & {13l} & {156} & { - 22l} \\ { - 13l} & { - 3l^{2} } & { - 22l} & {4l^{2} } \\ \end{array} } \right]$$
(10)

The stiffness matrix of the beam element is

$$\left[ k \right]^{e} = \frac{EI}{{l^{3} }}\left[ {\begin{array}{*{20}c} {12} & { - 6l} & { - 12} & {6l} \\ { - 6l} & {4l^{2} } & {6l} & {2l^{2} } \\ { - 12} & {6l} & {12} & {6l} \\ {6l} & {2l^{2} } & {6l} & {4l^{2} } \\ \end{array} } \right]$$
(11)

The dynamic equation of the system can be written using Lagrange equation which is expressed as

$$\frac{\text{d}}{{{\text{d}}t}}\frac{\partial L}{{\partial \dot{a}}} - \frac{\partial L}{\partial a} + \frac{\partial R}{{\partial \dot{a}}} = 0$$
(12)
$$M\ddot{a}\left( t \right) + C\dot{a}\left( t \right) + Ka\left( t \right) = Q(t)$$
(13)

Equation (13) represents the dynamic finite element equation of the system which can be solved by the numerical techniques.

2.1 Matrix Formulation of Track System

Using the concepts discussed above, mass, stiffness and damping matrices are formed. To form the global matrix of the whole track system, appropriate boundary conditions are considered which helps in the reduction of the matrix size and speeds up the calculation. In this paper track system is considered to be simply supported at the ends, thus having only rotational degrees of freedom at the ends.

As per Fig. 1, mass matrix of the rail is

$$m_{r} = \frac{{\rho_{r} A_{r} l}}{420}\left[ {\begin{array}{*{20}c} {156} & { - 22l} & 0 & 0 & 0 & 0 & {54} & {13l} & 0 & 0 & 0 & 0 \\ { - 22l} & {4l^{2} } & 0 & 0 & 0 & 0 & { - 13l} & { - 3l^{2} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ {54} & { - 13l} & 0 & 0 & 0 & 0 & {156} & {22l} & 0 & 0 & 0 & 0 \\ {13l} & { - 3l^{2} } & 0 & 0 & 0 & 0 & {22l} & {4l^{2} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]$$
(14)

Similarly, mass matrix of the precast slab is

$$m_{s} = \frac{{\rho_{s} A_{s} l}}{420}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {156} & { - 22l} & 0 & 0 & 0 & 0 & {54} & {13l} & 0 & 0 \\ 0 & 0 & { - 22l} & {4l^{2} } & 0 & 0 & 0 & 0 & { - 13l} & { - 3l^{2} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {54} & { - 13l} & 0 & 0 & 0 & 0 & {156} & {22l} & 0 & 0 \\ 0 & 0 & {13l} & { - 3l^{2} } & 0 & 0 & 0 & 0 & {22l} & {4l^{2} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]$$
(15)

Mass matrix of the concrete support layer/tunnel invert is

$$m_{t} = \frac{{\rho_{t} A_{t} l}}{420}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {156} & { - 22l} & 0 & 0 & 0 & 0 & {54} & {13l} \\ 0 & 0 & 0 & 0 & { - 22l} & {4l^{2} } & 0 & 0 & 0 & 0 & { - 13l} & { - 3l^{2} } \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {54} & { - 13l} & 0 & 0 & 0 & 0 & {156} & {22l} \\ 0 & 0 & 0 & 0 & {13l} & { - 3l^{2} } & 0 & 0 & 0 & 0 & {22l} & {4l^{2} } \\ \end{array} } \right]$$
(16)

Mass matrix of the whole element can be written as

$$m = m_{r} + m_{s} + m_{t}$$
(17)

Using the similar concept of matrix formulation, stiffness matrix for the whole element can be written as

$$k = k_{r} + k_{s} + k_{t} + k_{p} + k_{c} + k_{h}$$
(18)

Here, \(k_{r} ,k_{s} ,k_{t} ,k_{p} ,k_{c}\) and \(k_{h}\) are the stiffnesses of rail beam, precast slab, tunnel invert, rail pads, cement mortar layer and HBL layer, respectively.

Damping matrix for the whole element can be written as

$$c = c_{r} + c_{p} + c_{c} + c_{h}$$
(19)

Here, \(c_{r}\) represents the proportional damping matrix of the rail, precast slab and tunnel invert. It is represented as

$$c_{r} = \alpha m_{r} + \beta k_{r} + \alpha m_{s} + \beta k_{s} + \alpha m_{t} + \beta k_{t}$$
(20)

The Rayleigh damping coefficients \(\alpha\) and \(\beta\) depend on the damping ratio and the natural frequencies of the system. \(c_{p} ,c_{c}\) and \(c_{h}\) are damping of rail pads, cement mortar layer and HBL layer, respectively.

Now, using the general rule of assembling element matrix, the global mass, stiffness, damping and load matrix are assembled and the final dynamic equation of the whole system is written as

$$M_{N \times N} \ddot{a}\left( t \right)_{N \times 1} + C_{N \times N} \dot{a}\left( t \right)_{N \times 1} + K_{N \times N} a\left( t \right)_{N \times 1} = Q(t)_{N \times 1}$$
(21)

Here, N is the degree of freedom of system.

3 Vehicle Model

A simplified model of the train represented as quarter-car is taken in the present study to understand the interaction between a wheel and a rail. The model consists of primary and secondary suspension spring and damper system as shown in Fig. 3 moving with constant velocity over a rail.

Fig. 3
figure 3

Quarter-car model

Full size image

Using law of mechanics, the equations of motion of the above system which is a second-order differential equation can be written in the matrix form as follows

$$M_{v} \ddot{a}_{v} + C_{v} \dot{a}_{v} + K_{v} a_{v} = Q_{v}$$
(22)

Here,

$$M_{v} = {\text{diag}}\left[ {\begin{array}{*{20}c} {m_{cr} } & {m_{bo} } & {m_{wh} } \\ \end{array} } \right]$$
(23)
$$C_{v} = \left[ {\begin{array}{*{20}c} {c_{cr} } & { - c_{cr} } & 0 \\ { - c_{cr} } & {c_{cr} + c_{bo} } & { - c_{bo} } \\ 0 & { - c_{bo} } & {c_{bo} } \\ \end{array} } \right]$$
(24)
$$K_{v} = \left[ {\begin{array}{*{20}c} {k_{cr} } & { - k_{cr} } & 0 \\ { - k_{cr} } & {k_{cr} + k_{bo} } & { - k_{bo} } \\ 0 & { - k_{bo} } & {k_{bo} } \\ \end{array} } \right]$$
(25)
$$Q_{v} = \left[ {\begin{array}{*{20}c} { - m_{cr} g} \\ { - m_{bo} g} \\ { - m_{wh} g + P} \\ \end{array} } \right]$$
(26)

‘P’ is the wheel–rail interaction force arising due to a relative displacement between wheel and rail at the contact point.

4 Wheel–Rail Interaction

The interaction between the two subsystems, that is, vehicle and track is achieved through the wheel–rail interaction forces arising at the rail–wheel interface. Many theories have been put forward to study the interaction forces. In the present study nonlinear Hertzian contact theory had been used to generate the contact forces.

$$P = \left[ {\begin{array}{*{20}c} {\frac{1}{{G^{1.5} }}\left| {v_{wi} - \left( {v_{ri} + \eta_{i} } \right)} \right|^{1.5} } & {{\text{if}}\;\left| {v_{wi} - \left( {v_{ri} + \eta_{i} } \right)} \right|^{1.5} < 0} \\ 0 & {{\text{if}}\;\left| {v_{wi} - \left( {v_{ri} + \eta_{i} } \right)} \right|^{1.5} > 0} \\ \end{array} } \right.$$
(27)

Equation (27) represents the contact forces in which \(v_{wi}\), \(v_{ri}\) and \(\eta_{i}\) are wheel displacement, rail displacement and irregularity, respectively, at the ith wheel rail contact point and is a function of speed of a train. As discussed by authors like [21, 22] in their study that for ground vibrations study vertical track irregularities are predominant factor for vibration generation, thus vertical random track irregularities are considered in this paper, which is generated based on the power spectrum density(PSD) formula given by the Federal Railroad Administration of America (FRA). For the metro vibrations generally grade 5 or grade 6 track PSD function is used to generate the random track irregularity.

4.1 Solution Method

The dynamic responses of the rail and track system are solved separately using the Newmark integration scheme in which if solution at time step ‘t’ is known then the solution at time step ‘t + dt’ can be obtained by using the following formula

$$\left( {K + a_{1} M + a_{2} C} \right)a^{{t + {\text{d}}t}} = Q^{{t + {\text{d}}t}} + M\left( {a_{1} a^{t} + a_{3} \dot{a}^{t} + a_{4} \ddot{a}^{t} } \right) + C\left( {a_{2} a^{t} + a_{5} \dot{a}^{t} + a_{6} \ddot{a}^{t} } \right)$$
(28)

Here, \(a_{1}\) to \(a_{6}\) are the Newmark constants.

Since the Hertzian forces acting at the wheel–rail contact point is nonlinear in nature, thus it becomes important to iterate the value at each time using suitable iteration technique as suggested by Yang and Fonder [23] at each time step of Newmark till the required convergence criteria is fulfilled.

5 Results and Discussions

The vehicle and track parameters used in this study are of CRH3 train and CRTS II slab track, respectively. The following assumptions are made:

  • In the present analysis only bouncing vibration of the vehicle is considered.

  • Due to symmetry of the system only half of the vehicle track coupling system is used for the analysis.

  • At initial time step it is assumed that wheel–rail interaction force is solely due to the irregularity of the track.

  • The relative displacement between wheel and track is assumed to be zeros at initial time step.

  • The convergence range considered in the iteration technique lies between \(10^{ - 5}\) and \(10^{ - 10}\).

The purpose of this study is to validate our model with existing available literature so that a full-scale model can be developed for our case study of Delhi Metro. To validate our data, responses generated in the proposed model are compared with the results of Lei et al. [24], for same track length and vehicle speed.

The comparison done in Table 1 clearly indicates that the order of result obtained in both the models is the same. Though the results don’t match exactly which might be due to the differences in the track properties and the vehicle model taken, we can say that the proposed model can be used to study the vibration generation due to the metro trains and to get a more realistic data a full-scale model of the vehicle, and a track system can be developed based on the methodology discussed in this paper.

Table 1 Comparison of results
Full size table

Then, to study the behavior of the responses generated by the model, a track length of 120 m is taken and vehicle is made to run at two different speeds of 10 and 40 m/s. Track irregularity as shown in Fig. 4 is used in this study.

Fig. 4
figure 4

Track irregularity

Full size image

  • For L = 120 and v = 10 m/s

  • For L = 120 m and v = 40 m/s

Figures 5 and 8 show that amplitude of the wheel–rail interaction force increases with the increase in speed of the vehicle. Moreover, the midpoint deflection of the rail also increases with the increase in speed as visible from Figs. 6 and 9. A similar trend was observed for the acceleration computed at the midpoint of the rail, which can be seen in Figs. 7 and 10.

Fig. 5
figure 5

Wheel–rail interaction force

Full size image
Fig. 6
figure 6

Midpoint deflection of rail

Full size image
Fig. 7
figure 7

Midpoint acceleration of rail

Full size image
Fig. 8
figure 8

Wheel–rail interaction force

Full size image
Fig. 9
figure 9

Midpoint deflection of rail

Full size image
Fig. 10
figure 10

Midpoint acceleration of rail

Full size image

6 Conclusions

The responses generated from the coupled model of vehicle and slab track were compared with those existing in the literature. Since the results obtained were of the same order we can conclude that the model adopted in the present paper can be used to study the dynamic responses of train-track–tunnel–soil system generated through the wheel–rail interaction. To capture a more realistic behavior a full-scale model of vehicle and slab track considering more degrees of freedom can be developed based on the computation technique discussed in this paper.