Keywords

1 Introduction

One of the problems concerning creating resonant vibration machines with unbalance vibration exciters is to ensure the specified modes of oscillations at fluctuating process load. Here, the fluctuation of the technological load is understood as the change in its mass and its location on the machine’s working body. These changes significantly affect the dynamic characteristics of the machine and at a given excitation frequency lead to undesirable changes in the amplitudes and modes of the system, as well as change in the required type of the vibration exciters synchronization (differences between the phases of unbalanced rotation) [1,2,3], which ultimately leads to disruption of vibrational processing.

The solution to this problem can be found by using automated control systems that monitor these changes and adjust the system parameters and excitation [4,5,6,7,8,9,10,11]. So in [9], a system for control resonant oscillations of one-dimensional single-mass system excited by a single unbalance vibration exciter of a synchronous type, based on the use of autoresonance excitation, was proposed. In [10, 11], a system for controlling the resonant oscillations based on usage of combinational parametric resonance was considered for a similar dynamic scheme of the machine. In the previous works of the authors [12], a number of algorithms for the control system of an asynchronous unbalance exciter based on the measurement of mutual phase shift between the exciting force and system oscillations were proposed. The developed control systems made it possible to efficiently track the change in the system’s mass and quickly reconfigure it to the required near-resonant oscillations mode [13].

For planar oscillatory systems with two unbalance exciters, the effect of self-synchronization of vibration exciters plays a significant role. Moreover, the type of synchronization of the vibration exciters rotation and the form of the system’s oscillations have a mutual influence on each other [2].

It is obvious that in cases of planar oscillations of the vibratory machine’s working body it is necessary to take into account not only the change in mass of the process load, but also its location on the working body. In [14], the effect of the mass center’s displacement of the technological load relative to the axis of system’s structural symmetry on its frequency characteristics and the type of the debalances synchronization depending on their rotational frequency is shown. In [4, 8], the possibilities of separate control of the vibration exciters’ driving motors to create the required type of their synchronous rotation were investigated. However, with independent control of vibration exciters a forced synchronization mode is set, which leads to increased loads on the electric motors, reducing their reliability, as well as increasing energy consumption.

In this paper, the authors based on the results of a numerical dynamics analysis of a vibration machine with two self-synchronizing vibration exciters of asynchronous type, consider the possibility of creating rational algorithms for controlling its resonant oscillations under conditions of the variable arrangement of the technological load on the working body. Within the framework of the problem statement under consideration, it is assumed that to ensure the required efficiency of the working process it is necessary to provide the excitation of unidirectional vertical oscillations of the machine working body in near-resonant modes, regardless of the position of the process load’s center of mass.

2 Mathematical Model of Vibrating Machine

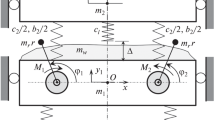
The design scheme is a single-mass mechanical system, in which planar oscillations are excited by two self-synchronizing unbalance vibration exciters driven by asynchronous motors (Fig. 1).

Fig. 1
figure 1

Design scheme

Full size image

A platform imitating the machine’s working body is considered as a rigid body supported in the directions of its plane motion (vertical, horizontal, and angular) by elastic-viscous elements with linear characteristics. There are two almost identical asynchronous type exciters installed on the platform symmetrically with respect to the vertical axis passing through its center of mass. The rotors’ axes are parallel to each other and perpendicular to the plane of the platform’s motion. Both motors are connected to a three-phase AC power supply source using a single inverter so that their rotors rotate in opposite directions.

The technological load (the weight) is modeled by a rigid body with mass mw and moment of inertia Jw about its center of mass at the point Ow, rigidly fixed on the platform, which position is set by parameters ax, ay—distances from the central axis of symmetry to its center of mass (see Fig. 1).

The principal feature of this design scheme is the possibility of taking into account the interaction of the oscillating system with vibration exciters of limited power, inertial parameters of the process load, and its location on the machine’s working body.

Motion of the system is considered relative to the fixed coordinate system yOx, whose origin coincides with the position of the platform’s center of mass in the undeformed state, and is described by displacements of the platform’s center of mass in the Oy and Ox directions, the angle φ of the platform rotation and the rotors rotational angles φ1 and φ2. All angular coordinates are counted from the Ox axis counterclockwise. Differential equations of motion of the system have the following form:

$$ {\mathbf{M}}\left( {\mathbf{X}} \right){\ddot{\mathbf {X}}} + {\mathbf{B}}\dot{\mathbf{X}} + {\mathbf{CX}} = {\mathbf{F}}\left( {{\dot{\mathbf{X}}},{\mathbf{X}} ,t} \right) $$
(1)

where

\( {\mathbf{M}}\left( {\mathbf{X}} \right) = \left[ {\begin{array}{*{20}c} M & 0 & {\mu_{13} } & { - m_{r1} r_{1} \sin \varphi_{1} } & { - m_{r2} r_{2} \sin \varphi_{2} } \\ 0 & M & {\mu_{23} } & {m_{r1} r_{1} \cos \varphi_{1} } & {m_{r2} r_{2} \cos \varphi_{2} } \\ {\mu_{31} } & {\mu_{32} } & J & {\mu_{34} } & {\mu_{35} } \\ { - m_{r1} r_{1} \sin \varphi_{1} } & {m_{r1} r_{1} \cos \varphi_{1} } & {\mu_{43} } & {J_{1} } & 0 \\ { - m_{r2} r_{2} \sin \varphi_{2} } & {m_{r2} r_{2} \cos \varphi_{2} } & {\mu_{53} } & 0 & {J_{2} } \\ \end{array} } \right] \)

\( \begin{aligned} \mu_{13} = \mu_{13} = - m_{w} \left( {a_{y} \cos \varphi + a_{x} \sin \varphi } \right) - \sum\limits_{j = 1}^{2} {m_{rj} } \rho \sin \left( {\delta_{j} + \varphi } \right), \hfill \\ \mu_{23} = \mu_{32} = - m_{w} \left( {a_{y} \sin \varphi + a_{x} \cos \varphi } \right) - \sum\limits_{j = 1}^{2} {m_{rj} } \rho \cos \left( {\delta_{j} + \varphi } \right), \hfill \\ \mu_{34} = \mu_{43} = m_{r1} r_{1} \rho \cos \left( {\delta_{1} + \varphi - \varphi_{1} } \right), \hfill \\ \mu_{35} = \mu_{53} = m_{r2} r_{2} \rho \cos \left( {\delta_{2} + \varphi - \varphi_{2} } \right), \hfill \\ \end{aligned} \)

$$ {\mathbf{B}} = \left[ {\begin{array}{*{20}c} {b_{x} } & 0 & 0 & 0 & 0 \\ 0 & {b_{y} } & 0 & 0 & 0 \\ 0 & 0 & {b_{\varphi } } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]{\mathbf{,C}} = \left[ {\begin{array}{*{20}c} {c_{x} } & 0 & 0 & 0 & 0 \\ 0 & {c_{y} } & 0 & 0 & 0 \\ 0 & 0 & {c_{\varphi } } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right],{\mathbf{X}} = \left[ {\begin{array}{*{20}c} x \\ y \\ \varphi \\ {\varphi_{1} } \\ {\varphi_{2} } \\ \end{array} } \right],{\mathbf{F}}\left( {{\dot{\mathbf{X}}},{\mathbf{X}},t} \right) = \left[ {\begin{array}{*{20}c} {F_{1} } \\ {F_{2} } \\ {F_{3} } \\ {F_{4} } \\ {F_{5} } \\ \end{array} } \right] $$
$$ F_{1} = \left[ {m_{w} \left( {a_{x} \cos \varphi - a_{y} \sin \varphi } \right) + \mathop \sum \limits_{j = 1}^{2} m_{rj} \rho \cos \left( {\delta_{j} + \varphi } \right)} \right]\dot{\varphi }^{2} + \mathop \sum \limits_{j = 1}^{2} m_{rj} r_{j} \cos \varphi_{j} \dot{\varphi }_{j}^{2} , $$
$$ F_{2} = \left[ {m_{w} \left( {a_{y} \cos \varphi + a_{x} \sin \varphi } \right) + \mathop \sum \limits_{j = 1}^{2} m_{rj} \rho \cos \left( {\delta_{j} + \varphi } \right)} \right]\dot{\varphi }^{2} + \mathop \sum \limits_{j = 1}^{2} m_{rj} r_{j} \sin \varphi_{j} \dot{\varphi }_{j}^{2} - Mg, $$
$$ F_{3} = - \mathop \sum \limits_{j = 1}^{2} m_{rj} r_{j} \rho \sin \left( {\delta_{j} + \varphi - \varphi_{j} } \right)\dot{\varphi }_{j}^{2} - m_{w} g\left( {a_{x} \cos \varphi - a_{y} \sin \varphi } \right) - \mathop \sum \limits_{j = 1}^{2} m_{rj} g\rho \cos \left( {\delta_{j} + \varphi } \right), $$
$$ F_{4} = \sigma_{1} L_{1} - 0.5m_{r1} r_{1} \dot{\varphi }_{1}^{2} k_{f1} sign\left( {\dot{\varphi }_{1} } \right) + m_{r1} r_{1} \rho \sin \left( {\delta_{1} + \varphi - \varphi_{1} } \right)\dot{\varphi }^{2} + m_{r1} gr_{1} \cos \varphi_{1} , $$
$$ F_{5} = \sigma_{2} L_{1} - 0.5m_{r2} r_{2} \dot{\varphi }_{2}^{2} k_{f2} sign\left( {\dot{\varphi }_{2} } \right) + m_{r2} r_{2} \rho \sin \left( {\delta_{2} + \varphi - \varphi_{2} } \right)\dot{\varphi }^{2} + m_{r2} gr_{2} \cos \varphi_{2} , $$

where mrj (j = 1, 2)—imbalanced mass of jth debalance, rj—eccentricity of jth debalance, \( J_{j} = J_{rj} + m_{rj} r_{j}^{2} \), Jrj—inertia moment of jth rotor; \( M = m_{pl} + m_{w} + \mathop \sum \nolimits_{j = 1}^{2} m_{rj} \)—total mass of the system; \( m_{pl} \)—mass of the platform with exciters; cx, cy, cφ, bx, by, bφ—stiffness and damping coefficients of elastic-viscous elements in horizontal, vertical and angular directions correspondingly; ρ—distance between the platform’s center of mass and centers of debalances rotation; δj—angle between axis Ox and the axis connecting the platform’s center of mass with the center of jth debalance rotation, \( J = J_{pl} + J_{w} + m_{w} \left( {a_{x}^{2} + a_{y}^{2} } \right) + \mathop \sum \nolimits_{j = 1}^{2} m_{rj} \rho^{2} \)—reduced inertia moment of the system relative to the platform’s center of mass; Jpl—moment of inertia of the platform with exciters; g—gravity acceleration; σ1 = +1, σ1 = −1—the constants determining direction of the debalances rotation; \( k_{fj} \)—coefficient of friction in the jth rotor supports.

The driving moments L1, L2 on the right side of Eq. (1) are described by the static characteristic of the motors according to the Kloss formula:

$$ L_{j} = 2M_{crj}^{*} /\left( {s_{j} /s_{crj} + s_{crj} /s_{j} } \right), s_{j} = 1 - P\left| {\dot{\varphi }_{j} } \right|/\omega_{0j} , $$
(2)
$$ M_{crj}^{*} = \left\{ {\begin{array}{*{20}c} {M_{crj} \;{\text{for}} \;f_{e} \le f_{ej}^{nom} } \\ {\frac{{f_{ej}^{nom} }}{{f_{e} }}M_{crj} \; {\text{for}} \;f_{e} > f_{ej}^{nom} } \\ \end{array} } \right. , $$
(3)

where Mcrj—critical (maximum) driving torque of jth electric motor, \( s_{crj} \)—critical slip corresponding to critical torque, \( s_{j} \)—current slip, determined by the frequency \( \omega_{0j} = 2\pi f_{e} \) and angular speeds of the rotors \( \dot{\varphi }_{1} \) and \( \dot{\varphi }_{2} \), \( f_{e} \)—power supply frequency, \( f_{ej}^{nom} \)—nominal power supply frequency of jth motor, P = 2—number of pole pairs. Formula (3) takes into account the change in critical moment when the power frequency applied exceeds the nominal power frequency of the electric motor.

3 Simulation Results

Numerical simulation was carried out in the MATLAB software with a sequential step change in frequency of the supply voltage fe in the frequency range from 30 to 90 Hz with a step of 0.5 Hz and an exposure for 5 s. Such a change ensured the establishment of steady oscillations at each excitation frequency. The calculations were carried out at the following values of the system parameters: mpl = 12.46 kg, mw = 1 kg, mr1 = mr2 = 0.029 kg, Jpl = 0.11 kg m2, Jw = 0.01 kg m2, Jr1 = Jr2 = 0.8 · 10−3 kg m2, r1 = r2 = 0.09 m, ρ = 0.128 m, ay = 0.05 m, δ1 = 22.5°, δ2 = 157,5°, cx = 580 kN/m, cy = 470 kN/m, cφ = 1.8 kN m/rad, bx = 300 N s/m, by = 200 N s/m, bφ = 1.5 N s2/m, g = 9.81 m/s2, Mcr1 = Mcr2 = 1.19 N m, scr1 = scr2 = 0.6, P = 2, \( f_{e1}^{nom} = f_{e2}^{nom} \) = 50 Hz, kf1 = kf2 = 0.005.

Figures 2, 3, and 4 show the dependences of the amplitudes of horizontal (Fig. 2), vertical (Fig. 3) and angular (Fig. 4) platform’s oscillations on the power supply frequency for different displacements of the weight relative to the vertical axis of symmetry (ax = 0, ax = 0.4ρ, ax = 0.8ρ). In the frequency range under consideration, two characteristic frequencies are observed at which the maxima of the oscillation amplitudes corresponding to the resonant oscillations of the system are reached. The expected third resonance, corresponding to the mode of simultaneous angular and horizontal oscillations, turned out to be beyond the investigated frequency range of the supply voltage.

Fig. 2
figure 2

Amplitudes of horizontal oscillations of the platform depending on power supply frequency for different weight’s displacements ax: 1 − ax = 0; 2 − ax = 0.4ρ; 3 − ax = 0.8ρ

Full size image
Fig. 3
figure 3

Amplitudes of vertical oscillations of the platform depending on power supply frequency for different weight’s displacements ax: 1 − ax = 0; 2 − ax = 0.4ρ; 3 − ax = 0.8ρ

Full size image
Fig. 4
figure 4

Amplitudes of angular oscillations of the platform depending on power supply frequency for different weight’s displacements ax: 1 − ax = 0; 2 − ax = 0.4ρ; 3 − ax = 0.8ρ

Full size image

In case of the weight’s center of mass is located on the vertical axis of symmetry, the mode of system’s oscillation near the first resonant frequency corresponds to the excitation of simultaneous angular and horizontal oscillations, and near the second resonant frequency, the mode of oscillations corresponds to the excitation of strictly vertical oscillations. The displacement of the weight from the vertical axis of symmetry leads to a change in the oscillation’s shape—simultaneous oscillations in all coordinates are excited near the second resonance. Moreover, the more displacement, the higher amplitudes of the horizontal and angular oscillations. As the supply frequency increases, the passage of the second resonances is accompanied by a jump wise decrease in the amplitudes of the vertical oscillations and an increase in the amplitudes of the horizontal and angular oscillations of the platform. The displacement of the weight leads to a decrease in the frequency of the supply voltage, at which the oscillations jump occurs; in the range of the second resonance, at a displacement of ax = 0.8ρ, the frequency reduction reaches 8%.

Figures 5, 6 and 7 show the frequency responses of horizontal (Fig. 5), vertical (Fig. 6), and angular (Fig. 7) platform oscillations depending on the debalances rotational speed for the same values of weight displacement. In contrast to the graphs, in Figs. 2, 3, and 4 curves contain discontinuities in excitation frequency during the passage resonant frequencies, which is a demonstration of nonlinearity caused by the interaction of the linear oscillatory system with vibration exciters of limited power. The rest of the characteristic features of the curves are the same.

Fig. 5
figure 5

Amplitudes frequency response of horizontal oscillations of the platform depending on excitation frequency for different weight’s displacements ax: 1 − ax = 0; 2 − ax = 0.4ρ; 3 − ax = 0.8ρ

Full size image
Fig. 6
figure 6

Amplitudes frequency response of vertical oscillations of the platform depending on excitation frequency for different weight’s displacements ax: 1 − ax = 0; 2 − ax = 0.4ρ; 3 − ax = 0.8ρ

Full size image
Fig. 7
figure 7

Amplitudes frequency response of angular oscillations of the platform depending on excitation frequency for different weight’s displacements ax: 1 − ax = 0; 2 − ax = 0.4ρ; 3 − ax = 0.8ρ

Full size image

Figures 8 and 9 show the graphs of the debalances rotational speeds (frequencies) averaged over a revolution, depending on the frequency of power supply voltage at central (Fig. 8) and shifted (Fig. 9) weight’s arrangement (ax = 0.8ρ). Here one can see that both debalances rotate with the same angular velocity in absolute value. When approaching the resonant frequencies, a decrease in the rate of increase in the motors rotational frequency is observed with increasing frequency of the supply voltage. With the passage through the resonant frequencies of the system, there is an abrupt change in the debalances rotational speeds associated with the jump of the system’s oscillations into behind-resonance range. The weight displacement leads to a decrease in power supply frequency at which system resonances occur.

Fig. 8
figure 8

Frequencies of rotation of the right-hand-side (curve 1) and left-hand-side (curve 2) debalances depending on power supply frequency at central weight’s arrangement (ax = 0)

Full size image
Fig. 9
figure 9

Frequencies of rotation of the right-hand-side (curve 1) and left-hand-side (curve 2) debalances depending on power supply frequency at shifted weight’s arrangement (ax = 0.8ρ)

Full size image

Figures 10 and 11 show the graphs of the change in mutual phase of debalances rotation of the right-hand-side exciter relative to the left-hand-side exciter depending on the frequency of the supply voltage at the central position of the weight and at its shifted positions (ax = ±0.8ρ) in positive (Fig. 10) and negative (Fig. 11) directions. In case of the central position of the weight (curves 1), one of two possible types of the debalances synchronization is realized in the system—with a mutual phase shift of 0° in the frequency range before the first resonance and after the second resonance, and with a mutual phase shift of 180° in the frequency range between the first and second resonances. The phase shift sharply changes when passing through a resonance. The displacement of the weight from the axis of symmetry leads to a change in the indicated above phase relations. In this case, in the indicated frequency ranges, the phase shift becomes dependent on the power supply frequency. An increase in weight’s displacement leads to an increase in deviations of the phase shift from the corresponding values for a system with the central position of the weight. Moreover, the direction of the phase shift deviation depends on the direction of displacement of the weight to the left or to the right.

Fig. 10
figure 10

Mutual phase of debalances at the central location of the weight (curve 1) and at shifted to the right position of the weight by the value | ax | = 0.8ρ (curve 2) depending on power supply frequency

Full size image
Fig. 11
figure 11

Mutual phase of debalances at the central location of the weight (curve 1) and at shifted to the left position of the weight by the value | ax | = 0.8ρ (curve 2) depending on power supply frequency

Full size image

4 Conclusion

The features revealed here about the behavior of the mutual phase shift of the debalances rotation depending on power supply frequency when the weight’s center of mass is shifted relative to the machine’s structural axis of symmetry make it possible to determine an initially unknown displacement of the oscillatory system’s center of mass. Taking into account the changes in the motor’s characteristics when regulating their rotational frequency did not allow to overcome the third resonance with increasing power supply frequency due to their limited power. Thus, when developing algorithms for controlling the resonant modes of vibration technological machines operation, measuring the mutual phase shift between self-synchronizing rotating debalances will make it possible to establish the correction value of the vibration exciters’ power supply frequency when an uncontrolled shift of technological load occurs.