Properties of Vibration Fields in a Two-Dimensional Lattice Structure Colliding with an Obstacle

Abstract

The paper discusses the dynamic properties of flat lattice structures colliding with a fixed limiter. Lattice structures are actively used in many branches of modern industrial production. A very noticeable subclass of these objects is 2D-lattices. They can be the basis of the designs of a number of mining, sorting, and also screening machines, with their help it is possible to carry out mathematical modeling of common 2D objects—panels, plates, membranes, a number of building structures. Corresponding models can provide analysis of nonlinear waves in various composite materials with regular reinforcement, in flat acoustic metamaterials, crystals, nanostructured surface and subsurface layers of structural materials, and many other systems. The paper presents the results of studying vibration fields in string lattices with square cells. Lattice nodes can collide with flat fixed stops. Analytical frequency-time methods of analysis of vibro-impact systems, as well as experimental methods using modern vibration measuring equipment were used.

1 Introduction

Various of lattice structures and lattice-like systems is fairly widespread in the ship and aircraft industry, as well as in other branches of modern engineering and construction. Flat (2D) lattices constitute an important class of such objects. They are included in the construction of many sorting, sifting, and mountain machines. Also, these systems play a great role in modeling of numerous 2D-objects, such as membranes, plates, panels, building structures. One should mention also the models of waves in metamaterials, crystals, composite materials with periodic reinforcement, nanostructured surfaces, and near-surface layers of materials [1,2,3,4,5,6,7,8].

At the same time, the dynamics of lattice structures has not been much investigated for a number of reasons and works related to the dynamics of lattice vibro-impact systems are rare (see papers [9,10,11,12,13]).

Let us study the rectangular string lattices, which are understood as two systems of mutually perpendicular inertialess elastic strings forming rectangular cells. In the nodes of the lattices, absolutely solid point bodies are placed. String lattices with massive nodes turn out to be a natural 2D-generalization of the well-known “string with beads” model, which played a fundamental role in the theory of oscillations [14].

In this article, the results of the study of string lattices with rectangular cells are given. Lattice nodes collide with a fixed limiter. Analytical methods of the theory of vibro-impact systems are based on the time–frequency analysis of periodic vibro-impact processes [15, 16]. And at the same time, experimental studies use modern vibration measuring equipment.

2 Statement of the Problem

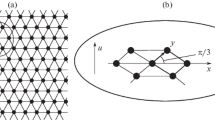
Let us consider a string lattice in a rectangular frame which is vibrating near a fixed limiter [9]—Fig. 1.

Fig. 1

String lattice near the wall

The lattice is assembled of two families of mutually perpendicular identical linear strings, which are pinched at the ends and have lengths l₁ and l₂ correspondingly (Fig. 1). The strings are numbered by the indices k = 1, 2, …, N₁ and q = 1, 2 …, N₂. The lattice nodes are point solids with the same mass m.

The rectangular lattice cells are the same, but the lengths and widths of their sides may be unequal to each other. Generally speaking, the lattice is anisotropic. We consider string elements as inertia-free. The fastening of the strings in the nodes is assumed to be absolutely rigid, with the tension being large, so that its possible changes during linear oscillations can be neglected.

Each “horizontal” side of the cells is of length Δl₁; “vertical” is of Δl₂. Let the tension of the corresponding inertialess intervals be $\tau_{1}$ and $\tau_{2}$.

The dynamics of the lattice structure is described by means of the N functions of the deflections u_kq(t), where $N = N_{1} N_{2}$. All the functions u_kq(t) vary along some axes perpendicular to the plane of the static equilibrium of the lattice.

Suppose wall is installed that a flat parallel to the plane of the static equilibrium of the lattice at a fixed distance Δ < 0. The wall is a limiter with which the nodes can collide. Thus, the system may contain up to N impact pairs (Fig. 1). We assume that all the impacts are momentary, direct, and central.

In this case, the impact conditions can be described using Newton’s hypothesis: if an impact in a node $(n,h)$ occurs at an arbitrary time $t = t_{\alpha nh}$, then

$$ \dot{u}(t_{\alpha nh} + 0) = - R\dot{u}(t_{\alpha nh} - 0),{ 0 < }R \le 1 $$

(1)

The equations of motion of the lattice nodes are

$$ \begin{aligned} & m\ddot{u}_{kq} + c_{1} ( 2u_{kq} { - }u_{ (k - 1,q )} { - }u_{ (k + 1,q )} )+ c_{2} ( 2u_{kq} { - }u_{ (k,q - 1 )} { - }u_{ (k,q + 1 )} ) { + }\varPhi_{kq} (u_{kq} ,\dot{u}_{kq} ) \\ & = \varepsilon g_{kq} (p;t,u_{kq} ) ; { } \end{aligned} $$

(2)

Here $c_{i} = \tau_{i}^{ - 1} \Delta l_{i}$; $\varepsilon$ is small parameter, $p \equiv {d \mathord{\left/ {\vphantom {d {dt}}} \right. \kern-0pt} {dt}}; \, g_{kq} (p;t,u_{kq} )$ are operator functions describing non-conservative forces. Expressions $\varPhi_{kq} (u_{kq} ,\dot{u}_{kq} )$ denote impact forces defined by means of $\delta$-functions. In accordance with (1), given that the coordinate of the limiter $\Delta < 0$ [15, 16]:

$$ \varPhi_{0kq} [u_{kq} (t_{\alpha kq} ),\dot{u}_{kq} (t_{\alpha kq} )] = J_{kq} \delta (t - t_{\alpha kq} ), $$

(3)

Values $J_{kq}$ are impulses of impacts. From formula (1), it follows: $J_{kq} = - (1 + R)m|\dot{u}_{kq} (t_{\alpha kq} - 0)|$. The boundary conditions, in this case, have the form:

$$ u_{kq} = 0, \, k = 0;N_{1} , \, q = 0;N_{2} $$

(4)

If necessary, the initial conditions could also appear here.

System (2), (4) can be written in the operator form [13, 15]

$$ u_{kq} (t )= \sum\limits_{n = 1}^{N - 1} {\sum\limits_{j = 1}^{N - 1} {L_{kq,nj} } } (p ) [\varepsilon g_{nj} (p;t,u_{nj} )- \, \varPhi_{nj} (u_{nj} ,\dot{u}_{nj} )], $$

(5)

where $\{ L_{kq,nj} (p)\}$—a system of operators of dynamic compliance of the lattice, each of which puts in correspondence the response (displacement) of the node (k, q) with the action (force) applied at the node (n, j).

The types of motion of the lattice in question are obviously quite diverse. Our goal is to study and describe in a certain sense some of the “most ordered” movements.

3 Equations of Free Oscillations with Impacts

Consider free oscillations with collisions. In this case, the impact is elastic and R = 1, and the impact impulse in formula (3) is $J_{kq} = - 2m|\dot{u}_{kq} (t_{\alpha kq} - 0)|$.

We use the operator Eq. (5) with $\varepsilon$ = 0. Representations for operators $\{ L_{kq,nj} (p)\}$ were found in [3, 10]:

$$ L_{kq,nj} (p) = C_{0} \sum\limits_{r = 1}^{{N_{1} - 1}} {\sum\limits_{h = 1}^{{N_{2} - 1}} {(\varOmega_{rh}^{2} + p^{2} )^{ - 1} \sin \frac{kr\pi }{{N_{1} }}} } \sin \frac{qh\pi }{{N{}_{2}}}\sin \frac{nr\pi }{{N_{1} }}\sin \frac{jh\pi }{{N{}_{2}}}. $$

(6)

normalization coefficient $C_{0}$ = 2[(N₁ − 1)(N₂ − 1)]⁻². The natural frequencies of the lattice {$\varOmega_{rh}^{{}}$} are determined by [3]:

$$ \varOmega_{rh}^{2} = \frac{{2\tau_{1} }}{{\Delta l_{1} }}(1 - \cos \frac{r\pi }{{N_{1} }}) + \frac{{2\tau_{2} }}{{\Delta l_{2} }}(1 - \cos \frac{h\pi }{{N_{2} }}) . $$

(7)

To describe free oscillations with impacts of a period $T = 2\pi \omega^{ - 1}$, in accordance with the time–frequency analysis methods, it is necessary to switch to a system of nonlinear Hammerstein-type integral equations [15, 16]. From Eq. (5) for periodic modes we find:

$$ u_{kq} (t )= - \sum\limits_{n = 1}^{N - 1} {\sum\limits_{j = 1}^{N - 1} {\int\limits_{0}^{T} {\chi_{kq,nj} (t - s)} } } \varPhi_{0nj} [u_{nj} (s),\dot{u}_{nj} (s)]ds, $$

(8)

The kernels of Eq. (8) are the set of periodic Green functions (PFG) [15] of the lattice considered. Its terms are defined by the set {L_kq,nj(p)} (6) by means of Fourier series of the form:

$$ \chi_{kq,nj} (t) = \frac{{C_{0} }}{{T^{ - 1} }}\sum\limits_{\nu = - \infty }^{\infty } {\sum\limits_{r = 1}^{{N_{1} - 1}} {\sum\limits_{h = 1}^{{N_{2} - 1}} {\frac{\exp (i\nu \omega t)}{{\varOmega_{rh}^{2} - \nu^{2} \omega^{2} }}\sin \frac{kr\pi }{{N_{1} }}} } } \sin \frac{qh\pi }{{N{}_{2}}}\sin \frac{nr\pi }{{N_{1} }}\sin \frac{jh\pi }{{N{}_{2}}} , $$

(9)

which on the periodicity interval 0 ≤ t < T can be written as

$$ \chi_{kq,nj} (t) = \frac{{C_{0} }}{{T^{ - 1} }}\sum\limits_{r = 1}^{{N_{1} }} {\sum\limits_{h = 1}^{{N{}_{2}}} {\chi_{rh} (t)sin\frac{kr\pi }{{N_{1} }}} } \sin \frac{qh\pi }{{N{}_{2}}}\sin \frac{nr\pi }{{N_{1} }}\sin \frac{jh\pi }{{N{}_{2}}} , $$

(10)

where $\chi_{rh} (t)$—PFG linear oscillators with frequencies $\{ \varOmega_{rh}^{{}} \}$. It is known [13] that

$$ \chi_{rh} (t) = \frac{1}{{2\varOmega_{rh} }}\frac{{\cos [\varOmega_{rh} (t - \tfrac{1}{2}T)]}}{{\sin \tfrac{1}{2}\varOmega_{rh} T}}, \, t \in [0,T]. $$

For the modes of motion with one impact in for the period of motion from formula (3), we find

$$ \varPhi_{kq} [u_{kq} (t_{kq} ),\dot{u}_{kq} (t_{kq} )] = J_{kq} \delta^{T} (t - \varphi_{kq} ); \, \delta^{T} (t) = \sum\limits_{n = - \infty }^{\infty } {\delta (t - kT)} , $$

(11)

The generalized T-periodic function $\delta^{T} (t)$ is also called the Dirac comb. Periodic Green’s functions are reactions of linear systems to precisely such force impacts [15]. Here $\varphi_{kq}$ are the moments of impacts.

Using formulas (11) and (8), we find

$$ u_{kq} (t) = \sum\limits_{n = 1}^{{N_{1} - 1}} {\sum\limits_{j = 1}^{{N_{2} - 1}} {J_{nj} \chi_{kq,nj} } } (t - \varphi_{nj} ), \, k = \, 1,2, \ldots ,N_{1} , \, q = \, 1,2, \ldots ,N_{2} , $$

(12)

Movement parameters, namely, impulses and phases should be determined from the impact conditions:

$$ \begin{aligned} & \Delta = u_{kq} (\varphi_{kq} ) = \sum\limits_{n = 1}^{{N_{1} - 1}} {\sum\limits_{j = 1}^{{N_{2} - 1}} {J_{nj} \chi_{kq,nj} } } (t - \varphi_{nj} ) \, ; \hfill \\ & J_{kq} = - 2m\sum\limits_{n = 1}^{{N_{1} - 1}} {\sum\limits_{j = 1}^{{N_{2} - 1}} {J_{nj} \left| {\frac{d}{dt}} \right.\chi_{kq,nj} } } (\varphi_{kq} - \varphi_{nj} - 0\left. ) \right|, \, k = \, 1,2, \ldots ,N_{1} \, , \, q \, = \, 1,2, \ldots ,N_{2} . \hfill \\ \end{aligned} $$

(13)

Now we are ready to study any configuration of vibro-impact modes. By varying the parameters of the system, we can investigate different types of lattices. Non-conservative forces can be accounted for by using relations similar to (12), (13), which, however, can be rather cumbersome.

4 In-Phase Modes in an Isotropic Square Lattice

We will carry out further simplifications. Let the lattice be isotropic and have square cells ($N_{1} { = }N_{2}$) with the same sides $(\Delta l_{1} = \Delta l_{2} \equiv \Delta l)$, with the tensions of all the strings, forming the lattice, being also the same $(\tau_{1} = \tau_{2} \equiv \tau )$. Then in Eq. (2), we have $c_{1} = c_{2} = \tau^{ - 1} \Delta l$. The structure of the set of natural frequencies of the lattice is simplified:

$$ \varOmega_{rh}^{2} = \frac{{2\tau_{{}} }}{{\Delta l_{{}} }}(2 - \cos \frac{r\pi }{{N_{{}} }} - \cos \frac{h\pi }{{N_{{}} }}), $$

(14)

Thus, the matrix $\left\| \varOmega \right.\left. {_{rh}^{2} } \right\|$ is quadratic and symmetric. This entails significant simplifications when making transformations with PFG $\chi_{kq,nj} (t)$.

Periodic-free oscillations with one impact over a period are described by the solutions of system (13), which determines the 2 N² motion parameters ($J_{kq} ;\varphi_{kq}$).

Of special attention are the solutions with the simplest structure, which correspond to in-phase, anti-phase, or localized modes [13, 17, 18]. As a rule, such regimes, or similar ones, were registered experimentally. They correspond to nonlinear resonant modes. Sometimes with their help, one can “design” more complicated modes of motion.

Consider the movements of in-phase claps type. At such movements, synchronization of the impacts occurs in different impact pairs. Claps were deeply studied in one-dimensional systems [17, 18]. In lattice structures, they were considered in [9,10,11].

For in-phase oscillations: $\varphi_{kq} = \varphi , \, k,q \, = \, 1,2, \ldots ,N \,$ and the first group of equations (7) gives for impulses a linear system of N² algebraic equations, while the second group of equations becomes an identity that can be derived from the PFG properties [15]. As an example, we take a system with four degrees of freedom—an isotropic square lattice $2 \times 2$. In this case, for all values of the indexes, the displacements of the nodes are the same ($u_{kq} (t) \equiv u(t)$) and can be given by the expression

$$ u(t) = - \Delta \frac{{\cos \varOmega_{11} (t - {\raise0.7ex\hbox{$T$} \!\mathord{\left/ {\vphantom {T 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}})}}{{\cos \varOmega_{11} {\raise0.7ex\hbox{$T$} \!\mathord{\left/ {\vphantom {T 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}, \, t \in [0,T] , $$

(15)

where $\varOmega_{11} = 2\tau_{1} (\Delta l_{1} )^{ - 1}$. Representation (15) coincides with the representation of the law of motion of a vibro-impact system with one degree of freedom (impact oscillator) [19].

The function graph $u(t)$ is shown in Fig. 2. Figure 3 shows the dependence of the amplitude of oscillations on the frequency in each of the four shock pairs.

Fig. 2

The low motion of lattice nodes

Fig. 3

Amplitude and frequency characteristic

$$ A(\omega ) = \frac{1}{2}(\hbox{max} u - \Delta ) = \frac{\Delta }{2}(sec\frac{\pi \varOmega }{\omega } - 1), $$

(16)

It is easily seen that this graph is similar to that obtained for an impact oscillator [15, 19]. The figure marked frequencies $\varOmega {}_{0}$ = $\varOmega_{11}$; $\varOmega^{0}$ = 2 $\varOmega_{11}$. The polysemy of the graph at the frequency is associated with the existence of linear oscillations with arbitrary amplitudes before reaching the obstacle.

5 Experimental Stand

The study of in-phase resonant modes was carried out using a specially designed and manufactured stand “Alligator Square” [12, 13] (Fig. 4). Following the traditions of the nonlinear theory of oscillations, resonant oscillations are understood as no small displacements of the systems caused by small excitatory factors with a small level of energy dissipation.

Fig. 4

Experimental stand

The stand consists of a work installation and a system of control and registration. The work installation includes a vibration exciter (V) and square replaceable lattices (L) with dimensions (250 × 250 mm) that consist of aluminum profile frames and mutually perpendicular stretched rubber strings with a diameter of 1 mm.

Cell sizes are controlled by precision rulers. The frame of the lattice (2 × 2, 3 × 3, 4 × 4) is attached to the rod of the vibroexciter. The frame design allows for the lattice parameters (number of strings, cell sizes, etc.) to be changed. The lattice nods are formed by toroidal washers with diameters d = 9 mm and masses m₀ = 1.1 g. Washers made of hardened steel, placed at the intersections of the strings and are not fixed rigidly.

The control and recording system consist of a control computer (CC) that solves the tasks of controlling both the vibrator and time-frequency analysis of the recorded information. Also used a power amplifier (A), digital strobe (SL), meter to measure the amplitude of vibration of the rod of the vibroexciter (MA), together with force sensors (F_nj). Camera (C) registered the profiles of standing waves, in the regime of photo-graphing or accelerated video.

The signals from the force sensors ($\phi_{nj}$) are conveyed to the control computer, where they can be visualized and presented in both the frequency and time ranges. The strobe lamp (SL) provides visualization of the standing wave profiles.

6 Impact-Free Movements

The stand, described in the previous paragraph, was used for a detailed description of the behavior of string lattices if no impacts take place. The characteristic profiles of standing waves in the case of motion according to the first form $\varTheta_{11}$ [12] are given in Fig. 5: Fig. 5a, b demonstrate $2 \times 2$ lattice and $3 \times 3$ lattice correspondingly. The evolution of the standing wave profiles for $4 \times 4$ dimension lattice is shown in Fig. 6.

Fig. 5

Lattice profiles. The first form

Fig. 6

Standing wave evolution

Consider the amplitude-frequency characteristics (AFC) of impact-free motion on the basic form $\varTheta_{11}$. Figure 7 shows a family of amplitude-frequency characteristics of 2 × 2 lattice. Furthermore, it is assumed that the amplitude appears to be a semi-range of oscillations of the selected characteristic point of the lattice. For a given lattice, the characteristic point was chosen somewhere in the middle of span between neighboring nodes, etc. Curves 1–3 correspond to the amplitudes of the vibrator rod, which are respectively, a₁= 0.3 mm; a₂= 0.6 mm; a₃= 1.4 mm.

Fig. 7

Amplitude-frequency characteristics in the absence of impacts

It is seen that when the amplitude of excitation increases, the lattice loses linearity. Its AFC is distorted as it happens in the case of systems with, for example, geometric nonlinearity.

Nonlinear distortions manifest themselves, in particular, in the deviation of the contours of the lattice cells from the square. Their shape becomes trapezoid-like (see also [12]).

7 In-Phase Vibro-Impact Modes of Motion (Claps)

Using the described stand, it was found that after the passage of the first natural frequency of oscillations, one can observe stable periodic modes with simultaneous collisions with the limiter of all nodes. At the same time, the vibro-impact mode at the linear resonance frequency turns out to be complicated (see below).

The profiles of standing waves are shown in Fig. 8 (2 × 2 lattice) and Fig. 9 (3 × 3 lattice). These modes and are the claps in the string lattice. The fact that the impacts are in-phase was established both visually and by comparing the synchronizing signals from the force sensors F_nj. For one-dimensional case (balls on a stretched string), claps were experimentally described in [17, 18].

Fig. 8

Clap in a string lattice

Fig. 9

Clap in a string lattice

Figure 8 demonstrates the moment of the impact (a limiter with no sensors was chosen). The overlay of several photographs demonstrates the evolution of the standing wave profile (Fig. 9). Oscillations are limited to the surface of a truncated octahedron.

Figure 10 shows three curves numbered in accordance with Fig. 7 numbering. The curves correspond to the amplitudes of the claps (the half-range of oscillations of characteristic points of the lattices, near the geometric center).

Fig. 10

Amplitude-frequency characteristic of the standing waves at in-phase claps

It can be seen that as the excitation frequency increases, the amplitude increases until a sudden cessation of oscillations with collisions. This dynamic phenomenon is called pulling by frequency. It is characteristic of the classical impact oscillator and clap in one-dimensional chains and strings [15, 17,18,19]. When striving for frequencies of sudden disruption of intensive oscillations, the amplitudes forces of impact strive for the maximum possible.

With the passage of the frequency range after sudden disruption, claps can be obtained only by giving the elements of the lattices some triggering impulse (hard triggering phenomenon) or after a significant return of frequency closer to the linear resonance value.

It should be noted that the nonlinearity of impact-free system, that is, the nonlinearity of the string lattice itself is practically not manifested when getting to a periodic vibro-impact mode. Thus, it is possible to say, in this case, that more “weak nonlinearity”, arising due to usually weak nonlinear geometrical or physical factors, is suppressed by strong non-linearity, caused by the impacts.

Note that, perhaps, a noticeable discrepancy between the theoretical and experimental curves (Figs. 3 and 10) is caused by the fact that the model neglects a great deal of factors connected with the obvious imperfections of the lattices. These factors, in particular, lead to a deviation of the system from linear between the impacts.

At the same time, the main resonance properties of the claps (pulling, sudden disruption of oscillation, hard start necessity) remain qualitatively the same and, as indicated, are clearly distinct.

In a small neighborhood (about 0.3 Hz) of the linear resonance frequency, we observed complicated weakly ordered motions with impacts, accompanied by chatter [15]. Further, periodic regimes were observed up to emergence of steady claps. These modes were accompanied by the impacts of only several nodes.

Modes of a complicated type were recorded in some frequency zones after the frequency of the sudden disruption. The highest forms of claps were not recorded.

We note in conclusion that with a change in the parameters of the gratings, a qualitative change in the character of standing waves is possible. In article [20], standing waves in gratings with wider cells than in the grids described above were investigated. The phenomenon of the formation of periodic standing waves—claps with synchronous collisions of all nodes was transformed into the effect of the emergence of periodic regimes with more complicated profiles.

A 3 × 3 lattice was considered. Initially, eight peripheral nodes collided simultaneously, and then the central one. At the same time, a number of the above properties, characteristic of nonlinear resonant modes, were preserved. The effect of synchronization of all collisions manifested itself in the simultaneous achievement by all the nodes of the lattice of some intermediate coordinate different from the value of the gap.

These results require a detailed theoretical study, as well as a number of clarifications concerning the clarification of the role of the number of nodes, widths of spans, and some other factors that can affect the dynamics of string lattices in vibro-impact modes.