Design and Optimization of the KDamper Concept for Seismic Protection of Bridges

Abstract

The KDamper is a novel passive vibration isolation and damping concept, based essentially on the optimal combination of appropriate stiffness elements, which include a negative stiffness element. The KDamper concept ensures the static stability of the structure, does not require heavy masses, and can achieve better dynamic characteristics, compared to the “Quazi-Zero Stiffness” (QZS) isolators and the traditional Tuned Mass Damper (TMD). Contrary to the TMD and its variants, the KDamper substitutes the necessary high inertial forces of the added mass by the stiffness force of the negative stiffness element. Among others, this can provide comparative advantages in the very low-frequency range (Kapasakalis et al. in GRACM, 2018 [1]). The paper proceeds to a systematic approach for the optimal design and selection of the KDamper parameters, for a typical bridge structure. The design of the KDamper follows the scope of a general vibration isolation and damping concept considering Base Acceleration Excitation/Relative Structure Displacement Response Transfer Function and/or Base Acceleration Excitation/Absolute Structure Acceleration Response Transfer Function. Furthermore, an alternative design approach, incorporating an optimization algorithm is examined. The system is subjected to artificial accelerograms and real earthquake records. The proposed system is compared to the initial undamped model as well as similar structures employing other seismic isolation techniques. Comparative results prove the efficiency of the proposed KDamper system, used as an alternative or supplement to conventional seismic isolation techniques.

1 Introduction

Following from [2], seismic isolation is probably the best-established design approach of antiseismic protection [3] because it relies on reducing the seismic demand (usually increasing the natural period of the structure) rather than increasing the earthquake resistance capacity of the structure. Isolation systems implemented in the bases of the structures, typically provide horizontal isolation from the effects of earthquake shaking, by disjoining the superstructure from the base-foundation during earthquakes. Therefore, a number of isolation devices such as the elastomeric bearings (with lead core or without) [4], frictional/sliding bearings, roller bearings have been developed.

Following this direction, the last years has been proposed the introduction of negative stiffness elements (Negative Stiffness Devices and “Quazi-Zero Stiffness” oscillators). True negative stiffness is defined as a force that assists motion instead of resisting it, like a positive stiffness spring. The idea of introducing negative stiffness elements (or “anti-springs”) is not new, being introduced for the first time in the pioneering publication of Molyneaux [5], as well as in the milestone developments of Platus [6]. The basic idea of these approaches is the significant reduction of the stiffness of the isolator and as a consequence the reduction of the natural frequency of the system at almost zero levels, as in Carella et al. [7], called “Quazi-Zero Stiffness” (QZS) oscillators. An introductory overall analysis of such designs can be found in Ibrahim [8]. The negative stiffness behavior is mainly accomplished by special mechanical designs comprising of typical positive stiffness prestressed elastic mechanical elements, such as post-buckled beams, plates, shells, and pre-compressed springs, organized in appropriate geometrical shapes. Some interesting designs are described in [9, 10]. Also, QZS oscillators find a large array of applications in seismic isolation [11,12,13,14,15,16,17,18].

Among the numerous passive and active control techniques, the implementation of an additional mass (Tuned Mass Dampers), is probably the most popular and mature theory. A Tuned Mass Damper (TMD), also known as a dynamic vibration absorber, is a classical engineering device that consists of a mass, a spring, and a viscous damper. Usually, it is attached to a vibrating primary system, to suppress any unwanted vibrations induced by wind and earthquake loads. The first application of the TMD concept was made by Frahm [19]. Since Den Hartog’s [20] first proposition of optimal design theory for the TMD for an undamped SDoF structure, the TMD has been employed on a vast array of systems with the most interesting case being skyscrapers [21,22,23]. An interesting approach is the connection of a TMD to a BIS, [24,25,26,27] because in base-isolated structures at the level of the isolator occurs the maximum relative displacement. Furthermore, this placement of the TMD keeps the load of the superstructure at the same level. Even though TMDs are known for their effective and reliable use, they pose significant disadvantages. The properties of the TMD may be altered by environmental influences and other external factors, disturbing its tuning. As a consequence, the performance of the device can be heavily reduced [28]. Another vital limitation of the TMD is that it requires a large oscillating mass, in order to achieve significant vibration reduction, making its construction and placement procedure rather demanding.

As an alternative, in this paper, the novel Kdamper vibration absorption concept is presented as a seismic Base Absorber. The KDamper, introduced by Antoniadis et al. [29], incorporates the beneficial properties of both Negative Stiffness Elements and Tuned Mass Dampers. The proposed device combines a negative stiffness element, which can display exceptional damping properties, without the disadvantages of TMDs or QZS oscillators. The design of the KDamper is made in order to present the same overall (static) stiffness, as a traditional reference original oscillator. However, it displays differences compared to both original SDoF oscillators, as well as from the known negative stiffness oscillators, because of the proper redistribution of the individual stiffness elements and the reallocation of the damping. Even though unstable behavior is a characteristic of the negative stiffness elements, the proposed device is planned in order to be statically and dynamically stable. In order to reduce the effects of a vibrating load an additional mass is added, which operates as an energy dissipation mechanism identical to the additional mass of the TMDs. However, the KDamper overcomes the sensitivity problems of TMDs, as the negative stiffness elements control the tuning. When a system’s parameters are optimally selected, the system displays exceptional damping behavior. The method for the optimal selection of the KDamper parameters can pursue the classical minmax (H∞) method, proposed firstly by Den Hartog [20]. Relevant procedures are described in Antoniadis et al. [29] for a Force Excitation/Displacement Response Transfer Function and in [30,31,32,33] for a Base Acceleration Excitation/Relative Structure Displacement Response Transfer Function. An alternative design approach, incorporating an optimization algorithm, can be found in Syrimi et al. [34]. For the optimization process, a new metaheuristic algorithm is chosen, the harmony search algorithm (HS). First introduced by Geem et al. [35] in 2001, HS can manage problems with both discrete and continuous variables [36, 37] and is defined by the distinguishing features of algorithm simplicity and search effectiveness. Not being a hill-climbing algorithm, the likelihood of becoming entrapped to a local optimum is significantly diminished. Furthermore, it adopts a stochastic random search instead of a gradient search, which enhances its simplicity. Stochastic derivatives are useful for numerous scientific and engineering problems where mathematical derivatives cannot be determined or easily handled [38] and also reduce the required number of iterations. The previous advantages render HS useful for various optimization problems such as the traveling salesman problem [35], optimization of data classification systems [39], pipe network design [40], and generalized orienteering problem [41]. As far as structural problems are involved, HS has been successfully implemented to the optimum design of truss structures [42], steel sway frames [43], and grillage systems [44]. Lately, HS has been utilized for the optimum design of the application of TMDs to multistory buildings [45, 46].

In this paper, the implementation of the KDamper concept as an alternative or supplement to conventional seismic isolation concepts of bridges is examined. The objective is to optimally select the KDamper parameters for seismic isolation of a typical bridge structure and to assess the resulting benefits to the dynamic behavior of the structure. The KDamper concept is introduced in Sect. 2 of the paper, together with a preliminary conceptual presentation on its fundamental concept and on the reasons why this concept offers the potential to overcome the disadvantages of the traditional vibration absorbers: Quazi-Zero Stiffness Oscillators and Tuned Mass Dampers. The optimal selection approach of the KDamper parameters is introduced in Sect. 3, which follows exactly the same steps of Den Hartog [18], considering Base Acceleration Excitation/Relative Structure Displacement Response Transfer Function minimization and Base Acceleration Excitation/Absolute Structure Acceleration Response Transfer Function minimization. Alternatively, an optimization algorithm is employed, which has been successfully applied to several engineering problems, to obtain optimum design parameters for a typical bridge structure under seismic excitation. The set of the optimized parameters considering the HS optimization algorithm is obtained for a set of 10 Artificial Accelerograms, the generation of which is described in Sect. 4 of this paper, using as an objective function the Root Mean Square of the displacement ratio and a constraint for the maximum absolute acceleration of the deck. The dynamic response of the bridge is examined before and after the implementation of the KDamper concept. Comparative results with a highly damped seismic isolated structure, confirm that the KDamper concept can be used efficiently as an alternative or supplement of the conventional seismic isolation approaches, improving the dynamic behavior of the structure in terms of the deck’s relative displacement and absolute acceleration.

2 The KDamper Concept

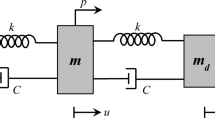
As in [2], Fig. 1 displays the main design of the fundamental vibration isolation and damping concepts to be examined. They are all designed to achieve minimal response x(t) of an undamped or low damped, SDoF system of mass m and static stiffness k of to a base excitation of x_G(t). The idea of the Negative Stiffness isolator, displayed in Fig. 1a, is the addition of a negative stiffness element k_N in parallel to the original stiffness k of the system in order for the overall stiffness of the system to become k_QZS = k + k_N ≤ k. However, this caps the static loading capacity of the structure, which may result in unsolvable problems, especially in the case of vertical vibration isolation. Figure 1c displays the basic concept of KDamper. Like the NS isolator, it uses a negative stiffness element k_N. However, unlike the NS isolator, the first essential requirement of the KDamper is that the overall static stiffness of the system is maintained:

Fig. 1

Schematic presentation of the considered vibration absorption concepts a Quasi-Zero Stiffness (QZS) oscillator, b Tuned Mass Damper (TMD) and c KDamper

$$k_{R} + \frac{{k_{P} k_{N} }}{{k_{P} + k_{N} }} = k$$

(1)

As a result, the KDamper can overcome the basic disadvantage of the NS isolator. Compared to the TMD damper (Fig. 1b), the KDamper makes use of an additional negative stiffness element k_N, which connects the additional mass to the base. Consequently, the equation of motion of the KDamper is

$$m\ddot{u}_{S} + c_{D} (\dot{u}_{S} - \dot{u}_{D} ) + k_{R} u_{S} + k_{P} (u_{S} - u_{D} ) = - ma_{G}$$

(2a)

$$m_{D} \ddot{u}_{D} - c_{D} (\dot{u}_{S} - \dot{u}_{D} ) - k_{P} (u{}_{S} - u_{D} ) + k_{N} u_{D} = - m_{D} a{}_{G}$$

(2b)

or equal to:

$$m\ddot{u}_{S} + k_{R} u_{S} + m_{D} \ddot{u}_{D} + k_{N} u_{D} = - (m + m_{D} )a_{G}$$

(3a)

$$m_{D} \ddot{u}_{D} - c_{D} (\dot{u}_{S} - \dot{u}_{D} ) - k_{P} (u{}_{S} - u_{D} ) + k_{N} u_{D} = - m_{D} a{}_{G}$$

(3b)

Expecting a harmonic excitation of $a_{G} (t) = A_{G} \exp (j\omega t)$ and a constant state response of $u_{S} (t) = \tilde{U}_{S} \exp (j\omega t)$ and $u_{D} (t) = \tilde{U}_{D} \exp (j\omega t)$, where $\tilde{U}_{S}$, $\tilde{U}_{D}$ stand for complex quantities, the equations of motion (Eqs. 2a, 2b) of the KDamper become

$$- \omega^{2} m\tilde{U}_{S} + j\omega c_{D} (\tilde{U}_{S} - \tilde{U}_{D} ) + k_{R} \tilde{U}_{S} + k_{P} (\tilde{U}_{S} - \tilde{U}_{D} ) = - mA_{G}$$

(4a)

$$- \omega^{2} m_{D} \tilde{U}_{D} - j\omega c_{D} (\tilde{U}_{S} - \tilde{U}_{D} ) - k_{P} (\tilde{U}_{S} - \tilde{U}_{D} ) + k_{N} \tilde{U}_{D} = - m_{D} A_{G}$$

(4b)

or equal to

$$- \omega^{2} m\tilde{U}_{S} + k_{R} \tilde{U}_{S} - \omega^{2} m\tilde{U}_{D} + k_{N} \tilde{U}_{D} = - (m + m_{D} )A_{G}$$

(5a)

$$- \omega^{2} m_{D} \tilde{U}_{D} - j\omega c_{D} (\tilde{U}_{S} - \tilde{U}_{D} ) - k_{P} (\tilde{U}_{S} - \tilde{U}_{D} ) + k_{N} \tilde{U}_{D} = - m_{D} A_{G}$$

(5b)

A precise study of Eqs. 4a, 4b shows that the amplitude F_MD of the inertia force of the additional mass and the amplitude F_N of the negative stiffness force

$$F_{MD} = - \omega^{2} m_{D} \left| {\tilde{U}_{D} } \right|$$

(6a)

$$F_{N} = k_{N} \left| {\tilde{U}_{D} } \right| \le 0$$

(6b)

are exactly in phase, because of the negative value of k_N. Hence, the KDamper can be treated as an indirect way to raise the inertia effect of the additional mass m_D without a direct increase of the mass m_D. Furthermore, it should be noted that the value of F_MD depends on the frequency, while the value of F_N is constant in the full frequency range, an important fact for low-frequency vibration isolation and displays an essential dynamic advantage as opposed to the inerter.

2.1 Formulation of Transfer Functions

A number of Transfer Functions of the KDamper result from Eqs. (4a, 4b).

$$\tilde{H}_{US} = \frac{{\tilde{U}_{S} }}{{A_{G} }} = - \frac{{\tilde{N}_{US} }}{{\tilde{D}}}$$

(7a)

$$\tilde{H}_{UD} = \frac{{\tilde{U}_{D} }}{{A_{G} }} = \frac{{(j\omega c_{D} + k_{P} )H_{US} - m_{D} }}{{( - \omega^{2} m_{D} + j\omega c_{D} + k_{p} + k_{N} )}} = \frac{{\tilde{N}_{UD} }}{{\tilde{D}}}$$

(7b)

$$\tilde{H}_{AS} = \frac{{\tilde{A}_{S} }}{{A_{G} }} = 1 - \omega^{2} \tilde{H}_{US} = \frac{{\tilde{N}_{AS} }}{{\tilde{D}}}$$

(7c)

where

$$\tilde{N}_{US} = - \omega^{2} mm_{D} + j\omega c_{D} (m + m_{D} ) + m(k_{P} + k_{N} ) + m_{D} k_{P}$$

(8a)

$$\tilde{N}_{UD} = - \omega^{2} mm_{D} + j\omega c_{D} (m + m_{D} ) + mk_{P} + m_{D} (k_{R} + k_{P} )$$

(8b)

$$\tilde{N}_{AS} = - \omega^{2} m_{D} k_{R} + j\omega c_{D} (k_{R} + k_{N} ) + k(k_{P} + k_{N} )$$

(8c)

$$\tilde{D} = \omega^{4} mm_{D} - j\omega^{3} (m + m_{D} )c_{D} - \omega^{2} [m(k_{P} + k_{R} ) + m_{D} (k_{P} + k_{R} )] + j\omega c_{D} (k_{R} + k_{N} ) + k(k_{P} + k_{N} )$$

(8d)

where k is the total static stiffness of the system, as described in Eq. (1). The procedure for the optimal selection of the KDamper parameters can follow the classical minmax (H∞) approach, first proposed by Den Hartog [18]. Relevant procedures are described in Hashimoto et al. [27] for a Force Excitation/Displacement Response Transfer Function and in [28,29,30,31] for a base acceleration excitation/relative structure displacement response transfer function. An alternative design approach, incorporating an optimization algorithm, can be found in Sapountzakis et al. [32].

However, the results of the optimization present significant differences, depending on the transfer function to be selected for optimization, as shown in Sect. 3 of this paper. Finally, the following parameters are introduced:

$$\kappa = - k_{N} /(k_{P} + k_{N} );\mu = m{}_{D}/m;\mu = m{}_{D}/m;q = \omega /\omega_{0}$$

(9a, b, c, d)

$$\omega {}_{0} = \sqrt {k/m} ;\omega {}_{D} = \sqrt {k_{D} /m_{D} } ;\zeta {}_{D} = c_{D} /2\sqrt {k_{D} m_{D} }$$

(9e, f, g)

2.2 Basic Properties of the KDamper

Increasing the absolute value of the stiffness k_N may endanger the static stability of the structure. Although theoretically the value of k_N is selected according to Eq. (1) to ensure the static stability, due to various reasons, such as temperature variations, manufacturing tolerances, or nonlinear behavior, k_N may present significant variations in practice, since almost all negative stiffness designs result from unstable nonlinear systems. Consequently, an increase of the absolute value of k_N by a factor ε may lead to a new value of k_NL where the structure becomes unstable:

$$k_{R} + \frac{{k_{P} k_{NL} }}{{k_{P} + k_{NL} }} = 0 \Leftrightarrow k_{NL} = - \frac{{k_{R} k_{P} }}{{k_{R} + k_{P} }} = (1 + \varepsilon )k_{N}$$

(10)

Substitution of Eqs. (17a) to (17c) into (10) leads to the following estimate for the static stability margin:

$$\varepsilon = \frac{1}{{\kappa [1 + (1 + \kappa )^{2} \mu \rho^{2} ]}}$$

(11)

3 Optimal Design Approach for the KDamper

3.1 Harmony Search Algorithm and Optimization Process

In this section, the HS metaheuristic algorithm is shortly described and is also presented with a comprehensive example of the recommended optimization procedure. The four key steps of the algorithm are presented below.

Step 1: Initialization of the HS Memory matrix (HM). HM matrix consists of vectors representing potential solutions to the examined optimization problem. The original HM matrix is formed using randomly generated results. For an n-dimension problem, HM has the form:

$$HM = \left[ {\begin{array}{*{20}c} {x_{1}^{1} ,x_{2}^{1} , \ldots ,x_{n}^{1} } \\ {x_{1}^{2} ,x_{2}^{2} , \ldots ,x_{n}^{2} } \\ . \\ . \\ . \\ {x_{1}^{HMS} ,x_{2}^{HMS} , \ldots ,x_{n}^{HMS} } \\ \end{array} } \right]$$

(12)

where [x ¹₁ , x ¹₂ , …, x ¹_n ] (i = 1, 2,…, HMS) is a result candidate. HMS is generally set to values between 50 and 100. The value of the objective function is determined for every solution vector of the HM matrix.

Step 2: Improvisation of a [x ^′₁ , x ^′₁ , …, x ^′₁ ] new result from the HM. Each one of the components of this new result, x ^′_j , is gained based on the Harmony Memory Considering Rate (HMCR), which is described as the probability of selecting a component from the HM members. 1—HMCR is, thus, the probability of creating a new component at random. If x ^′_j is elected from the HM matrix, it is further altered according to the Pitching Adjusting Rate (PAR), which regulates the probability of a candidate from the HM to be altered.

Step 3: Update of the HM matrix. The value of the objective function of the new result, gained in Step 2, is determined and measured to the ones that correlate to the original HM matrix vectors. If the outcome is a better fitness than that of the worst member in the HM, it will take over that one. If there are more than one member in the HM with bigger values of the objective function that the new solution, the result with the higher value is replaced. Otherwise, the new solution is erased and HM matrix remains untouched.

Step 4: Repetition of Steps 2 and 3 until a preset termination benchmark is satisfied. A frequently used termination benchmark is the maximum number of total iterations.

The flowchart of the suggested HS algorithm is shown in Fig. 2.

Fig. 2

Flowchart of the proposed HS algorithm

KDamper concept optimization process. Succeeding the method and flowchart presented above, the features of the inspected optimization problems can be calculated.

Firstly, the two parameters are selected, whose values shall be optimized, that control the device’s performance κ, and ζ_D. The additional mass ratio of the KDamper device is selected 5% equal to the other optimized set of parameters that will be employed in Sect. 5. Secondly, the restrains of the design variables are decided. Their choice relies on safety, stability, and manufacturing parameters that need to be considered. These parameters may alter from structure to structure, yet, as far as bridges are involved, the restrains presented below produce satisfying results in most cases.

In Table 1 are demonstrated the lower and upper caps of the two design variables. As far as the ratio ζ_D is concerned, its value is upper limited because of manufacturing causes, in order for the system to be economic and to have an easy to construct and place the device. The restrains of the design variable, κ, are guided by the basic stability specification of the KDamper. The latter is introduced in the KDamper design technique in order to stay away from excessive values of the negative stiffness element that could disrupt the static stability of the system. The aimed stability is provided by the indication of the static stability margin, ε. In this case, ε is set to be 10%. Thus, the frequency ratio ρ is obtained as a function of μ, κ, and ε (Eq. 11).

Table 1 Variable design limits

As far as the parameters inherently involved in the HS algorithm are concerned, a common practice is to adopt commonly found values found in relative literature (Table 2). The same is true for the termination criterion, as the maximum number of repetitions is pre-determined.

Table 2 Values of the HS algorithm parameters

With the intention of finding the optimum solution for all 10 Artificial Accelerograms to which the considered bridge is exposed to, the Root Mean Square (RMS) of the displacement ratio (deck displacement of the isolated structure over the deck displacement of the original structure) is determined as the objective function, that needs to be minimized.

Finally, the restraints of the inspected optimization problem are specified, and more specifically a constraint concerning the maximum deck’s absolute acceleration to be lower than the maximum PGA of the Artificial Accelerograms.

3.2 Optimal Acceleration Response Under Base Excitation

Equation (7c) can be written in the following form:

$$\widetilde{\rm H}_{AS} = - \frac{{A + (j2\zeta_{D} )B}}{{C + (j2\zeta_{D} )D}};H_{AS} = \frac{{\left| {\widetilde{A}_{S} } \right|}}{{A_{G} }} = \frac{{A_{S} }}{{A_{G} }} = \sqrt {\frac{{A^{2} + (2\zeta_{D} )^{2} B^{2} }}{{C^{2} + (2\zeta_{D} )^{2} D^{2} }}}$$

(13a,b)

where

$$A = - q^{2} [1 + \kappa (1 + \kappa )\mu \rho^{2} ] + \rho^{2} ;{\rm B} = \rho q(1 + \kappa^{2} \mu \rho^{2} )$$

(14a,b)

$$C = q^{4} - q^{2} [1 + \rho^{2} + (1 + \kappa^{2} )\mu \rho^{2} ] + \rho^{2} ;D = \rho q[(1 + \kappa^{2} \mu \rho^{2} ) - q^{2} (1 + \mu )]$$

(14c,d)

By setting κ = 0 to Eq. (13b) leads to the corresponding transfer function for the TMD. The transfer function in Eq. (13b) is now a four-parameter function of: κ, μ, ρ, ζ_D. At first, the selection of the parameters μ and κ is made. Next, we get the optimal value of ρ as a function of κ, μ (Eq. 27), following the minmax approach defined in Appendix 1. Considering the selection of ζ_D, many approaches are available, the exact treatment of which is beyond the scope of the present paper. Α clear approach is the numerical calculation of ζ_D so that it minimizes the peak of the Transfer Function H_AS(q, ζ_D) (Fig. 3b). Figure 3 shows the fluctuation of H_US(f, μ) and H_AS(f, μ) due to shifts of μ. It must be noted, that for the optimum value of ζ_Dopt = ζ_min, both peaks of the Transfer Function H_AS(q, ζ_D) have equal values and are minimized (Fig. 3b).

Fig. 3

Dependence of the transfer functions a H_US and b H_AS on the mass ratio μ, for acceleration response optimization

3.3 Optimal Relative Displacement Response Under Base Excitation

Equation (7a) can be written in the following form:

$$\tilde{H}_{US} = \frac{{\tilde{U}_{S} }}{{A_{G} }} = - \frac{1}{{\omega_{0}^{2} }}\frac{{A + (j2\zeta_{D} )B}}{{C + (j2\zeta_{D} )D}};H_{US} = \frac{{\left| {\widetilde{U}_{S} } \right|}}{{A_{G} }} = \frac{{U_{S} }}{{A_{G} }} = \frac{1}{{\omega^{2} }}\sqrt {\frac{{{\rm A}^{2} + (2\zeta_{D} )^{2} B^{2} }}{{C^{2} + (2\zeta_{D} )^{2} D^{2} }}}$$

(15a,b)

where

$$A = \rho^{2} [1 + (1 + \kappa )\mu ] - q^{2} ;B = \rho q(1 + m)$$

(16a,b)

$$C = q^{4} - q^{2} [1 + \rho^{2} + (1 + \kappa^{2} )\mu \rho^{2} ] + \rho^{2} ;D = \rho q[(1 + \kappa^{2} \mu \rho^{2} ) - q^{2} (1 + \mu )]$$

(16c,d)

By setting κ = 0 to Eq. (15b) leads to the corresponding transfer function for the TMD. The transfer function in Eq. (15b) is a four-parameter function of: κ, μ, ρ, ζ_D. At first, the selection of the parameters μ and κ is made. Next, we get the optimal value of ρ as a function of κ, μ (Eq. 37), following the minmax approach defined in Appendix 2. Considering the selection of ζ_D, many approaches are available, the exact treatment of which is beyond the scope of the present paper. Α clear approach is the numerical calculation of ζ_D so that it minimizes the peak of the Transfer Function H_US(q, ζ_D) (Fig. 4a). Figure 4 shows the fluctuation of H_US(f, μ) and H_AS(f, μ) due to shifts of μ. It must be noted, that for the optimum value of ζ_Dopt = ζ_min, both peaks of the Transfer Function H_US(q, ζ_D) have equal values and are minimized (Fig. 4a).

Fig. 4

Dependence of the transfer functions a H_US and b H_AS on the mass ratio μ, relative displacement response optimization

Once the values of the mass m and the total stiffness k are established, the values of the elements of the KDamper finally result as follows:

$$k_{N} /k = \kappa_{\rm N} = - \kappa \mu \rho^{2} ;k_{P} /k = \kappa_{\rm P} = (1 + \kappa )\mu \rho^{2} ;k_{R} /k = \kappa_{S} = 1 + \kappa (1 + \kappa )\mu \rho^{2}$$

(17a,b,c)

$$m_{D} = \mu m;c_{D} = 2\zeta_{D} \sqrt {(k_{P} + k_{N} )m_{D} }$$

(17d,e)

4 Base Acceleration Excitations

Considering [2] strong earthquake time histories are created from one out of three essential types of accelerograms: real accelerograms recorded during earthquakes (not all soil combinations are involved, not polished spectra), synthetic records retrieved from seismological models and artificial records, suitable for a specific design response spectrum, with the latter being the most satisfactory for Code-based spectrum design. Following this, there is a necessity for the creation of the design response spectrum-compatible ground acceleration excitations.

For this reason, the approach adopted in this paper is based on first creating a sample of artificial accelerograms whose response spectra is approximately compatible with the design response spectra (EC8). Artificial spectrum-compatible accelerograms can be created through SeismoArtif Software [47]. The Artificial Accelerograms utilized in this paper are drafted to match a highly challenging but realistic case: the EC8 response spectrum for a particular ground type, in this case, ground type C, for spectral acceleration 0.36 g, spectrum type I, importance class II.

Nevertheless, real earthquake ground motions are neither motionless nor have a fixed time span. So, it is extremely important to investigate the effectiveness of the proposed vibration control method also with real accelerograms recorded in earthquakes. Three natural earthquake signals are reviewed: Northridge, L’Aquila, and Tabas, with their PGA and duration, are given in Table 1. The mean PGA of the 10 Artificial Accelerograms of the database is 0.529 g. The response acceleration spectrum of each one of the reviewed real accelerograms along with the mean of the 10 Artificial Accelerograms acceleration response spectrum of the database are described in Fig. 5 (Table 3).

Fig. 5

Acceleration response spectrum of the investigated real earthquake records and the mean of the 30 Artificial Accelerograms acceleration in the database

Table 3 PGA and duration of investigated real earthquake records

5 Implementation

A typical single-pier concrete bridge of mass m_S = 729.3 tn with two spans of 25 m each is considered. The deck is 9.50 m wide. A schematic representation of the bridge is given in Fig. 6. The pier is considered stiff enough to be neglected. The initial system (IN) has a natural period of 2 s and conventional isolation bearings with a damping ratio of 5%. A highly damped isolated system with a natural period of 2 s and an increased damping ratio of 20% is considered (Lead Rubber Bearings) and will be referred hereafter as the LRB system. A possible implementation of the KDamper is presented in Fig. 1c. The equations of motion of the new system are Eqs. 2a and 2b. The new system’s parameters μ, κ, and ρ are selected according to Sect. 3 of this paper. The first set of the KDamper parameters will be referred hereafter as S1, and the procedure followed is described in Sect. 3.1 using the Harmony Search optimization algorithm. The second and third set of parameters, S2 and S3, follows the procedure described in Sects. 3.2 and 3.3 respectively for acceleration response and relative displacement response optimization, under base excitation. In all sets of parameters, the mass ratio μ is selected 5% and ε = 10%. Finally, for all the sets of the KDamper parameters, the nominal KDamper frequency f₀ is selected to be equal to the low frequency (0.5 Hz) of the initial conventional base-isolated system.

Fig. 6

Schematic representation of the bridge considered. a Longitudinal section, b Transverse section

5.1 Transfer Functions

Figure 7 presents the transfer functions of the main system responses for all the considered sets of parameters, concerning the KDamper parameters and the LRB system. The transfer function H_US (Fig. 7a) is improved in all frequency range with the implementation of the KDamper system, compared with the LRB system. The acceleration transfer function H_AS, considering the H_US set of parameters, presents the worst behavior similar to the LRB system. The H_AS and the HS set of parameters greatly improve the dynamic behavior of the system, in terms of both acceleration and relative displacement response. The KDamper’s relative displacement response H_UD improves in the following order: H_US set, H_AS set, and HS set.

Fig. 7

Transfer functions of the main system responses a structure’s absolute acceleration H_US, b structure’s relative displacement H_AS and c KDamper relative displacement H_UD for all the considered sets of parameters of the KDamper system and the LRB system

5.2 Dynamic Responses

The systems main dynamic responses, considering the max values of the dynamic responses for all the Artificial Accelerograms in the database (mean of 10 max), as well as the selected real earthquake records in this paper, of the examined bridge structure, are presented in Tables 4 and 5, for all the examined systems.

Table 4 List of deck’s maximum absolute acceleration (m/sec²), considering max values of the dynamic responses, and the % reduction compared with the PGA of the respective earthquake records

Table 5 List of deck’s relative displacement, considering max values of the dynamic responses, and the % reduction compared with the initial conventional base-isolated structure’s (IN) deck’s relative displacement maximum values

Comparative results between the highly damped LRB system and the Harmony set KDamper system, are presented in Figs. 8 and 9. The presented time histories relate to (1) a characteristic Artificial Accelerogram and (2) Tabas real earthquake record.

Fig. 8

Comparative results, a in terms of deck’s relative displacement (m) and b deck’s absolute acceleration (m/sec²), between the highly damped LRB system and the Harmony set KDamper system, for an artificial acceleration

Fig. 9

Comparative results, a in terms of deck’s relative displacement (m) and b deck’s absolute acceleration (m/sec²), between the highly damped LRB system and the Harmony set KDamper system, for the Tabas earthquake excitation

6 Conclusions

In this paper as in [2], the KDamper concept is implemented as an alternative or supplement of conventional seismic isolation approaches for the seismic protection of bridge structures. A database of Artificial Accelerograms is generated, designed to match the EC8 acceleration response spectrum, and several real earthquakes records are considered. Different approaches to the optimal selection of the KDamper parameters are considered. The KDamper is implemented with a nominal frequency equal to the low frequency (0.5 Hz) of the conventional seismic isolation approaches. Finally, the following conclusive comments can be made:

• The optimal design of the KDamper, considering Base Acceleration Excitation/Absolute Structure Acceleration Response Transfer Function, provides an improved dynamic behavior, in terms of the structure’s responses, compared with Base Acceleration Excitation/Relative Structure Displacement Response Transfer Function. The selection of the KDamper parameters, incorporating an optimization algorithm, present an improved structural dynamic behavior, in almost all frequency range.

• The KDamper with a nominal frequency equal to the low frequency of a conventional base isolation system (0.5 Hz), presents similar reductions to the deck’s maximum absolute accelerations compared with the highly damped isolated system (LRB). At the same time, the deck’s relative displacement is significantly reduced compared with the LRB system, thus making the KDamper concept a possible alternative or supplement to the conventional seismic isolation approaches.

• The selection of the KDamper parameters considering Base Acceleration Excitation/Absolute Structure Acceleration Response Transfer Function present an improved dynamic behavior of the system, comparable with the optimization algorithm approach, without the need to consider proper objective function and constraints, as in the case of the Harmony Search procedure.

Appendices

Appendix 1: Acceleration Response Optimization

In the limit cases of ζ_D = 0 or ζ_D $\to \infty$, H_AS of Eq. (13b) becomes:

$$H_{AS} (0) = \left| {\frac{A}{C}} \right|;H_{AS} (\infty ) = \left| {\frac{B}{D}} \right|$$

(18)

The transfer function H_AS(q, ζ_D) of Eq. (13b) has two poles for two different values of q and therefore, it presents two different maximal values (peaks) at these points. The optimal selection of the parameters of the KDamper requires that both these peaks are minimized and become equal to each other. This is ensured by the optimal design approach followed in Den Hartog [18], which will be also used in the current paper. The approach is based on the identification of a pair of frequencies q_L < 1 and q_R > 1, where the values H_AS(q_L) and H_AS(q_R) become independent of ζ_D. The first step for the optimization procedure is the requirement that the values of the transfer functions at these points are equal:

$$H_{AS} \left( {q_{L} } \right) \, = H_{AS} \left( {q_{R} } \right) \, = H_{ASI} = H_{AS} \left( \infty \right)$$

(19)

In order that a solution for such a pair of frequencies exists, two alternative conditions must be fulfilled as in Den Hartog [18]:

$${\text{Case I}}:AD = BC$$

(20a)

$${\text{Case II}}:AD = - BC$$

(20b)

As it can be verified, no solution of Eq. (20a) exists for a positive q², when the values κ, μ, and ρ are positive. Elaboration of Eq. (20b) results in

$$(A_{2} D_{2} + B_{0} )q^{4} + (A_{0} D_{2} + A_{2} D_{0} + B_{0} C_{2} )q^{2} + (A_{0} D_{0} + B_{0} C_{0} ) = 0$$

(21)

where

$$A = A_{2} q^{2} + A_{0} ;B = B_{0} \rho q;C = q^{4} + C_{2} q^{2} + C_{0} ;D = (D_{2} q^{2} + D_{0} )\rho q$$

(22a,b,c,d)

$$A_{2} = A_{2\rho } \rho^{2} + A_{20} ;A_{0} = A_{0\rho } \rho^{2} + A_{00} ;B_{0} = B_{0\rho } \rho^{2} + B_{00} ;C_{2} = C_{2\rho } \rho^{2} + C_{20}$$

(23a,b,c,d)

$$C_{0} = C_{0\rho } \rho^{2} + C_{00} ;D_{2} = D_{2\rho } \rho^{2} + D_{20} ;D_{0} = D_{0\rho } \rho^{2} + D_{00}$$

(23e,f,g)

$$A_{\rho } = (A_{0\rho } D_{2\rho } + A_{2\rho } D_{0\rho } + B_{0\rho } C_{2\rho } )D_{20} - 2(A_{2\rho } D_{20} + A_{20} D_{2\rho } + B_{0\rho } )D_{0\rho }$$

(24a)

$$B_{\rho A} = [(A_{0\rho } D_{20} + D_{2\rho } A_{00} ) + (A_{2\rho } D_{00} + D_{0\rho } A_{20} ) + (B_{0\rho } C_{20} + C_{2\rho } B_{00} )]D_{20}$$

(24b)

$$B_{\rho B} = - 2(A_{2\rho } D_{20} + A_{20} D_{2\rho } + B_{0\rho } )D_{00} - 2(A_{20} D_{20} + B_{00} )D_{0\rho }$$

(24c)

$$B_{\rho } = B_{\rho A} + B_{\rho B}$$

(24d)

$$C_{\rho } = (A_{00} D_{20} + A_{20} D_{00} + B_{00} C_{20} )D_{20} - 2(A_{20} D_{20} + B_{00} )D_{00}$$

(24e)

and the coefficients in the Eqs. (23a,b,c,d, 23e,f,g) are defined in Table 6.

Table 6 Coefficients in Eqs. 23a,b,c,d, 23e,f,g

As a result of Eq. (21), the pair of roots of Eq. (21) must satisfy

$$q_{L}^{2} + q_{R}^{2} = - \frac{{(A_{0} D_{2} + A_{2} D_{0} + B_{0} C_{2} )}}{{(A_{2} D_{2} + B_{0} )}}$$

(25)

Additionally, both roots q_L and q_R must fulfill Eq. (18), which results in

$$\frac{{B_{0} }}{{D_{0} + D_{2} q_{L}^{2} }} = - \frac{{B_{0} }}{{D_{0} + D_{2} q_{R}^{2} }} \Rightarrow q_{L}^{2} + q_{R}^{2} = - \frac{{2D_{0} }}{{D_{2} }}$$

(26)

The combination of Eqs. (25) and (26) leads to an equation for the optimal value of the parameter ρ:

$$A_{\rho } \rho^{4} + {\rm B}_{\rho } \rho^{2} + C_{\rho } = 0$$

(27)

The optimal value of ρ is selected as the minimum positive value of the two roots of (27).

Appendix 2: Relative Displacement Response Optimization

In the limit cases of ζ_D = 0 or ζ_D $\to \infty$, Eq. (15.b) becomes

$$H_{US} (0) = \frac{1}{{\omega_{0}^{2} }}\left| {\frac{A}{C}} \right|;H_{US} (\infty ) = \frac{1}{{\omega_{0}^{2} }}\left| {\frac{B}{D}} \right|$$

(28a,b)

In view of Eq. (15.b), the Transfer Function H_US(q, ζ_D) has two poles for two different values of q, and therefore, it presents two different maximal values (peaks) at these points. The optimal selection of the parameters of the KDamper requires that both these peaks are minimized and become equal to each other. This is ensured by the optimal design approach followed in Den Hartog [18]. The approach is based on the identification of a pair of frequencies q_L < 1 and q_R > 1, where the values H_US(q_L) and H_US(q_R) become independent of ζ_D. The first step for the optimization procedure is the requirement that the values of the Transfer Functions at these points are equal

$$H_{US} (q_{L} ) = H_{US} (q_{R} ) = H_{USI} = H_{US} (\infty )$$

(29)

In order that a solution for such a pair of frequencies exists, two alternative conditions must be fulfilled as in Den Hartog [18]:

$${\text{Case I}}:AD = BC$$

(30a)

$${\text{Case II}}:AD = - BC$$

(30b)

As it can be verified, no solution of Eq. (30a) exists for a positive q², when the values κ,μ, and ρ are positive. Elaboration of Eq. (30b) results in

$$(A_{2} D_{2} + B_{0} )q^{4} + (A_{0} D_{2} + A_{2} D_{0} + B_{0} C_{2} )q^{2} + (A_{0} D_{0} + B_{0} C_{0} ) = 0$$

(31)

where

$${\rm B}_{{\rho {\rm A}}} = [({\rm A}_{0\rho } D_{20} + D_{2\rho } {\rm A}_{00} ) + ({\rm A}_{2\rho } D_{00} + D_{0\rho } {\rm A}_{20} ) + ({\rm B}_{0\rho } C_{20} + C_{2\rho } {\rm B}_{00} )]D_{20}$$

(32a)

$$B_{\rho B} = - 2(A_{2\rho } D_{20} + A_{20} D_{2\rho } + B_{0\rho } )D_{00} - 2(A_{20} D_{20} + B_{00} )D_{0\rho }$$

(32b)

$$B_{\rho } = {\rm B}_{{\rho {\rm A}}} + {\rm B}_{{\rho {\rm B}}}$$

(32c)

$$C_{\rho } = (A_{00} C_{20} + A_{20} C_{00} + B_{00} C_{20} )D_{20} - 2(A_{20} D_{20} + B_{00} )D_{00}$$

(32d)

where A_0ρ, D₂₀, D_2ρ, A₀₀, A_2ρ, D₀₀, D_0ρ, A₂₀, B_0ρ, C₂₀, C_2ρ and B₀₀ are derived from Table 7.

Table 7 Coefficients in Eqs. 32a, 32b, 32c, 32d

As a result of Eq. (31), the pair of roots of Eq. (31) must satisfy

$$q_{L}^{2} + q_{R}^{2} = - \frac{{(A_{0} D_{2} + A_{2} D_{0} + B_{0} C_{2} )}}{{(A_{2} D_{2} + B_{0} )}}$$

(33)

Additionally, both roots q_L and q_R must fulfill Eq. (29), which results in

$$\frac{{B_{0} }}{{D_{0} + D_{2} q_{L}^{2} }} = - \frac{{B_{0} }}{{D_{0} + D_{2} q_{R}^{2} }} \Rightarrow q_{L}^{2} + q_{R}^{2} = - \frac{{2D_{0} }}{{D_{2} }}$$

(34)

The combination of Eqs. (33) and (34) leads to an equation for the optimal value of the parameter ρ:

$$A_{\rho } \rho^{4} + {\rm B}_{\rho } \rho^{2} + C_{\rho } = 0$$

(35)

Since A_ρ = 0, the optimum value of ρ for a set of parameters κ,μ results as

$$\rho = \sqrt { - \frac{{C_{\rho } }}{{{\rm B}_{\rho } }}}$$

(36)

After successive substitution of the coefficients of Table 7 into Eq. (37) we get the following:

$$\rho (\kappa ,\mu ) = \sqrt {\frac{ - (\mu - 2)}{{\kappa^{2} \mu (\mu - 2) + (2 + 2\mu + 3\kappa \mu )(1 + \mu )}}}$$

(37)