Design of 2-Degree of Freedom Fractional Order PID Controller for Magnetic Levitation Plant with Time Delay

Abstract

This work presents the design of a two Degree of Freedom fractional order PID (2-DOF FOPID) controller to stabilize a second order unstable magnetic levitation plant having time delay. To achieve the optimum performance of the system, the controller gains have been tuned using Monarch Butterfly Optimization (MBO), a recently developed evolutionary algorithm. The performance of the 2-DOF FOPID controller has been compared with its 1-DOF counterpart. The obtained results validate that the 2-DOF FOPID enhances the performance of the system in both frequency and time domains and also exhibits superior robustness to external disturbances and parameter uncertainties.

1 Introduction

Time delay is one of the major causes of instability and degraded performance of real time plants. Several industrial processes, such as stirred tanks, bio-reactors, polymerization reactors, etc have time delays and are also open loop unstable. Designing a controller for an open loop unstable system with time delay is a challenging task, which is the reason it has attracted the attention of researchers worldwide. Many researchers are focused on formulating Proportional-Integral Derivative (PID) control schemes for unstable plants with time delay.

Due to its simple structure, ease of realization and availability of simple tuning methods, PID controller is being used in more than 90% of industrial closed loops [1]. However, it has also been reported in literature that PID control proves to be inefficient for nonlinear, time-delay and uncertain systems [1, 2].

Since few decades, researchers have done significant advancement in the modeling and applications of Fractional PID controller (FOPID) [3]. In an FOPID controller, the derivative and integral actions are of non-integer order, the values of which may vary from 0 to 2. It has been confirmed in literature, that FOPID performs better than PID, whether used with an integer order or a fractional order plant. A comprehensive review of the applications of FOPID controller can be found in [4, 5]. Recently, several works report the design or parameter tuning of FOPID controller using recently proposed meta-heuristics such as Symbiotic Organisms Search (SOS) [6], Monarch Butterfly Optimization (MBO) [7], Teaching Learning based Optimization (TLBO) [8], Chaotic Atom Search Optimization Algorithm (CASO) [9]. A multivariable multiobjective genetic algorithm (MMGA) has also been applied to tune FOPID controller in [10].

This work illustrates the development of a 2-DOF FOPID controller to stabilize a second order unstable magnetic levitation system having time delay. The controller parameters have been tuned using MBO, after formulating an objective function. The obtained results are then, compared with those of 1-DOF FOPID controller.

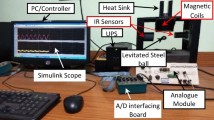
2 Magnetic Levitation System (Maglev)

The basic illustration of the magnetic levitation plant is shown in Fig. 1. The maglev system considered for this work is an experimental hardware-in-loop setup from Feedback Instruments Ltd. [11]. The setup consists of a metallic ball suspended in air using an electromagnet, which is excited through an input control voltage. The real time kit works in conjunction with MATLAB Simulink. The controller signal to the real time maglev system and the real time system response from the maglev system are sent/received through an A/D board which handles all the communications between MATLAB Simulink and the real time maglev kit.

Fig. 1

Basic block diagram of maglev

The dynamics of the maglev system may be expressed as [6, 12]:

$$\begin{aligned} m\ddot{x}=mg-k\dfrac{i^2}{x^2} \end{aligned}$$

(1)

Since (1) is a nonlinear plant, it needs to be linearized to obtain the transfer function and proceed with further analysis. The linearization of (1) may be done by:

$$\begin{aligned} \Delta \ddot{x}=-\dfrac{\partial f(x,i)}{\partial x}\Biggr \vert _{i_0,x_0} \Delta x -\dfrac{\partial f(x,i)}{\partial i}\Biggr \vert _{i_0,x_0} \Delta i \end{aligned}$$

(2)

where $f(x,i)=g-k\frac{i^2}{x^2}$. $\Delta x$ and $\Delta i$ are the negligibly small deviations from $x_0$ and $i_0$, the equilibrium value of position and current. After calculating the partial derivatives and applying Laplace Transform to (2), we get:

$$\begin{aligned} \dfrac{\Delta x}{\Delta i}=\dfrac{-k_c}{s^2-k_p} \end{aligned}$$

(3)

where $k_c=\frac{2g}{i_0}$ and $k_p=\frac{2g}{x_0}$ [6, 12]. Substituting the values of all the constants from [11], we get the plant transfer function

$$\begin{aligned} G_p(s)=\dfrac{-3518.85}{s^2-2180} \end{aligned}$$

(4)

It is evident that (4) is an open loop unstable system. In this work, we add time delay into the system. The delay transfer function is defined by:

$$\begin{aligned} G_p(s)=\dfrac{-3518.85 e^{-sT_\text {d}}}{s^2-2180} \end{aligned}$$

(5)

where $T_\text {d}$ is time delay.

3 Fractional Order PID Controller (FOPID)

The control law of an FOPID controller is defined by:

$$\begin{aligned} u_{\text {fopid}}(t)=K_pe(t)+K_i[{_0D^{-\rho }_t}e(t)]+K_d[{_0D^{\sigma }_t}e(t)] \end{aligned}$$

(6)

where $\rho$, $\sigma$, $K_p$, $K_i$, $K_d$ are the non-integer integral order, non-integer derivative order, proportional gain, integral gain and derivative gain, respectively. The transfer function may, thus, be expressed as:

$$\begin{aligned} U_{\text {fopid}}(s)=K_p+\dfrac{K_i}{s^{\rho }}+K_ds^{\sigma } \end{aligned}$$

(7)

where $0<\rho ,\sigma <2$. By looking at (7) it becomes evident that the performance of FOPID controller depends on five parameters. The increased number of tunable parameters has its own advantage and disadvantage. Advantage: More number of system specifications, both from time and frequency domain, can be controlled simultaneously, giving the designer more control over the plant. Disadvantage: Tuning the FOPID is complex compared to PID. The FOPID controller, just like PID, may be implemented in different configurations. This work focuses on the 1-degree of freedom (DOF) and 2-DOF configurations. The schematics of the 1-DOF FOPID and 2-DOF FOPID configurations are illustrated in Figs. 2 and 3, respectively.

Fig. 2

Block diagram of 1-DOF FOPID configuration

Fig. 3

Block diagram of 2-DOF FOPID configuration

It becomes evident from Fig. 2, that in 1-DOF configuration, the controller zeros appear in the forward path. These zeros introduce excess overshoot in the closed loop system response. This problem is overcome by using the 2-DOF configuration. It is clear from Fig. 3, that in a 2-DOF configuration, the controller zeros appear in the feedback path; while the integral term appears in the forward path. Elimination of zeros from the forward path reduces the overshoot in the closed loop response [12]. The PD controller $q_2s+q_1$, further, helps in improving the speed of response [13]. Note that the loop transfer function for both the configurations remain same.

4 Monarch Butterfly Optimization

Wang et. al. proposed a meta-heuristic in 2015, namely, Monarch Butterfly Optimization (MBO) [14]. This optimization algorithm is inspired from the southward migration, spanning thousands of kilometers, of North American monarch butterflies during summer/autumn. Due to its minimal dependency on control parameters/constants, it has been employed to solve optimization problems in several fields like controller tuning, optimal power flow and more.

The MBO consists of two operators, namely, (1) Migration operator and (2) Butterfly adjusting operator. Initially, a population is generated, wherein each butterfly represent a candidate solution to the problem. The total population is split into two sub-populations, namely, Subpopulation-1 and Subpopulation-1. The migration operator generates a new Subpopulation-1, whereas, the butterfly adjusting operator generates a new Subpopulation-2, for the upcoming generation.

4.1 Migration Operator

Let the total number of butterflies be NB. If p percent of butterflies are assumed to be located in Land-1, then the number of butterflies in Subpopulation-1 will be $\text {NB}_1=p \times \text {NB}$ and that in Subpopulation-2 will be $\text {NB}_2=\text {NB}-\text {NB}1$. The position of a butterfly in Subpopulation-1, in the next generation is given by [14]:

$$\begin{aligned} x_{i,k}^{t+1}= {\left\{ \begin{array}{ll} x_{r_1,k}^t,\;\;\;\text {if}\;\;r \le p\\ x_{r_2,k}^t,\;\;\;\text {if}\;\;r>p \end{array}\right. } \end{aligned}$$

(8)

where, t represents the present generation; $x_{i,k}^{t+1}$ is the kth dimension of the ith butterfly in $t+1$th generation; $x_{r_1,k}^t$ is the kth dimension of the r1-th butterfly randomly chosen from Subpopulation-1 and $x_{r_2,k}^t$ is the kth dimension of the r2-th butterfly randomly chosen from Subpopulation-2. Note that, $r_1 \in \{1,2 \ldots ,\text {NB}_1\}$ and $r_2 \in \{1,2\ldots , \text {NB}_2\}$. So, the butterflies of the Subpopulation-1 in the next generation will be the off-springs of butterflies from Subpopulation-1 and Subpopulation-2. The factor r is found by $r=\text {rand} \times peri$, where peri indicates migration period and has been set to 1.2 [14] and $\text {rand}$ is a random number uniformly distributed between [0,1].

4.2 Butterfly Adjusting Operator

The location of the butterflies is also updated using this operator. This operator is applied only to the butterflies in Subpopulation-2. The position of a butterfly of Subpopulation-2, in the next generation is given by [14]:

$$\begin{aligned} x_{j,k}^{t+1}= {\left\{ \begin{array}{ll} x_{best,k}^t,\;\;\;\text {if}\;\;\text {rand} \le p\\ x_{r_3,k}^t,\;\;\;\text {if}\;\;\text {rand}>p \\ x_{j,k}^t+\alpha \times (dx_k-0.5),\;\;\;\text {if}\;\;\text {rand}>BAR \end{array}\right. } \end{aligned}$$

(9)

The terms in (9) are defined as: $\text {d}x=\text {Levy}(x_j^t)$ is the step-size of the random walk taken by a monarch butterfly; $\text {BAR}$ is butterfly adjusting rate; $x_{\text {best},k}^t$ is the kth dimension of the best monarch butterfly; $x_{r_3,k}^t$ is the kth dimension of the $r_3$th monarch butterfly randomly chosen from Subpopulation-2. Note that $r_3 \in \{1,2, \ldots , \text {NB}2\}$. rand is a random number uniformly distributed between [0, 1]; $\alpha =\frac{S_{\text {max}}}{t^2}$, where $S_{\text {max}}$ is the maximum step-size that a monarch butterfly may take and t is the present generation.

After completion of both the operators, the two sub-populations are merged and sorted as per the fitness value. The resulting new population is again divided into two sub-populations. This procedure is repeated until the termination condition is achieved or the algorithm reaches the maximum number of generations.

5 Simulation

For tuning the FOPID controllers using the MBO algorithm, it is important to define the search space, i.e. the lower limit and upper limit of the parameters. Note that the plant transfer function has negative dc-gain [refer to Eq. (5)]. To stabilize the plant, controller gains $K_p$, $K_i$ and $K_d$ must be negative. The search space considered in this work is $-5<K_p,K_i,K_d<0$, $0<\rho <2$ and $0<\sigma <2$. To tune a 2-DOF controller, the controller gains are, first tuned, keeping $q_2$=0 and $q_1$=ki. $q_2$ may then be tuned to achieve the desired speed of response. Population size and maximum iteration count of MBO are kept at 50 and 1000, respectively. Other required parameters are set as: $p=0.45$, $\text {peri}=1.2$ and $\text {BAR}=5/12$, $S_{\text {max}}=1.0$. The algorithm is executed for 30 independent runs.

Th objective function proposed for the purpose is given in (10)

$$\begin{aligned}&J(K_p,K_i,K_d,\rho ,\sigma )=\omega _1\text {ISE}+\omega _2t_s+\omega _3M_p \nonumber \\&{\text {subject to}}\;\; ||S||_{\infty }<2\;\text {and}\;||T||_{\infty }<2 \end{aligned}$$

(10)

where J(.) is the objective function, signifying the minimization of integal square error ($\text {ISE}$), settling time ($t_s$) and peak overshoot ($M_p$) of the system response. $\omega _1$, $\omega _2$ and $\omega _3$ are weighing factors, such that $\omega _1+\omega _2+\omega _3=1$. $||S||_{\infty }$ and $||T||_{\infty }$ represent the infinity norms of sensitivity and complementary sensitivity of the closed loop system. The constraints have been imposed to achieve satisfactory robustness to external disturbances and parameter uncertainties.

Table 1 Best results of MBO, over 30 independent runs

The best results obtained from MBO, over 30 runs, is summarized in Table 1. The time domain specifications $t_s$, $M_p$, rise time ($t_r$), $\text {ISE}$, J, $||S||_{\infty }$ and $||T||_{\infty }$ of the compensated system are given in Table 2. Results summarized in the table reveal the superior performance of 2-DOF FOPID configuration.

Table 2 Time domain specifications for the optimum solution

The system responses for 1-DOF and 2-DOF FOPID controllers are shown in Fig. 4. The excessively prominent overshoot in the response with 1-DOF controller is because of the existence of controller-zeros along with zeros of the delay term ($e^{-sT_d}$), in the forward path. It is clear, that the 2-DOF configuration mitigates the overshoot occurring in the system response of the time-delay plant. Also, the values of sensitivity and complementary sensitivity being less than 2 signify satisfactory robustness.

Fig. 4

Comparison between responses of the compensated system for 1-DOF and 2-DOF FOPID controllers

Fig. 5

Response of the system subject to periodic output disturbance

Fig. 6

Bode plot of compensated system

For examine the robustness of the closed loop system to external disturbances, it is subjected to a periodic output disturbance signal of magnitude 0.02 and time period 10 s. The output of the system, in presence of output disturbance, is shown in Fig. 5. It is clear that the system exhibits satisfactory robustness to external disturbance. Figure 6 reveals that the phase plot of the compensated system is flat in the vicinity of gain cross-over frequency. This means that the system exhibits iso-damping behaviour, which verifies that the closed loop system will remain robust to gain and parameter variations/uncertainties.

6 Conclusion

A 2-DOF FOPID controller has been designed to stabilize a second order unstable magnetic levitation plant, having time delay. The parameters of the controller have been tuned using Monarch Butterfly Optimization algorithm by to minimizing the proposed objective function. The results and responses of the 2-DOF FOPID controller have been compared with its 1-DOF counterpart and it has been verified that the 2-DOF FOPID controller exhibits better performance bringing significant reduction in settling time and peak overshoot. The system, compensated with 2-DOF FOPID controller exhibits iso-damping property, thereby displaying good robustness to external disturbance and parameter uncertainties. Control of systems having fractional-order time delay, uncertain plant models and more are some of the areas which are open to be explored.