Keywords

1 Introduction

Queueing system is an important tool for designing and analyzing the systems ranging from IOT, blockchain technology to telecommunication systems [1,2,3]. Suitable queueing models have been designed for different systems. Erlang loss queueing model is applicable in many domains like telecommunication networks, transportation systems, etc. [5, 6]. Such systems are designed better and analyzed on the basis of their performance measures. In order to evaluate performance measures, the systems are assumed to be in a steady state. Based on this assumption, the systems are analyzed. The reason for this assumption is that stationary solutions are easy to obtain. However, in reality, the systems are not in steady state and steady-state solutions are far from reality. The arrival and service rates are not constant; rather, they are a function of time. For instance, the pattern of calls or vehicles on road is different in morning and in evening [7, 8]. The non-stationary solutions of the queueing models are difficult to obtain. So, the researchers are trying to obtain approximations [6, 7]. Several approximations have been found in the literature to approximate and analyze the non-stationary queueing systems. Some of these are simple stationary approximation (SSA), pointwise stationary approximation (PSA), modified offer load (MOL), etc [9,10,11,12,13]. The arrival and service rates are assumed to be in sinusoidal form to test these approximations. In this paper, we have opted time-dependent perturbation (TDP) theory, extensively used to solve numerous problems of quantum mechanics [13,14,15]. TDP is applied on the non-stationary Erlang loss model with time-varying arrival and service rates. The sinusoidal rates are generally used so that we can accurately estimate the performance of the approximation scheme, although this method can also be applied for general perturbed rates.

The rest of the chapter is as follows: After the introduction section, Sect. 2 presents a literature review of non-stationary queues. Section 3 provides Erlang loss model and its CR equations. Time-dependent perturbation theory is briefly discussed in Sect. 4. Section 5 presents numerical results. The last section is the conclusion.

2 Literature Review

Non-stationary queueing models developed for analyzing the systems are complex in nature [13]. Simulation techniques can predict the behavior of the queueing models but these techniques, for example, Monte Carlo simulation, take more computational power as well as time. People choose approximation methods based on steady-state results to predict the behavior of systems. These approximations are much easier and require less computation. Simple stationary approximation (SSA) is one of the techniques based on steady-state solution. The average rate is calculated over a time interval and inserted in steady-state formula. Mathematically, the average arrival rate (similarly average service rate) over a time of length T is given by:

$$ \bar{\uplambda } = \frac{1}{T}\int \limits _0^T {\uplambda (t){\text {d}}t} $$

All Markovian queues can be evaluated by using these average arrival rates. However, SSA method ignores non-stationarity behavior and provides stationary solution for the number of jobs in the system. Green et al. [10] found that SSA gives a reasonable approximation if the arrival rate function varies by only 10% about its average arrival rate. Green et al. [10] proposed pointwise stationary approximation (PSA) method used to compute non-stationary behavior. PSA provides time-dependent behavior based on steady-state behavior of a stationary model. It uses arrival and/or service rate that prevails at the time at which we want to describe the performance. For example, the blocking probability \(P_B(t)\) which is the probability that no server is available is calculated approximately for M(t)/M(t)/s/s queue as:

$$\begin{aligned} {P_B}(t) \approx \frac{{\rho {{(t)}^s}/s!}}{{\sum \nolimits _{i = 0}^s {\rho {{(t)}^s}/i!} }} \end{aligned}$$

where \(\rho (t) = \uplambda (t)/\mu (t)\)

The expected number of busy servers E[S(t)] can be given approximately as

$$\begin{aligned} E[S(t)] \approx (1 - P_B(t))\rho (t) \end{aligned}$$

Massey and Whitt [12] showed that PSA is asymptotically correct as arrival rate changes less rapidly. Modified offered load (MOL) model was introduced to approximate telephone traffic [12]. MOL is applicable to only Erlang loss models and works effectively if the blocking probability is small.

3 Erlang Loss Model

Consider a queueing system with s number of servers and with zero buffer size. That is, there can be at most s jobs in the system that are under service. The arrival pattern follows Poisson process with a non-negative time-varying rate \(\uplambda (t)\). The service of each job follows exponential distribution with rate \(\mu (t)\). Let p(n, t) be the probability of n jobs in the system at time t. The Chapmann–Kolmogorov (CR) equations for M(t)/M(t)/s/s queueing system [5] are given:

$$\begin{aligned} \begin{aligned} \frac{{\text {d}}}{{{\text {d}}t}}p(0,t)&= - \uplambda (t)p(0,t) + \mu (t)p(1,t)\\ \frac{{\text {d}}}{{{\text {d}}t}}p(n,t)&= \uplambda (t)p(n - 1,t)\mathrm{{ - }}(\uplambda (t) + n\mu (t))p(n,t) + (n + 1)\mu (t)p(n + 1,t)\\ \frac{{\text {d}}}{{{\text {d}}t}}p(s,t)&= \uplambda (t)p(s - 1,t) - s\mu (t)p(s,t)\\&\quad \quad \mathrm{{0}} < n \le s\\ \end{aligned} \end{aligned}$$
(1)

The non-autonomous linear differential equation in matrix form of above set of CR equations can be written as:

$$\begin{aligned} \frac{{{\text {d}}P(t)}}{{{\text {d}}t}} = M(t)P(t) \end{aligned}$$
(2)

where

$$\begin{aligned} P(t) = {(p(0,t),\mathrm{{ }}p(1,t), \ldots , p(s,t))^T} \end{aligned}$$

and M(t) be a matrix obtained from the set of differential equations. The solution of Eq. (2), if M(t) is constant (\(M(t)=M_0\)), can easily be obtained by matrix differential equation with constant coefficients. If the initial condition p(n, 0) is known, then the solution is given by

$$\begin{aligned} P(t) = \sum \limits _{i = 1}^{s + 1} {{a_i}{\mathrm{{e}}^{ - {b_i}t}}{m_i}} \end{aligned}$$
(3)

where \(b_i\) is the eigenvalue and \(m_i\) is the corresponding eigenvector of \(M_0\) and coefficients \(a_i\) can be easily obtained by the initial probability values. However, if the entries of matrix M(t) in Eq. (2) are time-dependent, then it is complex to obtain the exact solution. For solving the differential Eq. (2), researchers proposed a different method. For the support of their method, researchers assumed that the time-varying rates are periodic in sinusoidal form [12]. But, these methods can also be applied on general rates. In the light of this assumption [13], we assume that the time-varying rates can be split into two parts: a constant and some perturbed part. The perturbation part of the rates is in sinusoidal form. Formally, the rates can be written as

$$\begin{aligned} \uplambda (t) = \uplambda + {\eta _\uplambda }\sin ({\tau _\uplambda }t + {\phi _\uplambda }) \end{aligned}$$
$$\begin{aligned} \mu (t) = \mu + {\eta _\mu }\sin ({\tau _\mu }t + {\phi _\mu }) \end{aligned}$$

The matrix M(t) thus can be seen as a sum of two matrices \(M_0\) and X(t) where \(M_0\) is constant and X(t) is sinusoidal form.

4 Time-Dependent Perturbation (TDP) Theory

The matrix differential equations with time-dependent coefficients are generally found in quantum mechanics, for instance, the Schrodingers wave equation with time-dependent Hamiltonian [14,15,16]. TDP theory has been very successful in computing the solution of such problems. Equation (2) can be rewritten where the coefficient matrix is the sum of constant and perturbed part, i.e.,

$$\begin{aligned} \frac{{{\text {d}}P(t)}}{{{\text {d}}t}} = ({M_0} + X(t))P(t), \quad \quad P\left( 0 \right) \mathrm{{ }} = \mathrm{{ }}{\mathrm{{p}}_0}. \end{aligned}$$
(4)

In case of M(t) as constant, the solution of Eq. (4) as discussed in the previous section is given by

$$\begin{aligned} P(t) = \sum \limits _{i = 1}^{s + 1} {{a_n}{\mathrm{{e}}^{-{b_i}t}}{m_i}} \end{aligned}$$
(5)

In a similar fashion, if the coefficient matrix as given in Eq. (4) is time-dependent, the unknown coefficients \(a_n\) must be a(n, t). The general solution of Eq. (4) can be written as

$$\begin{aligned} P(t) = \sum \limits _{i = 1}^{s + 1} {a(i,t){\mathrm{{e}}^{-{b_i}t}}{m_i}} \end{aligned}$$
(6)

Substituting the value of P(t) given in Eq. (6) into (4) and simplifying it, we have

$$\begin{aligned} \sum \limits _i {\frac{{{\text {d}}a(i,t)}}{{{\text {d}}t}}{e^{ - {b_i}t}}{m_i} = c\sum \limits _i {a(i,t)} } {e^{ - {b_i}t}}{m_i} \end{aligned}$$
(7)

If \({m_j}'\) is left eigenvector corresponding to eigenvalue \(b_j\) and \(m_i\) is right eigenvector corresponding to \(b_i\), then \({m_j}'m_i\ne 0\), if \(i=j\), otherwise 0 [17]. So, we multiply reduced Eq. (7) by \({m_j}'\) from left-hand side

$$\begin{aligned} \begin{aligned} \frac{{{\text {d}}a(j,t)}}{{{\text {d}}t}}&= c\sum \limits _n {{m_j}'X(t){m_i}{e^{({b_i} - {b_j})t}}a(i,t)} \\&= c\sum \limits _n {a(i,t){X_{ij}}{e^{({b_i} - {b_j})t}}} \end{aligned} \end{aligned}$$
(8)

where \(X_{ij}={m_j}'X(t){m_i}\).

The term a(i, t) can be expanded in the power of c as a perturbation approximation

$$\begin{aligned} a(n,t) = {a(n,t)}^{(0)} + {c ^1}{a(n,t)}^{(1)} + {c ^2}{a(n,t)}^{(2)} + \ldots \end{aligned}$$
(9)

Using this expression into Eq. (8) and on equating the coefficients of equal power of c, one can obtain

$$\begin{aligned} \frac{{{\text {d}}{a_j}^0(t)}}{{{\text {d}}t}} = 0 \end{aligned}$$
(10)

The first-order coefficients are evaluated by

$$\begin{aligned} \frac{{{\text {d}}{a_j}^{(1)}(t)}}{{{\text {d}}t}} = \sum \limits _i {{X_{ij}}{e^{({b_i} - {b_j})t}}{m_i}{a_i}^{(0)}} \end{aligned}$$
(11)

Similarly, higher-order coefficients can be calculated using

$$\begin{aligned} \frac{{{\text {d}}{a_j}^{(r + 1)}(t)}}{{{\text {d}}t}} = \sum \limits _i {{X_{ij}}{e^{({b_i} - {b_j})t}}{m_i}{a_i}^{(r)}(t)} \end{aligned}$$
(12)

The zeroth-order coefficients a(n, 0) are obtained from initial condition

$$\begin{aligned} \zeta (0) = \sum \limits _i {{a_i}^{(0)}{m_i}} \end{aligned}$$

which is given in the problem. The first-order coefficients can be obtained by using zeroth-order coefficients. The higher-order coefficients can be obtained in the same manner [17,18,19].

Fig. 1.
figure 1

Average number of customers in M(t)/M/5/5. (\(\uplambda =10+7{\text {sin}}(2t),\mu =2\))

Full size image

5 Numerical Results

In this section, we implemented TDP method on Erlang loss model. The results obtained from TDP(correct up to first and second order), MOL and PSA are compared with the solution obtained by the ode45 function available in MATLAB ODE suit. The relative error RE of the existing and TDP methods is computed to get insights by

$$\begin{aligned} RE = \frac{{\mathrm{{Value\_obtained\_by\_ode45 - Approx\_value}}}}{{\mathrm{{Value\_obtained\_by\_ode45}}}} \end{aligned}$$

We take M(t)/M(t)/5/5 queue as an instance to gain insight on how the solution based on TDP correct up to first and second order performs. We take arrival rate

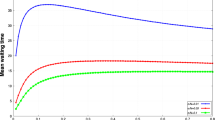
$$\begin{aligned} \uplambda (t) = 3 + 0.2\sin (2t) \end{aligned}$$

and service rate \(\mu (t)=4\). In Fig. 1, we can easily see that TDP (second-order approx.) performs better than the other approximations (PSA, MOL, TDP (first-order approx.)). Figure 2 shows the relative error of PSA, MOL, TDP (first-order and second-order approx). For better clarity, Fig. 3 shows only the relative error of only MOL and TDP (second-order approx). From Figs. 2 and 3, it can be easily seen that the TDP method outperforms the other existing methods.

Fig. 2.
figure 2

Relative error of TDP(second approx.) (\(\uplambda =10+7{\text {sin}}(2t),\mu =2\))

Full size image
Fig. 3.
figure 3

Relative error of TDP(second approx.)(\(\uplambda =10+7sin(2t),\mu =2\))

Full size image

6 Conclusion

In this chapter a time-dependent perturbation theory is used for computing probability distribution and blocking probability for non-stationary Erlang loss model. The scope of this study covers a plethora of systems with dynamic organization. The numerical results show that the opted theory outperforms the existing approximations. The theory can be applied extensively to obtain approximations for various non-stationary queueing models.