Keywords

1 Introduction

There are many optimization problems in the real society, and these problems are often composed of multiple objectives that conflict and affect each other, which are called multi-objective optimization Problems (MOPs) [1]. Since the early 1960s, MOPs have attracted more and more researchers from different backgrounds [2, 3], and it has very important scientific and practical significance to solve multi-objective optimization problems. However, with the continuous development of society, many engineering problems have become more and more complicated, and the mathematical model is no longer a simple multi-objective optimization model. The many-objective optimization problems (MaOPs) [4] (when the objectives of optimization reach four or more) have been appeared in real life, such as wing design problem [5], water distribution system [6] and car engine calibration problem [7].

Whether in scientific research [8] or engineering applications [9], optimization issues generally involve multiple conflicting objective functions. Therefore, there are a set of optimal solution sets, which composed of numerous Pareto optimal solutions in MaOPs. In recent years, many-objectives evolutionary algorithms (MaOEAs) [10] have been researched by many scholars for MaOPs. And these evolutionary algorithms can be divided into the following three categories.

  1. (1)

    Many-objective evolutionary algorithm based on pareto-dominance. For example, NSGA-III [11], NSGAIII-NE [12], etc. The disadvantage of this approach is that there are many parameters in the algorithm, which requires adjust heuristically.

  2. (2)

    Many-objective evolutionary algorithm based on decomposition [13]. The main idea is that the algorithm decomposes the complex MaOPs into a series of sub-problems, and then solves them one by one. This method effectively overcomes the diversity maintenance difficulties, but it is still in its infancy.

  3. (3)

    Many-objective evolutionary algorithm based on performance indicators [14]. For example, a density estimation strategy that uses a simple coordinate transformation to put the solution with poor convergence into crowded area.

Reference-point based non-dominated sorting strategy uses widely distributed reference points (one reference direction can be associated with multiple solutions) to maintain diversity. However, as the number of objective increases, the pareto-dominance makes the selection pressure of the strategy insufficient. Therefore, in order to effectively improve the performance of the algorithm, this paper combines the balanceable fitness estimation strategy and the adaptive penalty distance boundary intersection strategy to increase the selection pressure. And on this basis, a dynamic threshold selection strategy is proposed. The specific principle is as follows:

  1. 1)

    Balanceable fitness estimation strategy is used to balance the solution of convergence and diversity.

  2. 2)

    Reference-point based non-dominated sorting strategy is used to achieve the goal of distributing the non-dominated solution in the objective space as uniform as possible.

  3. 3)

    Adaptive penalty distance boundary intersection strategy is designed to dynamically adjust the impact of convergence and diversity on the algorithm.

  4. 4)

    Dynamic threshold selection strategy is proposed to ensure that the algorithm emphasizes diversity in the early stage and convergence in the late stage to make sure that the results are closer to the real non-dominant front.

The structural of this paper is organized as follows: Sect. 2 introduces related works about balanceable fitness estimation and reference-point based non-dominated sorting strategy. Section 3 describes the proposed algorithm in detail. The simulation of several algorithms has been experimented in Sect. 4. Section 5 gives the conclusion of this paper.

2 Related Works

This section describes the balanceable fitness estimation strategy and the reference-point based non-dominated sorting strategy, which are important components of MaOEA-TES.

2.1 Balanceable Fitness Estimation Strategy (BFE)

Balanceable fitness estimation (BFE) [15] is a strategy which combined the diversity and convergence distance to balance the convergence and diversity for each solution in objective space.

Suppose that the population \(P = \{ {p_1},{p_2},...,{p_N}\}\) includes N individuals. Each individual has the position \({X_i}\). For each individual \({p_i}\), the value of BFE \(BFE({p_i},P)\) is consisted of two components: the diversity distance and the convergence distance, the equation is as follows:

$$\begin{aligned} BFE({p_i},P) = \alpha \times Cd({p_i},P) + \beta \times Cv({p_i},P) \end{aligned}$$
(1)

where \(Cd({p_i},P)\) and \(Cv({p_i},P)\) represent the diversity and convergence distances of \({p_i}\), respectively. Both \(\alpha \) and \(\beta \) are the weight factors, when calculating the value of BFE, each objective of population \({p_i}\) will be normalized firstly by using the maximum and minimum values of the corresponding objective. This normalization approach helps to eliminate the impact of different amplitudes on multiple objectives. The normalized objective \({f'_k}\left( {{p_i}} \right) \) of \({p_i}\) is obtained with the following equation:

$$\begin{aligned} {f'_k}({p_i}) = \frac{{{f_k}({p_i}) - {f_k}min}}{{{f_k}max - {f_k}min}} \end{aligned}$$
(2)

where \({f_k}max\) and \({f_k}min\) are the maximum and minimum values of the \(k - th\) objective obtained from the non-dominated solutions available in the external archive, respectively. And the objective \({f'_k} \left( {{p_i}} \right) \) is normalized to [0, 1]. Then, the normalized diversity distance \(Cd({p_i},P)\) is showed as follows:

$$\begin{aligned} Cd({p_i},P) = \frac{{SDE({p_i}) - SD{E_{\min }}}}{{SD{E_{\max }} - SD{E_{\min }}}} \end{aligned}$$
(3)

where \(SD{E_{\max }}\) and \(SD{E_{\min }}\) are the maximum and minimum SDE distances in the population, respectively. \(SDE({p_i})\) is the original SDE distance defined in [4], which uses the shifted euclidean distance to the nearest neighbor, the equation is showed as follow:

$$\begin{aligned} SDE({p_i}) = \mathop {\min }\limits _{{p_j} \in P,j \ne i} \sqrt{\sum \limits _{k = 1}^m {sde{{({f'_k}({p_i}),{f'_k}({p_j}))}^2}} } \end{aligned}$$
(4)
$$\begin{aligned} sde({f'_k}({p_i}),{f'_k}({p_j})) = \left\{ {\begin{array}{*{20}{c}} {{f'_k}({p_j}) - {f'_k}({p_i})}&{}{\mathrm{{if }}\,{f'_k}({p_j}) > {f'_k}({p_i})}\\ 0&{}{otherwise} \end{array}} \right. \end{aligned}$$
(5)

And the convergence distance \(Cv({p_i},P)\) is used to reflect the convergence ability of \({f'_k}\left( {{p_i}} \right) ({} {} k = 1,2,...,m)\) with respect to the ideal point \({z^*}\). The equation is calculated as follows:

$$\begin{aligned} Cv({p_i},P) = 1 - \frac{{dis({p_i})}}{{\sqrt{m} }} \end{aligned}$$
(6)

where \(dis({p_i})\) denotes the euclidean distance from \({f'_k}({p_i})({} {} k = 1,2,...,m)\) to the ideal point \({z^*}\). It can be computed as follows:

$$\begin{aligned} dis({p_i}) = sqrt(\sum \limits _{k = 1}^m {{f'_k}{{({p_i})}^2}} ) \end{aligned}$$
(7)

The larger the value of \(Cd({p_i},P)\), the further away the neighborhood is from \({p_i}\). The larger the value of \(Cv({p_i},P)\), the closer the distance between the \({f'_k}({p_i})({} {} k = 1,2,...,m)\) and the ideal point \({z^*}\). To minimize all the objectives, individuals with larger convergence distances should be prioritized to increase selection pressure, and selected individuals should move toward ideal points when external archive are updated. At the same time, in order to balance the diversity distance and the convergence distance, the two weight factors \(\alpha \) and \(\beta \) can be used to adjust the individual weights adaptively on the basis of their original diversity distance and convergence distance.

2.2 Reference-Point Based Non-dominated Sorting Strategy (RNS)

In reference-point based non-dominated sorting strategy, the diversity maintenance is achieved by initializing a set of reference points [12]. Supposed that the initial population is \({P_t}\) and the size is \(N\,\left( {N \approx H} \right) \), the offspring population is \({Q_t}\), and the combined population \({S_t} = {P_t}\,\cup \,{Q_t}\). Then, the population \({S_t}\) selects individuals of different non-domination levels \(({F_1},{F_2},...,{F_l},...)\) at the same time, the termination condition is that the size of \({S_t}\) is equal to or larger than N. Suppose that the current level is the \(l - th\) level. Select \({F_{l - 1}}\) individuals from \({S_t}\) and put them into the next generation population \({P_{t + 1}}\). The rest individuals \(N - number({S_t}({F_{l - 1}}))\) are chosen from \({F_l}\) by the reference points strategy. The reference points strategy needs to normalize the objective function values. Also, the ideal point of the population \({z^*}\) is defined as (0, ..., 0) and reference points just lie on this normalized hyper-plane. Then, the perpendicular distance between each individual in \({S_t}\) with reference line is calculated and the individual of minimum distance belongs to the niche corresponding to the reference point. The ones associated with the reference points whose niche counts are small have better chances to be selected. The procedure is presented in Algorithm 1.

figure a

3 The Proposed Algorithm

In this section, the detailed process of the proposed MaOEA-TES algorithm is described in Sect. 3.1. And then, designed strategies are given in Sect. 3.2, 3.3.

3.1 Many-Objective Evolutionary Algorithm Based on Threshold Elite Selection Strategy (MaOEA-TES)

In this section, a many-objective evolutionary algorithm with threshold elite selection strategy (MaOEA-TES) is proposed. A reference-point based non-dominated sorting strategy is used to select good individuals. The non-dominated sorting strategy can be layered according to the level of individual non-dominated solutions, and the pareto optimal solution can be quickly searched. Furthermore, based on the reference point and adaptive penalty distance boundary intersection strategy, individuals with uniform distribution in the objective space can be selected to enhance the diversity of the population, and the convergence information can be combined to ensure convergence and distribution of the population. Furthermore, the dynamic threshold selection strategy is adopted to ensure that the BFE method can replace the general environment selection mechanism in the later stage of the algorithm, so that the algorithm can balance the convergence and distribution well in the whole group evolution process. The pseudo code is shown in Algorithm 2.

figure b

3.2 Adaptive Penalty Distance Boundary Intersection Strategy (APDBI)

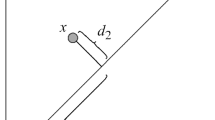
As shown in Fig. 1, it can be seen that the perpendicular distance between the individual and the reference line is \({d_2}\) in the non-dominated sorting strategy based on the reference point. However, \({d_2}\) represents the diversity of individuals and does not balance well with the relationship between convergence and diversity.

Therefore, \(d(x) = {d_{j,1}}(x)\, +\, \theta \times {d_{j,2}}(x)\) is used to replace \({d_2}\), and then the value of \(\theta \) can dynamically balance adaptive penalty distance of boundary intersect with the number of iterations increases, which makes the solution closer to PF.

Fig. 1.
figure 1

The description of APDBI

Full size image

And the equations are showed as follows:

$$\begin{aligned} d(x) = {d_{j,1}}(x) + \theta \times {d_{j,2}}(x) \end{aligned}$$
(8)
$$\begin{aligned} {d_{j,1}}(x) = \frac{{\left\| {{{(w - F(x))}^T}\sigma } \right\| }}{{\left\| \sigma \right\| }} \end{aligned}$$
(9)
$$\begin{aligned} {d_{j,2}}(x) = \left\| {f(x) - (w - {d_1}\sigma )} \right\| \end{aligned}$$
(10)
$$\begin{aligned} \theta = \sigma \cdot {e^{M\mathrm{{ - 1}} \cdot \frac{{gen + 1}}{{maxgen}} \cdot \left\| {{w^j}} \right\| }} \end{aligned}$$
(11)

where w represents the ideal point, M is the number of objective, gen represents the current iterations number, and the maximum iterations number is maxgen, \(\sigma \) is the reference point and \(\theta \) is the adaptively defined penalty parameter. Also, \({d_{j,1}}(x)\) represents the distance between the point that the individual maps to the reference line and the ideal point, \({d_{j,2}}(x)\) is the distance between the individual and reference line.

3.3 Dynamic Threshold Selection Strategy (DTS)

Because of the different proportions of convergence and diversity in the different evolution stages of the algorithm, dynamic threshold selection strategy is adopted to balance them in the evolution process dynamically. And a threshold is set to select different strategy in the algorithm. When the condition is met, the algorithm uses the reference point strategy to select the offspring, otherwise balanceable fitness estimation strategy is used to select offspring. The equation for this threshold is as follows:

$$\begin{aligned} Thre = \frac{{t + 1}}{{MaxIt}} \end{aligned}$$
(12)

where t represents the current generation, MaxIt represents the maximum generation, and the threshold Thre increases with the number of iterations. A random number rand within [0, 1] is generated. If rand is larger than the threshold, the reference-point based non-dominated sorting strategy is selected, otherwise, the balanceable fitness estimation strategy is selected.

4 Experimental Results and Analysis

This section will evaluate the performance of MaOEA-TES and discuss results. Firstly, we will describe the test problems DTLZ [16]. Meanwhile, the performance indicator is used in the experiment. Then we will introduce three most advanced algorithms for comparison and corresponding parameter design. Finally, the experimental results are discussed. The simulation results of MaOEA-TES on three to fifteen objective optimization problems are provided. Seven problems are used as test problems in DTLZ. DTLZ problems are non-convex, multi-modal, non-connected and non-uniform Pareto front. These benchmark issues are challenging to evaluate the performance of MaOEAs.

Table 1. Population size corresponding to different objective numbers
Full size table

In the evaluation criterion, the inverse intergenerational distance (IGD) [17] is chose as the performance indicator to evaluate the quality of the solution set, as a separate measure, which can provide a combination of information about the convergence and diversity of the obtained solutions. By calculating the average Euclidean distance and standard deviation between the Pareto optimal solution set and the obtained optimal solution set (in parentheses), the formulas are as follows:

$$\begin{aligned} IGD(A,Z) = \frac{1}{{\left| Z \right| }}\sum \limits _{i = 1}^{\left| z \right| } {\mathop {\min }\limits _{j = 1}^{\left| A \right| } d\left( {{z_i},{a_j}} \right) } \end{aligned}$$
(13)

where \(d\left( {{z_i},{a_j}} \right) = {\left\| {{z_i} - {a_i}} \right\| _2}\). The IGD value is smaller, the solution set obtained by the algorithm is closer to the PF. If the IGD value is large, it proves that no solution related to the reference point has been found.

For each algorithm, the number of iterations is 10000 generations, running 30 times independently, and the best, median and worst IGD performance values are reported. For all algorithms, performance indicators are computed using the final solution set. Table 1 shows the different population sizes for different objective sizes.

Fig. 2.
figure 2

Coordinates of the solutions obtained by five algorithms on DTLZ2 with five objectives. (a) NSGAIII (b) KnEA (c) SPEA2 (d) MaOEA-TES

Full size image
Table 2. IGD comparisons the four algorithms on DTLZ test suite
Full size table

It can be seen from Table 2 that the average value of the algorithm MaOEA-TES is better than other algorithms. The feasibility and accuracy of the algorithm are verified. It can be seen from DTLZ1 that MaOEA-TES is significantly better than other algorithms. For DTLZ2, the reason of the proposed is slightly worse than KnEA is that KnEA adopts the inflection point strategy which is suitable for solving the concave problem. And for DTLZ3, MaOEA-TES receives the best performance on 8, 10, 15 objectives, which is caused by the balanceable fitness estimation strategy. At the same time, by comparing the IGD value and standard deviation (in parentheses) on DTLZ4-7, it can be concluded that the MaOEA-TES algorithm has a significant role in promoting population convergence and diversity. Observing from the pareto front of the algorithm, and the results are shown in Fig. 2. It can be seen that the solution set of MaOEA-TES is at the center of the pareto, which can maintain a better diversity.

5 Conclusion

Due to the non-dominated sorting strategy based on the reference-point lacks the pareto selection pressure and the diversity maintenance mechanism is insufficient in the late stage of algorithm. In order to solve this problem, a many-objective evolutionary algorithm with threshold elite selection strategy MaOEA-TES is proposed in this paper. The proposed algorithm combines balanceable fitness estimation with reference-point based non-dominated sorting strategy. Meanwhile, dynamic threshold selection strategy is designed to better balance the diversity and convergence of population. The experiment results show that the proposed MaOEA-TES is superior to other advanced algorithms.