Provably Secure Server-Assisted Verification Threshold Proxy Re-signature Scheme

Abstract

Aiming at the problems of limited computing power and high security requirements of terminal equipment, which affects people’s good experience on some network resources, we proposes a provably secure server-assisted verification threshold proxy re-signature scheme. Threshold proxy re-signature can effectively disperse the power of the agent, and solve the security problem that the agent’s rights are too concentrated. In the server-assisted authentication protocol, the verifier transfers the complex bilinear pairing operation to the server through the interaction, reducing the computational complexity of the verifier. Under the standard model, the scheme can effectively resist collusion attacks and adaptive selection of message attacks. Performance analysis results show that compared with Yang’s scheme, the signature length of the new scheme is at least twice shorter and the verification efficiency is increased by at least 57%.

1 Introduction

With the development of network technology and the continuous growth of technology in mobile communication, mobile devices become an important part of people’s life. However, due to the limited computing power of terminal equipment and limited energy supply, it has affected people’s good experience of some network resources. The emergence of server-assisted verification technology has effectively solved this problem. A secure server-assisted verification signature scheme was given in [1]. However, this solution does not effectively defend against server and signer collusion attacks. Later, in the [2], Niu et al. proposed a server-assisted verification signature scheme and the scheme can resist the attack, but the scheme needs to consume large broadband expenditure. Combined with aggregation signature and server-assisted verification signatures, Yang et al. proposed a cryptosystem that saves broadband expenditures in [3]. This scheme reduces broadband expenditure by converging different signatures corresponding to multiple messages into one signature. Saves verification time and improves verification efficiency.

Agent re-signature is an important research direction of cryptography. Domestic and foreign scholars have done a lot of work in this direction. The security model of proxy re-signature was first proposed in the literature [4], and two schemes with strict security under the random oracle model are given in this paper. A general combinable proxy re-signature scheme was proposed in [5]. However, this scheme not un-forgeable. In order to overcome this problem, a modification of the above scheme was proposed in the [6]. In recent years, the wide practicality of proxy re-signature has attracted the attention of scholars. Some proxy re-signature schemes with special properties have been proposed successively, such as proxy-based signature scheme based on polynomial isomorphism [7], lattice proxy re-signature [8], identity-based proxy re-signature [9], etc. However, these identity-based or certificate-based proxy re-signature schemes have problems such as certificate management and key escrow. In order to overcome these problems, a certificate-less proxy re-signature scheme with aggregation property was designed in [10]. This scheme effectively reduces the computational cost and communication cost in the verification process. In addition, in order to avoid the agent obtaining the detailed content of the converted message, Mi et al. proposed a blind proxy re-signature scheme in [11], however, the verifier in this scheme is pre-specified in practical application. Therefore, there are limitations in practical applications and lack of security. Aiming at this problem, a partial blind proxy re-signature scheme with security was given in [12]. This scheme not only realizes the conversion of the signature between the trustee and the agent when the message content is not public. Moreover, it also effectively prevents the trustee from illegally using the re-signature.

Although the proxy re-signature scheme has been widely used, it still has many drawbacks. For example, once the re-signature key is compromised, the security of the solution will be compromised. In addition, the agent’s rights are too concentrated and need to be decentralized in order to make the solution more reliable. Then the concept of threshold proxy re-signature was proposed. Threshold proxy re-signature is a process of dealing with the threshold of proxy re-signature, so that the proxy’s signature rights are dispersed. Threshold proxy re-signature schemes can be used to reduce public key management expenditures, space-saving specific path traversal certificates, and generate manageable weak group signatures [13, 14].

In [15], a server-assisted verification proxy re-signature scheme was proposed, which improves the efficiency of signature verification. However, in the proxy re-signature process of this scheme, there is only one agent, so the agent’s rights are too concentrated. Once the agent is attacked, the re-signature key is leaked and the security of the scheme is destroyed. Aiming at this problem, we proposed a one-way variable threshold proxy re-signature scheme in [16]. In this paper, we introduce the secret sharing model and threshold technology, and propose a new provably secure server-assisted verification threshold proxy re-signature scheme. On the one hand, in the process of server-assisted authentication protocol, the verifier and the server transfer the complex bilinear pairing operation task to the server through the interaction protocol between them, so that the verifier has a smaller computational cost. The signature was verified to improve the verification efficiency of the signature. On the other hand, the dispersal of the agent’s rights enhances the security of the scheme. Finally, simulation experiments show that the scheme is efficient.

2 Preliminaries

2.1 Bilinear Pairings

Let $p$ be a large prime, $G_{1}$ and $G_{2}$ are two $p$ - ordered cyclic groups, and $g$ is a generator of group $G_{1}$. $e:G_{1} \times G_{1} \to G_{2}$ is a bilinear map and satisfies the following conditions:

• (1) Bilinear: For arbitrary $x,y \in Z_{q}^{*}$, satisfied $e(g^{x} ,g^{y} ) = e(g,g)^{xy}$.

• (2) Non-degenerate: There exist $g_{1} ,g_{2} \in G_{1}$, which satisfied $e(g_{1} ,g_{2} ) \ne 1$.

• (3) Computability: There exists a valid algorithm $e(g_{1} ,g_{2} )$, where $g_{1} ,g_{2} \in G_{1}$.

2.2 CDH Hypothesis

Definition 1 (CDH problem):

For any unknown $x,y \in Z_{q}^{*}$, when $\left( {g,g^{x} ,g^{y} } \right) \in G_{1}^{3}$ is known, we can calculate $g^{xy} \in G_{1}$.

Definition 2 (CDH Hypothesis):

The CDH problem in the group $G_{1}$ can be solved with a large probability in polynomial time. The algorithm that satisfies the above conditions does not exist.

2.3 Secret Sharing Model

Distribution stage: Let $q$ be a prime number and secret $s \in Z_{q}^{*}$ to be distributed. Suppose there is a threshold of $(t,n)$, namely in a group with $n$ members $P_{i} (i = 1,2, \ldots ,n)$, the secret $s$ can be recovered when at least $t$ members cooperate. The basic idea is: first randomly generate $a_{1} ,a_{2} , \ldots ,a_{t - 1}$ and generate the function $F(x) = s + a_{1} x + \ldots + a_{t - 1} x^{t - 1}$, then calculate $X_{i} = F(i) \in Z_{q}^{*}$ and issue $(i,X_{i} )$ to each member $P_{i}$, note that we can get $X_{0} = F(0) = s$, when $i = 0$.

Reconstruction stage: Let $\Phi \subseteq \left\{ {1,2, \ldots ,n} \right\}$, $\left|\Phi \right| \ge t$, where $|.|$ represents the order of the set. Then, let the function, $F({\text{x}}) = \sum\limits_{{j \in\Phi }} {\lambda_{{X_{\text{j}} }}^{\Phi } X_{\text{j}} }$, $\lambda_{{{\text{x}}_{\text{j}} }}^{\Phi } \in Z_{q}^{*}$, where parameter $\lambda_{{x_{j} }}^{\Phi } = \prod\limits_{{{\text{k}} \in\Phi ,k \ne j}} {\frac{x\, - \,k}{j\, - \,k}}$. Finally, we can recover the $s = F(0) = \sum\limits_{{j \in\Phi }} {\lambda_{{0{\text{j}}}}^{\Phi } x_{\text{j}} }$, where $\lambda_{0\,j}^{\Phi } = \prod\limits_{{k \in\Phi ,k \ne {\text{j}}}} {\frac{0\, - \,k}{j\, - \,k}}$.

3 Scheme Model and Security Definitions

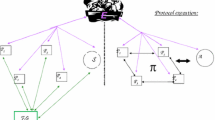
3.1 Two-Way Server-Assisted Verification Threshold Proxy Re-signature Scheme Model

The server-assisted verification threshold proxy re-signature scheme generally includes the following eight algorithms.

• (1) $Setup$: Given a constant $k$, the system parameter $cp$ are obtained by operation $(1^{k} ) \to cp$ and disclosed.

• (2) $Keygen$: Enter the system $cp$ parameter obtained based on the (1) process, and by $(cp) \to (pk,sk)$, we obtain the public and private key pairs $(pk,sk)$ of the user.

• (3) $Rekey$: Firstly, enter the public and private key pairs $(pk_{B} ,SK_{B} )$, $(pk_{A} ,sk_{A} )$ of Bob and Alice, respectively. Secondly, the re-signature key $rk_{A \to B}$ is distributed $n$ parts by the algorithm and randomly assigned them to the agents. Finally, a corresponding re-signature key $rk_{{A \to B_{i} }}$ and a re-signature public key $pk_{{A \to B_{i} }}$ are respectively generated for each agent, so that each agent can convert Alice’s signature into Bob’s partial re-signature through his own re-signed key. It should be noted that $sk_{A}$ is not necessary in this algorithm.

• (4) $Sign$: Randomly given the signature message $m$ and Alice’s private key $sk_{A}$ can generate an original signature $\sigma_{A(m)}$ of the message $m$ corresponding to the public key $pk_{A}$.

• (5) $Resign$: Firstly, the compositor needs to collect a partial re-signature obtained by each agent through its own re-signature key. Secondly, when the compositor has at least $t$ legal resigned parts, the compositor combines these legal parts into a signature to obtain a re-signature $\sigma_{B(m)}$ and outputs it.

• (6) $Verify$: Given the public key $pk$, the signature message $m$, and the signature $\sigma$ to be verified, if $\sigma$ is a valid signature obtained by the public key $pk$ for the message $m$, output $1$; otherwise, output $0$.

• (7) $Server - setup$: Enter a parameter $cp$ to generate a string $Vst$ for the verifier.

• (8) $Server - verify$: For the string $Vst$, public key $pk$ and message signature pairs $(m,\sigma )$, if the server lets the verifier determine that $\sigma$ is a valid signature, output $1$; otherwise, output $0$.

3.2 Security Definition

The security of the scheme is ensured by the robustness and unforgeability of the threshold proxy and the completeness of the server-assisted authentication protocol. The so-called robustness and unforgeability means that even if the attacker can unite with $t - 1$ agents, the signature scheme can still be implemented correctly, but the attacker cannot re-sign. This ensures that a legal signature of a new message cannot be generated in the case of a joint attack. The so-called server-assisted authentication protocol completeness means that the server cannot enable the verifier to determine the legality of an illegal signature. In [15], the completeness of the server-assisted authentication protocol under joint attack and adaptive selective message attack is defined by designing two games, Game1 and Game2.

Definition 3:

If the attacker approaches the probability that the game can be victorious in the Game1 and Game2 games in [15], the server-assisted verification protocol in the scheme is said to be complete.

Definition 4:

If the threshold proxy re-signature scheme satisfies both of the following conditions, it indicates that the scheme is safe in the case of collusion attacks and selective message attacks.

• (1) In the case of adaptive selection of message attacks, there is both unforgeability and robustness.

• (2) The server-assisted verification protocol is complete.

4 A New Two-Way Server-Assisted Verification Threshold Proxy Re-signature Scheme

In this part we construct a provably secure server-assisted verification threshold proxy re-signature scheme. Participants in the program are: Trustee Alice (responsible for generating the original signature of the message), Delegator Bob, Verifier (by verifying the validity of the signature by interacting with a semi-trusted server), $n$ semi-trusted agents and a server.

• (1) $Setup$: Let $q$ be a prime number of length $k$, and $G_{1}$, $G_{2}$ are respectively circular multiplicative groups of order $q$. Let $g$ be a generator in group $G_{1}$, $e\left( {G_{1} \times G_{1} \to G_{2} } \right)$ is a bilinear map, arbitrarily select positive integers $q_{0} < q_{1 < } q_{2 < .. < } q_{n - 1}$, satisfying conditions $gcd\text{(}q_{i} \text{,}q_{j} \text{) = 1}$ and $gcd\text{(}q_{i} \text{,}q\text{) = 1}$, where $0 \le i \le j \le n - 1$. Let $F = q_{0} q_{1} q_{2} \ldots q_{n - 1}$ and opening the parameter $(cp) = (e,q,G_{1} ,G_{2} ,g,H,F,q_{0} ,q_{1} ,q_{2} , \ldots ,q_{n - 1} )$.

• (2) $Keygen$: The user inputs the parameter and randomly selects $a \in Z_{q}$ and obtains the corresponding public-private key pair $(pk,sk) = (g^{a} ,a)$.

• (3) $Rekey$: After entering Alice and Bob’s private keys $sk_{A} = a$ and $sk_{B} = b$, then proceed as follows:

  • (1) In the interval $[1,q - 1]$, randomly select two numbers $l,m$ and then calculate $\alpha_{\text{i}} = l_{i} m_{i} \prod\limits_{j = 0}^{{{\text{i}} - 1}} {q_{j} } (mod\,F),i = 1,2, \ldots n - 1$. By applying the Chinese remainder theorem, we can calculate $\alpha_{0} \in Z_{F}$, which satisfies $\alpha_{0} = sk_{B} = b\,mod\,q_{i} ,$ $i = 0,1, \ldots ,n - 1$. Then, construct a $n - 1$ degree polynomial about the variable $x$. When a positive integer $t(1 \le t \le n)$ is given, there is a polynomial $f_{t} (x) = f(x)mod_{qt - 1} = b + \sum\limits_{\text{i = 1}}^{t - 1} {\alpha_{i} x^{i} }$ corresponding to $t - 1$.

  • (2) Let $X_{j} = g^{{\alpha_{j} /a}}$, $Y_{j} = g^{\alpha j}$, $j = 0,1, \ldots ,n - 1$. Re-signature key $rk_{A \to B}^{i} \in Z_{F}$, $rk_{A \to B}^{i} = \frac{{f_{t} (i)}}{a}mod\,q_{t - 1}$, $t = 1,2, \ldots ,n$ can be solved by Chinese remainder theorem. Then send the information $\left( {i,rk_{A \to B}^{i} } \right)$ to the agent $P_{i} ,i = 1,2, \ldots ,n$, where $X_{0} = g^{b/a} ,Y_{0} = pk_{B} = g^{b}$.

  • (3) The agent $P_{i} (1 \le i \le n)$ first calculates $rk_{A \to B}^{n,i} = rk_{A \to B}^{i} \,mod\,q_{n - 1}$ and then determines whether the obtained sub-key is valid by verifying the following Eqs. (1) and (2):

    $$ g^{{rk_{A \to B}^{n,i} }} = \prod\limits_{j = 0}^{n - 1} {X_{j}^{{i^{j} }} } $$

    (1)
    $$ e\left( {\prod\limits_{j = 0}^{n - 1} {X_{j} ,pk_{A} } } \right) = e\left( {\prod\limits_{j = 0}^{n - 1} {Y_{j} ,g} } \right) $$

    (2)

    If both of the above equations are true, then the generated sub-key $rk_{A \to B}^{i}$ is valid. Given any positive integer $t(1 \le t \le n)$, the agent $P_{i}$ can compute $rk_{A \to B}^{t,i} = rk_{A \to B}^{i} modq_{t - 1}$ independently and publish its verification public key $vk_{t,i} = g^{{f_{t} (i)}} = \prod\limits_{j = 0}^{t - 1} {Y_{j}^{{i^{j} }} }$ with the re-signature key $rk_{A \to B}^{i}$ originally obtained.

• (4) $Sign$: We give the trustee’s private key $a$ and a message $m = \left( {m_{1} ,m_{2} , \ldots ,m_{{n_{m} }} } \right) \in \left\{ {0,1} \right\}^{{n_{m} }}$ of length $n_{m} bit$, and then output an original signature $\upsigma_{A} = H\left( m \right)^{a} = \left( {\upsigma_{A1} ,\upsigma_{A2} } \right) = \left( {\text{g}_{1}^{a} \varpi^{\alpha } ,\,\text{g}^{\alpha } } \right)$ of the message $m$ corresponding to the public key $pk_{A}$, where $g_{1} ,g_{2} ,u_{1} , \ldots ,u_{{n{\text{m}}}} \in G_{1} ,\alpha \in_{R} Z_{q}$ and $\varpi = g_{2} \prod\limits_{i = 1}^{{n_{m} }} {\left( {u_{i} } \right)^{{m_{i} }} }$.

• (5) $\text{Re} sign$:

  • (1) Partial key generation: Assume that the threshold is $t\left( {1 \le t \le n} \right)$. Enter the threshold $t$, public key $pk_{A}$, message $m$, and signature $\sigma_{A}$. First check if $Verify(pk_{A} ,m,\sigma ) = 1$ is true. If the equation is true, enter the re-signature sub-key $rk_{A \to B}^{t,i}$ and output the partial re-signature $\sigma_{Bi} = (\sigma_{A} )^{{rk_{A \to B}^{t,i} }}$, where $i = 0,1, \ldots ,t$. If the equation is not true, namely it does not pass the verification, output $0$.

  • (2) Re-signature generation: After the re-signature combiner obtains some partial re-signatures, the following formula is verified:

    $$ e\left( {\sigma_{B,i} ,g} \right) = e\left( {\nu k_{t,i} ,H\left( m \right)} \right), $$

    (3)

    where $\nu k_{t,i}$ represents the verifiable public key of some agents. If the combiner obtains at least $t$ legal partial re-signatures $\left( {\sigma_{{B,i_{1} }} ,\sigma_{{B,i_{2} }} , \ldots ,\sigma_{{B,i_{k} }} } \right)$, its re-signature is $\sigma_{B} = (\sigma_{B,1} ,\sigma_{B,2} ) = (\prod\limits_{i = 1}^{t} {\left( {\sigma_{{B,i_{1} }} } \right)^{{\gamma_{0,i} }} } \text{,}\,\prod\limits_{i = 1}^{t} {\left( {\sigma_{{B,i_{2} }} } \right)^{{\gamma_{0,i} }} } )$, where $\gamma_{0,i}$ is the coefficient of the Lagrange interpolation polynomial.

• (6) $Verify$: When the public key $pk_{A}$, message $m$, and signature $\sigma$ are entered,

  $$ {\text{if}}\;{\text{the}}\;{\text{equation}}\;e\left( {\sigma ,g} \right) = e\left( {H\left( m \right),pk_{A} } \right) $$

  (4)

  is satisfied, output $1$, otherwise output $0$.

• (7) $Server - setup$: Given the system parameter $cp$, the verifier randomly selects an element $x \in Z_{q}^{ *}$ and assumes a string $Vst = x$.

• (8) $Server - verify$: Given $Vst = x$, a public key $pk$ and a signed message pair $\left( {m,\sigma = \left( {\sigma_{1} ,\sigma_{2} } \right)} \right)$, the server-assisted authentication interaction protocol between the verifier and the server is as follows:

  • (1) The verifier calculates $\sigma^{'} = \left( {\sigma_{1}^{'} ,\sigma_{2}^{'} } \right) = \left( {\left( {\sigma_{1} } \right)^{x} ,\,\left( {\sigma_{2} } \right)^{x} } \right)$ and sends $\left( {m,\sigma^{'} } \right)$ to the server.

  • (2) The server calculates $\eta_{1} = e\left( {\sigma_{1}^{{\prime }} ,g} \right)$, $\eta_{2} = e\left( {\varpi ,\sigma_{2}^{{\prime }} } \right)$ and sends $(\eta_{1} ,\eta_{2} )$ to the verifier.

  • (3) The verifier needs to determine whether the verifier considers $\sigma$ is the legal signature of the message $m$ by calculating whether equation

    $$ \eta_{1} = \left( {pk} \right)^{x} \eta_{2} $$

    (5)

    is true. If it is true, it outputs $1$; otherwise, it outputs $0$.

5 A New Two-Way Server-Assisted Verification Threshold Proxy Re-signature Scheme

5.1 Correctness Analysis

Theorem 1:

When the threshold is $t$, if the Eqs. (1) and (2) are true, the obtained re-signature sub-key is valid.

Proof:

By $rk_{A \to B}^{n,i} = rk_{A \to B}^{i} modq_{n - 1}$, then $g^{{rk_{A \to B}^{n,i} }} = g^{{rk_{A \to B}^{i} modq_{n - 1} }} = \prod\limits_{j = 0}^{n - 1} {X_{j}^{{i^{j} }} }$, and because of $X_{j} = g^{{\alpha_{j} /a}}$, $Y_{j} = g^{{\alpha_{j} }}$, then

$$ e\left( {\mathop \prod \limits_{j = 0}^{n - 1} X_{j} ,pk} \right) = e\left( {\mathop \prod \limits_{j = 0}^{n - 1} g^{{\frac{{\alpha_{j} }}{\alpha }}} ,g^{\alpha } } \right) = e\left( {\mathop \prod \limits_{j = 0}^{n - 1} g^{{\alpha_{j} }} ,g} \right) = e\left( {\mathop \prod \limits_{j = 0}^{n - 1} Y_{j} ,g} \right) $$

In addition, we have

$$ \begin{array}{*{20}l} {\quad rk_{A \to B}^{t,i} = rk_{A \to B}^{i} modq_{t - 1} = h^{{\frac{{f_{t} \text{(}i\text{)}}}{\alpha }}} ,} \hfill \\ {\nu k_{t,i} = \mathop \prod \limits_{j = 0}^{t - 1} Y_{j}^{{i^{j} }} = \mathop \prod \limits_{j = 0}^{t - 1} g^{{\alpha_{j}^{{i^{j} }} }} = g^{{\sum\limits_{j = 0}^{t - 1} {\alpha_{j}^{{i^{j} }} } }} = g^{{f_{t} \left( i \right)}} .} \hfill \\ \end{array} $$

Theorem 2:

When the threshold is $t$, if the Eq. (3) is established, the obtained partial re-signature is valid.

Proof:

From the properties of the bilinear pair, we get

$$ e\left( {g,s_{i} } \right) = e\left( {g,H\left( m \right)^{{f_{t} \left( i \right)}} } \right) = e\left( {g^{{f_{t} \left( i \right)}} ,H\left( m \right)} \right) = e\left( {\nu k_{t,i} ,H\left( m \right)} \right). $$

Theorem 3:

When the threshold is $t$, if the Eq. (4) is established, the obtained threshold proxy re-signature is valid.

Proof:

From the properties of the bilinear pair, we get

$$ e\left( {\sigma ,g} \right) = e\left( {H\left( m \right)^{\alpha } ,g} \right) = e\left( {H\left( m \right),g^{\alpha } } \right) = e\left( {pk,H\left( m \right)} \right). $$

Theorem 4:

If the Eq. (5) is true, the verifier is confident that $\sigma$ is the legal signature of the message $m$.

Proof:

From the re-signature $\sigma_{B} = \left( {\sigma_{B1} ,\upsigma_{B2} } \right) = \left( {g_{1}^{b} \varpi^{r} ,g^{r} } \right)$ of Bob and string $Vst = x$, we obtain

$$ \begin{array}{*{20}l} {\eta_{1} = e\left( {\sigma_{B1}^{{\prime }} ,g} \right) = e\left( {\left( {\sigma_{B1} } \right)^{x} ,g} \right) = e\left( {\left( {g_{1}^{b} \varpi^{r} } \right)^{x} ,g} \right) = e (g_{1}^{b} ,g )^{x} e\left( {\varpi^{rx} ,g} \right)} \hfill \\ { = e (g_{1} ,g^{b} )^{x} e\left( {\varpi ,g^{rx} } \right) = \left( {pk_{B} } \right)^{x} e\left( {\varpi ,g^{rx} } \right) = \left( {pk_{B} } \right)^{x} e\left( {\varpi ,\left( {g^{r} } \right)^{x} } \right)} \hfill \\ { = \left( {pk_{B} } \right)^{x} e (\varpi ,\left( {\sigma_{B2} )^{x} } \right) = \left( {pk_{B} } \right)^{x} e\left( {\varpi ,\sigma_{B2}^{{\prime }} } \right) = \left( {pk_{B} } \right)^{x} \eta_{2} .} \hfill \\ \end{array} $$

Through the above derivation process, it can be proved that when the threshold is $t$, the re-signature sub-key, partial re-signature and re-signature verification algorithm are effective, and the correctness of the server-assisted verification protocol is obtained. Since the length of the original signature and the length of the re-signature are the same, the scheme has the characteristics of transparency and versatility. We can get it through the operation $r_{A \to B} = b/a = 1/r_{B \to A}$, so the solution satisfies the two-way nature. In addition, because of $sk_{A} ,sk_{B} ,rk_{A \to B} \in Z_{q}^{*}$, this scheme has the characteristics of key optimality.

5.2 Security Analysis

The following analysis will analyze the scheme proposed in this paper with unforgeability and robustness, and the server verification protocol of the scheme satisfies the completeness. However, this scheme has unforgeability under the standard model. The proof has been given in [17], and its security problem can be attributed to the CDH hypothesis. Therefore, in order to prove the security of our proposed new solution, we only need to prove the robustness of the scheme and the completeness of the server-assisted verification protocol.

Theorem 5:

Under the standard model, when $n \ge 2t - 1$, the scheme is robust to any attacker who can unite $t - 1$ agents.

Proof:

• (1) Since the combiner has the ability to verify whether a partial re-signature is legal, it can be rejected when a malicious agent is found.

• (2) Because there are at least $t$ honest agents among the $n$ agents, and these honest agents calculate their respective partial re-signatures through their own re-signature keys, and the combiner can also obtain the set $\Phi (|\Phi |\, \ge \,t)$ of the sequence number $i$ of the honest agents, so the combiner can always have $t$ legal partial re-signatures to synthesize and calculate the re-signature corresponding to the message $m$.

• (3) When the combiner has $t$ legal partial re-signatures to synthesize and calculate the re-signature corresponding to the message $m$, the number of joint attackers is up to $2t - 1 - t = t - 1$. According to the $(t,n)$ threshold condition, the attacker cannot succeed break through.

  In summary, we can conclude that the scheme is robust when $n \ge 2t - 1$.

Theorem 6:

In the case of adaptive selection of messages and collusion attacks, $Server - verify$ is complete.

Before giving the proof of Theorem 6, we first introduce the following two lemmas.

Lemma 1:

If the server collides with Alice to become an attacker $A_{1}$, the attacker asks the challenger $C$ to determine that an illegal original signature is legal. The probability that the event is true is zero.

Proof:

In this process, $A_{1}$ plays the role of the server and in the agreement, $C$ plays the role of verifier. Given the illegal original signature of a message, the goal of $A_{1}$ is to let $C$ make sure that the illegal signature is legitimate. The interaction between them is as follows:

Establishment: Challenger $C$ performs the initialization algorithm to generate system parameter $cp$, randomly selects $x^{*} ,\gamma \in Z_{q}^{*}$, lets $Vst = x$ and calculates the public-private key pair $(pk_{A} ,sk_{A} ) = (e(g_{1} ,g^{\gamma } ),\gamma )$ of the trustee Alice and then sends $\{ cp,pk_{A} ,sk_{A} \}$ to the attacker $A_{1}$.

Query: The attacker $A_{1}$ can make a limited number of secondary verification queries to the server. In the process of each inquiry of $(m_{i} ,\sigma_{i} )$, both the challenger $C$ and the attacker $A_{1}$ perform server-assisted verification to obtain the authentication protocol, and then respond to the output of the protocol and return it to the attacker $A_{1}$.

Output: Finally, the attacker $A_{1}$ outputs the forged message $m^{ *}$ and the string $\sigma^{ *} = \left( {\sigma_{1}^{ *} ,\sigma_{2}^{ *} } \right)$, and let the set of all legal signatures that make the message $m^{ *}$ corresponding to the public key $pk_{A}$ is $\Gamma _{{m^{*} }}$, and satisfies $\sigma^{ *} \notin\Gamma _{{m^{ *} }}$. When the challenger $C$ receives $(m^{*} ,\,c^{*} ,\,\sigma^{1*} )$, it computes $\left( {\sigma^{ *} } \right)^{{\prime }} = \left( {\left( {\sigma_{1}^{ *} } \right)^{{\prime }} ,\left( {\sigma_{2}^{ *} } \right)^{{\prime }} } \right) = \left( {\left( {\left( {\sigma_{1}^{ *} } \right)^{{x^{ *} }} } \right),\left( {\sigma_{2}^{ *} } \right)^{{x^{ *} }} } \right)$ with the given string $Vst$ and sends it to the attacker $A_{1}$. Then, $A_{1}$ obtains $\eta_{1}^{ *} = e\left( {\left( {\sigma_{1}^{ *} } \right)^{{\prime }} ,g} \right)$ and $\eta_{2}^{ *} = e\left( {\varpi^{ *} ,\left( {\sigma_{1}^{ *} } \right)^{{\prime }} } \right)$ by operation and returns them to $C$. The following is a detailed derivation of the probability that the equation $\eta_{1}^{ *} = \left( {pk_{A} } \right)^{{x^{ *} }} \eta_{2}^{ *}$ is established is $1/\left( {q - 1} \right)$.

• (1) Because of $\left( {\sigma^{ *} } \right)^{{\prime }} = \left( {\sigma^{ *} } \right)^{{x^{ *} }}$ and $x^{ *} \in_{R} Z_{q}^{ *}$, the probability of attacker $A_{1}$ forging $\left( {\sigma^{ *} } \right)^{{\prime }}$ from $\sigma^{ *}$ is $1/\left( {q - 1} \right)$.

• (2) Assuming that the attacker $A_{1}$ returns $\left( {\eta_{1}^{ *} ,\eta_{2}^{ *} } \right)$, which satisfies $\eta_{1}^{ *} = \left( {pk_{A} } \right)^{{x^{ *} }} \eta_{2}^{ *}$, then we have $log_{{pk^{*} }} \,\eta_{1}^{*} = x^{*} + log_{{pk_{A} }} \,\eta_{2}^{*}$, because $x^{ *}$ is an element selected arbitrarily from $Z_{q}^{ *}$, the probability that the attacker tries to get $x^{ *}$ to make the above equation true is $1/\left( {q - 1} \right)$.

From the above analysis, it can be seen that the probability that attacker $A_{1}$ makes $C$ believe that message signature $(m^{*} ,\sigma^{*} )$ is legitimate is $1/\left( {q - 1} \right)$. Since $q$ is a large prime, the probability that attacker $A_{1}$ let $C$ decide that an illegal original signature is legitimate is zero.

Lemma 2:

If the server collides with the $t$ proxy agents to become an attacker $A_{2}$. The probability that $A_{2}$ lets $C$ decide that an illegal re-signature is legal is negligible.

Proof:

In this process, $A_{2}$ plays the role of the server and in the agreement $C$ plays the role of verifier. When an illegal signature of a message is given, the goal of $A_{2}$ is to let $C$ make sure the illegal signature is legal. The interaction between the two is as follows:

Establishment: Challenger $C$ obtains system parameter $cp$ by running a system initialization algorithm, selects three elements $x^{*} ,\,\alpha ,\,\beta$ from $Z_{q}^{ *}$, and computes $\left( {pk_{A} ,sk_{A} } \right) = \left( {e\left( {g_{1} ,g^{\alpha } } \right),\alpha } \right)$, $\left( {pk_{B} ,sk_{B} } \right) = \left( {e\left( {g_{1} ,g^{\beta } } \right),\beta } \right)$ and $rk_{A \to B} = b/a$. Then Challenger $C$ sends $cp,pk_{A} ,pk_{B}$ and $rk_{A \to B}$ to $A_{2}$.

Query: Same as the interrogation response process in Lemma 1.

Output: Finally, the attacker $A_{2}$ outputs the forged message $m^{*}$ and the string $\sigma^{*} = (\sigma_{1}^{*} ,\sigma_{2}^{*} )$, and let the set of all legal signatures that make the message $m^{*}$ corresponding to the public key $pk_{B}$ is $\Gamma _{{m^{*} }}$, and satisfies $\sigma^{*} \notin\Gamma _{{m^{*} }}$. Similarly, in the analysis process in Lemma 1, attacker $A_{2}$ let $C$ make sure that the probability that $\left( {m^{ *} ,\sigma^{ *} } \right)$ is a legal signature is $1/(q - 1)$. Therefore, the probability that attacker $A_{2}$ makes $C$ convinced that $\left( {m^{ *} ,\sigma^{ *} } \right)$ is a legitimate signature is negligible.

Based on the above analysis, we know that the two-way server-assisted verification threshold proxy re-signature scheme proposed in this paper is safe in the case of adaptive selection of message attacks and collusion attacks.

Next, we present a performance analysis of the server-assisted verification threshold proxy re-signature scheme.

5.3 Performance Analysis

5.3.1 Efficiency Analysis

In order to compare performance with the existing threshold proxy re-signature algorithm, the following symbols are defined in this paper (Table 1).

Table 1. The symbolic representation of the solution

It should be noted that since the calculation amount of addition, multiplication, HMAC algorithm and hash function are relatively small, we only consider the computational exponential operation and the bilinear pairing operation with large computational complexity when considering the computational overhead.

The following will be analyzed from secret segmentation, signature algorithm, re-signature algorithm, and signature verification, where the re-signature algorithm includes the partial re-signature algorithm and the synthetic re-signature algorithm. The calculation amount of the algorithm in the scheme of this paper is shown in Table 2 below.

Table 2. Calculation amount of the scheme

Two different threshold proxy re-signature schemes are presented in [18] and [19]. The comparison between the proposed signature algorithm and the existing two algorithms based on their signature length and computational overhead is shown in Table 3 below.

Table 3. Calculation overhead and security attributes of blind proxy re-signature algorithm

From Table 3, it can be seen that the computational cost of the re-signature generation algorithm in this scheme only includes two bilinear pairing operations and one exponentiation operation compared with that in [18, 19], so the computational cost of this scheme is less than that in [18, 19]. In addition, the length of the signature in this scheme is shorter, and the computational cost in signature verification is also lower than that in [18, 19]. In this scheme, two bilinear pairings are needed in the process of signature verification, and only three exponentiation operations are needed in the server-assisted verification protocol. Therefore, the new algorithm proposed in this paper has more advantages than the previous ones.

In the new scheme of this paper, the bilinear pairing computation task with high computational complexity is transferred to the server by the interaction protocol between the server and the verifier, so the bilinear pairing operation with large computational complexity is not needed in signature verification, which solves the problem of limited computing power of mobile terminal devices in mobile Internet environment. In addition, under the standard model, the proposed scheme is unforgettable and complete in the case of adaptive selection of messages. Therefore, the server-assisted verification threshold proxy re-signature scheme proposed in this paper is secure under adaptive selection message attack and collusion attack, thus satisfying the high security requirements due to the complexity of mobile Internet environment. In conclusion, this paper proposes a server-assisted verification threshold proxy re-signature scheme, which can be better adapted to terminal devices in mobile Internet environment.

5.4 Numerical Experiments

In this part, we simulate the schemes of [18] and [19] for verifier’s time overhead, verification efficiency and message signature of different orders of magnitude. The environment of the simulation experiment is CPU for Intel Core i5-8300H processor, clocked at 2.3 GHz, memory 8 GB, software environment: 64-bit Window 10 operating system, MyEclipse2015.

It can be seen from Fig. 1 that for the signature messages of the same length, the verification time overhead of the scheme is lower than that of the literature [18] and [19]. In addition, in the schemes of [18] and [19], the verifier needs to perform 8 and 5 bilinear pairings, respectively. As the length of the signature message increases, the time overhead of the verifier in the scheme increases greatly. However, in this scheme, the computationally complex bilinear pair operation is transferred to the server through the interaction protocol between the verifier and the server. The verifier only needs to perform 3 times exponential operation, so in this scheme as the length of the signature message increases, the time cost of the verifier changes little.

Fig. 1.

Relationship between verification time overhead and message length.

It can be seen from Fig. 2 that the verification efficiency of the scheme is improved by at least 68% and 57%, respectively, compared with the schemes of [18] and [19], which greatly reduces the time cost of the verifier and saves the verification cost.

Fig. 2.

Relationship between verification efficiency and message length.

6 Conclusion

In this paper, we propose a provably secure server-assisted verification threshold proxy re-signature scheme. In this scheme, on the one hand, in the process of server-assisted verification protocol, the verifier and the server transfer the complex bilinear pairing operation task to the server through the interaction protocol between them, which makes the verifier verify the signature with a small computational cost and improves the verification efficiency of the signature. On the other hand, the decentralization of the rights of agents enhances the security of the scheme and meets the higher security requirements of the mobile internet. Finally, the simulation results show that the scheme has higher verification efficiency and shorter signature length than other existing threshold proxy re-signature schemes, which satisfies the low-end computing devices with weak computing power and limited energy supply.