Keywords

1 Introduction

Integral transforms have been recognized [1] to be introduced by Leonhard Euler (1707–1783) for the solution of second-order linear differential equations, as presented in his acclaimed compendium Institutiones Calculi Integralis [2]. In general terms, his proposition introduces the integral transformation of a function f(x) in the form [1]:

$$F\left( n \right) = \int\limits_{{x_{0} }}^{{x_{1} }} {K\left( {x,n} \right)f\left( x \right)dx}$$
(1)

with the aid of a transformation kernel K(x, n), yielding a transformed dependent variable F(n) that involves a parameter n, which should in principle be a posteriori obtainable from a simpler transformed algebraic (or differential) problem, upon integral transformation of the original ordinary (or partial) differential system. Then, an inverse transformation is required to recover the original function f(x) from the transformed one, F(n). If additional independent variables are considered in Eq. (1), multiple integral transformations, with respect to each variable, can be adopted to reduce the original differential system by eliminating these variables in the resulting integral transformed system. The choices of kernels and integration bounds in Eq. (1), and consequently of the required inverse transformation, have been historically identified with the names of their particular proposers, such as the best-known Laplace and Fourier transforms.

The finite Fourier transform, of major relevance in the present context, can be said to have been introduced in a series of papers by Joseph Baptiste Fourier (1768–1830) and consolidated in his famous heat conduction treatise of 1822 [3]. It can be interpreted that from the application of separation of variables to the linear transient heat conduction equation in Cartesian coordinates, Fourier reached the eigenvalue problem, later on generalized as the so-called Sturm–Liouville problem, that naturally provided the transformation kernel and inverse formulae in terms of the associated eigenfunctions, essentially sines and cosines in the particular case of heat conduction in a slab. A number of contributions followed that dealt with the proposition of integral transforms of linear partial differential equations in different coordinates systems, such as the Hankel and Legendre transforms, respectively, for cylindrical and spherical geometries. In the popular book by Academician Nikolai Sergeevich Koshlyakov (1891–1958), published with the translated title of “Basic Differential Equations of Mathematical Physics” [4], the finite integral transform technique was formalized to handle nonhomogeneous problems, already in terms of eigenfunction expansions obtained from the generalized Sturm–Liouville problem. A number of classical works have then followed, such as in [5,6,7,8,9,10,11,12,13,14,15,16,17], expanding and consolidating this knowledge from the mathematical point of view and providing exact analytical solutions to various physical applications, notably in heat and mass diffusion, as systematically illustrated for seven different classes of problems [17].

Despite the usefulness of exact analytical solutions for such linear diffusion problems, the limitation of the classical integral transform approach was soon recognized when dealing with a priori non-transformable problems, such as in the case of time-dependent equation and/or boundary conditions coefficients [18, 19], yielding coupled infinite transformed ordinary differential systems with variable coefficients, of unknown analytical treatment. Approximate analytical solutions were yet made available in [18, 19] by considering only the diagonal of the coupled transformed system, until a hybrid numerical–analytical framework was introduced in [20] for the solution of a moving boundary mass diffusion problem, combining the integral transform method with the error-controlled numerical solution of ordinary differential systems. This hybrid approach was coined as the Generalized Integral Transform Technique (GITT) [20], following the terminology previously proposed for the approximate solution of non-transformable linear problems [18, 19]. In a natural development sequence, the GITT was then gradually extended to handle different classes of problems, including the first considered class of non-transformable linear problems with time-dependent coefficients [21]. It would not take long until this methodology was challenged to handle irregular geometries [22] and nonlinear formulations [23], followed by the solution of the boundary layer and Navier–Stokes formulations of heat and fluid flow problems [24, 25]. The various applications and extensions that were then pursued through the GITT, led to the first compilation of such developments as a monograph [26] and to a couple of invited articles [27, 28], that allowed for a broader dissemination of the methodology among the thermal sciences community.

During the participation as a keynote lecturer at the International Heat Transfer Conference in Brighton, UK [27], the first author had the unique opportunity of being properly introduced to Prof. Brian Spalding, who then kindly commented on the GITT development and provided suggestions for future work. The possibility of obtaining independent reference benchmark results in different classes of problems was one of the positive aspects, as pointed out by Prof. Spalding, to be further pursued, and he also referred us to some of the test cases that were then being tackled by the CHAM development team, such as the IAHR diverging channel test case [29], that would have numerical results compiled in electronic format through Phoenics version 2.2.1 in 1996. The handling by GITT of the suggested test case dealing with the Navier–Stokes formulation in an irregular domain was then pursued and first provided in [30], and later on presented as a dedicated article [31].

Since then, the GITT hybrid approach has been further extended and widely applied in different physical contexts, as compiled in various sources up to recent reviews [32,33,34,35,36,37,38,39]. The present chapter provides a general description of the methodology, that is, here focused on the solution of diffusion, convection–diffusion, and conjugated problems in irregular domains and/or heterogeneous media. In terms of formalism, first general solutions are provided for nonlinear diffusion problems, either considering linear or nonlinear eigenvalue problems. Second, convection–diffusion problems are discussed, either as a direct application of the previous formal solution of diffusion problems in the total transformation scheme or by skipping the integral transformation along the coordinate of predominant convective effects, through the so-called partial transformation scheme. Alternatively, the total transformation of convection–diffusion problems adopting convective eigenvalue problems is also described. Third, the treatment of eigenvalue problems by GITT is briefly reviewed, including the direct integral transformation for irregular domains, followed by the description of a single domain reformulation strategy, which markedly facilitates the handling of both heterogeneous domains and irregular regions, including the class of conjugated heat transfer problems here emphasized. Finally, selected test cases for laminar flow and convection in corrugated channels and conjugated heat transfer are described. The GITT approach results are examined in terms of convergence rates and critically compared to results from general-purpose numerical computer codes. The chapter is concluded with a discussion on the progress achieved within the last fifty years and on the next steps toward the full establishment of this computational–analytical (CAFD) approach in heat and fluid flow.

2 Diffusion Problems

Let us consider a fairly general nonlinear transient diffusion problem for the potential T(x, t), defined in the arbitrary region V, with all equation and boundary conditions coefficients written as functions of the independent and dependent variables, including the respective nonlinear source terms, P(x, t, T) and ϕ(x, t, T), given as

$$w({\mathbf{x}},t,T)\frac{{\partial {\kern 1pt} T({\mathbf{x}},t)}}{{\partial {\kern 1pt} t}} = \nabla .k({\mathbf{x}},t,T)\nabla T - d({\mathbf{x}},t,T)T + P({\mathbf{x}},t,T),\quad {\text{in}}\;{\mathbf{x}} \in V,\;t > 0$$
(2a)

with initial and boundary conditions

$$T({\mathbf{x}},0) = f({\mathbf{x}}) , \quad {\mathbf{x}} \in V$$
(2b)
$$\alpha ({\mathbf{x}},t,T) T({\mathbf{x}},t) + \beta ({\mathbf{x}},t,T) k({\mathbf{x}},t,T)\frac{{\partial {\kern 1pt} T}}{{\partial {\kern 1pt} {\mathbf{n}}}} = \phi ({\mathbf{x}},t,T),\quad {\mathbf{x}} \in S,\;t > 0$$
(2c)

where α and β are the nonlinear boundary condition coefficients that allow for recovering the three most usual kinds of boundary conditions, and n is the outward-drawn normal vector to surface S. Although more general situations could be considered, such as accounting for elliptic- and hyperbolic-type formulations, through appropriate t-operators, and including coupled multiple potentials [38], Eq. (2a) provides enough information to fully illustrate the methodology.

The most usual formal integral transform solution of problem (2b) involves the selection of a linear eigenvalue problem, which offers the basis for the eigenfunction expansion that represents the potential, as introduced in [23]. This is in fact equivalent to rewriting problem (2c) with characteristic linear coefficients that have only x dependence, i.e. w(x), k(x), d(x), α(x), and β(x), while the nonlinear source terms then incorporate the remaining nonlinear portions of the equation and boundary conditions operators. This more traditional approach is thoroughly documented in previous reviews [32,33,34,35,36,37,38,39], and therefore is not repeated here. Instead, a more general formalism is presented, as introduced in [40], which adopts a nonlinear eigenvalue problem, with all the nonlinear coefficients present in the formulation. Thus, consider the following nonlinear eigenvalue problem:

$$\nabla .k({\mathbf{x}},t,T)\nabla \uppsi_{i} ({\mathbf{x}};t) + \left[ {\mu_{i}^{2} (t)w({\mathbf{x}},t,T) - d({\mathbf{x}},t,T)} \right]\uppsi_{i} ({\mathbf{x}};t) = 0,\quad {\mathbf{x}} \in V$$
(3a)

with boundary conditions

$$\upalpha ({\mathbf{x}},t,T)\uppsi_{i} ({\mathbf{x}};t) + \upbeta ({\mathbf{x}},t,T){\text{k}}({\mathbf{x}},t,T)\frac{{\partial \uppsi_{i} ({\mathbf{x}};t)}}{{\partial {\mathbf{n}}}} = 0,\quad {\mathbf{x}} \in S$$
(3b)

The solution for the associated time-dependent eigenfunctions, ψi(x; t), and eigenvalues, μi(t), has been presented in [40], as will be discussed in what follows. Thus, the following integral transform pair is defined from problem (3a):

$$\bar{T}_{i} (t) = \int\limits_{{{\kern 1pt} V}} w ({\mathbf{x}},t,T)\;\uppsi_{i} ({\mathbf{x}};t)\,{\rm T}({\mathbf{x}},t)\;dv,\quad {\text{transform}}$$
(4a)
$${\rm T} ({\mathbf{x}},t) = \sum\limits_{i = 1}^{\infty } {\frac{1}{{N_{i} (t)}}\uppsi_{i} } ({\mathbf{x}};t)\bar{T}_{i} (t),\quad {\text{inverse}}$$
(4b)

with the normalization integral given as

$$N_{i} (t) = \int\limits_{{{\kern 1pt} V}}^{{}} {w({\mathbf{x}},t,T)\uppsi_{i}^{2} ({\mathbf{x}};t) dv}$$
(4c)

After application of the integral transformation procedure through the operator \(\int_{{{\kern 1pt} V}}^{{}} {( - )\uppsi_{i} ({\mathbf{x}};t) dv}\) , the resulting ODE system for the transformed potentials, \(\overline{{T_{i} }} (t),\) is written as

$$\frac{{d\bar{T}_{i} (t)}}{dt} + \sum\limits_{j = 1}^{\infty } {A_{i,j} (t,{\bar{\mathbf{T}}})} \bar{T}_{j} (t) = \bar{g}_{i} (t,{\bar{\mathbf{T}}}),\quad t > 0,i,j = 1,2 \ldots$$
(5a)

with initial conditions

$$\bar{T}_{i} {(0) = }\bar{f}_{i}$$
(5b)

where

$$A_{i,j} (t,{\bar{\mathbf{T}}}) = \delta_{ij} \mu_{i}^{2} (t) + A_{i,j}^{*} (t,{\bar{\mathbf{T}}})$$
(5c)
$$A_{i,j}^{*} (t,{\bar{\mathbf{T}}}) = - \frac{1}{{N_{j} (t)}}\int\limits_{{{\kern 1pt} V}} { \frac{\partial }{\partial t}[} w({\mathbf{x}},t,T)\uppsi_{i} ({\mathbf{x}};t)\,]\uppsi_{j} ({\mathbf{x}};t) dv$$
(5d)
$$\bar{g}_{i} (t,{\bar{\mathbf{T}}}) = \int\limits_{{{\kern 1pt} V}}^{{}} {\uppsi_{i} ({\mathbf{x}};t){\kern 1pt} P({\mathbf{x}},t,T) dv} + \int\limits_{{{\kern 1pt} S}}^{{}} {\upphi ({\mathbf{x}},t,T)\left( {\frac{{\uppsi_{i} ({\mathbf{x}};t) - k({\mathbf{x}},t,T)\frac{{\partial \uppsi_{i} }}{{\partial {\mathbf{n}}}}}}{{\upalpha ({\mathbf{x}},t,T) + \upbeta ({\mathbf{x}},t,T)}}} \right) ds}$$
(5e)
$$\bar{f}_{i} = \mathop \smallint \nolimits_{V} w({\mathbf{x}},0,T{\mathbf{(x}},0))\tilde{\uppsi }_{i} ({\mathbf{x}};0)f{\mathbf{(x}})dv$$
(5f)

This more general solution path provides a formal solution that encompasses the usual formalism with a linear eigenvalue problem and has been shown to result in improved convergence rates [40, 41]. On the other hand, it has the drawback of requiring that the eigenvalue problem be solved simultaneously with the transformed ODE system, yielding time-dependent transformed potentials, eigenvalues, and eigenfunctions. The GITT solution of the nonlinear eigenvalue problem (3) has been presented in [40], and will be later on reviewed, by considering an auxiliary linear eigenvalue problem of known solution to offer an eigenfunction expansion for the nonlinear eigenfunctions, leading, upon integral transformation, to a nonlinear algebraic eigenvalue problem that needs to be solved simultaneously with the ODE system (5). Alternatively, the algebraic eigenvalue problem can be differentiated with respect to the \(t\) variable and solved as a larger coupled ODE system jointly with the transformed potentials, Eq. (5a).

It should be noted that the above formal solution derivation did not account for the employment of a filtering solution, either explicit or implicit, so as to reduce the importance of the source terms in the convergence behavior, which essentially leads to the same system (2) but with redefined source terms and initial conditions. Also, only the total transformation scheme of the GITT has been so far described, when all space variables in the position vector x are eliminated through integral transformation. Alternatively, one may also consider the partial transformation scheme [42, 43], when one of the spatial variables is left out of the transformation process, thus leading to a transformed partial differential system with only time and one spatial coordinate as independent variables, as will be briefly described in the next section for convection–diffusion problems.

3 Convection–Diffusion Problems

Now consider an also fairly general convection–diffusion problem, which is essentially the nonlinear formulation of Eq. (2a) plus a nonlinear convective term, defined for a nonlinear velocity vector u(x, t, T):

$$w({\mathbf{x}},t,T)\frac{{\partial {\kern 1pt} T({\mathbf{x}},t)}}{{\partial {\kern 1pt} t}} + {\mathbf{u}}({\mathbf{x}},t,T).\nabla T = \nabla .k({\mathbf{x}},t,T)\nabla T - d({\mathbf{x}},t,T)T + P({\mathbf{x}},t,T) , \quad {\text{in}}\;{\mathbf{x}} \in V,{t} > 0$$
(6)

with similar initial and boundary conditions as in Eq. (2b, 2c).

The most usual formalism in dealing with the integral transformation of Eq. (6), similarly to the above diffusion problem (2), is to consider a linear diffusive eigenvalue problem with space dependent coefficients only, while incorporating the above nonlinear convection term and the remaining nonlinear terms, into the nonlinear source term, as introduced in [44] and widely employed throughout the development of the GITT approach. In addition, one may again merge the convection term, \({\mathbf{u}}({\mathbf{x}},t,T).\nabla T,\) into the nonlinear equation source term, \(P({\mathbf{x}},t,T),\) in Eq. (6), while keeping the remaining nonlinear coefficients in the equation to be transformed, thus being accounted for by the nonlinear diffusive eigenvalue problem. This derivation is not repeated here, since it is essentially a direct application of the methodology in Sect. 2. However, two alternative solution paths for convection–diffusion problems are here described, that have also been successfully employed in different classes of applications.

3.1 Partial Transformation

In the treatment of transient convection–diffusion problems with a preferential convective direction, one possible approach with relative merits is to consider the integral transformation in all but this one space coordinate, yielding an infinite coupled system of partial differential equations for the transformed potentials, to be solved numerically. This partial integral transformation scheme offers an interesting combination of advantages between the eigenfunction expansion approach and the selected numerical method for handling the coupled system of one-dimensional partial differential equations that results from the transformation procedure. To illustrate this procedure, a transient convection–diffusion problem is considered, separating the preferential direction that is not to be integral transformed. The vector \({\mathbf{x}} = \{ x_{1} ,x_{2} ,x_{3} \}\) is then formed by the space coordinates that will be eliminated through integral transformation, here denoted by \({\mathbf{x}}^{*} = \{ x_{1} ,x_{2} \}\) , as well as by the space variable to be retained in the transformed partial differential system, here denoted by x3. In addition, a linear eigenvalue problem is here preferred, by selecting characteristic x* dependent coefficients and incorporating the remaining terms in the source terms, including the nonlinear convection term and all the remaining nonlinear terms. The problem to be solved is now written in the following form:

$$w({\mathbf{x}}^{*} )\frac{{\partial \,T({\mathbf{x}},t)}}{{\partial {\kern 1pt} t}} = \nabla^{*} \cdot \left( {k({\mathbf{x}}^{*} )\nabla^{*} T({\mathbf{x}},t)} \right) - d({\mathbf{x}}^{*} )T({\mathbf{x}},t) + P({\mathbf{x}}^{*} ,x_{3} ,t,T),\quad {\mathbf{x}} \in V,t > 0$$
(7a)

where the operator \(\nabla^{*}\) refers only to the coordinates to be integral transformed, x*, and with initial and boundary conditions given, respectively, by

$$T({\mathbf{x}},0) = f({\mathbf{x}}),\;{\mathbf{x}} \in V;\left[ {\alpha ({\mathbf{x}}^{*} ) + \beta ({\mathbf{x}}^{*} )k({\mathbf{x}}^{*} )\frac{\partial }{{\partial {\kern 1pt} {\mathbf{n}}^{*} }}} \right]T({\mathbf{x}},t) = \phi ({\mathbf{x}}^{*} ,x_{3} ,t , T),\quad {\mathbf{x}}^{*} \in S^{*} , t > 0$$
(7b,c)
$$\left[ {\lambda (x_{3} ) + ( - 1)^{l + 1} \gamma (x_{3} )\frac{\partial }{{\partial {\kern 1pt} x_{3} }}} \right]T({\mathbf{x}},t) = \varphi ({\mathbf{x}}^{*} ,x_{3} ,t,T), x_{3} \in S_{3} = \{ x_{3,l} \} ,\quad l = 0,1,t > 0$$
(7.d)

where n* denotes the outward-drawn normal to the surface S* formed by the coordinates x* and S3 refers to the boundary values of the coordinate x3. The coefficients in Eq. (7a) inherently carry the information to the auxiliary eigenvalue problem that will be chosen for the eigenfunction expansion, and all the remaining terms from this rearrangement are collected into the source terms, \(P({\mathbf{x}}^{*} ,x_{3} ,t , T)\) and \(\phi ({\mathbf{x}}^{*} ,x_{3} ,t,T),\) including the existing nonlinear terms and diffusion and/or convection terms with respect to the dimensional variable x3. By performing the integral transformation of Eq. (7a) with respect to the selected space coordinates \({\mathbf{x}}^{*} = \{ x_{1} ,x_{2} \}\), one obtains the following transformed system dependent on the remaining variables \(t\) and \(x_{3}\):

$$\frac{{\partial \bar{T}_{i} (x_{3} ,t)}}{\partial t} + \mu_{i}^{2} \bar{T}_{i} (x_{3} ,t) = \bar{g}_{i} (x_{3} ,t,\overline{{\mathbf{T}}} ),i = 1,2, \ldots ,\quad {\text{x}}_{3} \in V_{3} , t > 0,$$
(8a)
$$\bar{g}_{i} (x_{3} ,t,\overline{{\mathbf{T}}} ) = \int\limits_{{V^{*} }} {\uppsi_{i} ({\mathbf{x}}^{*} )P({\mathbf{x}}^{*} ,x_{3} ,t,\overline{{\mathbf{T}}} )dv^{*} } + \int\limits_{{S^{*} }} {\phi ({\mathbf{x}}^{*} ,x_{3} ,t,T)} \left[ {\frac{{\uppsi_{i} ({\mathbf{x}}^{*} ) - k({\mathbf{x}}^{*} )\frac{{\partial \uppsi_{i} ({\mathbf{x}}^{*} )}}{{\partial {\mathbf{n}}^{*} }}}}{{\alpha \left( {{\mathbf{x}}^{*} } \right) + \beta \left( {{\mathbf{x}}^{*} } \right)}}} \right]ds^{*}$$
(8b)
$$\bar{T}_{i} (x_{3} ,0) = \bar{f}_{i} (x_{3} ) \equiv \int\limits_{{V^{*} }} {w({\mathbf{x}}^{*} ){\kern 1pt} \uppsi_{i} ({\mathbf{x}}^{*} )f({\mathbf{x}})dv^{*} }$$
(8c)
$$\begin{aligned} \left[ {\lambda (x_{3} ) + ( - 1)^{l + 1} \gamma (x_{3} )\frac{\partial }{{\partial {\kern 1pt} x_{3} }}} \right]\bar{T}_{i} (x_{3} ,t) & = \overline{\varphi }_{{\ddot{i}}} (x_{3} ,t,\overline{{\mathbf{T}}} ) \equiv \int\limits_{{\text{v}^{*} }} {w({\mathbf{x}}^{*} ){\kern 1pt} \uppsi_{i} ({\mathbf{x}}^{*} )\varphi ({\mathbf{x}}^{*} ,x_{3} ,t,\overline{{\mathbf{T}}} )dv^{*} } , \\ & \quad x_{3} \in S_{3} = \{ x_{3,l} \} ,l = 0,1,t > 0 \\ \end{aligned}$$
(8d,e)

Equation (8a–e) form an infinite coupled system of nonlinear partial differential equations for the transformed potentials, \(\bar{T}_{i} (x_{3} ,t).\) After truncation to a sufficiently large finite order, this PDE system can be numerically solved. For instance, the Mathematica system provides the routine NDSolve, which implements the Method of Lines in the numerical solution of this problem, under automatic absolute and relative error control.

3.2 Convective Eigenvalue Problems

Quite recently, an alternative solution was proposed adopting a convective eigenvalue problem, again either linear or nonlinear, that through a coefficient transformation could allow to rewrite Eq. (6) as a generalized diffusion problem [45]. Consider that the convective term coefficient vector u can be represented in the three-dimensional situation by the three components {ux, uy, uz}, here illustrating the transformation in the Cartesian coordinates system, x = {x, y, z}. Then, Eq. (6) can be rewritten in the generalized diffusive form as

$$\begin{aligned} w^{*} ({\mathbf{x}},t,T)\frac{{\partial T({\mathbf{x}},t)}}{\partial t} = \frac{1}{{\hat{k}_{x} ({\mathbf{x}},t,T)}}\frac{\partial }{\partial x}[\hat{k}_{x} ({\mathbf{x}},t,T)\frac{{\partial T({\mathbf{x}},t)}}{\partial x}] \hfill \\ + \frac{1}{{\hat{k}_{y} ({\mathbf{x}},t,T)}}\frac{\partial }{\partial y}[\hat{k}_{y} ({\mathbf{x}},t,T)\frac{{\partial T({\mathbf{x}},t)}}{\partial y}] \hfill \\ + \frac{1}{{\hat{k}_{z} ({\mathbf{x}},t,T)}}\frac{\partial }{\partial z}[\hat{k}_{z} ({\mathbf{x}},t,T)\frac{{\partial T({\mathbf{x}},t)}}{\partial z}] \hfill \\ - d^{*} ({\mathbf{x}},t,T)T({\mathbf{x}},t) \hfill \\ + P^{*} ({\mathbf{x}},t,T),\quad {\mathbf{x}} \in V,\quad t > 0 \hfill \\ \end{aligned}$$
(9a)

where

$$\begin{aligned} w^{*} ({\mathbf{x}},t,T) & = w({\mathbf{x}},t,T)/k({\mathbf{x}},t,T);\quad d^{*} ({\mathbf{x}},t,T) = d({\mathbf{x}},t,T)/k({\mathbf{x}},t,T); \\ P^{*} ({\mathbf{x}},t,T) & = P({\mathbf{x}},t,T)/k({\mathbf{x}},t,T);\quad {\mathbf{u}}^{{\mathbf{*}}} ({\mathbf{x}},t,T) = \frac{1}{{k({\mathbf{x}},t,T)}}\left[ {{\mathbf{u}}({\mathbf{x}},t,T) - \nabla k({\mathbf{x}},t,T)} \right]; \\ \hat{k}({\mathbf{x}},t,T) & = \hat{k}_{x} ({\mathbf{x}},t,T)\hat{k}_{y} ({\mathbf{x}},t,T)\hat{k}_{z} ({\mathbf{x}},t,T) \\ \hat{k}_{x} ({\mathbf{x}},t,T) & = e^{{ - \int {u_{x}^{*} ({\mathbf{x}},t,T)dx} }} ;\quad \hat{k}_{y} ({\mathbf{x}},t,T) = e^{{ - \int {u_{y}^{*} ({\mathbf{x}},t,T)dy} }} ;\quad \hat{k}_{z} ({\mathbf{x}},t,T) = e^{{ - \int {u_{z}^{*} ({\mathbf{x}},t,T)dz} }} \\ \end{aligned}$$
(9b-i)

In the special simpler case when the transformed diffusion coefficients are functions of only the corresponding space coordinate, or \(\hat{k}_{x} ({\mathbf{x}},t,T) = \hat{k}_{x} (x),\quad \hat{k}_{y} ({\mathbf{x}},t,T) = \hat{k}_{y} (y);\quad \hat{k}_{z} ({\mathbf{x}},t,T) = \hat{k}_{z} (z),\) with the consequent restrictions on the related coefficients k and u, a diffusion formulation is constructed which leads to a self-adjoint eigenvalue problem [45]. Alternatively, one may seek an adjoint eigenvalue problem that allows for the construction of a biorthogonal eigenfunctions set. This convective eigenvalue problem solution path was recently implemented in the analysis of conjugated heat transfer problems, also with significant convergence rates improvement [46].

4 Vector Eigenfunction Expansion

Although flow problems governed either by the boundary layer or full Navier–Stokes equations formulations can be cast into the general form of Eq. (6), with corresponding initial and boundary conditions, their GITT treatment deserves some special considerations that are here briefly reviewed, while the most recent developments are pointed out.

As mentioned before, the first GITT solution of the boundary layer equations was proposed in [24], in the primitive variables formulation; while the Navier–Stokes equations were first solved by GITT in [25], but preferring instead the streamfunction-only formulation, which eliminates the pressure field and automatically satisfies the continuity equation, while introducing a fourth-order differential eigenvalue problem. A number of contributions then followed extending the applicability of the GITT to different classes of flow problems, also considering the GITT solution for the Navier–Stokes equations in the primitive variables formulation [47], including, for instance, transient problems, compressible flow, three-dimensional formulations, variable physical properties, non-Newtonian fluids, porous and partially porous media, irregular regions, MHD flows, among others, as reviewed in [39].

Recently, a unified framework was proposed, based on a vector eigenfunction expansion [48], which includes the streamfunction formulation treatment as a special case, while generalizing the GITT in dealing with heterogeneous media and three-dimensional flow problems. The vector eigenfunction expansion represents all velocity components with one set of transformed potentials and an appropriately chosen vector eigenfunction basis, while the velocity vector field can be interpreted as the result of the influence of an infinite number of vortices disturbing a base flow. Consider the transient Navier–Stokes equations for incompressible flow, in dimensionless vector form:

$$\nabla \cdot {\mathbf{u}} = 0,\quad {\mathbf{x}} \in V$$
(10a)
$$\frac{{\partial {\mathbf{u}}}}{\partial t} + \nabla \cdot \left( {{\mathbf{u}} \otimes {\mathbf{u}}} \right) = - \nabla p + \frac{1}{{\text{Re}}}\nabla^{2} {\mathbf{u}} + {\mathbf{b}},\quad {\mathbf{x}} \in V$$
(10b)

where V represents the domain occupied by the Newtonian fluid, u is the dimensionless velocity vector, p is the dimensionless pressure field, Re is the Reynolds number, \({\mathbf{b}}\) is a volumetric source term.

The first step in the GITT solution, as usual, is the proposition of a filtering solution to reduce the importance of source terms, specially to homogenize the boundary conditions, in the form:

$${\mathbf{u}}\left( {{\mathbf{x}},t} \right) = {\hat{\mathbf{u}}}\left( {{\mathbf{x}},t} \right) + {\mathbf{u}}_{{\mathbf{f}}} \left( {{\mathbf{x}};t} \right)$$
(11)

The vector eigenfunction expansion for the filtered velocity field is then proposed as

$${\hat{\mathbf{u}}}\left( {{\mathbf{x}},t} \right) = \sum\limits_{i = 1}^{\infty } {\bar{u}_{i} \left( t \right)\left( {\nabla \times {\tilde{\varvec{\Phi}}}_{i} } \right)}$$
(12)

where Eq. (12) warrants mass conservation, as in the streamfunction-only formulation, dropping the need to further deal with Eq. (10a). A self-adjoint fourth-order vector eigenvalue problem, extracted from the analytical solution for the limiting linear situation of Re → 0 (Stoke’s flow), is given by [49]:

$$\nabla^{2} \left( {\nabla \times \nabla \times {\tilde{\varvec{\Phi}}}_{i} } \right) + \lambda_{i}^{2} \left( {\nabla \times \nabla \times {\tilde{\varvec{\Phi}}}_{i} } \right) = {\mathbf{0}}$$
(13)

The orthogonality property of the eigenfunction from Eq. (13) allows for the proposition of a transformed velocity, in the form:

$$\bar{u}_{i} \left( t \right) = \int\limits_{V} {\left( {\nabla \times {\tilde{\varvec{\Phi}}}_{i} } \right) \cdot {\hat{\mathbf{u}}}\left( {{\mathbf{x}},t} \right)dv}$$
(14)

Equations (12) and (14) thus provide the inverse-transform pair required for the integral transformation process, following the same formalism as in the usual application of the GITT above described. The integral transformation of the Navier–Stokes equations, with the curl of the solution of Eq. (13) as kernel, then proceeds, leading to the transformed problem below, as detailed in [49]:

$$\frac{{d\bar{u}_{i} }}{dt} + \frac{{\lambda_{i}^{2} }}{\text{Re}}\bar{u}_{i} \left( t \right) + \sum\limits_{k = 1}^{\infty } {\sum\limits_{j = 1}^{\infty } {A_{ijk} \bar{u}_{j} \left( t \right)\bar{u}_{k} \left( t \right)} } + \sum\limits_{j = 1}^{\infty } {B_{ij} \left( t \right)\bar{u}_{j} \left( t \right)} = \bar{g}_{j} \left( t \right)$$
(15a)

with integral coefficients given by

$$A_{ijk} = - \int\limits_{V} {\nabla \left( {\nabla \times {\tilde{\varvec{\Phi}}}_{i} } \right) \cdot \left[ {\left( {\nabla \times {\tilde{\varvec{\Phi}}}_{j} } \right) \otimes \left( {\nabla \times {\tilde{\varvec{\Phi}}}_{k} } \right)} \right]dv}$$
(15b)
$$B_{ij} \left( t \right) = - \int\limits_{V} {\nabla \left( {\nabla \times {\tilde{\varvec{\Phi}}}_{i} } \right) \cdot \left[ {\left( {\nabla \times {\tilde{\varvec{\Phi}}}_{j} } \right) \otimes {\mathbf{u}}_{{\mathbf{f}}} + {\mathbf{u}}_{{\mathbf{f}}} \otimes \left( {\nabla \times {\tilde{\varvec{\Phi}}}_{j} } \right)} \right]dv}$$
(15c)
$$\bar{g}_{i} \left( t \right) = \int\limits_{V} {\left( {\nabla \times {\tilde{\varvec{\Phi}}}_{i} } \right) \cdot \left\{ {{\mathbf{b}} + \frac{1}{\text{Re}}\nabla^{2} {\mathbf{u}}_{{\mathbf{f}}} - \frac{{\partial {\mathbf{u}}_{{\mathbf{f}}} }}{\partial t} - \nabla \cdot \left( {{\mathbf{u}}_{{\mathbf{f}}} \otimes {\mathbf{u}}_{{\mathbf{f}}} } \right)} \right\}}$$
(15d)

It is noteworthy that the automatic elimination of the pressure gradient term from the transformed problem is achieved through the use of the proper integral transform kernel, thus dropping the need to directly deal with the pressure term. Notwithstanding, the pressure field can be determined a posteriori from the original Navier–Stokes equations, once the velocity field is known.

5 Eigenvalue Problems and Irregular Domains

As seen in the previous sections, the accurate solution of the associated eigenvalue problems is a crucial step in the application of the GITT approach. Except for those simpler cases in which an exact analytical solution is available for the Sturm–Liouville problem, it is necessary to implement a more general and automatic procedure for its computational–analytical solution. The GITT itself can be used for this purpose, including the treatment of nonlinear eigenvalue problems and irregular domains, as now reviewed. Thus, consider the nonlinear eigenvalue problem defined in region V and boundary surface S:

$$L\uppsi ({\mathbf{x}};t) = \mu^{2} (t)w({\mathbf{x}},t,T)\uppsi ({\mathbf{x}};t),\quad {\mathbf{x}} \in V$$
(16a)
$$B\uppsi ({\mathbf{x}};t) = 0,\quad {\mathbf{x}} \in S$$
(16b)

where the operators L and B are given by

$$L = - \nabla \cdot \left( {k({\mathbf{x}},t,T)\nabla } \right) + d({\mathbf{x}},t,T)$$
(16c)
$$B = \alpha ({\mathbf{x}},t,T) + \beta ({\mathbf{x}},t,T)k({\mathbf{x}},t,T)\frac{\partial }{{\partial {\mathbf{n}}}}$$
(16d)

The problem given by Eq. (16a–d) can be rewritten as

$$\hat{L}\uppsi ({\mathbf{x}};t) = \left( {\hat{L} - L} \right)\uppsi ({\mathbf{x}};t) + \mu^{2} (t)w({\mathbf{x}},t,T)\uppsi ({\mathbf{x}};t),\quad {\mathbf{x}} \in V$$
(17a)
$$\hat{B}\uppsi ({\mathbf{x}};t) = (\hat{B} - B)\uppsi ({\mathbf{x}};t),\quad {\mathbf{x}} \in S$$
(17b)

where \(\hat{L}\) and \(\hat{B}\) are simpler operators with linear coefficients that define an auxiliary eigenvalue problem of known solution for the eigenvalues, λ, and corresponding eigenfunctions, Ω(x), given by

$$\hat{L} {\Omega} ({\mathbf{x}}) = \lambda^{2} \hat{w}({\mathbf{x}}) {\Omega} ({\mathbf{x}}), \quad {\mathbf{x}} \in V$$
(18a)
$$\hat{B} {\Omega} ({\mathbf{x}}) = 0, \quad {\mathbf{x}} \in S$$
(18b)

where

$$\hat{L} = - \nabla \cdot \left( {\hat{k}({\mathbf{x}})\nabla } \right) + \hat{d}({\mathbf{x}})$$
(18c)
$$\hat{B} = \hat{\alpha }({\mathbf{x}}) + \hat{\beta }({\mathbf{x}})\hat{k}({\mathbf{x}})\frac{\partial }{{\partial {\mathbf{n}}}}$$
(18d)

Problem (18) thus allows definition of the following integral transform pair:

$$\bar{\uppsi }_{i} (t) = \int\limits_{V} {\hat{w}({\mathbf{x}})\tilde{ {\Omega} }_{i} ({\mathbf{x}})\uppsi ({\mathbf{x}};t)dv} ,\quad {\text{transform}}$$
(19a)
$$\uppsi ({\mathbf{x}};t) = \sum\limits_{i = 1}^{\infty } {\tilde{ {\Omega} }_{i} ({\mathbf{x}})\bar{\uppsi }_{i} (t)} ,\quad {\text{inverse}}$$
(19b)

where the normalized auxiliary eigenfunctions and corresponding norms are given by

$$\tilde{ {\Omega} }_{i} ({\mathbf{x}}) = \frac{{ {\Omega}_{i} ({\mathbf{x}})}}{{\sqrt {N_{{ {\Omega}_{i} }} } }},{\text{with}}\quad N_{{ {\Omega}_{i} }} = \int\limits_{V} {\hat{w}({\mathbf{x}}) {\Omega}_{i}^{2} ({\mathbf{x}})dv}$$
(19c, d)

Problem (17) is now operated on with \(\int_{V} {\tilde{ {\Omega} }_{i} ({\mathbf{x}})\left( \cdot \right)} dv,\) to yield the transformed nonlinear algebraic system, truncated to the Mth order, in matrix form, as

$$({\mathbf{A}}(t) + {\mathbf{C}})\left\{ {{\bar{\mathbf{\uppsi }}}(t)} \right\} = {\varvec{\upmu}}^{{\mathbf{2}}} (t){\mathbf{B}}(t)\left\{ {{\bar{\mathbf{\uppsi }}}(t)} \right\}$$
(20a)

with the elements of the M x M matrices and vector μ(t) given by

$$a_{ij} (t) = - \int\limits_{S} {\gamma_{i} (\hat{B} - B)\tilde{ {\Omega} }_{j} ({\mathbf{x}})ds} - \int\limits_{V} {\tilde{ {\Omega} }_{i} ({\mathbf{x}})(\hat{L} - L)\tilde{ {\Omega} }_{j} ({\mathbf{x}})dv}$$
(20b)
$$c_{ij} = \lambda_{i}^{2} \delta_{ij}$$
(20c)
$$b_{ij} (t) = \int\limits_{V} {w({\mathbf{x}},t,T)\tilde{ {\Omega} }_{i} ({\mathbf{x}})\tilde{ {\Omega} }_{j} ({\mathbf{x}})dv}$$
(20d)
$${\varvec{\upmu}}(t) = \left\{ {\mu_{1} (t),\mu_{2} (t), \ldots ,\mu_{M} (t)} \right\}$$
(20e)
$$\gamma_{i} = \frac{{\tilde{ {\Omega} }_{i} ({\mathbf{x}}) - \hat{k}({\mathbf{x}})\frac{{\partial \tilde{ {\Omega} }_{i} ({\mathbf{x}})}}{{\partial {\mathbf{n}}}}}}{{\hat{\alpha }({\mathbf{x}}) + \hat{\beta }({\mathbf{x}})}}$$
(20f)

The nonlinear algebraic eigenvalue problem, Eq. (20a–f), should now be solved simultaneously with the transformed system, Eq. (5a–f), or the equivalent for convection–diffusion problems, yielding the time evolution of the transformed potentials, eigenvalues and eigenfunctions. For linear eigenvalue problems, system (18) is solved only once, prior to the numerical solution of the transformed system (5).

The expressions here derived are valid for any arbitrary region V and corresponding surface S, and essentially require the evaluation of the volume and surface integrals defined in the transformed coefficients and source terms of the transformed ODE system, Eq. (5d–f), and in the coefficients of the transformed eigenvalue problem, Eq. (20b, d). In the more general situation of complex geometric configurations, domain decomposition techniques can be handy in the automatic computational evaluation of such integral transformations. However, in a fairly wide class of problems for which the domain bounding surfaces, in one coordinate, can successively be expressed as functions of the remaining space variables, the volume integral can be organized so as to permit a direct integration of the irregular region [50, 51], including the generalization to nonlinear moving boundaries, i.e. V(t) and S(t) [52]. For instance, considering such a region in the Cartesian coordinates system, the bounding surfaces in each spatial coordinate, may be written as

$$x_{0} (t) \le x \le x_{1} (t),\quad y_{0} (x,t) \le y \le y_{1} (x,t),\quad z_{0} (x,y,t) \le z \le z_{1} (x,y,t)$$
(21a)

Then, the auxiliary eigenfunction (or directly the original eigenfunction or the potential), can be expressed as an eigenfunction expansion of the product of one-dimensional eigenfunctions in each coordinate, as

$$\tilde{ {\Omega} }_{n} ({\mathbf{x}};t) = \tilde{X}_{j} (x;t)\tilde{Y}_{k} (y;x,t)\tilde{Z}_{m} (z;x,y,t)$$
(21b)

and the corresponding integral transform pair, in terms of this auxiliary eigenfunction basis, would be

$$\bar{\uppsi }_{n} (t) = \int\limits_{V(t)} {\hat{w}({\mathbf{x}})\tilde{ {\Omega} }_{n} ({\mathbf{x}};t)\uppsi ({\mathbf{x}};t)dv} ,\quad {\text{transform}}$$
(21c)
$$\uppsi ({\mathbf{x}};t) = \sum\limits_{n = 1}^{\infty } {\tilde{ {\Omega} }_{n} ({\mathbf{x}};t)\bar{\uppsi }_{n} (t)} ,\quad {\text{inverse}}$$
(21d)

while the volume integrals are undertaken in the appropriate sequence as

$$\int\limits_{V(t)} {( - )\tilde{ {\Omega} }_{n} ({\mathbf{x}};t)dv} \equiv \int\limits_{{x_{0} (t)}}^{{x_{1} (t)}} {\{ \int\limits_{{y_{0} (x,t)}}^{{y_{1} (x,t)}} {[\int\limits_{{z_{0} (x,y,t)}}^{{z_{1} (x,y,t)}} {( - )\tilde{Z}_{m} (z;x,y,t)dz} ]\tilde{Y}_{k} (y;x,t)dy} \} \tilde{X}_{j} (x;t)dx}$$
(21e)

The special case of boundary surfaces mapped as functions of the space coordinates, as discussed above, is particular advantageous in the analytical or semi-analytical evaluation of the transformation integrals [53], and an appropriate choice of the positioning of the coordinates system may allow for this direct integration in many situations. In any case, as discussed above, domain decomposition with numerical or semi-analytical integration provides a more general-purpose algorithm for determination of the transformed coefficients and source terms [42, 54].

6 Single Domain Formulation

In dealing with heterogeneous media, either defined in regular or irregular subregions, the derivation task of the integral transform process can become tedious, especially for multiple regions. Besides, the computational task itself can become cumbersome, since many transformed subregions will lead to a large coupled transformed system to be numerically solved for. Therefore, a single domain formulation strategy was proposed in [55], originally aimed at solving conjugated heat transfer problems when solid and fluid subregions would require separate integral transformations or solving coupled eigenvalue problems. The strategy is based in rewriting the diffusion or convection–diffusion equations for each subdomain, with their respective physical properties and source terms, as one single formulation for the whole region, with spatially variable coefficients and functions that vary abruptly at the interfaces of the subregions, representing the original heterogeneities. This approach was then employed in various classes of conjugated heat transfer problems [56,57,58], heat conduction applications [59], natural convection in partially porous media [60], and convective mass transfer problems [61].

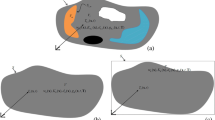
To illustrate the single domain formulation strategy, consider a nonlinear diffusion problem, defined in a multi-region configuration that is formed by nV subregions of volumes Vl, l = 1, 2, …, nV, with potential and flux continuity at the interfaces, as illustrated in Fig. 1a, in the form

Fig. 1
figure 1

a Diffusion or convection–diffusion problem in a complex multidimensional configuration with nV sub-regions; b Single domain representation keeping the original overall domain

Full size image
$$\begin{aligned} w_{l} ({\mathbf{x}},t,T_{l} )\frac{{\partial T_{l} ({\mathbf{x}},t)}}{\partial t} = \nabla \cdot \left[ {k_{l} ({\mathbf{x}},t,T_{l} )\nabla T_{l} ({\mathbf{x}},t)} \right] - d_{l} ({\mathbf{x}},t,T_{l} )T_{l} ({\mathbf{x}},t) \hfill \\ + P_{l} ({\mathbf{x}},t,T_{l} ),\quad {\mathbf{x}} \in V_{l} ,t > 0,l = 1,2, \ldots ,n_{V} \hfill \\ \end{aligned}$$
(22a)

with initial, interface and boundary conditions given, respectively, by

$$T_{l} ({\mathbf{x}},0) = f_{l} ({\mathbf{x}}),\quad {\mathbf{x}} \in V_{l}$$
(22b)
$$T_{l} ({\mathbf{x}},t) = T_{m} ({\mathbf{x}},t);\quad k_{l} ({\mathbf{x}},t,T_{l} )\frac{{\partial T_{l} ({\mathbf{x}},t)}}{{\partial {\mathbf{n}}}} = k_{m} ({\mathbf{x}},t,T_{m} )\frac{{\partial T_{m} ({\mathbf{x}},t)}}{{\partial {\mathbf{n}}}},\quad {\mathbf{x}} \in S_{l,m} , t > 0$$
(22c, d)
$$\left[ {\alpha_{l} ({\mathbf{x}},t,T_{l} ) + \beta_{l} ({\mathbf{x}},t,T_{l} )k_{l} ({\mathbf{x}},t,T_{l} )\frac{\partial }{{\partial {\kern 1pt} {\mathbf{n}}}}} \right]T_{l} ({\mathbf{x}},t) = \phi_{l} ({\mathbf{x}},t,T_{l} ),\quad {\mathbf{x}} \in S_{l} , t > 0$$
(22e)

where n denotes the outward-drawn normal to the interfaces among the different subregions, Sl,m, and at the external surfaces, Sl.

The idea in the single domain reformulation is, as illustrated in Fig. 1.b, to merge all the Eq. (22a) into one single equation, for the whole region V, and to represent the various properties and source terms in each subregion as one single set of nonlinear space variable coefficients accounting for the abrupt variations at the interfaces. Then, problem (22) is simply rewritten in identical form to problem (1), with the appropriate reformulation of the coefficients, thus requiring only a single integral transformation process, yielding a single transformed ODE system, and carrying the information on the domain heterogeneity to the associated single region eigenvalue problem with spatially variable coefficients.

7 Test Cases

The chosen test cases to illustrate the hybrid GITT methodology are closely related to the suggestions of Prof. Spalding, which motivated the present review. First, laminar flow inside a corrugated microchannel is analyzed [62], followed by the convective heat transfer analysis. This flow problem has been previously analyzed through the GITT methodology [63], but recently it has been observed that the domain singularity at the corrugated duct inlet could introduce some numerical disturbances, which are here corrected for. Also, the heat transfer problem was also previously considered, including upstream and downstream axial diffusion effects, but employing an analytical approximate velocity field representation for very low Reynolds numbers [64]. More recently, the substrate conjugation in the micro-system thermal behavior was also accounted for [37, 65], again by considering a simplified velocity field for low Reynolds number. Here, the full set of Navier–Stokes equations for the fluid flow are solved for and employed in the solution of the corresponding energy equation for the fluid. Second, the analysis of conjugate heat transfer problems is considered to illustrate the single domain reformulation approach in dealing with heterogeneous and irregular regions. A multi-stream perfused substrate configuration with channels of polygonal cross section is then considered and handled through the partial transformation scheme [58]. The adoption of a convective eigenvalue problem in handling conjugated heat transfer is also demonstrated, considering a transient two-dimensional formulation in the total transformation scheme [66].

7.1 Steady Heat Transfer and Fluid Flow in Corrugated Channel

The first test case deals with the steady forced convection heat transfer in a wavy wall channel. The geometrical duct configuration and the physical aspects of this problem are similar to that analyzed in the work of Wang and Chen [62]. Thus, we consider incompressible laminar flow of a Newtonian fluid within a wavy irregular channel in simultaneous hydrodynamic and thermal developments, with fully developed velocity and uniform temperature profiles at the inlet. Viscous dissipation is disregarded and constant physical properties are imposed. The channel walls are maintained at a uniform dimensional temperature T*w. Figure 2 shows a schematic representation of the problem and the respective boundary conditions. This problem is governed by the continuity, Navier–Stokes and energy equations in two dimensions, which in terms of the streamfunction-only formulation is written in dimensionless form as

Fig. 2
figure 2

Geometric configuration and boundary conditions for the problem of forced convection heat transfer within a wavy walls channel

Full size image
$$\frac{\partial \uppsi }{\partial y}\left( {\frac{{\partial^{3} \uppsi }}{{\partial x^{3} }} + \frac{{\partial^{3} \uppsi }}{{\partial x\partial y^{2} }}} \right) - \frac{\partial \uppsi }{\partial x}\left( {\frac{{\partial^{3} \uppsi }}{{\partial x^{2} \partial y}} + \frac{{\partial^{3} \uppsi }}{{\partial y^{3} }}} \right) = \frac{1}{\text{Re}}\left( {\frac{{\partial^{4} \uppsi }}{{\partial x^{4} }} + 2\frac{{\partial^{4} \uppsi }}{{\partial x^{2} \partial y^{2} }} + \frac{{\partial^{4} \uppsi }}{{\partial y^{4} }}} \right)$$
(23a)
$$\frac{\partial \uppsi }{\partial y}\frac{\partial T}{\partial x} - \frac{\partial \uppsi }{\partial x}\frac{\partial T}{\partial y} = \frac{1}{{\text{Re} \Pr }}\left( {\frac{{\partial^{\text{2}} T}}{{\partial x^{\text{2}} }} + \frac{{\partial^{\text{2}} T}}{{\partial y^{\text{2}} }}} \right)$$
(23b)

subjected to the following inlet, outlet, and boundary conditions:

$$\uppsi (0,y) = k_{1} + \frac{3}{2}\left( {y - \frac{{y^{3} }}{3}} \right) + 1;\quad \frac{\partial \uppsi (0,y)}{\partial x} = 0;\quad T({0},y) = 1$$
(23c–e)
$$\frac{{\partial \upomega (x_{out} ,y)}}{\partial x} = \frac{{\partial^{3} \uppsi (x_{out} ,y)}}{{\partial x^{3} }} + \frac{{\partial^{3} \uppsi (x_{out} ,y)}}{{\partial x\partial y^{2} }} = 0;\quad \frac{{\partial \uppsi (x_{out} ,y)}}{\partial x} = 0;\quad \frac{{\partial T(x_{out} ,y)}}{\partial x} = 0$$
(23f–h)
$$\uppsi (x, - y_{1} (x)) = k_{1} ;\quad \frac{{\partial \uppsi (x, - y_{1} (x))}}{{\partial {\mathbf{n}}}} = 0;\quad T(x, - y_{1} (x)) = 0$$
(23i–k)
$$\uppsi (x,y_{2} (x)) = k_{2} ;\quad \frac{{\partial \uppsi (x,y_{2} (x))}}{{\partial {\mathbf{n}}}} = 0;\quad T(x,y_{2} (x)) = 0$$
(23l–n)

where n, k1, and k2 represent the outward-drawn normal vector to the channel wall and the values of the streamfunction at the duct walls, respectively, which are associated through the overall mass balance with the volumetric flow rate per unit length Q, as k2 = Q+k1. In the streamfunction-only formulation the continuity equation is automatically satisfied, and the velocity components are related to the streamfunction through its definition:

$$u = \frac{\partial \uppsi }{\partial y};\quad v = - \frac{\partial \uppsi }{\partial x}$$
(24a, b)

Also, the following dimensionless groups were employed in Eqs. (22a–e) to (23a–n):

$$\begin{aligned} x = \frac{{x^{*} }}{b};\quad y = \frac{{y^{*} }}{b};\quad {\text{y}}_{1} (x) = \frac{{{\text{y}}_{1}^{*} (x^{*} )}}{b};\quad {\text{y}}_{2} (x) = \frac{{{\text{y}}_{2}^{*} (x^{*} )}}{b}; \hfill \\ u = \frac{{u^{*} }}{{u_{0} }};\quad v = \frac{{v^{*} }}{{u_{0} }};\quad T = \frac{{T^{*} - T_{w}^{*} }}{{T_{0}^{*} - T_{w}^{*} }};\quad \text{Re} = \frac{{u_{0} b}}{\nu };\quad \Pr = \frac{\nu }{\upalpha } \hfill \\ \end{aligned}$$
(25a–h)

where b is the half-spacing between the plates at the straight sections, \(u_{0}\) is the average velocity at the channel inlet, y1(x) and y2(x) are the functions that describe the wall contours, Re and Pr are the Reynolds and Prandtl numbers, respectively.

The functions that define the channel walls are here taken as

$$y_{2} (x) = - y_{1} (x) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{for}}\;{0} \le x \le x_{s} } \hfill \\ {1 + \upalpha \sin [\uppi (x - x_{s} )],} \hfill & {{\text{for}}\;x_{\text{s}} \le x \le x_{l} } \hfill \\ {1,} \hfill & {{\text{for}}\;x_{l} \le x \le x_{out} } \hfill \\ \end{array} } \right.$$
(26)

where α = a/b is the dimensionless channel amplitude, and xs =  x*s/b and xl =  x*l/b are the dimensionless lengths for the beginning and the end of the wavy walls, respectively, and xout =  x*out/b is the dimensionless channel length, which is taken equal to 20. The geometry selected for illustration has the parameters xs = 3 and xl = 15, yielding six complete sinusoidal waves in the corrugated part of the channel.

In order to avoid incorrect solutions stemming from the discontinuity of the derivatives of the function defined in Eq. (26), an approximate continuous unit step function is introduced to smooth the transition between the straight and sinusoidal sections of the channel depicted in Fig. 2. The modified geometry is then given by

$${\text{y}}_{2} (x) = - {\text{y}}_{1} (x) = 1 + \upalpha \sin [\uppi (x - x_{s} )]\left[ {U_{s} \left( {x,x_{s} } \right) - U_{s} \left( {x,x_{1} } \right)} \right]$$
(27a)

with a continuous approximate unit step written as,

$$U_{s} \left( {x,x^{\prime}} \right) = \frac{1}{{1 + \exp \left[ { - \beta \left( {x - x^{\prime}} \right)} \right]}}$$
(27b)

where β is an adjustable parameter.

Simplifying Eq. (13) for two-dimensional problems in the Cartesian coordinate system, there is only one component of \({\tilde{\varvec{\Phi}}}_{i}\) different from zero, resulting in a scalar eigenvalue problem [49]. For that case, the curl of the vector base automatically reproduces the streamfunction-only formulation [48]. Therefore, the problem defined by Eqs. (23a–n) is solved via the GITT approach by eliminating the transversal coordinate through integral transformation, considering a biharmonic-type fourth-order eigenvalue problem for the flow problem and a classical Sturm–Liouville problem for the temperature problem, both yielding x-variable eigenvalues and eigenfunctions due to the irregular contours of the wavy walls.

7.2 Conjugated Heat Transfer

The second application is aimed at illustrating the single domain reformulation, the partial transformation scheme, and the convective eigenvalue problem alternative in handling conjugated heat transfer. Consider the thermally developing flow inside one or multiple straight channels of arbitrarily irregular cross section, perfusing a rectangular prismatic substrate. The single domain dimensionless formulation for the energy balance is given by

$$\begin{aligned} W(X,Y)\frac{\partial \theta }{\partial \tau } + U(X,Y)\frac{\partial \theta }{\partial X} & = \frac{K(X,Y)}{{{\text{Pe}}^{2} }}\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{\partial }{\partial Y}\left( {K(X,Y)\frac{\partial \theta }{\partial Y}} \right) + \frac{\partial }{\partial Z}\left( {K(X,Y)\frac{\partial \theta }{\partial Z}} \right), \\ & \quad 0 < X < L_{X} ,\quad 0 < Y < L_{Y} ,\quad 0 < Z < L_{Z}, \;\tau > 0 \\ \end{aligned}$$
(28a)

where

$$U(X,Y) = \left\{ {\begin{array}{*{20}l} {U_{f} (X,Y),} \hfill & {\text{in fluid region}} \hfill \\ {0,} \hfill & {\text{in solid region}} \hfill \\ \end{array} } \right.;\quad K(X,Y) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\text{in fluid region}} \hfill \\ {k_{s} /k_{f} ,} \hfill & {\text{in solid region}} \hfill \\ \end{array} } \right.$$
(28b, c)
$$W(X,Y) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\text{in fluid region}} \hfill \\ {w_{s} /w_{f} ,} \hfill & {\text{in solid region}} \hfill \\ \end{array} } \right.$$
(28d)

with the following dimensionless groups:

$$\begin{aligned} X = \frac{{x/L_{ref} }}{\text{RePr}} = \frac{x}{{L_{ref} {\text{Pe}}}};\quad Y = \frac{y}{{L_{ref} }};\quad Z = \frac{z}{{L_{ref} }}; \hfill \\ U = \frac{u}{{4u_{av} }};\quad \theta = \frac{{T - T_{in} }}{{T_{w} - T_{in} }};\quad K = \frac{k}{{k_{f} }};\quad W = \frac{w}{{w_{f} }}{\text{Re}} = \frac{{u_{av} 4L_{ref} }}{\nu }; \hfill \\ \Pr = \frac{\nu }{\alpha };\quad {\text{Pe}} = {\text{Re}}\Pr = \frac{{u_{av} 4L_{ref} }}{\alpha };\quad \alpha = \frac{{k_{f} }}{{w_{f} }};\quad \tau = \frac{\alpha t}{{L_{ref}^{2} }} \hfill \\ \end{aligned}$$
(28e)

where \(x\) is the longitudinal coordinate, \(y\) and \(z\) are the transversal space coordinates (height and width, respectively). In order to more closely illustrate the conjugated heat transfer application, two examples are analyzed. The first example considers multiple parallel fluid streams perfusing a substrate through channels with polygonal cross sections, illustrating the handling of arbitrary geometries and the partial integral transformation procedure, while the second one considers heat and fluid flow inside parallel plates, illustrating the total integral transformation procedure and the convergence gains achieved with the convective eigenvalue problem alternative previously discussed.

7.2.1 Multiple Irregular Regions

The transversal view of the multi-stream perfused substrate with parallel channels of irregular cross section is illustrated in Fig. 3.

Fig. 3
figure 3

Schematic representation of the multi-stream perfused substrate cross section

Full size image

The substrate and fluid inlet region is assumed to be at the dimensionless temperature \(\theta_{in} = 0,\) the outlet surface is considered adiabatic, and the four lateral surfaces are considered at the prescribed dimensionless temperature \(\theta_{w} = 1.\) In order to obtain the velocity field inside the fluid flow regions, \(u_{f} (Y,Z),\) the single domain formulation was also employed for the momentum equation in the longitudinal direction (\(X\)), assuming that the flow is fully developed and governed by

$$\frac{\partial }{\partial Y}\left( {\nu (Y,Z)\frac{{\partial u_{f} (Y,Z)}}{\partial Y}} \right) + \frac{\partial }{\partial Z}\left( {\nu (Y,Z)\frac{{\partial u_{f} (Y,Z)}}{\partial Z}} \right) - \frac{C(Y,Z)}{\rho (Y,Z)} = 0$$
(29a)

with

$$\begin{aligned} C(Y,Z) = \left\{ {\begin{array}{*{20}l} {\frac{dp}{dX} = \Delta p/L_{X} ,} \hfill & {\text{ in the fluid region}} \hfill \\ {0,} \hfill & {\text{in the solid region}} \hfill \\ \end{array} } \right.; \hfill \\ \nu (Y,Z) = \left\{ {\begin{array}{*{20}l} {\nu_{f} ,} \hfill & {\text{in the fluid region}} \hfill \\ {\nu_{s} \to \infty ,} \hfill & {\text{in the solid region}} \hfill \\ \end{array} } \right. \hfill \\ \end{aligned}$$
(29b, c)
$$\rho (Y,Z) = \left\{ {\begin{array}{*{20}l} {\rho_{f} ,} \hfill & {\text{in the fluid region}} \hfill \\ {\rho_{s} ,} \hfill & {\text{in the solid region}} \hfill \\ \end{array} } \right.$$
(29d)

where νf and ρf stand for the kinematic viscosity and density of the fluid, and νs and ρs for the solid. For νs it suffices to choose a sufficiently large value, when the value for ρs will no longer affect the final result and the calculated velocities in the solid region will recover the no slip condition, as physically expected. The dimensionless velocity is calculated from Uf =  uf/uav. The solution of problem (29a) is readily handled through GITT based upon an eigenvalue problem with space variable coefficients, as detailed in [58]. The energy equation is solved through the partial transformation scheme, described in Sect. 3.1, in which the longitudinal variable, X, is not integral transformed, leading to a PDE system to be numerically solved, as described in [58].

7.2.2 Convective Eigenvalue Problem

Consider a laminar incompressible internal flow between parallel plates, as illustrated in Fig. 4. In this case, the lateral coordinate \(Z\) can be neglected in Eq. (28a), and the space variable coefficients are function of the Y-coordinate only, leading to a 2D transient problem.

Fig. 4
figure 4

Schematic representation of the transient conjugated heat transfer example

Full size image

The flow is considered fully developed, with known parabolic velocity profile, the inlet surface and the external walls are considered at a prescribed dimensionless temperature \(\theta_{in} = \theta_{w} = 0,\) and the initial condition is taken as \(\theta_{0} = 1.\) Adopting the procedure described in Sect. 3.2, the energy equation can be rewritten in the following generalized diffusive form:

$$\hat{W}\frac{\partial \theta }{\partial \tau } = \frac{{\hat{K}_{Y} }}{{{\text{Pe}}^{2} }}\frac{\partial }{\partial X}\left( {\hat{K}_{X} \frac{\partial \theta }{\partial X}} \right) + \hat{K}_{X} \frac{\partial }{\partial Y}\left( {\hat{K}_{Y} \frac{\partial \theta }{\partial Y}} \right),\quad 0 < Y < L_{Y} ,\quad 0 < X < L_{X} ,\tau > 0$$
(30a)
$$\hat{K}_{X} (X,Y) = e^{{ - \int {{\text{Pe}}^{2} U_{X}^{*} dX} }} ;\;\hat{K}_{Y} (Y) = e^{{ - \int {U_{Y}^{*} dY} }}$$
(30b, c)
$$U_{X}^{*} = \frac{U(Y)}{K(Y)};\quad U_{Y}^{*} = - \frac{1}{K(Y)}\frac{dK(Y)}{dY};\quad \hat{W}(X,Y) = \frac{{W(Y)\hat{K}_{x} (X,Y)\hat{K}_{Y} (Y)}}{K(Y)}$$
(30d–f)

Separation of variables is then applied to problem (28a), yielding the following non-classical eigenvalue problem:

$$\frac{{\hat{K}_{Y} }}{{{\text{Pe}}^{2} }}\frac{\partial }{\partial X}\left( {\hat{K}_{X} \frac{\partial \psi }{\partial X}} \right) + \hat{K}_{X} \frac{\partial }{\partial Y}\left( {\hat{K}_{Y} \frac{\partial \psi }{\partial Y}} \right) + \mu_{i}^{2} \psi = 0,\quad 0 < Y < L_{Y} ,\quad 0 < X < L_{X}$$
(31)

with boundary conditions analogous to the original problem. This eigenvalue problem is non-self-adjoint, meaning the eigenfunctions \(\psi_{i} (X,Y),\) \(i = 1,2,3 \ldots\) , do not follow the same orthogonality property as for the classical Sturm–Liouville problem. Also, the corresponding eigenvalues spectrum is not known a priori and eventually complex quantities may be present. This eigenvalue problem does not allow for explicit analytic solution, but the integral transforms procedure described in Sect. 5 can be employed in its solution. The solution to problem (30) can be written as

$$\theta (X,Y,\tau ) = \sum\limits_{i = 1}^{\infty } {A_{i} \psi_{i} (X,Y)e^{{ - \beta_{i}^{2} t}} }$$
(32)

where the expansion coefficients \(A_{i}\) must be determined from the initial condition. Hence, operating on Eq. (30a) with \(\int_{0}^{1} {\int_{0}^{{L^{*} }} {\psi_{j} (X,Y)\left( \cdot \right)} } dXdY\) at \(\tau = 0\) yields the following system:

$$\begin{gathered} \int\limits_{0}^{{L_{Y} }} {\int\limits_{0}^{{L_{X} }} {\psi _{j} (X,Y)} } dXdY = \sum\limits_{{i = 1}}^{\infty } {A_{i} \int\limits_{0}^{{L_{Y} }} {\int\limits_{0}^{{L_{X} }} {\psi _{i} (X,Y)\psi _{j} (X,Y)} } dXdY} , \hfill \\ i = 1,2,3 \ldots ,\quad j = 1,2,3 \ldots \hfill \\ \end{gathered}$$
(33)

which, after truncated to a finite order N, can be solved for the coefficients \(A_{i}\) , and the expansion given by Eq. (33) can be readily used to calculate the dimensionless temperature \(\theta\) at any position \((X,Y)\) and time τ.

8 Results and Discussion

8.1 Steady Heat Transfer and Fluid Flow in Corrugated Channel

Numerical results are presented for the forced convection heat transfer problem in the wavy walls channel described in Sect. 7.1. For the sake of reporting numerical results, it is considered the case of Re = 400, Pr = 6.93, and α = 0.1. Results for the streamfunction and isotherms along the wavy walls channel are presented. In Fig. 5.a, the streamfunction isolines show that recirculation zones are present in almost all cavities along the duct walls. Figure 5b shows the isotherms, and it can be noticed that the temperature distribution is affected mainly in the vicinity of the channel walls and it remains practically unchanged in the central regions of the channel.

Fig. 5
figure 5

Patterns of a streamlines and b isotherms for Re = 400, Pr = 6.93, and α = 0.1

Full size image

Figure 6 shows the comparison of the present GITT results with those generated by using the software COMSOL Multiphysics, and one may observe a good agreement between the two sets of results. Figure 6a shows the results for the product of the skin-friction coefficient by the Reynolds number, \({\text{C}}_{\text{f}} {\text{Re}} = - \left. {\left( {\frac{{\partial {\text{u}}}}{{\partial {\text{y}}}} + \frac{{\partial {\text{v}}}}{{\partial {\text{x}}}}} \right)} \right|_{{{\text{y}} = {\text{y}}_{2} \left( {\text{x}} \right)}}\) , and one can readily observe the oscillatory behavior for this parameter along the channel. In Fig. 6.b, it is shown the axial velocity component at the centerline, Uc, and it is also noted the expected oscillatory behavior accompanying the distribution of peaks and valleys along the channel, slightly increasing until the flat outlet region of the duct is reached. Finally, Fig. 6.c shows the distribution of the local Nusselt number, Nu, along the channel. One can observe that the Nusselt number increases in the constricted regions and decreases in the diverging ones. This behavior can be explained due to an increase in the average flow velocity and temperature gradients in such constricted areas.

Fig. 6
figure 6

Parameters related to the velocity and temperature fields for Re = 400, Pr = 6.93, and α = 0.1: a Product CfRe; b centerline axial velocity; c local Nusselt number

Full size image

8.2 Conjugated Heat Transfer

Numerical results are now presented for the conjugated heat transfer examples described in Sect. 7.2. As test case, an application with water as the working fluid and acrylic as the channel substrate is here considered, leading to the adopted dimensionless values \(k_{s} /k_{f} = 0.25\) and \(w_{s} /w_{f} = 0.35.\)

8.2.1 Multiple Irregular Regions

The flexibility of the single domain approach in handling arbitrary domains is here illustrated by considering the multi-stream perfused substrate with the five microchannels shown in Fig. 7, which can be modeled as a single domain by properly defining the space variable coefficients so as to capture the five microchannels geometries. The wall and fluid temperature profiles are plotted in Fig. 7a, b in steady-state regime (\(\tau \to \infty\)) for Pe = 1, comparing the GITT and COMSOL solutions for different longitudinal positions, (a) along \(Z,\) at \(Y = 0.2,\) and (b) along \(Y\) at \(Z = 0.\) Both across the thickness of the micro-system and along its width, taking just half of the width due to symmetry, one may observe the perfect adherence to the graphical scale between the two sets of temperature results. Clearly, the transitions between the solid and fluid regions are accurately accounted for by the single domain formulation and its corresponding eigenfunctions.

Fig. 7
figure 7

Comparisons between GITT and COMSOL solutions for the fluid and wall temperature profiles: a along Z, at \(Y = 0.2,\) and b along \(Y\) at \(Z = 0,\) for different longitudinal positions (\(X\)), for the multiple irregular regions situation

Full size image

Besides the remarkable adherence between the hybrid and numerical solutions observed in Figs. 7, Tables 1 and 2 illustrate the convergence behavior of the GITT solution with respect to the number of terms employed in the temperature field expansion, N, where it can be observed a convergence of three significant digits to within the truncation orders considered. In these results, the eigenvalue problem was also solved using GITT, as described in Sect. 5, keeping the truncation order constant with M = 120 terms.

Table 1 Convergence behavior of the steady-state temperature profile along \(Y\) with respect to the truncation order of the expansion (\(N\)), with fixed \(M = 120\) terms in the eigenvalue problem solution (multiple irregular regions), at \(X = 0.1\)
Full size table
Table 2 Convergence behavior of the steady-state temperature profile along \(Y\) with respect to the truncation order of the expansion (\(N\)), with fixed \(M = 120\) terms in the eigenvalue problem solution (multiple irregular regions), at \(X = 0.2\)
Full size table

8.2.2 Convective Eigenvalue Problem

In order to demonstrate the convergence rate gains in adopting the convective eigenvalue problem formulation, three representative situations are considered in the analysis, with Pe = 1, 10, and 100. In all cases, it was employed M = 75 as the truncation order in the eigenvalue problem solution via GITT (Sect. 5). Figure 8a–c graphically illustrate the convergence behaviors for Pe = 1, 10, and 100, respectively, by presenting some transversal temperature profiles calculated with different truncation orders (N = 3, 6, 9) together with purely numerical solutions calculated with COMSOL (automatically generated mesh with the “extremely fine” option), demonstrating that a truncation order as small as N = 9 is enough to provide curves fully converged to the graph scale and in full agreement with the numerical solutions.

Fig. 8
figure 8

Transversal temperature profiles at. \({\text{XPe}} = 0.01,0.02,0.03\,{\text{and}}\,0.05\) and \(\tau = 0.01,\) calculated employing the convective eigenvalue problem and the truncation orders N = 3 (green dots-dashes), N = 6 (blue dashes), N = 9 (solid black), and COMSOL (red dots). a Pe = 1, b Pe = 10, c Pe = 100

Full size image

Tables 3, 4, 5 further illustrate the convergence behavior, by presenting the results in tabular form for Pe = 1, 10, and 100, respectively, demonstrating that with only N = 18 terms, a full convergence of five to six significant digits is observed at the selected positions, despite the increase in the Péclet number, clearly demonstrating the importance of incorporating the convective term into the eigenvalue problem.

Table 3 Convergence behavior of the calculated temperatures at \(X{\text{Pe}} = 0.05,\) \(\tau = 0.01,\) for Pe = 1, employing the convective eigenvalue problem
Full size table
Table 4 Convergence behavior of the calculated temperatures at \(X{\text{Pe}} = 0.05\), \(\tau = 0.01\), for Pe = 10, employing the convective eigenvalue problem
Full size table
Table 5 Convergence behavior of the calculated temperatures at \(X{\text{Pe}} = 0.05\), \(\tau = 0.01\), for Pe = 100, employing the convective eigenvalue problem
Full size table

9 Closing Remarks

Fifty years ago, roughly by the late 60s and early 70s, the classical integral transform method for the solution of linear diffusion problems reached a maturity level that is evident from the seminal contributions published in this period, as here reviewed [10,11,12,13,14]. Also around this period, the limitations on the classical approach were faced, in the pioneering works of Ozisik and Murray [18] and Mikhailov [19], that provided the first approximate analytical solutions for non-transformable linear problems, and would plant the seeds for the development of the hybrid numerical–analytical approach [20,21,22,23,24,25,26,27,28], nowadays known as the Generalized Integral Transform Technique, GITT, that has been extended to various classes of linear and nonlinear diffusion and convection–diffusion problems along about thirty years, as here briefly described. Also, fifty years ago, Prof. Spalding and his collaborators were breeding a sequence of academic contributions on the finite volume method, that would lead to the very first version of the Phoenics code, launched in 1981, inaugurating the era of modern CFD & HT. This achievement was soon followed by developments on other classical numerical approaches that also led to the establishment of general-purpose computational tools based on the finite element, finite differences, and boundary element methods. The need for independent benchmarks of classical heat and fluid flow test cases, toward the verification and critical comparison of competing numerical schemes, was the original motivation in the parallel development of the hybrid GITT approach along this period. The analytical nature behind the GITT, which concentrates most of the numerical work in one single independent variable, has proved to offer error-controlled solutions with mild computational costs that, once derived and implemented for a certain class of problems, become an interesting alternative path for computational simulation, especially when associated with very computer intensive tasks such as optimization, inverse problem analysis, and simulation under uncertainty.

More recently, with the aid of mixed symbolic-numerical systems [67], the construction of a Unified Integral Transforms (UNIT) algorithm has been advanced [42, 54], offering both an automatic symbolic-numerical open source solver and a development platform for researchers and practitioners interested in this class of hybrid methods for partial differential equations. In parallel to the attempt of offering a more general-purpose hybrid simulation tool, the method has been advanced through both mathematical and computational novel aspects, as here partially described, to challenge applications from now on that, even nowadays pose difficulties to the well-established numerical methods, such as in dealing with the wide classes of unstable nonlinear problems and multiscale phenomena.