Dynamical Properties of Coastal Currents in the Northwestern Part of Iriomote Island Part. 2—Funauki and Shirahama Bays

Abstract

This chapter presents investigation of the physical properties of tidal flows in two semi-closed bays connected with a channel based on theoretical, observational and numerical frameworks. Shirahama Bay with shallower water and Funauki Bay with deeper water in the northwestern part of Iriomote Island are mutually connected by a channel. Tidal flows in both bays are expected to be much more complex than those of Sakiyama and Amitori bays, discussed in Chap. 4. According to the tidal flow dynamics in Chap. 4, the seawater exchange in Shirahama Bay is more active because of its shallower water floor, whereas the seawater exchange in Funauki Bay is more stagnant because of its deeper water floor. Consequently, the low-salinity water originating from a river is likely to be retarded in Funauki Bay under near-calm conditions. In the case of a smaller aspect ratio (shallower and longer) of the connecting channel, the seawater exchange among the bays becomes inactive. In the case of the moderate aspect ratio of the connecting channel, which is comparable with those of both bays, the seawater exchange among the bays reaches a maximum. For a larger aspect ratio (deeper or shorter) of the connecting channel, the seawater exchange will stagnate not only between the bays, but also between the bays and the open ocean. The aspect ratio of the connecting channel, which strongly affects the tidal currents in both bays, is expected to strongly influence on the dispersions of eggs and seeds in the coastal ocean ecosystems in this region.

This chapter is based on works reported by Yoshino et al. (2016, 2018).

1 Introduction

In the coastal area in the northwestern part of Iriomote Island, there are intricate semi-closed bays consisting of (from south to north) Sakiyama Bay, Amitori Bay, Funauki Bay and Shirahama Bay (referred to Sect. 1.1, Sect. 1.2 and Fig. 1.1). Funauki and Shirahama bays, which are located north of the Sakiyama and Amitori bays discussed in Chap. 4, have respective vertical depths of 80 m and 40 m, giving rise to a great difference in the depth. We can infer that such a great difference leads to differences in the physical properties of coastal currents among the bays. The heads of Funauki and Shirahama bays have river mouths of Kuira River and Nakara River, respectively. Moreover, they are mutually linked by a connecting channel. The existence of that connecting channel might cause complicated tidal flows. The behaviors will therefore be more complex than those of Sakiyama and Amitori bays discussed in Chap. 4.

The heads of Funauki and Shirahama bays are home to the tropical seaweed Enhalus acoroides, as discussed in Sect. 1.5, in which the Yaeyama Islands, Okinawa, Japan are situated at the northern extreme. The Enhalus acoroides generally develop colonies near the river mouth, where waves are constantly calm (Yoshida et al. 2007). Recently, however, Enhalus acoroides has come to be listed as a category II endangered species in the Red List by the Ministry of the Environment. Its colonies are reported to be decaying and disappearing from Funauki and Shirahama bays (Takeyama et al. 2014). Especially in Funauki Bay, although some colonies of Enhalus acoroides have existed in the past, most are currently disappearing, because of feeding damage inflicted by green turtles (Mizutani et al. 2016) among other reasons. To conserve and restore the Enhalus acoroides colonies in this region, the seed and fruit dispersion processes in this region must be understood. To elucidate those processes, it is important in turn to discuss the physical properties of tidal flows in Funauki and Shirahama bays with their connecting channel.

This chapter describes the theoretical, observational and numerical investigations on the coastal currents in Funauki and Shirahama bays, which are mutually connected by a single channel.

2 Tidal Flow Dynamics in a Complex Channel Network

• (a) Theoretical formula

We first examine the physical properties of tidal flow in Funauki and Shirahama bays in the northwestern part of Iriomote Island, based on the tidal flow theory in a complex channel network (Unoki 1993). The existence of a connecting channel linking Funauki and Shirahama bays is expected to complicate the flow structure, compared to a single channel such as that in Sakiyama and Amitori bays, discussed in Chap. 4. This section explains the tidal flow dynamics in the complex channel network. Subsequently, we discuss the influence of the connecting channel on Funauki and Shirahama bays.

Funauki and Shirahama bays with a connecting channel are simplified and idealized herein by three channels and two bays, as shown in the schematic diagram in Fig. 5.1. Bay 1 and Bay 2 have the same area A. They are connected respectively with the open ocean by Channel 1 and Channel 2. Bay 1 and Channel 1 are associated with Shirahama Bay. Bay 2 and Channel 2 correspond to Funauki Bay. Bay 1 and Bay 2 are mutually connected by Channel 3, analogous to the connecting channel. $\eta_{0}$ represents the tidal level in the open ocean. Also, $\eta_{1}$ and $\eta_{2}$ respectively stand for the tidal levels in Bay 1 and Bay 2. In the three channels, $u$, $w$, $l$ and $h$ respectively denote the velocity, width, length, and depth. Their suffix represents the number of three channels. The current velocity $u_{1}$ ($u_{2}$) from the open ocean to Bay 1 (Bay 2) is positive. Velocity $u_{3}$ from Bay 1 to Bay 2 is positive. Consequently, the momentum equations in Channel 1, Channel 2 and Channel 3 and the mass continuity equations in Bay 1 and Bay 2 are described as shown below.

Fig. 5.1

Referred from Yoshino et al. (2016)

Schematic diagram showing tidal flow dynamics in a complex channel network, simplifying Shirahama and Funauki bays with a connecting channel.

$$\frac{{{\text{d}}u_{1} }}{{{\text{d}}t}} = - g\frac{{\eta_{1} - \eta_{0} }}{{l_{1} }} - \frac{{\beta u_{1} }}{{h_{1} }}$$

(5.1)

$$\frac{{{\text{d}}u_{2} }}{{{\text{d}}t}} = - g\frac{{\eta_{2} - \eta_{0} }}{{l_{2} }} - \frac{{\beta u_{2} }}{{h_{2} }}$$

(5.2)

$$\frac{{{\text{d}}u_{3} }}{{{\text{d}}t}} = - g\frac{{\eta_{2} - \eta_{1} }}{{l_{3} }} - \frac{{\beta u_{3} }}{{h_{3} }}$$

(5.3)

$${\rm A}\frac{{{\text{d}}\eta_{1} }}{{{\text{d}}t}} = w_{1} h_{1} u_{1} - w_{3} h_{3} u_{3}$$

(5.4)

$${\rm A}\frac{{{\text{d}}\eta_{2} }}{{{\text{d}}t}} = w_{2} h_{2} u_{2} + w_{3} h_{3} u_{3}$$

(5.5)

In those equations, $g$ represents gravitational acceleration. The ocean bottom drag expressed by the second terms in Eqs. (5.1), (5.2), and (5.3) is assumed to be proportional to the first power of the current velocity, where $\beta = (8/3\pi )C_{f} \hat{U} = 6.85 \times 10^{3}$. In these equations, the meteorological forcing is negligible under near-calm conditions.

To solve the linear equations system above, the temporal variations of the tidal level $\eta$ and current velocity $u$ respondent to the tidal level $\eta_{0}$ in the open ocean can be represented as the following exponential forms.

$$\begin{aligned} & \eta_{0} = M{\text{e}}^{i\sigma t} ,\eta_{1} = \hat{\eta }_{1} {\text{e}}^{i\sigma t} ,\eta_{2} = \hat{\eta }_{2} {\text{e}}^{i\sigma t} , \\ & u_{1} = \hat{u}_{1} {\text{e}}^{i\sigma t} ,u_{2} = \hat{u}_{2} {\text{e}}^{i\sigma t} ,u_{3} = \hat{u}_{3} {\text{e}}^{i\sigma t} \\ \end{aligned}$$

(5.6)

In those expressions, $M$ (real number) stands for the amplitude of the tidal level in the open ocean. Also, $\hat{\eta }$ and $\hat{u}$ (complex number) represent the amplitude and phase change of the tidal level and current velocity. The amplitude of tidal level and current is expressed, respectively, by $|\hat{\eta }|$ and $|\hat{u}|$. The phase change of the tidal level and current is presented, respectively, as $\arg (\hat{\eta })$ and $\arg (\hat{u})$. $\sigma$ ($= 2\pi /T$) is the radian frequency of the tidal level $\eta_{0}$ in the open ocean with a period $T$ of 12 h. Substituting Eq. (5.6) into Eqs. (5.1), (5.2), (5.3), (5.4) and (5.5), we can obtain the following first-order algebraic equations system as

$$\hat{\eta }_{1} + A\hat{u}_{1} = M$$

(5.7)

$$\hat{\eta }_{2} + B\hat{u}_{2} = M$$

(5.8)

$$\hat{\eta }_{1} - \hat{\eta }_{2} + C\hat{u}_{3} = 0$$

(5.9)

$$\hat{\eta }_{1} - a\hat{u}_{1} + c\hat{u}_{3} = 0$$

(5.10)

$$\hat{\eta }_{2} - b\hat{u}_{2} - c\hat{u}_{3} = 0$$

(5.11)

where $A$ and $a$ in Eqs. (5.7), (5.8), (5.9), (5.10) and (5.11) are complex number as

$$\begin{aligned} & A = \left( {i\sigma + \frac{\beta }{{h_{1} }}} \right)\frac{{l_{1} }}{g},\quad a = - i\frac{{w_{1} h_{1} }}{\sigma A} \\ & B = \left( {i\sigma + \frac{\beta }{{h_{2} }}} \right)\frac{{l_{2} }}{g},\quad b = - i\frac{{w_{2} h_{2} }}{\sigma A} \\ & C = \left( {i\sigma + \frac{\beta }{{h_{3} }}} \right)\frac{{l_{3} }}{g},\quad c = - i\frac{{w_{3} h_{3} }}{\sigma A} \\ \end{aligned}$$

(5.12)

where $i$ is the imaginary unit. It is better to express these equations in matrix form as

$$\left[ {\begin{array}{*{20}c} 1 & 0 & A & 0 & 0 \\ 0 & 1 & 0 & B & 0 \\ 1 & { - 1} & 0 & 0 & { - C} \\ 1 & 0 & { - a} & 0 & c \\ 0 & 1 & 0 & { - b} & { - c} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{\eta }_{1} } \\ {\hat{\eta }_{2} } \\ {\hat{u}_{1} } \\ {\hat{u}_{2} } \\ {\hat{u}_{3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} M \\ M \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]$$

(5.13)

Because Eq. (5.13) is described in the form of ${\mathbf{Ax}} = {\mathbf{b}}$, the solution vector ${\mathbf{x}}$ is solvable using the Cramer’s rule. Consequently, the exact solutions of $\hat{u}_{1} ,\hat{u}_{2} ,\hat{u}_{3}$,$\hat{\eta }_{1}$, and $\hat{\eta }_{2}$ are obtainable as presented below.

$$\hat{u}_{1} = \frac{2Bc + (B + b)C}{A(B + b)c + (A + a)Bc + (A + a)(B + b)C}M$$

(5.14)

$$\hat{u}_{2} = \frac{2Ac + (A + a)C}{A(B + b)c + (A + a)Bc + (A + a)(B + b)C}M$$

(5.15)

$$\hat{u}_{3} = \frac{ - A(B + b) + (A + a)B}{A(B + b)c + (A + a)Bc + (A + a)(B + b)C}M$$

(5.16)

$$\hat{\eta }_{1} = \frac{(Ab + aB)c + a(B + b)C}{A(B + b)c + (A + a)Bc + (A + a)(B + b)C}M$$

(5.17)

$$\hat{\eta }_{2} = \frac{(Ab + aB)c + (A + a)bC}{A(B + b)c + (A + a)Bc + (A + a)(B + b)C}M$$

(5.18)

As discussed in the preceding chapter, because both Funauki and Shirahama bays are categorized as deep bays, the assumptions of $A + a \approx a$ and $B + b \approx b$ can be valid. Therefore, Eqs. (5.14), (5.15), (5.16), (5.17) and (5.18) can be simplified as

$$\hat{u}_{1} = \frac{2Bc + bC}{Abc + aBc + abC}M$$

(5.19)

$$\hat{u}_{2} = \frac{2Ac + aC}{Abc + aBc + abC}M$$

(5.20)

$$\hat{u}_{3} = \frac{ - Ab + aB}{Abc + aBc + abC}M$$

(5.21)

$$\hat{\eta }_{1} = \frac{Abc + aBc + abC}{Abc + aBc + abC}M = M$$

(5.22)

$$\hat{\eta }_{2} = \frac{Abc + aBc + abC}{Abc + aBc + abC}M = M$$

(5.23)

which are the approximate solutions in deep bays. These equations indicate that the tidal flows in Channel 1 (Bay 1) and Channel 2 (Bay 2) are influenced by the flow of Channel 3 (connecting channel), because Eqs. (5.19), (5.20), and (5.21) include complex parameters $C$ and $c$ representing the Channel 3 shape. Conversely, the tidal flow in Channel 3 also depends on the flows in Channel 1 (Bay 1) and Channel 2 (Bay 2), implying that all channels mutually interact in a complex manner. However, the amplitudes of tidal levels in Bay 1 and Bay 2 are nearly equal to the amplitude in the open ocean $M$, suggesting that the amplitude reduction and phase shift are sufficiently small to be negligible when Bay 1 and Bay 2 are “deep bays.”

• (b) Case of Funauki and Shirahama bays

Based on the exact solutions of Eqs. (5.14), (5.15), (5.16), (5.17) and (5.18), one can next consider the tidal flows in Funauki and Shirahama bays. The depth of Shirahama Bay (i.e., Channel 1) is estimated as $h_{1} = 40$ m. The depth of Funauki Bay (i.e., Channel 2) is estimated as $h_{2} = 80$ m. In this study, to simplify the problem, width $w$ and length $l$ in Funauki and Shirahama bays are mutually coincident. Therefore, the areas of the two bays are set to the same values. We herein assume the representative values $l_{1} = l_{2} = 5000$ m, $w_{1} = w_{2} = 500$ m and $A = 2,500,000$ m². Then, the aspect ratio of Shirahama Bay (Channel 1) is $l_{1} /h_{1} = 125$. That of Funauki Bay (Channel 2) is $l_{2} /h_{2} = 62.5$. Furthermore, the width, length, and depth of the connecting channel (i.e., Channel 3) are assumed to be $w_{3} = 50$ m, $l_{3} = 1000$ m, and $h_{3} = 5$ m, resulting in an aspect ratio of $l_{3} /h_{3} = 500$, which is much larger than those of Channel 1 and Channel 2. Under the topographic conditions, the tidal flows in Funauki and Shirahama bays are calculated using a tidal level of $M = 0.5$ m in the open ocean.

Figure 5.2 shows time series of current velocities $u_{1}$ and $u_{2}$ in Channel 1 (Shirahama Bay) and Channel 2 (Funauki Bay) during a one-day period. Because both Channel 1 and Channel 2 are categorized as “deep bays,” a greater aspect ratio in those channels (with shallower and longer water) produces a greater amplitude of the current velocity. For example, Shirahama Bay, with its lager aspect ratio, has amplitude of about 0.009 m/s, which is double the corresponding value (0.0045 m/s) in Funauki Bay. It is consistent with Eq. (4.21) in Chap. 4 that the aspect ratio of Channel 1 is double the aspect ratio of Channel 2, and that the phases of tidal currents ${\text{arg(}}\hat{u}_{1} )$ and ${\text{arg(}}\hat{u}_{2} )$ are 1/4T (3 h) earlier than the phase of the ocean tide ${\text{arg(}}M )$.

Fig. 5.2

Time series of ocean tidal level and current velocity in Channel 1 and Channel 2

Figure 5.3 presents a time series of current velocity $u_{3}$ in Channel 3 (the connecting channel) during a one-day period. The tidal current amplitude is close to 0.02 m/s, which is much larger than that of either Channel 1 or Channel 2. Another characteristic is that the phase of tidal current ${\text{arg(}}\hat{u}_{3} )$ is delayed by 1/4T (3 h). That result indicates that the flow from Bay 1 (Bay 2) to Bay 2 (Bay 1) occurs in the outgoing tide (incoming tide).

Fig. 5.3

Referred from Yoshino et al. (2016)

Time series of tidal level $\hat{\eta }$ and current velocity $\hat{u}$ in Channel 3, simulated using the theory of tidal flow dynamics in a complex channel network.

• (c) Physical properties of the connecting channel

The previous subsection describes a strong tidal flow in Channel 3 between Bay 1 and Bay 2, in which the phase of current velocity ${\text{arg(}}\hat{u}_{3} )$ is 1/4T (3 h) earlier than the phase of the ocean tide ${\text{arg(}}M )$. Consequently, the water and material exchanges that occur near the surface are expected to be active between Bay 1 (Shirahama Bay) and Bay 2 (Funauki Bay). We herein discuss what physical processes can control the tidal current in Channel 3. The width, length and depth of Channel 3 are set as $w_{3} = 50$ m, $l_{3} = 1000$ m, and $h_{3} = 5$ m as the reference state. Then the respective sensitivities of depth $h_{1}$ and length $l_{1}$ are investigated.

First, Fig. 5.4 shows the time series of the current velocities $u_{3}$ of tidal flows simulated with depths $h_{1}$ of seven types in Channel 1: 10, 20, 40, 80, 160, 320, and 640 m, assuming that all other parameters are fixed. The results indicate that the amplitude of current velocity $\left| {\hat{u}_{3} } \right|$ is intensified by the difference of depth between Channel 1 and Channel 2. For $h_{1} < h_{2}$, the phase of current velocity ${\text{arg(}}\hat{u}_{3} )$ is shifted by −1/4T (−3 h) from that of the ocean tide ${\text{arg(}}M )$. In the case of $h_{1} = h_{2}$, the amplitude of the tidal velocity $\left| {\hat{u}_{3} } \right|$ will be zero, implying that no tidal flow passes through Channel 3. In the case of $h_{1} > h_{2}$, the phase of current velocity ${\text{arg(}}\hat{u}_{3} )$ is shifted by +1/4T (+3 h) from that of the ocean tide ${\text{arg(}}M )$. Consequently, it is suggested that the flow pattern in the connecting channel is mainly controlled by the differences of depth among Funauki and Shirahama bays.

Fig. 5.4

Referred from Yoshino et al. (2016)

Time series of tidal level $\hat{\eta }$ and current velocity $\hat{u}$ in Channel 3 in each of sensitivity experiments with changing depth of Channel 1.

Such a phase shift presented in Fig. 5.4 is explainable by the approximated Eq. (5.21). The inequality $Ab \gg aB$ in Eq. (5.21) will hold if the Channel 1 depth is assumed to be much larger than that of Channel 2 ($h_{1} \ll h_{2}$). Equalities A ≫ C and B ≫ C in Eq. (5.21) will be valid if the aspect ratio of Channel 3 is assumed to be much larger than those of Channel 1 and Channel 2 ($l_{3} /h_{3} \gg l_{1} /h_{1}$ and $l_{3} /h_{3} \gg l_{2} /h_{2}$). Then, Eq. (5.21) can be approximated as shown below.

$$\hat{u}_{3} \approx \frac{ - Ab}{Abc}M = - \frac{M}{c} = - i\frac{\sigma A}{{w_{3} h_{3} }}M$$

(5.24)

Therefore, the approximated equation indicates that the large difference of depth between Channel 1 and Channel 2 ($h_{1} \ll h_{2}$) causes the phase delay of the current velocity ${\text{arg(}}\hat{u}_{3} )$ of Channel 3 by 1/4T (3 h) from the ocean tide ${\text{arg(}}M )$ (T = 12 h) because of the “$- i$” multiplier in Eq. (5.24).

Next, Fig. 5.5 presents a time series of the current velocities $u_{3}$ of tidal flows simulated with lengths $l_{1}$ of seven types in Channel 1: 625, 1,250, 2,500, 5,000, 10,000, 20,000, and 40,000 m, assuming that all the other parameters are fixed. The results suggest that the amplitude of current velocity $\left| {\hat{u}_{3} } \right|$ in Channel 3 is intensified by the difference of length between Channel 1 and Channel 2. In the case of $l_{1} < l_{2}$, Channel 3 will have a phase shift $\arg (\hat{u}_{3} )$ of +1/4T (+3 h) from the ocean tide ${\text{arg(}}M )$. In the case of $l_{1} = l_{2}$, the amplitude $\left| {\hat{u}_{3} } \right|$ and phase shift ${\text{arg(}}\hat{u}_{3} )$ in Channel 3 will be zero. In the case of $h_{1} > h_{2}$, the phase of current velocity ${\text{arg(}}\hat{u}_{3} )$ in Channel 3 will be delayed by −1/4T (−3 h) from the ocean tide ${\text{arg(}}M )$. Consequently, the difference of length between Channel 1 and Channel 2 shows an opposite response to that of depth presented in Fig. 5.4, implying that not only depths but also lengths in both Funauki and Shirahama bays control the tidal flow in the connecting channel.

Fig. 5.5

Referred from Yoshino et al. (2016)

Time series of tidal level $\hat{\eta }$ and current velocity $\hat{u}$ in Channel 3 in each of sensitivity experiments with changing length of Channel 1.

Such a phase shift ${\text{arg(}}\hat{u}_{3} )$ depicted in Fig. 5.5 can be understood from the rearrangement of the theoretical equation written in Eq. (5.21). The inequality $Ab \ll aB$ in Eq. (5.21) will hold if the difference of length between Channel 1 and Channel 2 is sufficiently large ($l_{1} \ll l_{2}$). The equalities $A \gg C$ and $B \gg C$ in Eq. (5.21) will be valid if the aspect ratio of Channel 3 is much larger than those of Channel 1 and Channel 2 ($l_{3} /h_{3} \gg l_{1} /h_{1}$ and $l_{3} /h_{3} \gg l_{2} /h_{2}$). Then Eq. (5.21) can be approximated as presented below.

$$\hat{u}_{3} \approx \frac{aB}{aBc}M = \frac{M}{c} = i\frac{\sigma A}{{w_{3} h_{3} }}M$$

(5.25)

As a result, the large difference of length between Channel 1 and Channel 2 induces the tidal flow $u_{3}$ in Channel 3 with a phase shift of +1/4T (+3 h) from the ocean tide ${\text{arg(}}M )$ (T = 12 h) because of the “$+ i$” multiplier in Eq. (5.25).

Based on the results described above for the sensitivity experiments of changes of depth and length in Channel 1 on the tidal flows in Channel 3, results show that the difference of aspect ratio $l/h$ between Channel 1 and Channel 2 mainly influences the response of tidal flows $u_{3}$ in the connecting channel. The aspect ratio of Shirahama Bay is 125, which is double the aspect ratio of Funauki Bay (62.6). The greater the difference in aspect ratio between the two bays, the greater the magnitude of tidal velocity $\left| {\hat{u}_{3} } \right|$ in Channel 3. The phase of tidal velocity ${\text{arg(}}\hat{u}_{3} )$ in Channel 3 is delayed by 1/4T (3 h) from the ocean tide ${\text{arg(}}M )$.

3 Tidal Flow Simulations in a Complex Channel Network

• (a) Basic equation system

Next, to identify the degree to which the aspect ratio of Channel 3 influences the tidal flows and seawater exchanges in Shirahama Bay (Channel 1 and Bay 1) and Funauki Bay (Channel 2 and Bay 2), the numerical experiments using a two-layer nonlinear tidal flow model in a complex channel network are conducted in this section. The tidal flow model will include the effects of river flow and mass transport, which are ignored in the one-layer linear model used in the preceding section.

As presented in Fig. 5.6, an idealized topography representing Shirahama Bay (Channel 1 and Bay 1) and Funauki Bay (Channel 2 and Bay 2) with the connecting channel (Channel 3) is applied in this model. Assuming that the difference of depth between Channel 1 and Channel 2 is sufficiently large, the respective depths of Channel 1 and Channel 2 are set as 10 and 100 m. Bay 1 and Bay 2 are connected to the open ocean by Channel 1 and Channel 2, respectively, and are mutually linked by Channel 3. Furthermore, the river waters of River 1 and River 2 flow respectively into Bay 1 and Bay 2. Under near-calm conditions in summers, a saltwater wedge among the upper-level freshwater and low-level saltwater can be often observed in the bays, implying that the bay areas can be generally categorized as a type of “weak mixing.” Therefore, the momentum and mass continuity equations in the tidal flow model can be divisible into two layers, consisting of upper-level freshwater layer (denoted by suffix U) and lower-level saltwater layer (denoted by suffix L).

Fig. 5.6

Referred from Yoshino et al. (2018)

Schematic diagram showing two-layer tidal flow model in a complex channel network representing Shirahama and Funauki bays with a connecting channel.

$\eta_{U0}$ and $\eta_{L0}$ respectively stand for the sea-level anomalies in the open ocean at the upper and lower layers. $\eta_{U1}$ and $\eta_{L1}$ ($\eta_{U2}$ and $\eta_{L2}$) respectively represent the sea-level anomalies in Bay 1 (Bay 2) at the upper and lower layers. The area is defined as ${\rm A}$ in both Bay 1 and Bay 2, assuming the same length and width as each other. $u_{U1}$ and $u_{L1}$ ($u_{U2}$ and $u_{L2}$) respectively show current velocities at the upper and lower layers in Channel 1 (Channel 2), assuming that a flow from the open ocean to Bay 1 (Bay 2) is positive. $u_{U3}$ and $u_{L3}$ are the same but in Channel 3, assuming that a flow from Bay 1 to Bay 2 is positive. The respective width, length and depth of the three channels are $w$, $l$ and $h$, which are labeled with suffixes by the channel layer (U and L) and channel number (1, 2, and 3). Consequently, the momentum conservation equations at the upper layer in Channel 1, Channel 2 and Channel 3 are the followings.

$$\frac{{{\text{d}}u_{U1} }}{{{\text{d}}t}} = - g\frac{{\eta_{U1} - \eta_{U0} }}{{l_{1} }} - \frac{{\tau_{i1} }}{{\rho_{U1} h_{U1} }}$$

(5.26)

$$\frac{{{\text{d}}u_{U2} }}{{{\text{d}}t}} = - g\frac{{\eta_{U2} - \eta_{U0} }}{{l_{2} }} - \frac{{\tau_{i2} }}{{\rho_{U2} h_{U2} }}$$

(5.27)

$$\frac{{{\text{d}}u_{U3} }}{{{\text{d}}t}} = - g\frac{{\eta_{U2} - \eta_{U1} }}{{l_{3} }} - \frac{{\tau_{i3} }}{{\rho_{U3} h_{U3} }}$$

(5.28)

Also, the momentum conservation equations at the lower layer in Channel 1, Channel 2 and Channel 3 are expressed as,

$$\frac{{{\text{d}}u_{L1} }}{{{\text{d}}t}} = - g(1 - \varepsilon )\frac{{\eta_{U1} - \eta_{U0} }}{{l_{1} }} - g\varepsilon \frac{{\eta_{L1} - \eta_{L0} }}{{l_{1} }} + \frac{{\tau_{i1} }}{{\rho_{L1} h_{L1} }} - \frac{{\tau_{b1} }}{{\rho_{L1} h_{L1} }}$$

(5.29)

$$\frac{{{\text{d}}u_{L2} }}{{{\text{d}}t}} = - g(1 - \varepsilon )\frac{{\eta_{U2} - \eta_{U0} }}{{l_{2} }} - g\varepsilon \frac{{\eta_{L2} - \eta_{L0} }}{{l_{2} }} + \frac{{\tau_{i2} }}{{\rho_{L2} h_{L2} }} - \frac{{\tau_{b2} }}{{\rho_{L2} h_{L2} }}$$

(5.30)

$$\frac{{{\text{d}}u_{L3} }}{{{\text{d}}t}} = - g(1 - \varepsilon )\frac{{\eta_{U2} - \eta_{U1} }}{{l_{3} }} - g\varepsilon \frac{{\eta_{L2} - \eta_{L1} }}{{l_{3} }} + \frac{{\tau_{i3} }}{{\rho_{L3} h_{L3} }} - \frac{{\tau_{b3} }}{{\rho_{L3} h_{L3} }}$$

(5.31)

where $g$ represents the gravitational acceleration, $\rho_{U}$ and $\rho_{L}$ respectively denote the density of seawater at the upper and lower layers, leading to $\varepsilon = (\rho_{L} - \rho_{U} )/\rho_{L} = 0.03$. The interfacial and bottom friction drags $\tau_{i}$ and $\tau_{b}$ are parameterized by the following equations.

$$\tau_{i} = \frac{1}{2}\rho_{U} f_{i} \left| { \, u_{U} - u_{L} } \right|\left( {u_{U} - u_{L} } \right)$$

(5.32)

$$\tau_{b} = \rho_{L} C_{f} \left| { \, u_{L} } \right|u_{L}$$

(5.33)

Therein, $f_{i}$ signifies the coefficient of interfacial friction drag. The empirical formulas of Nakayama et al. (1998) are used in this study. In addition, $C_{f}$ denotes the dimensionless coefficient of bottom friction drag. It is set as 0.0026 and ignores the presence of seaweed and coral at the bottom.

Furthermore, mass conservation equations at the upper layer in Bay 1 and Bay 2 are described as,

$$A\frac{{{\text{d}}\eta_{U1} }}{{{\text{d}}t}} = w_{1} h_{U1} u_{U1} + w_{1} h_{L1} u_{L1} - w_{3} h_{U3} u_{U3} - w_{3} h_{L3} u_{L3} + Q_{R1}$$

(5.34)

$$A\frac{{{\text{d}}\eta_{U2} }}{{{\text{d}}t}} = w_{2} h_{U2} u_{U2} + w_{2} h_{L2} u_{L2} + w_{3} h_{U3} u_{U3} + w_{3} h_{L3} u_{L3} + Q_{R2}$$

(5.35)

where $Q_{R1}$ and $Q_{R2}$, respectively, represent the river flow rates into Bay 1 and Bay 2. They are set as a constant value of 0.01 [m³/s] in both of the rivers, based on the observations made near other similar rivers under calm conditions. The mass conservation equations at the lower layer in Bay 1 and Bay 2 are given as

$$A\frac{{{\text{d}}\eta_{L1} }}{{{\text{d}}t}} = w_{1} h_{L1} u_{L1} - w_{3} h_{L3} u_{L3} - AE(u_{U1} - u_{L1} )$$

(5.36)

$$A\frac{{{\text{d}}\eta_{L2} }}{{{\text{d}}t}} = w_{2} h_{L2} u_{L2} + w_{3} h_{L3} u_{L3} - AE(u_{U2} - u_{L2} )$$

(5.37)

where $E$ is the coefficient of entrainment at the interface between upper and lower layers. It is estimated using the empirical formula reported by Suga and Takahashi (1976). Moreover, the salinity conservation equations at the upper layer in Bay 1 and Bay 2 are introduced as

$$\begin{aligned} V_{1} \frac{{\partial S_{U1} }}{\partial t} & = S_{0} \hbox{max} (w_{1} h_{U1} u_{U1} ,0.0) + S_{U1} \hbox{min} (w_{1} h_{U1} u_{U1} ,0.0) \\ & \quad - S_{U1} \hbox{max} (w_{3} h_{U3} u_{U3} ,0.0) - S_{U2} \hbox{min} (w_{3} h_{U3} u_{U3} ,0.0) \\ & \quad + E{\rm A}(S_{U1} - S_{0} )(u_{U1} - u_{L1} ) + S_{R1} Q_{R1} \\ \end{aligned}$$

(5.38)

$$\begin{aligned} V_{2} \frac{{\partial S_{U2} }}{\partial t} & = S_{0} \hbox{max} (w_{2} h_{U2} u_{U2} ,0.0) + S_{U2} \hbox{min} (w_{2} h_{U2} u_{U2} ,0.0) \\ & \quad + S_{U1} \hbox{max} (w_{3} h_{U3} u_{U3} ,0.0) + S_{U2} \hbox{min} (w_{3} h_{U3} u_{U3} ,0.0) \\ & \quad + E{\rm A}(S_{U2} - S_{0} )(u_{U2} - u_{L2} ) + S_{R2} Q_{R2} \\ \end{aligned}$$

(5.39)

where $S_{U1}$ and $S_{U2}$, respectively, denote the salinities at the upper layer in Bay 1 and Bay 2. They can be considered as passive tracer in the bays. Furthermore, $V_{1}$ and $V_{2}$ are the respective volumes of seawater at the upper layer in Bay 1 and Bay 2. $S_{0}$ represents the salinity of the open ocean which is fixed at 35.0 ‰. Also, $S_{R1}$ and $S_{R2}$ respectively represent the salinities of the river water incoming to Bay 1 and Bay 2, and are set as a constant of 0.0 ‰. Because the volume of the lower layer is much greater than that of the upper layer, the salinities at the lower layer in Bay 1 and Bay 2 are assumed to be fixed at 35.0 ‰, which is same as that in the open ocean.

The differential equations presented above in Eqs. (5.26)–(5.39) are numerically integrated using the Runge–Kutta method during a period of 200 days. The tidal level in the open ocean at the upper level and lower level ($\eta_{U0}$ and $\eta_{L0}$) is given by a sine function with a period of 12 h and a peak value of 0.5 m. The last 24 h in the simulations are used for analysis.

• (b) CNTRL: moderate aspect ratio for the connecting channel

First, we discuss the result of a control experiment (CNTRL), in which the parameters used in the model are presented in Fig. 5.6. The parameters in CNTRL are set to realistic values in Channel 1 (Bay 1), Channel 2 (Bay 2) and Channel 3. Those orders are in good agreement with the actual conditions. The aspect ratio of Channel 1 is $l_{1} /h_{1} = 500$; that of Channel 2 is $l_{2} /h_{2} = 50$. The aspect ratio of Channel 3 is assumed to be $l_{3} /h_{3} = 500$, which is the same value as that of Channel 1.

Figure 5.7 shows a time series of the tidal level in each bay and the upper-level water flow rate in each channel during 24 h in CNTRL. Figure 5.8 presents a time series of the salinity in the respective bays during 24 h in CNTRL. Upper-level flows in both Channel 1 and Channel 2 are oscillating with a phase shift of +1/4T (+3 h) from the ocean tide (T = 12 h). The upper-level flow rate in Channel 1 with shallower water ($h_{1} = 10$ m) is much greater than that in Channel 2 with deeper water ($h_{2} = 100$ m). The upper-level flow rate in Channel 3 is considerably higher than that in Channel 2. It is about half of that in Channel 1. Moreover, it oscillates with a phase shift of −1/4T (−3 h) from the ocean tide (T = 12 h). The connecting channel therefore transports surface waters from Bay 2 (Bay 1) to Bay 1 (Bay 2) in the incoming tide (outgoing tide). The salinity in Bay 2 with lower seawater exchanges is lower than that in Bay 1 with higher seawater exchanges because of the stagnation of flow and freshwater in Bay 2.

Fig. 5.7

Referred from Yoshino et al. (2018)

Time series of tidal-level and upper-level water flows in Channel 1, Channel 2 and Channel 3 simulated using CNTRL.

Fig. 5.8

Referred from Yoshino et al. (2018)

Time series of tidal level and upper-level salinity in Bay 1 and Bay 2 simulated using CNTRL.

Figure 5.9 presents a summary of the tidal exchange rate and constant flow rate in respective channels and the salinity in respective bay, averaged during 24 h in CNTRL. Although the upper-level tidal exchange in Channel 3 is quite large (0.065 m³/s), a clear difference in salinities is apparent between Bay 1 (32.8 ‰) and Bay 2 (30.6 ‰). This difference derives from a large difference in the tidal exchange between Channel 1 (0.173 m³/s) and Channel 2 (0.021 m³/s). According to the linear theory for “deep bays” in Chap. 4, the tidal exchange in Channel 1 with shallower water ($h_{1} = 10$ m) is active, but that in Channel 2 with deeper water ($h_{2} = 100$ m) is inactive.

Fig. 5.9

Referred from Yoshino et al. (2018)

Tidal flows, constant flows and salinity in respective channels and bays simulated using CNTRL.

One can consider the physical properties of tidal current in each channel in CNTRL based on the theoretical equations in the previous subsection. Under the aspect ratios of three channels in CNTRL, the assumptions $C \approx A \gg B$ and $c \approx a \ll b$ will hold; then Eqs. (5.19), (5.20), and (5.21) can be approximated as shown below.

$$\hat{u}_{1} \approx \frac{bC}{Abc + abC}M = \frac{M}{c + a}$$

(5.40)

$$\hat{u}_{2} \approx \frac{Ac + aC}{Abc + abC}M = \frac{M}{b} \, ( \to 0)$$

(5.41)

$$\hat{u}_{3} \approx \frac{ - Ab}{Abc + abC}M = - \frac{M}{c + a}$$

(5.42)

In the case of the moderate aspect ratio of the connecting channel, the tidal flow in Channel 1 is strong, but that in Channel 2 is weak. It is noteworthy that the tidal exchange in Channel 3 is comparable with that in Channel 1.

• (c) CASE 1: large aspect ratio for the connecting channel

Next, we discuss the result of a sensitivity run (CASE 1), in which the aspect ratio of Channel 3 is set at an extremely high value of 50,000. The experimental setting assumes that the connecting channel in CASE 1 is much longer and shallower than that in CNTRL. The other parameters used are the same as the CNTRL run, as presented in Fig. 5.6.

Figure 5.10 summarizes the tidal exchange rate and constant flow rate in each channel and the salinity in each bay, averaged during 24 h in CASE 1. The upper-level tidal exchange in the connecting channel is 0.017 m³/s, which is about 4 times lower in CASE 1 than in CNTRL. As a consequence, the difference in salinity between Bay 1 (33.1 ‰) and Bay 2 (27.3 ‰) is enlarged in CASE 1. In common with CNTRL, the tidal exchange in Channel 1 is active (0.181 m³/s), and that in Channel 2 is inactive (0.019 m³/s). The longer and shallower Channel 3 in CASE 1 weakens the mutual interference among the bays and distinguishes different intrinsic features among individual bays.

Fig. 5.10

Referred from Yoshino et al. (2018)

Tidal flows, constant flows and salinity in respective channels and bays simulated using CASE 1.

One can then assess the physical properties of tidal currents in each channel in CASE 1 based on the theoretical equations presented in the preceding subsection. Under the aspect ratios of three channels in CASE 1, the assumptions $C \gg A \gg B$ and $c \ll a \ll b$ will hold; then Eqs. (5.19), (5.20), and (5.21) can be approximated as presented below.

$$\hat{u}_{1} \approx \frac{bC}{abC}M = \frac{M}{a}$$

(5.43)

$$\hat{u}_{2} \approx \frac{aC}{abC}M = \frac{M}{b}( \to 0)$$

(5.44)

$$\hat{u}_{3} \approx \frac{ - Ab}{abC}M = - \left( {\frac{A}{C}} \right)\frac{M}{a}( \to 0)$$

(5.45)

In the case of a large aspect ratio of the connecting channel, the tidal exchange in Channel 3 is expected to be inactive. For that reason, Channel 1 and Channel 2 will not mutually interact. As a result, the tidal flows in both channels show clear individual features as a single bay, as described in Chap. 4.

• (d) CASE 2: small aspect ratio for the connecting channel

Next, one can discuss the sensitivity run results (CASE 2) in which the aspect ratio of Channel 3 is set at an extremely low value of 0.5. The experimental setting includes the assumption that the connecting channel in CASE 2 is much shorter and deeper than that in CNTRL. The other parameters are the same as those used for the CNTRL run, as presented in Fig. 5.6.

Figure 5.11 presents a summary of the tidal exchange rate and constant flow rate in each channel and the salinity in each bay, as averaged during 24 h in CASE 2. The upper-level tidal exchange in the connecting channel is reduced to nearly 0.0 m³/s in CASE 2. Not only Channel 3 but also Channel 1 decreases the upper-level tidal exchange to 0.035 m³/s, which is equivalent to that (0.034 m³/s) in Channel 2. Consequently, the tidal current over the entire channel network stagnates because of the small aspect ratio of the connecting channel. The upper-level salinity is also decreased by the stagnations of freshwater in both Bay 1 (26.7 ‰) and Bay 2 (26.8 ‰). The shorter and deeper (smaller aspect ratio) characteristics of the connecting channel can contribute to a slower tidal exchange over the whole channel network because of the dominance of the effects of Channel 2.

Fig. 5.11

Referred from Yoshino et al. (2018)

Tidal flows, constant flows, and salinity in respective channels and bays simulated using CASE 2.

One can consider the physical properties of tidal current in each channel in CASE 2 based on the theoretical equations given in the previous subsection. Under the aspect ratios of three channels in CASE 2, the assumptions $C \ll B \ll A$ and $c \gg b \gg a$ will hold; then Eqs. (5.19), (5.20) and (5.21) can be approximated as shown below.

$$\hat{u}_{1} \approx \frac{Bc}{Abc}M = \left( {\frac{B}{A}} \right)\frac{M}{b}( \to 0)$$

(5.46)

$$\hat{u}_{2} \approx \frac{Ac}{Abc}M = \frac{M}{b}( \to 0)$$

(5.47)

$$\hat{u}_{3} \approx \frac{ - Ab}{Abc}M = - \frac{M}{c} \, ( \to 0)$$

(5.48)

In the case of the small aspect ratio of the connecting channel, the tidal flow by Channel 3 will stagnate. Then the tidal exchange in Channel 1 is influenced by those in Channel 2, resulting in tidal flow suppression over the whole channel network.

• (e) Relations between aspect ratio and tidal flow

The sensitivities of the aspect ratio of the connecting channel (Channel 3) are investigated next. Figure 5.12 shows the relations between the aspect ratio $l_{3} /h_{3}$ of Channel 3 and upper-level tidal exchange rates in each bay. When aspect ratio $l_{3} /h_{3}$ of Channel 3 is a moderate value equivalent to $l_{1} /h_{1}$, the tidal exchange in Channel 3 becomes maximum, leading to active exchange between Bay 1 and Bay 2. Whether $l_{3} /h_{3}$ is larger or smaller than the value, the seawater exchange at the connecting channel will be suppressed. The tidal flow in Channel 2 (i.e., Funauki Bay) responds only slightly to the change of $l_{3} /h_{3}$ at all. It is always inactive through the open ocean because of its deeper water floor. By contrast, the tidal flow in Channel 1 (i.e., Shirahama Bay) is strongly affected by the change of $l_{3} /h_{3}$. The active (inactive) tidal flow in Channel 1 is attributed mainly to a larger (smaller) $l_{3} /h_{3}$ in Channel 3. Consequently, when it comes to the upper-level tidal exchange, Shirahama Bay rather than Funauki Bay is likely to be affected by the topographic change of the connecting channel.

Fig. 5.12

Referred from Yoshino et al. (2018)

Relations between aspect ratio of Channel 3 $l_{3} /h_{3}$ and tidal flow in respective channels.

Figure 5.13 presents relations between the aspect ratio $l_{3} /h_{3}$ of Channel 3 and upper-level salinity in each bay. The upper-level mass exchanges, such as fruits and seeds of coastal ocean ecosystems, can be estimated indirectly because salinity at the surface level can be regarded as a passive tracer. In the case of the larger $l_{3} /h_{3}$, the upper-level tidal exchange in Channel 3 becomes inactive, leading to an independent environment with the greater difference in salinity between Bay 1 and Bay 2. It is considered that in such a condition, the dispersion of fruits and seeds from coastal ocean ecosystems is stronger in Shirahama Bay than in Funauki Bay. Moreover, the dispersion through the connecting channel is weaker. For smaller $l_{3} /h_{3}$, the upper-level tidal exchanges in the whole channel network become inactive, resulting in a stagnant environment with the lower salinity in Bay 1 and Bay 2 than in the open ocean. The dispersion ability in the whole bays is regarded as weakened. In the case of the moderate $l_{3} /h_{3}$, the upper-level tidal exchange in Channel 3 becomes active, creating a mutually interactive environment with less difference in salinity between Bay 1 and Bay 2. The dispersion capability among the bays is probably enhanced. Consequently, the upper-level dispersion of fruits and seeds in both Funauki and Shirahama bays are likely to be influenced by the topographic changes of their mutually connective channel.

Fig. 5.13

Referred from Yoshino et al. (2018)

Relations between the aspect ratio of Channel 3 $l_{3} /h_{3}$ and salinity in respective bays.

4 Observations and Simulations

This section presents examination of details of the physical features of tidal flows in Funauki and Shirahama bays with the connecting channel, based on results of in situ observations and CCM simulations. Detailed information is presented in relation to observational instruments in Chap. 2. The coastal current model “CCM” is explained in Chap. 3.

• (a) In situ observations

First, observational features of water quality in Funauki and Shirahama bays are discussed in this subsection. We conducted in situ observations using a conductivity-temperature-depth profiler (CTD) during high-tide and low-tide periods on September 15, 2014, August 15, 2014, and October 20, 2015. The moving observations were conducted using a small boat with the CTD profiler at 26–36 points and at every 0.1-m depth. Influences of the movements of the small boat may be reduced to a great degree, because the observations were done during the near-calm conditions with a wind speed of less than 6 m/s, at AMeDAS Iriomote (observed by JMA: referred to Sect. 1.3). The CTD profiler used for this study (RINKO-Profiler ASTD102; JFE Advantech Co. Ltd.) can detect depth, temperature, salinity, dissolved oxygen, turbidity and chlorophyll simultaneously.

We herein specifically examine the results of the observations taken at 6:50 JST (low tide) and 14:00 JST (high tide) on October 20, 2015.

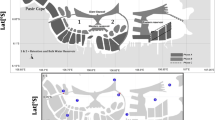
Figure 5.14 depicts the horizontal distributions of salinity in 0.1-m depth at 6:50 JST (low tide) and 14:00 JST (high tide) on October 20, 2015. Figure 5.15 portrays the horizontal distributions of temperature in 0.1-m depth at 6:50 JST (low tide) and 14:00 JST (high tide) on October 20, 2015. In both of the low and high tides, a low-salinity water mass (less than 20 ‰) is apparent near the connecting channel in Funauki Bay. Low-salinity areas tend to show a low temperature. Although low-salinity water exists in a small area of Shirahama Bay, most of it tends to show high-salinity water (30–36 ‰) over the bay. The low-salinity water mass observed in Funauki Bay is regarded as originating a freshwater from Kuira River located at the head of Funauki Bay, or partially originating in freshwater via the connecting channel from Nakara River located at the head of Shirahama Bay because of tidal exchanges.

Fig. 5.14

Referred from Yoshino et al. (2016)

Observed distributions of salinity in surface 0.1-m layer at a 6:50 JST October 20, 2015 (low tide) and b 14:00 JST October 20, 2015 (high tide).

Fig. 5.15

Observed distributions of temperature in surface 0.1-m layer at a 6:50 JST October 20, 2015 (low tide) and b 14:00 JST October 20, 2015 (high tide)

Figure 5.16 presents vertical profiles of salinity and temperature at five points at the low tide time (6:50 JST on October 20, 2015). Figure 5.17 also presents vertical profiles of salinity and temperature at five points at the high tide time (14:00 JST on October 20, 2015). St. 2 and St. 3 close to the head of Funauki Bay show tendencies of low salinity and low temperature near 10 cm depth. The river-originating water mass at the surface layer is visible in both low-tide and high-tide periods. Seawater exchange in Funauki Bay is regarded as stagnant for a longer period under the calm conditions. In Shirahama Bay, although transient low-salinity water is visible occasionally, it disappears promptly because of the strong seawater exchange.

Fig. 5.16

Referred from Yoshino et al. (2016)

Vertical profiles of salinity at five observational points at a 6:50 JST October 20, 2015 (low tide) and b 14:00 JST October 20, 2015 (high tide).

Fig. 5.17

Vertical profiles of temperature at the five observational points at a 6:50 JST October 20, 2015 (low tide) and b 14:00 JST October 20, 2015 (high tide)

Consequently, in situ observations by the CTD profiler indicate that the low-salinity and low-temperature water mass originating from the rivers is likely to be stagnant, especially in Funauki Bay with deeper water. This feature is consistent with our findings related to the theory and simulations of tidal flow dynamics in a complex channel network described in previous sections.

• (b) CCM simulations

Next in this subsection, we discuss the physical features of tidal flow in Funauki and Shirahama bays with the connecting channel, which might influence the surface layer water quality. To identify the tidal flow behavior in complex terrain, a numerical simulation is conducted using the multi-sigma coordinate coastal current model CCM (Murakami et al. 2004). In these simulations, salinity and temperature conservation equations are not included to simplify the problem, so the barotropic structures in the ocean are solved using momentum equations and mass continuity equations. The horizontal grid spacing of CCM is 50 m × 50 m. Two simulation periods are employed: June 9–May 16, 2014 (7 days) in summer and November 2–November 9, 2014 (7 days) in winter. The lateral boundary conditions for the sea-level height are added along the open boundaries using NAO.99jb (Matsumoto et al. 2000). As the meteorological forcing, the wind speed and direction observed at Amitori Village (operated by Okinawa Regional Research Center, Tokai University) are inputted homogeneously at the upper ocean boundary. Consequently, the currents in CCM are induced by current by tide (lateral boundary) and by current by wind (upper boundary). To compare tidal and wind influences, a CCM simulation without meteorological forcing, in which the wind speed is set to 0 m/s during the simulation period, is also conducted.

Figure 5.18 presents the horizontal distributions of the 7-day averaged surface current speed and vectors in summer and winter, as simulated by CCM. The time-average procedure can eliminate the high-frequency periodic tidal currents and can retain the steady-state residual currents only. In summer, the main wind direction is southwesterly winds, but its wind speeds are very weak. As a result, the surface residual current is not readily visible in the bays and channel. By contrast, in winter, northeasterly monsoon winds dominate. Strong residual currents develop from the north to the south in the bays. In winter, surface water is advected steadily from Shirahama Bay (north) to Funauki Bay (south) because of by the strong northeasterly wind.

Fig. 5.18

Horizontal distributions of surface current speed and vectors averaged during 7 days in a summer and b winter simulated by CCM with wind forcing

Figure 5.19 shows the horizontal distributions of the surface current speed and vectors averaged at the incoming tides in summer and winter, as simulated by CCM. For comparison between tide-induced currents and wind-induced currents, Fig. 5.20 shows the values as portrayed in Fig. 5.19, but without wind forcing. Such a time-average procedure can identify the typical flow structure in the incoming tides. The current velocities become maximum in the direction from the open ocean to the bays because those bays are categorized as “deep bays.” In summer, no clear difference is apparent in surface currents between those with and without wind forcing. Strong incoming flow dominates in the head of the bays. The surface tidal current in the connecting channel is directed from Funauki Bay (south) to Shirahama Bay (north). In winter, the strong northerly (southward) winds compensate for the northward tidal current in the connecting channel.

Fig. 5.19

Horizontal distributions of surface current speed and vectors averaged at incoming tide in a summer and b winter simulated by CCM with wind forcing

Fig. 5.20

Same as Fig. 5.19, but without wind forcing

Figure 5.21 presents the horizontal distributions of the surface current speed and vectors averaged at the outgoing tides in summer and winter, as simulated by CCM. For comparison between tide-induced currents and wind-induced currents, Fig. 5.22 shows the values as shown in Fig. 5.21, but without wind forcing. The current velocities become maximum in the direction from the bays to the open ocean, as described above. In summer, no clear difference is apparent in surface currents between those with and without wind forcing. Strong outgoing flow dominates in the head of the bays. The surface tidal current in the connecting channel is directed from Shirahama Bay (north) to Funauki Bay (south). In winter, strong northerly (southward) winds further enhance the southward tidal current in the connecting channel.

Fig. 5.21

Referred from Yoshino et al. (2016)

Horizontal distributions of surface current speed and vectors averaged at outgoing tide in a summer and b winter simulated by CCM with wind forcing.

Fig. 5.22

Same as Fig. 5.21, but without wind forcing

Figure 5.23 presents time series of the tidal level and surface current velocity in the connecting channel. In these figures, the positive velocity denotes the current in the direction from Shirahama Bay to Funauki Bay. Negative velocity denotes the current in the direction from Funauki Bay to Shirahama Bay. Without wind forcing, a periodic tidal current develops in the connecting channel. The phase of the current velocity is delayed by 1/4T (3 h) from that of the tidal level (T = 12 h). In other words, the ocean tide induces strong flows from Funauki Bay (Shirahama Bay) to Shirahama Bay (Funauki Bay) in the incoming (outgoing) tide. The amplitude of the current velocity in the connecting channel is on the order of 0.01 m/s when the amplitude of the sea level in the open sea is 0.5 m. Such a change is consistent with results of theory (Sect. 5.2) and simulations (Sect. 5.3) of tidal flow dynamics in a complex channel network. It is noteworthy that the theory and simulations produce a sine wave pattern for the tidal velocity in the connecting channel, but the CCM simulations indicate an asymmetric pattern in which the velocity component increases more slowly in the outgoing tides, although the velocity component decreases more rapidly in the incoming tides. The underlying causes of the asymmetric velocity changes might not be understood up to this point, but they might be related to the unconsidered processes in the theory of tidal flow dynamics explained in preceding sections. Considering wind forcing at the ocean surface, the current velocity in the connecting channel in summer has a phase shift of −1/4T (−3 h) for the tidal level (T = 12 h). In winter, the periodic flows by the ocean tide are not readily discernable. It is noteworthy that the phase shift of the current velocity in the connecting channel does not occur under the strong meteorological forcing and that strong southward currents in the high tide are enhanced by the strong northerly winds. Meteorological forcing such as that which occurs by strong wind is expected to change the tidal flow pattern considerably, but further study is necessary to ascertain the effects of meteorological forcing on the coastal currents in this region.

Fig. 5.23

Time series of tidal level (orange color lines) and surface current component (blue color lines) at the connecting channel in a summer simulated without wind forcing, b summer simulated with wind forcing, c winter simulated without wind forcing, and d winter simulated with wind forcing

It is readily apparent that the connecting channel linking Funauki and Shirahama bays causes the surface water exchange among the bays under near-calm conditions in summer. Their amplitude is closely related to the aspect ratio of the channels. As a consequence, the existence of the connecting channel drastically changes the water quality in the bays. Moreover, it might affect the dispersions of fruits and seeds of their respective coastal ocean ecosystems.

5 Concluding Remarks

This chapter presented discussion of the physical features of coastal current in Funauki and Shirahama bays in the northwestern part of Iriomote Island, based on theoretical, observational, and numerical investigations.

Because Shirahama Bay with shallower water and Funauki Bay with deeper water are connected by a channel, the respective flow pattern in the bays is very complex compared with those of Sakiyama Bay and Amitori Bay, as discussed in Chap. 4. Seawater exchange in Shirahama Bay would be more active than that in Funauki Bay if there is no connecting channel. As a result, the low-salinity water originating from rivers is more stagnant in Funauki Bay than in Shirahama Bay. Theoretical considerations have indicated that the flow in the connecting channel is controlled by the aspect ratio (ratio of length to depth) of the bays. The existence of the connecting channel strongly influences the flow and water quality patterns throughout the bays. In the realistic case (the moderate aspect ratio of the connecting channel), the connecting channel actively exchanges surface water among the bays. In the case of the smaller aspect ratio (longer or shallower) of the connecting channel, the seawater exchange at the connecting channel becomes inactive, leading to the greater difference in salinity among the bays. For a higher aspect ratio (shorter or deeper) of the connecting channel, not only bay–bay exchange but also ocean–bay exchange becomes inactive, resulting in stagnant and low-salinity conditions throughout the bays.

The possibility exists that the existence of the connecting channel changes the tidal currents and water quality in both bays and affects the dispersion processes of fruits and seeds of coastal ocean ecosystems.