Dynamical Properties of Coastal Currents in the Northwestern Part of Iriomote Island Part. 1—Sakiyama and Amitori Bays

Abstract

The physical properties of coastal currents in semi-closed bays (e.g., Sakiyama and Amitori bays) in the northwestern part of Iriomote Island are discussed in this chapter, based on the results of theoretical, observational, and numerical investigations. According to the tidal flow dynamics in a single channel, these bays in this region are categorized as “deep bays,” in which little difference in phase and amplitude of the tidal levels exists from the open ocean. Ocean waters therefore flow in a bay in the incoming tide. By contrast, bay waters flow out to the open ocean in the outgoing tide. In Sakiyama Bay with its shallower waters, surface seawater exchange between the bay and ocean is active under near-calm conditions, leading to an environment in which the river water mass near the surface layer is more likely to flow out to the open ocean. By contrast, in Amitori Bay with the deeper waters, near-surface river water is stagnant under near-calm conditions. It selectively distributes to the eastern side of the bay because of the Earth’s rotation. The theory of tidal flow dynamics in a single channel suggests that differences of coastal currents between Sakiyama and Funauki bays are mainly attributable to the difference of the aspect ratio, the length to depth ratio, between the two bays. Such a difference in physical properties in the coastal currents is expected to affect the coastal ocean ecosystem distribution in this region.

This chapter is based on works reported by Yoshino et al. (2011, 2016).

1 Introduction

The northwestern part of Iriomote Island has rich coastal oceanic ecosystems with intricate topography, leading to the considerable spatial variation of reef-building corals (Sect. 1.4), mangrove forests, and Enhalus acoroides (Sect. 1.5). Its coastal oceanic ecosystems are strongly influenced by various environmental factors, which comprise physical factors (i.e., radiations, temperature, wave, current, and turbidity), chemical factors (i.e., dissolved oxygen, salinity, and nutrients), topographical/geological factors (i.e., depth and bottom sediments), biological factors (i.e., competitors and enemies), and anthropogenic factors (i.e., landfill and sediment discharge). Because the physical factors are especially important in this region, we require quantitative estimation of the coastal current fields to develop the strategies to improve biodiversity and to preserve natural ecosystems.

In the northwestern part of Iriomote Island, semi-enclosed bays continue from south to north: Sakiyama Bay, Amitori Bay, Funauki Bay, and Shirahama Bay (see Sects. 1.1 and 1.2, and Fig. 1.1). In addition, each of the bays has a few rivers. Sakiyama Bay is a shorter and shallower bay of about 2 km length and about 10 m depth, with two major rivers: Painta River and Ubo River. Amitori Bay next to Sakiyama Bay is longer and deeper, about 3 km long and about 70 m deep, with two major rivers: Ayanda River and Udara River. Such topographical differences among the bays might engender differences of physical factors, consequently influencing the distributions of respective coastal oceanic ecosystems in this region.

In this chapter, differences of coastal current fields in Sakiyama and Amitori bays located in the northwestern part of Iriomote Island are discussed based on theoretical, observational, and numerical perspectives.

2 Tidal Flow Dynamics in a Single Channel

• (a) Theoretical Formulae

First, the theory of the tidal flow dynamics in a single channel, which is simplified as a rectangular bay portrayed in Fig. 4.1, is introduced. Then, the physical properties of tidal currents in Sakiyama and Amitori bays are discussed. The basic equation system of this theory comprises a momentum equation and a mass continuity equation describing an idealized rectangular semi-closed bay (Unoki 1993). In these equations, $\eta_{0}$ represents the tidal level in the open ocean given by a simple sine curve with a period of $T$, and $\eta$ denotes the resultant tidal level homogeneous in a channel (bay) with area of ${\rm A}$. The width, length, and depth in a channel are expressed, respectively, as w, l, and $h$. Therefore, the channel area is expressed as ${\rm A} = wl$. The current velocity is $u$ in a channel, where the direction from offshore to onshore is positive. We assume that the meteorological forcing and river discharge can be ignored under calm conditions. Then, the momentum equation and mass continuity equation in a channel are described as follows:

Fig. 4.1

Schematic diagram of tidal flow dynamics in a single channel

$$\frac{{{\text{d}}u}}{{{\text{d}}t}} = - g\frac{{\eta - \eta_{0} }}{l} - \frac{\beta \, u}{h}$$

(4.1)

$$\frac{{{\text{d}}\eta }}{{{\text{d}}t}} = \frac{whu}{\rm A} = \frac{hu}{l}$$

(4.2)

where the first term on the right side of the momentum equation Eq. (4.1) is the sea surface gradient force and $g$ represents the gravitational force. The second term on the right side of Eq. (4.1) expresses the ocean bottom drag as linearly approximated by $\beta = (8/3\pi )C_{f} \hat{U}$ and $C_{f} = 0.0026$. Also, $\hat{U}$ stands for the amplitude of tidal current velocity $u$ of which optimal value is found by the successive iteration method. The right side of the mass continuity equation Eq. (4.2) expresses the rate of discharge in a channel. The linear equation systems Eqs. (4.1) and (4.2) are solvable by assuming that variations of the tidal level $\eta$ and current velocity $u$ in a channel responded by the tidal level $\eta_{0}$ in the open ocean can be represented in the following exponential forms.

$$\eta_{0} = M{\text{e}}^{i\sigma t} ,\eta = \hat{\eta }{\text{e}}^{i\sigma t} ,u = \hat{u}{\text{e}}^{i\sigma t}$$

(4.3)

Therein, $M$ (real number) denotes the amplitude of tidal level in the open ocean, $\hat{\eta }$ and $\hat{u}$ (complex number), respectively, express the amplitude and phase change of tidal level and current velocity in a channel. The amplitudes of tidal level and current in a channel are expressed, respectively, by $|\hat{\eta }|$ and $|\hat{u}|$. The phase change of tidal level and current in a channel are written, respectively, by $\arg (\hat{\eta })$ and $\arg (\hat{u})$. $\sigma ( = 2\pi /T)$ is the radian frequency of tidal level in the open ocean with a period $T$ of 12 h. Based on Eqs. (4.1), (4.2), and (4.3), we obtain the following first-order algebraic equation system.

$$\hat{\eta } + A\hat{u} = M$$

(4.4)

$$\hat{\eta } - a\hat{u} = 0$$

(4.5)

Then, we can solve $\hat{\eta }$ and $\hat{u}$ as shown below.

$$\hat{u} = \frac{1}{A + a}M$$

(4.6)

$$\hat{\eta } = \frac{a}{A + a}M$$

(4.7)

In those equations, $A$ and $a$ are the complex number expressed in seconds.

$$A = \left( {\frac{\beta }{h} + i\sigma } \right)\frac{l}{g}$$

(4.8)

$$a = - i\frac{wh}{{\sigma {\text{A}}}} = - \frac{i}{\sigma }\frac{h}{l}$$

(4.9)

Therein, $i$ is the imaginary unit. Denominator $A + a$ in Eqs. (4.6) and (4.7) is derived as the following.

$$A + a = \frac{\beta l}{gh \, } + i \, \left( {\frac{\sigma l}{g} - \frac{h}{\sigma l}} \right)$$

(4.10)

Then, the relations between the complex parameters $A$ and $a$ defined by Eqs. (4.8) and (4.9) are compared. In these definitions, $A$ and $a$ include two parameters “length $l$” and “depth $h$” of a channel, implying that the aspect ratio “$l/h$” is an important parameter to express tidal currents in a channel. Figure 4.2 presents the relations of aspect ratio ($l/h$) and complex parameters ($A$ and $a$) with fixed length of $l$ = 10,000 m. Because $A$ is a complex number obtained from the momentum equation Eq. (4.1) and because $a$ is pure imaginary number obtained from the mass continuity equation Eq. (4.2), the real part (solid lines) and imaginary part (dashed lines) are individually compared. Figures 4.3 and 4.4, respectively, show the relations of aspect ratio ($l/h$) and the amplitude of current velocity $|\hat{u}|$ and tidal level $|\hat{\eta }|$ with a fixed ocean tide of $M = 1\,{\text{m}}$ . In this comparison, the radian frequency of ocean tide and gravitational force are set, respectively, to $\sigma = 1.45 \times 10^{ - 4} \,1/{\text{s}}$ and $g = 9.8\,{\text{m/s}}^{ 2}$.

Fig. 4.2

Relations between the aspect ratio of the channel $l/h$ and complex parameters ($\text{Re} (A)$, ${\text{Im(}}A)$, and ${\text{Im(}}a)$)

Fig. 4.3

Relation between the channel aspect ratio $l/h$ and the amplitude of the current velocity $|\hat{u}|$

Fig. 4.4

Relation between the aspect ratio $l/h$ and tidal amplitude $|\hat{\eta }|$

In the smaller aspect ratio of a channel ($l/h < 2.18 \times 10^{3}$), complex parameter $a$ derived from the mass continuity equation becomes more dominant. Such a bay is designated as a “deep bay” in this study. In this case, the larger the aspect ratio $l/h$ of a bay, the lager the amplitude of current velocity $|\hat{u}|$ in a bay. Then, the amplitude of tidal level $|\hat{\eta }|$ in a bay is nearly 1.0 m, which is same size as the amplitude of the tidal level $M$ in the open ocean.

In the moderate aspect ratio of a channel ($2.18 \times 10^{3}$ ≤ $l/h$ < $4.63 \times 10^{4}$), two complex parameters, $A$ and $a$, are mutually comparable, implying that the each of the terms in both the momentum equation and mass continuity equation must act comparably on the tidal currents. Such a bay is designated as a “shallow bay” in this study. When the aspect ratio of a bay becomes $l/h$ = $6.85 \times 10^{3}$, the amplitude of current velocity $|\hat{u}|$ in a bay corresponds roughly to a peak value of 0.7 m/s. The amplitude of tidal level $|\hat{\eta }|$ in a bay is about 0.7 m, which is less than that (M = 1.0 m) of the open ocean.

In the larger aspect ratio of a channel ($l/h$ ≥ $4.63 \times 10^{4}$), the complex parameter $A$ derived from the momentum equation Eq. (4.1) dominates the complex parameter $a$ obtained from the mass continuity equation Eq. (4.2). Such a bay is designated as a “very shallow bay” in this study. In this case, the larger the aspect ratio $l/h$ of a bay, the smaller the amplitudes of tidal current $|\hat{u}|$ and level $|\hat{\eta }|$, respectively, approaching 0 m/s and 0 m.

Next, we intend to extend the detailed discussion to elucidate the bays’ three types: “very shallow bay,” “shallow bay,” and “deep bay.”

• (b) Case of “very shallow bay”

First, we consider $l/h$ = $4.63 \times 10^{4}$ in which ${\text{Im(}}A)$ and ${\text{Im(}}a)$ are the same size but which are at least one order of magnitude smaller than $\text{Re} (A)$, according to Fig. 4.2. Such a shallow-floor bay is categorized as a “very shallow bay” for this study. In this situation, the term of the mass continuity equation in Eq. (4.2) is smaller, but the terms of the momentum equation, especially for the second term of the ocean bottom drag ($\beta /h$ in $\text{Re} (A)$) in Eq. (4.1), become more dominant. Because the imaginary part of $A + a$ in Eq. (4.10) is nearly 0, one can obtain depth $h$ of this case as presented below.

$$h = \frac{{\sigma^{2} \, l^{2} }}{g}$$

(4.11)

If depth $h$ satisfies Eq. (4.11) (i.e., $l$ = 10,000 m and $h$ = 0.22 m), then $A + a$ in Eq. (4.10) can be approximated as shown below.

$$A + a \approx \frac{\beta \, l}{g \, h \, }$$

(4.12)

In addition, one can obtain the approximated forms of Eqs. (4.6) and (4.7) such that

$$\hat{u} \approx \frac{g}{\beta }\left( {\frac{l}{h}} \right)^{ - 1} M$$

(4.13)

$$\hat{\eta } \approx - i\frac{g}{\sigma \, \beta \, }\left( {\frac{l}{h}} \right)^{ - 2} M$$

(4.14)

The amplitudes of current velocity $|\hat{u}|$ and tidal level $|\hat{\eta }|$ in a bay, shown in Eqs. (4.13) and (4.14), provide high accuracy in a “very shallow bay” with the larger aspect ratio of a channel. In $l/h$ ≥ $4.63 \times 10^{4}$, the effect of ocean bottom drag contributes greatly to the temporal change of tidal current velocity $\hat{u}$, as shown in Eq. (4.13) and Fig. 4.3. Therefore, $|\hat{u}|$ is proportional to depth $h$ in a bay and is inversely proportional to length $l$ of a bay. That is, $|\hat{u}|$ is inversely proportional to the aspect ratio $l/h$ of a bay. The positive maximum of $u$ in a bay (from ocean to bay) appears at the high-tide time, although the negative minimum of $u$ in a bay (from bay to ocean) appears at the low-tide time. Therefore, no phase difference exists between tidal flow ${\text{arg(}}\hat{u} )$ in a bay and tidal level ${\text{arg(}}M )$ in the open ocean. The ocean bottom drag effect also influences the temporal change of tidal level $\hat{\eta }$, as shown in Eq. (4.14) and Fig. 4.4, so $|\hat{\eta }|$ is proportional to the square of depth $h$ in a bay and is inversely proportional to the square of length $l$ in a bay. Consequently, $|\hat{\eta }|$ is inversely proportional to the square of the aspect ratio $l/h$ of a bay. The phase of tidal level ${\text{arg(}}\hat{\eta } )$ in a bay lags behind that ${\text{arg(}}M )$ of the open ocean by 1/4 $T$ (3 h) because of the existence of “$- i$” in Eq. (4.14).

• (c) Case of “shallow bay”

If $l/h$ = $6.85 \times 10^{3}$, which is smaller than the previous threshold $( = 4.63 \times 10^{4} )$, then the amplitude of tidal velocity $|\hat{u}|$ in a bay reaches a peak, as presented in Fig. 4.3. In such a case, $\text{Re} (A)$ and ${\text{Im(}}a)$ are the same size, but are almost one order larger than ${\text{Im(}}A)$, according to Fig. 4.2. In other words, the effect of ocean bottom drag gradually decreases with depth $h$, although the effect of mass conservation gradually increases with depth $h$. These effects on the amplitude of tidal velocity $|\hat{u}|$ in a bay are mutually compensatory, becoming a peak of $|\hat{u}|$. Such a transitional bay is categorized as a “shallow bay” in this study. Because the real part of Eq. (4.8) is just equal to the imaginary part of Eq. (4.9), the following holds.

$$h = l \, \sqrt {\frac{\sigma \, \beta }{g}}$$

(4.15)

If the depth $h$ satisfies Eq. (4.15) (i.e., $l$ = 10,000 m and $h$ = 1.53 m), then $A + a$ in Eq. (4.10) can be approximated as shown below.

$$A + a \approx \frac{\beta l}{gh \, } - i \, \frac{\beta l}{gh \, }$$

(4.16)

One can obtain the approximated forms of Eqs. (4.6) and (4.7) as the following.

$$\hat{u} \approx \frac{1}{2}\frac{g}{\beta }\left( {\frac{l}{h}} \right)^{ - 1} (1 + i)M$$

(4.17)

$$\hat{\eta } \approx \frac{1}{2}\frac{g}{\sigma \beta \, }\left( {\frac{l}{h}} \right)^{ - 2} (1 - i)M$$

(4.18)

The amplitude of tidal velocity $|\hat{u}|$ and tidal level $|\hat{\eta }|$ in a bay, estimated by Eq. (4.17) and (4.18), are 0.7 m/s and 0.7 m, respectively, which are consistent with the values estimated by exact solutions in Eqs. (4.6) and (4.7). In this case, the ocean bottom drag effect decreases gradually with depth $h$, thereby increasing $|\hat{u}|$. In contrast, the effect of mass conservation also increases with depth $h$, leading to the decrease of $|\hat{u}|$. When these two effects approximately balance, then the amplitude of tidal current $|\hat{u}|$ in a bay shows a peak. The phase of tidal current ${\text{arg(}}\hat{u} )$ in a bay is earlier by 1/8 $T$ (1.5 h) from that ${\text{arg(}}M )$ in the open ocean. For this reason, Eq. (4.17) includes “$1 + i$” making the phase shift earlier. According to Eq. (4.18), although the magnitude of tidal level $|\hat{\eta }|$ in a bay is decayed by the ocean bottom drag, the phase of tidal level ${\text{arg(}}\hat{\eta } )$ in a bay is delayed by 1/8 $T$ (1.5 h) from that ${\text{arg(}}M )$ of the open ocean, because of “$1 - i$”, making the phase shift later.

• (d) Case of “deep bay”

If aspect ratio $l/h$ is smaller than $6.85 \times 10^{3}$, then the amplitude of tidal velocity $|\hat{u}|$ declines thereafter, according to Fig. 4.3. Also, Fig. 4.2 shows that, in the case of $l/h$ = $2.18 \times 10^{3}$, $\text{Re} (A)$ and ${\text{Im(}}A)$ are mutually comparable and are one order smaller than ${\text{Im(}}a)$. In other words, the ocean bottom drag effect can be safely neglected. The mass conservation becomes a dominant effect. Such a bay is categorized as a “deep bay” in this study. Because the real part $\text{Re} (A)$ in Eq. (4.8) is equal to the imaginary part ${\text{Im(}}A)$ in Eq. (4.8), the following expression can be obtained.

$$h = \frac{\beta }{\sigma }$$

(4.19)

If depth $h$ satisfies with Eq. (4.19) (i.e., $l$ = 10,000 m and $h$ = 4.58 m), then the complex parameter $A + a$ is approximated to the complex parameter $a$. For $h$ = 4.58 m, $A + a$ in Eq. (4.10) become a simple form as shown below, because of $|A| << |a|$.

$$A + a \approx a = - \frac{i}{\sigma }\frac{h}{l}$$

(4.20)

As a result, Eqs. (4.6) and (4.7) can be simplified.

$$\hat{u} \approx \frac{1}{a}M = i\sigma \left( {\frac{l}{h}} \right)M$$

(4.21)

$$\hat{\eta } \approx M$$

(4.22)

These two equations, Eqs. (4.21) and (4.22), are sufficiently accurate to account for the tidal velocity $\hat{u}$ and tidal level $\hat{\eta }$ in the deep bay with an aspect ratio $l/h$ of less than $6.85 \times 10^{3}$. In this case, the ocean bottom drag effect seldom influences the tidal currents. According to Eq. (4.21) and Fig. 4.3, the effect of the mass conservation equation Eq. (4.2) mainly dominates that of the momentum equation Eq. (4.1). Also, Eq. (4.21) includes “$i$”. Therefore, the phase of tidal current ${\text{arg(}}\hat{u} )$ in a bay is 1/4 $T$ (3 h) earlier than that ${\text{arg(}}M )$ of the ocean tide. As a consequence, the maximum peaks of $u$ in a bay appear at incoming tide. The minimum peaks of $u$ in a bay emerge at outgoing tide. The tidal velocity magnitude $|\hat{u}|$ is proportional to length $l$ and inversely proportional to depth $h$. Actually, $|\hat{u}|$ is proportional to aspect ratio $l/h$. Apparently, Eq. (4.22) and Fig. 4.4 suggest that the amplitude of tidal level $|\hat{\eta }|$ is no longer affected by the ocean bottom drag and is nearly corresponding to the amplitude of the ocean tide $M$. The phase of tidal level ${\text{arg(}}\hat{\eta } )$ is no longer delayed from that ${\text{arg(}}M )$ of the open ocean, irrespective of the aspect ratio $l/h$.

• (e) Cases of Sakiyama and Amitori bays

Based on the discussions presented above, one can then turn to consider the properties of tidal currents in the Sakiyama and Amitori bays, which are similar to the idealized rectangular semi-closed bays discussed in the previous subsections.

In Sakiyama Bay, the representative length $l$ and depth $h$ are estimated, respectively, as approximately 2000 and 2 m. Figure 4.5 shows a time series of tidal velocity and tidal level during one day under the settings of Sakiyama Bay, when $M$ = 0.5 m. The tidal level in the bay corresponds to that of the open ocean. Amplitude decay and phase lag no longer occur. The amplitude of tidal velocity $|\hat{u}|$ in the bay is 0.073 m/s, and the phase of tidal velocity $\arg (\hat{u})$ in the bay is 1/4 $T$ (3 h) earlier than that $\arg (M)$ of the open ocean. The aspect ratio $l/h$ in Sakiyama Bay is 1000, which is categorized as a “deep bay” ($A = 0.00164 + i0.0297$, $a = - 6.88i$). Its physical features are consistent with those presented in the earlier discussion.

Fig. 4.5

Time series of tidal level $\hat{\eta }$ and current velocity $\hat{u}$ in Sakiyama Bay, as predicted by the theory of tidal flow dynamics in a single channel

In Amitori Bay, located at the next to Sakiyama Bay, the representative length $l$ and depth $h$ are estimated, respectively, as about 3000 and 50 m. Figure 4.6 shows a time series of tidal velocity $u$ and tidal level $\eta$ during one day under the settings of Amitori Bay, when $M$ = 0.5 m. The amplitude of tidal level $\left| {\hat{\eta }} \right|$ in the bay corresponds to that $M$ of the open ocean. The amplitude decay and phase lag no longer occur as they do in Sakiyama Bay. The amplitude of tidal velocity $|\hat{u}|$ in the bay is 0.0043 m/s. The phase of tidal current $\arg (\hat{u})$ is 1/4 $T$ (3 h) earlier than that $\arg (M)$ of the ocean tide. The aspect ratio $l/h$ of Amitori Bay is 60, which is also categorized as a “deep bay” ($A$ = $0.0000581 + i0.0445$, $a$ = −114i).

Fig. 4.6

Time series of tidal level $\hat{\eta }$ and current velocity $\hat{u}$ in Amitori Bay, as predicted using the theory of tidal flow dynamics in a single channel

Both Sakiyama and Amitori bays show “deep bay” behavior, but the aspect ratio $l/h$ of Sakiyama Bay is about 17 times higher than that of Amitori Bay. Furthermore, the amplitude of tidal velocity $u$ in Sakiyama Bay is about 17 times larger than that of Amitori Bay, consistent with Eq. (4.21) in the “deep bay” theory. In Sakiyama Bay with larger $l/h$, the seawater exchange at the near-surface layer might take place actively. In Amitori Bay with smaller $l/h$, surface seawater is likely to stagnate in a bay. Such a difference of physical properties might strongly influence the soil particle transport from rivers and the resultant distributions of coastal oceanic ecosystems.

Any bay in the northwestern part of Iriomote Island is classified as a “deep bay,” which is explainable by Eqs. (4.21) and (4.22) in the previous subsection. It should be remembered that the distributions of physical properties are never homogeneous in a realistic bay, while the tidal flow theory in this study is assumed to be horizontally homogeneous in an idealized bay.

3 Observations and Simulations

In this section, we next examine detailed current fields within Amitori Bay, based on results of in situ observations and numerical simulations.

• (a) In situ observations

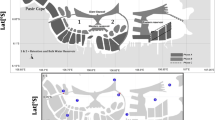
First, observational results of coastal currents within Amitori Bay are discussed in this subsection. We conducted in situ observations during two months from October 2010. Detailed explanations have been made of the observational instruments used for this study in Chap. 2. As presented in Fig. 4.7, a total of five observational points are present within the area in Amitori Bay. Those points are distributed uniformly and broadly within Amitori Bay to identify the horizontal properties of coastal currents in the semi-closed bay. Observed data are the temperature (Points 1, 2, 3, 4, and 5 at three depths), salinity (Points 1 and 5 at two depths), illuminance (Points 1, 3, 4, and 5 at a one depth), tidal level (Point 2), significant wave height (Point 2), wave direction (Point 2), wave direction (Point 2), and current velocity (Point 2).

Fig. 4.7

Referred from Yoshino et al. (2011)

Computational domain of CCM shown with five observational points in Amitori Bay.

As described herein, we specially examine the observational results of temperature and salinity. Figure 4.8 shows time series of three-depth temperatures at the five observational points during November 2–7, 2010, under mostly cloudy conditions with weaker meteorological forcing. Especially at Points 1, 3, and 5, a considerable temperature drop is apparent at a 1 m depth. Such a large temperature drop in the surface layer might be regarded as attributable to “radiative cooling” during night time. However, that reason might be excluded from several possible causes, suggesting cloudy conditions during this period and no temperature drop at Point 2. Radiative cooling might occur homogeneously, depending not on the observational points because the target bay is sufficiently narrow that it is not affected by inhomogeneities of meteorological forcing. Granting that there may be substantial radiative cooling at the ocean surface, one might infer that temperature drops would take place anywhere in Amitori Bay. One another reason for surface temperature drops might be “vertical mixing (entrainment)” with cold deep water. However, that might be incorrect because the deeper water has higher temperature than the surface water, as presented in Fig. 4.8. The “horizontal advection” of cold river water may be another reason for partial temperature drops in Amitori Bay. We can infer that the river water with a lower temperature at the surface layer in this season flows out from the bay to the ocean. It would hardly be surprising if horizontal advection of the river water occurs selectively in the bay, except for Points 2 and 4.

Fig. 4.8

Referred from Yoshino et al. (2011)

Time series of temperature at −1 m from the sea surface, +15 m from the bottom, +5 m from the bottom, and at the five observational points shown in Fig. 4.7.

The assumption of “horizontal advection” can be justified by the tidal flow dynamics discussed in the previous section. Figure 4.9 shows a time series of the tidal level at Point 2 during the same period as Fig. 4.8. Because Amitori Bay is classified as a “deep bay,” the tidal level within the bay changes in phase with the ocean tide, and the tidal current within the bay stagnates uniformly. Comparison between Figs. 4.8 and 4.9 indicates that surface temperature drops are synchronized with outgoing tide during night time. The phase lag of temperature drop at Point 1 is regarded as resulting from the longer traveling time from the river mouth to Point 1. The night-time temperature drops in the outgoing tide are visible at the eastern side of Amitori Bay (e.g., Point 1), but not at the opposite (western) side (e.g., Point 2). The amount of temperature drop at Point 3 is larger than that at the opposite side (Point 4). The temperature drops in the outgoing tide have not been observed during the daytime, perhaps because of the compensation of low-temperature advections and weak radiation heating. Consequently, a distinct west–east asymmetry is apparent in the mixing processes between tidal water flow and river water flow within Amitori Bay.

Fig. 4.9

Referred from Yoshino et al. (2011)

Time series of sea level height at Point 2 in Amitori Bay.

Figure 4.10 shows the horizontal distributions of observed surface temperatures averaged temporally over six-day periods and interpolated horizontally. Higher ocean water temperatures are located at the western side of Amitori Bay. Lower river water temperatures are shifted to the opposite (eastern) side. It is readily apparent that there is a strong west–east asymmetry of surface temperature. The averaged distributions show clear asymmetry, implying that asymmetric tidal currents dominates steadily under calm conditions with cloudy skies and low wind speeds. In situ observations suggest that for some reason, low-temperature and low-salinity river water is likely to flow selectively in the eastern side in Amitori Bay. By contrast, high-temperature and that high-salinity ocean water is prone to dominate in the western side in Amitori Bay.

Fig. 4.10

Referred from Yoshino et al. (2011)

Horizontal distribution of sea surface temperatures averaged during 6 days observed in Amitori Bay.

• (b) Numerical simulations

Next, the physical properties of tidal currents in Amitori Bay can be discussed based on the results of numerical simulations obtained using a multi-sigma-coordinate coastal current model (CCM) (Murakami et al. 2004). Detailed information related to the CCM is presented in Chap. 3. The computational domain having grid size of 50 m is presented in Fig. 4.7. In the lateral boundary conditions of CCM, the tidal level is defined by the outputs of ocean tidal model NAO (Matsumoto et al. 2000). The salinity in the open ocean is set to 34.4 ‰, held constant during the simulation periods. In the two rivers located at the head of Amitori Bay, the river flow rate and salinity are fixed, respectively, at 0.01 m³/s and 0‰ during the simulation periods. The momentum, temperature, mass, and salinity conservation equations are numerically integrated during October 4–9, 2010 (a total of five days) with a time step interval of 1 s.

Because the numerical simulations in this study are designed to elucidate the mixing processes between the ocean water and river water in Amitori Bay, meteorological forcing at the sea surface (the fluxes of water, heat, radiation, and momentum) is fixed at zero in CCM. Therefore, no circulation occurs in the bay driven by wind and buoyancy. We can consider the salinity as a passive tracer.

Figure 4.11 portrays the horizontal distributions of salinity and current velocity vectors at the surface layer in the outgoing tide (21:00UTC October 7, 2010) and incoming tide (15:00UTC October 7, 2010). In the outgoing tide presented in Fig. 4.11a, low-salinity water originating from two rivers spreads from the head to the mouth of Amitori Bay. As shown previously, the low-salinity river water selectively flows out to the eastern side of Amitori Bay (right side of the figure). In the incoming tide presented in Fig. 4.11b, the upwelling of the high-salinity water originating from the open ocean is apparent near the head of the bay. Upwelling flows near Point 5 result from the exit of the sea valley portrayed in Fig. 4.7. At the time of the incoming tide, the low-salinity river water from the river mouth is trapped close to the head of the bay. The low-salinity river water in the middle of the bay, which is transported in the previous incoming tide, is mixed with the high-salinity ocean water near the center. The mixing processes between river water and ocean water never reach to the western side of Amitori Bay. Such physical properties of tidal flow in Amitori Bay are characterized as a deep bay in which tidal velocity is weaker and as calm conditions in which the meteorological forcing is weaker.

Fig. 4.11

Referred from Yoshino et al. (2011)

Horizontal distributions of surface current vectors and surface salinity simulated in Amitori Bay in a falling tide and b rising tide.

Figure 4.12 shows the horizontal distributions of salinity and current velocity vectors at the surface layer averaged during the three-day periods (last half of the simulation periods). It is readily apparent that the river water, on average, is consistently flowing out to the eastern side of the bay and that it is unlikely to affect the opposite (western) side of the bay. Such a west–east asymmetry of tidal currents is expected to control, indirectly, the asymmetries of the horizontal distribution and coverage of coral reefs, which is apparent in Amitori Bay.

Fig. 4.12

Referred from Yoshino et al. (2011)

Horizontal distributions of surface current vectors and surface salinity averaged during 3 days simulated in Amitori Bay.

Why does the west–east asymmetry of tidal currents appear at the surface layer in Amitori Bay? When we assume that river water flows at the surface without the effects of friction and entrainment, then the potential vorticity ${\text{PV}}$ of a river water mass should be conserved as shown below.

$${\text{PV}} = \frac{{\zeta_{z} + f}}{h} = {\text{const}} .$$

(4.23)

In that equation, $h$ represents the river water depth, $\zeta_{z}$ signifies the vertical vorticity of the river water, $f$ denotes the planetary vorticity ($= 2\varOmega { \sin }\phi$), $\varOmega$ expresses the angular velocity of the Earth’s rotation, and $\phi$ stands for the latitude. In Amitori Bay, located in the Northern Hemisphere, the initial value of ${\text{PV}}$ is expected to be greater than 0 because of $\zeta_{z}$ = 0 and $f$ > 0. When a water mass flows out from the mouth of river, then the water mass will spread out with decreasing depth $h$. To conserve the potential vorticity ${\text{PV}}$, the vertical vorticity $\zeta_{z}$ is expected to be less than 0. As a result, negative vertical vorticity ($\zeta_{z}$ < 0) may cause a counterclockwise rotation of the river flow. In other words, the Earth’s rotation changes northward currents from the river to the eastward. Therefore, the river flow is steered toward right side (left side) in the Northern (Southern) Hemisphere. At the equator, the Earth’s rotation never affects the river flow in the bay.

Figure 4.13 shows the horizontal distributions of salinity and current velocity vectors at the surface layer averaged during the three-day periods (last half of the simulation periods) in the case of (a) Northern Hemisphere ($\phi$ = +24°), (b) equator ($\phi$ = 0°), and (c) Southern Hemisphere ($\phi$ = −24°). These sensitivity experiments indicate that, in Amitori Bay, the surface river water is likely to flow to the eastern (western) side of the bay in the case of the Northern (Southern) Hemisphere, and shows no west–east asymmetry in the case of the equator. Consequently, it can be concluded that the asymmetric flow of a surface river water mass, which can be confirmed in observations and simulations, results from the effect of the Earth’s rotation called as the “Colioris force.”

Fig. 4.13

Horizontal distributions of surface current vectors and surface salinity averaged during 3 days simulated as a $\phi$ = 24°, b $\phi$ = 0° and c $\phi$ = −24°

However, when entrainment, ocean bottom drag, and meteorological forcing are strong, then the conservation law of potential vorticity expressed in Eq. (4.23) is not valid, leading to a lack of asymmetric pattern of a surface river flow. It is expected that such an asymmetric pattern is a typical phenomenon under the “deep bay” (i.e., small aspect ratio of a bay) with the “calm conditions” (i.e., low wind speeds).

4 Concluding Remarks

The physical properties of coastal currents in semi-closed bays in the northwestern part of Iriomote Island were examined as described in this chapter based on theoretical, observational, and numerical investigations.

The tidal flow dynamics in a single channel, introduced in this chapter, indicated that Sakiyama and Amitori bays were classified as “deep bays,” for which the amplitude and phase of tidal level in the bay were the almost same as those in the open ocean and for which the tidal velocity in incoming tide (outgoing tide) showed a maximum (minimum) peak. In Sakiyama Bay with its lager aspect ratio (with shallower floor), the tidal seawater exchange was relatively high. Surface river water flowed easily out to the open ocean under calm conditions. In Amitori Bay with a smaller aspect ratio (with deeper floor), the tidal seawater exchange was relatively weak. Surface river water from the head of the bay was likely to stagnate. Under calm conditions, the stagnant river water flowed selectively out to the eastern side of the bay because of the effects of Earth’s rotation. The differences of physical properties between Sakiyama and Amitori bays can be explained by the different aspect ratio of the bays.

Such influential differences of tidal flow patterns are regarded as affecting the differences of distribution and structure of coastal ocean ecosystems in this area.