Keywords

1 Introduction

1.1 Capsule Network Architecture

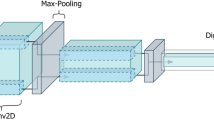
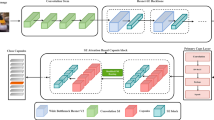
The vector based encoder–decoder neural architecture [1] mainly comprises of six layers namely convolutional 2D layer, primary capsule layer, digit capsule layer along with three fully connected layers while handling a total of 8,238,608 parameters during the process of image reconstruction.

The detailed architecture is as demonstrated (see Fig. 1).

Fig. 1
figure 1

Layer wise Capsule Network architecture

Full size image

A detailed breakdown of the layers of the capsule network is as follows.

Encoder. The encoder accepts the input image and predicts the set of structure variables corresponding to transformation matrices while dealing with margin as well as reconstruction loss. The functionality of each of the layers is as described below.

Convolutional 2D Layer. The layer with 9 × 9 × 1 28 kernels with stride 1, accepts the 28 × 28 input image and outputs a 20 × 20 × 256 tensor and has 20,992 trainable parameters in all.

Primary Caps Layer. This layer which is composed of 32 primary capsule units, accepts the 20 × 20 × 256 tensor from the previous layer, applies 9 × 9 × 256 convolutions to the input volume and produces combinations of the already detected features. The output of this layer is a 6 × 6 × 8 tensor and has 5,308,672 trainable parameters.

Digit Caps Layer. The 10 digit capsules layer accepts the 6 × 6 × 328 dimensional tensor and maps the input to a 16D capsule output space. These coefficients are then used in routing [2]. The layer has 149,760 trainable parameters per capsule.

The loss of the system is defined by

$$ {\text{loss}}\, = \,{\text{margin}}\_{\text{loss}}\, + \,{\text{reconstruction}}\_{\text{loss}} $$
(1)

where the reconstruction loss function is defined by a regularization factor which doesn’t dominate over the marginal loss. The margin loss function for each category c is defined by a zero loss when correct prediction occurs with probability greater than 0.9 or when an incorrect prediction occurs having a probability less than 0.1 (non zero otherwise in either case). The same can be mathematically represented as follows:

$$ L_{c} = T_{c} \hbox{max} \left( {0, \, m^{ + } - \, ||v_{c} ||} \right)^{2} + \, \lambda \, \left( {1 - T_{c} } \right) \, \hbox{max} \left( {0, \, \left| {\left| {v_{c} } \right|} \right| \, - \, m^{ - } } \right)^{2} $$
(2)

where λ is the numerical stability constant, and for a matching training label, there is only one correct DigitCaps capsule while the rest nine remain incorrect. The equation then retracts all values accordingly.

Decoder. The decoder part of the capsule system accepts the image format previously processed by the encoder and produces the final reconstructed output image after passing the input through three fully connected layers which also perform denoising thus, supporting routing by agreement. Each of the layers of the decoder accept processed input from the previous layers and pass the input to the next layer in a feed-forward manner while calculating number of parameters based on bias. The structure of each of the layers is as described below.

Fully Connected Layer #1. The layer with the ReLU activation function accepts the 16 × 10 input from the Digit CapsLayer and produces a 512 vector output while dealing with 82,432 parameters.

Fully Connected Layer #2. This ReLU activated layer accepts the 512 vector output from the previous fully connected layer and produces a 1024 vector output while dealing with 525,312 parameters.

Fully Connected Layer #3. The Sigmoid activated layer accepts the 210 vector output from the previous fully connected layer and produces a 784 vector which is also the 28 × 28 reconstructed output while dealing with 803,600 parameters.

1.2 Orthogonality in Weights

As the training of neural networks is laborious due to vanishing or exploding gradients [3], proliferation or fluctuation in saddle points [4], and/or feature statistic shifts [5], introducing orthogonality in weights ensures faster and more stable convergence during training and is enforced through variants of Frobenius norm regularizer, mutual coherence or restricted isometric properties [6]. Orthogonality implies energy preservation and hence, stabilizes the distribution of activations over the concerned layer. The various methods for enforcement of orthogonalilty are as described below.

Double soft orthogonality regularizer. The soft orthogonality regularizer defined by:

$$ \lambda{||W^{T} W - I||_F}^{2} $$
(3)

is expanded to compensate for under and over complete cases using

$$ \lambda\left({||W^{T} W - I||_{F}}^{2} + {||WW^{T} - I||_{F}}^{2} \right) $$
(4)

where \( W^{T} W \, = \, WW^{T} = \, I \) for an orthogonal W.

Mutual coherence regularizer. The mutual coherence regularization can be defined by:

$$ \lambda \left( {|| \, W^{T} W \, {-} \, I \, ||_{\infty } } \right) $$
(5)

where the gradient can be solved with smoothing techniques applied to the |∞ norm [7].

Spectral restricted isometry property regularizer. This regularization is defined by the following equation:

$$ \lambda \, \sigma \, \left( {W^{T} W \, {-} \, I} \right) $$
(6)

where W is well-conditioned and regularizes computation cost from O(n3) to O(mn2)

2 Related Work

2.1 Capsule Network Architecture

Fundamental research. While capsule networks are still in a nascent stage of research, experiments have been carried out around implementing additional inception blocks [8], and enabling sparsity in activation value distribution of capsules in primary capsule layer [9, 10].

Application research. Capsules have, in recent times, been employed in multitude of tasks including audio processing [11], mobility-on-demand network coordination [12], gait recognition [13], traffic classification for smart cities [14, 15], natural language tasks like sentiment analysis [16] and healthcare applications [17, 18].

2.2 Weight Orthogonality

Past research along the lines of weight orthogonality have been specifically focused toward reducing internal covariate shifts [19, 20], avoiding gradient explosions, exploring soft and hard constraints [21], using nonlinear dynamics to stabilize weight layer-wise activation distribution [20].

3 Methodology

The following section describes the architectural frameworks and the detailed experimental setup used to obtain the results described in Sect. 4.

A pytorch implementation of Capsule Networks was run on a tesla K40c GPU environment while implementing the same on the FashionMNIST [21] dataset. Since, under simplified assumptions [22], it’s concluded that random initialisations produce similar convergence rates as in case of unsupervised pretraining, initial orthogonality wouldn’t necessarily sustain throughout training and could breakdown if improperly regularized. With proper regularization, experimentation proves that adding orthogonality regularizations can impact accuracy as well as empirical convergence. However, the following regularizations and optimizations ensure faster convergence, and hence, have been executed for 20 epochs as the results are known to stabilize thereafter.

The modifications incorporated into the original architecture is as detailed below.

Activation or Transfer function. Activation functions are nonlinear complex functional mappings between incoming data and response variables. Capsule Networks by default employs the ReLU [23] activation function which can be mathematically represented as:

$$ A\left( x \right)\, = \,\hbox{max} \left( {0,x} \right) $$
(7)

However, our past experimentation [24] has shown that newer nonlinear transformations like Swish [22] outperforms standard ReLU. Ramachandran et al. proposed function can hereby be defined in terms of the sigmoid as:

$$ f\left( x \right) \, = \, x.{\text{sigmoid}}\left( {\beta x} \right) $$
(8)

Softmax optimization. In order to enhance the object recognition performance, additional softmax layers [25] are augmented into the decoder of the Capsule architecture and tend to have the same number of nodes as that of the previous layer [26]. The softmax layer computes the probability distributions for all involved classes and is mathematically:

$$ P(y = j|x) = e_{{w_{j} }} T_{{x + b_{j} }} /\sum\limits_{k \in K} {e^{w} k^{{T_{x} }} + b_{k} } $$
(9)

Optimizer. As optimizers like Adam [27] fail to stably converge at extreme learning rates, newer techniques like Adabound [28] tend to work better where the lower bound is ηt and upper bound is ηu with gradient clipping that enhances adaptive moment estimation with dynamic bounds.

Weight orthogonality. The capsnet system has two types of weights: (a) the weights between the primary and digit caps and (b) the dynamic weight connections. Applying the orthogonality equations to both of these ensures coherent and faster convergence.

4 Results and Discussions

The results of the experiments are as follows. The baseline is the original capsule network architecture which achieves maximum accuracy of 93.8% while the architecture with the above-suggested modifications achieves maximum accuracy of 96.3%. Hence, a relative increase of 3.4765% can be observed in the average accuracy values. The same are tabulated (see Table 1).

Table 1 Comparison between the original and the modified Capsule Network architecture in terms of accuracy
Full size table

A visual representation of the same is as follows (see Fig. 2).

Fig. 2
figure 2

Comparison between accuracy of original and modified Capsule Network architecture with reference to discussed dataset

Full size image

5 Conclusion and Future Work

It is evident from the above experimentation that implementation of weight orthogonality along with other optimizations and activation functions, ensure faster convergence and hence, lesser training time while enhancing reconstruction performance. Future work could entail aforementioned optimizations applied to more complex models or further enhancements to the architecture like experimenting with newer techniques and methodologies. While the scientific community continues to explore capsule networks and other upcoming systems, the future could spur out challenging avenues to explore current and newer problems in interdisciplinary spaces as in case of nuclear variability in galaxies [29].