Keywords

1 Introduction

Most of the natural systems around us are subjected to the presence of delayed feedback and are influenced by the uncontrolled environmental noise. For instance, the growth of the cancer cells is non-instantaneous but responds only after some time lag, r > 0. Cancer cells also subject to the uncontrolled factors such as blood pressures variations and individual characteristics like genes and stress impacts [1]. The most suitable mathematical equations describing such system is stochastic delay differential equations (SDDEs). In SDDEs, time delay and noisy behaviour are incorporating to its deterministic counterpart. Due to the presence of both effects, solving SDDEs is not an easy task. Analytical solutions of SDDEs are often unavailable. Thus, numerical methods provide a way to solve problem. The development of numerical methods for SDDEs is now among of the research interest. Amongst of the recent works are [2,3,4]. They proposed explicit numerical methods for solving SDDEs. The convergence and stability analysis of the semi-implicit method for linear SDDEs has been presented in [5]. It is the aimed of this paper to investigate the performance of explicit and semi-implicit Euler methods in approximating the solution of SDDEs. This paper is arranged as follows; Sect. 2 presents the mean-square stability properties of explicit and semi implicit Euler methods. Numerical experiment is conducted in Sect. 3. Concluding remarks are given in Sect. 4.

2 Stochastic Delay Differential Equations

Consider SDDEs of Ito form

$$ \begin{aligned} & dX(t) = f(X(t),X(t - r))dt + g(X(t),X(t - r))dW(t),\,\,\,\,\,t \in [ - r,T] \\ & X(t) =\Phi (t),\,\,\,\,t \in [ - r,0]\, \\ \end{aligned} $$
(1)

where \( \left\{ {W_{t} :t \in {\mathbb{R}}} \right\} \) is a standard Wiener process with W0 = 0 and the increments W(t) − W(s) ∼ N(0, t − s), 0 ≤ s ≤ t. \( f:{\mathbb{R}} \times {\mathbb{R}} \to {\mathbb{R}},\,\,g:{\mathbb{R}} \times {\mathbb{R}} \to {\mathbb{R}} \) are drift and diffusion functions, respectively and Φ(t) is an initial function defined on interval [−r, 0] which is F0 − measurable and right continuous, E‖Φ‖2 < ∞,  where ‖Φ‖ \( \mathop {\sup }\limits_{ - r \le s \le 0} \)|Φ(s)| Φ(t) does not depends on W(t) and r > 0 is a positive fixed delay. Linear SDDEs is written by

$$ \begin{aligned} & dX(t) = \left[ {aX(t) + bX(t - 1)} \right]dt + \left[ {cX(t) + dX(t - 1)} \right]dW(t),\,\,\,\,\,t \in [ - r,T] \\ & X(t) = 1 + t,\,\,\,\,t \in [ - r,0]\, \\ \end{aligned} $$
(2)

2.1 Euler Scheme for SDDEs

Let consider

$$ \begin{aligned} & X_{n + 1} = X_{n} + \left[ {\alpha \left( {aX_{n + 1} + bX_{n + 1 - m} } \right) + \left( {1 - \alpha } \right)\left( {aX_{n} + bX_{n - m} } \right)} \right]h \\ & + \left( {cX_{n} + dX_{n - m} } \right)\Delta W_{n} \\ \end{aligned} $$
(3)

where α is a parameter with 0 ≤ α ≤ 1 and h > 0 satisfies r = mh,  for positive integer, m and tn = nh. Xn is an approximate solution to X(tn). If tn ≤ 0, Xn = Φ(tn). The increment ΔWn = W(tn+1) − W(tn) are independent and normally distributed with mean zero and variance, Δt.

A method is said to be explicit if α = 0,  hence we have

$$ X_{n + 1} = X_{n} + \left( {aX_{n} + bX_{n - m} } \right)h + \left( {cX_{n} + dX_{n - m} } \right)\Delta W_{n} $$
(4)

A semi-implicit Euler scheme is given by (2) for 0 < α ≤ 1.

2.2 Convergence and Mean Square Stability of Euler Scheme

The following results are cited from [5].

Theorem 1

([5]) Assume that ahα < 1. The numerical solution produced by ( 3 ) is convergent to the exact solution of ( 1 ) in the mean square sense with order of 0.5, i.e. there exists a positive constant C such that

$$ \mathop {\hbox{max} }\limits_{1 \le n \le N} \left( {E\left( {\varepsilon_{n} } \right)^{2} } \right)^{{\frac{1}{2}}} \le Ch^{{\frac{1}{2}}} \,\,\,\,\,\,\,\,{\text{as }}h \to 0 $$
(5)

where ɛn = X(tn) − Xn is defined as a global error.

Lemma 1

([5]) If

$$ a < - |b| - \frac{1}{2}c^{2} $$
(6)

then the solution of ( 2 ) is mean square stable, that is

$$ \mathop {\lim }\limits_{t \to \infty } E\left| {X(t)} \right|^{2} = 0 $$
(7)

Definition 1

([5]) Under condition (6) a numerical method is said to be general mean square stable (GMS), if there exists h0(a,b,c,d) > 0, such that any application of the method to problem (1) generates numerical approximations, Xn which satisfy

$$ \mathop {\lim }\limits_{n \to \infty } E\left| {X_{n} } \right|^{2} = 0 $$
(8)

for every stepsize \( h = \frac{r}{m}. \)

Definition 2

([5]) Under condition (6) a numerical method is said to be mean square stable (MS), if there exists h0(a,b,c,d) > 0, such that any application of the method to problem (1) generates numerical approximations, Xn which satisfy

$$ \mathop {\lim }\limits_{n \to \infty } E\left| {X_{n} } \right|^{2} = 0 $$
(9)

for all h ∊ (0,h0(a,b,c,d)) with \( h = \frac{r}{m}. \)

Theorem 2

([5]) Under condition (6) and let

$$ K = \frac{|a| + |b|}{2|a|} + \frac{{2a + 2|b| + \left( {|c| + |d|} \right)^{2} }}{{2|a|\left( {|a| + |b|} \right)}} $$
(10)

If K < 0, then for all α ∊ [0, 1], the Euler method ( 3 ) is GMS stable. If K ≥ 0, then for α ∊ (K, 1], the Euler method ( 3 ) is GMS stable and for α ∊ [0, K], it is MS-stable and h0(a,b,c,d) = min{h′,h ′′}, where \( h' = \hbox{max} \{ h_{1}\,,h_{2} \} ,\,\,\,\,\,h'' = \hbox{max} \left\{ {\frac{1}{|a|},h_{2} } \right\} \) and \( h_{1} = \hbox{min} \left\{ {\frac{1}{|a|},\frac{{ - (2a + 2|b| + (|c| + |d|)^{2} }}{{(a + |b|)^{2} }}} \right\},\,\,h_{2} = \frac{{ - (2a + 2|b| + (|c| + |d|)^{2} }}{{(a + |b|)^{2} }}. \)

3 Numerical Experiments

Let consider linear SDDE (2) with sets of coefficients are given in Table 1.

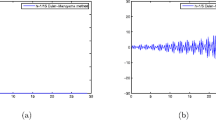
Table 1 Coefficients of linear SDDEs and the corresponding values of K and h0
Full size table

By Theorem 2, SDDE (2) is GMS-stable for set of coefficients C1 if 0.1693 < α ≤ 1 and it is MS-stable for 0 ≤ α ≤ 0.1693. For C2, a linear SDDE (2) is GMS-stable for 0 ≤ α ≤ 1 when h ∊ (0,1.250). For C3, the solution obtained is GMS-stable for α ∊ (0,1] and it is MS-stable if α = 0 when h ∊ (0,1.0). Theoretically, it shows that a set of coefficients C1 produce unstable solution if the explicit Euler method is applied, but it is GMS-stable and MS-stable for semi-implicit method under certain values of α. Moreover, the solution is GMS-unstable for α < 0.1693. Linear SDDE generates from C2 is GMS-stable for both methods. Linear SDDE generates from C3 is MS-stable for both methods and GMS-unstable for explicit method. The theoretical results are confirmed by applying explicit Euler method (4) and semi implicit (3) with fixed parameter α = 0, 0.1 and 1.0. Table 2 shows the corresponding methods for each α.

Table 2 Explicit and semi-implicit Euler methods
Full size table

In Figs. 1, 2 and 3, the stepsize is fixed to \( h = \frac{1}{10} \) and the parameter α is changed according to Table 2.

Fig. 1
figure 1

Simulation result for C1 with fixed stepsize \( h = \tfrac{1}{10} \) for α = 0, 0.1 and 1.0

Full size image
Fig. 2
figure 2

Simulation result for C2 with fixed stepsize \( h = \tfrac{1}{10} \) for α = 0, 0.1 and 1.0

Full size image
Fig. 3
figure 3

Simulation result for C3 with fixed stepsize \( h = \tfrac{1}{10} \) for α = 0, 0.1 and 1.0

Full size image

For α = 0 and 0.1, the simulated results for C2 are mean-square unstable. This indicates that for small values of α (when the method is reduced to explicit scheme) the results become unstable for C2. However, for C1 and C3, the results tend to negative values for α = 0 and 0.1, hence indicates instability of the solution. However, the simulated result produced by semi-implicit method with α = 1.0 possess the stability in mean-square for C1, C2 and C3.

4 Conclusions

It can be concluded that the stability of explicit and semi-implicit methods are influenced by the values of hand α. Small values of αproduce instable results compare than large value of α (for α = 1.0).