Keywords

1 Introduction

In recent years, more and more ultra-low permeability reservoirs in the Ordos Basin have been put into development, and most of them have been developed by water flooding [1]. The areal sweep efficiency is one of the important indexes for evaluating the development effect of water flooding. Therefore, it is necessary to accurately calculate the areal sweep efficiency under water flooding in ultra-low permeability reservoirs.

A large number of physics experiments have shown that the fluid has a threshold pressure gradient when flowing in ultra-low permeability reservoirs. The flow law no longer meets Darcy’s law, showing non-Darcy flow characteristics [2,3,4,5,6]. At the same time, natural fractures are usually developed in ultra-low permeability reservoirs, which make the reservoirs have the anisotropic characteristics of permeability. Injected water preferentially protrudes in the direction of high permeability in the water injection process [7,8,9,10]. Moreover, in the process of water flooding in ultra-low permeability reservoirs, the difference in viscosity of oil and water has a great influence on the areal sweep coefficient of water flooding [11]. Therefore, it is necessary to consider the influence of non-Darcy flow characteristics, permeability anisotropy characteristics and oil-water viscosity difference when calculating the areal sweep coefficient of ultra-low permeability reservoirs. These factors make it difficult to accurately calculate the areal sweep coefficient of water flooding in ultra-low permeability reservoirs.

Former researchers have conducted extensive researches on the areal sweep coefficient. The literature [12,13,14] used numerical simulation method to calculate the areal sweep coefficient under water flooding, but this method failed to consider the non-Darcy flow characteristics of ultra-low permeability reservoirs. Ji Bingyu [15] used the flow steam-tube method to deduce the production formula of different well patterns considering the non-Darcy flow characteristics of ultra-low permeability reservoirs, and proposed the concepts of starting angle and starting coefficient. Based on this, the literatures [16,17,18,19,20,21,22] derived the areal sweep coefficient of different well patterns considering the threshold pressure gradient. The above literatures did not consider the influence of the permeability anisotropy and oil-water viscosity difference. Therefore, they cannot be directly used to calculate the areal sweep coefficient under water flooding in ultra-low permeability reservoirs.

In view of the characteristics of non-Darcy flow and permeability anisotropy in extra-low permeability reservoirs under the process of water flooding, we obtained streamlines distribution through solving the stream function based on coordinate transformation, and derived the areal sweep efficiency formula considering oil-water two phases non-piston displacement by streamline integral method. In combination with actual oilfield data, the effects of the ratio of oil to water, the threshold pressure gradient, the permeability anisotropy, pressure difference and well spacing on the areal sweep efficiency were analyzed with this method.

2 Mathematical Model

2.1 Basic Assumptions of the Mathematical Model

The mathematical model is subject to the following basic assumptions:

  1. (1)

    The fluid is oil-water two-phase and non-piston displacement.

  2. (2)

    Do not consider the compressibility of porous media and fluids.

  3. (3)

    Do not consider the effect of capillary force and gravity.

  4. (4)

    The formation is a homogeneous and uniform single oil layer.

  5. (5)

    The threshold pressure gradient of oil phase and water phase are the same.

2.2 Characteristics of Ultra-Low Permeability Reservoirs

Due to the threshold pressure gradient in ultra-low permeability reservoirs, the flow no longer meets the Darcy law. The non-Darcy flow formula is

$$\nu = - \frac{k}{\mu }\nabla P\left( {1 - \frac{\lambda }{{\left| {\nabla P} \right|}}} \right)$$
(1)

Ultra-low permeability reservoirs often exhibit permeability anisotropy. The anisotropic reservoir can be converted to an equivalent isotropic reservoir based on coordinate transformation, and the coordinate transform formula is

$$\left\{ {\begin{array}{*{20}l} {x = x^{{\prime }} \sqrt {k/k_{x} } } \hfill \\ {y = {\text{y}}^{{\prime }} \sqrt {k/k_{y} } } \hfill \\ {k = \sqrt {k_{x} k{}_{y}} } \hfill \\ \end{array} } \right.$$
(2)

2.3 Streamline Distribution

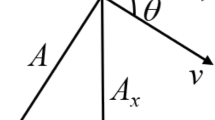
In an isotropic reservoir, according to symmetry, an injection-production well group in the five-point well pattern can be divided into four identical seepage units (Fig. 1), and the seepage unit △ABD can be further divided into two similar seepage units (unit △ABC and unit △ACD), A is an injector, B, D are production wells, and C is the midpoint of BD. According to Eq. (1), and by the superposition theory of potentials, the pressure at any point in the seepage unit ΔABC is

Fig. 1.
figure 1

Schematic of 5-spot well pattern

Full size image
$$\begin{aligned} P(x,y) & = p_{i} - \frac{\mu q}{2\pi k}\ln \left[ {\frac{d}{{r_{\text{w}} }}\sqrt {\frac{{x^{2} + y^{2} }}{{(x - d)^{2} + y^{2} }}} } \right] \\ & \quad - \lambda \left[ {d + \sqrt {x^{2} + y^{2} } - \sqrt {(x - d)^{2} + y^{2} } } \right] \\ \end{aligned}$$
(3)

From the above formula, the seepage velocity component \(v_{\text{x}}\) is

$$\begin{aligned} \nu_{\text{x}} & = \frac{q}{2\pi }\frac{{xd\left[ {d - 2x} \right] + d(x^{2} + y^{2} )}}{{(x^{2} + y^{2} )\left[ {(x - d)^{2} + y^{2} } \right]}} \\ & \quad - \frac{k\lambda }{\mu }\left[ {\frac{x - d}{{\sqrt {(x - d)^{2} + y^{2} } }} - \frac{x}{{\sqrt {x^{2} + y^{2} } }}} \right] \\ \end{aligned}$$
(4)

Based on Eq. (4), the steam function can be written as

$$\begin{aligned} \psi (x,y) & = \int {v_{\text{x}} } {\text{d}}y = \frac{q}{2\pi }\left[ \begin{aligned} \arctan \left( {\frac{y}{x - d}} \right) \hfill \\ + \arctan \left( {\frac{y}{x}} \right) \hfill \\ \end{aligned} \right] \\ & \quad - \frac{k\lambda }{\mu }\left[ {(x - d)\ln ((x - d)^{2} + y^{2} ) - x\,\ln (x^{2} + y^{2} )} \right] \\ \end{aligned}$$
(5)

Therefore, the streamline equation for the seepage unit ΔABC is

$$\begin{aligned} & \frac{q}{2\pi }\left[ {\arctan \left( {\frac{y}{x - d}} \right) + \arctan \left( {\frac{y}{x}} \right)} \right] \\ & \quad - \frac{k\lambda }{\mu }\left[ {\begin{array}{*{20}l} {(x - d)\ln ((x - d)^{2} + y^{2} )} \hfill \\ { - x\,\ln (x^{2} + y^{2} )} \hfill \\ \end{array} } \right] = {\text{C}}_{1} \\ \end{aligned}$$
(6)

where \(C_{1} = \psi\).

Near the injection wells, \(x \to 0\), \(y \to 0\), the streamline equation can be approximated as

$$y = \tan {\text{C}}_{2} \cdot x$$
(7)

where \({\text{C}}_{2} = \frac{2\pi }{q}\left( {{\text{C}}_{1} + \frac{k\lambda d\,\ln d}{\mu }} \right)\).

Near the production wells, \(x \to d\), \(y \to 0\), the streamline equation can be approximated as

$$y = - \tan {\text{C}}_{2} \cdot (x - d)$$
(8)

Therefore, for the sake of simple calculation, this article uses the above two intersecting straight lines to approximate the real streamlines (the solid line in Fig. 2 is the real streamline), and the approximate streamline distribution is shown in dotted lines in Fig. 2.

Fig. 2.
figure 2

Streamlines for seepage unit ΔABC

Full size image

2.4 The Derivation of Areal Sweep Coefficient

In seepage unit ΔABC shown as Fig. 2, \({\angle }{\text{CAB}} = \alpha_{\text{m}}\), \({\angle }{\text{CBA}} = \beta_{\text{m}}\), and \(\alpha_{\text{m}} {\text{ = artan}}(y/d)\), \(\beta_{\text{m}} = \alpha_{\text{m}}\). Take a stream line AEB, and the angle between the injection well and ∠EAB is \(\alpha\), and the angle between the production well and ∠EBA is \(\beta\). The length of steam line AEB is L. The velocity of oil-water two-phase flow on streamline AEB is

$$\nu = \frac{{p_{\text{i}} - p_{\text{w}} - \lambda L}}{{\frac{{\mu_{\text{o}} }}{k}\int_{0}^{{x_{\text{f}} }} {\frac{{{\text{d}}x}}{{\mu_{\text{r}} k_{\text{rw}} { + }k_{\text{ro}} }}} { + }\frac{{\mu_{\text{o}} (L - x_{\text{f}} )}}{k}}}$$
(9)

where \(\frac{{\mu_{\text{o}} }}{k}\int_{0}^{{x_{\text{f1}} }} {\frac{{{\text{d}}x}}{{\mu_{\text{r}} k_{\text{rw}} { + }k_{\text{ro}} }}}\) is the total flow resistance in oil-water mixing zone, and it can be rewritten as

$$\begin{aligned} & \frac{{\mu_{\text{o}} }}{k}\int\limits_{0}^{{x_{\text{f1}} }} {\frac{{{\text{d}}x}}{{\mu_{\text{r}} k_{\text{rw}} { + }k_{\text{ro}} }}} \\ & \quad { = }\frac{{\mu_{\text{w}} }}{k}\frac{{x_{\text{f1}} }}{{f_{\text{w}}^{{\prime }} (s_{\text{wf}} )}}\int\limits_{0}^{{f_{\text{w}}^{{\prime }} (s_{\text{wf}} )}} {\frac{{f_{\text{w}} ( {\text{S}}_{\text{w}} )}}{{k_{\text{rw}} }}{\text{d}}f_{\text{w}}^{{\prime }} (s_{\text{w}} )} = \frac{{\mu_{\text{w}} x_{\text{f1}} }}{k}\alpha \\ \end{aligned}$$
(10)

where \(\alpha = \frac{1}{{f_{\text{w}}^{{\prime }} (s_{\text{wf}} )}}\int_{0}^{{f_{\text{w}}^{{\prime }} (s_{\text{wf}} )}} {\frac{{f_{\text{w}} ( {\text{S}}_{\text{w}} )}}{{k_{\text{rw}} }}{\text{d}}f_{\text{w}}^{{\prime }} (s_{\text{w}} )}\), \(f_{\text{w}}^{{\prime }} (s_{\text{wf}} )\) is water cut rate.

When the pressure difference between injection and production remains unchanged, the position of the water flooding frontier meets

$$x_{\text{f}} = \frac{{f_{\text{w}}^{{\prime }} (s_{\text{wf}} )}}{\phi }\int\limits_{0}^{t} v {\text{d}}t$$
(11)

Combining Eq. 9 and Eq. 10, we can get

$$x_{\text{f}} = \frac{{f_{\text{w}}^{{\prime }} (s_{\text{wf}} )}}{\phi }\int\limits_{0}^{t} {\frac{{p_{\text{i}} - p_{\text{w}} - \lambda L}}{{\lambda_{\text{w}}^{{\prime }} x_{\text{f}} { + }\lambda_{\text{o}}^{{\prime }} (L - x_{\text{f}} )}}} {\text{d}}t$$
(12)

where \(\lambda_{\text{w}}^{{\prime }} = \frac{{\mu_{\text{w}} \alpha }}{k}\), \(\lambda_{\text{o}}^{{\prime }} = \frac{{\mu_{\text{o}} }}{k}\).

After derivation and integral of Eq. 12, we can get

$$\frac{{(\lambda_{\text{w}}^{{\prime }} { - }\lambda_{\text{o}}^{{\prime }} )}}{2}x_{\text{f}}^{2} { + }\lambda_{\text{o}}^{{\prime }} Lx_{\text{f}} { - }\frac{{f_{\text{w}}^{{\prime }} (s_{\text{wf}} )(p_{\text{i}} - p_{\text{w}} - \lambda L)t}}{\phi } = 0$$
(13)

By solving the above formula, the position distribution of the water flooding frontier at different time points on different streamlines can be obtained. When \(\lambda_{\text{w}}^{{\prime }} { < }\lambda_{\text{o}}^{{\prime }}\), the position is

$$x_{\text{f}} = \frac{{ - D - \sqrt {D^{2} + 4E} }}{2}$$
(14)

where \(D = \frac{{2\lambda_{\text{o}}^{{\prime }} L}}{{(\lambda_{\text{w}}^{{\prime }} { - }\lambda_{\text{o}}^{{\prime }} )}}\), \(E = \frac{{2f_{\text{w}}^{{\prime }} (s_{\text{wf}} )(p_{\text{i}} - p_{\text{w}} - \lambda L)t}}{{\phi (\lambda_{\text{w}}^{{\prime }} { - }\lambda_{\text{o}}^{{\prime }} )}}\).

When \(\lambda_{\text{w}}^{{\prime }} { = }\lambda_{\text{o}}^{{\prime }}\), the position is

$$x_{\text{f}} = \frac{{f_{\text{w}}^{{\prime }} (s_{\text{wf}} )(p_{\text{i}} - p_{\text{w}} - \lambda L)t}}{{\lambda_{\text{o}}^{{\prime }} L\phi }}$$
(15)

With Eq. 14, the time when the frontier edge of the main stream AB reaches the inflection point e, \(t_{1}\), and the time when the frontier edge of the main steam AB reaches production well B, \(t_{2}\), can be obtained.

When \(t \le t_{1}\), the swept area of flow unit ΔABC is

$$s_{1} = \frac{1}{2}\int\limits_{0}^{{\alpha_{0} }} {x_{\text{f}}^{2} } {\text{d}}\alpha$$
(16)

where \(\alpha_{0}\) is the starting angle

When \(t_{1} < t \le t_{2}\), the swept area of flow unit ΔABC is

$$s_{1} = \left\{ {\begin{array}{*{20}l} {\frac{1}{2}d^{2} \frac{{\sin \alpha_{0} \sin \beta_{0} }}{{\sin (\alpha_{0} + \beta_{0} )}} - \frac{1}{2}\int\limits_{0}^{{\beta_{0} }} {(L - x_{\text{f}} )^{2} } {\text{d}}\beta } \hfill & {{\text{for}}\;\;\alpha_{1} \ge \alpha_{0} } \hfill \\ {\frac{1}{2}d^{2} \frac{{\sin \alpha_{1} \sin \beta_{1} }}{{\sin (\alpha_{1} + \beta_{1} )}} - \frac{1}{2}\int\limits_{0}^{{\beta_{1} }} {(L - x_{\text{f}} )^{2} } {\text{d}}\beta + \frac{1}{2}\int\limits_{{\alpha_{1} }}^{{\alpha_{0} }} {x_{\text{f}}^{2} } {\text{d}}\alpha } \hfill & {{\text{for}}{\kern 1pt} \;\;\alpha_{1} < \alpha_{0} } \hfill \\ \end{array} } \right.$$
(17)

When \(t > t_{2}\), the swept area of flow unit ΔABC is

$$s_{1} = \left\{ {\begin{array}{*{20}l} {\frac{1}{2}d^{2} \frac{{\sin \alpha_{0} \sin \beta_{0} }}{{\sin (\alpha_{0} + \beta_{0} )}} - \frac{1}{2}\int\limits_{{\beta_{2} }}^{{\beta_{0} }} {(L - x_{\text{f}} )^{2} } {\text{d}}\beta } \hfill & {{\text{for}}\;\;\alpha_{1} \ge \alpha_{0} } \hfill \\ {\frac{1}{2}d^{2} \frac{{\sin \alpha_{1} \sin \beta_{1} }}{{\sin (\alpha_{1} + \beta_{1} )}} - \frac{1}{2}\int\limits_{{\beta_{2} }}^{{\beta_{1} }} {(L - x_{\text{f}} )^{2} } {\text{d}}\beta + \frac{1}{2}\int\limits_{{\alpha_{1} }}^{{\alpha_{0} }} {x_{\text{f}}^{2} } {\text{d}}\alpha {\kern 1pt} } \hfill & {{\text{for}}\;\;\alpha_{1} < \alpha_{0} } \hfill \\ \end{array} } \right.$$
(18)

Similarly, the swept area of flow unitΔADC is s2. Based on the symmetry of the five-point well pattern and the area of flow unit ofΔABC is \(s_{0} = 0.25d \cdot y\), and therefore, the areal sweep efficiency of flow unit of ΔABC is

$$\eta = \frac{{s_{1} + s_{2} }}{{s_{0} }}$$
(19)

3 Results and Discussion

Taking a typical ultra-low-permeability reservoir in Changqing as an example, the effect of oil-water viscosity ratio, threshold pressure gradient, and injection-production parameters on the areal sweep efficiency under water flooding at five-spot well pattern in ultra-low permeability reservoirs was analyzed. The reservoir parameters are as follows: the porosity is 0.15; the permeability is 2 mD, the degree of permeability anisotropy (kx/ky) is 3; the oil viscosity is 5.0 mPa s; the water viscosity is 1.0 mPa s; threshold pressure gradient is 0.04 MPa/m; Water cut rate is 10 and \(\alpha = 1.5\).

3.1 Effect of Oil-Water Viscosity Ratio

In the case of well spacing of 250 × 150 m, injection and production pressure difference of 18 MPa, and threshold pressure gradient of 0.04 MPa/m, the effect of oil-water viscosity ratio on areal sweep efficiency of five-spot well pattern is shown in Table 1. It shows that the greater the oil-water viscosity ratio, the smaller the areal sweep efficiency at the time of water breakthrough. This is mainly because the greater the oil-water viscosity ratio, the greater the difference in oil-water two-phase flow ability. Therefore, for ultra-low permeability reservoirs with large differences in oil-water viscosity, the oil-water viscosity ratio can be appropriately reduced through chemical reagents, so as to increase the areal sweep coefficient at the time of water breakthrough.

Table 1. Results of water breakthrough time and areal sweep efficiency for different viscosity ratio of oil and water
Full size table

3.2 Effect of Threshold Pressure Gradient

In the case of well spacing of 250 × 150 m, injection and production pressure difference of 18 MPa, the effect of threshold pressure gradient on areal sweep efficiency of five-spot well pattern is shown in Fig. 3. It shows that before the production well water breakthrough, the areal sweep coefficient slowly increases with time and then increases rapidly. The larger the threshold pressure gradient, the longer the time of water breakthrough. This is because with the increase of the threshold pressure gradient, the additional resistance generated during the water flooding process will be greater.

Fig. 3.
figure 3

The effect of threshold pressure gradient on areal sweep efficiency (The asterisk indicates water breakthrough)

Full size image

3.3 Effect of the Degree of Permeability Anisotropy

In the case of well spacing of 250 × 150 m, injection and production pressure difference of 18 MPa, the threshold pressure gradient of 0.04 MPa/m and the viscosity ratio of oil and water of 5, the effect of the degree of permeability anisotropy on areal sweep efficiency of five-spot well pattern is shown in Figs. 4 and 5. It shows that in the current well pattern condition, when the degree of permeability anisotropy is 3, the time of water breakthrough is the latest (Fig. 4), and the areal sweep coefficient at the time of water breakthrough is the largest (Fig. 5). The literature [9] also pointed out that the well spacing should be adjusted appropriately for anisotropic reservoirs based on permeability anisotropy in order to achieve an equilibrium displacement. When the ratio of well spacing to row spacing is equal to the square root of the degree of permeability anisotropy, the displacement is the most balanced.

Fig. 4.
figure 4

Water breakthrough time at different anisotropy degrees

Full size image
Fig. 5.
figure 5

Areal sweep efficiency at different anisotropy degrees

Full size image

3.4 Effect of Injection-Production Parameters

In the case of well spacing of 250 × 150 m, the threshold pressure gradient of 0.04 MPa/m and the viscosity ratio of oil and water of 5, the degree of permeability anisotropy of 5, the effect of injection and production pressure difference on areal sweep efficiency of five-spot well pattern is analyzed. Meanwhile, In the case of injection and production pressure difference of 18 MPa, the threshold pressure gradient of 0.04 MPa/m and the viscosity ratio of oil and water of 5, the degree of permeability anisotropy of 5, the effect of well spacing on areal sweep efficiency of five-spot well pattern is analyzed. The result is shown in Table 2. It shows that the larger the pressure difference between injection and production, the earlier the time of water breakthrough and the larger the areal sweep coefficient at the time of water breakthrough. Under the current well pattern conditions (250 × 150 m), when the row distance is reduced from 190 m to 150 m, the areal sweep coefficient of seepage unit △A’B’D’at the time of water breakthrough increases significantly. When the row spacing is further reduced, the areal sweep coefficient of the seepage unit △A’B’D’ at the time of water breakthrough is reduced.

Table 2. Results of water breakthrough time and areal sweep efficiency for different pressure differences and well spacing
Full size table

4 Conclusions

In this paper, a new mathematical model for areal sweep coefficient under water flooding in ultra-low permeability reservoir is set up. The following conclusions can be derived as follows:

  1. (1)

    When calculating the sweep coefficient under water flooding in ultra-low permeability reservoirs, it is necessary to consider not only the characteristics of non-linear flow, but also the influence of permeability anisotropy and oil-water viscosity difference.

  2. (2)

    In view of the characteristics of non-Darcy flow and permeability anisotropy in extra-low permeability reservoirs under the process of water flooding, streamlines distribution was obtained through solving the stream function based on coordinate transformation, and the areal sweep efficiency formula considering oil-water two phases non-piston displacement was derived by streamline integral method. Example calculations show that the derived formula can be reasonably calculated areal sweep coefficient of ultra-low permeability reservoir.

  3. (3)

    The larger the oil-water viscosity ratio or the smaller the injection pressure difference, the smaller the areal sweep coefficient at the time of water breakthrough. Adjusting the well spacing is an effective method to improve the areal sweep coefficient of water flooding, and the balanced displacement can be achieved when the ratio of well spacing to row spacing is equal to the square root of permeability anisotropy intensity.