Metasurfaces for Band-Pass Filter in Ka-Band

Abstract

This paper establishes a coupled-mode theory (CMT) to help understand the inherent physics governing the transmission properties of a band-pass filter, based on which a two-layer metasurface exhibiting a wide band pass in Ka-band is designed. This method can be easily extended to other frequency regimes.

1 Introduction

Recently, plasmonic systems have attracted a lot of attention due to their application in practice and scientific. Direct and indirect coupling of optical resonators enable open plasmonic open systems to achieve light manipulation through restructuring of eigenstates with contrasting Q factors, while exhibiting many fascinating optical phenomena, such as Fano resonance, Rabi oscillation, and plasmon-induced transparency (PIT). This method was employed in the design of a band-pass filter working at X-band [1].

In this paper, we employ a coupled-mode model to design a band-pass filter based on two-layer metasurfaces in Ka-band. By analyzing the two-layer metasurfaces using coupled-mode theory [2, 3], we discover that the crucial properties (i.e., position and bandwidth) of each transmission peak within the band pass are solely determined by a particular set of model parameters describing both the inter-layer near-field couplings and the far-field radiations. Our theory is fully justified by both full-wave simulations and microwave experiments.

2 Coupled-Mode Theotry

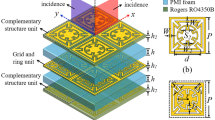
We start our discussion with a typical electromagnetic metasurface structure. As shown in Fig. 1, the metasurface structure is comprised of two identical layers printed with periodic arrays of subwavelength metallic structures, and the substrate is F4B (ε = 2.2 and h = 0.2 mm). Each layer is composed of a metallic Jerusalem cruciform resonator surrounded by a metallic mesh and the distance between the two layers is. The metallic mesh is optically opaque, and the two resonators induce optical transparency at two resonating frequencies [4].

Fig. 1

a Schematic diagram of metal structures stacked in space, where blue represents a dielectric substrate with ε = 2.2, h = 0.2 mm, and d is the distance between two metal structures. b A unit of metal structure, P = 3.5, ω = 0.25, α = 2, b = 1, c = 0.3, all in units of mm

Figure 2 illustrates the CMT model of such a system, which consists of 2 scattering channels and 2 modes embedded inside an opaque background. These two modes are contributed by the localized Jerusalem cruciform resonators.

Fig. 2

A schematic diagram of the CMT model showing the two ports and two resonators

By “turning off” the optical mode’s radiation toward the scattering channel, the resonator amplitude $\alpha_{j} \left( {j = 1,2} \right)$ can be expressed as

$$ \frac{1}{2\pi }\frac{d}{dt}\left( {\begin{array}{*{20}c} {\alpha_{1} } \\ {\alpha_{2} } \\ \end{array} } \right) = i\widehat{H}\left( {\begin{array}{*{20}c} {\alpha_{1} } \\ {\alpha_{2} } \\ \end{array} } \right) = i\left( {\begin{array}{*{20}c} {f_{0} + \kappa^{\prime}} & \kappa \\ \kappa & {f_{0} + \kappa^{\prime}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\alpha_{1} } \\ {\alpha_{2} } \\ \end{array} } \right) $$

(1)

where $f_{0}$ denotes the resonating frequency of resonator, $\kappa$ and $\kappa^{\prime}$ denote the near-field coupling [5, 6].

Through unitary transformation, $\widehat{H}$ can be diagonalized as

$$ \widetilde{H} = M.\widehat{H}.M^{T} = \left( {\begin{array}{*{20}c} {\widetilde{{f_{s} }}} & 0 \\ 0 & {\widetilde{{f_{a} }}} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {f_{0} + \kappa + \kappa^{\prime}} & \kappa \\ \kappa & {f_{0} - \kappa + \kappa^{\prime}} \\ \end{array} } \right) $$

(2)

where $M = \frac{1}{\sqrt 2 }\left( {\begin{array}{*{20}c} { - 1} & 1 \\ 1 & 1 \\ \end{array} } \right)$. We have proved that if $MM^{T} = I$, the constraint of CMT parameters would not change.

Therefore, we can apply the CMT model to obtain the formula as

$$ \frac{1}{2\pi }\frac{d}{dt}\left( {\begin{array}{*{20}c} {\widetilde{\alpha }_{s} } \\ {\widetilde{\alpha }_{a} } \\ \end{array} } \right) = i\left( {\begin{array}{*{20}c} {\widetilde{f}_{s} } & 0 \\ 0 & {\widetilde{f}_{a} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\widetilde{\alpha }_{s} } \\ {\widetilde{\alpha }_{a} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} { - \widetilde{\Gamma }_{s} } & {\widetilde{X}} \\ {\widetilde{X}} & { - \widetilde{\Gamma }_{a} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\widetilde{\alpha }_{s} } \\ {\widetilde{\alpha }_{a} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {\tilde{d}_{1s} } \\ {\tilde{d}_{1a} } \\ \end{array} } \right)S_{1} $$

(3)

where $\tilde{d}_{1i}$ denotes the coupling between the collective mode and the port.

$(r_{0} = - 1,t_{0} = 0)$, we can use the standard two-mode two-port CMT to analyze the transmission coefficient of the two-layer system [1, 7]. By referring to the standard CMT, the transmission coefficient can be approximately expressed as

$$ t \approx \frac{{\widetilde{W}_{a} \tilde{d}_{1,s} \tilde{d}_{2,s} + \widetilde{W}_{s} \tilde{d}_{1,a} \tilde{d}_{2,a} + \widetilde{X}\left( {\tilde{d}_{1,s} \tilde{d}_{2,a} + \tilde{d}_{2,s} \tilde{d}_{1,a} } \right)}}{{\widetilde{W}_{s} \widetilde{W}_{a} - \widetilde{X}^{2} }} $$

(4)

where $\widetilde{W}_{j} = i\left( {f - \tilde{f}_{j} } \right) + \widetilde{\Gamma }_{j}$ and $\tilde{f}_{j}$ and $\widetilde{\varGamma }_{j}$, respectively, denote the resonance frequency and the damping caused by radiations of the two ports. Here j = s, a definer the symmetrical (s) or antisymmetrical (a) mode. $\tilde{d}_{1,j}$ and $\tilde{d}_{2,j}$ (j = s, a) denote the couplings between the jth mode and the two ports, and $\widetilde{X}$ describes the interactions between the two resonant modes. $\widetilde{X}$ and $\widetilde{\Gamma }_{j}$ are not independent parameters, since $\widetilde{X} = - \left( {\tilde{d}_{1,s}^{*} \tilde{d}_{1,a} + \tilde{d}_{2,s}^{*} \tilde{d}_{2,a} } \right)/2$ and $\widetilde{\Gamma }_{j} = \left( {\left| {\tilde{d}_{1,j} } \right|^{2} + \left| {\tilde{d}_{2,j} } \right|^{2} } \right)/2$ according to the CMT [2].

The curve shown in Fig. 3a is the best-fitted CMT spectra.

Fig. 3

a Results of the two-layer structure transmittance FDTD and CMT fitting, where, b bandwidth of collective symmetric and antisymmetrical mode fit the simulated spectra

With parameters given by $\widetilde{\Gamma }_{a} = 2.3$, $\widetilde{\Gamma }_{s} = 5.1$, $\tilde{f}_{a} = 36.9$ and $\tilde{f}_{s} = 28.6$, all in units of GHz. We note that in the limit of X = 0, Eq. (4) can be further simplified as $t = \frac{{\tilde{d}_{1,s} \tilde{d}_{2,s} }}{{\widetilde{W}_{s} }} + \frac{{\tilde{d}_{1,a} \tilde{d}_{2,a} }}{{\widetilde{W}_{a} }}$, which describes the responses of the two independent oscillators. We then calculate the transmission spectra contributed by the symmetrical (j = s) and antisymmetrical (j = a) modes separately, and plot them in Fig. 3b. We find that the position and the bandwidth of the jth transmission peak can be described by $\tilde{f}_{j}$ and $\widetilde{\varGamma }_{j}$.

In order to understand this two-layer system, we repeated the CMT analyses on a series if two-layer systems with different inter-layer distance d, and retrieved the corresponding CMT parameters in different cases. Figure 4a–c illustrates the relationship between CMT parameters and inter-layer distance d. It can be clearly seen in Fig. 4a that $\kappa$ and $\kappa^{\prime}$ decrease as d increases, so tuning d can change the near-field coupling. In return, the near-field coupling can control the peak width of the two peaks, as shown in Fig. 4b. Figure 4d depicts the FDTD simulated transmission spectra for different distance d.

Fig. 4

Retrieved CMT fitting parameters of the two-layer metasurface: a coupling coefficients ($\kappa$, $\kappa^{\prime}$); b bandwidths of two peaks $\widetilde{\Gamma }_{a}$, $\widetilde{\Gamma }_{s}$ (blue and red symbols); c damping parameters $(d_{i,j} )$ as function of inter-layer distance; d distance dependence of transmittance spectra computed by FDTD simulations

3 Conclusions

We have established a highly efficient approach to designing an optical band-pass filter based on the coupled-mode theory. We have established that the peak positions and the peak width in the transmission spectrum of a coupled two-layer metasurface are closely related to the collective modes and can be described by near-field coupling. Based on the coupled-mode theory, we have designed a structure that can serve as a band-pass filter in Ka-band with 28.6–36.9 GHz.

Our design approach is robust, intuitive, fast and can have many applications in practice.