Second-Order Differentiator Based on Long-Period Waveguide Grating

Abstract

In this paper, a structure of second-order differentiator based on long-period waveguide grating (LPWG) is proposed. The second-order differentiator consists of two segment uniform gratings, one segment waveguide and electrode correspondingly deposited on both sides of waveguide on x-cut lithium niobate (LN) crystal. The performances of the second-order differentiator are analyzed and simulated. It shows that it can be implemented by introducing π-phase shift by adjusting voltage according to the electro-optic effect of LN.

1 Introduction

An N-th photonic differentiator can realize the N-th time derivative of input optical signal and has important applications in analog–digital conversion, pulse shaping, and optical processing of microwave signals [1]. In recent years, second-order differentiators based on long-period fiber grating (LPFG) have been proposed and experimentally verified [2, 3]. It normally uses the elastic-optical effect in fiber to obtain the differentiated function, resulting in low tuning speed. Lithium niobate (LN) has advantages of good electro-optic effect and fast tuning speed. Therefore, second-order differentiator based on LN long-period waveguide grating (LPWG) has potential applications in high-speed differentiator.

In this paper, a structure of second-order differentiator based on LPWG is proposed. And the second-order differentiator is analyzed theoretically and simulated by MATLAB. The fabrication of LPWG based on LN is investigated.

2 Principle

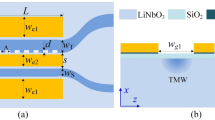
The structure of second-order differentiator based on LPWG is shown in Fig. 1. It consists of two segments of uniform LPWG gratings, one segment of waveguide and electrodes correspondingly deposited on both sides of waveguide on x-cut LN crystal.

Fig. 1

Structure of second-order differentiator based on long-period waveguide grating

According to transfer-matrix method, the matrix of differentiator can be expressed as [6].

$$F = F2 \times P \times F1$$

(1)

where F₁ is the transfer matrix of the 1-th grating and F₂ is the transfer matrix of the 2-th grating. P is transfer matrix of the waveguide.

F₁ is expressed as

$$\begin{aligned} F_{i} & = \left[ {\begin{array}{*{20}c} {\cos \left( {sl_{i} } \right) + j\frac{\delta }{s}\sin \left( {sl_{i} } \right)} & {j\frac{\kappa }{s}\sin \left( {sl_{i} } \right)} \\ {j\frac{\kappa }{s}\sin \left( {sl_{i} } \right)} & {\cos \left( {sl_{i} } \right) - j\frac{\delta }{s}\sin \left( {sl_{i} } \right)} \\ \end{array} } \right] \\ i & = 1,2 \\ \end{aligned}$$

(2)

where $l_{i}$ is length of the ith grating (i = 1, 2), $\delta = \frac{{\pi \left( {N_{{{\text{co}}}} - N_{{{\text{cl}}}} } \right)}}{\lambda } - \pi /\Lambda$ and $\kappa = \frac{\pi }{\lambda }\Delta N$ are the detuning and coupling coefficient of the grating, respectively. $N_{{{\text{co}}}}$ and $N_{{{\text{cl}}}}$ are effective refractive index of the core and cladding of waveguide, $\Delta N$ is modulation amplitude of the grating, ${\Lambda }$ is the period of the grating and s = $\sqrt {\kappa^{2} + \delta^{2} }$.

P is expressed as

$${\text{P}} = \left[ {\begin{array}{*{20}c} {{\text{e}}^{{ - j\frac{\theta }{2}}} } & 0 \\ 0 & {{\text{e}}^{{j\frac{\theta }{2}}} } \\ \end{array} } \right]$$

(3)

According to electro-optic effect of LN [7], $\theta$ is

$$\theta = \frac{2 \cdot \pi \cdot L}{\lambda } \cdot \left( {N_{{{\text{co}}}} - \frac{V}{2d}\gamma_{33} N_{{{\text{co}}}}^{3} } \right)$$

(4)

where L is the length of waveguide, V is the voltage added on electrode with gap d. $\gamma_{33} = 30.8\,{\text{pm}}/{\text{V}}$ is used for the electric field is parallel to the optical axis z.

Suppose a voltage is applied across the waveguide to produce π phase shift, the transfer function of the differentiator is

$$\begin{aligned} F\left[ {1,1} \right] & = - j\frac{{\delta^{2} }}{{s^{2} }}\cos s\left( {l_{1} + l_{2} } \right) \\ & \quad - j\frac{{\kappa^{2} }}{{s^{2} }}\cos s\left( {l_{1} - l_{2} } \right) + \frac{\delta }{s}\sin s\left( {l_{1} + l_{2} } \right) \\ \end{aligned}$$

(5)

Expanding F(1,1) into Taylor series analytically around the central frequency ω₀.

$$\begin{aligned} F\left[ {1,1} \right] & = F\left( {\omega_{0} } \right) + \frac{1}{2}F^{\prime } \left( {\omega_{0} } \right)\left( {\omega - \omega_{0} } \right) \\ & \quad + \frac{1}{6}F^{\prime \prime } \left( {\omega_{0} } \right)\left( {\omega - \omega_{0} } \right)^{2} + \ldots \\ \end{aligned}$$

(6)

For the second-order differentiator, it is required that the constant term and the first-order term are zero. According to Eqs. (5) and (6), we can obtain

$$\kappa l_{1} = \frac{3\pi }{4} \quad \kappa l_{2} = \frac{\pi }{4}$$

(7)

As a result, in order to obtain a second-order differentiator, θ should be equal to π, and length ratio of two segments LPWG should be l₁:l₂ = 3:1. According to Eq. (4), π phase shift can be achieved by adjusting the voltage V.

3 Results

The second-order differentiator is verified by MATLAB in the following. In simulation, we set N_co = 2.139, N_cl = 2.137, ∆N = 0.5 × 10⁻⁴, Λ = 775 μm, L = 3.6 mm, d = 7 μm, and set l₁ = 20.4 mm, l₂ = 6.8 mm according to theoretical analysis.

Figure 2 shows the relationship between the phase shift and voltage. It can be seen that the tuning efficiency of the phase is 0.1 π/V, which will be increased by using a longer length of waveguide. From Fig. 2, π-phase shift can be obtained by applying 10 V voltage.

Fig. 2

Phase shift versus voltage V

According to theoretical analysis, the second-order differentiator can be implemented by π-phase shift inserted between two LPWG with l₁:l₂ = 3:1, and the spectra of two LPWG are shown in Fig. 3.

Fig. 3

Transmission spectra of two-segment grating a spectrum of the 1th grating, b spectrum of the 2th grating

The spectrum of the second-order differentiator is shown in Fig. 4. As can be seen from Fig. 4, the transmission spectrum of it is approximately a quadratic function near the resonance frequency.

Fig. 4

Transmission function of second-order differentiator based on LPWG

Gaussian pulse was spectrally centered at the LPWGs’ resonance frequency and subsequently propagated through the LPWG structure. The output waveform is shown in Fig. 5. From Fig. 5b, there is a fairly good agreement between the theoretically predicted and output time-domain waveform. Thus, it verifies feasibility of second-order differentiator based on LPWG.

Fig. 5

Spectrum and time domain of Gaussian pulse derived by second-order differentiators based on LPWG. a Spectrum; b time domains

Figure 6 shows the relationship between amplitude of second-order differentiator and ∆N. As can be seen, amplitude of second-order differentiator is inversely proportional to ∆N.

Fig. 6

Amplitude of second-order differentiator vesus ∆N

4 Conclusion

In this paper, a structure of second-order differentiator based on long-period waveguide grating (LPWG) is proposed. The second-order differentiator is verified theoretically by MATLAB. The second-order time derivative of Gaussian pulses is obtained by introducing a π phase shift by adjusting voltage at 3/4 of the length of the grating.