A Generalisation of Stone Duality to Orthomodular Lattices

Abstract

With each orthomodular lattice L we associate a spectral presheaf $\underline{\varSigma }^{L}$, generalising the Stone space of a Boolean algebra, and show that (a) the assignment $L\mapsto \underline{\varSigma }^{L}$ is contravariantly functorial, (b) $\underline{\varSigma }^{L}$ is a complete invariant of L, and (c) for complete orthomodular lattices there is a generalisation of Stone representation in the sense that L is mapped into the clopen subobjects of the spectral presheaf $\underline{\varSigma }^{L}$. The clopen subobjects form a complete bi-Heyting algebra, and by taking suitable equivalence classes of clopen subobjects, one can regain a complete orthomodular lattice isomorphic to L. We interpret our results in the light of quantum logic and in the light of the topos approach to quantum theory.

1 Introduction

Classical dualities and the lack of dualities for nondistributive/ noncommutative algebras. Stone duality [1] is one of the classical dualities. It relates a kind of algebras (Boolean algebras) to a kind of topological spaces (Stone spaces). There are many variants and generalisations of Stone duality [2], which are all similar in spirit. Another important classical duality is Gelfand duality, relating $C^*$-algebras and locally compact Hausdorff spaces. (Again, there are a number of variants.) The classical dualities always have on one side some kind of distributive or commutative algebras, organised into a category, and on the other side a corresponding kind of topological spaces, forming another category, related by a dual equivalence.

Yet, in quantum theory and in a vast number of mathematical situations, non-distributive and noncommutative algebras are of interest. For these, there mostly are no general functorial correspondences or dualities with suitable (generalised) spaces known. In fact, much of the difficulty consists in determining what kind of dual spaces would be suitable. These generalised spaces would have to be noncommutative spaces, in a sense to be made precise. Of course, the vast field of noncommutative geometry has as one of its starting points the assumption that there should be spaces corresponding to noncommutative algebras, and that there is much to be gained from using geometric methods when dealing with noncommutative algebras. This is doubtlessly true and has led to many deep and beautiful results, but since concrete noncommutative spaces are often lacking, noncommutative geometry is mostly done as algebra and only implicitly deals with spaces and geometric objects.

The spectral presheaf of an orthomodular lattice as a dual space. In this article, we will go another route: we will provide a new, concrete kind of dual space for any orthomodular lattice L. Here, orthomodular lattices (OMLs) are seen as a natural, generally nondistributive generalisation of Boolean algebras.

The dual space that we will assign to an OML will be a presheaf, which means it is not a single set (equipped with a topology), but a ‘diagram’ of sets (in fact, topological spaces), canonically linked together by continuous functions. More specifically, the spectral presheaf $\underline{\varSigma }^{L}$ of an orthomodular lattice L consists of the Stone spaces of all the Boolean subalgebras of L, organised into a presheaf over the partially ordered set of these Boolean subalgebras. This seemingly simple-minded construction raises the question whether one does not lose too much information: is it possible to encode an orthomodular lattice, as a nondistributive structure, by considering the (Stone spaces of) its Boolean, distributive parts only? Maybe surprisingly, the answer is in the affirmative. One of our main results shows that two orthomodular lattices L and M are isomorphic if and only if their spectral presheaves $\underline{\varSigma }^{L}$ and $\underline{\varSigma }^{M}$ are isomorphic (Theorem 3.18). In order to show this, we first have to develop the necessary categorical background in some detail, including the notion of morphisms between presheaves over different base categories, and a dual notion of copresheaves and their morphisms. Among other things, we show that the assignment $L\rightarrow \underline{\varSigma }^{L}$ is contravariantly functorial.

We also provide a certain generalisation of Stone representation to complete orthomodular lattices. Recall that every Boolean algebra B is isomorphic to the concrete Boolean algebra of clopen subsets of the Stone space $\varSigma _B$ of B. In a similar fashion, every complete orthomodular lattice L can be represented within the clopen subobjects of its spectral presheaf $\underline{\varSigma }^{L}$. The representing map is called daseinisation. The clopen subobjects of $\underline{\varSigma }^{L}$ form a complete bi-Heyting algebra, and by using the adjoint of daseinisation, we can form suitable equivalence classes such that the set of equivalence classes becomes a complete OML that is canonically isomorphic to L. This is the content of our second main result (Theorem 4.19).

The topos approach and physical interpretation. This work is of course inspired by the so-called topos approach to quantum theory [3,4,5,6,7,8]. A spectral presheaf was first defined by Isham, Hamilton, and Butterfield for the noncommutative von Neumann algebra $\mathscr {B}(\mathscr {H})$ of all bounded operators on a Hilbert space $\mathscr {H}$ [9] and was later generalised to arbitrary von Neumann algebras [10]. In the topos approach, the spectral presheaf plays the role of a generalised state space for a quantum system, providing a topological-geometric perspective that is not available ordinarily. Just as in classical physics, propositions about the values of physical quantities are represented by (clopen) sub‘sets’ of the quantum state space. This led to the development of a new form of logic for quantum systems, based upon the internal logic of the topos of presheaves in which the spectral presheaf lies [4, 11, 12]. In [13, 14], the second author considered the question if the spectral presheaf determines a von Neumann algebra up to isomorphism (it does not, but it determines the algebra up to Jordan-$*$-isomorphism).

Orthomodular lattices are key structures in quantum logic [15, 16], where they represent algebras of propositions about a quantum system. The lattice operations are interpreted logically as conjunction and disjunction, while the orthocomplement is interpreted as negation. We provide a topological-geometric underpinning of this kind of quantum logic by providing a concrete dual space for every orthomodular lattice. Moreover, we represent the elements of a complete OML by clopen subsets (technically, subobjects) of this dual space. The fact that the clopen subsets form a complete bi-Heyting algebra and not a complete OML may seem to be a disadvantage at first sight, but in fact it is a great improvement over standard quantum logic, since many conceptual problems are avoided. For example, there is a material implication. Moreover, one can use the adjoint of daseinisation to map back to the complete OML. We will briefly discuss some of the interpretational advantages of the bi-Heyting algebra representation in Sect. 4.4.

Overview and organisation. This article is largely self-contained. Section 2 provides some mathematical background on orthomodular lattices, Stone duality etc. and some preliminary results, in particular concerning the Boolean substructure of an orthomodular lattice. In Sect. 3, we introduce the spectral presheaf of an orthomodular lattice (Sect. 3.1) and consider maps between spectral presheaves (Sect. 3.2). There is some detailed discussion of categories of presheaves over varying base categories and with values in another category $\mathscr {D}$ (Sect. 3.3), as well as of copresheaves with values in $\mathscr {C}$ (Sect. 3.4). A dual equivalence between $\mathscr {C}$ and $\mathscr {D}$ lifts to a dual equivalence between $\mathbf {Copresh}(\mathscr {C})$ and $\mathbf {Presh}(\mathscr {D})$, and we apply this to Stone duality in particular (Sect. 3.5). These results are then employed to show that two orthomodular lattices are isomorphic if and only if their spectral presheaves are isomorphic, and the isomorphisms can be constructed explicitly from each other (Sects. 3.6, 3.7; Theorem 3.18). We provide some interpretation, including physical interpretation, of this result in (Sect. 3.8) and also show the analogous result for complete orthomodular lattices (Sect. 3.9; Theorem 3.29). In Sect. 4, we are concerned with the representation of complete OMLs. We define clopen subobjects of the spectral presheaf (Sect. 4.1), show that they form a complete bi-Heyting algebra ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ (Sect. 4.2), and then introduce the map called daseinisation that takes elements of a complete OML L to clopen subobjects of its spectral presheaf $\underline{\varSigma }^{L}$. We interpret this as a representation of L within ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ (Sect. 4.3) and give some physical interpretation in (Sect. 4.4). The adjoint of daseinisation is introduced and some of its properties are discussed in (Sect. 4.5). We then show that using this adjoint, one can form equivalence classes of clopen subobjects such that the set E of equivalence classes becomes a complete OML isomorphic to L in a natural way, which means that we have a generalisation of Stone representation to complete orthomodular lattices (Sect. 4.6; Theorem 4.19). Section 5 concludes with a list of some open problems.

2 Background and Preliminary Results

We assume familiarity with some basics of order and lattice theory such as the definitions of partially ordered sets (posets), meets (greatest lower bounds), joins (least upper bounds), lattices, and complete lattices [17, 18]. Additionally, some familiarity with category theory is assumed, including the definitions (but no advanced properties) of presheaves, copresheaves, dual equivalences, and topoi; see, e.g., [19,20,21,22,23,24].

Throughout, we will denote the category of posets and monotone maps between them as Pos, the category of sets and functions between them as $\mathbf {Set}$, and the category of Boolean algebras and Boolean algebra homomorphisms as $\mathbf {BA}$.

2.1 Ortholattices and Orthomodular Lattices

Our results focus on orthomodular lattices, which we now define. Good references are [16, 25].

Definition 2.1

An orthocomplementation function on a lattice L is a map $a\mapsto a'$ for each lattice element a, satisfying

• 1. $a' \vee a = 1$, $a' \wedge a = 0$        (Complement Law),

• 2. $a''= a$                                (Involution Law),

• 3. If $a\le b$, then $b' \le a'$        (Order-Reversing).

Definition 2.2

An orthocomplemented lattice, also called an ortholattice, is a bounded lattice with an orthocomplementation function.

Definition 2.3

An orthomodular lattice (OML) L is an ortholattice such that for any $x,y \in L$ with $x \le y$, it holds that $x \vee ( x' \wedge y) = y$. This is the orthomodularity property.

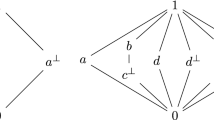
Figure 1 depicts four small ortholattices. Ortholattices (i), (iii), and (iv) have a unique orthocomplementation function, as shown. The second has three valid orthocomplementation functions; the orthocomplement of a could be any of b, c, or d. Of these ortholattices, (i), (ii), and (iv) are orthomodular lattices. In (iii), elements $b'$ and a satisfy $b' \le a$, but

$$\begin{aligned} b' \vee (b \wedge a) = b' \vee 0 = b' \ne a. \end{aligned}$$

(1)

Fig. 1

Four valid ortholattices. An arrow $a \rightarrow b$ means $a \le b$

Another example of an OML is the lattice of subspaces of any inner product space, with the orthogonal complement operation on these subspaces as the orthocomplementation function. The closed subspaces of a separable Hilbert space form a complete orthomodular lattice; such lattices are at the heart of Birkhoff-von Neumann style quantum logic [26], where the closed subspaces represent propositions about the values of physical quantities of a quantum system. More generally, the projections in any von Neumann algebra $\mathscr {N}$ form a complete OML $\mathscr {P}(\mathscr {N})$.

We will refer to an orthocomplement-preserving lattice homomorphism between two OMLs as an orthomodular lattice homomorphism. Orthomodular lattices and orthomodular lattice homomorphisms form a category $\mathbf {OML}$. It will be useful to note that De Morgan’s laws, which are an important property of Boolean algebras, hold in the more general case for all ortholattices (and thus all orthomodular lattices).

2.2 Distributive Substructure of an Orthomodular Lattice

We will consider Boolean sublattices of orthomodular lattices (OMLs).

Definition 2.4

A Boolean sublattice, also called a Boolean subalgebra, of an orthomodular lattice L is a complemented distributive sublattice with complements given by the orthocomplementation function of L.

Lemma 2.5

Every element a of an orthomodular lattice L is in some Boolean subalgebra of L.

For $a \ne 0,1$, one Boolean subalgebra containing a is the four-element sublattice $\{0,a,a',1\}$.

Proposition 2.6

Let L be an ortholattice. L is orthomodular if and only if for all elements $a,b \in L$ with $a\le b$ there is a Boolean subalgebra of L containing both a and b.

Proof

The forward implication can be found in [17]; concretely, for $a,b \ne 0,1$, a Boolean sublattice of L containing a and b is displayed in Fig. 2. For the converse, assume that for all $a\le b$ in L there is some Boolean subalgebra of L containing both a and b. Then elements a and b and their complements satisfy distributivity, meaning

$$\begin{aligned} a \vee (a' \wedge b) = (a \vee a') \wedge (a \vee b) = 1 \wedge b = b. \end{aligned}$$

(2)

This is the orthomodularity condition, so as it holds for all $a \le b$ then L is orthomodular.

Fig. 2

Boolean sublattices of an orthomodular lattice L containing (i) element a, and (ii) elements a and b with $a \le b$

This is the reason we consider orthomodular lattices instead of ortholattices, as Proposition 2.6 plays a key role in the proofs of Lemma 2.12 and Proposition 2.13 and subsequently in Theorem 3.17, which is the main result of Sect. 3.

2.2.1 The Context Category $\mathscr {B}(L)$

Definition 2.7

For an orthomodular lattice L, let $\mathscr {B}(L)$ denote the poset of Boolean sublattices of L, where the partial order on $\mathscr {B}(L)$ is given by inclusion. $\mathscr {B}(L)$ is also called the context category of L.

Seen as a category, the poset $\mathscr {B}(L)$ has a unique arrow from Boolean subalgebra $B'$ to Boolean subalgebra B whenever $B' \subseteq B$. This arrow will be denoted $i_{B',B}$, and simply indicates that $B' \subseteq B$.

Additionally, whenever $B' \subseteq B$, one can define an inclusion map between Boolean subalgebras $inc_{B', B}: B' \rightarrow B$ given by $inc_{B',B}(b) = b$ for all $b \in B'$. As $B'$ is closed under meets, joins, and orthocomplements, it follows that $inc_{B',B}$ is a Boolean algebra homomorphism, that is, a morphism in category $\mathbf {BA}$.

Let $\varphi : L \rightarrow M$ be an orthomodular lattice homomorphism. If B is a Boolean subalgebra of L, then

$$ \varphi |_B:B \longrightarrow \varphi [B] $$

is a morphism of Boolean (sub)algebras, since the image $\varphi [B]$ clearly is a Boolean subalgebra of M. Hence, every morphism $\varphi :L\mapsto M$ of OMLs induces a morphism between their context categories:

$$\begin{aligned} \tilde{\varphi }:\mathscr {B}(L)&\longrightarrow \mathscr {B}(M)\end{aligned}$$

(3)

$$\begin{aligned} B&\longmapsto \varphi [B]. \end{aligned}$$

(4)

If $\varphi :L\rightarrow M$ is an isomorphism of OMLs, then clearly $\varphi |_B:B\rightarrow \varphi [B]$ is an isomorphism of Boolean algebras. Summing up,

Proposition 2.8

There is a functor from $\mathscr {B}:\mathbf {OML}\rightarrow \mathbf {Pos}$ sending each orthomodular lattice L to its context category $\mathscr {B}(L)$ and each homomorphism $\varphi :L\rightarrow M$ of OMLs to the corresponding morphism $\tilde{\varphi }:\mathscr {B}(L)\rightarrow \mathscr {B}(M)$.

Since functors preserve isomorphisms, we have

Lemma 2.9

If $\varphi : L\rightarrow M$ is an isomorphism of orthomodular lattices, then $\tilde{\varphi }: \mathscr {B}(L)\rightarrow \mathscr {B}(M)$ is an order isomorphism in $\mathbf {Pos}$.

2.2.2 The Partial Orthomodular Lattice $L_{\!part}$

The Boolean sublattices of an OML can also be used to generate a second structure, called the partial orthomodular lattice associated with L.

Definition 2.10

Let L be an OML. The partial orthomodular lattice $L_{part}$ associated with L has the same elements and orthocomplements as L, as well as lattice operations $\vee$ and $\wedge$ inherited from L but only defined for finite families of elements $(a_i)_{i \in I}$ in L such that there is some $B \in \mathscr {B}(L)$ that contains $a_i$ for all $i \in I$. Such families of elements are called compatible families.

Definition 2.11

A morphism of partial orthomodular lattices is a function $p: L_{part}\rightarrow M_{part}$ that preserves orthocomplements and existing finite meets and joins.

The following lemma depends critically on orthomodularity:

Lemma 2.12

If $a\le b$ in orthomodular lattice L and $p:L_{part} \rightarrow M_{part}$ is a partial orthomodular lattice homomorphism, then $p(a) \le p(b)$.

Proof

Suppose $a,b \in L$ and $a \le b$. By Proposition 2.6, there is some Boolean subalgebra of L that contains both a and b. This means that the meet $a \wedge b = a$ is defined in $L_{part}$, and thus is preserved by any partial orthomodular lattice homomorphism p:

$$\begin{aligned} p(a) = p(a \wedge b) = p(a) \wedge p(b). \end{aligned}$$

(5)

From this it follows that $p(a) \le p(b)$.

Partial orthomodular lattices associated with OMLs and partial orthomodular lattice homomorphisms form a category $\mathbf {POML}$. The motivation for considering partial OMLs comes from the ‘Bohrification’ construction that can be applied to an orthomodular lattice, as will be explained in Sect. 3; $L_{part}$ can be seen as a topos-external description of the Bohrification ${\overline{\mathscr {L}}}$ of L, which is an object in the topos $\mathbf {Set}^{\mathscr {B}(L)}$ of (covariant) functors from the context category $\mathscr {B}(L)$ to $\mathbf {Set}$.

Proposition 2.13

Let L and M be OMLs, and $L_{part}$ and $M_{part}$ their associated partial OMLs. There is a bijective correspondence between isomorphisms $L\rightarrow M$ in $\mathbf {OML}$ and isomorphisms $L_{part}\rightarrow M_{part}$ in $\mathbf {POML}$.

Proof

Let $\varphi : L\rightarrow M$ be an isomorphism in $\mathbf {OML}$. As a homomorphism between orthomodular lattices, it preserves orthocomplements and finite meets and joins. In particular, it preserves all meets and joins that are defined in $L_{part}$, meaning that it induces a homomorphism $\varphi :L_{part} \rightarrow M_{part}$. As $\varphi :L\rightarrow M$ is an isomorphism, so is $\varphi :L_{part}\rightarrow M_{part}$.

Conversely, let $p:L_{part} \rightarrow M_{part}$ be an isomorphism of partial ortholattices in $\mathbf {POML}$. Let $(a_i)_{i\in I}$ be any finite family of elements in L; our goal is to show that

$$\begin{aligned} p\left( \bigvee _{i \in I} a_i\right) = \bigvee _{i \in I} p(a_i), \end{aligned}$$

(6)

which implies that p preserves all joins, not just those joins that are defined in $L_{part}$. The same result for meets then follows by taking orthocomplements.

First, suppose that there is some Boolean subalgebra B of L such that $a_i \in B$ for all $i \in I$. Thus $\bigvee _{i\in I} a_i$ is defined in $L_{part}$, and as partial orthomodular lattice isomorphism p preserves all joins that are defined in $L_{part}$,

$$\begin{aligned} p\left( \bigvee _{i \in I} a_i\right) = \bigvee _{i \in I} p(a_i). \end{aligned}$$

(7)

Now, assume there is no $B \in \mathscr {B}(L)$ such that $a_i\in B$ for all $i \in I$. Consider the element $\bigvee _{i\in I} a_i$ of L. Note that for each i, $a_i \le \bigvee _{i\in I} a_i$, meaning that by Lemma 2.12, $p(a_i) \le p\left( \bigvee _{i\in I} a_i\right) .$ As this is true for all i, it follows that

$$\begin{aligned} \bigvee _{i\in I} p(a_i) \le p\left( \bigvee _{i\in I} a_i\right) . \end{aligned}$$

(8)

Now, let $p^{-1}: M_{part} \rightarrow L_{part}$ be the inverse of partial orthomodular lattice isomorphism p, which is also a partial orthomodular lattice isomorphism. For all i, $p(a_i) \le \bigvee _{i\in I} p(a_i).$ Again by Lemma 2.12, $p^{-1}$ preserves inequalities, so this equation becomes

$$\begin{aligned} a_i = p^{-1}(p(a_i)) \le p^{-1}\left( \bigvee _{i\in I} p(a_i)\right) . \end{aligned}$$

(9)

As this is true for all $i\in I$, it follows that

$$\begin{aligned} \bigvee _{i \in I}a_i \le p^{-1}\left( \bigvee _{i\in I} p(a_i)\right) . \end{aligned}$$

(10)

Applying p to the above equation and again invoking Lemma 2.12, this becomes

$$\begin{aligned} p\left( \bigvee _{i \in I}a_i\right) \le p\left( p^{-1}\left( \bigvee _{i\in I} p(a_i)\right) \right) = \bigvee _{i\in I} p(a_i) \end{aligned}$$

(11)

Equations 8 and 11 together imply

$$\begin{aligned} p\left( \bigvee _{i \in I}a_i\right) = \bigvee _{i\in I} p(a_i), \end{aligned}$$

(12)

showing that p preserves all joins in L, not only those joins which are defined in $L_{part}$.

Showing that p preserves all meets in L follows easily. Let $(a_i)_{i\in I}$ be any family of elements in L. Then $(a_i')_{i\in I}$ is also a family of elements in L, and we know

$$\begin{aligned} p\left( \bigvee _{i \in I}a_i'\right) = \bigvee _{i\in I} p(a_i').\end{aligned}$$

(13)

Recall that orthocomplementation is preserved by p and satisfies De Morgan’s laws. Then,

$$\begin{aligned} p\left( \bigwedge _{i \in I}a_i\right)&= p\left( \left[ \bigvee _{i \in I} a_i'\right] '\right) = \left[ p\left( \bigvee _{i \in I}a_i'\right) \right] ' = \left[ \bigvee _{i\in I} p(a_i')\right] ' \end{aligned}$$

(14)

$$\begin{aligned}&= \bigwedge _{i \in I} \left[ p(a_i')\right] ' = \bigwedge _{i \in I} p(a_i'') = \bigwedge _{i \in I} p(a_i) .\end{aligned}$$

(15)

Thus, as p preserves all meets and joins in L, as well as all orthocomplements, p is in fact an isomorphism of OMLs, $p:L\rightarrow M$.

As $p: L_{part}\rightarrow M_{part}$ and $p:L\rightarrow M$ are the same on every element of L, and $\varphi : L\rightarrow M$ and the induced $\varphi : L_{part}\rightarrow M_{part}$ are the same on every element of L, then there is a bijective correspondence between isomorphisms $\varphi : L\rightarrow M$ and isomorphisms $p:L_{part} \rightarrow M_{part}$.

Note it is in the construction of an isomorphism of OMLs from an isomorphism of partial OMLs that the orthomodularity condition (in the form of Lemma 2.12) is essential. This result does not hold for arbitrary ortholattices, and is the reason we consider orthomodular lattices instead.

2.2.3 Example

We now consider a small OML $L^*$, and examine $\mathscr {B}(L^*)$ and $L^*_{part}$. Let $L^*$ be as in Fig. 3. Consider the Boolean sublattices of $L^*$. The two-element Boolean lattice $B_0 = \{0,1\}$ is a sublattice of $L^*$. The four element Boolean lattice (Fig. 1i) appears as a sublattice of L five times, as $B_a$, $B_b$, $B_c$, $B_d$, and $B_e$. The eight element Boolean lattice (Fig. 1iv) appears twice, as $B_{a,b,c}$ and $B_{c,d,e}$. This yields the context category shown in Fig. 3.

Fig. 3

An orthomodular lattice $L^*$ with twelve elements and its context category $\mathscr {B}(L^*)$

The partial orthomodular lattice $L^*_{part}$ has the same elements as $L^*$ but meets and joins only defined for compatible elements. Table 1 lists all pairs of elements in $L^*$ that do not have a well-defined meet or join. For $L^*$, larger families of elements are compatible precisely when they contain none of the pairs in Table 1, though this is not the case in general. To see this, consider $L^*$ with additional elements f and $f'$ such that $B_{e,f,a}$ is a Boolean sublattice. Then, for elements a, c, and e, all pairwise meets and joins are defined but not the meet or join of all three elements.

Table 1 Pairs of elements that are not compatible in $L^*$; that is, pairwise meets and joins between these elements are not defined in $L^*_{part}$

2.3 Stone Duality

There is a well-known duality between Boolean algebras and Stone spaces. We recall the main definitions and fix the notation for later use, see also, e.g., [27].

Definition 2.14

A Stone space is a compact totally disconnected Hausdorff space.

There is a category $\mathbf {Stone}$ whose objects are Stones spaces and whose arrows are continuous functions between these topological spaces. Let $\{0,1\}$ denote the two element Boolean algebra consisting of only a bottom element 0 and a top element 1.

Definition 2.15

The Stone space of a Boolean algebra B is the topological space $\varSigma _B$ with set of elements

$$\begin{aligned} \varSigma _B = \{ \lambda : B\rightarrow \{0,1\} \mid \lambda&\text { is a Boolean algebra homomorphism,}\end{aligned}$$

(16)

$$\begin{aligned}&\text {also called a state or an ultrafilter in}\, B \} \end{aligned}$$

(17)

and topology generated by a basis of, for all $b \in B$, the sets

$$\begin{aligned} U_b:=\{ \lambda \in \varSigma _B: \lambda (b) = 1\}. \end{aligned}$$

(18)

We use the notation $\varSigma _B$ instead of the more common $\varOmega _B$ (or just $\varOmega$), since we will generalise the Stone space $\varSigma _B$ to the spectral presheaf $\underline{\varSigma }^{L}$ of an orthomodular lattice L, and the notation $\underline{\varSigma }$ (or $\underline{\varSigma }^{\mathscr {N}}$) for the spectral presheaf of a von Neumann algebra $\mathscr {N}$ is already established. Moreover, the spectral presheaf is an object in a topos, and the subobject classifier in a topos is traditionally denoted $\varOmega$, which could lead to confusion.

Each $\lambda \in \varSigma _B$ is also called a state of B, and states correspond bijectively to ultrafilters: given $\lambda$, the set

$$ F_{\lambda }:= \{a\in B \mid \lambda (a)=1\} $$

is an ultrafilter in B.

We can construct a contravariant functor $\varSigma :\mathbf {BA}\rightarrow \mathbf {Stone}$ from the category of Boolean algebras and Boolean algebra homomorphisms to the category of Stone spaces and continuous functions, given

• (i) on objects: for each $B\in Ob({\mathbf {BA}})$, let $\varSigma (B):=\varSigma _B$, the Stone space of B,

• (ii) on arrows: for each morphism $(\phi :B'\rightarrow B)\in Arr({\mathbf {BA}})$ of Boolean algebras, let

  $$\begin{aligned} \varSigma (\phi ):\varSigma (B)&\longrightarrow \varSigma (B')\end{aligned}$$

  (19)
  $$\begin{aligned} \lambda&\longmapsto \lambda \circ \phi . \end{aligned}$$

  (20)

Furthermore, to each Stone space X we can associate a canonical Boolean algebra. Let $cl_X$ denote the set of subsets of X that are simultaneously closed and open, i.e. clopen. With meets given by intersections and joins given by unions, this is a Boolean algebra. Additionally considering morphisms, we obtain a functor $cl:\mathbf {Stone}\rightarrow \mathbf {BA}$, given

• (i) on objects: for all $X\in Ob({\mathbf {Stone}})$, let $cl(X):=cl_X$,

• (ii) on arrows: for all $(f:X\rightarrow X')\in Arr({\mathbf {Stone}})$, let

  $$\begin{aligned} cl(f):cl_{X'}&\longrightarrow cl_X\end{aligned}$$

  (21)
  $$\begin{aligned} S&\longmapsto f^{(-1)}(S), \end{aligned}$$

  (22)

  where $f^{(-1)}$ denotes the inverse image function of f.

Throughout, we will use the notation $f^{-1}$ to denote function inverses and $f^{(-1)}$ to denote inverse image functions.

If we replace each clopen subset $S\subseteq X$ by its characteristic function $\chi _S:X\rightarrow \{0,1\}$, we can write $cl(f)(\chi _S)=\chi _S\circ f$, which makes the morphism part of the functor $cl:\mathbf {Stone}\rightarrow \mathbf {BA}$ formally identical to the morphism part of $\varSigma :\mathbf {BA}\rightarrow \mathbf {Stone}$.

The two functors give rise to a dual equivalence between the categories $\mathbf {BA}$ and $\mathbf {Stone}$:

That is, there are natural isomorphisms $Bo: Id_{\mathbf {BA}} \rightarrow cl \circ \varSigma$ in $\mathbf {BA}$ and ${St: Id_{\mathbf {Stone}}\rightarrow \varSigma \circ cl}$ in $\mathbf {Stone}$. In particular, the components of these isomorphisms are given as follows:

$$\begin{aligned} Bo_B: B&\rightarrow cl(\varSigma _B)\end{aligned}$$

(23)

$$\begin{aligned} b&\mapsto U_b=\{ \lambda \in \varSigma _B \mid \lambda (b) = 1\}\end{aligned}$$

(24)

$$\begin{aligned} St_X: X&\rightarrow \varSigma (cl(X))\end{aligned}$$

(25)

$$\begin{aligned} x&\mapsto \lambda _x \end{aligned}$$

(26)

where $\lambda _x: cl(X) \rightarrow \{0,1\}$ is given by

$$\begin{aligned} \lambda _x(S) = \left\{ \begin{array}{lr} 1 &{}: x \in S\\ 0 &{}: x \notin S \end{array} \right. \end{aligned}$$

(27)

Later, it will be of use to know the explicit components of $Bo^{-1}: cl \circ \varSigma \rightarrow Id_{\mathbf {BA}}$. Each component $Bo_B^{-1}$ is a map from $cl(\varSigma _B)$ to B. Let S be any clopen subset in $cl(\varSigma _B)$. As S is closed and the subset of a compact space $\varSigma _B$, S is compact. As S is open, it can be written as the union of basic open sets. Compactness implies that this open cover has a finite subcover of basic open sets, which are of the form $U_b=\{\lambda \in \varSigma _B \mid \lambda (b)=1\}$. That is, for some finite index set $J\subseteq B$,

$$ S = \bigcup _{b\in J} U_b. $$

Let

$$\begin{aligned} s_* = \bigvee _{b \in J} b \in B. \end{aligned}$$

(28)

Then, the action of $Bo_B^{-1}$ is as follows.

$$\begin{aligned} Bo_B^{-1}: cl (\varSigma _B)&\longrightarrow B \end{aligned}$$

(29)

$$\begin{aligned} S&\longmapsto {s_*}. \end{aligned}$$

(30)

2.4 Complete Orthomodular Lattices and Their Boolean Substructure

All of the concepts defined above for orthomodular lattices also hold for complete orthomodular lattices (cOMLs). Let $\mathbf {cOML}$ denote the category of complete orthomodular lattices, and $\mathbf {cBA}$ the subcategory of complete Boolean algebras. Morphisms in both categories preserve all meets, all joins, and orthocomplements.

The following two results are immediate, and the Boolean algebras stated to exist are the same as in Fig. 2:

Proposition 2.16

Every element a of complete orthomodular lattice L is in some complete Boolean subalgebra of L.

Proposition 2.17

In a complete orthomodular lattice L, for any elements $a,b \in L$ satisfying $a\le b$ there is complete Boolean subalgebra of L containing both a and b.

We define the complete analogue of the context category $\mathscr {B}(L)$:

Definition 2.18

The complete context category of a complete orthomodular lattice L, denoted ${\mathscr {B}_c(L)}$, is the poset of complete Boolean subalgebras of L, ordered by inclusion.

As before, when we consider the poset ${\mathscr {B}_c(L)}$ as a category, arrows will be denoted in the form $i_{B',B}:B'\hookrightarrow B$. We will usually drop the ‘complete’ and just call ${\mathscr {B}_c(L)}$ the context category of L.

Any morphism $\varphi : L \rightarrow M$ of cOMLs induces an order-preserving map $\tilde{\varphi }: {\mathscr {B}_c(L)}\rightarrow \mathscr {B}_c(M)$ between the context categories, where on each complete Boolean subalgebra B of L,

$$ \tilde{\varphi }(B):= \varphi [B]. $$

Clearly, $\varphi |_B:B\rightarrow \varphi [B]$ is a morphism of complete Boolean algebras.

Summing up, there is a functor $c\mathscr {B}: \mathbf {cOML}\rightarrow \mathbf{Pos}$, given

• (i) on objects: for each $L\in \mathbf {cOML}$, let $c\mathscr {B}_L:={\mathscr {B}_c(L)}$, the (complete) context category of L,

• (ii) on arrows: for each morphism $\varphi :L\rightarrow M$ of cOMLs, let

  $$\begin{aligned} c\mathscr {B}(\varphi ):= \tilde{\varphi }: {\mathscr {B}_c(L)}&\longrightarrow \mathscr {B}_c(M)\end{aligned}$$

  (31)
  $$\begin{aligned} B&\longmapsto \varphi [B]. \end{aligned}$$

  (32)

There is also a complete version of the partial Boolean algebra $L_{part}$ associated with an orthomodular lattice L:

Definition 2.19

Let L be a complete orthomodular lattice. The partial complete orthomodular algebra $L^c_{part}$ associated with L has the same elements and orthocomplements as L, and has lattice operations $\bigvee$ and $\bigwedge$ inherited from L but only defined for (possibly infinite) families of elements $(a_i)_{i \in I}$ in L such that there is a $B \in {\mathscr {B}_c(L)}$ that contains $a_i$ for all $i \in I$. Such families of elements are called compatible families.

Definition 2.20

A morphism of partial complete orthomodular algebras is a function $p: L^c_{part}\rightarrow M^c_{part}$ that preserves orthocomplements and existing meets and joins.

There is a category $\mathbf {pcOML}$ of partial cOMLs and morphisms of partial cOMLs between them. The complete versions of Lemma 2.12 and Proposition 2.13 are

Lemma 2.21

If $a\le b$ in complete orthomodular lattice L and $p:L_{part} \rightarrow M_{part}$ is a morphism of partial cOMLs, then $p(a) \le p(b)$.

Proposition 2.22

Let L and M be complete orthomodular lattices, and $L_{part}$ and $M_{part}$ their associated partial complete orthomodular lattices. There is a bijective correspondence between isomorphisms $L\rightarrow M$ in $\mathbf {cOML}$ and isomorphisms $L_{part}\rightarrow M_{part}$ in $\mathbf {pcOML}$.

As before, Lemmas 2.21 and 2.22 depend on orthomodularity and do not hold for arbitrary complete ortholattices.

2.5 Stonean Spaces and Stone Duality for Complete Boolean Algebras

Just as there is a duality between Boolean algebras and Stone spaces, there is a duality between complete Boolean algebras and Stonean spaces.

Definition 2.23

A Stonean space is an extremely disconnected compact Hausdorff space.

In an extremely disconnected topological space, the closure of every open subspace is open and the interior of every closed subspace is closed. Recall that a Stone space is a totally disconnected compact Hausdorff space. As ‘extremely disconnected’ is a stronger condition than ‘totally disconnected,’ all Stonean spaces are also Stone spaces but not vice versa. The following lemmas characterise the relation between Stonean spaces and complete Boolean algebras.

Proposition 2.24

([2]) A Boolean algebra is complete if and only if its Stone space is Stonean.

Proposition 2.25

([28]) The clopen subsets of a Stonean space form a complete Boolean algebra. Complementation is given by set-theoretic complementation, and meets and joins for a family of clopen subsets $\{ S_i \mid i \in I\}$ are given by:

$$\begin{aligned} \bigvee _{i \in I} S_i&= {\text {cls}}(\bigcup _{i \in I} S_i) \end{aligned}$$

(33)

$$\begin{aligned} \bigwedge _{i \in I} S_i&= {\text {int}}(\bigcap _{i \in I} S_i) \end{aligned}$$

(34)

Here ${\text {cls}}$ denotes the closure and ${\text {int}}$ the interior of a subset with respect to the Stone topology.

The correspondence between complete Boolean algebras and Stonean spaces can be extended to a dual equivalence of categories. There is a category $\mathbf {Stonean}$, whose objects are Stonean spaces and whose morphisms are continuous open maps.

Proposition 2.26

([29]) There is a dual equivalence of categories between $\mathbf {cBA}$ and $\mathbf {Stonean}$:

This duality is witnessed by the natural isomorphisms $Bo: Id_\mathbf {cBA}\rightarrow cl\circ \varSigma$ and $St: Id_{\mathbf {Stonean}} \rightarrow \varSigma \circ cl$ (where we use the same notation as in Stone duality for OMLs and BAs). Propositions 2.24 and 2.25, above, are consequences of this dual equivalence, but the references listed above provide explicit proofs that give more intuition as to why such results are true.

As corollaries of Proposition 2.26, we also have the following facts that will later be essential for extending the isomorphism result of Theorem 3.18 to complete orthomodular lattices.

Fact 2.27

For every $B \in Ob(\mathbf {cBA})$, the component $Bo_B$ of the natural isomorphism Bo is an isomorphism of cBAs.

Proof

$Bo_B: B \rightarrow cl(\varSigma _B)$ is an arrow in $\mathbf {cBA}$.

Fact 2.28

If $\eta :X \rightarrow Y$ is any continuous open map between Stonean spaces, then $cl(\eta )$ is a morphism of cBAs.

Proof

$cl(\eta ): cl(Y) \rightarrow cl(X)$ is an arrow in $\mathbf {cBA}$.

2.6 Galois Connections and the Adjoint Functor Theorem for Posets

We briefly recall the definition of Galois connections and the adjoint functor theorem for posets (in fact, for complete lattices) for later use, see also, e.g., [18].

Definition 2.29

Let P and Q be posets. A pair of monotone maps $f:P \rightarrow Q$ and $g: Q \rightarrow P$ is a Galois connection between P and Q if, for all $p \in P$ and all $q \in Q$,

$$\begin{aligned} f(p) \le q \text { iff } p \le g(q). \end{aligned}$$

(35)

A Galois connection is written (f, g), where f is called the lower adjoint (or left adjoint) of g, and g is called the upper adjoint (or right adjoint) of f.

Proposition 2.30

(Adjoint functor theorem for posets) Let P and Q be complete lattices and $f: P \rightarrow Q$ a monotone map. Then,

• 1. f preserves arbitrary joins if and only if f has an upper adjoint g, meaning (f, g) is a Galois connection. For all $q \in Q$, this map g is given by

  $$\begin{aligned} g(q) = \bigvee \{ p \in P \mid f(p) \le q\}. \end{aligned}$$

  (36)

• 2. f preserves arbitrary meets if and only if f has a lower adjoint h, meaning (h, f) is a Galois connection. For all $q \in Q$, this map h is given by

  $$\begin{aligned} h(q) = \bigwedge \{ p \in P \mid q \le f(p) \}. \end{aligned}$$

  (37)

There are more general versions of this theorem, but the above form is what we will need.

Galois connections have several interesting properties that will be of use to us.

Proposition 2.31

Let P and Q be complete lattices and $f: P \rightarrow Q$ and $g:Q \rightarrow P$ such that (f, q) is a Galois connection. The following hold:

• 1. f preserves arbitrary joins,

• 2. g preserves arbitrary meets,

• 3. For all $p \in P$, $p \le (g \circ f)(p)$,

• 4. For all $q \in Q$, $(f \circ g)(q) \le q$,

• 5. For all $p \in P$, $(f \circ g \circ f)(p) = f(p)$,

• 6. For all $q \in Q$, $(g\circ f \circ g)(q) = g(q)$.

3 The Spectral Presheaf of an Orthomodular Lattice

We now define and examine the spectral presheaf of an orthomodular lattice, the main focus of this work.

3.1 Definition

A spectral presheaf was originally defined for von Neumann algebras as part of an alternate topos-based formulation of quantum mechanics. However, one can also define the spectral presheaf of an orthomodular lattice as follows.

Definition 3.1

Let L be an orthomodular lattice with context category $\mathscr {B}(L)$. The spectral presheaf$\underline{\varSigma }^{L}$ of L is the contravariant, $\mathbf {Set}$-valued functor with domain $\mathscr {B}(L)$ given

• (i) on objects: for all $B\in Ob({\mathscr {B}(L)})$, let $\underline{\varSigma }^{L}_B:=\varSigma _B$, the Stone space of B. Here, $\underline{\varSigma }^{L}_B$ denotes the component of $\underline{\varSigma }^{L}$ at B.

• (ii) on arrows: for all $(i_{B'B}:B'\hookrightarrow B)\in Arr({\mathscr {B}(L)})$, let

  $$\begin{aligned} \underline{\varSigma }^{L}(i_{B'B}):\underline{\varSigma }^{L}_B&\longrightarrow \underline{\varSigma }^{L}_{B'}\end{aligned}$$

  (38)
  $$\begin{aligned} \lambda&\longmapsto \lambda |_{B'}. \end{aligned}$$

  (39)

  Here, $\lambda |_{B'}$ denotes the restriction of $\lambda$ to the subalgebra $B'$.

The spectral presheaf $\underline{\varSigma }^{L}$ of an OML L is an object in the functor category $\mathbf {Set}^{\mathscr {B}(L)^{{\text {op}}}}$ of contravariant, $\mathbf {Set}$-valued functors with domain $\mathscr {B}(L)$. The category $\mathbf {Set}^{\mathscr {B}(L)^{{\text {op}}}}$ is a topos. In fact, we will shortly also consider another category in which $\underline{\varSigma }^{L}$ is an object, namely the category of $\mathbf {Stone}$-valued presheaves. The advantage of considering $\underline{\varSigma }^{L}$ as a $\mathbf {Stone}$-valued presheaf is that the components of $\underline{\varSigma }^{L}$ are explicitly seen as topological spaces in $\mathbf {Stone}$ rather than simply as sets, and the restriction maps $\underline{\varSigma }^{L}(i_{B'B})$ are continuous functions (in fact, surjective, continuous and open functions).

3.1.1 Example

Consider the orthomodular lattice $L^*$ from Sect. 2.2.3. This lattice and its context category appear in Fig. 3. The spectral presheaf of $L^*$ is a functor from $\mathscr {B}(L)$ to $\mathbf {Set}$. Each Boolean subalgebra B of $L^*$ is mapped to its Stone space $\varSigma _B$.

We now consider the action of the spectral presheaf on an inclusion map in $\mathscr {B}(L)$. We know that $B_a \subseteq B_{a,b,c}$, meaning there is an arrow $i_{B_a, B_{a,b,c}}$ corresponding to this in $\mathscr {B}(L)$. Note the Stone space of $B_a$ has two elements, called $\lambda _a$ and $\lambda _{a'}$, where $\lambda _a(a) = 1$ and $\lambda _{a'}(a) = 0$. Additionally, the Stone space of $B_{a,b,c}$ has three elements $\lambda _{a,b}$, $\lambda _{a,c}$, and $\lambda _{b,c}$, where the subscripts denote the two elements out of a, b, and c that are mapped to 1, while the third is mapped to 0; this completely determines the functions’ values on all of $B_{a,b,c}$. Then, $\underline{\varSigma (L^*)}(i_{B_a, B_{a,b,c}})$ is a map r from $\varSigma _{B_{a,b,c}}$ to $\varSigma _{B_a}$ whose action on elements of $\varSigma _{B_{a,b,c}}$ simply restricts the domains of the homomorphisms to $B_a$:

$$\begin{aligned} r(\lambda _{a,b}) = \lambda _a \end{aligned}$$

(40)

$$\begin{aligned} r(\lambda _{a,c}) = \lambda _a \end{aligned}$$

(41)

$$\begin{aligned} r(\lambda _{b,c}) = \lambda _{a'} \end{aligned}$$

(42)

Note that as the inverse image of any open set of $\varSigma _{B_a}$ is open in $\varSigma _{B_{a,b,c}}$, then this map r is in fact a continuous map when $\varSigma _{B_a}$ and $\varSigma _{B_{a,b,c}}$ are considered as topological spaces rather than simply as sets. The images of other inclusion arrows under the spectral presheaf of $L^*$ can be determined similarly and are also continuous maps between topological spaces.

3.2 Maps Between Spectral Presheaves

The next obvious step is to consider maps between spectral presheaves of orthomodular lattices. Specifically, if L and M are orthomodular lattices and $\varphi : L\rightarrow M$ is a morphism of OMLs, then we want to define some map $\Phi$, determined by $\varphi$, from $\underline{\varSigma }^{M}$ to $\underline{\varSigma }^{L}$. This is done in two steps, below. The first step transforms $\underline{\varSigma }^{M}$ into a contravariant functor from $\mathscr {B}(L)$ to $\mathbf {Set}$, while the second step then gives a natural transformation within $\mathbf {Set}^{\mathscr {B}(L)^{{\text {op}}}}$ from this new functor to $\underline{\varSigma }^{L}$. In particular, such a map will be used to show that $L \cong M$ if and only if $\underline{\varSigma }^{L}\cong \underline{\varSigma }^{M}$, the goal of this section. This result implies that the spectral presheaf $\underline{\varSigma }^{L}$ determines up to isomorphism the orthomodular lattice L it comes from.

Step 1. Let $\varphi :L\rightarrow M$ be a morphism of OMLs. Recall from Sect. 2.2 that $\varphi :L\rightarrow M$ induces a monotone map $\tilde{\varphi }: \mathscr {B}(L)\rightarrow \mathscr {B}(M)$ between the context categories. This map $\tilde{\varphi }$ then induces a map between functor categories (topoi) $\tilde{\varphi }^*: \mathbf {Set}^{\mathscr {B}(M)^{{\text {op}}}}\rightarrow \mathbf {Set}^{\mathscr {B}(L)^{{\text {op}}}}$, given by ‘pullback’, that is, precomposition: for each $\underline{P}\in Ob({\mathbf {Set}^{\mathscr {B}(M)^{{\text {op}}}}})$, let

$$ \tilde{\varphi }^*(\underline{P}):= \underline{P}\circ \tilde{\varphi }, $$

which is the presheaf over $\mathscr {B}(L)$ with components

$$ \forall B\in \mathscr {B}(L): (\tilde{\varphi }^*(\underline{P}))_B = \underline{P}_{\tilde{\varphi }(B)}. $$

Those familiar with topos theory [20, 21, 23] will recognise the map $\tilde{\varphi }^*$ as the inverse image part the essential geometric morphism induced by the functor $\tilde{\varphi }:\mathscr {B}(L)\rightarrow \mathscr {B}(M)$ between the base categories of the topoi $\mathbf {Set}^{\mathscr {B}(L)^{{\text {op}}}}$ and $\mathbf {Set}^{\mathscr {B}(M)^{{\text {op}}}}$.

Thus, $\tilde{\varphi }^*$ maps $\underline{\varSigma }^{M}$ to some functor from $\mathscr {B}(L)$ to $\mathbf {Set}$, which is not necessarily $\underline{\varSigma }^{L}$. However, since a map from $\underline{\varSigma }^{M}$ to $\underline{\varSigma }^{L}$ is desired, it is now necessary to define a way to transform $\tilde{\varphi }^*(\underline{\varSigma }^{M})$ to $\underline{\varSigma }^{L}$ within the functor category $\mathbf {Set}^{\mathscr {B}(L)^{{\text {op}}}}$. This is done via a natural transformation as follows.

Step 2. Let $B \in \mathscr {B}(L)$. A morphism $\varphi : L\rightarrow M$ of OMLs induces a Boolean algebra homomorphism $\varphi |_B: B \rightarrow \tilde{\varphi }(B)$. By Stone duality, this corresponds to a unique morphism $\varSigma _{\tilde{\varphi }(B)}\rightarrow \varSigma _B$ of Stone spaces, sending $\lambda$ to $\lambda \circ \varphi |_B$. Note that $\varSigma _{\tilde{\varphi }(B)}$ is the component of $\tilde{\varphi }^*(\underline{\varSigma }^{M})$ at $B\in \mathscr {B}(L)$, and $\varSigma _B$ is the component of $\underline{\varSigma }^{L}$ at B. Hence, for each $B\in \mathscr {B}(L)$ we have a map

$$\begin{aligned} \zeta _{\varphi , B}: \tilde{\varphi }^*(\underline{\varSigma }^{M})_B = \underline{\varSigma }^{M}_{\tilde{\varphi }(B)}&\longrightarrow \underline{\varSigma }^{L}_B=\varSigma _B\end{aligned}$$

(43)

$$\begin{aligned} \lambda&\longmapsto \lambda \circ \varphi |_B. \end{aligned}$$

(44)

Lemma 3.2

The maps $\zeta _{\varphi , B}$, where $B\in \mathscr {B}(L)$, are the components of a natural transformation between functors in $\mathbf {Set}^{\mathscr {B}(L)^{{\text {op}}}}\!$:

$$\begin{aligned} \zeta _\varphi : \tilde{\varphi }^*(\underline{\varSigma }^{M}) \longrightarrow \underline{\varSigma }^{L}. \end{aligned}$$

(45)

Proof

Recall

$$\begin{aligned} \tilde{\varphi }^*(\underline{\varSigma }^{M})_B&= \underline{\varSigma }^{M}_{\tilde{\varphi }(B)} = \varSigma _{\tilde{\varphi }(B)} \end{aligned}$$

(46)

$$\begin{aligned} \tilde{\varphi }^*(\underline{\varSigma }^{M}) (i_{B', B})&=\underline{\varSigma }^{M}( i_{\tilde{\varphi }(B'), \tilde{\varphi }(B)}) = r_{\tilde{\varphi }(B), \tilde{\varphi }(B')} \end{aligned}$$

(47)

For $B', B \in \mathscr {B}(L)$, where $i_{B',B}$ is an inclusion arrow, to show $\zeta _\varphi$ is a natural transformation it is necessary to show that the following diagram commutes:

Let $\lambda : \tilde{\varphi }(B) \rightarrow \{0,1\}$ be any element of $\underline{\varSigma }^{M}_{\tilde{\varphi }(B)}$. Then,

$$\begin{aligned} \left[ \zeta _{\varphi , B'} \circ \underline{\varSigma }^{M}( i_{\tilde{\varphi }(B'), \tilde{\varphi }(B)})\right] ( \lambda )&= \zeta _{\varphi , B'} (\lambda |_{\tilde{\varphi }(B')}) \end{aligned}$$

(48)

$$\begin{aligned}&= \lambda |_{\tilde{\varphi }(B')} \circ \varphi |_{B'} \end{aligned}$$

(49)

$$\begin{aligned}&= (\lambda \circ \varphi )|_{B'},\end{aligned}$$

(50)

$$\begin{aligned} \left[ \underline{\varSigma }^{L}(i_{B',B})\circ \zeta _{\varphi , B}\right] (\lambda )&= \underline{\varSigma }^{L}(i_{B',B}) (\lambda \circ \varphi |_{B})\end{aligned}$$

(51)

$$\begin{aligned}&= (\lambda \circ \varphi |_{B})|_{B'} \end{aligned}$$

(52)

$$\begin{aligned}&= (\lambda \circ \varphi )|_{B'}. \end{aligned}$$

(53)

Thus, the diagram commutes and $\zeta _\varphi$ is a natural transformation.

The two maps $\tilde{\varphi }^*$ and $\zeta _\varphi$ defined above can be combined to give, for any homomorphism $\varphi : L \rightarrow M$, a map from $\underline{\varSigma }^{M}$ to $\underline{\varSigma }^{L}$, written $\Phi = \langle \tilde{\varphi }^*, \zeta _\varphi \rangle$. As $\tilde{\varphi }^*$ is completely determined by $\tilde{\varphi }$ (as is $\zeta _\varphi$), this can also equivalently be written $\Phi = \langle \tilde{\varphi }, \zeta _\varphi \rangle$. Note that the process described above is not a standard composition $\zeta _\varphi \circ \tilde{\varphi }^*$, as these two maps are not within the same category; $\tilde{\varphi }^*$ is a map between topoi $\mathbf {Set}^{\mathscr {B}(M)^{{\text {op}}}}$ and $\mathbf {Set}^{\mathscr {B}(L)^{{\text {op}}}}$, while $\zeta _\varphi$ is a natural transformation within $\mathbf {Set}^{\mathscr {B}(L)^{{\text {op}}}}$.

So far, we have shown that every morphism $\varphi :L\rightarrow M$ of OMLs induces a morphism $\langle \tilde{\varphi }, \zeta _\varphi \rangle :\underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$ in the ‘opposite’ direction between their spectral presheaves. In order to understand this properly as a contravariant functor, we will show this is an example of a more general construction and define a suitable category of presheaves over varying base categories and their morphisms.

3.3 The Category of $\mathscr {D}$-Valued Presheaves

The rather unintuitive definition of a map between spectral presheaves, above, can in fact be understood best as an arrow in a suitable category $\mathbf {Presh}(\mathbf {Stone})$. We now define and explore such presheaf categories. This subsection and the next considerably expand some work done by the second author in [13].

First, we develop some general theory of presheaf categories over varying base categories with values in a category $\mathscr {D}$. Since the base categories of such presheaves are not the same in general, the morphisms between the presheaves are not just natural transformations.

Let $H: \mathscr {K} \rightarrow \mathscr {J}$ be a functor between small categories. For clarity, the action of H on an object K of $\mathscr {K}$ will be written as H(K) rather than $H_K$. For any category $\mathscr {L}$, H induces a “pullback” map $H^*$, analogous to $\tilde{\varphi }^*$, above, from $\mathscr {L}^{\mathscr {J}}$ to $\mathscr {L}^{\mathscr {K}}$ which acts by precomposing by H. That is, on objects $R \in \mathscr {L}^{\mathscr {J}}$,

$$\begin{aligned} H^* R = R \circ H: \mathscr {K} \rightarrow \mathscr {L}. \end{aligned}$$

(54)

Specifically, for any $K \in \mathscr {K}$,

$$\begin{aligned} (H^*R)_K = (R\circ H)_K = R_{H(K)}. \end{aligned}$$

(55)

This is captured by the following commutative diagram for each $R \in \mathscr {L}^\mathscr {J}\!$:

We can additionally show $H^*$ satisfies the even stronger property of being a functor from $\mathscr {L^J}$ to $\mathscr {L^K}$ by defining its action on arrows of $\mathscr {L^J}$ as well. An arrow in $\mathscr {L}^{\mathscr {J}}$ is a natural transformation $\tau :R \rightarrow {R'}$, for $R,{R'}: \mathscr {J}\rightarrow \mathscr {L}.$ Applying $H^*$ produces a natural transformation $H^*\tau : H^*R \rightarrow H^*{R}'$ in $\mathscr {L}^{\mathscr {K}}$, where for each $K \in \mathscr {K}$,

$$\begin{aligned} (H^*\tau )_K = \tau _{H(K)}. \end{aligned}$$

(56)

Checking the necessary diagram shows that $H^*\tau$ is a valid natural transformation precisely because $\tau$ is.

Proposition 3.3

$H^*: \mathscr {L}^{\mathscr {J}} \rightarrow \mathscr {L}^{\mathscr {K}}$ is a functor.

Proof

One can verify, using the definition of $H^*$, that it preserves identity arrows and composition.

The following elementary facts about $H^*$ follow from the definition of $H^*$ and will be useful in later proofs.

Fact 3.4

For $H:\mathscr {J}' \rightarrow \mathscr {J}$ and induced functor $H^*: \mathscr {L}^{\mathscr {J}} \rightarrow \mathscr {L}^{\mathscr {J}'}$, $\tilde{H}:\mathscr {J}'' \rightarrow \mathscr {J}'$ and induced functor $\tilde{H}^*: \mathscr {L}^{\mathscr {J}'} \rightarrow \mathscr {L}^{\mathscr {J}''}$,

$$\begin{aligned} (H\circ \tilde{H})^* = \tilde{H}^* \circ H^*. \end{aligned}$$

(57)

Fact 3.5

Suppose $H: \mathscr {K}\rightarrow \mathscr {J}$, $R: \mathscr {J}\rightarrow \mathscr {L}$, and $S: \mathscr {L}\rightarrow \mathscr {M}$. Then

$$\begin{aligned} H^*(S \circ R) = S \circ (H^*R). \end{aligned}$$

(58)

That is, the following diagram commutes:

Fact 3.6

Let $Id: \mathscr {J} \rightarrow \mathscr {J}$ be the identity functor on category $\mathscr {J}$. Let $R, R' \in \mathscr {L}^{\mathscr {J}}$, and let $\eta : R \rightarrow R'$ be a natural transformation. Then $Id^*R = R$ and $Id^*\eta = \eta : R \rightarrow R'$.

We now proceed to use the functor $H^*$ to define a presheaf category.

Definition 3.7

The category $\mathbf {Presh}(\mathscr {D})$ of $\mathscr {D}$-valued presheaves has as its objects functors (presheaves) of the form $\underline{P}: \mathscr {J}\rightarrow \mathscr {D}^{op}$, where $\mathscr {J}$ is a small category. Arrows are pairs

$$\begin{aligned} \langle H,\eta \rangle : ({\underline{P}}': {\mathscr {J}}' \rightarrow \mathscr {D}^{op}) \rightarrow ({\underline{P}}: {\mathscr {J}} \rightarrow \mathscr {D}^{op}), \end{aligned}$$

(59)

where $H: {\mathscr {J}} \rightarrow {\mathscr {J}}'$ is a functor and $\eta : H^*{\underline{P}}' \rightarrow {\underline{P}}$ is a natural transformation in $(\mathscr {D}^{op})^{{\mathscr {J}}}\!$:

Let $\underline{P}_i: \mathscr {J}_i \rightarrow \mathscr {D}^{op}$, for $i = 1,2,3$, be functors. Given two arrows $\langle \tilde{H}, \tilde{\eta }\rangle : \underline{P}_3 \rightarrow \underline{P}_2$ and $\langle H, \eta \rangle : \underline{P}_2 \rightarrow \underline{P}_1$, the composition $\langle H, \eta \rangle \circ \langle \tilde{H}, \tilde{\eta }\rangle : \underline{P}_3 \rightarrow \underline{P}_1$ is given by

$$\begin{aligned} \langle H, \eta \rangle \circ \langle \tilde{H}, \tilde{\eta }\rangle = \langle \tilde{H} \circ H, \eta \circ H^*\tilde{\eta } \rangle ,\end{aligned}$$

(60)

where $\eta \circ H^*\tilde{\eta }$ denotes vertical composition of natural transformations. The intuition behind this definition of composition can be seen in the following diagram.

Lemma 3.8

$\mathbf {Presh}(\mathscr {D})$ is a category.

Proof

First, it is necessary to show that composition as given above is well-defined, that is, that $\langle H, \eta \rangle \circ \langle \tilde{H}, \tilde{\eta }\rangle$ is a valid arrow from $\underline{P}_3$ to $\underline{P}_1$. Consider the diagram above. Clearly $\tilde{H} \circ H$ is a functor from $\mathscr {J}_1$ to $\mathscr {J}_3$, as required. Then, the natural transformation $\eta \circ H^*\tilde{\eta }$ is from $H^*(\tilde{H}^*\underline{P}_3)$ to $H^*\underline{P}_2$ to $\underline{P}_1$ in $(\mathscr {D}^{op})^{\mathscr {J}_1}$. As $H^*\circ \tilde{H}^* = (\tilde{H}\circ H)^*$ by Fact 3.4, it follows that $\eta \circ H^*\tilde{\eta }: (\tilde{H}\circ H)^*\underline{P}_3 \rightarrow \underline{P}_1$, as required.

It is also necessary to show that this composition is associative, which will be done algebraically. Suppose $\underline{P}_4: \mathscr {J}_4 \rightarrow \mathscr {D}^{op}$ is a presheaf and $\hat{H}: \mathscr {J}_3 \rightarrow \mathscr {J}_4$ is a functor, and that $\langle {\hat{H}}, \hat{\eta } \rangle$ is an arrow from $\underline{P}_4$ to $\underline{P}_3$. Then, by the definition of composition, the functoriality of $H^*$, the associativity of functors and natural transformations, and Fact 3.4,

$$\begin{aligned} \left( \langle {H} , {\eta } \rangle \circ \langle \tilde{H} , \tilde{\eta } \rangle \right) \circ \langle \hat{H} , \hat{\eta } \rangle&= \langle \tilde{H} \circ H, \eta \circ H^*\tilde{\eta } \rangle \circ \langle \hat{H} , \hat{\eta } \rangle \end{aligned}$$

(61)

$$\begin{aligned}&= \langle \hat{H} \circ \left( \tilde{H} \circ H\right) , \left( \eta \circ H^*\tilde{\eta } \right) \circ (\tilde{H} \circ {H})^* \hat{\eta } \rangle \end{aligned}$$

(62)

$$\begin{aligned}&= \langle \hat{H} \circ \left( \tilde{H} \circ H\right) , \eta \circ \left( H^*\tilde{\eta } \circ (H^* \circ \tilde{H}^*)\hat{\eta } \right) \rangle \end{aligned}$$

(63)

$$\begin{aligned}&= \langle \left( \hat{H} \circ \tilde{H} \right) \circ H, \eta \circ H^*\left( \tilde{\eta } \circ \tilde{H}^* \hat{\eta }\right) \rangle \end{aligned}$$

(64)

$$\begin{aligned}&=\langle {H} , {\eta } \rangle \circ \langle \hat{H} \circ \tilde{H}, \tilde{\eta } \circ \tilde{H}^* \hat{\eta } \rangle \end{aligned}$$

(65)

$$\begin{aligned}&= \langle {H} , {\eta } \rangle \circ \left( \langle \tilde{H} , \tilde{\eta } \rangle \circ \langle \hat{H} , \hat{\eta } \rangle \right) \end{aligned}$$

(66)

Finally, it remains only to show that every object $\underline{P}: \mathscr {J}\rightarrow \mathscr {D}^{op}$ of $\mathbf {Presh}(\mathscr {D})$ has an identity arrow. If $Id_J: \mathscr {J}\rightarrow \mathscr {J}$ is the identity functor on J and $id_{\underline{P}}: \underline{P} \rightarrow \underline{P}$ is the identity natural transformation on $\underline{P}$, then $\langle Id_J, id_{\underline{P}}\rangle$ is the appropriate identity arrow on $\underline{P}$, which can be easily verified using the definitions above. Thus, $\mathbf {Presh}(\mathscr {D})$ is a valid category.

It is possible to view spectral presheaves and spectral presheaf maps as defined in the previous subsection as a subcategory of $\mathbf {Presh}(\mathbf {Set})$. Specifically, it is the subcategory with objects and arrows determined as follows.

$$\begin{aligned} \text {Objects: }&\{ \underline{\varSigma }^{L}: \mathscr {B}(L)\rightarrow \mathbf {Set}\ \mid L \text { is an orthomodular lattice.} \} \end{aligned}$$

(67)

$$\begin{aligned} \text {Morphisms: }&\{ \langle \tilde{\varphi }, \zeta _\varphi \rangle \mid \varphi \text { is an orthomodular lattice homomorphism.} \} \end{aligned}$$

(68)

The latter is an arrow in $\mathbf {Presh}(\mathbf {Set})$, depicted here:

In fact, this subcategory is the image of a functor; there is a contravariant functor $SP:\mathbf {OML}\rightarrow \mathbf {Presh}(Set)$ which acts as follows for all orthomodular lattices L and all orthomodular lattice homomorphisms $\varphi : L\rightarrow M$:

$$\begin{aligned} SP(L)&= \underline{\varSigma }^{L}\end{aligned}$$

(69)

$$\begin{aligned} SP(\varphi )&= \langle \tilde{\varphi }, \zeta _\varphi \rangle : \underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}. \end{aligned}$$

(70)

Proposition 3.9

SP is a functor.

Proof

First, we must check that SP preserves identities. Suppose $i: L \rightarrow L$ is the identity orthomodular lattice homomorphism on L. Then, $\tilde{i}: \mathscr {B}(L)\rightarrow \mathscr {B}(L)$ is also clearly the identity functor on category $\mathscr {B}(L)$. Furthermore, $\zeta _{i}$ has components given by

$$\begin{aligned} \zeta _{i, B}: \underline{\varSigma }^{L}_B&\rightarrow \underline{\varSigma }^{L}_B \end{aligned}$$

(71)

$$\begin{aligned} \lambda&\mapsto \lambda \circ i = \lambda \end{aligned}$$

(72)

Thus, as each $\zeta _{i, B}$ is just the identity map on $\underline{\varSigma }^{L}_B$ in $\mathbf {Set}$, it follows that $\zeta _{i}$ is the identity natural transformation on $\underline{\varSigma }^{L}$. Thus, $\langle \tilde{i}, \zeta _{i}\rangle$ is the identity arrow of $\underline{\varSigma }^{L}$ in category $\mathbf {Presh}(\mathbf {Set})$.

Next, it is necessary to show that SP preserves composition. Suppose $\varphi : L\rightarrow M$ and $\rho : M \rightarrow N$ are orthomodular lattice homomorphisms. Recalling that SP is contravariant, we wish to show that $SP(\rho \circ \varphi ) = SP(\varphi ) \circ SP(\rho )$. Consider the following diagram, which depicts arrows $SP(\varphi ): \underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$ and $SP(\rho ): \underline{\varSigma }^N\rightarrow \underline{\varSigma }^{M}$ in $\mathbf {Presh}(\mathbf {Set})$:

Recall the definition of composition in $\mathbf {Presh}(\mathbf {Set})$:

$$\begin{aligned} SP(\varphi ) \circ SP(\rho ) = \langle \tilde{\varphi }, \zeta _\varphi \rangle \circ \langle \tilde{\rho } , \zeta _\rho \rangle&= \langle \tilde{\rho } \circ \tilde{\varphi }, \zeta _\varphi \circ \tilde{\varphi }^*\zeta _\rho \rangle \end{aligned}$$

(73)

Note also that the map from $\mathscr {B}(L)$ to $\mathscr {B}(N)$ induced by the composition $\rho \circ \varphi$ is precisely $\tilde{\rho }\circ \tilde{\varphi }$, which follows from the definition in Sect. 2.2 of such induced maps. Thus,

$$\begin{aligned} SP(\rho \circ \varphi ) = \langle \tilde{\rho } \circ \tilde{\varphi }, \zeta _{\rho \circ \varphi }\rangle \end{aligned}$$

It simply remains to show that the natural transformations $\zeta _\varphi \circ \tilde{\varphi }^*\zeta _\rho$ and $\zeta _{\rho \circ \varphi }$ from presheaf $\tilde{\varphi }^*\tilde{\rho }^*\underline{\varSigma }^N$ to presheaf $\underline{\varSigma }^{L}$ in $\mathbf {Set}^{\mathscr {B}(L)^{{\text {op}}}}$ are equal. Consider any element $B \in \mathscr {B}(L)$. Recall, from Fact 3.4 and previous definitions, that

$$\begin{aligned} (\tilde{\varphi }^*\tilde{\rho }^*\underline{\varSigma }^N)_B = ((\tilde{\rho }\circ \tilde{\varphi })^*\underline{\varSigma }^N)_B = \underline{\varSigma }^N_{(\tilde{\rho }\circ \tilde{\varphi })(B)} = \varSigma _{(\tilde{\rho }\circ \tilde{\varphi })(B)}. \end{aligned}$$

(74)

The action of the component at B of natural transformation $\zeta _{\rho \circ \varphi }$ is, by the definition of $\zeta$,

$$\begin{aligned} \zeta _{\rho \circ \varphi }: \varSigma _{(\tilde{\rho }\circ \tilde{\varphi })(B)}&\rightarrow \varSigma _B \end{aligned}$$

(75)

$$\begin{aligned} \lambda&\mapsto \lambda \circ ( \rho \circ \varphi )|_B \end{aligned}$$

(76)

Now consider natural transformation $\zeta _\varphi \circ \tilde{\varphi }^*\zeta _\rho$.

$$\begin{aligned} \left( \zeta _\varphi \circ \tilde{\varphi }^*\zeta _\rho \right) _B = \zeta _{\varphi ,B} \circ (\tilde{\varphi }^*\zeta _\rho )_B = \zeta _{\varphi ,B} \circ \zeta _{\rho , \tilde{\varphi }(B)} \end{aligned}$$

The action of this composition is given as follows.

$$\begin{aligned} \zeta _{\varphi ,B} \circ \zeta _{\rho , \tilde{\varphi }(B)}: \underline{\varSigma }^N_{(\tilde{\rho }\circ \tilde{\varphi })(B)} \rightarrow \underline{\varSigma }^{M}_{\tilde{\varphi }(B)} \rightarrow&\underline{\varSigma }^{L}_B \end{aligned}$$

(77)

$$\begin{aligned} \lambda \mapsto \lambda \circ \rho |_{\tilde{\varphi }(B)} \mapsto&\lambda \circ \rho |_{\tilde{\varphi }(B)} \circ \varphi |_B \end{aligned}$$

(78)

$$\begin{aligned}&= \lambda \circ ( \rho \circ \varphi )|_B \end{aligned}$$

(79)

As the two natural transformations we are considering have the same component for every $B \in \mathscr {B}(L)$, then they must be the same natural transformation, implying SP preserves composition and is a functor.

Thus, the image in $\mathbf {Presh}(\mathbf {Set})$ of functor SP, consisting of the spectral presheaves of orthomodular lattices and the spectral presheaf maps between them, is a category. Of note, the functor SP is neither full nor faithful.

3.4 The Category of $\mathscr {C}$-Valued Copresheaves

Dual to the notion of a presheaf is that of a copresheaf. This definition yields another category $\mathbf {Copresh}(\mathscr {C})$ as follows.

Definition 3.10

Let $\mathscr {C}$ be a category. The category $\mathbf {Copresh}(\mathscr {C})$ of $\mathscr {C}$-valued copresheaves has as its objects functors (copresheaves) of the form ${\overline{Q}}: \mathscr {J}\rightarrow \mathscr {C}$, where $\mathscr {J}$ is a small category. Arrows are pairs

$$\begin{aligned} \langle I,\theta \rangle : ({\overline{Q}}: \mathscr {J}\rightarrow \mathscr {C}) \rightarrow ({{\overline{Q}}}': \mathscr {J}' \rightarrow \mathscr {C}), \end{aligned}$$

(80)

where $I: \mathscr {J}\rightarrow \mathscr {J}'$ is a functor and $\theta : {\overline{Q}}\rightarrow I^*{\overline{Q}}'$ is a natural transformation in $\mathscr {C}^\mathscr {J}$:

Let ${\overline{Q}}_i: \mathscr {J}_i \rightarrow \mathscr {C}$, for $i = 1,2,3$, be functors. Given two arrows $\langle {I}, {\theta }\rangle : {\overline{Q}}_1 \rightarrow {\overline{Q}}_2$ and $\langle \tilde{I}, \tilde{\theta }\rangle : {\overline{Q}}_2 \rightarrow {\overline{Q}}_3$, the composition $\langle \tilde{I}, \tilde{\theta }\rangle \circ \langle {I}, {\theta }\rangle : {\overline{Q}}_1\rightarrow {\overline{Q}}_3$ is given by

$$\begin{aligned} \langle \tilde{I}, \tilde{\theta }\rangle \circ \langle I, {\theta }\rangle = \langle \tilde{I} \circ {I}, (I^* \tilde{\theta }) \circ \theta \rangle , \end{aligned}$$

(81)

where $(I^* \tilde{\theta }) \circ \theta$ denotes vertical composition of natural transformations within functor category $\mathscr {C}^{\mathscr {J}_1}$. The intuition behind this definition of composition can be seen in the following diagram.

Just as with category $\mathbf {Presh}(\mathscr {D})$, it follows that $\mathbf {Copresh}(\mathscr {C})$ is a well-defined category, though this proof is omitted due to its similarities to the proof above.

3.5 Dual Equivalences and Stone Duality

3.5.1 Lifting Dual Equivalences to Presheaf and Copresheaf Categories

Having defined the categories of $\mathscr {D}$-valued presheaves and $\mathscr {D}$-valued copresheaves and their morphisms, we now turn to the question of how such categories relate if $\mathscr {C}$ and $\mathscr {D}$ are dually equivalent. In [13], the following result was proven:

Lemma 3.11

Let $\mathscr {C}$, $\mathscr {D}$ be two categories that are dually equivalent,

Then there is a dual equivalence

The actions of the functors F and G are defined in the proof of the above theorem in the following way. First, consider $G: \mathbf {Presh}(\mathscr {D}) \rightarrow \mathbf {Copresh}(\mathscr {C})$. If $\underline{P}: \mathscr {J}\rightarrow {\mathscr {D}^{op}}$ is an object of $\mathbf {Presh}(\mathscr {D})$, then $G(\underline{P}): \mathscr {J}\rightarrow \mathscr {C}$ is the (covariant) functor $g \circ \underline{P}$. That is, for all objects J and arrows $a: J' \rightarrow J$ in $\mathscr {J}$,

$$\begin{aligned} G(\underline{P})_J&= (g\circ \underline{P})_J = g(\underline{P}_J) \in Ob(\mathscr {C}) \end{aligned}$$

(82)

$$\begin{aligned} G(\underline{P})(a)&= (g \circ \underline{P})(a) \in Morph(\mathscr {C}) \end{aligned}$$

(83)

It is now time to consider the action of G on morphisms on $\mathbf {Presh}(\mathscr {D})$. Let

$$\begin{aligned} \langle H,\eta \rangle : ({\underline{P}}': {\mathscr {J}}' \rightarrow \mathscr {D}^{op}) \rightarrow ({\underline{P}}: {\mathscr {J}} \rightarrow \mathscr {D}^{op}) \end{aligned}$$

(84)

be an arrow in $\mathbf {Presh}(\mathscr {D})$. Then, as G is contravariant, $G(\langle H, \eta \rangle )$ is an arrow in $\mathbf {Copresh}(\mathscr {C})$ from $G(\underline{P}) = g\circ \underline{P}$ to $G(\underline{P}') = g \circ \underline{P}'$. Specifically,

$$\begin{aligned} G(\langle H, \eta \rangle ) = \langle H, g(\eta ) \rangle , \end{aligned}$$

(85)

where $g(\eta ): g\circ \underline{P} \rightarrow H^*(g \circ \underline{P}')$ is a natural transformation with components

$$\begin{aligned} (g(\eta ))_J = g(\eta _J): (g\circ \underline{P})_J \rightarrow (g \circ H^* \underline{P}')_J. \end{aligned}$$

(86)

Because g is a contravariant functor, components $g(\eta )_J$ are arrows in the opposite direction of components $\eta _J$. The following diagram is not a commutative diagram, but is intended to give some visual intuition behind the definitions above and why $\langle H, g(\eta )\rangle : G(\underline{P}) \rightarrow G(\underline{P}')$ is in fact a morphism in $\mathbf {Copresh}(\mathscr {C})$.

In [13], the action of contravariant functor $F: \mathbf {Copresh}(\mathscr {C})\rightarrow \mathbf {Presh}(\mathscr {D})$ is defined as follows. On an object ${\overline{Q}}: \mathscr {J}\rightarrow \mathscr {C}$ of $\mathbf {Copresh}(\mathscr {C})$, F acts as postcomposition by $f: \mathscr {C}\rightarrow {\mathscr {D}^{op}}$. That is,

$$\begin{aligned} F({\overline{Q}}) = f \circ {\overline{Q}}: \mathscr {J}\rightarrow \mathscr {C}\rightarrow \mathscr {D}^{op}. \end{aligned}$$

(87)

On morphisms $\langle I, \theta \rangle : ({\overline{Q}}: \mathscr {J}\rightarrow \mathscr {C}) \rightarrow ({{\overline{Q}}}': \mathscr {J}' \rightarrow \mathscr {C})$ in $\mathbf {Copresh}(\mathscr {C})$, contravariant functor F acts as follows:

$$\begin{aligned} F(\langle I, \theta \rangle ) = \langle I, f(\theta )\rangle , \end{aligned}$$

(88)

where $f(\theta ): I^*(F({\overline{Q}}')) \rightarrow F({\overline{Q}})$ is a natural transformation with components, for each $J \in \mathscr {J}$, given by

$$\begin{aligned} f(\theta )_J = f(\theta _J): (f \circ I^*{\overline{Q}}')_J \rightarrow (f\circ {\overline{Q}})_J \end{aligned}$$

(89)

As the functor $f: \mathscr {C}\rightarrow {\mathscr {D}^{op}}$ is contravariant, the natural transformations $f(\theta )$ and $\theta$ are in opposite directions. The following is again not a commutative diagram, but captures the intuition behind this definition of F.

3.5.2 Stone Duality, the Spectral Presheaf, and the Bohrification of an OML

Recall there is a dual equivalence between the category $\mathbf{BA}$ of Boolean algebras and the category Stone of Stone spaces, given by functors ${\varSigma }: \mathbf {BA}\rightarrow \mathbf {Stone}^{{\text {op}}}$ and $cl:\mathbf {Stone}^{{\text {op}}}\rightarrow \mathbf {BA}$. By Lemma 3.11, there is then a duality

We now define the actions of $\overline{CL}$ and $\underline{\varSigma } \!\!\!\! \varSigma$ on so-called Bohrifications in the category $\mathbf {Copresh}(\mathbf {BA})$ and spectral presheaves in the category $\mathbf {Presh}(\mathbf {Stone})$. The Bohrification of a unital $C^*$-algebra was introduced by Heunen, Landsman, and Spitters in [8]. Our construction for orthomodular lattices is analogous, it is the tautological inclusion copresheaf:

Definition 3.12

For an orthomodular lattice L, the Bohrification ${\overline{\mathscr {L}}}$ of L is the copresheaf from $\mathscr {B}(L)$ to BA given by:

$$\begin{aligned} \text {On objects: }&{\overline{\mathscr {L}}}_B = B \end{aligned}$$

(90)

$$\begin{aligned} \text {On morphisms: }&{\overline{\mathscr {L}}}(i_{B', B}) = inc_{B',B}\text {, the inclusion homomorphism} \end{aligned}$$

(91)

Recall $i_{B', B}$ denotes the arrow in poset $\mathscr {B}(L)$ from $B'$ to B which signifies that $B' \subseteq B$, while $inc_{B', B}$ denotes the Boolean algebra homomorphism that maps each element in $B'$ to the same element of B.

Functor $\underline{\varSigma } \!\!\!\! \varSigma$: We are interested in the action of the functor $\underline{\varSigma } \!\!\!\! \varSigma$ on Bohrifications of orthomodular lattices and maps between them. First consider the action of $\underline{\varSigma } \!\!\!\! \varSigma$ on the Bohrification ${\overline{\mathscr {L}}}$ of an orthomodular lattice L, which is an object in $\mathbf {Copresh}(\mathbf {BA})$. $\underline{\varSigma } \!\!\!\! \varSigma$ acts by postcomposition with $\varSigma$, that is,

$$\begin{aligned} \underline{\varSigma } \!\!\!\! \varSigma ({\overline{\mathscr {L}}}) = \varSigma \circ {\overline{\mathscr {L}}}: \mathscr {B}(L) \rightarrow \mathbf{BA} \rightarrow \mathbf{Stone} \end{aligned}$$

(92)

Specifically, on objects B of $\mathscr {B}(L)$, the functor $\underline{\varSigma } \!\!\!\! \varSigma ({\overline{\mathscr {L}}})$ in $\mathbf {Presh}(\mathbf {Stone})$ acts as follows: for all $B\in \mathscr {B}(L)$,

$$\begin{aligned} \underline{\varSigma } \!\!\!\! \varSigma ( {\overline{\mathscr {L}}}) _B = (\varSigma \circ {\overline{\mathscr {L}}})_B = \varSigma ({\overline{\mathscr {L}}}_B) = \varSigma _B. \end{aligned}$$

(93)

On arrows $i_{B',B}$ in $\mathscr {B}(L)$, this functor $\underline{\varSigma } \!\!\!\! \varSigma ({\overline{\mathscr {L}}})$ has the following action:

$$\begin{aligned} \underline{\varSigma } \!\!\!\! \varSigma ({\overline{\mathscr {L}}})(i_{B',B}) = (\varSigma \circ {\overline{\mathscr {L}}})(i_{B',B}) = \varSigma (inc_{B', B}) = r_{B, B'}, \end{aligned}$$

(94)

where r denotes the restriction map, that is, precomposition with the inclusion map. Note that as $\varSigma \circ {\overline{\mathscr {L}}}$ is a presheaf from $\mathscr {B}(L)$ to Stone with the same action on both objects and arrows of $\mathscr {B}(L)$ as $\underline{\varSigma }^{L}$, then in fact $\varSigma \circ {\overline{\mathscr {L}}}= \underline{\varSigma }^{L}$. That is,

$$\begin{aligned} \underline{\varSigma } \!\!\!\! \varSigma ({\overline{\mathscr {L}}}) = \underline{\varSigma }^{L}. \end{aligned}$$

(95)

Now consider the action of functor $\underline{\varSigma } \!\!\!\! \varSigma$ on morphisms between Bohrifications, that is, on arrows $\langle I, \theta \rangle : {\overline{\mathscr {L}}}\rightarrow {\overline{\mathscr {M}}}$ in $\mathbf {Copresh}(\mathbf {BA})$. By Eq. 88,

$$\begin{aligned} \underline{\varSigma } \!\!\!\! \varSigma (\langle I, \theta \rangle ) = \langle I, \varSigma (\theta )\rangle ,\end{aligned}$$

(96)

where $\varSigma (\theta )$ is the natural transformation with components $\varSigma (\theta )_B = \varSigma (\theta _B)$ for all $B \in \mathscr {B}(L)$.

Functor $\overline{CL}$: We are interested in the action of the functor $\overline{CL}$ on a spectral presheaf $\underline{\varSigma }^{L}\in \mathbf {Presh}(\mathbf {Stone})$, for some orthomodular lattice L. $\overline{CL}$ acts on $\underline{\varSigma }^{L}$ as postcomposition with $cl:\mathbf {Stone}\rightarrow \mathbf {BA}$, yielding $cl \circ \underline{\varSigma }^{L}$, a functor with domain $\mathscr {B}(L)$ in $\mathbf {Copresh}(\mathbf {BA})$. The functor $\overline{CL}(\underline{\varSigma }^{L})$ acts on objects $B \in \mathscr {B}(L)$ by

$$\begin{aligned} \overline{CL}(\underline{\varSigma }^{L})_B = (cl\circ \underline{\varSigma }^{L})_B = cl(\underline{\varSigma }^{L}_B) = cl(\varSigma _B), \end{aligned}$$

(97)

where $cl(\varSigma _B)$ is the Boolean algebra of clopen subsets of $\varSigma _B$. On arrows $i_{B,B'}: B' \rightarrow B$ in $\mathscr {B}(L)$,

$$\begin{aligned} \overline{CL}(\underline{\varSigma }^{L})(i_{B',B}) = (cl \circ \underline{\varSigma }^{L})(i_{B',B}) = cl(r_{B,{B'}}): cl(\varSigma _{B'})\rightarrow cl(\varSigma _B). \end{aligned}$$

(98)

Recall functor cl maps a morphism to its inverse image morphism, denoted by exponent $(-1)$. For any clopen subset S of $\varSigma _{B'}$, the map $cl(r_{B,B'})$ acts as

$$\begin{aligned} cl(r_{B,B'})(S) = r_{B, B'}^{(-1)} (S) = \{ \lambda \in \varSigma _B: \lambda |_{B'} \in S \}, \end{aligned}$$

(99)

which is a clopen subset of $\varSigma _{B}$.

Now, consider how the map $\overline{CL}$ acts on spectral presheaf morphisms $\langle \tilde{\varphi }, \zeta _\varphi \rangle : \underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$ in $\mathbf {Presh}(\mathbf {Stone})$. From Eq. 85,

$$\begin{aligned} \overline{CL}(\langle \tilde{\varphi }, \zeta _\varphi \rangle ) = \langle \tilde{\varphi }, cl(\zeta _\varphi ) \rangle \end{aligned}$$

(100)

where $cl(\zeta _\varphi )$ is a natural transformation between functors in $\mathbf {BA}^{\mathscr {B}(L)}$, from functor $\overline{CL}(\underline{\varSigma }^{L}) = cl\circ \underline{\varSigma }^{L}$ to functor $cl \circ \tilde{\varphi }^*(\underline{\varSigma }^{M})$. Map $cl(\zeta _\varphi )$ has components for each $B \in \mathscr {B}(L)$ that map from $cl(\underline{\varSigma }^{L}_B)= cl(\varSigma _B)$ to $cl((\tilde{\varphi }^*\underline{\varSigma }^{M})_B)= cl(\varSigma _{\tilde{\varphi }(B)})$, given by:

$$\begin{aligned} cl(\zeta _\varphi )_B = cl(\zeta _{\varphi , B}) = \zeta _{\varphi , B}^{(-1)}: cl(\varSigma _B) \rightarrow cl(\varSigma _{\tilde{\varphi }(B)}). \end{aligned}$$

(101)

Again, here the exponent denotes inverse image, rather than inverse. Specifically, the action of $cl(\zeta _\varphi )_B$ on a clopen subset S of $\underline{\varSigma }^{L}_B$ is given by

$$\begin{aligned} cl(\zeta _\varphi )_B (S) = \zeta _{\varphi , B}^{(-1)} (S) = \{ \lambda \in \varSigma _{\tilde{\varphi }(B)}: \zeta _{\varphi , B} (\lambda ) \in S\} = \{ \lambda \in \varSigma _{\tilde{\varphi }(B)}: \lambda \circ \varphi |_B \in S\}. \end{aligned}$$

(102)

3.6 Concrete Isomorphisms Between Spectral Presheaves and Bohrifications

Now that the action of the functors $\underline{\varSigma } \!\!\!\! \varSigma$ and $\overline{CL}$ has been defined, we explore the relationship between spectral presheaves in $\mathbf {Presh}(\mathbf {Stone})$ and Bohrifications in $\mathbf {Copresh}(\mathbf {BA})$ further. From Lemma 3.11 and Stone duality, it is not hard to see that if L and M are orthomodular lattices, with spectral presheaves $\underline{\varSigma }^{L}$ and $\underline{\varSigma }^{M}$ and Bohrifications ${\overline{\mathscr {L}}}$ and ${\overline{\mathscr {M}}}$, then there is an isomorphism $\underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$ in $\mathbf {Presh}(\mathbf {Stone})$ if and only if there is an isomorphism ${\overline{\mathscr {L}}}\rightarrow {\overline{\mathscr {M}}}$ in $\mathbf {Copresh}(\mathbf {BA})$. Our goal in this subsection is to construct such isomorphisms from each other explicitly. This is done in Theorem 3.15 below. The concrete form will be useful later in the proof of Theorem 3.18, one of the main results.

We first show ${\overline{\mathscr {L}}}$ and $\overline{CL}(\underline{\varSigma }^{L}) = cl \circ \underline{\varSigma }^{L}$ are naturally isomorphic in the functor category $\mathbf{BA}^{\mathscr {B}(L)}$. For each $B \in \mathscr {B}(L)$, this requires an isomorphism from ${\overline{\mathscr {L}}}_B$ to $(cl \circ \underline{\varSigma }^{L})_B$. Recall

$$\begin{aligned} {\overline{\mathscr {L}}}_B = B \text { and } (cl \circ \underline{\varSigma }^{L})_B = cl(\underline{\varSigma }^{L}_B) = cl(\varSigma _B). \end{aligned}$$

(103)

The dual equivalence between BA and Stone given in Sect. 2.3 is witnessed by a natural isomorphism $Bo: Id_{\mathbf {BA}} \rightarrow cl \circ \varSigma$ with components $Bo_B: B\rightarrow cl(\varSigma _B)$. Using those components of Bo corresponding to $B \in \mathscr {B}(L)$ gives a map $\{ Bo_B\}_{B \in \mathscr {B}(L)}:{\overline{\mathscr {L}}}\rightarrow cl\circ \underline{\varSigma }^{L}$, which we now show comprise a natural isomorphism as desired.

Lemma 3.13

The map $\{ Bo_B\}_{B \in \mathscr {B}(L)}: {\overline{\mathscr {L}}}\rightarrow cl\circ \underline{\varSigma }^{L}$ is a natural isomorphism. That is, these two functors are naturally isomorphic in the functor category BA$^{\mathscr {B}(L)}$.

Proof

First it is necessary to show that this map is a natural transformation, that is, that the following diagram commutes for every $B', B \in \mathscr {B}(L)$ such that $B' \subseteq B$:

Recall that

$$\begin{aligned} (cl \circ \underline{\varSigma }^{L})_B = cl(\underline{\varSigma }^{L}_B) = cl(\varSigma _B) = (cl \circ \varSigma )_B. \end{aligned}$$

(104)

Additionally, note that

$$\begin{aligned} (cl\circ \underline{\varSigma }^{L})(i_{B',B})&= cl(\underline{\varSigma }^{L}(i_{B', B})) = cl(r_{B, B'}) = cl(\varSigma (inc_{B',B})) = (cl\circ \varSigma )(inc_{B', B}). \end{aligned}$$

(105)

Thus, also applying the definition of ${\overline{\mathscr {L}}}$, the above diagram can be rewritten as

The above diagram commutes because $inc_{B', B}: B' \rightarrow B$ is a morphism in category BA and because $Bo: Id_\mathbf{BA} \rightarrow cl \circ \varSigma$ is a natural transformation. Thus, the collection $\{Bo_B\}_{B \in \mathscr {B}(L)}: {\overline{\mathscr {L}}}\rightarrow cl \circ \underline{\varSigma }^{L}$ is a valid natural transformation. As each arrow $Bo_B$ is an isomorphism then it is in fact a natural isomorphism.

Natural isomorphism $\{Bo_B\}_{B\in \mathscr {B}(L)}$ will now simply be written in a slight abuse of notation as Bo, and we will remember it only has components for all $B \in \mathscr {B}(L)$.

While the above lemma presents an interesting result, it will be more useful to know that the functors ${\overline{\mathscr {L}}}$ and $\overline{CL}(\underline{\varSigma }^{L}) = cl\circ \underline{\varSigma }^{L}$ are isomorphic in category $\mathbf {Copresh}(\mathbf {BA})$ rather than just naturally isomorphic in $\mathbf{BA}^{\mathscr {B}(L)}$.

Lemma 3.14

The morphism $\langle Id_{\mathscr {B}(L)}, Bo\rangle : {\overline{\mathscr {L}}}\rightarrow cl \circ \underline{\varSigma }^{L}$ is an isomorphism in $\mathbf {Copresh}(\mathbf {BA})$.

Proof

For natural isomorphism $Bo = \{Bo_B\}_{B\in \mathscr {B}(L)}$ there exists some inverse natural isomorphism which we denote by $Bo^{-1}: cl \circ \varSigma \rightarrow {\overline{\mathscr {L}}}$. We now use Fact 3.6 to show that morphism $\langle Id_{\mathscr {B}(L)} , Bo^{-1} \rangle : cl\circ \underline{\varSigma }^{L}\rightarrow {\overline{\mathscr {L}}}$ is an inverse to morphism $\langle Id_{\mathscr {B}(L)}, Bo\rangle$ in $\mathbf {Copresh}(\mathbf {BA})$:

$$\begin{aligned} \langle Id_{\mathscr {B}(L)}, Bo\rangle \circ \langle Id_{\mathscr {B}(L)}, Bo^{-1}\rangle&= \langle Id_{\mathscr {B}(L)} \circ Id_{\mathscr {B}(L)}, (Id_{\mathscr {B}(L)}^* Bo )\circ Bo^{-1} \rangle \end{aligned}$$

(106)

$$\begin{aligned}&= \langle Id_{\mathscr {B}(L)}, Bo\circ Bo^{-1} \rangle \end{aligned}$$

(107)

$$\begin{aligned}&= \langle Id_{\mathscr {B}(L)}, Id_{cl\circ \underline{\varSigma }^{L}} \rangle \end{aligned}$$

(108)

$$\begin{aligned} \langle Id_{\mathscr {B}(L)}, Bo^{-1}\rangle \circ \langle Id_{\mathscr {B}(L)}, Bo\rangle&= \langle Id_{\mathscr {B}(L)} \circ Id_{\mathscr {B}(L)}, (Id_{\mathscr {B}(L)}^* Bo^{-1} )\circ Bo\rangle \end{aligned}$$

(109)

$$\begin{aligned}&= \langle Id_{\mathscr {B}(L)}, Bo^{-1}\circ Bo \rangle \end{aligned}$$

(110)

$$\begin{aligned}&= \langle Id_{\mathscr {B}(L)}, Id_{{\overline{\mathscr {L}}}} \rangle \end{aligned}$$

(111)

Thus, $\langle Id_{\mathscr {B}(L)}, Bo\rangle$ is an isomorphism in $\mathbf {Copresh}(\mathbf {BA})$, meaning ${\overline{\mathscr {L}}}$ and $cl\circ \underline{\varSigma }^{L}$ are isomorphic in this category of copresheaves.

Theorem 3.15

Let L and M be orthomodular lattices, $\underline{\varSigma }^{L}$ and $\underline{\varSigma }^{M}$ their spectral presheaves, and ${\overline{\mathscr {L}}}$ and ${\overline{\mathscr {M}}}$ their Bohrifications. There is an isomorphism $\underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$ in the category $\mathbf {Presh}(\mathbf {Stone})$ if and only if there is an isomorphism ${\overline{\mathscr {L}}}\rightarrow {\overline{\mathscr {M}}}$ in the category $\mathbf {Copresh}(\mathbf {BA})$, and these isomorphisms can be explicitly constructed from each other.

Proof

Suppose there is an isomorphism $\langle H, \eta \rangle : \underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$ in $\mathbf {Presh}(\mathbf {Stone})$. Then, as functors preserve isomorphisms, there is an isomorphism in $\mathbf {Copresh}(\mathbf {BA})$ given by

$$\begin{aligned} \overline{CL}(\langle H, \eta \rangle ): \overline{CL}(\underline{\varSigma }^{L}) \rightarrow \overline{CL}(\underline{\varSigma }^{M}), \end{aligned}$$

(112)

or equivalently,

$$\begin{aligned} \langle H, cl(\eta ) \rangle : cl \circ \underline{\varSigma }^{L}\rightarrow cl \circ \underline{\varSigma }^{M}, \end{aligned}$$

(113)

where $cl(\eta )$ is the natural transformation with components, for all $B \in \mathscr {B}(L)$, given by $cl(\eta )_B= cl(\eta _B) = \eta ^{(-1)}_B$, where the exponent $(-1)$ denotes the inverse image function. By the previous lemma, there are isomorphisms in $\mathbf {Copresh}(\mathbf {BA})$

$$\begin{aligned} \langle Id_{\mathscr {B}(L)}, Bo \rangle&: {\overline{\mathscr {L}}}\rightarrow cl\circ \underline{\varSigma }^{L}\end{aligned}$$

(114)

$$\begin{aligned} \langle Id_{\mathscr {B}(M)}, Bo^{-1}\rangle&: cl \circ \underline{\varSigma }^{M}\rightarrow {\overline{\mathscr {M}}}\end{aligned}$$

(115)

Composing these two isomorphisms on either side of isomorphism $\langle H, cl(\eta )\rangle$ gives an isomorphism from ${\overline{\mathscr {L}}}$ to ${\overline{\mathscr {M}}}$, as desired. Specifically, this composition evaluates as follows:

$$\begin{aligned} \langle Id_{\mathscr {B}(M)}, Bo^{-1}\rangle \circ \langle H&, cl(\eta )\rangle \circ \langle Id_{\mathscr {B}(L)}, Bo \rangle \end{aligned}$$

(116)

$$\begin{aligned}&= \langle Id_{\mathscr {B}(M)}, Bo^{-1}\rangle \circ \langle H \circ Id_{\mathscr {B}(L)}, (Id_{\mathscr {B}(L)}^* cl(\eta )) \circ Bo \rangle \end{aligned}$$

(117)

$$\begin{aligned}&= \langle Id_{\mathscr {B}(M)} \circ H \circ Id_{\mathscr {B}(L)}, (H^* Bo^{-1}) \circ (Id_{\mathscr {B}(L)}^* cl(\eta )) \circ Bo\rangle \end{aligned}$$

(118)

$$\begin{aligned}&= \langle H, (H^* Bo^{-1}) \circ cl(\eta ) \circ Bo \rangle \end{aligned}$$

(119)

Some visual intuition is provided below:

We conclude whenever there is an isomorphism $\langle H, \eta \rangle : \underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$ in $\mathbf {Presh}(\mathbf {Stone})$, then $\langle H, (H^* Bo^{-1}) \circ cl(\eta ) \circ Bo\rangle : {\overline{\mathscr {L}}}\rightarrow {\overline{\mathscr {M}}}$ is an isomorphism in $\mathbf {Copresh}(\mathbf {BA})$, completing the first half of this proof.

Now, suppose that there is an isomorphism $\langle I, \theta \rangle : {\overline{\mathscr {L}}}\rightarrow {\overline{\mathscr {M}}}$ in $\mathbf {Copresh}(\mathbf {BA})$. Recall $\underline{\varSigma } \!\!\!\! \varSigma : \mathbf {Copresh}(\mathbf {BA})\rightarrow \mathbf {Presh}(\mathbf {Stone})$ that is dual to $\overline{CL}$. As functors preserve isomorphisms, there is an isomorphism in $\mathbf {Presh}(\mathbf {Stone})$ from $\underline{\varSigma } \!\!\!\! \varSigma ({\overline{\mathscr {M}}})$ to $\underline{\varSigma } \!\!\!\! \varSigma ({\overline{\mathscr {L}}})$, given by

$$\begin{aligned} \underline{\varSigma } \!\!\!\! \varSigma (\langle I, \theta \rangle ) = \langle I, \varSigma (\theta )\rangle , \end{aligned}$$

(120)

where $\varSigma (\theta )$ is the natural transformation with components $\varSigma (\theta )_B = \varSigma (\theta _B)$ for all B in $\mathscr {B}(L)$. Recalling from (95) that

$$\begin{aligned} \underline{\varSigma } \!\!\!\! \varSigma ({\overline{\mathscr {M}}}) = \varSigma \circ {\overline{\mathscr {M}}}= \underline{\varSigma }^{M}\text { and } \underline{\varSigma } \!\!\!\! \varSigma ({\overline{\mathscr {L}}}) = \varSigma \circ {\overline{\mathscr {L}}}= \underline{\varSigma }^{L}, \end{aligned}$$

(121)

it follows that $\langle I, \varSigma (\theta ) \rangle$ is an isomorphism in $\mathbf {Presh}(\mathbf {Stone})$ from $\underline{\varSigma }^{M}$ to $\underline{\varSigma }^{L}$, as desired.

3.7 The Spectral Presheaf of an OML Is a Complete Invariant

We now prove our first main result: two orthomodular lattices are isomorphic if and only if their spectral presheaves are isomorphic, hence the spectral presheaf is a complete invariant of an OML.

The proof is separated into the following two theorems.

Theorem 3.16

Let L and M be orthomodular lattices. If $\varphi : L \rightarrow M$ is an isomorphism in OML, then there is an isomorphism $\langle \tilde{\varphi }, \zeta _\varphi \rangle : \underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$ in $\mathbf {Presh}(\mathbf {Stone})$, where the natural transformation $\zeta _\varphi$ has components $\zeta _{\varphi , B} = \varSigma (\varphi |_B)$ for all B in $\mathscr {B}(L)$.

Proof

Suppose $\varphi : L \rightarrow M$ is an isomorphism of orthomodular lattices, with inverse ${\psi = \varphi ^{-1}}: M \rightarrow L$. Then, by Lemma 2.9, $\tilde{\varphi }: \mathscr {B}(L)\rightarrow \mathscr {B}(M)$ is an order isomorphism of posets, with inverse $\tilde{\psi }$. Additionally, for each $B \in \mathscr {B}(L)$, $\varphi |_B: B \rightarrow \varphi [B]$ is an isomorphism of Boolean algebras, with inverse $\psi |_{\tilde{\varphi }(B)}$.

By Stone duality, applying functor $\varSigma$ to Boolean algebra isomorphism $\varphi |_B: B \rightarrow \tilde{\varphi }(B)$ yields a continuous isomorphism $\varSigma (\varphi |_B): \varSigma _{\tilde{\varphi }(B)} \rightarrow \varSigma _{B}$ in Stone. As $\tilde{\varphi }(B) \in \mathscr {B}(M)$, then

$$\begin{aligned} \varSigma _{\tilde{\varphi }(B)} = \underline{\varSigma }^{M}_{\tilde{\varphi }(B)} = (\underline{\varSigma }^{M}\circ \tilde{\varphi })_B = (\tilde{\varphi }^*\underline{\varSigma }^{M})_B. \end{aligned}$$

(122)

Additionally, as $B \in \mathscr {B}(L)$, then $\varSigma _B = \underline{\varSigma }^{L}_B$. Thus, $\varSigma (\varphi |_B)$ is in fact a Stone space isomorphism from $(\tilde{\varphi }^*\underline{\varSigma }^{M})_B$ to $\underline{\varSigma }^{L}_B$. Let isomorphism $\varSigma (\varphi |_B)$ be denoted

$$\begin{aligned} \varSigma (\varphi |_B):= \zeta _{\varphi , B}: (\tilde{\varphi }^* \underline{\varSigma }^{M})_B\rightarrow \underline{\varSigma }^{L}_B. \end{aligned}$$

(123)

Note this coincides exactly with the definition of $\zeta _{\varphi , B}$ given in Step 2 of Sect. 3.2, where the action of isomorphism $\zeta _{\varphi , B}$ on a homomorphism $\lambda : \tilde{\varphi }(B) \rightarrow \{0,1\}$ is given by precomposition with ${\varphi |_B}$. The components $(\zeta _{\varphi ,B} )_{B \in \mathscr {B}(L)}$ thus form a natural isomorphism from $\tilde{\varphi }^*\underline{\varSigma }^{M}$ to $\underline{\varSigma }^{L}$, because as we proved in Lemma 3.2, for every $B' \subseteq B$ in $\mathscr {B}(L)$ the following diagram commutes:

Since $\tilde{\varphi }: \mathscr {B}(L) \rightarrow \mathscr {B}(M)$ is an isomorphism and $\zeta _{\varphi }: \tilde{\varphi }^*\underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$ is a natural isomorphism, then the composite

$$\begin{aligned} \langle \tilde{\varphi }, \zeta _\varphi \rangle : \underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}\end{aligned}$$

(124)

is an arrow in $\mathbf {Presh}(\mathbf {Stone})$, depicted here:

It only remains to show that this arrow has an inverse, that is, that it is an isomorphism in $\mathbf {Presh}(\mathbf {Stone})$. Recall that $\tilde{\psi }: \mathscr {B}(M) \rightarrow \mathscr {B}(L)$ is the inverse of $\tilde{\varphi }$, and consider the arrow

$$\begin{aligned} \langle \tilde{\psi }, \tilde{\psi }^* (\zeta _\varphi ^{-1} )\rangle : \underline{\varSigma }^{L}\rightarrow \underline{\varSigma }^{M}. \end{aligned}$$

(125)

This arrow is depicted in the following diagram:

That both compositions of arrow $\langle \tilde{\varphi }, \zeta _\varphi \rangle$ with its inverse give the identity morphism is now checked algebraically.

$$\begin{aligned} \langle \tilde{\psi }, \tilde{\psi }^* (\zeta _\varphi ^{-1} )\rangle \circ \langle \tilde{\varphi }, \zeta _\varphi \rangle&= \langle \tilde{\varphi }\circ \tilde{\psi }, \tilde{\psi }^*(\zeta _\varphi ^{-1}) \circ \tilde{\psi }^*\zeta _\varphi \rangle \end{aligned}$$

(126)

$$\begin{aligned}&= \langle Id_{\mathscr {B}(M)}, \tilde{\psi }^*(Id_{\tilde{\varphi }^*\underline{\varSigma }^{M}})\rangle \end{aligned}$$

(127)

$$\begin{aligned}&= \langle Id_{\mathscr {B}(M)}, Id_{\tilde{\psi }^*\tilde{\varphi }^*\underline{\varSigma }^{M}}\rangle \end{aligned}$$

(128)

$$\begin{aligned}&= \langle Id_{\mathscr {B}(M)}, Id_{\underline{\varSigma }^{M}} \rangle . \end{aligned}$$

(129)

$$\begin{aligned} \langle \tilde{\varphi }, \zeta _\varphi \rangle \circ \langle \tilde{\psi }, \tilde{\psi }^* (\zeta _\varphi ^{-1} )\rangle&= \langle \tilde{\psi } \circ \tilde{\varphi }, \zeta _\varphi \circ \tilde{\varphi }^*(\tilde{\psi }^*(\zeta _\varphi ^{-1})) \rangle \end{aligned}$$

(130)

$$\begin{aligned}&= \langle Id_{\mathscr {B}(L)}, \zeta _\varphi \circ (\tilde{\psi }\circ \tilde{\varphi })^* (\zeta _\varphi ^{-1})) \rangle \end{aligned}$$

(131)

$$\begin{aligned}&= \langle Id_{\mathscr {B}(L)}, \zeta _\varphi \circ (Id_{\mathscr {B}(L)})^* (\zeta _\varphi ^{-1}) \rangle \end{aligned}$$

(132)

$$\begin{aligned}&= \langle Id_{\mathscr {B}(L)}, \zeta _\varphi \circ \zeta _\varphi ^{-1} \rangle \end{aligned}$$

(133)

$$\begin{aligned}&= \langle Id_{\mathscr {B}(L)}, Id_{\underline{\varSigma }^{L}} \rangle . \end{aligned}$$

(134)

Thus, $\langle \tilde{\varphi }, \zeta _\varphi \rangle : \underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$ is an isomorphism in $\mathbf {Presh}(\mathbf {Stone})$, as desired.

In order to prove the next result, recall from Sect. 2.2.2 the definition of a partial orthomodular lattice, which captures all aspects of lattice structure within each boolean subalgebra of L, as well as capturing inclusion relations between Boolean subalgebras.

Theorem 3.17

Let L and M be orthomodular lattices. If there is an isomorphism $\langle H, \eta \rangle : \underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$ in $\mathbf {Presh}(\mathbf {Stone})$, then there is an isomorphism from L to M in OML that can be explicitly constructed from $\langle H, \eta \rangle$.

Proof

Let $\langle H, \eta \rangle : \underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$ be an isomorphism between spectral presheaves of orthomodular lattices. Note $H: \mathscr {B}(L)\rightarrow \mathscr {B}(M)$ is necessarily an isomorphism with inverse $H^{-1}: \mathscr {B}(M)\rightarrow \mathscr {B}(L)$. By Theorem 3.15, there exists a isomorphism from ${\overline{\mathscr {L}}}$ to ${\overline{\mathscr {M}}}$ in $\mathbf {Copresh}(\mathbf {BA})$, specifically,

$$\begin{aligned} \langle H, (H^* Bo^{-1}) \circ cl(\eta ) \circ Bo\rangle : {\overline{\mathscr {L}}}\rightarrow {\overline{\mathscr {M}}}. \end{aligned}$$

(135)

For simplicity, define

$$\begin{aligned} \rho := (H^* Bo^{-1}) \circ cl(\eta ) \circ Bo: {\overline{\mathscr {L}}}\rightarrow H^*{\overline{\mathscr {M}}}. \end{aligned}$$

(136)

This natural transformation $\rho$ has components for each $B\in \mathscr {B}(L)$ that map from ${\overline{\mathscr {L}}}_B = B$ to $(H^*{\overline{\mathscr {M}}})_B = {\overline{\mathscr {M}}}_{H(B)} = H(B)$, where H(B) is an element of $\mathscr {B}(M)$, that is, a Boolean subalgebra of M:

$$\begin{aligned} \rho _B: B \rightarrow H(B). \end{aligned}$$

(137)

By the construction of $\rho$ in the proof of Theorem 3.15, each component $\rho _B$ is a Boolean algebra isomorphism.

Suppose that $B', B \in \mathscr {B}(L)$ with $B' \subseteq B$, that is, $i_{B',B}$ is an arrow in $\mathscr {B}(L)$. Recall that ${\overline{\mathscr {L}}}(i_{B',B}) = inc_{B',B}$, the inclusion Boolean algebra homomorphism from $B'$ to B. Additionally, $H(i_{B',B})$ is an arrow in $\mathscr {B}(M)$ from $H(B')$ to H(B); as poset categories have at most one arrow with a given domain and codomain, it must be that $H(i_{B',B}) = i_{H(B'),H(B)}$. Then,

$$\begin{aligned} ({\overline{\mathscr {M}}}\circ H)(i_{B',B}) = inc_{H(B'), H(B)}.\end{aligned}$$

(138)

The naturality of $\rho$ then means that the following diagram commutes:

Let $a \in L$ such that $a \in B, B'$. Then

$$\begin{aligned} \rho _B(a) = (\rho _B \circ inc_{B',B})(a) = (inc_{H(B'),H(B)} \circ \rho _{B'})(a) = \rho _{B'}(a). \end{aligned}$$

(139)

From this, it follows that if element a is in any two Boolean subalgebras $B_1,B_2$ of L (not necessarily related by containment), then

$$\begin{aligned} \rho _{B_1}(a) = \rho _{B_1\cap B_2}(a) = \rho _{B_2}(a). \end{aligned}$$

(140)

As every element of L is in at least one Boolean subalgebra, this yields a well-defined map as follows:

$$\begin{aligned} \varphi : L_{part}&\rightarrow M_{part} \end{aligned}$$

(141)

$$\begin{aligned} a&\mapsto \rho _B(a)\text {, where}\, B \in \mathscr {B}(L)\, \text {is any Boolean subalgebra containing} a \end{aligned}$$

(142)

This map $\varphi$ is a partial orthomodular lattice homomorphism because it preserves all defined meets and joins, i.e. those within some Boolean subalgebra, as well as orthocomplementation. It remains to check that $\varphi$ is an isomorphism of partial orthomodular lattices.

As $\rho$ is a natural isomorphism, each component $\rho _B$ is an isomorphism of Boolean algebras and has an inverse $\rho _B^{-1}:H(B)\rightarrow B$; note the subscript in $\rho _B^{-1}$ reflects its codomain. Just as above, for any $m \in M$ and any $B_1,B_2 \in \mathscr {B}(M)$ that contain m, it can be shown that $\rho _{H^{-1}(B_1)}^{-1}(m) = \rho _{H^{-1}(B_2)}^{-1}(m)$. Thus, as any $m \in M$ is in at least one $B \in \mathscr {B}(M)$, it is possible to define a partial orthomodular lattice homomorphism

$$\begin{aligned} \psi : M_{part}&\rightarrow L_{part} \end{aligned}$$

(143)

$$\begin{aligned} m&\mapsto \rho ^{-1}_{H^{-1}(B)}(m)\text {, where}\, B \in \mathscr {B}(M)\, \text {is any Boolean subalgebra containing } m \end{aligned}$$

(144)

One can now verify that $\psi$ is an inverse to $\varphi$. Let $a \in L$, and let $B\in \mathscr {B}(L)$ contain a. Then,

$$\begin{aligned} ( \psi \circ \varphi )(a) = (\rho _B^{-1} \circ \rho _B)(a) = Id_B (a) = a \end{aligned}$$

(145)

Similarly, for any $m \in M$ contained in some Boolean algebra $B \in \mathscr {B}(M)$,

$$\begin{aligned} (\varphi \circ \psi )(m) = (\rho _{H^{-1}(B)} \circ \rho ^{-1}_{H^{-1}(B)})(m) = Id_B(m) = m \end{aligned}$$

(146)

Thus $\psi$ is an inverse to $\varphi$, meaning $\varphi$ is a partial orthomodular lattice isomorphism. By Proposition 2.13, $\varphi$ preserves all meets and joins, not just those within Boolean subalgebras, and as it also already preserves orthocomplementation this means that $\varphi :L\rightarrow M$ is an isomorphism of orthomodular lattices.

Specifically, for any element $a \in L$, the action of $\varphi$ on a as constructed in the proof above is given as follows. Let $B\in \mathscr {B}(L)$ be any Boolean subalgebra containing a. Then,

$$\begin{aligned} \varphi (a) = \rho _B(a) = ((H^* Bo^{-1}) \circ cl(\eta ) \circ Bo)_B(a) = ((H^* Bo^{-1}_B) \circ cl(\eta )_B \circ Bo_B)(a) \end{aligned}$$

(147)

$$\begin{aligned} = (Bo^{-1}_{H(B)} \circ cl(\eta _B) \circ Bo_B)(a). \end{aligned}$$

(148)

Recall that $Bo_B: B \rightarrow cl(\varSigma (B))$ is the component at B of the natural transformation that witnesses Stone duality; $Bo^{-1}_{H(B)}$ is the component at $H(B) \in \mathscr {B}(M)$ of the inverse of this same natural transformation; and $cl: \mathbf{Stone} \rightarrow \mathbf{BA}$ is one functor of the dual equivalence between $\mathbf {BA}$ and $\mathbf {Stone}$. Specific actions of these maps are given in Sect. 2.3. In practice, to calculate $\varphi (a) = \rho _B(a)$ it is simplest to choose $B = B_a = \{0,a,a',1\}$, the Boolean algebra with four elements, as we will do in the later proofs of Theorems 3.19 and 3.20.

Theorem 3.18

Two orthomodular lattices L and M are isomorphic in OML if and only if their spectral preserves $\underline{\varSigma }^{L}$ and $\underline{\varSigma }^{M}$ are isomorphic in $\mathbf {Presh}(\mathbf {Stone})$.

Proof

Theorems 3.16 and 3.17.

We give some interpretation of this result in Sect. 3.8, but first we present an even stronger result. For an orthomodular lattice isomorphism $\varphi :L \rightarrow M$, denote the spectral presheaf isomorphism constructed in the proof of Theorem 3.16 by $SP(\varphi ): \underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$. For a spectral presheaf isomorphism $\langle H, \eta \rangle : \underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$, denote the orthomodular lattice isomorphism constructed in the proof of Theorem 3.17 by $OML(\langle H, \eta \rangle ): L \rightarrow M$.

Theorem 3.19

For all orthomodular lattice isomorphisms $\varphi :L \rightarrow M$,

$$\begin{aligned} OML(SP(\varphi )) = \varphi . \end{aligned}$$

(149)

Proof

Consider an orthomodular lattice isomorphism $\varphi : L \rightarrow M$. Then, $\langle \tilde{\varphi }, \zeta _\varphi \rangle$ is an isomorphism in $\mathbf {Presh}(\mathbf {Stone})$, where $\zeta _\varphi$ is a natural isomorphism with components given by

$$\begin{aligned} \zeta _{\varphi , B}: \varSigma _{\tilde{\varphi }(B)}&\rightarrow \varSigma _B \end{aligned}$$

(150)

$$\begin{aligned} \lambda&\mapsto \lambda \circ \varphi |_B \end{aligned}$$

(151)

Each component $\zeta _{\varphi , B}$ is an isomorphism of Stone spaces. To construct $OML(\langle \tilde{\varphi }, \zeta _{\varphi }\rangle )$, consider the natural isomorphism in $\mathbf {Copresh}(\mathbf {BA})$

$$\begin{aligned} \rho = (\tilde{\varphi }^*Bo^{-1}) \circ cl(\zeta _\varphi ) \circ Bo: {\overline{\mathscr {L}}}\rightarrow \tilde{\varphi }^*{{\overline{\mathscr {M}}}}.\end{aligned}$$

(152)

Each component of this natural isomorphism is a Boolean algebra isomorphism from B to $\tilde{\varphi }(B)$ given by

$$\begin{aligned} \rho _B&= \left( (\tilde{\varphi }^*Bo^{-1}) \circ cl(\zeta _\varphi ) \circ Bo\right) _B\end{aligned}$$

(153)

$$\begin{aligned}&= (\tilde{\varphi }^*Bo^{-1})_B \circ cl(\zeta _\varphi )_B \circ Bo_B \end{aligned}$$

(154)

$$\begin{aligned}&= Bo_{\tilde{\varphi }(B)}^{-1} \circ \zeta _{\varphi , B} ^{(-1)} \circ Bo_B \end{aligned}$$

(155)

Let $a \in L$, and consider the Boolean algebra $B_a \subseteq L$ with elements $\{ 0,a,a',1\}$. $OML(\langle \tilde{\varphi }, \zeta _\varphi \rangle )$ is the homomorphism from L to M whose action on element a is $\rho _{B_a}(a)$, which we will now calculate. The Stone space of $B_a$ has two elements $\lambda _a$ and $\lambda _{a'}$, where $\lambda _a(a) = 1$, $\lambda _a(a') = 0$, and $\lambda _{a'}(a) = 0$, $\lambda _{a'}(a) = 0$. Thus,

$$\begin{aligned} Bo_{B_a} (a) = \{ \lambda \in \varSigma _{B_a} \mid \lambda (a) = 1\} = \{ \lambda _a\}. \end{aligned}$$

(156)

As $\varphi |_B$ is a Boolean algebra isomorphism, then $\tilde{\varphi }(B)$ is the four-element Boolean algebra with elements $\{ 0, \varphi (a), \varphi (a)', 1\}$, which we will denote $B_{\varphi (a)}$. The Stone space $\varSigma _{B_a}$ has two elements, which we denote $\lambda _{\varphi (a)}$ and $\lambda _{\varphi (a)'}$, where $\lambda _{\varphi (a)} (\varphi (a)) = 1$, $\lambda _{\varphi (a)} (\varphi (a')) = 0$ and $\lambda _{\varphi (a)'}(\varphi (a)) = 0$, $\lambda _{\varphi (a')} (\varphi (a)) = 0$. Then,

$$\begin{aligned} \zeta _{\varphi ,B}^{(-1)}(Bo_B(a))&= \zeta _{\varphi ,B}^{(-1)} (\{ \lambda _a\}) \end{aligned}$$

(157)

$$\begin{aligned}&= \{ \lambda \in \varSigma _{\tilde{\varphi }(B_a)} \mid (\lambda \circ \varphi |_{B_a}) (a) = 1\}\end{aligned}$$

(158)

$$\begin{aligned}&= \{ \lambda _{\varphi (a)} \}. \end{aligned}$$

(159)

In order to calculate $\rho _{B_a}(a) = Bo_{\tilde{\varphi }(B)}^{-1} (\{ \lambda _{\varphi (a)}\})$, recall the definition for the components of $Bo^{-1}$ given at the end of Sect. 2.3: write $S = \bigcup _{b \in J} U_b$ as a finite union of basic open sets for some index set J, then $Bo^{-1}(S) = \bigvee _{b \in J} b$. As $\{\lambda _{\varphi (a)} \} = U_{\varphi (a)}$ is itself a basic open set, then $Bo_{\tilde{\varphi }(B)}^{-1} (\{ \lambda _{\varphi (a)}\}) = \varphi (a)$. Thus,

$$\begin{aligned} \rho _{B_a}(a) = \left( Bo_{\tilde{\varphi }(B)}^{-1} \circ \zeta _{\varphi , B} ^{(-1)} \circ Bo_B\right) (a) = Bo^{-1}_{\tilde{\varphi }(B)} (\{ \lambda _{\varphi (a)} \}) = \varphi (a) \end{aligned}$$

(160)

Thus, $OML(\langle \tilde{\varphi }, \zeta _\varphi \rangle )$ is the orthomodular lattice homomorphism from L to M mapping a to $\rho _{B_a}(a) = \varphi (a)$, meaning that $\varphi = OML(\langle \tilde{\varphi }, \zeta _\varphi \rangle ) = (OML \circ SP)(\varphi )$.

Theorem 3.20

Let $\langle H, \eta \rangle : \underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$ be an isomorphism in $\mathbf {Presh}(\mathbf {Stone})$ between the spectral presheaves of two orthomodular lattices M and L. Then

$$\begin{aligned} SP(OML(\langle H, \eta \rangle )) = \langle H, \eta \rangle . \end{aligned}$$

(161)

Proof

Consider an isomorphism $\langle H, \eta \rangle : \underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$ in $\mathbf {Presh}(\mathbf {Stone})$. To construct $OML(\langle H, \eta \rangle ): L \rightarrow M$, consider natural isomorphism in $\mathbf {Copresh}(\mathbf {BA})$:

$$\begin{aligned} \rho = (H^*Bo^{-1}) \circ cl(\eta ) \circ Bo: {\overline{\mathscr {L}}}\rightarrow H^*{{\overline{\mathscr {M}}}}. \end{aligned}$$

(162)

Each component of this natural isomorphism is a Boolean algebra isomorphism from B to H(B) given by

$$\begin{aligned} \rho _B = Bo_{H(B)}^{-1} \circ \eta _B ^{(-1)} \circ Bo_B: B \rightarrow H(B). \end{aligned}$$

(163)

Let $a \in L$; the four-element Boolean $B_a$ contains a. We first want to calculate

$$\begin{aligned} OML(\langle H, \eta \rangle )(a) = \rho _{B_a}(a). \end{aligned}$$

(164)

Note that $H(B_a)$ is also a four-element Boolean algebra because H is an order isomorphism of posets; as there is no $B \in \mathscr {B}(L)$ such that $\{0,1\} \subset B \subset B_a$, then this also holds true for $H(B_a)$ in $\mathscr {B}(M)$. We name its elements $\{0,h(a),h(a)',1\}$. Note that we are not defining some function $h:L\rightarrow M$, but rather simply using function notation to indicate that the elements of $H(B_a)$ depend on the chosen element a. We now calculate

$$\begin{aligned} (\eta _{B_a} ^{(-1)} \circ Bo_{B_a} )(a)&= \eta _{B_a}^{(-1)}(\{\lambda _a\})\end{aligned}$$

(165)

$$\begin{aligned}&= \{ \lambda \in \varSigma _{H(B_a)} \mid \eta _{B_a}(\lambda ) = \lambda _a\}\end{aligned}$$

(166)

$$\begin{aligned}&= \{ \lambda \in \varSigma _{H(B_a)} \mid \eta _{B_a}(\lambda ) (a) = 1\} \end{aligned}$$

(167)

As $\eta _{B_a}:\varSigma _{H(B_a)} \rightarrow \varSigma _{B_a}$ is an isomorphism of Stone spaces, it must be that exactly one of the two elements $\sigma = \lambda _{h(a)}$ or $\sigma = \lambda _{h(a)'}$ of $\varSigma _{H(B_a)}$ satisfies $\eta _{B_a}(\sigma ) (a) = 1$. If $(\eta _{B_a} ^{(-1)} \circ Bo_{B_a} )(a) = \{ \lambda _{h(a)}\} = U_{h(a)}$, then applying $Bo_{H(B_a)}^{-1}$ yields h(a), while the other case yields $h(a)'$. Thus,

$$\begin{aligned} \rho _{B_a}(a) = \left\{ \begin{array}{lcc} h(a) &{}:&{} \eta _{B_a}(\lambda _{h(a)}) = \lambda _a \\ h'(a )&{}:&{} \eta _{B_a}(\lambda _{h(a)'}) = \lambda _a \end{array} \right. \end{aligned}$$

(168)

Thus, $OML(\langle H, \eta \rangle )$ is a homomorphism $\varphi : L \rightarrow M$ given by $\varphi (a) = \rho _{B_a}(a)$ as above.

We now want to show that $SP(\varphi ) = \langle H, \eta \rangle$. First, consider $\tilde{\varphi }$, and let B be any element of $\mathscr {B}(L)$. We want to show that $\tilde{\varphi }(B) = H(B)$. First, let $a \in L$ and consider the four-element Boolean subalgebra $B_a = \{0,a,a',1\}$. Recall that $H(B_a)$ has four elements which we call $\{0,h(a), h'(a), 1\}$, and note that either $\varphi (a) = h(a)$ and $\varphi (a') = h(a)'$, or $\varphi (a) = h(a)'$ and $\varphi (a') = h(a)$. In either case,

$$\begin{aligned} \tilde{\varphi }(B_a) = \{ \varphi (x) \mid x \in B_a\} = \{ 0,h(a), h(a)', 1\} = H(B_a).\end{aligned}$$

(169)

Now, let B be an arbitrary Boolean subalgebra of L. Let $\varphi (a)$ be any element in $\tilde{\varphi }(B)$, where a is some element of B. Then, $\varphi (a) \in \tilde{\varphi }(B_a) = H(B_a)$. As $B_a \subseteq B$, then $H(B_a) \subseteq H(B)$, meaning $\varphi (a) \in H(B)$ and thus $\tilde{\varphi }(B) \subseteq H(B)$.

Conversely, let $h \in H(B)$. Then $B_h = \{0,h,h',1\} \subseteq H(B)$, implying that

$$\begin{aligned} H^{-1}(B_h) \subseteq H^{-1}(H(B)) = B. \end{aligned}$$

(170)

$H^{-1}(B_h)$ is a four-element Boolean subalgebra of B because H is an order isomorphism, so because $\tilde{\varphi }$ and H are the same on four-element Boolean subalgebras then

$$\begin{aligned} \tilde{\varphi }(H^{-1}(B_h)) = H( H^{-1}(B_h)) = B_h. \end{aligned}$$

(171)

Thus $h \in B_h$ is equal to some element $\varphi (a)$ in

$$\begin{aligned} \tilde{\varphi }(H^{-1}(B_h)) = \{ \varphi (a) \mid a \in H^{-1}(B_h) \subseteq B \} . \end{aligned}$$

(172)

As a is thus also an element of B, then $h \in \tilde{\varphi }(B)$ implying $H(B) \subseteq \tilde{\varphi }(B)$ and thus $H(B) = \tilde{\varphi }(B)$ for all $B \in \mathscr {B}(L)$, so $\tilde{\varphi }= H$.

It only remains to show that $\zeta _\varphi = \eta$, i.e for all $B \in \mathscr {B}(L)$, $\zeta _{\phi , B} = \eta _B$. Recall $\zeta _{\varphi ,B}$ and $\eta _B$ are both isomorphisms from $\varSigma _{\tilde{\varphi }(B)} = \varSigma _{H(B)}$ to $\varSigma _B$. Fix $\lambda \in \varSigma _{\tilde{\varphi }(B)} = \varSigma _{H(B)}$ and fix $a \in B$; we want to show that $\zeta _{\varphi ,B}(\lambda )(a) = \eta _B(\lambda )(a)$.

As described in the proof of Theorem 3.16, component $\zeta _{\varphi , B}$ acts on an element $\lambda \in \varSigma _B$ by precomposing by $\varphi |_B$:

$$\begin{aligned} \zeta _{\varphi ,B}: \varSigma _{\tilde{\varphi }(B)}&\rightarrow \varSigma _B \end{aligned}$$

(173)

$$\begin{aligned} \lambda&\mapsto \lambda \circ \varphi |_B \end{aligned}$$

(174)

Thus,

$$\begin{aligned} \zeta _{\varphi ,B}(\lambda )(a) = \lambda (\varphi (a)). \end{aligned}$$

(175)

As $\eta$ is a natural transformation, then as $B_a$ is a Boolean algebra contained in B, the following diagram commutes:

In particular, this implies that

$$\begin{aligned} \eta _B(\lambda )(a) = \eta _B(\lambda )|_{B_a}(a) = \eta _{B_a}(\lambda |_{\tilde{\varphi }(B_a)})(a). \end{aligned}$$

(176)

Recall:

$$\begin{aligned} \varphi (a) = \left\{ \begin{array}{lcc} h(a) &{}:&{} \eta _{B_a}(\lambda _{h(a)}) = \lambda _a \Leftrightarrow \eta _{B_a}(\lambda _{h(a)}) (a) = 1 \\ h(a)' &{}:&{} \eta _{B_a}(\lambda _{h(a)'}) = \lambda _a \Leftrightarrow \eta _{B_a}(\lambda _{h(a)}) (a) = 0 \end{array} \right. \end{aligned}$$

(177)

Specifically, for any $\lambda |_{\tilde{\varphi }(B)} \in \varSigma _{H(B)} = \{ \lambda _{h(a)}, \lambda _{h(a)'}\}$, whether $\lambda |_{\tilde{\varphi }(B)} = \lambda _{h(a)}$ or $\lambda |_{\tilde{\varphi }(B)} = \lambda _{h(a)'}$, an exhaustive check shows

$$\begin{aligned} \lambda (\varphi (a)) = \lambda |_{\tilde{\varphi }(B_a)}(\varphi (a)) = \eta _{B_a}(\lambda |_{\tilde{\varphi }(B)}) (a). \end{aligned}$$

(178)

Combining this with Eqs. 175 and 176,

$$\begin{aligned} \zeta _{\varphi , B} (\lambda )(a) = \lambda (\varphi (a)) = \eta _{B_a}(\lambda |_{\tilde{\varphi }(B)}) (a) = \eta _B(\lambda )(a) \end{aligned}$$

(179)

Thus, $\zeta _\varphi = \eta$, meaning

$$\begin{aligned} SP(OML(\langle H, \eta \rangle )) = \langle H , \eta \rangle . \end{aligned}$$

(180)

Theorem 3.21

There are bijections SP and OML between orthomodular lattice isomorphisms $\varphi : L \rightarrow M$ and spectral presheaf isomorphisms $\langle H, \eta \rangle : \underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$.

Proof

Theorems 3.19 and 3.20.

3.8 Interpretation of the Results so Far

Mathematical aspects. Theorem 3.18 is of some mathematical interest. While the duality between Stone spaces and Boolean algebras has been well-known for many years, we are not familiar with any attempts to generalise this duality to general orthomodular lattices. The spectral presheaf of an orthomodular lattice provides a new notion of ‘dual space’ for an orthomodular lattice, given by a functor whose image is, rather than a single Stone space, a collection of Stone spaces linked together into a presheaf by continuous restriction maps. Theorem 3.18 implies that the assignment of the spectral presheaf $\underline{\varSigma }^{L}$ to an OML L (implicitly) preserves all the structure of an orthomodular lattice, as one would require in a duality type situation.

In the case where the orthomodular lattice L is in fact a Boolean algebra, the spectral presheaf does not quite reduce to the Stone space of the Boolean algebra, as our construction of the spectral presheaf considers all Boolean subalgebras of L while Stone duality does not. This is necessary to avoid certain no-go theorems about extending classical dualities [30]. Yet, for a Boolean algebra B the poset of contexts has a unique top element, which is B itself, and the component of the spectral presheaf $\underline{\varSigma }^B$ at B is the Stone space of B. In this sense, for Boolean algebras the spectral presheaf is very close to the Stone space.

Theorem 3.18 shows that the spectral presheaf of an orthomodular lattice is a complete invariant, hence determines the orthomodular lattice up to isomorphism and vice versa. This is stronger than the corresponding result for von Neumann algebras, where a spectral presheaf determines a von Neumann algebra only up to Jordan $*$-isomorphism rather than up to isomorphism [13].

Relation with earlier results by Harding and Navara. In [31], Harding and Navara prove that an isomorphism of context categories yields an isomorphism of orthomodular lattices, though this isomorphism is only unique when the orthomodular lattices have no maximal four-element Boolean subalgebras. We considered not just the context category but rather a functor on the context category; an isomorphism between spectral presheaves $\langle H, \eta \rangle$ consists of not only an isomorphism H between context categories but also a natural isomorphism $\eta$. The additional data of $\eta$ enables the proof of Theorem 3.21, that there is a concrete bijection between orthomodular lattice isomorphisms and spectral presheaf isomorphisms. Additionally, Theorem 3.17 provides a way to construct an isomorphism of orthomodular lattices from an isomorphism of their spectral presheaves by only considering four-element Boolean subalgebras; it is precisely when considering maximal four-element Boolean subalgebras that the process employed by [31] fails to construct a unique isomorphism.

Quantum logic and physical interpretation. Many considerations in physics can fundamentally be phrased in terms of propositions. Such propositions are of the form “the physical quantity A has a value in the (Borel) set $\varDelta \subseteq \mathbb {R}$”, short “$A\,\varepsilon \,\varDelta$”. Of course, the truth value of such a proposition depends on the state of the system.¹

In classical physics, a proposition such as “$A\,\varepsilon \,\varDelta$” is represented by a (Borel) subset of the state space $\mathscr {S}$ of the system. If $f_A:\mathscr {S}\rightarrow \mathbb {R}$ is the (Borel) function representing the physical quantity A, then the subset $f_A^{-1}(\varDelta )$ of $\mathscr {S}$ contains all the states for which A has a value in $\varDelta$: if $s\in f_A^{-1}(\varDelta )$, then $f_A(s)\in \varDelta$. Hence, $f_A^{-1}(\varDelta )$ represents the proposition “$A\,\varepsilon \,\varDelta$”. The Borel subsets of the state space $\mathscr {S}$ form a $\sigma$-complete Boolean algebra.

For quantum theory, such a state space picture is lacking. Instead, one uses the closed subspaces of Hilbert space as representatives of propositions. The closed subspaces form a complete orthomodular lattice, and this is the motivation to also consider more general orthomodular lattices as algebras modeling propositions in quantum theory and quantum logic.

The spectral presheaf $\underline{\varSigma }^{L}$ plays the role of a state space for the quantum system described by an OML L, akin to the classical state space $\mathscr {S}$. Our results so far show that the spectral presheaf is a complete invariant of an OML, which implies that instead of modeling quantum logic with the OML, one can model quantum logic based on the spectral presheaf without losing any information. To do so concretely, we will not just need the spectral presheaf $\underline{\varSigma }^{L}$ (this is like having the state space of a classical system only), but also a representation of the OML L, that is, of the propositions, by suitable subsets of the quantum state space (this is like having the algebra of Borel subsets of the form $f_A^{-1}(\varDelta )$). The representation of the OML L by subsets—technically, subobjects—of $\underline{\varSigma }^{L}$ should generalise the well-known Stone representation for Boolean algebras. For a concrete generalisation of the Stone representation theorem to complete orthomodular lattices, see Sect. 4 and in particular Theorem 4.19 below.

3.9 The Spectral Presheaf of a Complete OML Is a Complete Invariant

We finally treat the case of complete orthomodular lattices (cOMLs). Note that the isomorphism result of Theorem 3.18 doesn’t immediately apply to complete OMLs. This is because the isomorphism between orthomodular lattices L and M constructed from an isomorphism from $L_{part}$ to $M_{part}$ in the proof of Theorem 3.17 is not necessarily a morphism of complete orthomodular lattices, that is, it may only preserve finite meets and joins, not arbitrary meets and joins.

Luckily, the extra effort needed in proving the results for complete OMLs is very moderate, and with a little care the proofs carry over virtually unchanged, with just the additional ‘complete’ in the right places. For this reason, we will not give all the details here.

Recall from Sect. 2.5 that the clopen subsets of the Stone space of a complete Boolean algebra form a complete Boolean algebra, and that there is a duality between complete Boolean algebras and Stonean spaces, which are extremely disconnected compact Hausdorff spaces. The appropriate kind of morphisms between these spaces are continuous open maps.

We first define the spectral presheaf of a complete OML:

Definition 3.22

Let L be a cOML, and let ${\mathscr {B}_c(L)}$ be its context category consisting of the complete Boolean subalgebras of L. The spectral presheaf $\underline{\varSigma }^{L}$ of L is the contravariant functor over ${\mathscr {B}_c(L)}$ given

• (i) on objects: for all $B\in {\mathscr {B}_c(L)}$, let $\underline{\varSigma }^{L}_B:=\varSigma (B)$, the Stonean space of B,

• (ii) on arrows: for all inclusions $i_{B'B}:B'\rightarrow B$, let

  $$\begin{aligned} \underline{\varSigma }^{L}(i_{B'B}): \underline{\varSigma }^{L}_B&\longrightarrow \underline{\varSigma }^{L}_{B'}\end{aligned}$$

  (181)
  $$\begin{aligned} \lambda&\longmapsto \lambda |_{B'}. \end{aligned}$$

  (182)

If we consider the Stonean spaces $\underline{\varSigma }^{L}_B$, $B\in {\mathscr {B}_c(L)}$, with their topology (and not just as mere sets), the restriction maps $\underline{\varSigma }^{L}(i_{B'B})$ are surjective, continuous, closed, and open. In particular, they are open since the inclusion $B'\hookrightarrow B$ is a morphism of cBAs, and the restriction $\underline{\varSigma }^{L}(i_{B'B})$ is the dual map to this inclusion, so by Proposition 2.26, $\underline{\varSigma }^{L}(i_{B'B})$ is a morphism in $\mathbf {Stonean}$. Hence, the spectral presheaf $\underline{\varSigma }^{L}$ of a cOML L is an object in the category $\mathbf {Presh}(\mathbf {Stonean})$ of presheaves with values in Stonean spaces.

Definition 3.23

Let L be a cOML, and let ${\mathscr {B}_c(L)}$ be its context category. The Bohrification ${\overline{\mathscr {L}}}$ of L is the covariant functor over ${\mathscr {B}_c(L)}$ given

• (i) on objects: for each $B\in {\mathscr {B}_c(L)}$, let ${\overline{\mathscr {L}}}_B:=B$, the complete Boolean algebra B itself,

• (ii) on arrows: for each inclusion arrow $i_{B'B}$, let ${\overline{\mathscr {L}}}(i_{B'B}):B'\hookrightarrow B$ be the inclusion homomorphism of cBAs.

The Bohrification ${\overline{\mathscr {L}}}$ of a cOML L is an object in the category $\mathbf {Copresh}(\mathbf {cBA})$ of copresheaves with values in complete Boolean algebras.

We consider the action of the functors $\varSigma$ and $\overline{CL}$ of the dual equivalence between $\mathbf {Copresh}(\mathbf {cBA})$ and $\mathbf {Presh}(\mathbf {Stonean})$ on Bohrifications and spectral presheaves, respectively. A brief check shows that they are just as for the general case of arbitrary orthomodular lattices in Sect. 3.5:

$$\begin{aligned} \varSigma ({\overline{\mathscr {L}}})&= \underline{\varSigma }^{L}\end{aligned}$$

(183)

$$\begin{aligned} \varSigma (\langle I, \theta \rangle )&= \langle I, \varSigma (\theta )\rangle \end{aligned}$$

(184)

$$\begin{aligned} CL(\underline{\varSigma }^{L})&= cl \circ \underline{\varSigma }^{L}\end{aligned}$$

(185)

$$\begin{aligned} CL(\langle \tilde{\varphi }, \zeta _\varphi \rangle )&= \langle \tilde{\varphi }, \zeta _\varphi ^{(-1)}\rangle \end{aligned}$$

(186)

The lemmas and theorems of Sects. 3.6 and 3.7 also have analogous versions for the complete case:

Lemma 3.24

The map $\{ Bo_B\}_{B \in {\mathscr {B}_c(L)}}: {\overline{\mathscr {L}}}\rightarrow cl\circ \underline{\varSigma }^{L}$ is a natural isomorphism. That is, these two functors are isomorphic in the functor category $\mathbf {cBA}^{{\mathscr {B}_c(L)}}$.

The natural isomorphism $\{Bo_B\}_{B\in {\mathscr {B}_c(L)}}$ will now simply be written in a slight abuse of notation as Bo for the sake of simplicity.

Lemma 3.25

The morphism $\langle Id_{{\mathscr {B}_c(L)}}, Bo\rangle : {\overline{\mathscr {L}}}\rightarrow cl \circ \underline{\varSigma }^{L}$ is an isomorphism in $\mathbf {Copresh}(\mathbf {cBA})$.

Theorem 3.26

Let L and M be complete orthomodular lattices, $\underline{\varSigma }^{L}$ and $\underline{\varSigma }^{M}$ their spectral presheaves, and ${\overline{\mathscr {L}}}$ and ${\overline{\mathscr {M}}}$ their Bohrifications. Then there is an isomorphism $\underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$ in $\mathbf {Presh}(\mathbf {Stonean})$ if and only if there is an isomorphism ${\overline{\mathscr {L}}}\rightarrow {\overline{\mathscr {M}}}$ in $\mathbf {Copresh}(\mathbf {cBA})$, and these isomorphisms can be explicitly constructed from each other.

If $\langle H, \eta \rangle$ is an isomorphism between the spectral presheaves of cOMLs L and M, then the corresponding isomorphism from ${\overline{\mathscr {L}}}$ to ${\overline{\mathscr {M}}}$ in $\mathbf {Copresh}(\mathbf {cBA})$ is:

$$ \rho := \langle Id_{\mathscr {B}(M)}, Bo^{-1}\rangle \circ \langle H, cl(\eta )\rangle \circ \langle Id_{\mathscr {B}(L)}, Bo \rangle = \langle H, (H^* Bo^{-1}) \circ cl(\eta ) \circ Bo \rangle . $$

In particular, each component of the natural isomorphism $(H^* Bo^{-1}) \circ cl(\eta ) \circ B$ is an isomorphism in $\mathbf {cBA}$. This follows from Proposition 2.26, and in particular, Facts 2.27 and 2.28. That this isomorphism (renamed $\rho$ in the proof of Theorem 3.17 as it is above) preserves arbitrary meets and joins is essential for being able to construct an isomorphism of cOMLs from an isomorphism of spectral presheaves in Theorem 3.28 below.

Theorem 3.27

Let L and M be complete orthomodular lattices. If $\varphi : L \rightarrow M$ is an isomorphism in $\mathbf {cOML}$, then there is an isomorphism $\langle \tilde{\varphi }, \zeta _\varphi \rangle : \underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$ in $\mathbf {Presh}(\mathbf {Stonean})$, where the natural transformation $\zeta _\varphi$ has components $\zeta _{\varphi , B} = \varSigma (\varphi |_B)$ for all B in ${\mathscr {B}_c(L)}$.

Theorem 3.28

Let L and M be complete orthomodular lattices. If there is an isomorphism $\langle H, \eta \rangle : \underline{\varSigma }^{M}\rightarrow \underline{\varSigma }^{L}$ in $\mathbf {Presh}(\mathbf {Stonean})$, then there is an isomorphism from L to M in $\mathbf {cOML}$ that can be constructed explicitly from $\langle H,\eta \rangle$.

The proof of this theorem for cOMLs is made possible by the fact that $\rho$ is an isomorphism of complete Boolean algebras and thus induces an isomorphism of partial complete orthomodular lattices, which in turn determines a (unique) isomorphism of cOMLs. Summing up, we have:

Theorem 3.29

Two complete orthomodular lattices L and M are isomorphic in $\mathbf {cOML}$ if and only if their spectral presheaves $\underline{\varSigma }^{L}$ and $\underline{\varSigma }^{M}$ are isomorphic in $\mathbf {Presh}(\mathbf {Stonean})$.

4 Representing a Complete Orthomodular Lattice

The goal of this section is to find a ‘representation’ of a complete orthomodular lattice by clopen subobjects of its spectral presheaf, in analogy to the Stone representation of a Boolean algebra by clopen subsets of its Stone space.

In Sect. 4.1, we define and describe the clopen subobjects of the spectral presheaf of a complete orthomodular lattice, and in Sect. 4.2 we show that they form a complete bi-Heyting algebra. In Sect. 4.3, we define a map called ‘daseinisation’ from a complete orthomodular lattice to the clopen subobjects of its spectral presheaf. If we interpret the elements of the cOML as propositions about (the values of physical quantities of) a quantum system, then this map can be seen as a ‘translation’ of the quantum propositions into clopen subobjects of a generalised phase space. In Sects. 4.5 and 4.6, we use the adjoint of the daseinisation map to relate the lattice structure of the clopen subobjects of the spectral presheaf to the lattice structure of the original orthomodular lattice.

4.1 Clopen Subobjects of the Spectral Presheaf

For the remainder of this section, we assume L is a complete orthomodular lattice and $\underline{\varSigma }^{L}$ is its spectral presheaf.

Definition 4.1

Let $F: \mathscr {C} \rightarrow \mathbf {Set}$ be a functor. A functor $G: \mathscr {C}\rightarrow \mathbf {Set}$ is a subfunctor of F if for all $C \in Ob(\mathscr {C})$, $G_C\subseteq F_C$ and for all $a:C \rightarrow D$ in $Arr({\mathscr {C}})$, G(a) is the restriction of F(a) to domain $G_C$ and codomain $G_D$.

Note that this implies $G(a)(G_C)\subseteq G_D$.

Definition 4.2

A subobject of $\underline{\varSigma }^{L}$ is a subfunctor $\underline{S}: {\mathscr {B}_c(L)}^{op} \rightarrow \mathbf {Set}$ of $\underline{\varSigma }^{L}$.

This is the same definition of a subobject of $\underline{\varSigma }^{L}$ as in the topos sense. That is, recalling the definition of a subobject in a topos, subfunctors of $\underline{\varSigma }^{L}$ correspond precisely to monic arrows with codomain $\underline{\varSigma }^{L}$ in the functor category $\mathbf {Set}^{\mathscr {B}(L)^{{\text {op}}}}$ (see e.g. [23]).

Definition 4.3

A subobject $\underline{S}$ of $\underline{\varSigma }^{L}$ is clopen if for all $B \in {\mathscr {B}_c(L)}$, the component $\underline{S}_B$ is a clopen subset of $\underline{\varSigma }^{L}_B$. The set of clopen subobjects of $\underline{\varSigma }^{L}$ will be denoted ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$.

There is an obvious partial order on ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$: let $\underline{S}$ and $\underline{T}$ be clopen subobjects in ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$. Then define

$$ \underline{S} \le \underline{T} \quad :\Longleftrightarrow \quad \forall B\in {\mathscr {B}_c(L)}: \underline{S}_B\subseteq \underline{T}_B. $$

With respect to this partial order, all meets and joins exist. Let $(\underline{S}_i)_{i\in I}\subseteq {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ be an arbitrary family of clopen subobjects. Their meet resp. join is given by

$$\begin{aligned} \forall B\in {\mathscr {B}_c(L)}:\;&\left( \bigwedge _{i\in I}\underline{S}_i\right) _B = {\text {int}}\bigcap _{i\in I}\underline{S}_{i;B},\end{aligned}$$

(187)

$$\begin{aligned}&\left( \bigvee _{i\in I}\underline{S}_i\right) _B = {\text {cls}}\bigcup _{i\in I}\underline{S}_{i;B}, \end{aligned}$$

(188)

where $\underline{S}_{i;B}$ denotes the component of $\underline{S}_i$ at B. The interior resp. closure are taken with respect to the Stone topology. Since the Stone spaces of the complete Boolean (sub)algebras are Stonean, i.e. extremely disconnected, we obtain clopen subsets at each stage $B\in {\mathscr {B}_c(L)}$, and the meet and the join of clopen subobjects are clopen subobjects again as required.

Hence, ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ is a complete lattice. It is also distributive, since meets and joins are defined stagewise, at each $B\in {\mathscr {B}_c(L)}$ separately. At $B\in {\mathscr {B}_c(L)}$, the meet and the join are the meet and join of clopen subsets of the Stonean space $\underline{\varSigma }^{L}_B$ of B, which form a complete Boolean algebra (which of course is distributive). It is easy to show that in ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$, finite meets distribute over arbitrary joins and finite joins distribute over arbitrary meets.

4.2 The Clopen Subobjects Form a Complete Bi-Heyting Algebra

It was shown in [12] that ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ is a complete bi-Heyting algebra. For general information on bi-Heyting algebras, see [32]. For convenience of the reader, we briefly recall the definitions and main results.

Definition 4.4

A Heyting algebra is a bounded lattice H such that for all elements $a,b \in H$, there is a greatest element $x \in H$ such that $a \wedge x \le b$. Such an element x is called the relative pseudocomplement of a with respect to b or the Heyting implication from a to b and is denoted $a \Rightarrow b$. The pseudocomplement of a, also called the Heyting negation of a, is the element $\lnot a:= (a \Rightarrow 0)$.

In the above definition, the element $\lnot a$ is called a pseudocomplement of a because

$a \wedge \lnot a = 0$ but it is not necessarily true that $a \vee \lnot a = 1$.

Definition 4.5

A Heyting algebra is complete if it is complete as a lattice.

In a complete Heyting algebra, finite meets distribute over arbitrary joins [32].

One can also define the dual notion of a co-Heyting algebra, also called a Brouwer algebra.

Definition 4.6

A co-Heyting algebra (or Brouwer algebra) is a bounded lattice H such that for all elements $a,b \in H$, there is a least element $x \in H$ such that $a \le b \vee x$. Such an element x is called the co-Heyting implication from a to b, and is denoted $a \Leftarrow b$. The co-Heyting negation of a is the element $\sim a:= (1 \Leftarrow a)$.

Dually to the negation in a Heyting algebra, the co-Heyting negation satisfies $a \vee \sim a = 1$ but it might not necessarily be true that $a\wedge \sim a = 0$.

Definition 4.7

A co-Heyting algebra is complete if it is complete as a lattice.

In a complete co-Heyting algebra, finite joins distribute over arbitrary meets [32].

Definition 4.8

A bi-Heyting algebra is a bounded lattice that is both a Heyting algebra and a co-Heyting algebra. A bi-Heyting algebra is complete if it is complete as a lattice.

A bi-Heyting algebra is distributive, but generalises a Boolean algebra by splitting up the notion of complementation into two separate notions, Heyting negation and co-Heyting negation. Heyting negation is intuitionistic, satisfying $a \wedge \lnot a = 0$ but not necessarily $a \vee \lnot a = 1$; logically, this means that the law of excluded middle need not hold. The co-Heyting negation is paraconsistent, satisfying $a\vee \sim a = 1$ but not necessarily $a \wedge \sim a = 0$; logically, this means that the law of noncontradiction need not hold.

Proposition 4.9

${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ is a complete bi-Heyting algebra.

Proof

We already saw that ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ is a complete distributive lattice. It remains to show that there are both a Heyting and a co-Heyting structure on ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }$.

The map

$$\begin{aligned} \underline{S} \wedge (-): {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}&\longrightarrow {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}\end{aligned}$$

(189)

$$\begin{aligned} \underline{T}&\longmapsto \underline{S} \wedge \underline{T} \end{aligned}$$

(190)

is monotone and preserves arbitrary joins. Hence, by Proposition 2.30, this map has an upper adjoint which is denoted $\underline{S} \rightarrow (-)$ and is given by:

$$\begin{aligned} \underline{S} \Rightarrow (-): {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}&\longrightarrow {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}\end{aligned}$$

(191)

$$\begin{aligned} \underline{T}&\longmapsto (\underline{S} \Rightarrow \underline{T}):= \bigvee \{ \underline{R} \in {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}\mid \underline{S} \wedge \underline{R} \le \underline{T} \} \end{aligned}$$

(192)

Additionally, by Proposition 2.31, this map satisfies

$$\begin{aligned} \underline{S} \wedge (\underline{S} \Rightarrow \underline{T}) \le \underline{T}. \end{aligned}$$

(193)

The map $\underline{S}\Rightarrow (-):{\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}\rightarrow {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ gives a well-defined Heyting implication in the complete distributive lattice ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$, with $\underline{S}$ varying over ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$. Thus, ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ is a Heyting algebra. It is complete as ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ is a complete lattice. The Heyting negation of this algebra will be denoted $\lnot$, and is given by

$$\begin{aligned} \lnot : {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}&\longrightarrow {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}\end{aligned}$$

(194)

$$\begin{aligned} \underline{S}&\longmapsto \lnot \underline{S}:= (\underline{S} \Rightarrow \underline{0}). \end{aligned}$$

(195)

Here $\underline{0}$ is the clopen subobject of $\underline{\varSigma }^{L}$ with $\underline{0}_B = \emptyset$ for all $B \in \mathscr {B}_c(L)$, the bottom element of ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$.

Analogously, the following monotone map preserves arbitrary meets:

$$\begin{aligned} \underline{S} \vee (-): {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}&\longrightarrow {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}\end{aligned}$$

(196)

$$\begin{aligned} \underline{T}&\longmapsto \underline{S} \vee \underline{T} \end{aligned}$$

(197)

Thus, by Proposition 2.30, it has a lower adjoint which we will call $(-) \Leftarrow \underline{S}$ given by:

$$\begin{aligned} (-) \Leftarrow \underline{S}: {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}&\longrightarrow {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}\end{aligned}$$

(198)

$$\begin{aligned} \underline{T}&\longmapsto (\underline{T} \Leftarrow \underline{S}):= \bigwedge \{ \underline{R} \in {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}\mid \underline{T} \le \underline{S} \vee \underline{R} \} \end{aligned}$$

(199)

By Proposition 2.31, this map satisfies

$$\begin{aligned} \underline{T} \le \underline{S} \vee (\underline{T} \Leftarrow \underline{S}) \end{aligned}$$

(200)

It is clear by the definition of this map and Eq. 200 that this gives a co-Heyting implication for ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ (where $\underline{S}$ varies over ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$), demonstrating that ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ is a complete co-Heyting algebra and thus a complete bi-Heyting algebra. The co-Heyting negation is given by

$$\begin{aligned} \sim \;: {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}&\longrightarrow {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}\end{aligned}$$

(201)

$$\begin{aligned} \underline{S}&\longmapsto \;\sim \underline{S}:= (\underline{\varSigma }^{L}\Leftarrow \underline{S}). \end{aligned}$$

(202)

4.3 Daseinisation as Representation of a Complete OML

In this subsection we define a map from a complete orthomodular lattice L to the complete bi-Heyting algebra ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$, called the daseinisation map. This can be interpreted as an approximation map, which for each element a of L ‘brings into existence’ an approximation of a as a subspace of each of the Stonean spaces $\varSigma _B$ for $B \in {\mathscr {B}_c(L)}$ (hence the name). Daseinisation was first defined in a quantum theory context in [4] and discussed in detail in [11, 33] for the projection lattice of a von Neumann algebra. Here, we give a streamlined presentation and generalise to arbitrary complete OMLs.

Let L be a complete orthomodular lattice, let $a \in L$, and let $B \in \mathscr {B}_c(L)$ be a complete Boolean subalgebra of L, not necessarily containing a. Then, we define

$$\begin{aligned} \delta _B^o(a):= \bigwedge \{ b \in B\mid b \ge a\}, \end{aligned}$$

(203)

the smallest element of B that is greater than or equal to a. If $a \in B$, then $\delta _B^o (a) = a$. Note that the superscript of o denotes that this is outer daseinisation, that is, approximating element a in B from above. It is precisely at this step that completeness of orthomodular lattice L is required to define daseinisation; we need to know that the infinite meet in the definition of $\delta _B^o(a)$ exists.

Note that the inclusion map

$$\begin{aligned} B&\hookrightarrow L \end{aligned}$$

(204)

$$\begin{aligned} a&\mapsto a \end{aligned}$$

(205)

is a morphism of complete OMLs and hence preserves all meets in particular, so it has a lower adjoint, which is precisely

$$\begin{aligned} \delta _B^o: L&\longrightarrow B \end{aligned}$$

(206)

$$\begin{aligned} a&\longmapsto \delta _B^o(a). \end{aligned}$$

(207)

By Stone duality, we have an isomorphism between the complete Boolean algebra B and the clopen subobjects of its Stone space $\varSigma _B$, which is Stonean because B is complete. From Sect. 2.3, this isomorphism is given by

$$\begin{aligned} Bo_B: B&\longrightarrow cl(\varSigma _B) = cl(\underline{\varSigma }^{L}_B) \end{aligned}$$

(208)

$$\begin{aligned} b&\longmapsto \{ \lambda \in \underline{\varSigma }^{L}_B \mid \lambda (b) = 1 \} \end{aligned}$$

(209)

Recall cl is the functor which maps a Stone space to its Boolean algebra of clopen subsets. Here, $Bo_B$ is an isomorphism of complete Boolean algebras. In particular, the element $\delta _B^o(a)$ of B corresponds to the clopen subset of $\underline{\varSigma }^{L}_B$ given by:

$$\begin{aligned} {\underline{\delta }^o}_B(a):= Bo_B(\delta _B^o(a)) = \{ \lambda \in \underline{\varSigma }^{L}_B \mid \lambda (\delta _B^o(a) )= 1\}. \end{aligned}$$

(210)

(The reason for using the notation with underlining will become clear shortly.)

Suppose that $B' \subseteq B$ in $\mathscr {B}_c(L)$. Clearly, it holds that $\delta ^o_B(a) \le \delta ^o_{B'}(a)$. Then,

$$\begin{aligned} \lambda \in {\underline{\delta }^o}_B(a)&\Leftrightarrow \lambda ( \delta ^o_B(a)) = 1 \end{aligned}$$

(211)

$$\begin{aligned}&\Rightarrow \lambda (\delta ^o_{B'}(a)) = 1 \end{aligned}$$

(212)

$$\begin{aligned}&\Leftrightarrow \lambda |_{B'} (\delta ^o_{B'}(a)) = 1 \end{aligned}$$

(213)

$$\begin{aligned}&\Leftrightarrow \lambda |_{B'} \in {\underline{\delta }^o}_{B'}(a) \end{aligned}$$

(214)

We conjecture that this result can be strengthened to show that $\lambda \in {\underline{\delta }^o}_B(a)$ if and only if $\lambda |_{B'} \in {\underline{\delta }^o}_{B'}(a)$, but such a result is not necessary for our purposes so we do not pursue this line of investigation. Note that this result implies that for every inclusion arrow $i_{B', B}$ in $\mathscr {B}_c(L)$, the restriction of $\underline{\varSigma }^{L}(i_{B',B}) = r_{B,B'}$ to domain ${\underline{\delta }^o}_B(a) \subseteq \underline{\varSigma }^{L}_B$ has codomain contained in ${\underline{\delta }^o}_{B'}(a) \subseteq \underline{\varSigma }^{L}_{B'}$. This means that the functor from $\mathscr {B}_c(L)$ to Set which sends B to ${\underline{\delta }^o}_B(a)$ is a valid subfunctor of $\underline{\varSigma }^{L}$; we will call this functor ${\underline{\delta }^o}(a)$. Clearly this functor

$$\begin{aligned} {\underline{\delta }^o}(a):= \left( {\underline{\delta }^o}_B(a) \right) _{B \in \mathscr {B}_c(L)} \end{aligned}$$

(215)

is thus also a subobject of the spectral presheaf. It is a clopen subobject because for each $B \in {\mathscr {B}_c(L)}$, the subset ${\underline{\delta }^o}_B(a)$ of $\varSigma _B$ is clopen.

We are now ready to define the daseinisation map for complete orthomodular lattice L and discuss its properties.

Definition 4.10

The map

$$\begin{aligned} {\underline{\delta }^o}: L&\longrightarrow {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}\end{aligned}$$

(216)

$$\begin{aligned} a&\longmapsto {\underline{\delta }^o}(a) \end{aligned}$$

(217)

from the complete orthomodular lattice L to the complete bi-Heyting algebra ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ is called outer daseinisation, or more simply daseinisation.

The daseinisation map can be seen as a process by which an element a in the complete orthomodular lattice L is approximated in each classical context B and subsequently each Stone space $\varSigma _B$, ultimately yielding a clopen subobject of $\underline{\varSigma }^{L}$. Returning to the notion of an orthomodular lattice as a quantum logic whose elements are propositions, for each classical context B the daseinisation process first associates to proposition a the strongest proposition within B that must be true if proposition a is true, which above we called $\delta ^o_B(a)$. The next step of daseinisation associates to each of these strongest propositions the collection of local valuations (elements of the Stone space of B, i.e., Boolean algebra homomorphisms from B to $\{0,1\}$) for which the proposition holds, which we called ${\underline{\delta }^o}_B(a)$. These sets of local valuations are clopen and are linked together by the restriction maps to create a clopen subobject ${\underline{\delta }^o}(a)$. This analysis shows that the daseinisation process associates to each quantum proposition a subobject of the spectral presheaf of the complete orthomodular lattice to which it belongs, just as a classical proposition corresponds to a subset of the state space of the classical system.

Lemma 4.11

The daseinisation map ${\underline{\delta }^o}: L \rightarrow {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ has the following properties:

• 1. ${\underline{\delta }^o}(0) = \underline{0}$, ${\underline{\delta }^o}(1) = \underline{\varSigma }^{L}$,

• 2. ${\underline{\delta }^o}$ is monotone, that is, $a \le b$ in L implies ${\underline{\delta }^o}(a) \le {\underline{\delta }^o}(b)$ in ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$,

• 3. ${\underline{\delta }^o}$ is injective, but not surjective,

• 4. ${\underline{\delta }^o}$ preserves all joins.

Proof

(1) is obvious form the definition of ${\underline{\delta }^o}$; for all $B \in {\mathscr {B}_c(L)}$, $\delta ^o_B(0) = 0$ and ${\underline{\delta }^o}_B(0) = \emptyset$. Similarly, $\delta ^o_B(1) = 1$ and ${\underline{\delta }^o}_B(1) = \varSigma _B = \underline{\varSigma }^{L}_B$.

(2) also follows directly from the definition of ${\underline{\delta }^o}$. If $a \le b$, then $\delta ^o_B(a) \le \delta ^o_B(b)$ and ${\underline{\delta }^o}_B(a) \subseteq {\underline{\delta }^o}_B(b)$ for all $B \in {\mathscr {B}_c(L)}$, meaning that ${\underline{\delta }^o}(a) \le {\underline{\delta }^o}(b)$ in ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$.

For (3), let a and b be distinct elements of L. Then,

$$\begin{aligned} \bigwedge _{B \in {\mathscr {B}_c(L)}}&\delta ^o_B(a) = a \ne b = \bigwedge _{B \in {\mathscr {B}_c(L)}}\delta ^o_B(b) \end{aligned}$$

(218)

This implies that there must be some $B \in {\mathscr {B}_c(L)}$ such that $\delta ^o_B(a) \ne \delta ^o_B(b)$. As $Bo_B$ is a complete Boolean algebra isomorphism, it follows for this B that

$$\begin{aligned} {\underline{\delta }^o}_B(a) = Bo_B(\delta ^o_B(a)) \ne Bo_B(\delta ^o_B(a)) = {\underline{\delta }^o}_B(b) \end{aligned}$$

(219)

As ${\underline{\delta }^o}(a)$ and ${\underline{\delta }^o}(b)$ differ at this component, then they are not the same subobject of $\underline{\varSigma }^{L}$. Thus, ${\underline{\delta }^o}$ is injective. On the other hand, ${\underline{\delta }^o}$ clearly is not surjective, since not every clopen subobject of $\underline{\varSigma }^{L}$ is of the form ${\underline{\delta }^o}(a)$ for some $a\in L$.

For (4), note that joins are colimits, which are calculated stagewise, at each $B\in {\mathscr {B}_c(L)}$ separately. We saw that for each B, the map $\delta _B^o: L \rightarrow B$, $a \mapsto \delta _B^o(a)$, is the lower adjoint of the inclusion map $B\hookrightarrow L$, so it preserves all colimits. The map cl that takes $\delta _B^o(a)$ to ${\underline{\delta }^o}_B(a)$ is an isomorphism of complete Boolean algebras, so it preserves all joins.

Stone duality provides a representation of every complete Boolean algebra B by a concrete complete Boolean algebra, viz. the algebra of clopen subsets of the Stone space $\varSigma _B$,

$$\begin{aligned} B \longrightarrow cl(\varSigma _B). \end{aligned}$$

(220)

In analogy, and as a generalisation, daseinisation can be interpreted as providing a ‘representation’ of every complete orthomodular lattice L by a concrete algebra of clopen subobjects of a generalised Stone space, viz. the spectral presheaf $\underline{\varSigma }^{L}$,

$$\begin{aligned} L \longrightarrow {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}. \end{aligned}$$

(221)

We saw that $\underline{\varSigma }^{L}$ is a complete invariant of L (Theorem 3.18) and generalises the Stone space $\varSigma _B$ of a complete Boolean algebra B in a straightforward manner. Of course, the algebra ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ in which we are ‘representing’ the cOML L is not a cOML itself, but is a complete bi-Heyting algebra. The representation provided by ${\underline{\delta }^o}$ preserves top and bottom element, the order and all joins. Moreover, the representation is faithful, since ${\underline{\delta }^o}$ is an injective map (Lemma 4.11).

In Sect. 4.5, we will show that daseinisation has an adjoint, which will then allow us to regain the cOML L from the complete bi-Heyting algebra ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ in (Sect. 4.6), further strengthening the analogy with Stone representation. Bur first, we will give some physical interpretation of the results so far.

4.4 Some Physical Interpretation

The representation ${\underline{\delta }^o}:L\rightarrow \underline{\varSigma }^{L}$ of a complete orthomodular lattice L is structurally similar to the Stone representation of a Boolean algebra, and the interpretation of the spectral presheaf as a state space for the quantum system is vindicated.

Yet, the fact that we map from L into a complete bi-Heyting algebra (and not into another complete OML) may seem to be a drawback at first sight. We will give some brief arguments why, on the contrary, the bi-Heyting algebra picture provides many advantages compared to standard quantum logic [15, 16]. Some more discussion can be found in [4, 11, 12].

Distributivity and existence of a material implication. One key problem of standard quantum logic is the lack of a material implication. In a bi-Heyting algebra, the Heyting implication, $\Rightarrow$, plays the role of a material implication and hence is given as part of the structure. The existence of the Heyting implication depends on the distributivity of the underlying lattice (see the argument after Eq. (189)). The fact that the lattice in which we represent propositions about our quantum system is distributive has further advantages. The behaviour of meets and joins has a clear interpretation, and situations such as the ‘quantum breakfast’ do not pose any interpretational issues.²

Availability of higher-order logic. By daseinisation ${\underline{\delta }^o}:L\rightarrow \underline{\varSigma }^{L}$ we do not just map into a bi-Heyting algebra, but this algebra is given by the (clopen) subobjects of a presheaf, which is an object in the presheaf topos $\mathbf {Set}^{\mathscr {B}(L)^{{\text {op}}}}$. The topos comes equipped with an internal higher-order intuitionistic logic [20, 21, 23], which can now be employed for quantum theory. This is largely a task for the future.

Superposition without linearity. One characteristic feature of quantum theory is the existence of superposition. In a given (vector) state $\,|\psi \rangle$, the disjunction of two propositions P, Q can be true while neither of the propositions is true. For example, if p, q are one-dimensional subspaces that represent the propositions P, Q and the one-dimensional subspace $\mathbb {C}\,|\psi \rangle$ lies in the plane spanned by p and q (without being equal to either p or q), then the state $\,|\psi \rangle$ makes the proposition (P or Q) true without making P true or Q true. We see that superposition relates to the behaviour of joins, given by spans of subspaces of a linear space. Interestingly, our representation $L\rightarrow \underline{\varSigma }^{L}$ preserves all joins and hence preserves that structural aspect of orthomodular lattices which comes from superposition. This is true despite the fact that different from Hilbert space the spectral presheaf, which is the underlying (generalised) space, is not a linear space.

Good interpretation of all conjunctions. Every quantum system has incompatible physical quantities that cannot be measured simultaneously. In fact, a context is usually understood to be a subset of physical quantities that can be measured simultaneously. Accordingly, certain propositions of the form “$A\,\varepsilon \,\varDelta$ and $B\,\varepsilon \,\varGamma$” about the values of incompatible physical quantities should be meaningless, since there is no possible experiment that could measure A and B simultaneously. In an orthomodular lattice, any pair of elements has a meet, so there are many meets that have no good physical interpretation.

In our bi-Heyting algebra ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$, all meets exist as well, but nonetheless we avoid the interpretational problem described above: meets in ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ are taken stagewise, in each context separately. (Here, a context is a collection of compatible propositions, forming a Boolean algebra.) If we start from two incompatible propositions, we first apply a process of coarse-graining. Each proposition is approximated by a weaker proposition in every context (see Eq. (203)). The meet is then taken only between compatible propositions, each of which is a weakening of the original proposition. For example, if we consider a context B that contains an element p that represents the proposition “$A\,\varepsilon \,\varDelta$”, then $\delta ^o_B(p)=p$, so the ‘approximation’ to p within the context B is p itself, as expected. If q is another element of the OML that represents the (incompatible) proposition “$B\,\varepsilon \,\varGamma$”, then q is not contained in the context B, so $\delta ^o_B(q)\gneq q$, and the approximation of q within B represents a properly weaker proposition than the original one. The meet at B is the meet $p\wedge \delta ^o_B(q)$, and analogously for all other contexts, including those contexts $\tilde{B}$ that contain q (where p has to be properly approximated). In this way, we avoid taking any meets of incompatible elements.

Additional paraconsistent fragment of the logic. Apart from the Heyting algebra aspect, which provides an intuitionistic logic for every quantum system, there is also a co-Heyting algebra aspect. Logically, this represents a paraconsistent logic. Some properties of the Heyting and co-Heyting structure are discussed in [12]. A bi-Heyting algebra can be seen as a fairly modest generalisation of a Boolean algebra. The concept of negation becomes split into a Heyting negation (pseudocomplement) for which the law of the excluded middle does not hold (i.e., $a\wedge \lnot a=0$, but $a\vee \lnot a\le 1$), and a co-Heyting negation, for which the law of non-contradiction does not hold (i.e., $a\vee \sim a=1$, but $a\wedge \sim a\ge 0$). The latter property is a direct consequence of coarse-graining and is not problematic interpretationally.

Summing up, our representation ${\underline{\delta }^o}:L\rightarrow \underline{\varSigma }^{L}$ translates from standard quantum logic to a new, distributive form of logic for quantum systems that has many good interpretational properties. Daseinisation ‘creates’ distributivity and splits negation into two concepts, relating to the Heyting and the co-Heyting fragment, respectively.

In the following subsections, we will show that daseinisation has an adjoint that can be used to map back from the complete bi-Heyting algebra ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ to the complete OML L. This gives an even closer link between our new form of quantum logic and standard quantum logic formulated in OMLs.

4.5 The Adjoint of Daseinisation

${\underline{\delta }^o}$ is a join-preserving map between two complete lattices, so by Proposition 2.30, ${\underline{\delta }^o}$ has a meet-preserving upper adjoint $\varepsilon : {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}\rightarrow L$. This map $\varepsilon$ is defined by:

$$\begin{aligned} \varepsilon : {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}&\longrightarrow L \end{aligned}$$

(222)

$$\begin{aligned} \underline{S}&\longmapsto \bigvee \{ a \in L \mid {\underline{\delta }^o}(a) \le \underline{S} \}. \end{aligned}$$

(223)

The following lemma, adapted from an unpublished result by Carmen Constantin, provides more insight into this map $\varepsilon$.

Lemma 4.12

Let L be a complete orthomodular lattice, with spectral presheaf $\underline{\varSigma }^{L}$. The upper adjoint $\varepsilon$ of ${\underline{\delta }^o}$ is given by

$$\begin{aligned} \varepsilon : {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}&\rightarrow L \end{aligned}$$

(224)

$$\begin{aligned} \underline{S}&\mapsto \bigwedge _{B \in {\mathscr {B}_c(L)}} Bo_B^{-1} (\underline{S}_B) \end{aligned}$$

(225)

Proof

Suppose that a is some lower bound for the set $\{ Bo_B^{-1} (\underline{S}_B) \mid B \in {\mathscr {B}_c(L)}\}$. That is, for each $B \in {\mathscr {B}_c(L)}$,

$$\begin{aligned} a \le Bo_B^{-1}(\underline{S}_B). \end{aligned}$$

(226)

As $Bo_B^{-1}(\underline{S}_B)$ is an element of B that is greater than or equal to a and $\delta ^o_B(a)$ is the least element of B that is greater than or equal to a, then

$$\begin{aligned} a&\le Bo_B^{-1}(\underline{S}_B) \end{aligned}$$

(227)

$$\begin{aligned} \Leftrightarrow \delta _B^o(a)&\le Bo_B^{-1}(\underline{S}_B) \end{aligned}$$

(228)

$$\begin{aligned} \Leftrightarrow Bo_B( \delta _B^o(a) )&\subseteq Bo_B(Bo_B^{-1}(\underline{S}_B)) \end{aligned}$$

(229)

$$\begin{aligned} \Leftrightarrow {\underline{\delta }^o}_B(a)&\subseteq \underline{S}_B \end{aligned}$$

(230)

This exactly characterises the lower bounds a of the set $\{ Bo_B^{-1} (\underline{S}_B) \mid B \in {\mathscr {B}_c(L)}\}$. That is,

$$\begin{aligned} \{ a \in L \mid a \le Bo_B^{-1} (\underline{S}_B)\quad \forall \quad B \in {\mathscr {B}_c(L)}\}&= \{ a \in L \mid {\underline{\delta }^o}_B(a) \subseteq \underline{S}_B \forall \quad B \in {\mathscr {B}_c(L)}\} \end{aligned}$$

(231)

$$\begin{aligned}&= \{ a \in L \mid {\underline{\delta }^o}(a) \le \underline{S} \}. \end{aligned}$$

(232)

In a complete lattice, joins can be written in terms of meets. That is,

$$\begin{aligned} \bigwedge _{B \in {\mathscr {B}_c(L)}} Bo_B^{-1} (\underline{S}_B)&= \bigvee \{ a \in L \mid a \le Bo_B^{-1} (\underline{S}_B) \forall B \in {\mathscr {B}_c(L)}\} \end{aligned}$$

(233)

$$\begin{aligned}&= \bigvee \{ a \in L \mid {\underline{\delta }^o}(a) \le \underline{S} \} \end{aligned}$$

(234)

$$\begin{aligned}&= \varepsilon (\underline{S}). \end{aligned}$$

(235)

The previous lemma implies the following result, which is stronger than could be expected for an arbitrary Galois connection:

Lemma 4.13

$\varepsilon \circ {\underline{\delta }^o}= id_L$.

Proof

Let $a \in L$. Then,

$$\begin{aligned} (\varepsilon \circ {\underline{\delta }^o})(a) = \varepsilon ( {\underline{\delta }^o}(a))&= \bigwedge _{B \in {\mathscr {B}_c(L)}} Bo_B^{-1} ({\underline{\delta }^o}_B(a)) \end{aligned}$$

(236)

$$\begin{aligned}&= \bigwedge _{B \in {\mathscr {B}_c(L)}} Bo_B^{-1}( Bo_B( \delta ^o_B(a))) \end{aligned}$$

(237)

$$\begin{aligned}&= \bigwedge _{B \in {\mathscr {B}_c(L)}} \delta _B^o(a) \end{aligned}$$

(238)

$$\begin{aligned}&= a. \end{aligned}$$

(239)

From the general properties of a Galois connection, it also follows that

$$\begin{aligned} {\underline{\delta }^o}\circ \varepsilon \le id_{{\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}}. \end{aligned}$$

(240)

Lemma 4.14

The map $\varepsilon :{\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}\rightarrow L$ has the following properties:

• 1. $\varepsilon (\underline{0}) = 0$, $\varepsilon (\underline{\varSigma }^{L}) = 1$,

• 2. $\varepsilon$ is monotone,

• 3. $\varepsilon$ is surjective, but not injective,

• 4. $\varepsilon$ preserves all meets.

Proof

(1) and (2) are obvious. For (3), note that if $a\in L$, then $a=(\varepsilon \circ {\underline{\delta }^o})(a)$ by Lemma 4.13, so a is in the image of $\varepsilon$.

(4) holds since $\varepsilon$ is an upper adjoint, which preserves all limits, which are meets here.

4.6 Regaining a cOML from the Algebra of Clopen Subobjects

It is clear that a cOML L and the complete bi-Heyting algebra ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ cannot be isomorphic as lattices in general, because L is not necessarily distributive but ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ is. Additionally, ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ contains significantly more elements in general than L. However, we will show that by forming certain equivalence classes within ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$, we obtain a complete OML that is isomorphic to L. Of course, Lemma 4.13 already gives a clear hint that it is possible to reconstruct L from ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$, and we will make this explicit now.

We can use the map $\varepsilon$ to define an equivalence relation on ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$:

Definition 4.15

For $\underline{S}$, $\underline{T}$ in ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$, define $\underline{S} \sim \underline{T}$ if and only if $\varepsilon (\underline{S}) = \varepsilon (\underline{T})$.

This is clearly a well-defined equivalence relation. We will write $[\underline{S}]$ for the equivalence class of $\underline{S}$. Let

$$\begin{aligned} E:= \left\{ [\underline{S}] \mid \underline{S} \in {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}\right\} \end{aligned}$$

(241)

be the set of equivalence classes. We observe right away that E is a partially ordered set in a canonical manner: define

$$\begin{aligned} \,[\underline{S}]\le [\underline{T}]:\Leftrightarrow \varepsilon (\underline{S})\le \varepsilon (\underline{T}). \end{aligned}$$

(242)

Then $[\underline{\emptyset }]$ is the bottom element and $[\underline{\varSigma }^{L}]$ is the top element.

Lemma 4.16

Let $[\underline{S}]\in E$. Then $[({\underline{\delta }^o}\circ \varepsilon )(\underline{S})]=[\underline{S}]$ and $({\underline{\delta }^o}\circ \varepsilon )(\underline{S})$ is the smallest representative of $[\underline{S}]$.

Proof

By Proposition 2.31, we have $\varepsilon ({\underline{\delta }^o}\circ \varepsilon )(\underline{S})=\varepsilon (\underline{S})$, so $[({\underline{\delta }^o}\circ \varepsilon )(\underline{S})]=[\underline{S}]$. Moreover, if $\underline{T}$ is a representative of $[\underline{S}]$, then $\varepsilon (\underline{T})=\varepsilon (\underline{S})$ and since ${\underline{\delta }^o}\circ \varepsilon \le id_{{\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}}$,

$$\begin{aligned} \underline{T} \ge ({\underline{\delta }^o}\circ \varepsilon )(\underline{T}) = ({\underline{\delta }^o}\circ \varepsilon )(\underline{S}). \end{aligned}$$

(243)

Lemma 4.17

There is a bijective set map from E to the set underlying the complete orthomodular lattice L, given by

$$\begin{aligned} g: E&\longrightarrow L \end{aligned}$$

(244)

$$\begin{aligned} \,[\underline{S}]&\longmapsto \varepsilon (\underline{S}) \end{aligned}$$

(245)

Proof

Clearly g is well defined, as if $[\underline{S}] = [\underline{T}]$ then $g([\underline{S}]) = \varepsilon (\underline{S}) = \varepsilon (\underline{T}) = g([\underline{T}])$ by definition. Consider the function

$$\begin{aligned} f: L&\rightarrow E\end{aligned}$$

(246)

$$\begin{aligned} a&\mapsto [{\underline{\delta }^o}(a)] \end{aligned}$$

(247)

We will now show that f is an inverse to g, meaning E and L are isomorphic as sets. First, let $a \in L$. Then, by Lemma 4.13,

$$\begin{aligned} (g \circ f)(a) = g\left( [{\underline{\delta }^o}(a)]\right) = \varepsilon \left( {\underline{\delta }^o}(a)\right) = a. \end{aligned}$$

(248)

Now, let $\underline{S} \in {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$. Then,

$$\begin{aligned} (f \circ g)\left( [\underline{S}]\right) = f\left( \varepsilon (\underline{S})\right) = \left[ {\underline{\delta }^o}\left( \varepsilon (\underline{S})\right) \right] =[\underline{S}], \end{aligned}$$

(249)

where we used Lemma 4.16 in the last step. Thus, as both compositions of f and g are the identity, then $g: E \rightarrow L$ is a set bijection, and $f=g^{-1}$.

We can now use g (and $g^{-1}$) to equip E with the structure of a complete OML canonically: define the order by

$$\begin{aligned} \,[\underline{S}]\le [\underline{T}]:\Leftrightarrow g([\underline{S}])\le g([\underline{T}]). \end{aligned}$$

(250)

Since $g([\underline{S}])\le g([\underline{T}])\Leftrightarrow \varepsilon (\underline{S})\le \varepsilon (\underline{T})$, this is exactly the order we had defined on E before. Since g is a bijection (and an order isomorphism, as we now know), all meets and joins in E with respect to this order exist and correspond to those in L by construction. Moreover, following Eva [34], one defines an orthocomplementation on E by

$$\begin{aligned} ': E&\longrightarrow E\end{aligned}$$

(251)

$$\begin{aligned} \,[\underline{S}]&\longmapsto [\underline{S}]':= g^{-1}(g([\underline{S}])^{\perp }) = [{\underline{\delta }^o}(\varepsilon (\underline{S})^{\perp })]. \end{aligned}$$

(252)

This makes E into a cOML that is isomorphic to L. The maps g and $g^{-1}$ are isomorphisms of cOMLs.

We want to relate the lattice structure on $E={\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}\slash \sim$ more directly to the lattice structure on the bi-Heyting algebra ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ of clopen subsets. The meets in E can be written in terms of the meets in ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$ as follows:

Lemma 4.18

For all families $\left( [\underline{S}_i]\right) _{i \in I}$ of elements of E, where $\underline{S}_i \in {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$,

$$\begin{aligned} \bigwedge _{i \in I} [\underline{S}_i] = \left[ \bigwedge _{i\in I} \underline{S}_i\right] . \end{aligned}$$

(253)

Proof

We have

$$\begin{aligned} \bigwedge _{i\in I}[\underline{S}_i] = g^{-1}(\bigwedge _{i\in I}g([\underline{S}_i])) = [{\underline{\delta }^o}(\bigwedge _{i\in I}\varepsilon (\underline{S}_i))] = [{\underline{\delta }^o}(\varepsilon (\bigwedge _{i\in I}\underline{S}_i)] = [\bigwedge _{i\in I}\underline{S}_i], \end{aligned}$$

(254)

where we applied Lemma 4.16 in the last step.

As in any complete lattice, the joins in E can be written in terms of the meets. For all families $\left( [\underline{S}_i]\right) _{i \in I}$ of elements of E, where $\underline{S}_i \in {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$,

$$\begin{aligned} \bigvee _{i \in I} [\underline{S}_i]:= \bigwedge \{ [\underline{T}] \mid [\underline{S}_i] \le [\underline{T}] \forall i \in I \}. \end{aligned}$$

(255)

Note that in general,

$$\begin{aligned} \bigvee _{i \in I} [\underline{S}_i] \ne \left[ \bigvee _{i \in I} \underline{S}_i\right] . \end{aligned}$$

(256)

Summing up, we have the following generalisation of the Stone representation theorem to complete orthomodular lattices:

Theorem 4.19

For every complete orthomodular lattice L, there exists a map

$$\begin{aligned} {\underline{\delta }^o}: L&\longrightarrow {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}\end{aligned}$$

(257)

$$\begin{aligned} a&\longmapsto {\underline{\delta }^o}(a) \end{aligned}$$

(258)

called daseinisation into the complete bi-Heyting algebra of clopen subobjects of the spectral presheaf $\underline{\varSigma }^{L}$ of L. This map is injective, preserves top and bottom elements, the order and all joins.

The adjoint of ${\underline{\delta }^o}$ is a map

$$\begin{aligned} \varepsilon : {\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}&\longrightarrow L\end{aligned}$$

(259)

$$\begin{aligned} \underline{S}&\longmapsto \bigwedge _{B \in {\mathscr {B}_c(L)}} Bo_B^{-1} (\underline{S}_B) \end{aligned}$$

(260)

taking clopen subobjects to elements of the cOML L. The map $\varepsilon$ is surjective, preserves top and bottom elements, the order and all meets. The quotient $E={\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}\slash \sim$, where $\underline{S}\sim \underline{T}$ if and only if $\varepsilon (\underline{S})=\varepsilon (\underline{T})$, is canonically isomorphic to L as a complete orthomodular lattice.

5 Conclusion

We conclude with a list of some open problems:

• How does the complement in $E={\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}\slash \sim$, given by $[\underline{S}]'=[{\underline{\delta }^o}(\varepsilon (\underline{S})^\perp )]$, relate to the Heyting and co-Heyting negation in ${\text {Sub}}_{{\text {cl}}}\underline{\varSigma }^{L}$?

• Can the representation suggested in Sect. 4 be generalised from complete OMLs to all OMLs?

• Is there a characterisation of those posets that can show up as context categories of orthomodular lattices?

• How can we employ the logic of the presheaf topos $\mathbf {Set}^{\mathscr {B}(L)^{{\text {op}}}}$ to discuss higher-order aspects of the new logic for quantum systems?

• How does the work presented here relate to Quantum Set Theory and OML-valued models?³

In a more general perspective, one can ask which kind of nondistributive or noncommutative structures allow us to associate a spectral presheaf with them and prove duality type or (partial) representation results? A necessary precondition seems to be that the nondistributive or noncommutative structure under consideration has distributive or commutative parts which each have a dual space given by one of the classical dualities. For example, it is conceivable that compact Lie groups are amenable to methods similar to those developed in this article. A context in a compact Lie group would be a Lie-commuting compact subgroup. By Pontryagin duality, we obtain dual spaces that can be fit together into a spectral presheaf, and one can consider the question if this is a complete invariant of the compact Lie group. As a more direct generalisation of the algebras considered in this article, one could use the duality between spatial frames and sober spaces as a starting point. We hope to come back to these problems in the future.