Axisymmetric Modelling of Stretch Blow Moulding Using a Galerkin Mesh-Free Method

Abstract

Mesh-free methods are particularly suitable for material forming simulations, where application of the finite element method can be troublesome due to mesh distortion. This work involves the simulation of stretch blow moulding which is the main manufacturing process used to produce PET drink bottles, a market estimated to grow to $45 billion by the end of 2021. Due to the large deformation involved in the process, conventional finite element simulations can suffer from mesh related issues. This can require a re-meshing procedure and possible solution degradation. In this paper a Lagrangian mesh-free formulation is employed. Initial results confirm the effectiveness of mesh-free methods in simulating the free-blow process.

1 Introduction

Stretch blow moulding is a manufacturing process used to produce plastic bottles for the drink industry; an industry valued at an estimated $45 billion [1]. The process features two stages: an injection stage used to make the preform and a process to stretch and blow this preform into the shape of a bottle, Fig. 1. The preform is heated above its glass transition temperature and inserted into the mould, stretched axially by a stretch rod and radially expanded by high pressure air. In its early stages, preform design was a trial and error based process. In recent years, developments in the field of computational mechanics have allowed for this complex process to be simulated. Traditionally, this process has been simulated using the finite element method (FEM). However, the task of simulating the process is difficult due to the large deformation involved. This is particularly problematic for the FEM where the elements may become too distorted and force the solver to fail; implicating preform design as it is difficult to obtain accurate thickness distributions and contact conditions, degrading the quality of the simulation considerably in highly detailed regions.

In the last twenty years a new class of methods, which look to overcome the difficulties associated with the finite element method, have risen in popularity. These methods are termed mesh-free, or mesh-less methods, and were popularised by the element-free Galerkin method. Mesh-free methods have been applied to large deformation, fragmentation, and fracture problems, where mesh alignment, and distortion can cause issues. For an overview of the mesh-free methods, and applications, see the review comprehensive review by Chen et al. [2].

In this paper, a Galerkin mesh-free method is applied to simulate the free blow process of stretch blow moulding, which features the preform and the stretch-rod, but no mould. The benefits of using a mesh-free method in this work is the ability to simulate the process without encountering mesh related issues, such as mesh distortion during large deformation, and the difficulties associated with finer intricate details, such as logos and ribs. In the FEM these difficulties can lead to the need to adopt a re-meshing procedure, leading to possible solution degradation.

Fig. 1.

Stretch blow moulding

2 Mesh-Free Approximation Methods

In mesh-free methods, the approximation of any scalar field $u(\mathbf {x})$ is constructed based on a set of data points. In Galerkin based mesh-free methods the moving-least squares (MLS) [3] approximation has been applied frequently to construct the test and trial functions. The MLS approximation was used in the element-free Galerkin method [4], which proposes an approximation of the form:

$$\begin{aligned} u^h(x) = \sum _j^m p_j(x) a_j(x) \end{aligned}$$

(1)

where $p_j$ is a complete polynomial basis of a given order, and $a_j$ the coefficients of the approximation, which are obtained from a weighted least squares fit about the point x. The weighted least squares fit is defined by the functional $J(\mathbf {x})$:

$$\begin{aligned} J(x) = \sum _I^n w(x-x_i)[p^T(x_I)a(x) - u_I]^2 \end{aligned}$$

(2)

where $w(x-x_i)$ is the weight function.

Fig. 2.

Mesh-free discretisation

Minimisation of this function yields the moving least squares shape function, defined by:

$$\begin{aligned} \mathbf {\phi }_I = p^TA^{-1}B_I \end{aligned}$$

(3)

where A is a Gram matrix, defined as the product of the polynomial basis functions:

$$\begin{aligned} A(x) = \sum _I^N w(x-x_I)P(x_I)P^T(x_I) \end{aligned}$$

(4)

and $B_I$ is given by:

$$\begin{aligned} B_I(x) = w(x-x_I)p(x_I) \end{aligned}$$

(5)

The weight function $w_I$ defines a set of open covers $\omega _I$, Fig. 2, the union of which should fully contain the domain, i.e. $\varOmega \subseteq \cup _I \omega _I$. Points whose domain of influence contains the approximation point x possess a non zero and positive weight $w(x-x_I)>0$. Hence, contributing to the approximation at that point. In this work a cubic B-spline weight function, with a circular domain of influence (r) is used Eq. 6. The size of the domain of influence is obtained by enforcing a certain number of nodes lie within the support of a point, which is necessary for the Gram matrix A to invertible.

$$\begin{aligned} w(r) = {\left\{ \begin{array}{ll} \frac{2}{3} - 4r^2 + 4r^3, &{} \text {if } r \le \frac{1}{2} \\ \frac{4}{3} - 4r + 4r^2 - \frac{4}{3}r^3, &{} \text {if } \frac{1}{2 }< r \le 1 \\ 0 &{} \text {if } r > 1 \end{array}\right. } \end{aligned}$$

(6)

Finally, the MLS approximation can then be written in terms of the shape functions $\phi _I$ and the nodal values of the field $u_I$:

$$\begin{aligned} u^h(x) = \sum _I^N \phi _I(x)u_I \end{aligned}$$

(7)

3 Lagrangian Mesh-Free Formulation

Consider the equilibrium of a body initially occupying the region $\mathcal {B}_0$, with boundary $\varGamma$. It is assumed that the boundary can be divided into a displacement boundary, $\varGamma _u$, where boundary displacements are prescribed, and a traction boundary $\varGamma _t$, where prescribed loading is applied. Subject to external loading $\bar{T}$, and prescribed displacements $\bar{u}$ the body $\mathcal {B}_0$ will undergo a motion $\varphi (X,t)$, such that at any time t the coordinates of the body will be given by $\varOmega _t = \varphi (\mathcal {B}_0,t)$. Denote $\varOmega ^X$ the set of material coordinates X which define the body at $t=0$, i.e. $\varOmega ^X = \varphi (\mathcal {B}_0,0)$, along with the material boundaries $\varGamma ^X_t$ and $\varGamma ^X_u$. In each time instance $t \in [0,T],$ the motion $\varphi (X,t)$ should satisfy the following boundary value problem:

$$\begin{aligned} P_{iJ,J} = \rho _0 \ddot{\varphi }_i, ~X \in \mathcal {B}_0, ~t \in [0,T] \end{aligned}$$

(8)

subject to the boundary conditions:

$$\begin{aligned} P_{iJ} N_J = T_i ~\text {for all } X \in \varGamma _t^X \end{aligned}$$

(9)

$$\begin{aligned} \varphi _i = \bar{\varphi }_i ~\text {for all } X \in \varGamma _u^X \end{aligned}$$

(10)

Multiplying through (8) by a set of virtual displacements $\delta u$ yields:

$$\begin{aligned} (P_{iJ,J} - \rho \ddot{\varphi _i}) \cdot \delta u_i= 0 \end{aligned}$$

(11)

Integrating Eq. 11 and applying divergence theorem yields the well known principle of virtual work, given in terms of the material coordinates:

$$\begin{aligned} \int _{\varOmega ^X}{[\delta u_i \rho _0 \ddot{u}_i + \delta F_{ij} P_{ij}] d \varOmega } - \int _{\varGamma _t^X}{\delta u_i T_i d \varGamma } = 0 \end{aligned}$$

(12)

Substituting the MLS approximation (7) yields the semi-discrete equations:

$$\begin{aligned} m_I \ddot{u}_I = f_I^{ext} - f_I^{int} \end{aligned}$$

(13)

where $m_I$ is the mass of node I. The internal and external force vectors are given by

$$\begin{aligned} f_I^{ext} = \int _{\varGamma _t^X}{\phi _I \bar{T} d \varGamma }; \end{aligned}$$

(14)

$$\begin{aligned} f_I^{int} = \int _{\varOmega ^X}{B_I^T \hat{P} d \varOmega } \end{aligned}$$

(15)

where $\hat{P}$ is the Voigt form of the first Piola-Kirchoff stress tensor, and $B_I$ the strain-displacement matrix. These equations are integrated in time using an explicit central difference time stepping scheme [5].

3.1 Boundary Conditions

The MLS shape functions do not possess the Kronecker delta criteria ($\phi _I(X_J) \ne \delta _{IJ}$), which complicates boundary condition imposition. A number of different techniques have been proposed, including modification of the weak form [4], and transformation methods [6]. In explicit mesh-free methods, the optimum technique to apply boundary conditions is still an open-topic. However, in this work the method proposed by Joldes [7] is used. Where the boundary conditions are enforced using a predictor-corrector type approach, defined by:

$$\begin{aligned} u = u^{pre} + u^{corr} \end{aligned}$$

(16)

where $u^{corr}$ is obtained from the solution of a system of equations about the $(n + 1)th$ time step, which results in the following update formula:

$$\begin{aligned} u^{corr} = P(\bar{u} - \varPhi u) \end{aligned}$$

(17)

where $\varPhi$ is a matrix of shape function values at boundary points, and P a matrix that converts displacement corrections into the traction force that would be required to enforce the kinematic constraint.

3.2 Domain Integration

Domain integration is required to integrate the weak form. Conventionally, as in the finite element method, this is performed using Gauss integration. However, due to the non-polynomial characteristic of mesh-free shape functions, and misalignment of the supports with the integration point high errors can be attributed to this technique [8]. In lieu of this, nodal integration schemes have been proposed, however they have been shown to suffer from rank instabilities. In order to remove these instabilities Chen et al. [9] proposed a smoothed integration scheme. This integration scheme is constructed to satisfy the divergence free condition necessary for first order convergence:

$$\begin{aligned} \sum _I \nabla \phi _I = 0 \end{aligned}$$

(18)

In order to satisfy the divergence free condition the deformation gradient is smoothed around a nodal representative domain, constructed from a Delaunay tessellation. The smoothing is given by:

$$\begin{aligned} F_{iJ}(x_L) = \frac{1}{A_L} \int _{\varGamma _L}{\phi _{I}u_{Ii}n_J d \varGamma } + \delta _{iJ} \end{aligned}$$

(19)

4 Simulation

4.1 Material Model

Motivated by the rubber-like behaviour of PET above its glass transition temperature $T_g$, a hyperelastic material model was fitted to biaxial data. The biaxial data was obtained using the Queen’s biaxial stretcher [10] at a strain rate of $8s^{-1}$, and a temperature of $105\,^\circ$C (Fig. 3).

Fig. 3.

Material model

The Yeoh model was chosen based on this fit, the strain energy density function for this model is given by [11]

$$\begin{aligned} \psi (C_{10},C_{20},C_{30},\kappa ) = C_{10}(I_1^* - 3) + \\ C_{20}(I_1^* - 3)^2 + C_{30}(I_1^* - 3)^3 + \frac{\kappa }{2}(J - 1)^2 \end{aligned}$$

(20)

where $(C_{10},C_{20},C_{30},\kappa )$ are the material parameters in the Yeoh model, J the determinant of the deformation gradient F, and $I_1^*$ the first invariant of the deviatoric Cauchy deformation tensor C, defined by:

$$\begin{aligned} I_1^* = \text {trace}(C^*) \end{aligned}$$

(21)

where

$$\begin{aligned} C^* = \frac{1}{J^{2/3}}F^TF \end{aligned}$$

(22)

4.2 Loading

The material parameters, and the loading on the preform are summarised in Fig. 4. Both the stretch rod speed, and the pressure are ramped up over a short time period. The pressure is applied in two stages, an initial blow at a lower pressure (0.6 MPa), followed by a high pressure blow at 1.2 MPa, which is consistent with industrial practice.

Fig. 4.

Model inputs

Fig. 5.

Preform geometry

Fig. 6.

Deformation of the preform at t = 0.08, t = 0.12, and t = 0.20 s

Fig. 7.

Thickness distribution

4.3 Geometry

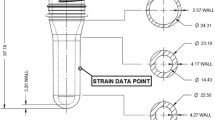
In this simulation a 31.7 g preform was used, the geometry of which is shown in Fig. 5(a). From this geometry, a simplified mesh-free axisymmetric model featuring 409 nodes was constructed, Fig. 5(b).

5 Results

The evolution of the bottle is shown in Fig. 6. As it can be seen at first the deformation is dominated by the effects of the stretch rod until a critical thickness is reached, at this point the bottle expands rapidly in the radial direction. The final shape of the bottle is consistent with those published in literature [12] In Fig. 7 the thickness distribution is plotted against the axial coordinate. The bottle is thickest at the bottom and the top, where the least stretching happens, it then reaches a minimum across the middle section of the bottle.

6 Conclusion

In this work a mesh-free Galerkin method has been applied to simulate the free blow process of stretch blow moulding. Results have highlighted the ability of mesh-free methods to deal with large deformation, without encountering mesh related issues which can cause difficulties for finite element based simulations.

7 Future Work

To progress this work further the mould has to be taken into account, and the direct pressure application replaced with a representative model for the air flow within the cavity [13].