Private Giving in Higher Education

Abstract

Why private giving in higher education in the USA by alumni and top philanthropists are significant but almost non-existent in a country like India? Introducing a public good (higher education) in Krugman’s (Krugman, J Int Econ, 9:469–479, 1979) model, we examine this dichotomy. In a country with a lower population base, the unit cost of production of the private good tends to be higher, and hence the price of giving lower, making public good much more attractive. The resulting per capita welfare in the two countries will likely differ. If national border control were removed, migration should equate per capita welfare with population in the two regions split even when private good technology exhibits economies of scale, unlike Krugman’s agglomeration hypothesis. Further, it is possible that per capita welfare turns out to be higher with the entire population situated in the more costly region with a higher price of the private good but higher overall provision of the public good. In Krugman’s world (without the public good), this is never possible.

1 Introduction

In India, failure of private giving to higher education is the norm. In particular, education at all levels is almost all publicly funded. The supply of good quality educational institutions is thus severely limited when viewed in relation to the huge demands by the country’s large population base at the young age group. Provision of education on profit motives is unlikely to be supported by the political class and the general public. Even with recent deregulation entry of non-profit private universities are very few and, to our knowledge, there is no documentation of noticeable initiatives by philanthropists. The end result is a sorry tale of pent-up demands.

The absence of philanthropists in Indian education sector provides a striking contrast when compared with the USA. Many of the top quality universities in the USA are private. While a large part of the costs of private education is borne by student fees, a substantial part of funding of US universities come in the form of big endowment donations by rich philanthropists and alumni.

A recent online report (dated June 28, 2017), “Giving USA 2017: Implications for Higher Education” has the following¹:

Giving USA estimates that giving to education organizations (of which giving to higher education accounts for 70% of the total) increased 3.6% in 2016 to $59.77 billion. The Council for Aid to Education’s Voluntary Support of Education (VSE) survey shows that individual giving (alumni and non-alumni) to education declined by 7.4%, while contributions from corporations and foundations grew by 14.8% and 7.3%, respectively. That said, giving from individuals still comprises the largest source of funds given.

Over the past two years, Giving USA estimates that giving to education grew 12.5%, which was surpassed only by the growth in giving to international affairs (20.7%) and environment/ animals (13.5%).

According to the VSE study, alumni giving accounted for 24.2% of total giving to higher education institutions in 2016, a smaller proportion than the previous year. However, this decline comes on the heels of extraordinary growth in individual giving in 2015 (10.2% from alumni and 23.1% for non-alumni).

Giving to education continues to be the most popular philanthropic cause for high net worth donors, according to the Wealth-X and Arton 2016 report, Changing Philanthropy: Trend Shifts in Ultra Wealthy Giving. This report notes that 47% of donations from high net worth individuals reportedly went to education, with 22% supporting higher education specifically. These results continue to bode well for higher education institutions.

University World News (http://www.universityworldnews.com/article.php?story=20110204222722977) runs the headline (dated February 06, 2011), “INDIA: Charity not beginning at home for universities” with excerpts such as the following:

It is interesting that many of the Ivy League colleges in the US have received donations from their Indian alumni. But the same alumni who have made it big in life because of an Indian education have failed to give back to their home institutions, said Prabhat Lal, professor of international relations at Jawaharlal Nehru University in New Delhi.

Philanthropic donations to Indian institutions are not completely absent but they are few and far between and pale in significance beside the huge donations, often by the same donors, made to western universities.

In this paper, we will view education as a consumption good but to be provided only voluntarily. The greater the collective contribution to education, the better the quality of institutions where young people can gather knowledge that serves them not only for future careers but also in enrichment of life experience. We will abstract from the career angle and focus on the utility enhancing part of consumption of education as a public good. Side by side education, there is also a private good that people buy to maximize their utility. The choice a typical consumer thus faces is how much to spend on the private good and how much to contribute to education as the public good. In an economy with relatively fewer population base, one might expect the supply of the voluntarily provided public good not to be that high. But it is also known that free riding in public good contribution generally increases with the population size (Andreoni 1988). Comparing a large country such as India, in terms of population size, and a “small” country such as the USA, how should voluntary provision of education compare is a theoretically interesting question. We provide an explanation of the different norms of giving in higher education in the two countries—greater generosity in the USA and almost negligible private initiatives in India.

Our main idea can be explained by an extension of Krugman (1979). Krugman had argued in an economy with only private goods, consumers with preference for product variety (as in Dixit and Stiglitz 1977), economies of scale in production and monopolistic competition, how different regions have a tendency to merge into a single conglomerate region. A merged region will sustain more private goods, thus serving consumers’ preference for greater product varieties. We consider an economy with one private good and one public good. Then we flip Krugman’s formulation to suggest that a larger region will bring down the unit cost of production of the private good due to supplies of many cheaper inputs.² This makes private good in the consumption basket more attractive compared to a public good (i.e. education). In contrast, high labour cost due to low population base makes private good more costly and public good relatively more attractive in the USA. In India, people are thus happier consuming the cheaper private good while the USA compensates by having their children educated in high-quality institutions. This, in a nutshell, is the key message of this paper.

In terms of formal results, we show the following. First, if national border control were not present so that people could move freely between countries, and production technologies in the two countries were uniform, there need not be concentration of population in a single country, i.e. agglomeration might not happen, as suggested by Krugman (1979). Instead, people might live separately in the two countries with uniform per capita welfare as the equilibrating force, as a special case of Proposition 2. As part of this process, the smaller country (USA in our example) may produce more of the public good. If one were to force agglomeration, per capita welfare would come down even with private good becoming cheaper because voluntary provision of the public good will suffer. Endogenous segregation of regions despite increasing returns to scale in the private good’s production and necessarily no other exogenous differences is a new and surprising result.

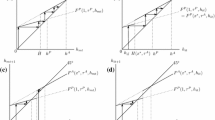
In fact, we show a range of possibilities: increases in population size may increase the equilibrium level of public good, lower it, or sometimes produce a non-monotonic effect by first increasing the level and then lowering it, while the cost of the private good always declines. As a result in some situations per capita welfare monotonically increases with population size, while in others per capita welfare exhibits an inverted-U pattern initially rising and then falling. Welfare may even initially increase, then decrease and eventually may rise again (Proposition 1, Figs. 1 and 2 and Table 1). The broad implication is that with free mobility of labour across countries (that are not integrated through trade, e.g. due to prohibitive trade/transportation costs), one may see either agglomeration or segmentation. Encompassing the alternative possibilities of agglomeration and segregation in one model enriches our understanding of migration similar to Tiebout models.

We also add couple of insights that we hope will improve our understanding of agglomeration. Specifically, an important issue in Krugman’s (1979) discussion involved how the initial distribution of population among different regions might influence which region attracts the population. For example, as long as labour productivity is the same everywhere, regions with the same population size would have no difference in welfare. However, if there is any difference in productivity, migration may lead to the wrong outcome. Consider, for example, a world with only two regions that are identical everywhere except that in one region private goods are more costly to produce. Then it is clearly desirable that all labour should move to the less costly region. But if the higher-cost region starts with a large population base, per capita welfare will be higher in that region drawing population towards it. Thus, in a model with only a private good, unless there are other exogenous differences, initially uneven distribution of population is the only reason for inefficient agglomeration (Proposition 3). However, in our model with both private good and a public good, even with identical distribution of initial population the more costly country might offer a better welfare prospect to cause migration to move in its direction (Proposition 4).³ This paradoxical result is easier to understand if one considers the improved appeal of the public good as the private good becomes more expensive. The utility loss from higher price of the private good could be more than made up for from higher quality (or quantity) of the public good.

The migration flow towards the inefficient region need not be a pathological outcome from wrong initial population distribution (including identical distribution). In fact, if one were to move the entire population to the less costly (in terms of private good’s production) region, per capita welfare could go down. In this sense, inefficient agglomeration could be welfare-dominant rather than welfare-immiserizing.

While we develop the analysis based on Krugman (1979), two papers have been instrumental in thinking about the main ideas explored in this paper. Pecorino’s (2009a) is the first analysis of public good in a general equilibrium setting in a variant of Krugman’s monopolistic competition model, studying specific conditions under which more population will lead to reduced voluntary provision.⁴ Pecorino, however, does not study Krugman’s original question of agglomeration.

Equally relevant is Epple and Romano (2003). The authors study voluntary provision of a public good along with dual provision (i.e. voluntary and tax-financed provision). For special type of public goods supported only by a minority of voters, it is shown that only voluntary provision can arise in equilibrium (Corollary to their Proposition 5). For voluntary provision, the examples cited are private funding of US medical research, private and corporate contributions to art museums, and historic preservation societies. Funding of higher education, strictly speaking, is not entirely by voluntary contributions because students are also charged tuition fees. However, to isolate the incentives for voluntary giving we view higher education as a consumable pure public good financed by large endowment gifts by corporate donors, philanthropists and alumni. Certainly major initiatives by rich private universities in the USA in hiring top quality faculties, setting up science and medical laboratories, starting a new department, etc., are made possible by big fund drives where universities are known to tap into potential big donors who are likely to support higher education. We take the view that these initiatives improve both the quality of education and its level, benefitting all citizens as stakeholders of higher education and learning.

The rest of the paper is organized as follows. In Sect. 2, we present the basic model. The main analysis of the public good economy is contained in Sect. 2.1, with Conclusion in Sect. 3. An Appendix contains a proof.

2 Preliminaries

There are two types of good in the economy—a pure public good, and a private good. The public good is produced using labour with a one-to-one technology that produces one unit of output using one unit of labour. The private good is produced using n number of different intermediate inputs. These inputs are combined using a CES aggregator to get the final output. We assume that final goods are produced in a perfectly competitive market structure while the market structure for the intermediate inputs is monopolistically competitive.⁵

There are L individuals (or consumers) who each inelastically supplies one unit of labour, earns a competitive wage w and spends it on the private good and contribution towards the public good. Denoting $g_j$ to be the dollar contribution towards the public good by consumer j, $G=\sum _{j=1}^L g_j$ is the total voluntary contribution by L consumers. G / w is the total amount of public good produced, with one unit of labour translating into one unit of public good.

The consumers have identical preferences summarized by a very general form of CES utility function (see Chap. 1 of Varian 1992) allowing for a broad range of substitutability between the public good and the private good. Representative consumer j solves:

$$\begin{aligned}&\max _{x_{j}, G}\;\;U_{j} = \big [\eta x_j^r + (1-\eta )G^{r}\big ]^\frac{1}{r},\quad \text{ where } \;\; 0\ne r\le 1, \;\;\eta \in (0,1), \end{aligned}$$

(1)

$$\begin{aligned}&~\qquad \text{ subject } \text{ to }\qquad p_xx_j + G = w_j+G_{-j}, \quad \text{ for } \text{ all }\;\; j=1,...,L. \end{aligned}$$

(2)

Consumption of the private good by person j is given by $x_j$ and its (per unit) price is denoted by $p_x$. The price of the public good is normalized at unity. We define the contribution by all people except j as $G_{-j}\equiv \sum _{k=1, k\ne j}^L g_{k}$ where $g_j$ is the contribution by person j only. The parameter $\eta$ in utility function (1) measures the preference bias for the private good.

We define the elasticity of substitution between the private good and the public good as $\epsilon =\frac{1}{1-r}\ge 0$. Setting the Lagrangian for the problem of maximizing (1) subject to (2), we derive the following first-order conditions:

$$\begin{aligned}&\frac{1}{r} \big [\eta x_j^r + (1-\eta )G^{r}\big ]^{\frac{1}{r} -1 }\; \eta \;r \;x_j^{r-1} =\lambda _j \;p_x, \end{aligned}$$

(3)

$$\begin{aligned}&\frac{1}{r} \big [\eta x_j^r + (1-\eta )G^{r}\big ]^{\frac{1}{r} -1 }\; \eta \;r \;G^{r-1} =\lambda _j. \end{aligned}$$

(4)

Equations (3) and (4) equalize the marginal benefit and cost of consuming private and public goods, respectively. The marginal utility of income of person j is denoted by the Lagrangian multiplier $\lambda _j>0$. Using Eqs. (3) and (4), we can write the demand for private good by agent j as

$$ x_j=G\left( \frac{\eta }{1-\eta } \frac{1}{p_x} \right) ^{\frac{1}{1-r}}. $$

Summing over all individuals, the aggregate demand for the private good is given by

$$\begin{aligned} X=\sum _{j=1}^L x_j = L\;G\left( \frac{\eta }{1-\eta } \frac{1}{p_x} \right) ^{\frac{1}{1-r}}. \end{aligned}$$

(5)

Using Eq. (2) and the definition of $G_{-j}$, the aggregate budget constraint for the entire economy can be written as $p_x\sum _{j=1}^L x_j + G =\sum _{j=1}^L w_j$. Since all individuals are alike, they earn the same wage, w. Therefore, using this aggregate budget equation and Eq. (5), we solve for the aggregate public good as,

$$\begin{aligned} G=\frac{w}{\left( \frac{\eta }{1-\eta } \right) ^{\frac{1}{1-r}} p_x^{-\frac{r}{1-r}}+\frac{1}{L}}. \end{aligned}$$

(6)

As is expected, the aggregate amount of public good is strictly increasing in the income/wealth of the individual (w) and in the size of the contributing group (L). The price of the private good affects G in the standard way depending upon the elasticity of substitution parameter r. For the Cobb–Douglas case with $r=0$, the public good is invariant to any change in the price of the private good. This completes the description of the demand side of the problem.

Turning to the supply side, we assume that the public good is produced using a one-to-one production technology as given by

$$\begin{aligned} L_G=G, \end{aligned}$$

(7)

where $L_G$ is the amount of labour used in producing the public good. Since the public good is produced competitively, and we normalize its price at unity, the wage rate is determined as

$$\begin{aligned} w=1. \end{aligned}$$

(8)

This implies that everybody earns an income equalized to unity and aggregate income is equal to L in the economy.

The private good is produced using n intermediate inputs as per the following CES production technology:

$$\begin{aligned} X=\left( \sum _{i=1}^n y_i^\theta \right) ^\frac{1}{\theta }, \;\;\text{ where }\; \theta \in (0,1). \end{aligned}$$

(9)

Define $\sigma =\frac{1}{1-\theta }$ to denote the elasticity of substitution among intermediate inputs in the final goods production function. Each intermediate input, $y_i$, is produced using labour and with the help of a linear production technology as given by

$$ l_i=\alpha + \beta y_i, \;\; i=1,...,n, $$

where $\alpha$ is the fixed labour requirement and $\beta$ is the marginal labour requirement. Therefore, it takes $l_i$ units of labour to produce $y_i$ units of the ith intermediate input.

The market structure for the final goods are assumed to be perfectly competitive. A final good producer maximizes profit by solving the following problem:

$$ \max _{\{y_i\}}\; \pi _X=\;p_x X - \sum _{i}^n p_{y_i} y_i \;\;\;\text{ subject } \text{ to } \text{ Eq. } \text{(9) }, $$

where $p_{y_i}$ denotes the price per unit of the ith intermediate input. This exercise generates the following demand for the ith intermediate input,

$$\begin{aligned} y_i=\frac{p_{y_i}^{-\frac{1}{1-\theta }} \;(p_x X)}{\sum _{i=1}^n p_{y_i}^{-\frac{\theta }{1-\theta }} }, \quad i=1,...,n. \end{aligned}$$

(10)

Using Eqs. (9) and  (10), we get the following expression of the price of the final private good in terms of price of the intermediate inputs,

$$\begin{aligned} p_x=\left( \sum _{i=1}^n p_{y_i}^{-\frac{\theta }{1-\theta }}\right) ^{-\frac{1-\theta }{\theta }}. \end{aligned}$$

(11)

Each intermediate input producer acts like a monopolist in its own market segment. The profit maximization problem of the ith intermediate input producer can be written as

$$ \max _{\{p_{y_i}\}}\; \pi _{y_i}=\; p_{y_i} y_i - w(\alpha + \beta y_i) \;\;\;\text{ subject } \text{ to } \text{ Eq. } \text{(10) }. $$

We assume the presence of large number of intermediate input producers so that each individual producer ignores the effect of others’ price on its own demand. Specifically, the term, $\sum _{i=1}^n p_{y_i}^{-\frac{\theta }{1-\theta }}$, in Eq. (10) is treated as a fixed value in the above profit maximization. Under this assumption and using Eq. (8), the profit maximizing price of ith intermediate input takes the following form:

$$\begin{aligned} p_{y_i}=\frac{\beta }{\theta }, \qquad \text{ for } \text{ all }\;\; i=1,...,n. \end{aligned}$$

(12)

Therefore, intermediate input prices become a constant mark-up over the marginal cost of production and this does not vary with i, given the identical production technology assumption. Henceforth, we get rid of the subscript i.

Free entry into the intermediate input production market implies zero profit. Setting $\pi _{y}=0$ and using Eq. (12), the equilibrium supply of ith intermediate input is given as

$$\begin{aligned} y_i=\frac{\alpha \theta }{(1-\theta )\beta }, \qquad \text{ for } \text{ all }\;\; i=1,...,n. \end{aligned}$$

(13)

Let us denote the aggregate demand for labour in production of intermediate inputs as $L_y=\sum _{i=1}^n l_i$. Then, using Eqs. (12) and (13), we get the following expressions,

$$\begin{aligned} L_y= & {} \frac{n\alpha }{1-\theta }, \end{aligned}$$

(14)

$$\begin{aligned} X= & {} n^{\frac{1}{\theta }}\;\frac{\alpha \theta }{(1-\theta )\beta },\end{aligned}$$

(15)

$$\begin{aligned} p_x= & {} n^{-\frac{1-\theta }{\theta }}\;\frac{\beta }{\theta }. \end{aligned}$$

(16)

Finally, equilibrium in the labour market (i.e. $L_G+L_y=L$) gives us the following solution for the number of intermediate inputs:

$$\begin{aligned} n=\frac{(1-\theta )(L-G)}{\alpha }. \end{aligned}$$

(17)

2.1 Solution

Using Eqs. (6), (8), (16) and (17), we get the following equilibrium condition involving G⁶:

$$\begin{aligned} LG= (L-G)^{\frac{\theta -r}{\theta (1-r)}}\Omega , \end{aligned}$$

(18)

where the expression $\Omega$ is a positive constant with $\Omega \equiv \left( \frac{\alpha }{1-\theta }\right) ^{\frac{r(1-\theta )}{\theta (1-r)}} \left( \frac{\beta }{\theta }\right) ^\frac{r}{1-r} \left( \frac{1-\eta }{\eta }\right) ^{\frac{1}{1-r}}$. We assume $1>\theta \ge r$ (i.e. $\sigma \ge \epsilon$) to guarantee the existence of a unique solution of G from Eq. (18). This assumption implies that intermediate inputs in the production function are more substitutable among each other than finals goods are in the utility function. From now onwards, we will interchangeably use the notations $\sigma$ and $\epsilon$ in place of $\theta$ and r, respectively.

Define the unique solution of G from Eq. (18) as $G^*(L)$. It can be shown that,

$$\begin{aligned} \frac{dG^*(L)}{dL}>(=;<) \;0 \quad \text{ iff }\quad G^*(L)>(=;<)\; \big (\frac{\epsilon -1}{\sigma -1}\big )L. \end{aligned}$$

(19)

When $\epsilon \le 1$, public good is increasing in population size. For $\epsilon >1$, $G^*(L)$ curve has a global maximum at $L=\hat{L}$. For all $L< (>)\hat{L}$, $G^*$ increases (decreases) with L. We are now interested to see the welfare properties of this model economy as a function of its population size and other cost parameters related to the production of the private good.

Table 1 Per capita welfare with $\beta =5$ and $\beta =10$ ($\sigma = 5, \; \epsilon = 3, \; \eta = 2/5, \;\alpha = 1$)

3 Welfare Effects

When the equilibrium level of final private good and the level of public good both increase with population size, welfare must increase. The equilibrium number of input varieties (denoted by n) always increase with population size irrespective of the value of $\epsilon$.⁷ When $\epsilon \le 1$, $G^*$ is strictly increasing in L, and hence, welfare must go up with population size in this case. For $\epsilon >1$, $G^*$ will decrease for all $L>\hat{L}$, so there is a possibility that welfare might decrease in L for some ranges of L. To show this formally, using Eqs. (5), (16), (17), (18), we rewrite the utility (or welfare) of a representative agent in (1) as follows:

$$\begin{aligned} U_j= \left( \frac{L-G^*}{LG^*}+1 \right) ^{\frac{1}{r}}G^*\;(1-\eta )^{\frac{1}{r}}. \end{aligned}$$

(20)

The expression, $\frac{L-G^*}{LG^*}$, in the right-hand side of the above expression always rises with L. To see this, just rewrite Eq. (18) as $\frac{L-G}{LG}= \frac{1}{\Omega }\; (L-G)^{\frac{r(1-\theta )}{\theta (1-r)}};$ and note that $(L-G)$ is an increasing function of L (see footnote 7). Thus as L increases, welfare goes up due to the (certain) reduction in price of the final private good, $p_x$. The possibility that welfare goes down with an increase in L arises only when $G^*$ decreases with L. We have seen that for $\epsilon >1$, $G^*$ is non-monotonic in L. In particular, $G^*$ is decreasing for all $L>\hat{L}$. Hence, welfare may fall with population size at some point in the range exceeding $\hat{L}$.

Given the complicated expression of (20) (as we need to solve for $G^*$), a neat characterization of per capita welfare with respect to population size is difficult. So for some of the results to follow, we will rely on numerical simulations. By fixing specific values for $(\alpha , \beta , \eta , \sigma , \epsilon )$, the values of U, equilibrium $p_x$ and equilibrium G for various values of L are reported in Table 1. We take two independent regions—region 1 and region 2. They share the same parameter values except for $\beta$. Region 1 has a lower $\beta$ value than region 2. Thus, the price of each intermediate input in region 2 is more than in region 1. This implies that, private good is more costly to produce in region 2 given the same number of intermediate inputs. Nevertheless, as we will see below, region 2 may provide better per capita welfare than region 1. This is because of the larger level of consumption of the public good in region 2.

Fig. 1

Inverted-U per capita welfare (Table 1: region 1)

We report the possibility of an inverted-U welfare. That is, welfare may initially go up and then down as population size increases.

As Table 1 shows, as population size increases, per capita welfare increases initially (in both regions), reaches maximum at $L=58$ in region 1 (at $L=144$ in region 2) and then starts falling: an inverted-U per capita welfare shown for region 1 in Fig. 1. However, welfare curve may even take a U-turn for large values of L as shown in Fig. 2 where L varies in the range $[2*10^5, 6*10^5]$ (and $\beta =5$).⁸ The reason is, for L becoming very large, G approaches zero while n approaches infinity (see Eq. (20) and note that $\frac{L-G^*}{LG^*}$ is proportional to n). Thus, the property that G is bounded below by zero makes it possible that per capita welfare might grow unbounded in L. We can summarize the above discussion as follows:

Proposition 1

(Per capita welfare)

(a):

Per capita welfare is increasing in L if $\epsilon \le 1$.

(b):

If $\epsilon > 1$, per capita welfare is increasing in L for $L\le \hat{L}$ but it may fall at some point in the range of $L>\hat{L}$, thus giving rise to an inverted-U pattern.

(c):

If $\epsilon > 1$, per capita welfare may exhibit U-turn after the inverted-U pattern as can be seen combining Figs. 1 and 2.

We also show the relationship between region’s population size and price of the private good and the level of public good in Figs. 3 and 4. Note that, the costly region (region 2) has higher prices (Fig. 4) but also provides higher amounts of the public good (Fig. 3). This result provides an explanation of why in the USA (respectively India) prices are higher (lower), and at the same time, voluntary giving to higher education is higher (lower). (Also, private good prices in both regions converge to zero as L become very large.)

Fig. 2

U-shape per capita welfare for L in the range $\in [2*10^5, 6*10^5]$ (region 1)

Fig. 3

Costly region with higher provision

Fig. 4

(Relative) price of the private good higher in region 2

3.1 Agglomeration or Segregation

Non-monotonic welfare (Proposition 1(b) and (c)) gives rise to either possibility—agglomeration or segregation of region—depending on total population size. To analyse this issue, we focus only on the inverted-U portion of the welfare curve.⁹ Let us assume that there are two identical regions each with $L=30$, the benefits from intermediate input varieties these regions produce are exclusive to the regions, there is no trade, and workers are immobile. From column 2 of Table 1 (region-1) individuals in these regions will enjoy a per capita welfare of 11.304. Now if we allow free mobility of workers across regions, do we see agglomeration? In this case, the answer is “yes” as the combined region will have a population size of 60, each enjoying welfare 13.321.

We next ask whether one big region can segregate into several smaller regions. Our answer, once again, is “yes”. An example is given following the next proposition. But the intuition is simple: a combined region may be on a downward-sloping part of the inverted-U welfare curve, which means there is always some split of the population size L into two regions, say, such that the welfare is higher in both those regions separately than the combined region. This creates an incentive for the region to break up. However, one has to be careful about how the segregation is going to play out. Segregation has to be welfare improving and migration-proof, the latter being a stability requirement. The following proposition provides a further guidance to the nature of segregation¹⁰:

Proposition 2

(Uniform segmentation) Starting from a single region of size L and assuming an inverted-U welfare curve (i.e. Proposition 1 part (b) applies), suppose there is a break up of the region into n smaller regions with population size in the $i^{th}$ region $L_i$, $i=1,...,M$ and $\sum _{i=1}^M L_i=L$. Then,

(a):

It must be the case that $L_i=L_j$ for all $i\ne j \,(=1,...,M)$; i.e. breakup must generate identical regions.

(b):

The equilibrium number of breakups, M, must satisfy: $U(\frac{L}{M})\ge \max \{U(\frac{L}{2M}), U(\frac{2L}{M})\}$.

To illustrate part (b) of Proposition 2, let us take a specific example from Table 1. Suppose initial population size of a region is $L=1000$. Breaking up into two equal-sized regions is perfectly possible in this case as $U(500)=6.738 > U(1000)=5.021$. Each region of size 500 will have a further incentive to break up since $U(250)=9.003 > U(500)$. We can now apply the result of part (b) of Proposition 2 to determine equilibrium n: it must be of the form $M=2^k$ for any positive integer k. For $k=3$, we have $M=8$ and can check from Table 1 that $U(1000/4=250)<U(1000/8=125)<\min \{U(\lfloor 1000/16 \rfloor = 62), U(\lfloor 1000/16\rfloor +1=63)\}$, so $M=8$ cannot be equilibrium (symbol $\lfloor z\rfloor$ denotes the largest integer contained in z). Next, for $M=16$ ($k=4$), we can check that inequality in part (b) is satisfied, with eight regions of size 62 and the remaining eight of size 63; this breakup is migration-proof not only against individual deviations but against coalitional deviations as in Conley and Konishi (2002).

Remark 1

In the proof of Proposition 2 in the Appendix, we check migration-proofness by simply comparing per capita welfare in different regions. If welfare differs between any two regions for any given population division, we say that there should be an incentive for some people to move from the low-welfare region to the high-welfare region. For our stability notion (or migration-proofness), the incentive refers to an individual member as opposed to any coalition of members (as in Conley and Konishi 2002). Since the argument we use for equality of regions is in the form of a “necessary condition”, looking at individual incentives rather than for arbitrary coalitions serve our purpose.

Remark 2

Our definition of migration-proof equilibrium has the notion stability built in it. The issue of stability is sometimes viewed separately from the equilibrium notion in partial equilibrium models with local public goods. For example, see Hindriks and Myles (2013, ch. 7).

3.2 Inefficient Agglomeration

With intermediate input varieties and only a private good, i.e. in a Krugman’s world, agglomeration is a natural outcome: one big region allows more firms to enter (due to scale economies), producing a greater variety of intermediate inputs and catering to a greater number of consumers, thus improving per capita welfare.¹¹ But which region ends up with the population depends on the initial distribution of population. As long as labour productivity is the same everywhere, regions with the same population size would have no difference in welfare among them. However, if there are regional differences in productivity, which region attracts the population will make a difference to people’s welfare—the process of migration may lead to the wrong outcome. Consider, for example, a world with only two regions that are identical everywhere except for the fact that the variable costs of production (of intermediate inputs) are higher in one region while fixed costs are the same. Then it is clearly desirable that all labour should move to the other (efficient) region. But if the higher-cost/inferior region starts with a large enough share of the population, per capita welfare could be higher in that region prompting migration to proceed towards the inefficient region. But if the two regions have the same initial population, the inefficient region will have a worse initial per capita welfare, prompting migration to move towards the efficient region. These observations that follow directly from Krugman (1979) are summarized below:

Proposition 3

(Agglomeration in Krugman world) In Krugman’s world, agglomeration is the logical outcome if one allows for free mobility of labour. Further, the following observations can be made:

(a):

Starting from two identical regions in terms of population size, tastes and technologies so that initial per capita welfare is the same, agglomeration is always welfare-neutral, i.e. to which region the population moves will not matter.

(b):

Starting from two regions with identical population and tastes but one being the higher-cost region, migration will always move towards the more efficient region: agglomeration is welfare-dominant.

(c):

Starting from two regions with identical tastes, if a higher-cost region (due to higher $\beta$ or $\alpha$ or both) has much higher population initially, then the migration may move towards this inferior region: agglomeration is inefficient and welfare-immiserizing.

One notable contrast of our model is that, even if we start with an identical distribution of initial population, inefficient region might yield higher welfare initially and may offer a better end-welfare prospect following agglomeration. This is purely due to the presence of the voluntarily provided public good.¹² Lower productivity in private intermediate goods production (i.e. higher values of $\beta$ and/or $\alpha$) either leads to higher prices or fewer varieties (or both). Both lead to an increase in the price of the final private good.

For gross substitutability in preferences ($\epsilon >1$), demand for the public good goes up and the final private good goes down. Collective higher provision of the public good and lower private good consumption (with fewer input varieties) will impact on per capita welfare in opposite directions. As a result, it may well happen that the inefficient region ends up providing, initially, a higher per capita welfare, triggering migration and attracting all the population. What is even more surprising is that even if one ignores the initial trigger for the migration and simply moves the entire population from inefficient to efficient region, per capita welfare might actually drop. The usual economic logic that if a region’s productivity were to improve, then people in that region should be better off (given the representative agent assumption), may fail to hold. Below we illustrate this possibility using numerical simulations.

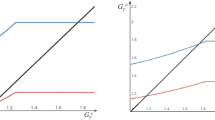
Consider once again Table 1. Marginal cost of intermediate inputs for region 2 is twice the marginal cost for region 1: $\beta =10$ versus $\beta =5$. Per capita welfare (U) in region 2 is higher for all reported population sizes, giving rise to the possibility of migration tipping towards the higher-cost, region 2. (We also report corresponding values of $p_x$ and G to highlight the trade-off between $p_x$ and G.) Now to illustrate the possibility that agglomeration in region 2 can be welfare-dominant (relative to region 1), let us go beyond Table 1 and consider Fig. 5. Here welfare curves are plotted for a continuum of $\beta$-values.¹³ Looking at the rising part of the welfare curve in colour red, consider regions 1 and 2 both of size $L=10^5$ and the $\beta$’s as specified earlier ($\beta =5$ for region 1 and $\beta =10$ for region 2). Initially, in region 1, $U \approx 1.29$ while for region 2, $U \approx 2.47$. This will move people from region 1 to region 2 resulting in per capita welfare $U\approx 1.98$ for the total population $L= 2* 10^5$ (refer the welfare curve in colour black (dashed curve)). However, if the same population were to be placed in the low-cost region 1, per capita welfare would have dropped to barely above $U=1.2$ (refer the black-coloured dashed curve against $\beta = 5$).

Fig. 5

U-shape welfare against marginal cost parameter $\beta$ [$L=10^5 \text {(red curve)}, L=2*10^5 \text {(black dashed curve)}, \sigma =5, \epsilon =3, \eta =2/5, \alpha =1$]

Next, for complementarity in preferences ($\epsilon <1$), welfare always goes down due to an increase in price of the final good. This is because, higher final good’s price would generate lower demand for both the final private good and the public good. Here one gets back Krugman’s result; that is, with identical population distribution, inferior region would generate lower per capita welfare. For the Cobb–Douglas case ($\epsilon =1$), G is unaffected to any change in the price of the final private good and hence per capita welfare would be lower in the high-cost/inefficient region.

We summarize the above observations in the following proposition:

Proposition 4

(Welfare-dominant inefficient agglomeration) Consider a world with CES utility and increasing returns in the production of the private goods as specified in Eqs. (1) and (9), intermediate inputs markets monopolistically competitive and public good voluntarily provided.

Starting from two regions with identical population sizes but differing technologies, any agglomeration will exhibit one of following characteristics:

(a):

Given complementarity in preferences, i.e. $\epsilon \le 1$, the technologically inferior region will always offer a lower per capita welfare initially. In such a case, agglomeration will be tipped towards the efficient region and will also be welfare-dominant.

(b):

Given substitutability in preferences, i.e. $\epsilon > 1$, the technologically inferior region may generate, initially, a higher or lower per capita welfare. In the case of the former, agglomeration will be tipped towards the inefficient region but it can be welfare-dominant.

Proposition 4 is an interesting demonstration of the economics of second-best. Two regions are compared which are identical in size, but one having worse technology of private good production. Inefficient production raises the price of the private good, and under substitutability raises provision of the public good. Given that the market equilibrium cannot provide the public good efficiently, it is indeed possible that welfare can be higher in the inefficient region.¹⁴

As already noted earlier, part (b) result of Proposition 4 does not conform to standard logic. The intuition is that more costly region, via its market process (fewer input varieties and high price of the final private good), makes higher voluntary provision of the public good sustainable that would not be possible in the low-cost region, and this public good effect sometimes comes to dominate. However, the result is not true generally. To see this, refer Fig. 5 and consider two $\beta$ values: $\beta =2.5$ (efficient) and $\beta =6$ (inefficient). Welfare along the red curve is higher at $\beta =6$ than at $\beta =2.5$, i.e. inefficient region offers higher per capita welfare with a population of $L=10^5$ compared to a similar sized region but with $\beta =2.5$. Let us check the per capita welfare if all population moves to the inefficient region rather than the efficient region. Looking at the black dashed curve, it is clear that the entire population should move to the efficient region as welfare at $\beta = 2.5$, $(U\approx 1.45)$, is higher than the welfare at $\beta =6\; (U\approx 1.3)$. Here, initially higher per capita welfare in the inefficient region triggers a movement that is welfare-immiserizing just like in Krugman (1979). If one were to apply the demanding, coalition-based notion of migration-proofness as in Conley and Konishi (2002), then in this example the entire population should relocate to the efficient region after the initial process of migration.

$\blacksquare$ Agent heterogeneity. In our representative agent model, the Nash equilibrium contribution of the public good is solved using symmetry of agent incomes (more precisely, labour endowment) and preferences. It is possible to allow income heterogeneity by considering two income classes, say the rich and the poor, where the rich contributes to the public good and the poor free rides similar to standard public good models without production. The incentives for agglomeration or segregation will have to be addressed more carefully; however, as the usual tension between the rich and the poor will resurface. While the rich and the poor will clash over the public good’s provision, the two groups will pull in the same direction with regard to the private goods: more population via Krugman-type agglomeration will tend to raise agents’ utilities due to greater intermediate input varieties. Our analysis here should be useful for a more elaborate modelling of this interesting issue.

4 Conclusion

Our modelling of voluntary contribution to higher education as a public good in a general equilibrium setting with identical agents differs from the literature’s partial equilibrium analysis. This way we are able to bring in a production sector explicitly where endogenously determined price of the private good impacts on the price of voluntary giving.

We do not model strategic aspects of donation in its full richness because of many agents and the general equilibrium structure. Also, we have remained silent on the role of fundraising drives in generating donations. In the USA, private universities actively solicit donations from alumni, corporate organizations and philanthropists. As Andreoni and Payne (2013) have discussed, people generally do not give unless asked explicitly by charities. So one reason private universities in the USA are so successful in receiving donations are due to their big fundraising initiatives. In this way the USA is unique. To our knowledge, Indian universities make no such major initiatives. This difference in approach in the two countries can of course explain part of the differential giving, besides the theoretical explanation we have offered here.

Last but not least, it might be argued that the Americans donate more simply because they are more wealthy. This argument is not entirely accurate. Big donations in higher education come mainly from rich alumni and philanthropists. The capacity of giving should not be any different whether one considers rich Americans or rich Indians. Generosity is not to be measured in terms of absolute dollar donations. Rather how much one gives relative to one’s wealth should be the correct indicator.

Appendix

Proof of Proposition 2. (a) We assume L to be a continuous variable.¹⁵ In equilibrium, all regions must enjoy the same level of welfare and there must not be any incentive for people to move from one region to another. Contrary to our claim suppose, there are two regions, i and j, such that $U(L_i)=U(L_j)$ and yet $L_i \ne L_j$ with $L_i>L_j$. Let welfare be maximized on the inverted-U curve at $L=\tilde{L}$. It must then be that $L_i>\tilde{L} > L_j$; all other possibilities can be ruled out given that $U(L_i)=U(L_j),\, L_i\ne L_j$ and U(L) is maximized at $\tilde{L}$ on the inverted-U curve. But then U(L) is increasing between $L_j$ and $\tilde{L}$. This implies that there is an incentive for some people to move from region i to region j, which is a contradiction.

(b) Suppose after the breakup, there are n identical regions. Using the result in part (a), each region will have $\frac{L}{n}$ population. That any further breakup is not possible requires $U(\frac{L}{2M})<U(\frac{L}{M})$. Also, no two regions should have the incentives to merge together: $U(\frac{2L}{M})<U(\frac{L}{M})$. Combining these two inequalities prove this part.    Q.E.D.