Keywords

1 Introduction

In recent years, the formation control of a group of autonomous marine vessels has received great attention from the control community due to its broad applications in navigation, such as exploration of natural resources, underway ship replenishment, surveillance of territorial waters, rescue missions and so on. Several methods have been proposed to achieve the desired formation, which include behavior-based, virtual structure, leader-follower strategy, and so on. Among these approaches, the leader-follower strategy has been much more preferred because of its simplicity and scalability.

The leader-follower approach plus the Lyapunov and backstepping technique has been used in [1]. A dynamic surface leader-follower formation controller based on neural network has been proposed for such systems in [2]. In [3], a linear sliding mode leader-follower formation control law has been designed. In [4], a Lagrangian formation control method is proposed for underactuated vessels. In [5], the multi-layer neural network and adaptive robust techniques are employed to design the controller for surface vessels with limited torques. However, all the methods mentioned above cannot guarantee the vessels to reach the desired formation in finite time.

In contrast, in this brief we develop a decentralized formation controller for underactuated vessels, using terminal sliding mode control (TSMC) approach combined with adaptive law. The TSMC approach proposed in [6] ensures the convergence of the system trajectories to the origin in finite time based on finite time stability theory. Meanwhile, in previous work, environmental disturbances are assumed to be upper bounded which is unrealistic in practical application and may cause acute chattering due to the over gain [12]. In this paper, the effects caused by environmental disturbances are cancelled by on-line upper bounds adaptive identification without any information in advance. Using this approach, a group of underactuated vessels can reach the desired formation in finite time under the influence of unknown disturbance.

2 Problem Formulation and Preliminaries

2.1 Vessel Communication Network

Graph theory is used to describe the communication (see for instance [7]). The communication network is \( G\left( {v,\varepsilon } \right) \), where \( v \) is a set of vertices and \( \varepsilon \) is a set of edges. The vertices represent the vessels in the formation and the number of vertices is equal to the number of vessels. The edges represent communication channels and are represented by \( \left( {v_{i} ,v_{j} } \right) \). If information transfer from \( v_{i} \) to \( v_{j} \) then \( \left( {v_{j} ,v_{i} } \right) \in \varepsilon \).

The adjacency matrix of the graph \( G \) is defined as \( A = \left\{ {a_{ij} } \right\} \in {\mathbb{R}}^{n \times n}, \) where \( a_{ii} = 0 \), \( a_{ij} = 1 \) if \( \left( {v_{i} ,v_{j} } \right) \in \varepsilon \) and \( a_{ij} = 0 \) otherwise. The in-degree matrix of the graph \( G \) is defined as \( D_{in} = diag\left[ {d_{in} \left( {v_{1} } \right), \ldots ,d_{in} \left( {v_{n} } \right)} \right], \) where \( d_{in} \left( {v_{n} } \right) \) is equal to the number of edges \( \left( {v_{j} ,v_{i} } \right) \in \varepsilon. \) The Laplacian matrix of \( G \) is defined as \( L = \left\{ {l_{ij} } \right\} \in {\mathbb{R}}^{n \times n}, \)where \( l_{ii} = \sum\nolimits_{j \ne i} {a_{ij} } \) and \( l_{ij} = - a_{ij} ,i \ne j \). The Laplacian matrix \( L = D_{in} - A \), the normalized directed Laplacian matrix is defined as \( \ell_{ij} = \frac{{l_{ij} }}{{l_{ii} }} \).

In this paper, for the formation control we consider is in the leader-follower framework, where the leader information is known. Moreover, the leader can only transmit information to the follower and does not influence by the follower. Thus the Laplacian matrix can be written as follows

$$ \ell = \left\{ {\ell_{ij} } \right\}_{{\left( {n + 1} \right) \times \left( {n + 1} \right)}} = \left[ {\begin{array}{*{20}c} 0 & {0_{1 \times n} } \\ {\ell_{1} } & {\ell_{2} } \\ \end{array} } \right] $$

Where

$$ \ell_{ij} = \left\{ {\begin{array}{*{20}l} 1 \hfill & { \, i = j \, and \, i \ne L} \hfill \\ {\frac{{l_{ij} }}{{l_{ii} }}} \hfill & {otherwise} \hfill \\ \end{array} } \right. $$
$$ \ell_{1} = \left[ {\begin{array}{*{20}c} {\ell_{1L} } \\ \vdots \\ {\ell_{nL} } \\ \end{array} } \right]\,{\text{and}}\,\ell_{2} = \left[ {\begin{array}{*{20}c} {\ell_{11} } & \cdots & {\ell_{1n} } \\ \vdots & {} & \vdots \\ {\ell_{nL} } & \cdots & {\ell_{nn} } \\ \end{array} } \right] $$

2.2 The Vessel Model

Consider a group of N underactuated surface vessels. The kinematics and dynamic models are as follows [8]

$$ \dot{\eta }_{i} = R\left( {\psi_{i} } \right)v_{i} ,\quad i = 1,2, \ldots ,N, $$
(1)
$$ M_{i} \dot{v}_{i} + C_{i} \left( v \right)v_{i} + D_{i} \left( v \right)v_{i} = \tau_{i} + \omega_{i} $$
(2)

Where \( \eta_{i} \, = \,[x_{i} ,y_{i} \, ,\,\psi_{i} ]^{T} \in {\mathbb{R}}^{3} \) denotes the position and orientation in the earth-fixed reference frame; \( v_{i} = \left[ {v_{xi} ,v_{yi} ,w_{zi} } \right]^{\rm T} \in {\mathbb{R}}^{3} \) denotes the velocity in the body-fixed reference frame. \( M_{i} \in {\mathbb{R}}^{{3{\text{x}}3}} \) is a symmetric positive-definite inertia matrix; \( C_{i} \left( v \right)v_{i} \in {\mathbb{R}}^{{3{\text{x}}3}} \) is a matrix of coriolis and centripetal matrix, \( D_{i} \left( v \right)v_{i} \in {\mathbb{R}}^{{3{\text{x}}3}} \) is the hydrodynamic damping matrix which is also symmetric and positive-definite; \( \tau_{i} \,{ = }\,\left[ {F_{xi} ,0,T_{zi} } \right]^{\rm T} \in {\mathbb{R}}^{3} \) denotes the vector of external force and torque; \( \omega_{i} \,{ = [}\,\omega_{x} ,\omega_{y} ,\omega_{z} ]^{T} \in {\mathbb{R}}^{3} \) denotes the unknown disturbances from the environment. The rotation matrix \( R\left( \psi \right) \), and dynamic matrices are defined as follows

$$ R\left( \psi \right) = \left[ {\begin{array}{*{20}l} {\cos \psi_{i} } \hfill & { - \sin \psi_{i} } \hfill & 0 \hfill \\ {\sin \psi_{i} } \hfill & {\cos \psi_{i} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right],\,M_{i} = \left[ {\begin{array}{*{20}l} {m_{11i} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {m_{22i} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {m_{33i} } \hfill \\ \end{array} } \right],\,C_{i} = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & {c_{13i} } \hfill \\ 0 \hfill & 0 \hfill & {c_{23i} } \hfill \\ { - c_{13i} } \hfill & { - c_{23i} } \hfill & 0 \hfill \\ \end{array} } \right] $$

Where \( c_{13i} = - m_{22i} v{}_{yi} - \frac{1}{2}\left( {m_{23i} + m_{32i} } \right)w_{zi} \) and \( c_{23i} = m_{11i} v_{xi}. \)

$$ D_{i} = \left[ {\begin{array}{*{20}c} {d_{11i} } & 0 & 0 \\ 0 & {d_{22i} } & 0 \\ 0 & 0 & {d_{33i} } \\ \end{array} } \right] $$
(3)

Then the simplified model can be obtained as follows

$$ \begin{aligned} & m_{11i} \dot{v}_{xi} - m_{22i} v_{yi} w_{zi} + d_{11i} v_{xi} = F_{xi} { + }\omega_{x} \\ & m_{22i} \dot{v}_{yi} + m_{11i} v_{xi} w_{zi} + d_{22i} v_{yi} = 0 + \omega_{y} \\ & m_{33i} \dot{w}_{zi} + m_{22i} v_{yi} v_{xi} - m_{11i} v_{xi} v_{yi} + d_{33i} w_{zi} = T_{zi} + \omega_{z} \\ \end{aligned} $$
(4)

3 Formation Controller Design and Stability Analysis

The dynamical model of the vehicle is represented by

$$ \begin{aligned} \dot{x}_{i} & = v_{xi} \cos \psi_{i} - v_{yi} \sin \psi_{i} \\ \dot{y}_{i} & = v_{xi} \sin \psi_{i} + v_{yi} \cos \psi_{i} \\ \dot{\psi }_{i} & = w_{zi} \\ \end{aligned} $$
(5)

From (4) we can get

$$ \begin{aligned} \dot{v}_{xi} & = \frac{{m_{22i} }}{{m_{11i} }}v_{yi} w_{zi} - \frac{{d_{11i} }}{{m_{11i} }}v_{xi} + \frac{1}{{m_{11i} }}F_{xi} + \frac{1}{{m_{11i} }}\omega_{x} \\ \dot{v}_{yi} & = - \frac{{m_{11i} }}{{m_{22i} }}v_{xi} w_{zi} - \frac{{d_{22i} }}{{m_{22i} }}v_{yi} + \frac{1}{{m_{22i} }}\omega_{y} \\ \dot{w}_{zi} & = \frac{{m_{11i} - m_{22i} }}{{m_{33i} }}v_{xi} v_{yi} - \frac{{d_{33i} }}{{m_{33i} }}w_{zi} + \frac{1}{{m_{33i} }}T_{zi} + \frac{1}{{m_{33i} }}\omega_{z} \\ \end{aligned} $$
(6)

Differentiating (5) we can get

$$ \begin{aligned} \ddot{x}_{i} \left( t \right) & = u_{1i} \left( t \right) + \tilde{\omega }_{x} \left( t \right) \\ \ddot{y}_{i} \left( t \right) & = u_{2i} \left( t \right) + \tilde{\omega }_{y} \left( t \right) \\ \ddot{\psi }_{i} \left( t \right) & = u_{3i} \left( t \right) + \tilde{\omega }_{z} \left( t \right) \\ \end{aligned} $$
(7)

Where

$$ \begin{aligned} u_{1i} \left( t \right) & = \left( {\frac{{m_{22i} }}{{m_{11i} }}v_{yi} w_{zi} - \frac{{d_{11i} }}{{m_{11i} }}v_{xi} - v_{xi} w_{zi} + \frac{1}{{m_{11i} }}F_{xi} } \right)\cos \psi_{i} + \left( {\frac{{m_{11i} }}{{m_{22i} }}v_{xi} w_{zi} - v_{xi} w_{zi} + \frac{{d_{22i} }}{{m_{22i} }}v_{yi} } \right)\sin \psi_{i} \\ u_{2i} \left( t \right) & = \left( {\frac{{m_{22i} }}{{m_{11i} }}v_{yi} w_{zi} - \frac{{d_{11i} }}{{m_{11i} }}v_{xi} - v_{yi} w_{zi} + \frac{1}{{m_{11i} }}F_{xi} } \right)sin\psi_{i} + \left( { - \frac{{m_{11} }}{{m_{22} }}v_{x} w_{z} + v_{x} w_{z} - \frac{{d_{22} }}{{m_{22} }}v_{y} } \right)\cos \psi \\ u_{3i} \left( t \right) & = \frac{{m_{11i} - m_{22i} }}{{m_{33i} }}v_{xi} v_{yi} - \frac{{d_{33i} }}{{m_{33i} }}w_{zi} + \frac{1}{{m_{33i} }}T_{zi} \\ \tilde{\omega }_{x} \left( t \right) & = \frac{1}{{m_{11i} }}\omega_{x} \cos \psi_{i} - \frac{1}{{m_{22i} }}\omega_{y} \sin \psi_{i} \\ \tilde{\omega }_{y} \left( t \right) & = \frac{1}{{m_{11i} }}\omega_{x} \sin \psi_{i} + \frac{1}{{m_{22i} }}\omega_{y} \cos \psi_{i} \\ \tilde{\omega }_{z} \left( t \right) & = \frac{1}{{m_{33i} }}\omega_{z} \\ \end{aligned} $$

The formation control objective for under-actuated ships can be stated as follows

$$ \mathop {\lim }\limits_{t \to \infty } e_{ij} \left( t \right) = \mathop {\lim }\limits_{t \to \infty } \left( {\eta_{i} \left( t \right) - \eta_{j} \left( t \right) - l_{ij} \left( t \right)} \right) = 0\,\,i, \,\, j = L,1, \ldots ,n $$
(8)

Where \( l_{ij} \left( t \right) \) denotes the relative position between the i-th ship and the j-th ship.

Furthermore, we introduce a generalized error state for the i-th ship as follows

$$ z_{i} \left( t \right) = \eta_{i} \left( t \right) - \frac{{a_{ij} }}{{\sum {_{j \ne i} a_{ij} } }}\sum {\left( {\eta_{i} (t) + l_{ij} (t)} \right)} \,\, i, \,\, j = 1, \ldots ,n $$
(9)

Lemma 1:

Define \( z = [z_{1}^{T}, \ldots ,z_{m}^{T} ]^{T}, \) where \( z_{i} \) is given by (9) we can get the conclusions as follows [9]

  1. (i)

    If \( z = 0 \), then \( e_{ij} = 0, \, i = 1, \ldots ,n,\,\,j = L, 1, \ldots ,n. \)

  2. (ii)

    If \( e_{ij} = 0,i = 1, \ldots ,n, \, \) \( j \in \left\{ {a_{ij} \ne 0,\,i,\,\,j = L,1, \ldots ,n} \right\} \), then \( z = 0. \)

The generalized error dynamics are obtained by taking the second time derivative of (9) and are given by

$$ \ddot{z}_{i} \left( t \right) = \ddot{\eta }_{i} \left( t \right) - \frac{{l_{ij} }}{{l_{ii} }}\sum {\left( {\ddot{\eta }_{j} \left( t \right) + \ddot{l}_{ij} \left( t \right)} \right)} \,{ = }\,\tilde{u}_{i} \left( t \right) + \varpi_{i} \left( t \right) + \ell_{iL} \ddot{\eta }_{L} - \frac{{l_{ij} }}{{l_{ii} }}\sum {\ddot{l}_{ij} } \left( t \right) $$
(10)

Where \( \tilde{u}_{i} \left( t \right)\,{ = }\,u_{i} \left( t \right) - \frac{{l_{ij} }}{{l_{ii} }}\sum\limits_{j \ne L} {u_{j} } \left( t \right) \), \( \varpi_{i} \left( t \right)\,{ = }\,\tilde{\omega }_{i} \left( t \right) - \frac{{l_{ij} }}{{l_{ii} }}\sum\limits_{j \ne L} {\tilde{\omega }_{i} \left( t \right)} \)

Next we define i-th nonlinear sliding mode surface respect to (13) as follows

$$ S_{i} \left( {z_{i} ,\dot{z}_{i} } \right) = \dot{z}_{i} \left( t \right) + C_{i} R_{i} \left( {z_{i} } \right)\left| {z_{i} } \right|^{{\frac{1}{2}}} $$
(11)

Where

\( C_{i} \;{ = }\;diag[c_{i1} ,c_{i2} ,c_{i3} ],c_{ij} > 0,R_{i} \left( {z_{i} } \right) = diag\left[ {sign\left( {z_{i1} } \right),sign\left( {z_{i2} } \right),sign\left( {z_{i3} } \right)} \right] \)

\( \left| {z_{i} } \right|^{{\frac{1}{2}}} = \left[ {\left| {z_{i1} } \right|^{{\frac{1}{2}}} ,\left| {z_{i2} } \right|^{{\frac{1}{2}}} ,\left| {z_{i3} } \right|^{{\frac{1}{2}}} } \right]^{T} \)

By using the sliding mode control theory and let \( \dot{S}_{i} \left( {z_{i} ,\dot{z}_{i} } \right)\,{\ = }\,0 \),we get

$$ \tilde{u}_{i} \left( t \right) = - \ell_{iL} \ddot{\eta }_{L} + \frac{{l_{ij} }}{{l_{ii} }}\sum {\ddot{l}_{ij} } \left( t \right) - \frac{1}{2}C_{i} p_{i} \left( {z_{i} ,\dot{z}_{i} } \right) - K_{i} sign\left( {S_{i} \left( {z_{i} ,\dot{z}_{i} } \right)} \right) $$
(12)

Where \( \left( {z_{i} ,\dot{z}_{i} } \right) \in q_{i} ,i = 1, \ldots ,n,K_{i} = diag\left[ {k_{i1} ,k_{i2} ,k_{i3} } \right] \),

$$ p_{i} \left( {z_{i} ,\dot{z}_{i} } \right) = \left[ {\dot{z}_{i1} \left| {z_{i1} } \right|^{{ - \frac{1}{2}}} ,\dot{z}_{i2} \left| {z_{i2} } \right|^{{ - \frac{1}{2}}} ,\dot{z}_{i3} \left| {z_{i3} } \right|^{{ - \frac{1}{2}}} } \right]^{T} ,i = 1, \ldots ,n, $$
$$ sign\left( {S_{i} \left( {z_{i} ,\dot{z}_{i} } \right)} \right)\,{ = }\,\left[ {\begin{array}{*{20}c} {sign\left( {S_{i1} \left( {z_{i} ,\dot{z}_{i} } \right)} \right)} \\ {sign\left( {S_{i2} \left( {z_{i} ,\dot{z}_{i} } \right)} \right)} \\ {sign\left( {S_{i3} \left( {z_{i} ,\dot{z}_{i} } \right)} \right)} \\ \end{array} } \right] $$

\( q_{i} = \left\{ {\left( {z_{i} ,\dot{z}_{i} } \right) \in {\mathbb{R}} \times {\mathbb{R}}:\left\| {p_{i} \left( {z_{i} ,\dot{z}_{i} } \right)} \right\|_{\infty } \le \lambda_{i} } \right\} , \)Where \( \lambda_{i} = \left\| {C_{i} } \right\|_{\infty } + \delta_{i} ,\delta_{i} > 0. \)

Remark 1:

\( q_{i} \) is the set where \( p_{i} \left( {z_{i} ,\dot{z}_{i} } \right) \) is bounded, and by setting \( p_{i} \left( {z_{i} ,\dot{z}_{i} } \right) \in q_{i} \) ,we can avoid the singularity problem of the controller.

Lemma 2:

if the sliding mode controller gain \( k_{ij} \) satisfies:

$$ k_{ij} = \alpha_{ij} + \sup \left\| \varpi \right\|_{\infty } $$
(13)

Where \( \alpha_{\text{ij}} > \frac{{\lambda^{2} - c_{ij} \lambda_{i} }}{2} > 0,\,i = 1, \ldots ,n,\,j = 1,2,3, \) then \( q_{i} \) is positively invariant set.

However, the upper bound of environment disturbance \( M \) is unknown in practical application. According to this circumstance, we introduce adaption law to the controller design. The estimated value of \( M \) is \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} \) , define the error between the two values are as follows:

$$ \tilde{M}\,{ = }\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} - M $$
(14)

Therefore, \( k_{ij} = \alpha_{ij} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M}_{i}, \) where \( \dot{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }_{i} \) satisfies

$$ \dot{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }_{i} \,{ = }\,\frac{{\left| {S_{ij} (z_{i} ,\dot{z}_{i} )} \right|}}{{\gamma_{i} }} $$
(15)

Next, for the condition \( \left( {z_{i} ,\dot{z}_{i} } \right) \notin q_{i}, \) we design an auxiliary sliding surface

$$ S_{iaux} \left( {z_{i} ,\dot{z}_{i} } \right) = \dot{z}_{i} $$
(16)

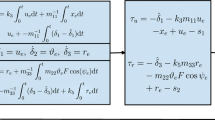
Let \( \dot{S}_{iaux} \left( t \right)\,{ = 0}, \) we obtain

$$ u_{iaux} = - \ell_{iL} \ddot{\eta }_{L} + \frac{{l_{ij} }}{{l_{ii} }}\sum {\ddot{l}_{ij} } \left( t \right) - K_{iaux} sign\left( {S_{iaux} \left( {z_{i} ,\dot{z}_{i} } \right)} \right) $$
(17)

Where \( \left( {z_{i} ,\dot{z}_{i} } \right) \notin q_{i} \) , \( K_{iaux} = diag\left[ {k_{i1aux} ,k_{i2aux} ,k_{i3aux} } \right] \)

$$ sign\left( {S_{iaux} \left( {z_{i} ,\dot{z}_{i} } \right)} \right){ = }\left[ {\begin{array}{*{20}c} {sign\left( {S_{i1aux} \left( {z_{i} ,\dot{z}_{i} } \right)} \right)} \\ {sign\left( {S_{i2aux} \left( {z_{i} ,\dot{z}_{i} } \right)} \right)} \\ {sign\left( {S_{i3aux} \left( {z_{i} ,\dot{z}_{i} } \right)} \right)} \\ \end{array} } \right] $$
$$ k_{ijaux} = \alpha_{ijaux} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M}_{{_{ijaux}, }} i = 1, \ldots ,n, \,\, j = 1,2,3,\,\dot{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }_{iaux} \,{ = }\,\frac{{\left| {S_{ijaux} (z_{i} ,\dot{z}_{i} )} \right|}}{{\gamma_{iaux} }} $$

Proof:

First, for the condition \( \left( {z_{i} ,\dot{z}_{i} } \right) \notin q_{i}, \) we consider a Lyapunov function as follows

$$ V_{i} \left( {S_{iaux} \left( {z_{i} ,\dot{z}_{i} } \right)} \right) = \frac{1}{2}S^{T}_{iaux} S_{iaux} + \frac{1}{2}\gamma_{iaux} \tilde{M}_{iaux}^{2} $$
(18)

Whose time derivative is given by

$$ \begin{aligned} \dot{V}_{i} & \;{ = } \;S^{T}_{iaux} \left( { - K_{iaux} sign\left( {S_{iaux} \left( {z_{i} ,\dot{z}_{i} } \right)} \right) + \varpi } \right) + \gamma_{iaux} \dot{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }_{iaux} \tilde{M}_{iaux} \\ & = - a_{ijaux} \left| {S_{ijaux} \left( {z_{i} ,\dot{z}_{i} } \right)} \right| - M_{iaux} \left| {S_{ijaux} \left( {z_{i} ,\dot{z}_{i} } \right)} \right|{ + }\varpi S_{ijaux} \left( {z_{i} ,\dot{z}_{i} } \right) \\ & \le - \sum\limits_{j = 1}^{3} {a_{ijaux} \left| {S_{ijaux} \left( {z_{i} ,\dot{z}_{i} } \right)} \right|} \le - \sum\limits_{j = 1}^{3} {\mathop {\hbox{min} }\limits_{j = 1,2,3} \left\{ {a_{ijaux} } \right\}\left| {S_{ijaux} \left( {z_{i} ,\dot{z}_{i} } \right)} \right|} = - \mathop {\hbox{min} }\limits_{j = 1,2,3} \left\{ {a_{ijaux} } \right\}\left\| {\dot{z}_{i} } \right\|_{1} \\ & \le - \sqrt 2 \mathop {\hbox{min} }\limits_{j = 1,2,3} \left\{ {a_{ijaux} } \right\}V_{{_{i} }}^{{\frac{1}{2}}} \left( {S_{ijaux} \left( {z_{i} ,\dot{z}_{i} } \right)} \right) \\ \end{aligned} $$
(19)

Thus, it follows [10] that the sliding surface is finite-time stable. Therefore, there exists a finite time T. At this time, the sliding mode controller switches from (12) to (17). Let \( T{ = }\max_{i = 1, \ldots ,n} \left\{ {T_{i} } \right\}, \) when \( t \ge T , \) we have \( \left( {z_{i} ,\dot{z}_{i} } \right) \in q_{i} ,i = 1, \ldots ,n. \)

Next consider the Lyapunov function candidate given by

$$ V_{i} \left( {S_{i} \left( {z_{i} ,\dot{z}_{i} } \right)} \right) = \frac{1}{2}S^{T}_{i} S_{i} + \frac{1}{2}\gamma_{i} \tilde{M}_{i}^{2} $$
(20)

Differentiating \( V_{i} \) with respect to time, we have

$$ \begin{aligned} \dot{V}_{i} & \;{ = } \;S^{T}_{i} \left( { - K_{i} sign\left( {S_{i} \left( {z_{i} ,\dot{z}_{i} } \right)} \right) + \varpi } \right) + \gamma_{i} \dot{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }_{i} \tilde{M}_{i} \\ & = - a_{ij} \left| {S_{ij} \left( {z_{i} ,\dot{z}_{i} } \right)} \right| - M_{i} \left| {S_{ij} \left( {z_{i} ,\dot{z}_{i} } \right)} \right|{ + }\varpi S_{ij} \left( {z_{i} ,\dot{z}_{i} } \right) \\ & \le - \sum\limits_{j = 1}^{3} {a_{ij} \left| {S_{ij} \left( {z_{i} ,\dot{z}_{i} } \right)} \right|} \le - \sum\limits_{j = 1}^{3} {\mathop {\hbox{min} }\limits_{j = 1,2,3} \left\{ {a_{ij} } \right\}\left| {S_{ij} \left( {z_{i} ,\dot{z}_{i} } \right)} \right|} = - \mathop {\hbox{min} }\limits_{j = 1,2,3} \left\{ {a_{ij} } \right\}\left\| {\dot{z}_{i} } \right\|_{1} \\ & \le - \sqrt 2 \mathop {\hbox{min} }\limits_{j = 1,2,3} \left\{ {a_{ij} } \right\}V_{{_{i} }}^{{\frac{1}{2}}} \left( {S_{ij} \left( {z_{i} ,\dot{z}_{i} } \right)} \right) \\ \end{aligned} $$
(21)

Thus, it follows from [10] that the error states can reach the sliding model surface in finite time. Furthermore, while on the sliding surface the close-loop error dynamics are characterized by

$$ \dot{z}_{i} = - C_{i} R_{i} \left( {z_{i} } \right)\left| {z_{i} } \right|^{{\frac{1}{2}}} $$
(22)

Consider the Lyapunov function as

$$ \bar{V}\left( {z_{i} } \right) = \left\| {z_{1} } \right\| $$
(23)

Whose time derivative is given by

$$ \dot{\bar{V}}\left( {z_{i} } \right)\,{ = }\,\sum\limits_{j = 1}^{3} {sign\left( {z_{ij} } \right)} \dot{z}_{ij} = - \sum\limits_{j = 1}^{3} {c_{ij} } \left| {z_{ij} } \right|^{{\frac{1}{2}}} \;\le \;- \left\| {C_{i}^{ - 1} } \right\|_{\infty }^{ - 1} \left( {V_{i} \left( {z_{i} } \right)} \right) $$
(24)

From [10], the error states converge to the origin in finite time.

4 Simulation

In this section, we consider a group of three ships with a communication network. The model parameters are given [8],

$$ m_{11} = 200\,kg,\,m_{22} = 250\,kg,\,m_{33} = 80\,kg, d_{11} = 70\,kg/s,\,d_{22} = 100\,kg/s,\,d_{33} = 50\,kg/s $$

The time-varying disturbances are given in [11], The path of the leader is parameterized as \( x_{L} = t,y_{L} = 3\cos \left( {0.1t} \right). \) The initial values are \( \eta_{1} = [\begin{array}{*{20}c} { - 3} & 2 & {\frac{5}{6}\pi } \\ \end{array} ] \),\( \eta_{2} = [\begin{array}{*{20}c} { - 5} & { - 2} & \pi \\ \end{array} ]. \) The sliding mode surface parameters and the control gain parameters are \( C_{1} = C_{2} = diag\left[ {\begin{array}{*{20}c} {1.2} & {1.2} & {1.2} \\ \end{array} } \right] \), \( a_{1} = a_{2} = a_{1aux} = a_{2aux} = diag\left[ {\begin{array}{*{20}c} {2.5} & {2.5} & {2.5} \\ \end{array} } \right], \)

\( \gamma_{1} = \gamma_{2} = \left[ {\begin{array}{*{20}c} 1 & 1 & 1 \\ \end{array} } \right] \), \( \gamma_{1aux} = \gamma_{2aux} = \left[ {\begin{array}{*{20}c} 1 & 1 & 1 \\ \end{array} } \right], \) Simulation result is presented as follows (Fig. 1).

Fig. 1.
figure 1

Formation trajectories in 2-D plane.

Full size image

5 Conclusions

In this paper, we investigate the formation control problem of underactuated vessels via adaptive terminal sliding mode control method. To tracking the desired trajectory in finite time, the adaptive sliding mode control method and finite time stability theory are combined to design a decentralized controller for underactuated vessels. Specifically, non-smooth sliding surface are designed to avoid the singularity problem. At last, the simulation results are given to illustrate the performance of the proposed scheme.