Keywords

2010 AMS Math. Subject Classification

1 Introduction

To obtain the solutions for engineering problems such as in magneto-hydro-dynamics or fluid dynamics whether through ordinary, partial or fractional differential equations, integral transform methods are often sought to the rescue. The advent is that they convert the differential problems to simplifiable algebraic problems in a possibly new domain with proxy units, the solution of which are then often inverted back to yield the sought solution. Fourier and Laplace transforms are the traditional integral transform icons in this regard [24, 45]. Based on the type of kernel used, various integral transforms and problem-solving techniques have risen to include Hankel, Mellin, Hilbert Jacobi, Gegenbauer, Radon, Wavelet and Curvelet transforms, and Z [43]. For instance, orthogonal polynomial kernels led to Legendre, Laguerre, and Hermite transforms [43].

For the function f(t) defined in the set \(A=\{f(t)|\exists M,\tau _{1},\tau _{2}>0,|f(t)|<Me^{\frac{|t|}{\tau _{j}}},\text {if}\ t\in (-1)^{j}\times [0,\infty )\}\), Natural transform is given by,

$$\begin{aligned} \begin{aligned} \mathbb {N}[f(t)]=R(s,u)&=\int _0^\infty e^{-st}f(ut)dt=\frac{1}{u}\int _0^\infty e^{-\frac{st}{u}}f(t)dt\\&=\frac{1}{s}\int _0^\infty e^{-t}f\left( \frac{ut}{s}\right) dt\ ;\ Re(s)>0,\ u\in (-\tau _1,\tau _2). \end{aligned} \end{aligned}$$
(1)

In (1), when \(u\equiv 1\) gives Laplace transform and \(s\equiv 1\) gives Sumudu transform, hence second and third integral equations define the respective Natural-Laplace dual (NLD) and Natural-Sumudu dual (NSD).

The above mentioned Natural transform combines the features of Laplace and Sumudu transforms and hence converges to both transforms upon variable substitutions in kernel. In this work, some Natural transform properties are reviewed and applied to fractional order diffusion equation in semi-infinite medium for its solution, and then for different values of \(\alpha \), the solution is analyzed. Followed by same, Natural transform is applied for Stokes–Ekman problem to obtain its layer thickness. Table comprising all new Natural transforms for certain functions is given. In the second half of this work, Sumudu transform applied for Stokes, Rayleigh, and Blasius problems to obtain their solutions and hence their layer thickness.

2 Natural Transform Properties

Properties and table of elementary functions and N transform are given with solutions of fluid flow over a plane wall is solved by the Natural transform (N-transform) in [1]. Assuming both initial and boundary conditions were null, Maxwell’s simultaneous equations were solved by Natural transform in [2]. Extensive properties including multiple shifting, dual nature to Laplace and Sumudu transforms, and all other required properties of Natural transform with list of tables were studied in [3]. A more generalized Laplace, Sumudu, and Natural transforms definitions are given in [3], (Eqs (1.4-5), and (2.12-13) in [3]). Natural and its inverse transforms were derived from Fourier integral in [3]. Bromwich contour integral and Heaviside’s expansions theorems for the inverse Natural transform were derived in [3] (Theorems 5.3 and 5.4, [3]). The same reference contains multiple shifting results related to products and divisions which were derived in terms of s as well as u in [3].

Transverse electromagnetic planar waves propagating in lossy medium (TEMP) are solved for electric field using Natural transform [4]. Maxwells equations were extended for n dimensions and studied using Natural transform in [5]. The relations of integral transforms and \(J_0(2\sqrt{vt})\) are studied in [6]. Fractional ODEs solved using Natural transform in [7]. Natural transform in distribution space \(\mathcal {D}^{'}\) and its dual space \(\mathcal {D}\) is studied in [8]. Natural transform in distribution space and Boehmians is studied in [9]. Integral equations solved using Natural transform in [10]. Decomposition method with Natural transform employeed for solving Schr\(\ddot{o}\)dinger equations in [11]. In [12] Q-theory of Natural transform discussed. Natural transform of basic functions calculated by Adomain decomposition method (ADM) in [13]. Laplace, Fourier, Sumudu, and Mellin transforms were back tracked from Natural transform in [14]. In [15], fractional PDEs are solved by Natural transform. Fluid PDEs are solved by Natural transform in [16]. Natural transform and the Homotopy Perturbation method (HPM) were hybridly joined to solve fractional PDEs in [17]. Fractional Natural transform, properties, and applications were studied in [18]. Some more applications of Natural transforms in solving PDEs were given in [19, 20].

Theorem 2.1

If \(f(t+NT)=-f(t)\), then

$$\begin{aligned} \mathbb {N}[f(t)]=-\frac{1}{u(1+e^{-\frac{sT}{u}})}\int _0^Te^{-\frac{st}{u}}f(t)dt. \end{aligned}$$
(2)

Proof

The proof is straightforward, rewriting the second integral of (1) in the interval [0, T] and \([T, \infty )\) so that \([0, \infty )=[0, T]\cup [T, \infty )\) and applying \(f(t+NT)=-f(t)\), simplifying gives (2). \(\square \)

Theorem 2.2

$$\begin{aligned} \mathbb {N}\left[ {\left\{ \begin{array}{ll} 0\ ;\ t<\frac{b}{a}\\ f(at-b)\ ;\ t>\frac{b}{a},\ a,\ b>0 \end{array}\right. }\right] =\frac{1}{a}e^{-\frac{sb}{au}}R\left( \frac{s}{a},u\right) . \end{aligned}$$
(3)

Proof

Applying second integral of (1) to the left-hand side of (3) and after simplifying completes the result. \(\square \)

3 Natural Transform Applications to Fractional Order Diffusion Equation in Semi-Infinite Medium and Stokes–Ekman Layer Problem

Example 3.1

(Fractional diffusion problem) The fractional order diffusion equation in semi infinite medium \(z>0\), where initial temperature is zero in the whole medium and temperature at the boundary is \(X_0f(t)\) given in [42]. The problem is described by the following equations.

$$\begin{aligned} \frac{\partial ^\alpha x(z,t)}{\partial t^\alpha }=\kappa \frac{\partial ^2x(z,t)}{\partial z^2}\ ;\ z\in (0,\infty )\ ,\ t>0. \end{aligned}$$
(4)

The initial and boundary conditions are, respectively, given by,

$$\begin{aligned} x(z,0)=0\ ;\ z>0. \end{aligned}$$
(5)
$$\begin{aligned} x(0,t)=X_0f(t)\ ;\ t>0\ \text {and}\ x(z,t)=0\ \text {as}\ z\rightarrow \infty . \end{aligned}$$
(6)

Letting \(\mathbb {N}[x(z,t)]=R(z,s,u)\) and \(\mathbb {N}[f(t)]=R(s,u)\), Natural transform of (4) after initial condition (5) and boundary condition (6) is given by,

$$\begin{aligned} \frac{d^2R(z,s,u)}{dz^2}-\left( \frac{s^\alpha }{\kappa u^\alpha }\right) R(z,s,u)=0\ ,\ z>0. \end{aligned}$$
(7)

and

$$\begin{aligned} R(0,s,u)=X_0R(s,u)\ ;\ R(z,s,u)\rightarrow 0\ \text {as}\ z\rightarrow \infty . \end{aligned}$$
(8)

Now the solution of (7) along with (8) is given by,

$$\begin{aligned} R(z,s,u)=X_0R(s,u)\exp \left( -z\sqrt{\frac{s^\alpha }{\kappa u^\alpha }}\right) . \end{aligned}$$
(9)

Inverse Natural transform of (9) from the application of convolution theorem of Natural transform [3] gives the solution of (4).

$$\begin{aligned} x(z,t)=X_0\int _0^tf(t-\tau )g(z,\tau )d\tau =X_0f(t)g(z,t). \end{aligned}$$
(10)

where

$$\begin{aligned} g(z,t)=\mathbb {N}^{-1}\left[ \exp \left( -z\sqrt{\frac{s^\alpha }{\kappa u^\alpha }}\right) \right] . . \end{aligned}$$
(11)

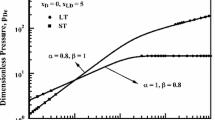
Now the solution x(z, t) of (4) with boundary condition \(f(t)=1\) in (6) for different values of \(\alpha \) in (4) is given in the Table 1.

Next the solution x(z, t) of (4) with boundary condition \(f(t)=t\) in (6) for different values of \(\alpha \) in (4) is given in the Table 2.

Hence, the general solution of (4) is given by (10) and (11). Finally, for different values of \(\alpha \) in (11), g(z, t) is given in Table 3.

Table 1 Solutions of (4) with boundary condition \(f(t)=1\) in (6) for different valus of \(\alpha \) in (4)
Full size table
Table 2 Solutions of (4) with boundary condition \(f(t)=t\) in (6) for different valus of \(\alpha \) in (4)
Full size table
Table 3 Solutions g(z, t) in (11) for different valus of \(\alpha \) in (11)
Full size table

Example 3.2

(Stokes–Ekman problem) When both fluid and disk rotate with uniform angular velocity \(\Omega \) about \(z-\) axis, unsteady boundary layer flow in a semi-infinite body of viscous fluid bounded by an infinite horizontal disk at \(z=0\) is given by the following equations [42].

$$\begin{aligned} \frac{\partial q(z,t)}{\partial t}+2\Omega iq(z,t)=\nu \frac{\partial ^2q(z,t}{\partial z^2}\ ;\ z>0\ ,\ t>0. \end{aligned}$$
(12)
$$\begin{aligned} q(z,t)=ae^{i\omega t}+be^{-i\omega t}\ \text {on}\ z=0\ ,\ t>0/ \end{aligned}$$
(13)
$$\begin{aligned} q(z,t)=0\ ;\ z\rightarrow \infty \ ,\ t>0. \end{aligned}$$
(14)
$$\begin{aligned} q(z,t)=0\ ;\ t\le 0\ \forall \ z>0. \end{aligned}$$
(15)

Here, q is the complex velocity field, \(\omega \) is frequency of oscillation of disk, and a and b are complex constants [42].

Let \(\mathbb {N}[q(z,t)]=R(z,s,u)\), Natural transform of (12) leads to,

$$\begin{aligned} \frac{d^2R(z,s,u)}{dz^2}-\left( \frac{s+2\Omega ui}{u\nu }\right) R(z,s,u)=0. \end{aligned}$$
(16)

Solution of (16) after initial and boundary conditions (8) and (7), respectively, yields,

$$\begin{aligned} R(z,s,u)=\frac{a}{s-i\omega u}\exp \left( -z\sqrt{\frac{s+2\Omega ui}{u\nu }}\right) +\frac{b}{s+i\omega u}\exp \left( -z\sqrt{\frac{s+2\Omega ui}{u\nu }}\right) .\nonumber \\ \end{aligned}$$
(17)

Inverse Natural transform of (17) gives the solution q(z, t) of (12).

$$\begin{aligned} q(z,t)=&\frac{ae^{i\omega t}}{2}\left[ \exp \left( -z\left( \frac{(2\Omega +\omega )i}{\nu }\right) \right) \text {erfc}\left( \frac{z}{2\sqrt{\nu t}}-\sqrt{t(2\Omega +\omega )i}\right) \right] \nonumber \\&+\frac{ae^{i\omega t}}{2}\left[ \exp \left( z\left( \frac{(2\Omega +\omega )i}{\nu }\right) \right) \text {erfc}\left( \frac{z}{2\sqrt{\nu t}}+\sqrt{t(2\Omega +\omega )i}\right) \right] \nonumber \\&+\frac{be^{-i\omega t}}{2}\left[ \exp \left( -z\left( \frac{(2\Omega +\omega )i}{\nu }\right) \right) \text {erfc}\left( \frac{z}{2\sqrt{\nu t}}-\sqrt{t(2\Omega +\omega )i}\right) \right] \nonumber \\&+\frac{be^{-i\omega t}}{2}\left[ \exp \left( z\left( \frac{(2\Omega +\omega )i}{\nu }\right) \right) \text {erfc}\left( \frac{z}{2\sqrt{\nu t}}+\sqrt{t(2\Omega +\omega )i}\right) \right] \nonumber \\ \end{aligned}$$
(18)

Upon \(\omega =0\) in (18) gives the Ekman layer thickness of order \(\sqrt{\frac{\nu }{2\Omega }}\).

For the functions in [41], table constituting list of exponential functions and their Natural transforms is given which will be useful for future study.

4 Sumudu Transform Literature Review

Over the past decade, a new theoretical framework has been developed to model anomalous diffusion. The new framework is based around the physics of continuous time random walks and the mathematics of fractional calculus. One can ask what would be a differential having as its exponent a fraction. Although this seems removed from Geometry . . . it appears that one day these paradoxes will yield useful consequences. Gottfried Leibniz Fractional Diffusion.

When \(s\equiv 1\) in (1), Natural transform converges to Sumudu transform, namely

$$\begin{aligned} \mathbb {S}[f(t)]=\int _0^\infty e^{-t}f(ut)dt=\frac{1}{u}\int _0^\infty e^{-\frac{t}{u}}f(t)dt\ ;\ u\in (-\tau _1,\tau _2). \end{aligned}$$
(19)

Sumudu transform is shown to dual of Laplace transform and used to solve production equation [21], followed by multiple shifting, convolutions, and table of Sumudu integral transforms given in [22]. Properties of shifting and derivative of functions, Taylor’s theorems, Sumudu transform applications and its relations to number theory and matrices given in [23]. From the Fourier integral, Sumudu transform is derived and applied for TEMP waves in [24]. Inverse Sumudu transform is applied and obtained the solution for Bessel’s differential equations and shown its relation to Laplace transform through Bessel function in [25]. In [26, 27, 29, 31, 32, 34] Sumudu transform applications used for fractional differential equations. In [28] Laplace transform defined for trigonometric functions and then new infinite series of trigonometric functions along with tables, examples discussed. Fractional Schnakenberg solved numerically in [30]. Fractional order systems in electrical circuits were studied in [33]. Boundary problems of double diffusiveness are studied in [35]. Sumudu transform applied for continuous everywhere and nowhere differentiable functions for smoothening the fracture in [36]. Sumudu computation in series format was derived through symbolic C\(++\) pseudocode, using the Sumudu definition without any additional decomposition schemes, in [37]. From the bimodular elliptic functions, Sumudu transform of \(\tan (x)\) and \(\sec (x)\) is derived as continued fractions in [38]. In [39] different Sumudu transform definition, its properties for trigonometric functions including table of new infinite series expansions of trigonometric functions were studied. Magnetic field solution of TEMP waves, numerical results and Maple graphical study were given in [40].

5 Sumudu Transform Applications to Stokes, Rayleigh and Blasius Problems

Example 5.1

(Stokes problem) Flow in unsteady boundary layer induced in semi-infinite viscous fluid is bounded by an infinite horizontal disk at \(z=0\) due to oscillations of disk in its own plane with given frequency \(\omega \). Corresponding PDE is given by [42],

$$\begin{aligned} \frac{\partial x(z,t)}{\partial t}=\nu \frac{\partial x(z,t)}{\partial z^2}\ ;\ z>0\ ,\ t>0. \end{aligned}$$
(20)

Initial conditions are

$$\begin{aligned} x(z,t)=0\ ;\ z\rightarrow \infty \ ,\ t>0. \end{aligned}$$
(21)
$$\begin{aligned} x(z,0)=0\ ;\ t\le 0\ ,\ \forall z>0. \end{aligned}$$
(22)

and the boundary condition is

$$\begin{aligned} x(z,t)=X_0e^{i\omega t}\ ;\ z=0\ ,\ t>0. \end{aligned}$$
(23)

Here, x(z, t) is velocity of fluid and \(\nu \) kinematic viscosity of fluid.

Let \(\mathbb {S}[x(z,t)]=G(z,u)\). Sumudu transform of (20) and after initial and boundary conditions yields,

$$\begin{aligned} G(z,u)=\frac{X_0}{1-i\omega u}\exp \left( -z\sqrt{\frac{1}{u\nu }}\right) . \end{aligned}$$
(24)

Sumudu inverting (24) gives velocity in unsteady boundary layer.

$$\begin{aligned} x(z,t)=\frac{X_0e^{i\omega t}}{2}\left[ e^{-z\sqrt{\frac{i\omega }{\nu }}}\text {erfc}\left( \frac{z}{2\sqrt{\nu t}}-\sqrt{i\omega t}\right) +e^{z\sqrt{\frac{i\omega }{\nu }}}\text {erfc}\left( \frac{z}{2\sqrt{\nu t}}+\sqrt{i\omega t}\right) \right] . \end{aligned}$$
(25)

From which the thickness of Stokes boundary layer is \(\sqrt{\frac{\nu }{\omega }}\).

Example 5.2

(Rayleigh problem) When the frequency \(\omega =0\) in Stokes problem, motion is generated from rest with constant velocity \(X_0\) in fluid [42]. Therefore, from (24).

$$\begin{aligned} G(z,u)=X_0\exp \left( -z\sqrt{\frac{1}{u\nu }}\right) . \end{aligned}$$
(26)

Sumudu inverting (26) gives the velocity x(z, t).

$$\begin{aligned} x(z,t)=X_0\,\text {erfc}\left( \frac{z}{2\sqrt{\nu t}}\right) . \end{aligned}$$
(27)

Thickness of Rayleigh boundary layer is \(\sqrt{\nu t}\).

Example 5.3

(Blasius problem) Unsteady boundary layer flow in semi-infinite body of viscous fluid is enclosed by infinite horizontal disk at \(z=0\) [42].

When the boundary condition is t in Stokes problem Example 5.1 leads to the Blasius problem. Therefore, Sumudu transformed (20)–(23) with \(x(z,t)=X_0t\) yields,

$$\begin{aligned} G(z,u)=X_0u\exp \left( -z\sqrt{\frac{1}{u\nu }}\right) . \end{aligned}$$
(28)

Inverse Sumudu transform of (28) using Maple gives the velocity profile of Blasius problem.

$$\begin{aligned} x(z,t)=\frac{X_0}{2}\left[ \left( \frac{z^2+2\nu v}{\nu }\right) \text {erfc}\left( \frac{z}{2\sqrt{\nu t}}\right) -2z\sqrt{\frac{t}{\pi \nu }}e^{-\frac{z^2}{4\nu t}}\right] . \end{aligned}$$
(29)
Table 4 Natural transform of elementary functions
Full size table

6 Conclusion

With respect to fractional diffusion problem, following observations were found. When the boundary condition is constant.

  • For \(\alpha =-2\), velocity profile x(z, t) is in terms of Bessel’s function.

  • For \(\alpha =-1\), velocity profile x(z, t) is in terms of hypergeometric function.

  • For \(\alpha =1\), velocity profile x(z, t) is in terms of complementary error function [42].

  • For \(\alpha =2\), velocity profile x(z, t) is in terms of Heaviside’s function.

  • When the boundary condition is t, velocity profiles for different \(\alpha \) are given in Table 2.

  • For \(\alpha >-2\) and \(\alpha >2\), velocity profile x(z, t) does not exists.

  • Therefore, for constant and t boundary conditions, velocity x(z, t) is defined for \(\alpha \in [-2,2]\).

Sumudu reciprocity property of [24] is shown in the realm of Stokes fluid flow problem and its descendent variations, and obtained solutions and layer thickness are in exact concordance with results in the literature [42].

For future studies, we relegate the still open problems regarding finding the velocity x(z, t) when \(\alpha \) takes fractional values in the interval \([-2, 2]\). Lists of Natural transforms of elementary functions given in Table 4 will be useful for further study. Moreover, we declare that we remain open to our readers comments, communications, and suggestions.