An Extension of the Shannon Wavelets for Numerical Solution of Integro-Differential Equations

Abstract

In this work, an extension of the algebraic formulation of the Shannon wavelets for the numerical solution of a class of Volterra integro-differential equation is proposed. Our approach is based on the connection coefficients of the Shannon wavelet and collocation method for constructing the algebraic equivalent representation of the problem. Also, the Shannon approximation is applied to solve one type of nonlinear integral equation arising from chemical phenomenon. An analysis of error for the problem is given. The obtained numerical results show the accuracy of the presented method.

1 Introduction

Integral, integro-differential, ordinary and fractional differential equations are used in modelling problems of engineering and science fields, including mathematical biology, electromagnetic theory, potential theory and chemical engineering, see [1, 2, 5, 7, 8, 11, 14] and references therein.

The main purpose in this article is to develop and to provide a numerical algorithm based on the coefficients of the Shannon wavelets for the following form of integro-differential equation

$$\begin{aligned} \sum _{i=0}^{1}\Gamma _{i} u^{(i)}(x)=f(x)+\int _{a}^{x} k(x,t) u(t) dt, \end{aligned}$$

(1)

$$\begin{aligned} u(a)=a_{0}, \end{aligned}$$

where $\Gamma _{i}$ are constants, k and f are given functions and u(x) is a solution to be determined. Noting that for $\Gamma _{1}=0$, (1) be transformed to integral equation.

Over the past few decades, the numerical solvability of these type of equations has been studied intensively by many authors, such as Chebyshev spectral solution [6], rationalized Haar functions [12] and Sinc-Legendre collocation method [13].

Wavelets are very powerful and useful tool in data compression, signal and operator analysis. The real part of the harmonic wavelets is Shannon wavelets. These wavelets can be used to study frequency changes as well as oscillations in a small range time interval [4].

This paper is organized as follows: Sect. 2 introduces some basic definitions and preliminaries of the Shannon wavelets. We derive formulas for a class of IDEs and give a numerical scheme based on proposed method in Sect. 3. Error analysis of our method is considered in Sect. 4. Finally, in Sect. 5, we report several numerical experiments to clarify the efficiency and accuracy of the proposed method.

2 Preliminary Definitions

Here, we give some basic definitions of the Shannon wavelets family [4, 9]. The Sinc function is defined on the whole real line by:

$$\begin{aligned} Sinc(x)=\left\{ \begin{array}{ll} \frac{\sin (\pi x)}{\pi x},&{}x\ne 0, \\ 1, &{}x=0. \end{array}\right. \end{aligned}$$

The Shannon scaling functions and mother wavelets can be defined as:

$$\begin{aligned} \left\{ \begin{array}{lll} \varphi _{j,k}(x)=2^{j/2}Sinc(2^{j}x-k)=2^{j/2}\dfrac{\sin \pi (2^{j}x-k)}{\pi (2^{j}x-k)}, &{} &{} j,k\in Z, \\ \psi _{j,k}(x)=2^{j/2}\dfrac{\sin \pi (2^{j}x-k-\frac{1}{2})- \sin 2\pi (2^{j}x-k-\frac{1}{2})}{\pi (2^{j}x-k-\frac{1}{2})},&{} &{} j,k\in Z,\\ \end{array}\right. \end{aligned}$$

we recall the following theorem from [3]:

Theorem 2.1

If $u(x)\in L_{2}(\mathbb {R})$, then

$$\begin{aligned} u(x)=\sum _{k=-\infty }^{\infty }\alpha _{k} \varphi _{0,k}(x)+\sum _{j=0}^{\infty }\sum _{k=-\infty }^{\infty }\beta _{j,k}\psi _{j,k}(x), \end{aligned}$$

(2)

with

$$\begin{aligned} \alpha _{k}=<u,\varphi _{0,k}>=\int _{-\infty }^{\infty } u(x)\varphi _{0,k}(x)dx, \end{aligned}$$

(3)

$$\begin{aligned} \beta _{j,k}=<u,\psi _{j,k}>=\int _{-\infty }^{\infty } u(x) \psi _{j,k}(x) dx. \end{aligned}$$

(4)

Using a finite truncated series of the above theorem, we can define an approximation function of the exact solution u(x) as follows:

$$\begin{aligned} u(x)\simeq \sum _{k=-M}^{M}\alpha _{k} \varphi _{0,k}(x)+\sum _{j=0}^{N}\sum _{k=-M}^{M}\beta _{j,k}\psi _{j,k}(x). \end{aligned}$$

(5)

The nth derivatives of u(x) in terms of the Shannon wavelets can be written as (see e.g. [9] for further details):

$$\begin{aligned} u^{(n)}(x)\simeq \sum _{k=-M}^{M}\alpha _{k} \varphi ^{(n)}_{0,k}(x)+\sum _{j=0}^{N}\sum _{k=-M}^{M}\beta _{j,k}\psi ^{(n)}_{j,k}(x), \end{aligned}$$

(6)

on the other hand, we have the following relations [4]:

$$\begin{aligned} \varphi ^{(n)}_{0,k}(x)=\sum _{h=-M}^{M}\lambda ^{(n)}_{kh} \varphi _{0,h}(x) \end{aligned}$$

(7)

$$\begin{aligned} \psi ^{(n)}_{j,k}(x)=\sum _{h=-M}^{M}\gamma ^{(n)jj}_{kh}\psi _{j,h}(x). \end{aligned}$$

(8)

Therefore, (6) rewritten as:

$$\begin{aligned} u^{(n)}(x)\simeq \sum _{k=-M}^{M}\alpha _{k}\sum _{h=-M}^{M}\lambda ^{(n)}_{kh} \varphi _{0,h}(x)+\sum _{j=0}^{N}\sum _{k=-M}^{M}\beta _{j,k}\sum _{h=-M}^{M}\gamma ^{(n)jj}_{kh}\psi _{j,h}(x), \end{aligned}$$

(9)

where

$$\begin{aligned} \lambda ^{(n)}_{kh}=\left\{ \begin{array}{lll} (-1)^{k-h}\frac{i^{n}}{2\pi }\sum _{s=1}^{n}\dfrac{l!\pi ^{s}}{s![i(k-h)]^{n-s+1}}[(-1)^{s}-1],&{} &{} k\ne h, \\ \dfrac{i^{n}\pi ^{n+1}}{2\pi (n+1)}[1+(-1)^{n}],&{} &{} k=h, \end{array}\right. \end{aligned}$$

(10)

$$\begin{aligned} \gamma ^{(n)jj}_{kh}=\left\{ \begin{array}{lll} \dfrac{i^{n} 2^{jn}}{2\pi }\Sigma _{m=1}^{n}(-1)^{n}\dfrac{n!\pi ^{m}(2^{m}-1)}{m![i(h-k)]^{n-m+1}}[(-1)^{m}-1],&{} &{} k\ne h, \\ \dfrac{i^{n} 2^{jn}\pi ^{n+1}}{2\pi (n+1)}[1+(-1)^{n}][2^{n+1}-1],&{} &{} k=h, \end{array}\right. \end{aligned}$$

(11)

which $\lambda ^{(n)}_{kh}$ and $\gamma ^{(n)jj}_{kh}$ are known as the connection coefficients.

Moreover, it is

$$\begin{aligned} \gamma ^{(n)jj}_{kh}=2^{n(j-1)}\gamma ^{(n)11}_{kh}. \end{aligned}$$

(12)

3 Numerical Treatment of the Problem

In this section, we will obtain formulas for numerical solvability of (1), based on the previous results. We define an approximation function $u^{'}(x)$ as follows:

$$\begin{aligned} u^{'}(x)\simeq \sum _{k=-M}^{M}\alpha _{k}\sum _{h=-M}^{M}\lambda ^{(1)}_{kh} \varphi _{0,h}(x)+\sum _{j=0}^{N}\sum _{k=-M}^{M}\beta _{j,k}\sum _{h=-M}^{M}\gamma ^{(1)jj}_{kh}\psi _{j,h}(x). \end{aligned}$$

(13)

By taking $n=1$ in (10), (11) and using simple computations, we obtain the following relations for $\lambda ^{(1)}_{kh}$ and $\gamma ^{(1)jj}_{kh}$:

$$\begin{aligned} \lambda ^{(1)}_{kh}=\left\{ \begin{array}{lll} -\frac{(-1)^{k-h}}{k-h},&{} &{} k\ne h, \\ 0,&{} &{} k=h, \end{array}\right. \quad \gamma ^{(1)jj}_{kh}=\left\{ \begin{array}{lll} \frac{2^{j}}{(h-k)},&{} &{} ~~~ k\ne h, \\ 0,&{} &{} ~~~k=h, \end{array}\right. ~~~~ \end{aligned}$$

(14)

and due to (12), we can write $\gamma ^{(1)jj}_{kh}=2^{(j-1)}\gamma ^{(1)11}_{kh},$ for $j>1$.

Now, we are ready to apply the obtained results for constructing the algebraic equivalent presentation of (1). Equation (1) can be rewritten as:

$$\begin{aligned} \Gamma _{0}u(x)+\Gamma _{1}u^{'}(x)=f(x)+\int _{a}^{x}k(x,t)u(t)dt, \end{aligned}$$

by substituting (5), (13) and (14) in the above equation, we have:

$$\begin{aligned}&\Gamma _{0}\left[ \sum _{k=-M}^{M}\alpha _{k} \varphi _{0,k}(x)+\sum _{j=0}^{N}\sum _{k=-M}^{M}\beta _{j,k}\psi _{j,k}(x)\right] \\&+\Gamma _{1}\left[ \sum _{k=-M}^{M}\alpha _{k}\sum _{h=-M}^{M}\lambda ^{(1)}_{kh}\varphi _{0,h}(x)+\sum _{j=0}^{N}\sum _{k=-M}^{M}\beta _{j,k}\sum _{h=-M}^{M}\gamma ^{(1)jj}_{kh}\psi _{j,h}(x)\right] \\&\qquad =f(x)+\int _{a}^{x}k(x,t)\left[ \sum _{k=-M}^{M}\alpha _{k}\varphi _{0,k}(t)+\sum _{j=0}^{N}\sum _{k=-M}^{M}\beta _{j,k}\psi _{j,k}(t)\right] dt, \end{aligned}$$

and by rearranging the above equation based on unknowns $\alpha _{k}$ and $\beta _{j,k}$, we get

$$\begin{aligned} \displaystyle&\sum _{k=-M}^{M}\alpha _{k}\left[ \Gamma _{0} \varphi _{0,k}(x)+\Gamma _{1}\sum _{h=-M}^{M}\lambda ^{(1)}_{kh} \varphi _{0,h}(x) -\int _{a}^{x}k(x,t) \varphi _{0,k}(t)dt\right] \\ \displaystyle +\sum _{j=0}^{N}\sum _{k=-M}^{M}&\beta _{j,k}\left[ \Gamma _{0} \psi _{j,k}(x)+\Gamma _{1}\sum _{h=-M}^{M}\gamma ^{(1)jj}_{kh}\psi _{j,h}(x)-\int _{a}^{x}k(x,t) \psi _{j,k}(t)dt\right] =f(x).\nonumber \end{aligned}$$

(15)

We may set

$$\begin{aligned}&\Phi _{k}(x)=\Gamma _{0} \varphi _{0,k}(x)+\Gamma _{1}\sum _{h=-M}^{M}\lambda ^{(1)}_{kh} \varphi _{0,h}(x)-\int _{a}^{x}k(x,t) \varphi _{0,k}(t)dt,\\&\Psi _{j,k}(x)=\Gamma _{0} \psi _{j,k}(x)+\Gamma _{1}\sum _{h=-M}^{M}\gamma ^{(1)jj}_{kh}\psi _{j,h}(x)-\int _{a}^{x}k(x,t) \psi _{j,k}(t)dt, \end{aligned}$$

therefore, we can write (15) as:

$$\begin{aligned} \sum _{k=-M}^{M}\alpha _{k}\Phi _{k}(x)+\sum _{j=0}^{N}\sum _{k=-M}^{M}\beta _{j,k}\Psi _{j,k}(x)=f(x). \end{aligned}$$

(16)

For obtaining $(2N+1)(2M+2)$ unknowns $\alpha _{k}$ and $\beta _{j,k}$, we take $x=x_{i}$ for $i=1,\ldots ,(2N+1)(2M+2)-1$, where $x_{i}$ be collocation points. So, we have

$$\begin{aligned} \sum _{k=-M}^{M}\alpha _{k}\Phi _{k}(x_{i})+\sum _{j=0}^{N}\sum _{k=-M}^{M}\beta _{j,k}\Psi _{j,k}(x_{i})=f(x_{i}). \end{aligned}$$

(17)

On the other hand, $u(a)=a_{0}$ can be written as

$$\begin{aligned} \sum _{k=-M}^{M}\alpha _{k} \varphi _{0,k}(a)+\sum _{j=0}^{N}\sum _{k=-M}^{M}\beta _{j,k}\psi _{j,k}(a)=a_{0}. \end{aligned}$$

(18)

According to above equations, a system of $(2N+1)(2M+2)$ linear equations is obtained. By solving the resulting system, unknowns $\alpha _{k}$ and $\beta _{j,k}$ can be determined and so the approximate solution u(x) will be obtained.

The following algorithm summarizes our proposed method:

4 Error Analysis

In this section, we will provided a convergence analysis of the numerical algorithm for a class of integro-differential equation (1).

Theorem 4.1

Assume that $\widetilde{u}(x)$ be the approximate solution of Eq. (1). If $u^{(1)}(x)\in L_{2}(\mathbb {R})$, then the obtained approximation solution of the proposed method converges to the exact solution, where $\alpha _{k}$ and $\beta _{j,k}$ are given in Theorem 2.1.

Proof

Note that

$$\begin{aligned} \widetilde{u}(x)&=\sum _{k=-\infty }^{\infty }<u,\varphi _{0,k}>\varphi _{0,k}(x)+\sum _{j=0}^{N-1}\sum _{k=-\infty }^{\infty }<u,\psi _{j,k}>\psi _{j,k}(x) \\&=\sum _{j=-\infty }^{N-1}\sum _{k=-\infty }^{\infty }<u,\psi _{j,k}>\psi _{j,k}(x).\nonumber \end{aligned}$$

(19)

Due to [9], the following relation holds

$$\begin{aligned} \Vert D^{(n)}\left[ \sum _{j=-\infty }^{N-1}\sum _{k=-\infty }^{\infty }<u,\psi _{j,k}>\psi _{j,k}(x)-u(x)\right] \Vert _{2}\rightarrow 0, ~~~as\,N\rightarrow \infty , \end{aligned}$$

or

$$\begin{aligned} \Vert \bigg [\sum _{k=-\infty }^{\infty }<u,\varphi _{0,k}>\varphi ^{(n)}_{0,k}(x)+\sum _{j=0}^{N-1}\sum _{k=-\infty }^{\infty }<u,\psi _{j,k}>\psi ^{(n)}_{j,k}(x)-u^{(n)}&(x) \bigg ]\Vert _{2}\rightarrow 0,\\ as\,N\rightarrow \infty ,&\end{aligned}$$

according to definitions of $\alpha _{k}$ and $\beta _{j,k}$ in Theorem 2.1 and Eqs. (7) and (8), for $n=1$ above relation can be written as

$$\begin{aligned} \lim _{N\rightarrow \infty } \left[ \sum _{k=-\infty }^{\infty }\alpha _{k}\sum _{h=-\infty }^{\infty }\lambda ^{(1)}_{kh} \varphi _{0,h}(x)+\sum _{j=0}^{N-1}\sum _{k=-\infty }^{\infty }\beta _{j,k}\sum _{h=-\infty }^{\infty }\gamma ^{(1)jj}_{kh}\psi _{j,h}(x)\right] =u^{(1)}(x), \end{aligned}$$

which proves the theorem.$\square$

Theorem 4.2

Let $u^{(1)}_{M}(x)$ be the first-order derivative of the approximate solution of Eq. (1), then there exist constants $C_{1}$ and $C_{2}$ independent of N and M, such that

$$\begin{aligned} \begin{array}{ll} \left| u^{(1)}(x)-\widetilde{u}^{(1)}_{M}(x)\right| &{} \le \left| C_{1}(u(-M-1)+u(M+1)) \right. \\ &{}-C_{2}\left[ \frac{3\sqrt{3}}{\pi } [u(2^{-N-1}(-M-\frac{1}{2}))+u(2^{-N-1}(M+\frac{3}{2}))]\right] |, \end{array} \end{aligned}$$

where $C_{1}=Max\{|\sum _{k} \sum _{h} \lambda _{kh}^{(1)}|\}$, $C_{2}=Max\{|\sum _{k} \sum _{h} \gamma _{kh}^{(1)jj}|\}$ and M, N refer to the given values of j and k.

Proof

See [10].

Detailed analysis of the proof of this theorem can be found in [9, 10], so we refrain from going into details.

5 Numerical Results

In this section, several test problems are considered to demonstrate the accuracy of the proposed method.

Example 5.1

Consider the following equation

$$\begin{aligned} \left\{ \begin{array}{llll} u^{'}(x)-2u(x)=f(x)+\int _{0}^{x}k(x,t) u(t)dt,\\ f(x)=1-2x-\dfrac{x^{4}}{2}-\dfrac{x^{3}}{3},\\ k(x,t)=x^{2}+t,\\ u(0)=0, \end{array}\right. \end{aligned}$$

(20)

with the exact solution $u(x)=x$.

Example 5.2

Consider the following equation

$$\begin{aligned} \left\{ \begin{array}{ll} u^{'}(x)-3 u(x)=f(x)+\int _{0}^{x}k(x,t) u(t)dt,\\ f(x)=-1+x-2xe^{x}-e^{x},\\ k(x,t)=x+t,\\ u(0)=1, \end{array}\right. \end{aligned}$$

(21)

with the exact solution $u(x)=e^{x}$.

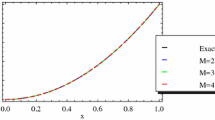
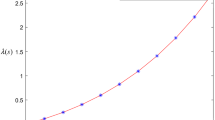
The computational results of Examples 5.1 and 5.2 have been reported in Tables 1 and 2, to show the accurate solution of mentioned algorithm. The exact and approximate solution of these examples for different values of M and N are compared in Figs. 1 and 2.

Table 1 Numerical results of Example 5.1 using Shannon approximation

Table 2 Numerical results of Example 5.2 using Shannon approximation

Fig. 1

Exact and approximate solution of Example 5.1 for different values of M and N using presented method

Fig. 2

Exact and approximate solution of Example 5.2 for different values of M and N using presented method

Table 3 Numerical results of Examples 5.3 and 5.4 using Shannon approximation

Example 5.3

Consider the following equation with the exact solution

$$u(x)=1-\sinh (x).$$

$$\begin{aligned} \left\{ \begin{array}{ll} u(x)=f(x)+\int _{0}^{x}k(x,t) u(t)dt,\\ f(x)=1-x-\dfrac{x^{2}}{2},\\ k(x,t)=x-t.\\ \end{array}\right. \end{aligned}$$

(22)

Examples 5.3 and 5.4, which are obtained by taking $\Gamma _{1}=0$, are integral equations. The numerical results of these examples are reported in Table 3. Also, Figs. 3 and 4 show the exact and approximate solution of Examples 5.3 and 5.4 for M $=$ 2 and N $=$ 3, respectively.

Fig. 3

Exact and approximate solution of Example 5.3 for M $=$ 2 and N $=$ 3 using presented method

Fig. 4

Exact and approximate solution of Example 5.4 for M $=$ 2 and N $=$ 3 using presented method

Table 4 Numerical results of Example 5.4 using Shannon approximation

Example 5.4

Consider the following equation

$$\begin{aligned} \left\{ \begin{array}{ll} u(x)=f(x)+\int _{0}^{x}k(x,t) u(t)dt,\\ f(x)=1,\\ k(x,t)=-x+t,\\ \end{array}\right. \end{aligned}$$

(23)

with the exact solution $u(x)=\cos (x)$.

Example 5.5

Consider the following equation

$$\begin{aligned} \left\{ \begin{array}{ll} u(x)=f(x)+\int _{0}^{1}k(x,t) (u(t))^{-1}dt,\\ f(x)=\dfrac{21-11e^{10}}{100}e^{(-10(1+x))}+\dfrac{1}{1+x},\\ k(x,t)=e^{-10(x+t)},\\ \end{array}\right. \end{aligned}$$

(24)

with the exact solution $u(x)=\dfrac{1}{1+x}$. This problem is a nonlinear Hammerstein integral equation which arising from chemical phenomenon. By choosing Shannon scaling functions, Example 5.5 has been solved. The reported results in Table 4 show that the Shannon approximation has produced highly numerical results. Good numerical results can be achieved by additional numerical experiments (e.g. with $N\ge 2$). This problem has been solved by $u(x)\simeq \sum _{k=1}^{2^{N}}\alpha _{k} \varphi _{N,k}(x)$.

6 Conclusions

In this present work, we applied an accurate and efficient method for solving a class of IDEs. We consider a special class of IE, which is a quantum chemistry, by the Shannon scaling functions. Our obtained results are in a good agreement with the exact solutions and are given to demonstrate the applicability of our proposed method.