Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Generalized continuum theories represent nowadays one of the most promising research fields in continuum mechanics. Sound theoretical results are already provided in the literature (see [8, 18, 21, 35, 38, 41, 49] for general results in higher gradient theory, [1, 22, 40, 42, 44,45,46] for pantographic and fibrous materials and [7, 19, 20] for second gradient fluids) together with interesting results concerning the more general field of microstructured/micromorphic continua (see for instance [28, 29, 32, 34, 47, 48], and in particular [2,3,4,5] for application to carbon nanotube and [6, 23, 25, 26] for biological application; a general introduction for the particular case of micropolar continua is [33]). In this framework pantographic structures represent, in the opinion of the authors, an ideal starting point for the theoretical understanding of generalized continua. In fact, they represent the simplest possible 2D continuum in wich second gradient effects naturally arise from the geometry of the microstructure. Moreover, availability of technologies such as 3D printing and other computer-aided techniques, allows a ready experimental comparison that reveals very fruitful in boosting the modeling process for pantografic sheets and for microstructured continua in general. In order to have this strict interaction between theoretical and experimental research properly working, suitable numerical tools should be provided since, with the exception of some particular cases (such as the examples presented in this work), it is in general impossible to provide closed-form solutions. The numerical tools employed are often borrowed from well-established techniques based mainly on Finite Element Method [9,10,11,12, 24, 39, 43], but sometimes high-regularity elements ensuring suitably strong continuity conditions needed by higher gradient models are required (e.g. [13,14,15,16, 27]).

The work is organized as follows. In Sect. 2 we recall the derivation of governing PDEs, obtained in [50] for a homogeneous D4 anisotropic two-dimensional second gradient elastic material. In this case, explicit form of stress and hyper stress components have been derived in terms both of the strain (and of its gradient) and of the displacement field (i.e., of first, of second and of third derivatives of its components). Thus, the stress divergence and the hyper stress double divergence vectors have been derived, so that the final form of the PDEs, that were first exposed in [50], have been re-obtained. In Sect. 3, the analytical solutions of the heavy sheet, of the non-conventional bending and of the trapezoidal cases, that have been shown in [50], will be analyzed. In particular, the strain, the strain-gradient, the stress and the hyper stress components will be derived. Besides, contact force and double force, for each of the four sides of the rectangular body, will be given, as well as the contact vertex forces for each of its four vertexes. In Sect. 4 the pantographic case has been analyzed, generalizing the results of [37] to the case where in the pantographic sheet springs are present instead of perfect hinges. In particular, we will show how the analytical solutions of the heavy sheet, of the non-conventional bending and of the trapezoidal cases, that have been obtained in [37], can be achieved with the presence of these internal rotational springs by applying a system of external couples, able to annihilate the effects of the internal rotational springs. Such a system of external couples will be identified with out-of-diagonal components of the external bulk double forces. Finally, the identification between the pantograph with internal rotational springs (the micro-model) and the continuous homogeneous D4 anisotropic two-dimensional elastic second gradient rectangular body (the macro-model) will give an explicit identification of the nine constitutive parameters of the macro-model in terms of constitutive characteristics of the micro-model. In Sect. 5 a simple form of the internal energy, in terms of the displacement field and of its first and second gradient components, will be shown. This form includes not only the contributions of both families of fibers, for axial and for bending deformations of the micro-beams, but also of the internal rotational springs. In Sect. 6 some conclusions will be driven.

Finally, a linguistic remark: in this paper (as well as in [36]) we use the expression “gedanken experiment” in order to describe the type of reasoning that allows us to find the constitutive parameters we search for. Since this linguistic choice has been argued sometimes, we would like to point out the following. According to the Stanford Encyclopedia of Philosophy [51], a gedanken experiment is a thought experiment, i.e. a device of the imagination used to investigate the nature of things. Gedanken experiments are used for diverse reasons in a variety of areas. The experiments should be imagined and schematically described, regardless of any possibility of practical realization. As model cases one can consider the well known experiments on the concept of simultaneity in Special Relativity or the EPR experiment by Einstein, Podolsky and Rosen (see for instance [52]). Our line of reasoning, though of course simpler, is nonetheless exactly of this type, and therefore we stick to our previous choice.

2 Outline of the Model

In this Section we briefly recall the main facts about the linear elastic second gradient D4 orthotropic two-dimensional continuum model employed in this paper, which can be found in more detail in [50].

\(\mathscr {B}\) is a 2-dimensional body that is considered in the reference configuration, where X denotes the coordinates of its material points. \(U\left( G,\nabla G\right) \) is the internal energy density functional, that is a function of the deformation matrix \(G=\left( F^{T}F-I\right) /2\) and of its gradient \(\nabla G\). Here, \(F=\nabla \chi \), where \(\chi \) is the placement function, \(F^{T}\) is the transpose of F, and \(\nabla \) is the gradient operator. The energy functional \(\mathscr {E}\left( u\left( \cdot \right) \right) \) depends on the displacement \(u=\chi -X\) and includes two contributions: the internal and the external energies,

$$\begin{aligned} \mathscr {E}\left( u\left( X\right) \right) =\int _{\mathscr {B}}\left[ U\left( G,\nabla G\right) -b^{ext}\cdot u-m^{ext}\cdot \nabla u\right] dA\\ -\int _{\partial \mathscr {B}}\left[ t^{ext}\cdot u+\tau ^{ext}\cdot \left[ \left( \nabla u\right) n\right] \right] ds-\int _{\left[ \partial \partial \mathscr {B}\right] }f^{ext}\cdot u.\nonumber \end{aligned}$$
(1)

Here, n is the unit external normal and the dot the scalar product between vectors or tensors. \(b^{ext}\) and \(m^{ext}\) are (per unit area) the external body force and double force, respectively; \(t^{ext}\) and \(\tau ^{ext}\) are (per unit length) the external force and double force; \(f^{ext}\) is the external concentrated force, that is applied on the vertices \(\left[ \partial \partial \mathscr {B}\right] \). The boundary \(\partial \mathscr {B}\) is assumed to be the union of m regular parts \(\Sigma _{c}\) (with \(c=1,\ldots ,m\)) and the so-called boundary of the boundary \(\left[ \partial \partial \mathscr {B}\right] \) is assumed to be the union of the corresponding m vertex-points \(\mathscr {V}_{c}\) (with \(c=1,\ldots ,m\)) with coordinates \(X^{c}\).

It is worth noting that the new contribution of [50] with respect to [36] is in the tensor \(m^{ext}\). This term will be crucial for the identification that we are going to perform.

It is well-established that in the general second gradient linear case we have

$$\begin{aligned} U\left( G,\nabla G\right) =\hat{U}\left( \varepsilon ,\eta \right) =\frac{1}{2}C_{IJ}\varepsilon _{I}\varepsilon _{J}+\frac{1}{2}A_{\alpha \beta }\eta _{\alpha }\eta _{\beta } \end{aligned}$$
(2)

where the indices I and J go from 1 to 3 and the indices \(\alpha \) and \(\beta \) go from 1 to 6. In [50], Eqs. (14), (16), (17), (19), \(\varepsilon \), \(\eta \), C and A are reported component-wise, respectively.

In [50], the computation of the minimum of \(\mathscr {E}\) is performed and (see Eq. (21) therein) the system of PDEs for anisotropic \(D_{4}\) elastic second gradient materials has been deduced in terms of the displacement field.

We now shall show some explicit computations which are instrumental for the identification procedure. Referring to the notation introduced in [50], Eqs. (5)–(8), the stress components read:

$$\begin{aligned}&S_{11}=\frac{\partial U}{\partial G_{11}}=\frac{\partial U}{\partial \varepsilon _{1}}=C_{1I}\varepsilon _{I}=C_{11}\varepsilon _{1}+C_{12}\varepsilon _{2}+C_{13}\varepsilon _{3}=c_{11}G_{11}+c_{12}G_{22},\end{aligned}$$
(3)
$$\begin{aligned}&S_{12}=S_{21}=\frac{1}{2}\frac{\partial U}{\partial G_{12}}=\frac{\sqrt{2}}{2}\frac{\partial U}{\partial \varepsilon _{3}}\nonumber \\&\qquad =\frac{\sqrt{2}}{2}C_{3I}\varepsilon _{I}=\frac{\sqrt{2}}{2}C_{31}\varepsilon _{1}+\frac{\sqrt{2}}{2}C_{32}\varepsilon _{2}+\frac{\sqrt{2}}{2}C_{33}\varepsilon _{3}=c_{33}G_{12},\end{aligned}$$
(4)
$$\begin{aligned}&S_{22}=\frac{\partial U}{\partial G_{22}}=\frac{\partial U}{\partial \varepsilon _{2}}=C_{2I}\varepsilon _{I}=C_{21}\varepsilon _{1}+C_{22}\varepsilon _{2}+C_{23}\varepsilon _{3}=c_{12}G_{11}+c_{11}G_{22}. \end{aligned}$$
(5)

The hyperstress components read:

$$\begin{aligned}&T_{111}=\frac{\partial U}{\partial G_{11,1}}=\frac{\partial U}{\partial \eta _{1}}=A_{1\alpha }\eta _{\alpha }=a_{11}G_{11,1}+a_{12}G_{22,1}+\sqrt{2}a_{13}G_{12,2},\end{aligned}$$
(6)
$$\begin{aligned}&T_{112}=\frac{\partial U}{\partial G_{11,2}}=\frac{\partial U}{\partial \eta _{5}}=A_{5\alpha }\eta _{\alpha }=a_{12}G_{22,2}+a_{22}G_{11,2}+\sqrt{2}a_{23}G_{12,1},\end{aligned}$$
(7)
$$\begin{aligned}&T_{121}=T_{211}=\frac{1}{2}\frac{\partial U}{\partial G_{12,1}}=\frac{\sqrt{2}}{2}\frac{\partial U}{\partial \eta _{6}}\nonumber \\&\qquad =\frac{\sqrt{2}}{2}A_{6\alpha }\eta _{\alpha }=\frac{\sqrt{2}}{2}a_{13}G_{22,2}+\frac{\sqrt{2}}{2}a_{23}G_{11,2}+a_{33}G_{12,1},\end{aligned}$$
(8)
$$\begin{aligned}&T_{122}=T_{212}=\frac{1}{2}\frac{\partial U}{\partial G_{12,2}}=\frac{\sqrt{2}}{2}\frac{\partial U}{\partial \eta _{3}}\nonumber \\&\qquad =\frac{\sqrt{2}}{2}A_{3\alpha }\eta _{\alpha }=\frac{\sqrt{2}}{2}a_{13}G_{11,1}+\frac{\sqrt{2}}{2}a_{23}G_{22,1}+a_{33}G_{12,2}, \end{aligned}$$
(9)
$$\begin{aligned}&T_{221}=\frac{\partial U}{\partial G_{22,1}}=\frac{\partial U}{\partial \eta _{2}}=A_{2\alpha }\eta _{\alpha }=a_{12}G_{11,1}+a_{22}G_{22,1}+\sqrt{2}a_{23}G_{12,2},\end{aligned}$$
(10)
$$\begin{aligned}&T_{222}=\frac{\partial U}{\partial G_{22,2}}=\frac{\partial U}{\partial \eta _{4}}=A_{4\alpha }\eta _{\alpha }=a_{11}G_{22,2}+a_{12}G_{11,2}+\sqrt{2}a_{13}G_{12,1}. \end{aligned}$$
(11)

It is worth to be noted that, by replacing the components of the strain and of the strain gradient tensors

$$\begin{aligned}&G_{11}=u_{1,1},\quad G_{12}=G_{21}=\frac{1}{2}\left( u_{1,2}+u_{2,1}\right) ,\quad G_{22}=u_{2,2},\end{aligned}$$
(12)
$$\begin{aligned}&G_{11,1}=u_{1,11},\quad G_{11,2}=u_{1,12},\quad G_{22,1}=u_{2,12},\quad G_{22,2}=u_{2,22},\end{aligned}$$
(13)
$$\begin{aligned}&G_{12,1}=G_{21,1}=\frac{1}{2}\left( u_{1,12}+u_{2,11}\right) ,\quad G_{12,2}=G_{21,2}=\frac{1}{2}\left( u_{1,22}+u_{2,12}\right) , \end{aligned}$$
(14)

into (3)–(11), we obtain, respectively, the stress and the hyperstress components in terms of the displacement fields,

$$\begin{aligned}&S_{11}=c_{11}u_{1,1}+c_{12}u_{2,2},\end{aligned}$$
(15)
$$\begin{aligned}&S_{12}=S_{21}=\frac{1}{2}c_{33}\left( u_{1,2}+u_{2,1}\right) ,\end{aligned}$$
(16)
$$\begin{aligned}&S_{22}=c_{11}u_{2,2}+c_{12}u_{1,1},\end{aligned}$$
(17)
$$\begin{aligned}&T_{111}=a_{11}u_{1,11}+a_{12}u_{2,12}+\frac{a_{13}}{\sqrt{2}}\left( u_{1,22}+u_{2,12}\right) ,\end{aligned}$$
(18)
$$\begin{aligned}&T_{112}=a_{12}u_{2,22}+a_{22}u_{1,12}+\frac{a_{23}}{\sqrt{2}}\left( u_{1,12}+u_{2,11}\right) ,\end{aligned}$$
(19)
$$\begin{aligned}&T_{121}=T_{211}=\frac{\sqrt{2}}{2}a_{13}u_{2,22}+\frac{\sqrt{2}}{2}a_{23}u_{1,12}+\frac{1}{2}a_{33}\left( u_{1,12}+u_{2,11}\right) ,\end{aligned}$$
(20)
$$\begin{aligned}&T_{122}=T_{212}=\frac{\sqrt{2}}{2}a_{13}u_{1,11}+\frac{\sqrt{2}}{2}a_{23}u_{2,12}+\frac{1}{2}a_{33}\left( u_{1,22}+u_{2,12}\right) ,\end{aligned}$$
(21)
$$\begin{aligned}&T_{221}=a_{12}u_{1,11}+a_{22}u_{2,12}+\frac{a_{23}}{\sqrt{2}}\left( u_{1,22}+u_{2,12}\right) ,\end{aligned}$$
(22)
$$\begin{aligned}&T_{222}=a_{11}u_{2,22}+a_{12}u_{1,12}+\frac{a_{13}}{\sqrt{2}}\left( u_{1,12}+u_{2,11}\right) , \end{aligned}$$
(23)

so that the first component of stress divergence in terms of the displacement field is

$$\begin{aligned} S_{11,1}+S_{12,2}=c_{11}u_{1,11}+c_{12}u_{2,12}+\frac{1}{2}c_{33}\left( u_{1,22}+u_{2,12}\right) . \end{aligned}$$
(24)

Besides, keeping in mind that

$$\begin{aligned}&T_{111,11}=a_{11}u_{1,1111}+a_{12}u_{2,1112}+\frac{a_{13}}{\sqrt{2}}\left( u_{1,1122}+u_{2,1112}\right) ,\\&T_{112,21}=a_{12}u_{2,1222}+a_{22}u_{1,1122}+\frac{a_{23}}{\sqrt{2}}\left( u_{1,1122}+u_{2,1112}\right) ,\\&T_{121,12}=\frac{\sqrt{2}}{2}a_{13}u_{2,1222}+\frac{\sqrt{2}}{2}a_{23}u_{1,1122}+\frac{1}{2}a_{33}\left( u_{1,1122}+u_{2,1112}\right) ,\\&T_{122,22}=\frac{\sqrt{2}}{2}a_{13}u_{1,1122}+\frac{\sqrt{2}}{2}a_{23}u_{2,1222}+\frac{1}{2}a_{33}\left( u_{1,2222}+u_{2,1222}\right) , \end{aligned}$$

the first component of the double divergence of the hyper-stress in terms of the displacement field is

$$\begin{aligned}&T_{1jh,hj}=a_{11}u_{1,1111}+a_{12}\left( u_{2,1112}+u_{2,1222}\right) \nonumber \\&\quad +\sqrt{2}\left( a_{13}+a_{23}\right) \left( u_{1,1122}+\frac{1}{2}u_{2,1112}+\frac{1}{2}u_{2,1222}\right) \nonumber \\&\quad \quad +a_{22}u_{1,1122}+a_{33}\left( u_{1,1122}+u_{2,1112}+u_{1,2222}+u_{2,1222}\right) . \end{aligned}$$
(25)

For the sake of brevity, from now on, whenever we will refer to an equation (n) in [50] we shall use the notation (n-P1). With this new notation it is now evident that (21-P1) is given by insertion of (24), and (25) into the integral argument of (3-P1).

3 Analytical Solutions

In this Section we shall elaborate on the top of analytical solutions proposed in [50] and give more details about the choice of compatible combinations of the external distributed bulk actions \(b^{ext}\) and \(m^{ext}\).

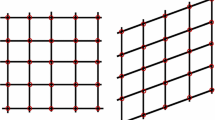
Since in [50] the case of a body of rectangular geometry is considered, in order to elaborate some of the analytical solutions proposed therein to perform identification through gedanken experiments, we shall do the same. In Fig. 1 the scheme of the rectangle considered in [50] is represented.

Fig. 1
figure 1

Nomenclature of the 2-dimensional body \(\mathscr {B}\)

Full size image

3.1 Heavy Sheet

The following displacement field is considered,

$$\begin{aligned} u_{1}=0,\qquad u_{2}=\frac{\rho g\left( X_{2}-l\right) \left( 3l+X_{2}\right) }{2c_{11}}. \end{aligned}$$
(26)

At the bottom the vertical displacement is

$$ u_{2}\left( X_{1},X_{2}=-l\right) =\frac{\rho g\left( -l-l\right) \left( 3l-l\right) }{2c_{11}}=-2\frac{\rho gl^{2}}{c_{11}}. $$

We have by derivation of (26)

$$\begin{aligned} u_{1,1}=u_{1,2}=u_{2,1}=0,\quad u_{2,2}=\frac{\rho g\left( X_{2}+l\right) }{c_{11}}. \end{aligned}$$
(27)

The strain components are by definition

$$\begin{aligned} G_{11}=0,\quad G_{12}=G_{21}=0,\quad G_{22}=\frac{\rho g\left( X_{2}+l\right) }{c_{11}} \end{aligned}$$
(28)

so that the strain gradient components are

$$\begin{aligned} G_{11,1}=G_{11,2}=G_{12,1}=G_{12,2}=G_{21,1}=G_{21,2}=G_{22,1}=0,\quad G_{22,2}=\frac{\rho g}{c_{11}}\,. \end{aligned}$$
(29)

Thus, from (15)–(17), the stress components are

$$\begin{aligned}&S_{11}=c_{11}G_{11}+c_{12}G_{22}=c_{12}\frac{\rho g\left( X_{2}+l\right) }{c_{11}},\end{aligned}$$
(30)
$$\begin{aligned}&S_{12}=S_{21}=2c_{33}G_{12}=0,\end{aligned}$$
(31)
$$\begin{aligned}&S_{22}=c_{12}G_{11}+c_{11}G_{22}=\rho g\left( X_{2}+l\right) , \end{aligned}$$
(32)

and, from (18)–(23), the hyperstress components are

$$\begin{aligned}&T_{111}=0,\end{aligned}$$
(33)
$$\begin{aligned}&T_{112}=a_{12}\frac{\rho g}{c_{11}},\end{aligned}$$
(34)
$$\begin{aligned}&T_{121}=T_{211}=\frac{\sqrt{2}}{2}a_{13}\frac{\rho g}{c_{11}},\end{aligned}$$
(35)
$$\begin{aligned}&T_{122}=T_{212}=0,\end{aligned}$$
(36)
$$\begin{aligned}&T_{221}=0,\end{aligned}$$
(37)
$$\begin{aligned}&T_{222}=a_{11}\frac{\rho g}{c_{11}}. \end{aligned}$$
(38)

From (4-P1), at the boundary sides with unit normal n we have the relations between, per unit length, the contact force t and double force \(\tau \) and the external force \(t^{ext}\) and double force \(\tau ^{ext}\),

$$\begin{aligned} t_{i}=t_{i}^{ext}+m_{ij}^{ext}n_{j},\qquad \tau _{i}=\tau _{i}^{ext}. \end{aligned}$$
(39)

Insertion of (24-P1)-(27-P1) into (39) and use of (30)–(38) gives for sides S, Q, R and T, respectively,

$$\begin{aligned}&t_{1}=t_{1}^{S}=c_{12}\frac{\rho g\left( X_{2}+l\right) }{c_{11}}=t_{1}^{ext,S}+m_{11}^{ext}=t_{1}^{ext,S},\end{aligned}$$
(40)
$$\begin{aligned}&t_{2}=t_{2}^{S}=0=t_{2}^{ext,S}+m_{21}^{ext}=t_{2}^{ext,S},\end{aligned}$$
(41)
$$\begin{aligned}&\tau _{1}=\tau _{1}^{S}=0=\tau _{1}^{S,ext},\end{aligned}$$
(42)
$$\begin{aligned}&\tau _{2}=\tau _{2}^{S}=\frac{\sqrt{2}}{2}a_{13}\frac{\rho g}{c_{11}}=\tau _{2}^{S,ext}.\end{aligned}$$
(43)
$$\begin{aligned}&t_{1}=t_{1}^{Q}=-c_{12}\frac{\rho g\left( X_{2}+l\right) }{c_{11}}=t_{1}^{ext,Q}-m_{11}^{ext}=t_{1}^{ext,Q},\end{aligned}$$
(44)
$$\begin{aligned}&t_{2}=t_{2}^{Q}=0=t_{2}^{ext,Q}-m_{21}^{ext}=t_{2}^{ext,Q},\end{aligned}$$
(45)
$$\begin{aligned}&\tau _{1}=\tau _{1}^{Q}=0=\tau _{1}^{Q,ext},\end{aligned}$$
(46)
$$\begin{aligned}&\tau _{2}=\tau _{2}^{Q}=\frac{\sqrt{2}}{2}a_{13}\frac{\rho g}{c_{11}}=\tau _{2}^{Q,ext}.\end{aligned}$$
(47)
$$\begin{aligned}&t_{1}=t_{1}^{R}=0=t_{1}^{ext,R}+m_{12}^{ext}=t_{1}^{ext,R},\end{aligned}$$
(48)
$$\begin{aligned}&t_{2}=t_{2}^{R}=\rho g\left( X_{2}+l\right) =2\rho gl+m_{22}^{ext}=t_{2}^{ext,R}+m_{22}^{ext}=t_{2}^{ext,R},\end{aligned}$$
(49)
$$\begin{aligned}&\tau _{1}=\tau _{1}^{R}=0=\tau _{1}^{R,ext},\end{aligned}$$
(50)
$$\begin{aligned}&\tau _{2}=\tau _{2}^{R}=a_{11}\frac{\rho g}{c_{11}}=\tau _{2}^{R,ext}. \end{aligned}$$
(51)
$$\begin{aligned}&t_{1}=t_{1}^{T}=0=t_{1}^{ext,T}-m_{12}^{ext}=t_{1}^{ext,T},\end{aligned}$$
(52)
$$\begin{aligned}&t_{2}=t_{2}^{T}=-\rho g\left( X_{2}+l\right) =-\rho g\left( -l+l\right) =0=t_{2}^{ext,T}-m_{22}^{ext}=t_{2}^{ext,T}, \qquad \end{aligned}$$
(53)
$$\begin{aligned}&\tau _{1}=\tau _{1}^{T}=0=\tau _{1}^{T,ext},\end{aligned}$$
(54)
$$\begin{aligned}&\tau _{2}=\tau _{2}^{T}=a_{11}\frac{\rho g}{c_{11}}=\tau _{2}^{T,ext}. \end{aligned}$$
(55)

At the vertices, from (42-P1) and (27), we have that the relevant combination of the hyperstress for characterization of vertex-forces are

$$ T_{112}+T_{121}=\left( a_{12}+\frac{\sqrt{2}}{2}a_{13}\right) \frac{\rho g}{c_{11}},\quad T_{212}+T_{221}=0 $$

so that, from (41-P1),

$$\begin{aligned} \left( f_{1}^{ext}\right) _{\mathscr {V}_{i}}=-\left( a_{12}+\frac{\sqrt{2}}{2}a_{13}\right) \frac{\rho g}{c_{11}},\quad i=1,3\end{aligned}$$
(56)
$$\begin{aligned} \left( f_{1}^{ext}\right) _{\mathscr {V}_{i}}=\left( a_{12}+\frac{\sqrt{2}}{2}a_{13}\right) \frac{\rho g}{c_{11}},\quad i=2,4\end{aligned}$$
(57)
$$\begin{aligned} \left( f_{2}^{ext}\right) _{\mathscr {V}_{i}}=0,\quad i=1,2,3,4. \end{aligned}$$
(58)

3.2 Non-conventional Bending

Let us take into account the following displacement field,

$$\begin{aligned} u_{1}=0,\qquad u_{2}=-\frac{aX_{1}^{2}}{2}. \end{aligned}$$
(59)

The maximum displacement (at side S) is

$$ u_{2}\left( X_{1}=L,X_{2}\right) =-\frac{aL^{2}}{2}. $$

We have by derivation of (59)

$$\begin{aligned} u_{1,1}=u_{1,2}=u_{2,2}=0,\quad u_{2,1}=-aX_{1}. \end{aligned}$$
(60)

The strain components are by definition

$$\begin{aligned} G_{11}=0,\quad G_{12}=G_{21}=-\frac{1}{2}aX_{1},\quad G_{22}=0, \end{aligned}$$
(61)

so that the strain gradient components are

$$\begin{aligned} G_{11,1}=G_{11,2}=G_{12,2}=G_{21,2}=G_{22,1}=G_{22,2}=0,\quad G_{12,1}=G_{21,1}=-\frac{1}{2}a. \end{aligned}$$
(62)

Thus, from (15)–(17), the stress components are

$$\begin{aligned}&S_{11}=c_{11}G_{11}+c_{12}G_{22}=0,\end{aligned}$$
(63)
$$\begin{aligned}&S_{12}=S_{21}=c_{33}G_{12}=-\frac{a}{2}X_{1}c_{33},\end{aligned}$$
(64)
$$\begin{aligned}&S_{22}=c_{12}G_{11}+c_{11}G_{22}=0, \end{aligned}$$
(65)

and, from (18)–(23), the hyperstress components are

$$\begin{aligned}&T_{111}=a_{11}G_{11,1}+a_{12}G_{22,1}+\sqrt{2}a_{13}G_{12,2}=0,\end{aligned}$$
(66)
$$\begin{aligned}&T_{112}=a_{12}G_{22,2}+a_{22}G_{11,2}+\sqrt{2}a_{23}G_{12,1}=-\frac{\sqrt{2}}{2}a_{23}a,\end{aligned}$$
(67)
$$\begin{aligned}&T_{121}=T_{211}=\frac{\sqrt{2}}{2}a_{13}G_{22,2}+\frac{\sqrt{2}}{2}a_{23}G_{11,2}+a_{33}G_{12,1}=-\frac{1}{2}a_{33}a,\end{aligned}$$
(68)
$$\begin{aligned}&T_{122}=T_{212}=\frac{\sqrt{2}}{2}a_{13}G_{11,1}+\frac{\sqrt{2}}{2}a_{23}G_{22,1}+a_{33}G_{12,2}=0,\end{aligned}$$
(69)
$$\begin{aligned}&T_{221}=a_{12}G_{11,1}+a_{22}G_{22,1}+\sqrt{2}a_{23}G_{12,2}=0,\end{aligned}$$
(70)
$$\begin{aligned}&T_{222}=a_{11}G_{22,2}+a_{12}G_{11,2}+\sqrt{2}a_{13}G_{12,1}=-\frac{\sqrt{2}}{2}a_{13}a. \end{aligned}$$
(71)

From (4-P1), at the boundary sides with unit normal n we have the relations between, per unit length, the contact force t and double force \(\tau \) and the external force \(t^{ext}\) and double force \(\tau ^{ext}\),

$$\begin{aligned} t_{i}=t_{i}^{ext}+m_{ij}^{ext}n_{j},\qquad \tau _{i}=\tau _{i}^{ext}. \end{aligned}$$
(72)

Insertion of (24-P1)-(27-P1) into (72) and use of (63)–(71) gives for sides S, Q, R and T, respectively,

$$\begin{aligned}& t_{1}=t_{1}^{S}=0=t_{1}^{ext,S}+m_{11}^{ext}=t_{1}^{ext,S}=0,\end{aligned}$$
(73)
$$\begin{aligned}&t_{2}=t_{2}^{S}=-\frac{a}{2}X_{1}c_{33}=t_{2}^{ext,S}+m_{21}^{ext}=t_{2}^{ext,S}-\frac{a}{2}c_{33}X_{1} \Rightarrow \ t_{2}^{ext,S}=0,\end{aligned}$$
(74)
$$\begin{aligned}&\tau _{1}=\tau _{1}^{S}=0=\tau _{1}^{S,ext},\end{aligned}$$
(75)
$$\begin{aligned}&\tau _{2}=\tau _{2}^{S}=-\frac{a}{2}a_{33}=\tau _{2}^{S,ext}. \end{aligned}$$
(76)
$$\begin{aligned}&t_{1}=t_{1}^{Q}=0=t_{1}^{ext,Q}-m_{11}^{ext}=t_{1}^{ext,Q}=0,\end{aligned}$$
(77)
$$\begin{aligned}&t_{2}=t_{2}^{Q}=\frac{a}{2}X_{1}c_{33}=t_{2}^{ext,Q}-m_{21}^{ext}=t_{2}^{ext,Q}+\frac{a}{2}c_{33}X_{1} \Rightarrow \ t_{2}^{ext,Q}=0,\end{aligned}$$
(78)
$$\begin{aligned}&\tau _{1}=\tau _{1}^{Q}=0=\tau _{1}^{Q,ext},\end{aligned}$$
(79)
$$\begin{aligned}&\tau _{2}=\tau _{2}^{Q}=-\frac{a}{2}a_{33}=\tau _{2}^{Q,ext}.\end{aligned}$$
(80)
$$\begin{aligned}&t_{1}=t_{1}^{R}=-\frac{a}{2}X_{1}c_{33}=t_{1}^{ext,R}+m_{12}^{ext}=t_{1}^{ext,R}-\frac{a}{2}X_{1}c_{33}=0\ \Rightarrow \ t_{1}^{ext,R}=0,\end{aligned}$$
(81)
$$\begin{aligned}&t_{2}=t_{2}^{R}=0=t_{2}^{ext,R}+m_{22}^{ext}=t_{2}^{ext,R}=0,\end{aligned}$$
(82)
$$\begin{aligned}&\tau _{1}=\tau _{1}^{R}=0=\tau _{1}^{R,ext},\end{aligned}$$
(83)
$$\begin{aligned}&\tau _{2}=\tau _{2}^{R}=-\frac{\sqrt{2}}{2}a_{13}a=\tau _{2}^{R,ext}.\end{aligned}$$
(84)
$$\begin{aligned}&t_{1}=t_{1}^{T}=\frac{a}{2}X_{1}c_{33}=t_{1}^{ext,T}-m_{12}^{ext}=t_{1}^{ext,T}+\frac{a}{2}X_{1}c_{33}\ \Rightarrow \ t_{1}^{ext,T}=0,\end{aligned}$$
(85)
$$\begin{aligned}&t_{2}=t_{2}^{T}=0=t_{2}^{ext,T}-m_{22}^{ext}=t_{2}^{ext,T},\end{aligned}$$
(86)
$$\begin{aligned}&\tau _{1}=\tau _{1}^{T}=0=\tau _{1}^{T,ext},\end{aligned}$$
(87)
$$\begin{aligned}&\tau _{2}=\tau _{2}^{T}=-\frac{\sqrt{2}}{2}a_{13}a=\tau _{2}^{T,ext}. \end{aligned}$$
(88)

From (42-P1) and (60), at the vertices we have that the relevant combinations of hyperstress for characterization of vertex-forces are

$$ T_{112}+T_{121}=-a\left( \frac{\sqrt{2}}{2}a_{23}+\frac{1}{2}a_{33}\right) ,\quad T_{212}+T_{221}=0 $$

so that, from (41-P1),

$$\begin{aligned} \left( f_{1}^{ext}\right) _{\mathscr {V}_{i}}=a\left( \frac{\sqrt{2}}{2}a_{23}+\frac{1}{2}a_{33}\right) ,\quad i=1,3\end{aligned}$$
(89)
$$\begin{aligned} \left( f_{1}^{ext}\right) _{\mathscr {V}_{i}}=-a\left( \frac{\sqrt{2}}{2}a_{23}+\frac{1}{2}a_{33}\right) ,\quad i=2,4\end{aligned}$$
(90)
$$\begin{aligned} \left( f_{2}^{ext}\right) _{\mathscr {V}_{i}}=0,\quad i=1,2,3,4. \end{aligned}$$
(91)

It is worth to be noted that the total external moment \(M_{S}^{ext}\) on side S is only due to the double force \(\tau _{2}^{ext,S}\) of (76)

$$\begin{aligned} M_{S}^{ext}=\int _{-l}^{l}\tau _{2}^{ext,S}ds=-a_{33}\frac{a}{2}\int _{-l}^{l}ds=-a_{33}al \end{aligned}$$
(92)

that provides an interpretation of the parameter a first introduced in (59), i.e.,

$$\begin{aligned} a=-\frac{M_{S}^{ext}}{a_{33}l}. \end{aligned}$$
(93)

3.3 Trapezoidal Case

Let us take into account the following displacement field

$$\begin{aligned}&u_{1}=0,\qquad u_{2}=bX_{1}X_{2}. \end{aligned}$$
(94)

We have by derivation of (94)

$$\begin{aligned} u_{1,1}=u_{1,2}=0,\quad u_{2,1}=bX_{2}\quad u_{2,2}=bX_{1}. \end{aligned}$$
(95)

The strain components are by definition

$$\begin{aligned} G_{11}=0,\quad G_{12}=G_{21}=\frac{1}{2}bX_{2},\quad G_{22}=bX_{1} \end{aligned}$$
(96)

so that the strain gradient components are

$$\begin{aligned} G_{11,1}=G_{11,2}=G_{12,1}=G_{21,1}=G_{22,2}=0,\quad G_{12,2}=G_{21,2}=\frac{1}{2}b\quad G_{22,1}=b. \end{aligned}$$
(97)

Thus, from (15)–(17), the stress components are

$$\begin{aligned}&S_{11}=c_{11}G_{11}+c_{12}G_{22}=bc_{12}X_{1},\end{aligned}$$
(98)
$$\begin{aligned}&S_{12}=S_{21}=c_{33}G_{12}=\frac{1}{2}bc_{33}X_{2},\end{aligned}$$
(99)
$$\begin{aligned}&S_{22}=c_{12}G_{11}+c_{11}G_{22}=bc_{11}X_{1}, \end{aligned}$$
(100)

and, from (18)–(23), the hyperstress components are

$$\begin{aligned} T_{111}= & {} a_{11}G_{11,1}+a_{12}G_{22,1}+\sqrt{2}a_{13}G_{12,2}=b\left( a_{12}+\frac{\sqrt{2}}{2}a_{13}\right) ,\end{aligned}$$
(101)
$$\begin{aligned} T_{112}= & {} a_{12}G_{22,2}+a_{22}G_{11,2}+\sqrt{2}a_{23}G_{12,1}=0,\end{aligned}$$
(102)
$$\begin{aligned} T_{121}= & {} T_{211}=\frac{1}{2}\sqrt{2}a_{13}G_{22,2}+\frac{1}{2}\sqrt{2}a_{23}G_{11,2}+a_{33}G_{12,1}=0,\end{aligned}$$
(103)
$$\begin{aligned} T_{122}= & {} T_{212}=\frac{1}{2}\sqrt{2}a_{13}G_{11,1}+\frac{1}{2}\sqrt{2}a_{23}G_{22,1}+a_{33}G_{12,2}\nonumber \\= & {} \frac{1}{2}b\left( \sqrt{2}a_{23}+a_{33}\right) ,\end{aligned}$$
(104)
$$\begin{aligned} T_{221}= & {} a_{12}G_{11,1}+a_{22}G_{22,1}+\sqrt{2}a_{23}G_{12,2}=b\left( a_{22}+\frac{\sqrt{2}}{2}a_{23}\right) ,\end{aligned}$$
(105)
$$\begin{aligned} T_{222}= & {} a_{11}G_{22,2}+a_{12}G_{11,2}+\sqrt{2}a_{13}G_{12,1}=0. \end{aligned}$$
(106)

Insertion of (24-P1)-(27-P1) into (39) and use of (63)–(71) gives for sides S, Q, R and T, respectively,

$$\begin{aligned}&t_{1}=t_{1}^{S}=c_{12}bX_{1}=c_{12}bL=t_{1}^{ext,S}+m_{11}^{ext}=t_{1}^{ext,S},\end{aligned}$$
(107)
$$\begin{aligned}&t_{2}=t_{2}^{S}=\frac{1}{2}bc_{33}X_{2}=t_{2}^{ext,S}+m_{21}^{ext}=t_{2}^{ext,S}+b\left( c_{12}+\frac{1}{2}c_{33}\right) X_{2}\nonumber \\&\qquad \Rightarrow \ t_{2}^{ext,S}=-bc_{12}X_{2},\end{aligned}$$
(108)
$$\begin{aligned}&\tau _{1}=\tau _{1}^{S}=b\left( a_{12}+\frac{\sqrt{2}}{2}a_{13}\right) =\tau _{1}^{S,ext},\end{aligned}$$
(109)
$$\begin{aligned}&\tau _{2}=\tau _{2}^{S}=0=\tau _{2}^{S,ext}. \end{aligned}$$
(110)
$$\begin{aligned}&t_{1}=t_{1}^{Q}=-bc_{12}X_{1}=0=t_{1}^{ext,Q}-m_{11}^{ext}=t_{1}^{ext,Q},\end{aligned}$$
(111)
$$\begin{aligned}&t_{2}=t_{2}^{Q}=-\frac{1}{2}bc_{33}X_{2}=t_{2}^{ext,Q}-m_{21}^{ext}=t_{2}^{ext,Q}-b\left( c_{12}+\frac{1}{2}c_{33}\right) X_{2}\nonumber \\&\qquad \Rightarrow \ t_{2}^{ext,Q}=bc_{12}X_{2},\end{aligned}$$
(112)
$$\begin{aligned}&\tau _{1}=\tau _{1}^{Q}=b\left( a_{12}+\frac{\sqrt{2}}{2}a_{13}\right) =\tau _{1}^{Q,ext},\end{aligned}$$
(113)
$$\begin{aligned}&\tau _{2}=\tau _{2}^{Q}=0=\tau _{2}^{Q,ext}. \end{aligned}$$
(114)
$$\begin{aligned}&t_{1}=t_{1}^{R}=\frac{1}{2}bc_{33}X_{2}=t_{1}^{ext,R}+m_{12}^{ext}=t_{1}^{ext,R}+b\left( c_{12}+\frac{1}{2}c_{33}\right) X_{2}=0 \nonumber \\&\qquad \Rightarrow t_{1}^{ext,R}=-bc_{12}X_{2}=-blc_{12}, \end{aligned}$$
(115)
$$\begin{aligned}&t_{2}=t_{2}^{R}=bc_{11}X_{1}=t_{2}^{ext,R}+m_{22}^{ext}=t_{2}^{ext,R},\end{aligned}$$
(116)
$$\begin{aligned}&\tau _{1}=\tau _{1}^{R}=\frac{b}{2}\left( \sqrt{2}a_{23}+a_{33}\right) =\tau _{1}^{R,ext},\end{aligned}$$
(117)
$$\begin{aligned}&\tau _{2}=\tau _{2}^{R}=0=\tau _{2}^{R,ext}. \end{aligned}$$
(118)
$$\begin{aligned}&t_{1}=t_{1}^{T}=-\frac{1}{2}bc_{33}X_{2}=t_{1}^{ext,T}-m_{12}^{ext}=t_{1}^{ext,T}-b\left( c_{12}+\frac{1}{2}c_{33}\right) X_{2}\nonumber \\&\qquad \Rightarrow \quad t_{1}^{ext,T}=-bc_{12}l, \end{aligned}$$
(119)
$$\begin{aligned}&t_{2}=t_{2}^{T}=0=t_{2}^{ext,T}-m_{22}^{ext}=t_{2}^{ext,T},\end{aligned}$$
(120)
$$\begin{aligned}&\tau _{1}=\tau _{1}^{T}=\frac{b}{2}\left( \sqrt{2}a_{23}+a_{33}\right) =\tau _{1}^{T,ext},\end{aligned}$$
(121)
$$\begin{aligned}&\tau _{2}=\tau _{2}^{T}=0=\tau _{2}^{T,ext}. \end{aligned}$$
(122)

From (42-P1) and (60), at the vertices we have that the relevant combination of the hyperstresses for characterization of vertex-forces are

$$ T_{112}+T_{121}=0,\quad T_{212}+T_{221}=b\left( a_{22}+\sqrt{2}a_{23}+\frac{1}{2}a_{33}\right) $$

so that, from (41-P1),

$$\begin{aligned}&\left( f_{1}^{ext}\right) _{\mathscr {V}_{i}}=0,\quad i=1,2,3,4\end{aligned}$$
(123)
$$\begin{aligned}&\left( f_{2}^{ext}\right) _{\mathscr {V}_{i}}=-b\left( a_{22}+\sqrt{2}a_{23}+\frac{1}{2}a_{33}\right) ,\quad i=1,3\end{aligned}$$
(124)
$$\begin{aligned}&\left( f_{2}^{ext}\right) _{\mathscr {V}_{i}}=b\left( a_{22}+\sqrt{2}a_{23}+\frac{1}{2}a_{33}\right) ,\quad i=2,4. \end{aligned}$$
(125)

4 Pantographic Case

Let us assume that the two families of fibers in the pantographic structure, modelled as Euler beams in the micro-model, are aligned with the axes of the frame of reference. A series of intuitive considerations are done in this section. In other words a set of gedanken experiments is conceived for the purpose of parameters identification.

4.1 Heavy Sheet

We can prove that the vertical displacement of side T is, in the micro-model, that of the free-side of a cantilever extensional beam of length 2l, with axial rigidity \(E_{m}A_{m}\) and with a distributed axial load \(b_{N}=b_{N}^{v}+b_{N}^{h}\) that is due to its own weight \(b_{N}^{v}=-\rho _{m}A_{m}g\) and to the weight of the horizontal beams \(b_{N}^{h}=b_{N}^{v}\)

$$\begin{aligned} u_{2}\left( X_{1},X_{2}=-l\right) =-\frac{2\rho gl^{2}}{c_{11}}=-\frac{4\rho _{m}gl^{2}}{E_{m}}, \end{aligned}$$
(126)

where g is gravity acceleration, \(\rho _{m}\) is the mass per unit volume of the micro beams and \(E_{m}\) is their Young modulus. Besides, equating the mass of the continuous macro model (\(\rho L2l\)) with the one of the micro model (\(\rho _{m}A_{m}L\frac{2l}{d_{m}}+\rho _{m}A_{m}2l\frac{L}{d_{m}}=2Ll\frac{2\rho _{m}A_{m}}{d_{m}}\)) yields the relation

$$\begin{aligned} \rho =\frac{2\rho _{m}A_{m}}{d_{m}}, \end{aligned}$$
(127)

where \(A_{m}\) is the cross section area of each micro beam and \(d_{m}\) is the distance between two adjacent families of micro beams. From (126) and (127) we have

$$\begin{aligned} c_{11}=E_{m}\frac{2\rho gl^{2}}{4\rho _{m}gl^{2}}=E_{m}\frac{2\rho _{m}A_{m}}{d_{m}}\frac{1}{2\rho _{m}}=\frac{E_{m}A_{m}}{d_{m}}. \end{aligned}$$
(128)

Further considerations based upon the heavy sheet configuration can be done. First of all, the natural absence of the Poisson effect in this configuration makes the horizontal force per unit length for the vertical sides, that are given from (40). This and (128) give

$$\begin{aligned} t_{1}^{ext,S}=\frac{\rho g\left( l+X_{2}\right) }{c_{11}}c_{12}=0,\quad \Rightarrow \quad c_{12}=0. \end{aligned}$$
(129)

The natural absence of double force in vertical sides gives from (43) and (128)

$$\begin{aligned} \tau _{2}^{ext,S}=\sqrt{2}\frac{a_{13}\rho g}{c_{11}}=0,\quad \Rightarrow \quad a_{13}=0. \end{aligned}$$
(130)

The natural absence of double force in horizontal sides gives from (51) and (128)

$$\begin{aligned} \tau _{2}^{R,ext}=\frac{\rho ga_{11}}{c_{11}}=0,\quad \Rightarrow \quad a_{11}=0. \end{aligned}$$
(131)

Moreover, in the same heavy sheet configuration, the natural absence of vertex forces gives from (56) and (128)

$$\begin{aligned} T_{112}+T_{121}=\frac{\left( a_{12}+\sqrt{2}a_{13}\right) \rho g}{2c_{11}}=0,\quad \Rightarrow \quad a_{12}+\sqrt{2}a_{13}=0, \end{aligned}$$
(132)

that yields with (130),

$$\begin{aligned} a_{12}=0. \end{aligned}$$
(133)

4.2 Non-conventional Bending

We set an equivalence of such a case with a pantograph composed of a number (i.e. \(\frac{2l}{d_{m}}\)) of horizontal beam that are bent due to an external couple \(M_{m}\) on the right-hand side of each beam, so that the total external moment \(M_{S}^{ext}\) on side S is related to \(M_{m}\),

$$\begin{aligned} M_{S}^{ext}=-\frac{2l}{d_{m}}M_{m}, \end{aligned}$$
(134)

and the vertical displacement of side S is

$$\begin{aligned} u_{2}\left( X_{1}=L,X_{2}\right) =-\frac{aL^{2}}{2}=-\frac{M_{m}L^{2}}{2E_{m}I_{m}}, \end{aligned}$$
(135)

where \(I_{m}\) is the moment of inertia of the micro-beams. Such an equivalence works nicely in the case of absence of internal rotational springs at the place of each internal hinges.

In the case where the internal rotational springs are present, we need to apply, in the micro-model, two moments at the position of each internal rotational springs. One moment \(M_{ext}^{H}\) on the horizontal fibers and the other moment \(M_{ext}^{V}\) on the vertical fibers. Such moments have the role to annihilate the effects of the moments, \(M_{rs}^{H\rightarrow V}\) and \(M_{rs}^{V\rightarrow H}\), that are due to the internal rotational springs and, therefore, are proportional to the relative angle \(\left( \theta _{H}-\theta _{V}\right) \) between the horizontal (\(\theta _{H}\) is the rotation of the horizontal beam) and the vertical \(\theta _{V}\) (\(\theta _{V}\) is the rotation of the vertical beam) beams. Let us take into account the horizontal beam. The internal rotational springs gives positive moment \(M_{rs}^{V\rightarrow H}\) on the beam

$$ M_{rs}^{V\rightarrow H}=-k_{r}\left( \theta _{H}-\theta _{V}\right) $$

because in this non-conventional bending case we have

$$ \theta _{V}=0,\qquad \theta _{H}=u_{2,1}=-aX_{1}, $$

that gives

$$ M_{rs}^{V\rightarrow H}=k_{r}aX_{1}. $$

The same internal rotational spring gives an opposite moment \(M_{rs}^{H\rightarrow V}\) on the vertical beam,

$$ M_{rs}^{H\rightarrow V}=-k_{r}\left( \theta _{V}-\theta _{H}\right) =-k_{r}aX_{1}. $$

In order to annihilate the effects of the internal rotational springs, the external moments \(M_{ext}^{H}\) and \(M_{ext}^{V}\) need to be the opposite of those given by the rotational springs, i.e.,

$$ M_{ext}^{H}=-M_{rs}^{V\rightarrow H}=-k_{r}aX_{1},\qquad M_{ext}^{V}=-M_{rs}^{H\rightarrow V}=k_{r}aX_{1}. $$

Thus, two moments have been applied at the position of each internal hinge-rotational-spring in the micro-model. In the macro-model, such positions are distributed on the two-dimensional body. Therefore, we need to apply distributed external moments that are modelled by a distributed external double force \(m^{ext}\). In particular only the out-of-diagonal components \(m_{12}^{ext}\) and \(m_{21}^{ext}\) have the role of distributed external couples. Since \(m_{12}^{ext}\) does work on the component \(u_{1,2}\) of the displacement gradient, then \(m_{12}^{ext}\) is interpreted as the negative distributed couple on the vertical beams

$$ m_{12}^{ext}=-M_{ext}^{V}=-k_{r}aX_{1}. $$

Because of (57-P1)

$$\begin{aligned} m_{12}^{ext}=-\frac{a}{2}c_{33}X_{1},\quad \Rightarrow \quad c_{33}=2k_{r}. \end{aligned}$$
(136)

Equations (93), (134) and (135) give

$$ a=-\frac{M_{S}^{ext}}{a_{33}l}. $$
$$\begin{aligned} a_{33}=-\frac{M_{S}^{ext}}{al}=\frac{2l}{d_{m}}M_{m}\frac{1}{al}=\frac{2l}{d_{m}}\frac{aL^{2}2E_{m}I_{m}}{2L^{2}}\frac{1}{al}=2\frac{E_{m}I_{m}}{d_{m}}. \end{aligned}$$
(137)

Moreover, in the non-conventional bending case, from (89), the natural absence of vertex forces gives,

$$\begin{aligned} T_{112}+T_{121}=\frac{a}{2}\left( a_{33}+\sqrt{2}a_{23}\right) =0,\quad \Rightarrow \quad a_{33}+\sqrt{2}a_{23}=0. \end{aligned}$$
(138)

4.3 Trapezoidal Case

From (124), assuming zero wedge forces, in the trapezoidal case we have

$$\begin{aligned} T_{212}+T_{221}=a_{22}+\sqrt{2}a_{23}+\frac{1}{2}a_{33}=0\ \Rightarrow \ 2a_{22}+2\sqrt{2}a_{23}+a_{33}=0. \end{aligned}$$
(139)

4.4 Summary

Equations (128)–(132), (136)–(139) completely characterize the orthotropic material. In particular the two constitutive matrices are represented as follows

$$\begin{aligned} \mathbf {C}=\frac{E_{m}A_{m}}{d_{m}}\left( \begin{array}{ccc} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 \end{array}\right) +2k_{r}\left( \begin{array}{ccc} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 1 \end{array}\right) =\left( \begin{array}{ccc} \frac{E_{m}A_{m}}{d_{m}} &{} 0 &{} 0\\ 0 &{} \frac{E_{m}A_{m}}{d_{m}} &{} 0\\ 0 &{} 0 &{} 2k_{r} \end{array}\right) , \end{aligned}$$
(140)
$$\begin{aligned} \mathbf {A}=\frac{E_{m}I_{m}}{d_{m}}\left( \begin{array}{cccccc} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 1 &{} -\sqrt{2} &{} 0 &{} 0 &{} 0\\ 0 &{} -\sqrt{2} &{} 2 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} -\sqrt{2}\\ 0 &{} 0 &{} 0 &{} 0 &{} -\sqrt{2} &{} 2 \end{array}\right) . \end{aligned}$$
(141)

4.5 About the Redundancy of Equations Coming from gedanken experiments

The same result in (136) could be achieved by identifying the component \(m_{21}^{ext}\) that does work on the component \(u_{2,1}\)of the displacement gradient. Thus, \(m_{21}^{ext}\) is interpreted as the positive distributed couple on the horizontal beams

$$ m_{21}^{ext}=M_{ext}^{H}=-k_{r}aX_{1}, $$

that, with (57-P1), gives the same identification (136).

We remark that the identification in (129) could also be achieved, in the trapezoidal case, assuming zero horizontal force on the vertical sides and that the one in (130) could also be achieved in the non-conventional bending case, from (84), assuming zero double force at horizontal sides.

We remark that the identification in (133) could also be achieved in the trapezoidal case, from (113) and with (132), assuming zero horizontal double force at vertical sides.

We remark that the identification in (136) could also be achieved in the non-conventional bending case, from (77)\(_{1}\) or from (73)\(_{1}\), assuming zero horizontal force per unit length at vertical sides or, from (81), by assuming zero horizontal force per unit length at horizontal sides. Alternatively it could be achieved in the trapezoidal case, from (78)\(_{2}\) and (74)\(_{2}\), by assuming zero vertical force per unit length at vertical sides or, from (81), by assuming zero horizontal force per unit length at horizontal sides.

We finally remark that the identification in (138) could also be achieved in the trapezoidal case, from (117), assuming zero horizontal double force at horizontal sides.

Further redundant identification formulas could be derived in the trapezoidal case that, for the sake of simplicity, are not made explicit in this paper.

5 Some Remarks on the Internal Energy

It is interesting to recognize that the internal energy (2) can now be computed with (14-P1), (15-P1) and with the definition, in the linear case, of the deformation matrix G and of its gradient \(\nabla G\),

$$\begin{aligned}&U\left( G,\nabla G\right) =\frac{1}{2}\frac{E_{m}A_{m}}{d_{m}}\left( G_{11}^{2}+G_{22}^{2}\right) +\frac{1}{2}2k_{r}2\left( G_{12}\right) ^{2}\\&+\frac{1}{2}\frac{E_{m}I_{m}}{d_{m}}\left[ G_{22,1}\left( G_{22,1}-2G_{12,2}\right) +2G_{12,2}\left( -G_{22,1}+2G_{12,2}\right) \right] \\&+\frac{1}{2}\frac{E_{m}I_{m}}{d_{m}}\left[ G_{11,2}\left( G_{11,2}-2G_{12,1}\right) +2G_{12,1}\left( -G_{11,2}+2G_{12,1}\right) \right] \end{aligned}$$

or, in terms of the displacement field,

$$\begin{aligned} U\left( G,\nabla G\right) =\frac{1}{2}k_{r}\left( u_{1,2}+u_{2,1}\right) ^{2}+\frac{E_{m}A_{m}}{2d_{m}}\left( u_{1,1}^{2}+u_{2,2}^{2}\right) +\frac{E_{m}I_{m}}{2d_{m}}\left( u_{1,22}^{2}+u_{2,11}^{2}\right) . \end{aligned}$$
(142)

Expression (142) is a useful form of the energy, as in it the contributions of both families of fibers, for axial and for bending deformations of the micro-beams, and also of the internal rotational springs, appear explicitly.

6 Conclusion

In the same fashion of [37], in this paper we have identified the whole set of nine parameters characterizing a homogeneous linear second gradient D4 orthotropic continuum model accounting for external distributed bulk double forces, developed in [50] and which can be considered an extension of the model presented in [36]. Analytical solutions proposed in [50] were employed in order to perform an identification in terms of the Young’s modulus of the fibers’ material, of their area, of the moment of inertia of their cross sections, of the rigidity of the internal rotational spring and of the step. A suitable form of the strain energy, that closely resembles the contributions of both families of fibers, for axial and for bending deformations of the micro-beams, and also of the internal rotational springs, has been derived.

The results can of course be generalized in various ways. For instance, interesting progresses in this line of investigation may involve multi-physics coupling between mechanical and electric effects (a case in which anisotropy plays of course a relevant role [53]), as well as more general beam models for the fibers [54,55,56]. The extension of the results to nonlinear second gradient continua is of course far from trivial and may require substantial theoretical progresses.