Boundary Objects Within a Replacement Unit Strategy for Mathematics Teacher Development

Abstract

We recognise that, for instructional innovations to take root in mathematics classrooms, curriculum redesign and teachers’ professional development are two necessary and mutually-reinforcing processes: a redesigned curriculum needs to be seen as an improvement in order to facilitate teachers’ buy-in—an ingredient for effective professional development; on the other hand, teachers’ professional development content needs to be directed towards actual useable classroom implements through the enterprise of collaborative curriculum redesign. In this chapter, we examine the interaction between researchers and teachers in this collaborative enterprise through the metaphor of boundary crossing. In particular, we study a basic model of how “boundary objects” located within a “Replacement Unit” strategy interact to advance the goals of professional development.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

For the past five years, we have been working with various schools in Singapore towards the goal of making Mathematics Problem Solving (MPS) a more integral part of the mathematics curriculum of secondary students. As part of our efforts to directly impact mathematics classrooms, we design our teacher development activities to be sustained, collaborative, practice-based (i.e., concerned with issues related to practice), and close to the genuine instructional concerns of practice. We recognise that heightening the prominence of MPS in classrooms does not happen overnight, hence the need for sustained engagements. We also recognise that schools and teachers themselves should develop an ownership for the reform initiative for real change to take root, thus the importance of close collaborations with the teachers. Also, to impact classrooms directly, discussions with teachers should be about issues of direct concern to them. Thus, our professional development work is centred around issues of classroom practice.

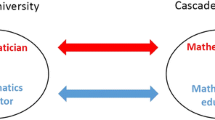
In this kind of school-based teacher professional development activities, two groups of people with their respective cultural and professional traditions are brought together in collaboration: (1) Mathematics teacher educators who are usually mathematicians or mathematics educators working in the university; and (2) mathematics teachers who are based in schools. Metaphorically, the interactions between these two groups of professionals can be likened to a boundary crossing—a stepping over the perceived limits of one’s professional ‘world’ into another social world. Seen in this way, the quality of teacher professional development can be studied through the activities around this boundary encounter.

2 Mathematics Teacher Professional Development as a Boundary Encounter

In defining professional development (PD) as a boundary encounter between researchers and teachers, we recognise that a natural boundary (Wenger 2000) exists between these two parties by virtue of the fact that they ordinarily operate in different domains and they possess different forms of expertise. Conventionally, researchers operate within universities or laboratories and are thought to possess more formal knowledge about practice; on the other hand, teachers operate within schools and possess more practical knowledge about practice (Cochran-Smith and Lytle 1999). PD provides a common domain or a boundary encounter where knowledge exchange, transfer, or creation can occur, which in theory can then lead to boundary crossings (Akkerman and Bakker 2011) of this knowledge benefitting both parties even as they return to operating in their usual domains.

While the potential for fruitful engagements within boundary encounters is evident, creating the conditions for successful boundary crossings is not straightforward. Three constructs highlighted by Sztajn et al. (2014) found within boundary encounters are helpful to consider when designing mathematics PD: Boundary brokers, boundary practices and boundary objects.

In teacher PD, the boundary brokers basically refer to the researchers and the teachers. As pointed out earlier, each of these two sets of individuals brings in different forms of expertise in the engagement. They also come in with a unique set of interests and expectations. These determine how each party acts as a broker for their respective domains.

Boundary practices, a result of boundary brokering, are the emerging or negotiated practices and norms which are carried out during the PD engagement. These define the manner in which knowledge is exchanged, transferred, or created.

Finally, boundary objects are the “representations of knowledge” (Sztajn et al. 2014) around which boundary practices are organised. Star and Griesemer (1989), from whom the term is originally attributed, describe boundary objects as

objects which are both plastic enough to adapt to local needs and constraints of the several parties employing them, yet robust enough to maintain a common identity across sites … They may be abstract or concrete … The creation and management of boundary objects is key in developing and maintaining coherence across intersecting social worlds. (p. 393)

In the context of teacher PD, boundary objects may refer to the reform principles being adopted, or to more tangible classroom artefacts such as students’ work. These objects do not necessarily hold the same meaning or value for the different parties in the boundary encounter. Cobb et al. (2009), for instance found that their use of students’ work in PD “was, for the teachers, a tool for retrospective assessment of prior instruction rather than a resource for the prospective planning of future instruction” (pp. 187–188, emphasis in the original). The meaning and value of boundary objects, however, could be negotiated and transformed through appropriate boundary practices.

We find that the boundary metaphor provides us with an alternative image and understanding of teacher PD. It particularly draws attention to how the disposition of boundary brokers, the boundary objects involved in the boundary encounter (or the PD engagement), and the practices established for these encounters contribute to the success or failure of boundary crossings. However, the metaphor does not specify how these encounters should look like so that successful crossings can take place. Such a portrait can aid in designing and conducting PD.

In the kind of PD activities we engage with teachers for MPS over time, some of the constructs in the boundary metaphor have gained greater clarity to us. Based on our experience working with these schools in such PD settings, boundary brokers are researchers and teachers who have a commitment to teach MPS. Boundary practices refer to the structure and schedule of engagements for the purpose of professional learning that have become standard practice for both researchers and teachers. (These practices are elaborated in Sect. 14.6.) There is, however, a need for greater clarity about the boundary objects in such an enterprise and the way these objects interact to forward PD goals.

Thus, we conducted an inquiry focused on characterising the appropriate boundary objects for successful practice-based mathematics PD. In our study, we identified the boundary objects that we think will help us—researchers—interact productively with the teachers of the research school. We particularly asked the following questions: How do the boundary objects that we identified interact with each other? Are the interactions productive of teacher PD?

In this chapter, we would like to propose a possible theoretical framework addressing these questions. We then demonstrate the suitability of this framework based on our curriculum development work with one school.

3 Boundary Objects During Mathematics Teacher PD

In crafting a basic working model of the boundary objects during mathematics teacher PD, we drew on the previously highlighted differences in the expertise and intentions of the two main brokers—the researchers and the teachers—when they participate in the encounter and imagined the boundary objects that they would contribute to the engagement. It led us to view PD as involving an interaction between two main boundary objects in the boundary encounter, namely the conceptualisations of reform ideas and the concretisations of reform ideas for classroom use. Figure 14.1 illustrates how these two objects are conceived to interact in PD.

Fig. 14.1

Boundary objects in mathematics teacher PD

Conceptualisations are provisional models informed by theoretical ideas from the disciplinary domain or from pedagogical principles. They represent the knowledge about how mathematics reform is conceived to be applied in the classroom. Essentially, these conceptualisations often come from the researchers in the teacher PD initiative. They have their starting points from actual problems of practice. It is through these objects that researchers communicate to teachers what is thought of as a possible classroom scenario in light of the classroom reforms being promoted in PD.

On the other hand, concretisations of reform ideas are often more tangible. They embody the conceptualisations of the reform ideas as they are to be deployed for classroom use. They may come in the form of lesson plans, manipulatives or other classroom-ready instructional materials. Typically, the form which these concretisations take often come from the teachers as they are the ones who can decide what is appropriate for use in their classrooms. It is through these objects that teachers communicate to researchers how they interpret the reform being promoted for classroom implementation.

During PD, these two boundary objects ‘interact’ in the sense that revisions in one can affect changes in the other. They are thus objects that can undergo refinements throughout the PD process. We advance our proposed 2-object model by locating it within our school-based PD engagement with a secondary school in Singapore, which was focused on infusing MPS in the mathematics curriculum. We carried this out via the Replacement Unit strategy.

4 Situating the Boundary Objects Within the Replacement Unit (RU) Strategy

The Replacement Unit (RU) strategy is both a strategy for curricular redesign as well as a strategy for teacher PD. Its curricular redesign feature is exemplified by its main tenet of redesigning a whole unit or topic of study in the curriculum for the purpose of replacing the old one. In their work, Cohen and Hill (2000) also used the term “replacement unit”. From a curricular redesign perspective, their definition of replacement units also coheres with our conception of it.

Replacement units are curriculum modules designed to be consistent with reforms that center on specific topics… or sets of topics. [The units are devised] to be coherent and comprehensive in their exploration of mathematical topics – to truly replace an entire unit in mathematics texts, rather than just add in activities to existing curricula – and to be supportive of teacher as well as student learning. (p. 305)

Thus, in the RU strategy, the curricular content of a specified unit of study as well as the development of all the relevant classroom-ready instructional materials are redesigned and restructured according to a set of adopted reform principles. And in order for a replacement unit to be acceptable for teachers’ implementation, the unit is redesigned without changing the time allocated for it in the school’s teaching schedule.

To us, the RU strategy is also a teacher PD strategy. This PD goal is embedded in the overall RU strategy of teacher involvement in the redesign of the curriculum. An RU strategy engagement will typically begin with an identification of the unit of the curriculum to be replaced. An initial meeting is held between the design collaborators—both researchers and teachers—to discuss ideas. Usually, researchers lead in this meeting. Teachers will then redesign curriculum materials based on the agreed-upon ideas and these will undergo review and possible modifications in subsequent unit review meetings. Here, teachers present their designs for scrutiny. After the unit is implemented by the teachers, the RU strategy engagement concludes with an evaluation meeting to review the designed curriculum based on the classroom implementations. It is largely in this collaborative process of redesign that we view the RU strategy as a boundary encounter between researchers and teachers.

A RU spans 4–8 h of classroom time. We find this to be realistic and reasonable in terms of the scope of the work demanded for the redesign process and in terms of the required period of engagement for PD. Focusing on a larger curricular unit at once might be daunting simply for the amount of time and work it would demand on the design collaborators. On the other hand, a single lesson might not always capture the totality of the reform principles we want to promote because of its short duration. Focusing on a RU to trial (and re-trial, if necessary) and refine, thus, makes it a more manageable and meaningful engagement for curriculum development and PD.

In the described RU strategy, we identified the main boundary objects, which are representations of knowledge, as: (1) The ideas about the MPS-infused curriculum unit (Conceptualisations); and (2) the teachers’ prepared instructional materials (Concretisations). In the rest of this chapter, we examine the interactions of these boundary objects within the context of designing a specific RU on probability. We begin by providing a brief background of the study.

5 Background of a Specific Case of RU-Design

The RU strategy engagement described herein was part of a broader design experiment entitled Mathematical Problem Solving for Everyone (MProSE). MProSE grew out of our desire to make MPS a more integral part of school mathematics in Singapore. This advocacy is consistent with the Singapore mathematics framework (Ministry of Education [MOE] 2006) which identified mathematical problem solving as “central to mathematics learning”. Despite the existing framework, however, we found that actual implementation of MPS in Singapore schools was such that it only played a peripheral role in the students’ mathematics learning rather than its envisioned central role (see for example Teong et al. 2009). That is, “problem solving” as enacted in mathematics classrooms was often relegated as a separate enrichment activity, sometimes packaged as an opportunity for students to encounter either recreational mathematics problems or problems that are considered as challenging. We also found that this situation was not unique to Singapore; in fact it was common for related international studies to report about how problem solving instruction still has not taken root in mathematics classrooms in spite of extensive past research (e.g. Doorman et al. 2007; Mok et al. 2005). This provided the motivation to embark on MProSE.

Currently in its fifth year of implementation, more details about MProSE, its implementation and outcomes can be obtained from our previous publications (Leong et al. 2014; Toh et al. 2011). In brief, MProSE can be described as having two main phases. The first phase, characterising our initial engagements with our partner secondary schools, was focused on the design and implementation of a 10-hour problem solving module which provided the students (and teachers) with the language and strategies used in problem solving. A central tool used in this module was the “Practical Worksheet” which was designed to habituate solvers to approach problem solving through the four stages of Pólya (1945/1973) model (i.e. Understand the Problem, Devise a Plan, Carry out the Plan and Check and Expand). (A compressed version of the Practical Worksheet as adapted by the research school reported in this chapter is found in Appendix A.)

A key activity of the module was solving “MProSE problems”. MProSE problems are problem solving tasks which are laid out in a Practical Worksheet. During class, students worked on these problems (individually or in small groups) for about 20 min, making use of the prompts in the Practical Worksheet to guide their MPS process. During this period, teachers were expected to monitor students’ work and scaffold students’ MPS processes.

Among the important outcomes of the first phase of MProSE was the common knowledge and understanding about MPS that was created among both teachers and students. It also resulted in a broader acceptance of a problem solving approach to teaching and learning mathematics. This paved the way for the next phase of MProSE which we are currently in the midst of.

The second phase of MProSE was focused on the actual infusion of problem solving in regular mathematics classes. This brought us further in making MPS a more integral part of the mathematics curriculum. Working within the regular curriculum, however, posed new challenges in our engagements with the schools. We adopted the RU strategy to maintain the manageability and meaningfulness of our engagements.

6 Implementing the RU Strategy in Eastpark Secondary School

Having previously established relationships with our research schools in the first phase of MProSE, Phase 2 formally started in Eastpark¹ Secondary School when the school expressed their willingness and readiness to proceed to infusion. They were then asked to identify a certain topic or unit of study which they found challenging to teach or which they wanted to infuse with problem solving. We describe in this section our implementation of the RU strategy in the school who expressed interest in transforming how they taught probability for their year eight classes. This unit spanned four one-hour lessons. It covered the definition of probability and computation of the probability of a single event.

The whole RU strategy—from curricular redesign, implementation and evaluation—spanned across 8 weeks. It started with an initial meeting² between the researchers and the relevant teachers of the school. In this meeting, the researchers presented their ideas about how the probability lesson infused with MPS can be carried out over the prescribed four-lesson requirement. Teachers then independently designed the actual lessons, which in Eastpark, were embodied in instructional worksheets for the classroom. Three teachers were involved in the actual redesign—Cindy, Diane and Emma. Of the three, only Cindy and Diane were teaching the RU lessons. Emma was involved in her capacity as subject coordinator for the level.

In the weeks that followed, the researchers, the teachers and Jake, the head of the mathematics department, came together four times to review the curricular unit. During these meetings, teachers shared drafts of the worksheets which they designed, discussing their content and organisation and the rationale behind them. In the process, ideas that were previously presented by the researchers were revisited. Thus, this stage in the RU strategy was the period wherein both teachers and researchers were actively working together to produce workable and concrete curriculum materials that would meet the requirements and standard of both parties. The researchers would propose further modifications, but the final content and organisation of the worksheets were ultimately left for the teachers to decide.

In implementation, teachers were given autonomy to execute the lessons according to how they saw fit. We³ made efforts to be kept posted of how the classes were implemented with minimal interrupts. We did not observe the teachers’ implemented classes first hand, but the classes were video-recorded; we reviewed each lesson video before the next lesson of the RU. This enabled us to provide feedback to the teachers via email correspondences when we thought it was warranted.

The RU strategy process ended with an evaluation meeting of the whole process after the teachers have implemented all the lessons. Figure 14.2 provides a schematic of the different activities that took place over the said period of time.

Fig. 14.2

The activities undertaken during the implementation of the RU strategy over the 8-week period

7 Capturing the Interaction Between Boundary Objects in the RU Strategy

As identified in an earlier section, the specific boundary objects in this study are (1) the researchers’ ideas about the MPS-infused probability unit, and (2) the teachers’ prepared worksheets of the redesigned unit. The former, as mentioned, is a conceptualisation, while the latter is a concretisation.

From reviewing the activities involved in the implemented RU strategy, we sought to locate the interactions between the conceptualisation and concretisation occurring in the unit review meetings when the drafts of the worksheets designed were clarified alongside the conceived ideas for the MPS-infused lessons. In the subsequent sections of this chapter, we provide empirical evidence of this dynamic interaction between conceptualisation and concretisation.

We primarily reviewed the initial meeting through written documentations of what transpired to establish how the MPS-infused unit on probability was conceptualised. We identified the focus of the lessons, their intended organisation, and other specific items that were suggested when the lessons were conceptualised. We then reviewed the final worksheets that the teachers designed and used for their lessons and evaluated their fidelity to the initial conceptualisations according to the same attributes reviewed. We took note of the similarities and deviations from the original conceptualisation. Finally, we also reviewed the video recordings of the unit review meetings in order to have a better appreciation of the design process carried out to produce the worksheets.

8 The RU on the Topic of Probability

In this section, we present the findings of our analysis by first providing a picture of how the lessons were conceptualised and then describing how the worksheets concretised these conceptualisations. We then provide an overview of the nature of the discussions during the unit review meetings related to the design of the worksheets.

8.1 Conceptualisation of the RU Lessons

The topic of probability was chosen for infusion of units for these reasons: (1) the teachers requested for it as they found the topic hard to teach. A RU-design on this topic was thus a practical way to improve the teaching of the topic and provide the accompanying teacher PD to match the redesign; (2) due to the rich set of problems usually associated with probability, it is a topic amenable to an emphasis on MPS. In conceptualising the RU, we incorporated what we identified were three essentials that would facilitate students’ understanding of probability better. First, the RU must be able to develop in students a motivation to quantify probability and not rely only on intuition. This involves instilling a discipline for careful study of the requirements when considering probability problems. We recognised that this should be developed progressively. Second, hand-in-hand with the first essential, the RU must be able to establish a common and formal language for communicating about probability in a progressive manner as well. This will facilitate the teaching and learning process. And finally, in line with the reform practice which we were advocating, the RU must feature infusion of problem solving to serve the purpose of deepening understanding in probability.

A description of how we conceived the four lessons is as follows:

Lesson One. The first lesson was essentially thought to provide students with an introduction to probability including some basic terms associated with it. We proposed beginning with tapping into the students’ intuitive knowledge of probability as a lead-in. A series of questions about the likelihood of certain everyday situations occurring could be posed to students. At this point, informal language could be used. We suggested using a horizontal line, with the two opposite ends labelled as “unlikely” and “likely” respectively, which can be marked to indicate an estimation of the degree of likelihood of a certain event to happen.

It was then proposed to hold a short activity to illustrate how intuition can be faulty, thus providing a motivation for a more careful consideration when computing for probability. The specific activity suggested was the “Choose a number”⁴ problem where students will be asked to choose and think of an integer between 1 and 200. [This is an adaptation to the “Birthday Problem”.] The activity was meant to create a surprise at finding the chance of getting a match as being higher than expected. This was to provide the motivation for developing a more formal way of studying probability.

Lesson 1 was then proposed to proceed with introducing some standard language used in probability by defining “experiment”, “outcome” and “event”. And according to these introduced definitions, “probability of an event” can be defined provisionally as

$$ {\text{Probability}}\,{\text{of}}\,{\text{an}}\,{\text{event}} = \frac{{{\text{no}}.\,{\text{of}}\,{\text{desired}}\,{\text{outcomes}}}}{{{\text{total}}\,{\text{no}} .\,{\text{of}}\,{\text{outcomes}}}} $$

(14.1)

Table 14.1 summarises how Lesson 1 was conceptualised according to the attributes identified in our analysis.

Table 14.1 Summary of how Lesson 1 was conceptualised

Lesson Two. We anticipated that students would have a tendency to still depend on intuition when responding to probability questions. Thus, in the second lesson we wanted students to develop a motivation for listing down all the outcomes in an experiment. We thought that this was a good opportunity for infusing MPS by allowing students to work on a MProSE problem featuring a probability situation where the intuitive outcomes were not equally likely. We thus provided some options that teachers could consider using––the “three children” problem, the “passenger seat” problem, and the “loaded die” problem. According to our conceptualisation, students would be given some time to independently work on this problem. After which a synthesis of the solution of the problem can be done, followed by introducing more formal probability language, in particular using “sample space” to denote the collection of all possible outcomes, and adjusting the definition of “probability” as found below to reflect this progression.

$$ {\text{Probability}}\,{\text{of}}\,{\text{an}}\,{\text{event}} = \frac{{{\text{no}}.\,{\text{of}}\,{\text{favourable}}\,{\text{outcomes}}}}{{{\text{no}} .\,{\text{of}}\,{\text{outcomes}}\,{\text{in}}\,{\text{the}}\,{\text{sample}}\,{\text{space}}}} $$

(14.2)

The importance of listing down the sample space with equally likely outcomes is to be emphasised, making reference to the students’ work with the problem posed at the start of the lesson. Table 14.2 summarises how Lesson 2 was conceptualised.

Table 14.2 Summary of how Lesson 2 was conceptualised

Lesson Three. In the third lesson, the definition of probability was to be extended to account for the case where the number of outcomes of a sample space was infinite. We thought that this was an important concept to include to provide the unit a better sense of completeness from a mathematical discipline perspective. To begin the lesson, it was suggested that teachers can pose an appropriate probability problem that can illustrate the inadequacy of the previously established definition of probability. Specific suggestions for the problem to pose included a spinner problem and a dart problem where the corresponding board has unequal sectors. After leading students to an intuitive solution to the problem, an extended definition of probability can then be formally introduced. In particular,

$$ {\text{Probability}}\,{\text{of}}\,{\text{an}}\,{\text{event}} = \frac{{{\text{measure}}\,{\text{of}}\,{\text{favourable}}\,{\text{event}}}}{{{\text{measure}}\,{\text{of}}\,{\text{sample}}\,{\text{space}}}} $$

(14.3)

Table 14.3 summarises how Lesson 3 was conceptualised.

Table 14.3 Summary of how Lesson 3 was conceptualised

Lesson Four. For the last lesson, we could include a MProSE problem that would utilise the concepts of probability taught in the previous lessons. We shared the “phoney Russian roulette” problem as a possible MProSE problem that could be used where students could be given time to independently work on the task before the discussion of the solution. It was then suggested that the lesson could end by returning to the “choose a number problem” introduced in Lesson 1. A summary of the conceptualisation of Lesson 4 is found in Table 14.4.

Table 14.4 Summary of how Lesson 4 was conceptualised

8.2 Lessons as Concretised in the RU Worksheets

The final worksheets used for the RU lessons were found to keep close fidelity to how they were conceptualised. We did, however, notice some deviations or additions. In the description that follows, we present an overview of these similarities and deviations.

Lesson One. The final worksheet prepared for Lesson 1 followed closely to how it was initially conceptualised. All the attributes as proposed in the conceptualisation were adapted (see Table 14.1). Figure 14.3 shows the actual portion of the worksheet for the first portion of the lesson.

Fig. 14.3

Part A of the final worksheet designed in Lesson 1

The definition of the probability of an event was presented as follows:

$$ {\text{Probability}}\,{\text{of}}\,{\text{an}}\,{\text{event}} = \frac{{{\text{no}}.\,{\text{of}}\,{\text{favourable}}\,{\text{outcomes}}}}{{{\text{total}}\,{\text{no}} .\,{\text{of}}\,{\text{possible}}\,{\text{outcomes}}}} $$

(14.4)

Finally, the worksheet concluded with a set of exercises where the first few questions did not only require students to find the probability of a certain event, but also require them to identify and characterise the experiment, the possible outcomes and the outcomes of the indicated event. The first of these problems is shown in Fig. 14.4.

Fig. 14.4

The first item in the exercises provided in the final worksheet designed for Lesson 1

Items that were in the concretisation that were not specified in the conceptualisation were these:

An exercise in the worksheet shown in Fig. 14.5 addressed P(not E) = 1 − P(E); also, the teachers included a worksheet for homework consisting of four questions that were meant to reinforce the concepts covered in Lesson 1.

Fig. 14.5

The first item in the exercises provided in the final worksheet designed for Lesson 1

Lesson Two. Again, all the attributes in Table 14.2 were adopted, with these minor modifications: (1) The first worksheet was a modified “three children” problem printed on the Practical Worksheet; (2) a homework sheet was also prepared for this lesson reinforcing the lessons learned; and (3) the second worksheet provided a recall of the definitions previously discussed but also brought in further use of formal notation and language by introducing the term “sample space”, thus redefining the terms “event” and “probability” in relation to the sample space. Thus, the definition of the probability of an event was now presented as

$$ {\text{P}}({\text{E}}) = \frac{{{\text{n}}({\text{E}})}}{{{\text{n}}({\text{S}})}} $$

(14.5)

Lesson Three. The worksheet for Lesson 3 began with a recall of the definition of probability of an even as presented in the previous lesson (i.e., P(E) = n(E)/n(S)). It then proceeded with two problems wherein the outcomes required a different measure. (The first problem involved area, while the second problem involved lengths.) It was followed by an extended definition of the probability of an event, where “measure” was used instead of “number”, exactly as that previously set in Definition 3. A set of practice questions then followed, covering different types of situations.

Lesson Four. The worksheet prepared for the last lesson consisted only of the “Phoney Russian roulette” problem which was printed on a Practical Worksheet. Thus, closing the unit by recalling and solving the “Choose a number” from Lesson 1 was not carried out as suggested in the conceptualisation.

8.3 Discussions During the Collaboration Sessions

The final worksheets adhered closely to how the unit was initially conceptualised. This can be taken as an indicator of how the two boundary objects interacted with each other. In this case, the worksheets drew heavily on the ideas for an MPS-infused unit on probability.

It may be argued, however, that the close correspondence of the worksheets to the conceptualisation can be interpreted differently. For instance, it can be said that teachers were just blindly or robotically complying with the ideas that they were presented with. Only through reviewing the original drafts of the worksheets and the unit review meetings can one fully appreciate the amount of clarification, negotiation, and transformation that went into the production of the final worksheets—and hence the dynamic interaction with the conceptualisation of the RU.

In reviewing the meetings, we took note of the various discussions that were undertaken in relation to the design of the worksheet. We identified four, not necessarily disjoint, aspects of the worksheet which were modified as a result of these discussions—sequence, coverage, task and wording.

Sequence. The first drafts of the worksheets did not all reflect the sequence of parts as found in the final worksheets. For example in Lesson 1, the “Choose a number” problem was initially designed to be a MProSE problem to be administered at the very beginning of the class instead of it being a short question or activity following the everyday probability questions as seen in Fig. 14.3. In Lesson 2, the “Three children” problem was thought to come after formally introducing the concepts of sample space and equal likelihood of outcomes. Discussions that led to changes to sequence of parts of the worksheet drew on consideration of the lesson rationale and the time constraints among other things.

Coverage. The content covered in the worksheets also saw some changes. A major change of course was the extension of the probability concept covered in Lesson 3. A more specific example was how the initial draft of the Lesson 3 worksheets included a statement about how the probability of a point lying on the boundary of certain shaded region is zero. It was agreed, however, that while this was something that teachers need to know, it might be prudent not to introduce this concept to the students unless they bring it up so as to not confuse them.

Task. The MProSE problems, exercises and examples appearing in the worksheets were carefully reviewed in the collaboration meetings. Their efficacy in producing the desired effect and their appropriateness were considered. Teachers would explain the inclusion of a certain task according to how they thought it can introduce a concept. (e.g. “The fifth [example] is to lead them on to impossible events and certain events”.) or reinforce a discipline they wanted students to develop (e.g. “I just thought that this one… will make them… list down all the possibilities”.).

The collective review of tasks would sometimes lead to revisions in or certain decisions about the task. For example, the ends of the horizontal line in Fig. 14.3 were originally labelled as “most likely and “most unlikely”. But it was pointed out that using the word “most” seemed to imply a need to compare events. Thus, “most” was replaced with “extremely”. Another example is how the original textbox in the exercise shown in Fig. 14.4 did not require the specification of the components of the experiment (i.e. the “Act” and what to “Observe”). But when it was recalled that it was something they wanted to reinforce, this was added. The decision to not include a simpler version of the “Choose a number” problem was also a result of a collective review of the conceptualised lesson. After trying out different versions of a simpler problem, revisiting the lesson goals, and considering the time allotted for the lesson, it was decided that this portion of the conceptualised lesson may not be necessary.

Wording. Apart from wording of the tasks, wording of the different statements and definitions appearing in the worksheets were also carefully scrutinised. Ensuring accuracy was a major consideration. For example, the beginning of the statement which defined “event” was corrected from “The event is” to “An event is”. Another example was the attention placed on ensuring that the probability definition included a clause about equal likelihood of outcomes when it was appropriate. Consistency was also a concern. This was reflected when efforts were made to make sure that definitions appearing across worksheets were identical whenever it was called for.

9 Discussion and Conclusion

In this study, drawing upon the boundary crossing metaphor, we sought to examine our proposed 2-object model which consists of the objects of conceptualisation and concretisation (Fig. 14.1). Each of the objects draws upon the forte of the respective “worlds” of researchers and teachers. Our interest lies in the potential of interaction, especially the conceptualisation → concretisation direction, between the objects.

As it turned out, the concretisations retain a high level of fidelity to the initial conceptualisation, with substantial teacher inputs that reflect their active sense-making for productive adoption in their classrooms. We interpret this to mean that the boundary encounter as facilitated by the two boundary objects provides a feasible platform for the teachers’ PD in the teaching of this topic.

As a thought experiment, we may suppose an alternative model where the PD was designed as mainly a one-object encounter. Specifically, suppose that the PD engagement was designed in such a way that the conceptualisations and the concretisations were packaged as a single object designed mainly by the researchers meant for the teachers’ ready use in their classrooms. In fact, this approach basically summarises the model of most reform engagements. In traditional reform models, the full works of curriculum development—which includes conceptualisation, design and production of curricular and instructional materials—are undertaken by “experts” engaged directly by policy-makers. In this model, teachers play at most a bit-part role of contributing feedback to the near-final documents. Mostly, teachers’ role is seen mainly as implementation of the designed curriculum. This results in teachers not having a direct stake in the concretisation which in itself is a form of personalised reconceptualization—which we think is necessary capacity-building to carry out the reform.

On the other hand, another conception of a one-object model is one where teachers take on the primary role of packaging both the conceptualisation and concretisation. This is essentially the model of the now-famous Lesson Study enterprise. In Lesson Study, teachers undertake the primary role of leading in conceptualisation and concretisation while university researchers (known as Knowledgeable Others) are invited in their teams. Because of their ‘guest’ status, their roles are normally limited to post-design advice that involves minor refinements to the teachers’ plans. In this case, however, the researchers’ higher vantage point in disciplinary and pedagogical matters is not sufficiently harnessed for significant improvements in curriculum design and teacher PD.

Admittedly, this study has not explored the full power of the boundary crossing metaphor. We have limited our field of study to the interaction of only the two objects of (mainly researcher-led) conceptualisation and (mainly teacher-owned) concretisation. Another important boundary object that can potentially advance communication between the two worlds is Actualisation—(video) images of how the concretised materials are harnessed during classroom enactment. We can expect this object to present a different set of affordances and tensions in the PD engagements. This is an example of how research building upon the boundary metaphor can proceed along. It is an area that we would like to explore in future research.

Appendices

Appendix A: A compressed version of the Practical Worksheet Used in Eastpark Secondary School

• Instructions

  • 1. You may proceed to complete the worksheet doing stages I–IV.

  • 2. If you wish, you have 15 min to solve the problem without explicitly using Polya’s model. Do your work in the space for Stage III.

    • If you are stuck after 15 min, use Polya’s model and complete all the stages I–IV.

    • If you can solve the problem, you must proceed to do stage IV—Check and Expand.

    • You may have to return to this section a few times. Number each attempt to understand the problem accordingly as Attempt 1, Attempt 2, etc.

• Stage I: Understand the Problem

• (a) Use some heuristics such as Draw a Diagram, Restate the problem, Use Suitable Numbers, etc., to help you.

• (b) I have understood the problem. (Circle your agreement below)

• Stage II & III: Devise a Plan and Carry it out

• (a) State your plan clearly, for example: (i) Use suitable Numbers and Look for Patterns; or (ii) Find the areas of all smaller triangles and work out their ratios.

• (b) Number each plan as Plan 1, Plan 2, etc.

• (c) Carry out the plan that you have stated.

• (d) Write down in the Control column, the key points where you make a decision or observation, for e.g. go back to check, try something else, look for resources or totally abandon the plan.

• Stage IV: Check and Expand

• (a) Write down how you checked your solution.

• (b) Write down a sketch of any alternative solution(s) that you can think of.

• (c) Give one or two adaptations, extensions or generalisations of the problem. Explain succinctly whether your solution structure will work on them.

Appendix B

Some of the specific problems suggested during the RU strategy

Problem name	Problem details
Choose a number	Write down an integer between 1 and 200. What is the probability/chance that there is a match?
Three children	Given a family with three children, what is the probability that the family has three boys?
Passenger seat	Mr. and Mrs. Tay and their son John goes into their family car. Mr. and Mrs. Tay can drive but John cannot. What is the probability of Mr. Tay sitting in the passenger seat? (Apart from the driver seat that must be filled, the other passengers can choose to sit in any of the remaining seats in the car.)
Loaded die	In an unbiased die, three faces are painted “1”, two faces are painted “2”, and the last face is painted “3”. Find the probability that when the die is rolled, “2” is obtained
Phoney Russian roulette	Two bullets are placed in two consecutive chambers of a 6-chamber revolver. The cylinder is then spun. Two persons play a safe version of Russian Roulette. The first points a gun at his hand phone and pulls the trigger. The shot is blank. Suppose you are the second person and it is now your turn to point the gun at your hand phone and pull the trigger. Should you pull the trigger or spin the cylinder another time before pulling the trigger?