An AHP-Based Scheme for Sales Forecasting in the Fashion Industry

Abstract

In this paper, we propose a novel aggregation–disaggregation scheme based on the analytic hierarchy process (AHP) to conduct sales forecasting in the fashion industry, where a stock keeping unit (SKU) is usually characterized by a short product life cycle and low sales volume because of various reasons such as the wide variety of products and the constant changes in fashion trends. To improve the accuracy of sales forecast, an AHP-based scheme is proposed to aggregate historical sales data so that future sales can be predicted with higher certainty, and then disaggregate forecast quantities over SKUs, products, or other entities of interest. The proposed scheme is evaluated by using real data collected from the fashion industry, and the experimental results show that under this scheme, the performance of two popular and well-established time series forecasting techniques, namely “moving average” and “exponential smoothing,” can be improved to predict the sales of the products with short history and low sales volumes. To continue this work, future research directions are also discussed.

1 Introduction

Forecasting is a very important topic in academic research and has been widely applied in many fields such as supply chain management (Cui et al. 2015; Schwartz et al. 2009; Jin et al. 2015), reliability engineering (Hu et al. 2011), and semiconductor manufacturing (Chen and Wang 2014; Luo et al. 2015). In reality, many companies with global supply networks suffer from market volatility and supply disruptions, which adversely affect both their short- and long-term profits (Asian and Nie 2014). Thus, forecasting is the preliminary step for many important business decisions such as production planning (Albey et al. 2015), spare parts management (Heinecke et al. 2013), and new product launch strategy (Cui et al. 2011) and hence a key driver to improve supply chain performance (Thomassey 2010).

For a fashion business , advanced statistical approaches and artificial intelligence techniques have been widely used to predict both future sales (Liu et al. 2013; Nenni et al. 2013) and fashion trend (Choi et al. 2012; Yu et al. 2012). Both of these problems are hard to solve because the fashion industry is characterized by short product life cycles, volatile customer demands, tremendous product varieties, and complex supply chains (Sen 2008). Also, the complexity of sales forecasting in the fashion industry is increased by the strong seasonality and the frequently changing market environment. Because of the great impact of forecasting on many aspects of the business such as operational performance (Danese and Kalchschmidt 2011), forecasting problems in fashion business have been studied extensively from many different perspectives in the literature. For example, by introducing advanced artificial intelligence techniques such as neural networks and fuzzy logic, Au et al. (2008) proposed an evolutionary neural networks approach in searching for the ideal network structure for a forecasting system and developed the optimized neural networks structure for the forecasting of apparel sales; Sun et al. (2008) applied a novel neural network technique called extreme learning machine (ELM) to investigate the relationship between sales volumes and some significant factors which affect demand , and Kaya et al. (2014) developed a fuzzy forecast combiner which calculates the final forecast using a weighted average of forecasts generated by independent methods. For different time spans, Du et al. (2015) proposed a multiobjective optimization-based neural network model to tackle the short-term replenishment forecasting problem in fashion industry , and Wong and Guo (2010) developed a hybrid intelligent (HI) model which comprises a data preprocessing component and an HI forecaster to tackle the medium-term fashion sales forecasting problem. Since time efficiency is also very important for the industry practices where data volume is very high, research efforts are also conducted to develop fast forecasting tools. For example, Yu et al. (2011) proposed a new fast forecasting model which employs both the extreme learning machine (ELM) and the traditional statistical methods as a quick and effective tool, and Choi et al. (2014) developed an intelligent forecasting algorithm which combines tools such as the extreme learning machine and the gray model to support operational decisions in fast fashion business.

It is observed that the sales of fashionable products follow unpredictable fashion trends associated with high volatility and strongly depend on many factors such as prices and economic conditions (Ren et al. 2015). Also, different from other traditional products, a product line always comprises a lot of stock keeping units (SKUs ), and the sales of those SKUs are usually correlated. Thus, fashion sales are not only influenced by some important factors such as color or price, but also by the sales of correlated items. To study a multidimensional relationship between sales volumes and other influence factors in fashion sales forecasting , Ren et al. (2015) developed a panel data method supported by particle filter and conducted a numerical experiment in terms of item and color categories. Although the method outperforms some other popular statistical and intelligent approaches in the literature, the correlation between items is not closely examined. Thus, it will be of great interest to explore new methods which can shed light on the quantitative relationship between the products under study as well as improve forecast accuracy.

In this paper, we propose a novel method based on the analytic hierarchy process (AHP) to study the quantitative relationship between fashion products, and then use it to improve forecast accuracy by taking advantage of data aggregation. In the fashion industry, even if the aggregate demand can be predicted with some certainty, it is still very difficult to predict how it will be distributed over the many products that are offered because of the low sales volumes of individual SKUs and the significant variation of the demand of the SKUs within a same product line (Mostard et al. 2011). As an effort to use aggregation–disaggregation process, Bruzzone et al. (2013) proposed a forecasting model based on multiple autoregressive algorithms and disaggregation policies. In our scheme, since products can be weighted by their percentages in the aggregate sales volume, it will be easy and straightforward to make a division over products that are offered for sales. Moreover, since the AHP-based scheme is a framework which is designed to aggregate historical observations and disaggregate forecast volumes properly, it can be applied to most, if not all, existing approaches whose effectiveness can be improved if there are more stable data for analysis.

The rest of this paper is organized as follows. First, we provide a brief introduction to the AHP and propose the forecasting aggregation and disaggregation scheme with all necessary details in Sect. 12.2. Then, we present numerical experiments and discuss findings in Sect. 12.3. Last, we conclude this paper in Sect. 12.4.

2 AHP-Based Scheme for Data Aggregation and Disaggregation in Fashion Sales Forecasting

2.1 Introduction to the AHP

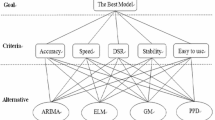
The AHP was first introduced by Saaty (1980) as a structured technique for complex decisions . Since then, it has been a popular approach among various multiple-criteria decision-making (MCDM) techniques proposed in the literature and applied in a wide variety of problems which comprise planning, selecting alternatives, allocating resources, and resolving conflicts (Subramanian and Ramanathan 2012). The AHP presents an effective way to combine subjective human knowledge with objective analysis and provides a solid framework to structure a problem and evaluate alternative solutions. In an AHP application, a decision problem will be decomposed into a hierarchy in a top-down structure with simpler subproblems. After the hierarchy is established, alternatives are compared in pairs under one or multiple criteria chosen by decision makers, and the solutions to the subproblems will be aggregated to obtain the final answer to the original problem under study. The AHP hierarchy may consist of many levels in which elements need to be compared pairwise. To avoid the inconsistency introduced by conflictive human judgments, the AHP introduces an eigenvector-based approach to check consistency. If the inconsistency cannot be tolerated, the pairwise comparison step will be performed repeatedly until comparison results are consistent. This feature overcomes the weakness of contradictory human knowledge and significantly improves the subjective comparisons and hence makes the AHP a popular MCDM tool which is widely used in practice.

In the literature, there are numerous applications of the AHP in many different areas such as supply chain management (Ramanathan 2013; Govindan et al. 2014), logistics (Barker and Zabinsky 2011), multisensor data fusion (Frikha and Moalla 2015), manufacturing (Sato et al. 2015), and data analysis (Chan et al. 2015). Moreover, research efforts are conducted to extend the power of the AHP. For example, Dong et al. (2013) proposed a new framework based on the 2-tuple linguistic modeling of AHP scale problems so that decision makers can use to generate numerical scales individually; Durbach et al. (2014) integrated the AHP with stochastic multicriteria acceptability analysis (SMAA) to allow uncertain pairwise comparisons; and Jalao et al. (2014) proposed a beta distribution to model the varying stochastic preferences of decision makers by using the method-of-moments methodology to fit the varying stochastic preferences of the decision makers into beta stochastic pairwise comparisons. All these works make the AHP more powerful and applicable.

Generally, a standard AHP application comprises the five steps below:

• 1. Hierarchy development: In this step, a top-down hierarchy will be established for the subsequent numerical computation in the AHP. First, it needs to identify the top level with a goal for the problem under study, one or multiple intermediate levels of criteria and subcriteria, and the bottom level which is usually a set of alternatives. Then, the correlated elements in different levels need to be connected to construct a top-down structure.

• 2. Pairwise comparison : After the hierarchy of an AHP model is established, the elements in each level, except the top goal level, need to be compared pairwise to evaluate their relative significance over others in the same level. Throughout the hierarchy, each element in an upper level will be used to compare the elements in the level immediately below with respect to it. Usually, this step relies on human knowledge, and a 1–9 scale will be used to measure the relative importance of two elements, which may introduce inconsistency because of contradictory or inaccurate human judgements. A comparison matrix shown in Eq. (12.1) will be obtained from the pairwise comparisons between the elements in each level.

  $$W = \left[ {\begin{array}{*{20}c} {\frac{{w_{1} }}{{w_{1} }}} & {\frac{{w_{1} }}{{w_{2} }}} & \cdots & {\frac{{w_{1} }}{{w_{n} }}} \\ {\frac{{w_{2} }}{{w_{1} }}} & {\frac{{w_{2} }}{{w_{2} }}} & \cdots & {\frac{{w_{2} }}{{w_{n} }}} \\ \vdots & \vdots & \ddots & \vdots \\ {\frac{{w_{n} }}{{w_{1} }}} & {\frac{{w_{n} }}{{w_{2} }}} & \cdots & {\frac{{w_{n} }}{{w_{n} }}} \\ \end{array} } \right],$$

  (12.1)

  where n is the number of the elements which are compared pairwise.

• 3. Eigenvalue and eigenvector calculation: An eigenvalue and eigenvector can be calculated from a comparison matrix shown in Eq. (12.1), and the values in the eigenvector indicate the significance of the elements which have been compared. Usually, the eigenvector will be normalized before it is aggregated to the final result.

• 4. Consistency check: For the accuracy of pairwise comparisons , the consistency of each comparison matrix needs to be checked by using consistency index (CI) or consistency ratio (CR). If a comparison matrix is not consistent, the corresponding pairwise comparisons should be repeated until the matrix is consistent.

• 5. Priority measurement: Usually, the priorities obtained from the pairwise comparisons at a level will be used to weigh the priorities in the level immediately below and then the weighted values of the elements in lower levels will be added to obtain their overall priority. This process needs to be repeated for every element until the final priorities of the alternatives in the bottom level of the AHP are obtained (Saaty 2008).

2.2 Data Aggregation and Disaggregation by the AHP

In a statistical analysis, variables can be classified into two types: qualitative and quantitative. Qualitative variables are non-numerical and usually associated with categorical values, while quantitative variables are numerical and their values are applicable for statistical techniques such as regression (Luo and Brodsky 2010). For example, item and color are two attributes which can be represented by qualitative variables, while the sales of a product is a quantitative variable over time. To gain better historical observations for forecasting , the low sales volumes of individual SKUs can be aggregated over qualitative variables. Although data aggregation is not difficult to implement, it is not easy to distribute the aggregate forecast over SKUs or products. However, the AHP provides a straightforward means to split the aggregate forecast . More specifically, the entities under study are weighted by the AHP based on their historical sales volumes with certainty, and then, the weights are used to distribute the aggregate forecast of future sales over those entities. Generally, the AHP hierarchy for such an application is shown in Fig. 12.1. In practice, the number of the levels of criteria is decided by the number of qualitative variables upon which raw data will be aggregated, and the alternatives can be any qualitative variable of interest such as SKUs or products. In each level, historical sales volumes, either original or aggregate, will be used for pairwise comparisons . Moreover, the element in a level may not be connected to all the elements in the level which is immediate above or below it, and whether a connection exists or not depends on the specific problem under study.

Fig. 12.1

AHP hierarchy for data aggregation and disaggregation in forecasting

In the fashion industry as well as many other industries, sales data are collected over time and hence attached with time labels, to which time series techniques (Cheng et al. 2015) can be used for sales forecasting . Because of the nature of the sales data, pairwise comparisons in our AHP model will also be conducted by using historical observations at discrete time points. Suppose $t = 1,2, \ldots ,T$ represents discrete time, $n = 1,2, \ldots ,N$ represents criteria levels in the hierarchy, and $m = 1,2, \ldots ,M_{n} \;(1 \le n \le N)$ represents the elements at criteria level n. Let S be the number of alternatives in the AHP, and $d_{s} (t)\;(1 \le s \le S,\;1 \le t \le T)$ be the sales of alternative s at time t, then the aggregate sale volume under category m at level n can be calculated by Eq. (12.2),

$$d_{m}^{n} (t) = \sum\limits_{{s \in \{ m_{n} \} }} {d_{s} (t)} ,\quad 1 \le n \le N,\;\;1 \le m \le M_{n} ,\;\;1 \le t \le T,$$

(12.2)

where $\{ m_{n} \}$ is the set of alternatives which belongs to category m at level n. Obviously, the bottom level of the AHP, which consists of alternatives, can be regarded as the (N + 1)th level of criteria, so $d_{s} (t)$ can be reformatted as Eq. (12.3). Thus, for level n, the comparison matrix of the elements at time t can be expressed by Eq. (12.4), and the final comparison matrix can be obtained by Eq. (12.5).

$$d_{m}^{N + 1} (t) = d_{m} (t),\quad 1 \le m \le S,\;\;1 \le t \le T,$$

(12.3)

$$W_{n} (t) = \left[ {\begin{array}{*{20}c} 1 & {\frac{{d_{1}^{n} (t)}}{{d_{2}^{n} (t)}}} & \cdots & {\frac{{d_{1}^{n} (t)}}{{d_{{M_{n} }}^{n} (t)}}} \\ {\frac{{d_{2}^{n} (t)}}{{d_{1}^{n} (t)}}} & 1 & \cdots & {\frac{{d_{2}^{n} (t)}}{{d_{{M_{n} }}^{n} (t)}}} \\ \vdots & \vdots & \ddots & \vdots \\ {\frac{{d_{{M_{n} }}^{n} (t)}}{{d_{1}^{n} (t)}}} & {\frac{{d_{{M_{n} }}^{n} (t)}}{{d_{2}^{n} (t)}}} & \cdots & 1 \\ \end{array} } \right],\quad 1 \le n \le N + 1,$$

(12.4)

$$V_{n} = \sum\limits_{t = 1}^{T} {a_{t} W_{n} (t)} ,\quad 1 \le n \le N + 1,$$

(12.5)

where $a_{t}$ is the weight of time period t. If the observations from all time periods are equally weighted, we have $a_{t} = 1\;(1 \le t \le T)$. The consistency of $W_{n} (t)$ is defined as follows.

Definition 1

In Eq. (12.4), $W_{n} (t)$ is consistent if and only if

$$\frac{{d_{i}^{n} (t)}}{{d_{j}^{n} (t)}} \cdot \frac{{d_{j}^{n} (t)}}{{d_{k}^{n} (t)}} = \frac{{d_{i}^{n} (t)}}{{d_{k}^{n} (t)}},\quad 1 \le i,j,k \le M_{n} ,\;\;i \ne j \ne k.$$

Let $\overrightarrow {{u_{n} }} = \left[ {u_{1}^{n} ,u_{2}^{n} , \ldots ,u_{{M_{n} }}^{n} } \right]^{{\prime }} \; (1 \le n \le N + 1)$ be the normalized eigenvector obtained from $V_{n}$, then $u_{m}^{n} \;(1 \le m \le M_{n} )$ is the local weight which indicates the significance of category or alternative m at level n comparing to others at the same level. The global weight which estimates the percentage of the sales volumes falling into such category or alternative can be calculated by Eq. (12.6).

$$g_{m}^{n} = u_{m}^{n} \sum\limits_{{m^{{\prime }} \subseteq \{ 1,2, \ldots ,M_{n - 1} \} }} {g_{{m^{{\prime }} }}^{n - 1} } ,\quad 1 \le n \le N + 1,$$

(12.6)

where $m^{{\prime }}$ is the set which consists of the parent elements of m at level $n - 1$.

2.3 Adjustment to Exceptional Results of Pairwise Comparison

For any level n and time t, $W_{n} (t)$ is always consistent because its entries are the results of pairwise comparisons which are conducted on a set of deterministic values. However, the final matrix at level n $(1 \le n \le N + 1)$, $V_{n}$, may not be consistent because the sales quantity of an alternative is a random variable over time (see the proof in Appendix for details). A main power of the AHP comes from its ability to measure and adjust inconsistent pairwise comparisons. In an application where human knowledge is used for pairwise comparisons, the inconsistency can be eliminated by repeating the process conducted by human experts until consistency is achieved. In our scheme, however, inconsistency cannot be adjusted in the traditional way because no human expert will be involved. To make $V_{n}$ consistent, a possible resolution is to adjust $a_{t}$ in Eq. (12.5). In case that $a_{t}$ cannot be adjusted, the entries in $V_{n} \;(1 \le n \le N + 1 )$ can also be changed for consistency by using some new values which comprise the comparison results shown in Eq. (12.7).

$$v_{i,j}^{n} = \frac{{\sum\nolimits_{t = 1}^{T} {d_{i}^{n} (t)} }}{{\sum\nolimits_{t = 1}^{T} {d_{j}^{n} (t)} }},\quad v_{j,i}^{n} = \frac{{\sum\nolimits_{t = 1}^{T} {d_{j}^{n} (t)} }}{{\sum\nolimits_{t = 1}^{T} {d_{i}^{n} (t)} }},\quad 1 \le i, \, j \le M_{n} ,\;\;i \ne j,$$

(12.7)

where $v_{i,j}^{n}$ is the entry at row i and column j of $V_{n}$, and $v_{j,i}^{n}$ is that at row j and column i.

Another common problem in pairwise comparisons is the occurrence of zero and infinite values. When the sales volume of an alternative or under a category is zero at time t, the related comparison results will be either zero or infinity, and hence, there will be infinite entries in the final matrix accordingly. Since it is not possible to calculate eigenvalues and eigenvectors from such a matrix, the infinite values must be replaced by finite numbers. Mathematically, suppose for element $i\;(1 \le i \le M_{n} )$ at level $n\;(1 \le n \le N + 1)$ during time period $t\;(1 \le t \le T)$, there is $d_{i}^{n} (t) = 0$, then there will be $w_{i,j}^{n} (t) = 0$ and $w_{j,i}^{n} (t) = \infty$ for any $j \ne i$, where $w_{i,j}^{n} (t)$ and $w_{j,i}^{n} (t)$ are the entries in $W_{n} (t)$. Consequently, there will be $v_{j,i}^{n} = \infty$, and hence, eigenvalues and eigenvectors cannot be calculated from $V_{n}$. In our scheme, we propose the resolution shown in Eq. (12.8).

$$v_{i,j}^{n} = \frac{1}{b},\quad v_{j,i}^{n} = b,\quad 1 \le n \le N + 1,\;\;1 \le i, \, j \le M_{n} ,\;\;i \ne j,$$

(12.8)

where b is a constant which can be either predefined or decided by some rules. Intuitively, b should be a large number because it is used to replace the infinity. However, this is not true for the sales forecasting in the fashion industry because of the nature of the business. More specifically, since individual SKUs usually have low sales volumes which may vary significantly, the actual portion of a SKU in the total sales volume can be distorted remarkably if b is very large. For example, if the sales of a high-volume product is zero during a period, which is not unusual in reality, large b values can lead to a small global weight for this product, and consequently, its sales volumes will be under-forecasted. Thus, a small or medium value is suggested for b in this study. In practice, the value of b can be set up by using the knowledge from business experts, or by numerical experiments to find an optimal value which minimizes forecast errors for the specific problem under study.

3 Numerical Experimentation

3.1 Data Set

In this section, the AHP -based scheme is tested by using real sales data from a fashion boutique in Hong Kong. The data include six fashion items (i.e., T-shirt, dress, bag, pant, accessory, and belt) and seven colors (i.e., black, blue, brown, red, white, green, and gray). Other than item and color, there are three attributes in a sales record: date, quantity, and price. The original data set covers time duration of forty-two weeks in total, and a sample piece is presented in Table 12.1. In this study, the original data are consolidated into a weekly bucket for simplicity, and the sales volumes are aggregated by item to test the scheme we propose. In Table 12.1, since the dates were in two different calendar weeks, the data can be aggregated into two weeks as shown in Table 12.2. There are 42 observations over time in our numerical analysis because the original data set covers 42 calendar weeks. The basic descriptive statistics of those observations under six item categories are provided in Table 12.3.

Table 12.1 Original sales data from a fashion boutique

Table 12.2 Aggregate sales data by item

Table 12.3 Global weight of item category (obs = 2, b = 3)

3.2 Experiment Design and Numerical Analysis

The original data set includes the prices of the products sold in history. It is a quantitative variable upon which many statistical techniques can be applied. However, how to set up this variable in aggregate sales data needs to be considered carefully. Otherwise, the information about the future sales to be predicted may be used implicitly, which will weaken the approach. For example, the average price weighted by sales volumes during a time period should not be used to forecast the sales during the same time period because it contains the information about the sales volumes to be predicted. As an initial research effort, this paper does not consider how to set up quantitative variables when sales data are aggregated. Thus, the AHP-based scheme is only applied to two basic time series forecasting methods , moving average (MA) and exponential smoothing (ES). To test its performance, the sales volumes per item in the last six weeks of the whole time span (i.e., week 37–42) are predicted with and without applying the AHP-based scheme, which means that the forecasting is made by four approaches : MA, MA based on the AHP (MA-AHP), ES, and ES based on the AHP (ES-AHP). In MA-AHP and ES-AHP, the global weights of the six item categories are generated by the AHP model whose hierarchy is shown in Fig. 12.2. Those weights are first generated under several different settings in terms of the number of historical observations and b values, and then are used to distribute the aggregate forecast over individual item categories.

Fig. 12.2

AHP hierarchy for numerical analysis

For week t, let $F_{t}$ be the total aggregate forecast over all SKUs, $d_{t}^{(i)}$ and $F_{t}^{(i)}$ be the aggregate sales and forecast volumes under item category i, respectively, and $g_{t}^{(i)}$ be the global weight of item category i generated by the AHP. Suppose K is the number of the most recent observations used by MA, and $\alpha \;(0 \le \alpha \le 1)$ is the smoothing constant for ES. Then, the four approaches can be expressed by Eqs. (12.9)–(12.12), respectively.

MA:

$$\quad F_{t}^{(i)} = \frac{1}{K}\sum\limits_{l = t - K}^{t - 1} {d_{l}^{(i)} } ,\quad 1 \le i \le 6,\;\;37 \le t \le 42.$$

(12.9)

MA-AHP :

$$F_{t} = \frac{1}{K}\sum\limits_{l = t - K}^{t - 1} {\sum\limits_{i = 1}^{6} {d_{l}^{(i)} ,F_{t}^{(i)} } } = \, g_{t}^{(i)} F_{t} ,\quad 1 \le i \le 6,\;\;37 \le t \le 42.$$

(12.10)

ES:

$$\quad F_{t}^{(i)} = \alpha d_{t - 1}^{(i)} + (1 - \alpha )F_{t - 1}^{(i)} ,\quad 1 \le i \le 6,\;\;37 \le t \le 42.$$

(12.11)

ES-AHP:

$$F_{t} = \alpha \sum\limits_{i = 1}^{6} {d_{t - 1}^{(i)} + (1 - \alpha )F_{t - 1} } , \, F_{t}^{(i)} = \, g_{t}^{(i)} F_{t} ,\quad 1 \le i \le 6,\;\;37 \le t \le 42.$$

(12.12)

Tables 12.3, 12.4, and 12.5 illustrate how the AHP-based scheme works by using the most recent two observations for sales forecasting (e.g., observations at weeks 35 and 36 are used for the forecasts at week 37). More specifically, Table 12.3 shows the global weights of the six item categories generated by the AHP, Table 12.4 shows the aggregate forecasts by MA and ES, and Table 12.5 shows the disaggregated forecast quantities per item category.

Table 12.4 Aggregate forecast by MA and ES (obs = 2, b = 3)

Table 12.5 Sales forecast by AHP-MA/AHP -ES (obs = 2, b = 3)

In the results analysis, the mean squared error (MSE) and the symmetric mean absolute percentage error (SMAPE) are used to measure the sales forecast accuracy of different approaches. MSE is one of the most popular measures which are widely used in both academic research and industrial practices. It is the average of the squared errors which implies how much an estimator deviates from a true value. Mathematically, MSE is defined in Eq. (12.13).

$${\text{MSE}} = \frac{1}{T}\sum\limits_{t = 1}^{T} {(F_{t} - A_{t} )^{2} } ,$$

(12.13)

where $F_{t}$ and $A_{t}$ represent forecast and true value at time t, respectively.

In the fashion industry , it happens from time to time that the sales volume of a product at a retail store is recorded to be zero during a time period. Because of this, there are many zero values in the data set used for our numerical study. Since the mean absolute percentage error (MAPE) is not suitable for handling this scenario , SMAPE, which is a relative measure based on percentage errors, is used as the second measurement of forecast accuracy instead. Mathematically, SMAPE is defined in Eq. (12.14).

$${\text{SMAPE}} = \frac{{\sum\nolimits_{t = 1}^{T} {\left| {F_{t} - A_{t} } \right|} }}{{\sum\nolimits_{t = 1}^{T} {(F_{t} + A_{t} )} }},$$

(12.14)

where $F_{t}$ and $A_{t}$ represent forecast and true value at time t, respectively.

To fully test the performance of the AHP-based scheme, the global weights of the item categories are generated by the AHP model under several different sets of obs and b values. Tables 12.6, 12.7, and 12.8 present the forecast accuracy in terms of MSE and SMAPE under short data history settings. From the numerical results, we can see that the overall performance of both MA and ES can be improved after the AHP-based scheme is applied. In particular, for item “belt” which has the smallest sales quantity among the six items, the forecast accuracy has been significantly increased in terms of MSE and SMAPE, which indicates that our scheme is an effective means to improve the forecast quality for the fashion products with short life cycle and low sales volumes. From Tables 12.6, 12.7 and 12.8, we can also see that the numerical results from the three experiments are similar, which indicates that the AHP -based scheme works consistently under similar parameter settings. Moreover, for item “belt,” there is a significant change in forecast accuracy when b changes, which indicates that low-volume items are more sensitive to b comparing to high-volume items.

Table 12.6 Forecast accuracy of four approaches (obs = 8, b = 4)

Table 12.7 Forecast accuracy of four approaches (obs = 8, b = 5)

Table 12.8 Forecast accuracy of four approaches (obs = 10, b = 4)

4 Conclusion and Future Work

Sales forecasting is a very challenging problem in the fashion industry . Although the wise use of information for conducting sales forecasting will be greatly helpful to enhance the operations management of fashion companies (Mishra et al. 2009), it is not easy to do so because the fashion products exhibit the features of short life cycles, low sales volumes, and significant volatility. In this paper, we propose a novel scheme based on the AHP to aggregate sales data for “better historical observations” on which the total future sales of multiple products (or SKUs ) can be predicted more accurately. The aggregate forecast can then be distributed over the business unit of interest to capture the future demand of those units more effectively. Notice that in the literature, many research efforts are conducted to improve a certain type of techniques for forecasting. For example, a multistep expectation maximization based algorithm was proposed by Luo et al. (2012) to improve piecewise surface regression for a better forecast quality. But unlike those works, this paper proposes a general framework which is developed to make a better use of historical data for forecasting instead of improving any specific techniques afterward for sales forecasting . Thus, it can be applied to help most existing approaches to enhance their performance in sales forecasting .

Future studies can be conducted in the following directions. First, as mentioned in Sect. 12.3.2, how to set up quantitative variables when sales data are aggregated has not been studied in the literature. By solving this problem, it will be possible to apply the AHP -based schema to many advanced forecasting techniques and hence the power of the method will be well extended. Second, the constant b in Eq. (12.8) is a predefined parameter in the numerical experiments presented in this paper; it is observed that the forecast accuracy may be significantly affected by the value of this parameter. To optimize the performance of the scheme, it will be greatly beneficial to develop a method which decides the optimal value of this parameter b. Last, this scheme is of great value in practice because of its runtime efficiency. Theoretically, this scheme should reduce the runtime of statistical approaches significantly because the number of statistical analysis will be decreased a lot when a large number of SKUs are aggregated together (as the runtime of the AHP model is very short comparing with statistical models). Thus, in an industrial application where data volume is extremely high, our proposed scheme will be highly preferred because of its great capability in runtime reduction even if it cannot improve forecast quality. However, the time performance of the AHP-based scheme cannot be tested in this study because we need much more data to do so. We thus relegate this extension to our future research .

Appendix

Lemma

The final comparison matrix in Eq. (12.5) can be inconsistent if it is aggregated from the comparison matrices in Eq. (12.4).

Proof

Suppose that at criteria level n, i, j, and k are three elements which are compared pairwise. Without loss of generality, let us assume that pairwise comparisons are conducted on the observations at two discrete times, namely 1 and 2, for which $a_{1} = a_{2} = 1$ is satisfied. Thus, Eqs. (12.15)–(12.17) can be obtained.

$$v_{i,j}^{n} = \frac{{d_{i}^{n} (1)}}{{d_{j}^{n} (1)}} + \frac{{d_{i}^{n} (2)}}{{d_{j}^{n} (2)}} = \frac{{d_{i}^{n} (1)d_{j}^{n} (2) + d_{i}^{n} (2)d_{j}^{n} (1)}}{{d_{j}^{n} (1)d_{j}^{n} (2)}},$$

(12.15)

$$v_{i,k}^{n} = \frac{{d_{i}^{n} (1)}}{{d_{k}^{n} (1)}} + \frac{{d_{i}^{n} (2)}}{{d_{k}^{n} (2)}} = \frac{{d_{i}^{n} (1)d_{k}^{n} (2) + d_{i}^{n} (2)d_{k}^{n} (1)}}{{d_{k}^{n} (1)d_{k}^{n} (2)}},$$

(12.16)

$$v_{j,k}^{n} = \frac{{d_{j}^{n} (1)}}{{d_{k}^{n} (1)}} + \frac{{d_{j}^{n} (2)}}{{d_{k}^{n} (2)}} = \frac{{d_{j}^{n} (1)d_{k}^{n} (2) + d_{j}^{n} (2)d_{k}^{n} (1)}}{{d_{k}^{n} (1)d_{k}^{n} (2)}}.$$

(12.17)

If the final comparison matrix in Eq. (12.5) is consistent, then there we have the following: $v_{i,j}^{n} \cdot v_{j,k}^{n} = v_{i,k}^{n}$. In this case, Eq. (12.18) must be true. Since sales volumes are random and Eq. (12.18) cannot be always satisfied, the lemma is proved.

$$d_{i}^{n} (1)d_{j}^{n} (2)d_{j}^{n} (2)d_{k}^{n} (1) + d_{i}^{n} (2)d_{j}^{n} (1)d_{j}^{n} (1)d_{k}^{n} (2) = 0.$$

(12.18)