Keywords

1 Introduction

Power divider/combiner (PDC) is commonly used in microwave circuits. They have various applications, such as combining the output power of high power amplifiers, [1–4]. The Wilkinson and Gysel structures are the most popular structures [5–8]. However, a major drawback of the conventional PDC is the presence of spurious response due to the adoption of quarter-wavelength TL [1–4].

Recently, PDC, hybrid and coupler with harmonic suppression performance or size reduction have been studied in some papers. Researchers Guan et al. and Wu et al. studied the PDCs with even-odd mode or ABCD matrix analysis method. Some studies [9, 10] use electromagnetic band gap (EBG) or defected ground structure (DGS) cells to make the suppression of harmonic frequency or size reduction.

In this paper, the design of equivalent cross-shaped TL cell is proposed to increase the harmonic suppression of modified Gysel PDC. In Sect. 2, the equivalent cross-shaped TL cell is analyzed by the ABCD matrix model. In Sect. 3, we present a simple process to design the proposed Gysel PDC with harmonic suppression characteristic by replacing the original TL in the Gysel PDC with equivalent cross-shaped TL. And in Sect. 4, for illustration, an example of Gysel PDC is fabricated and tested. In Sect. 5, we present the conclusion.

2 Design Cross-Shaped TL Cell for Harmonic Suppression

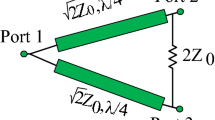
Figure 1 shows the original TL, equivalent cross-shaped TL and T-shaped [11] TL. In order to achieve the transmission zero at harmonic frequency fs [11], the electrical length θs of the open-stub in the equivalent TL cell can be calculate as below:

$$ \uptheta_{\text{s}} = \left( {\frac{\uppi}{2}} \right)\left( {\frac{{{\text{f}}_{0} }}{{{\text{f}}_{\text{s}} }}} \right) $$
(1)
Fig. 1
figure 1

a The original TL, b cross-shaped TL, c T-shaped TL

Full size image

The ABCD matrix of the original TL, the equivalent cross-shaped and T-shaped TL are as below:

$$ M_{0} = \left[ {\begin{array}{*{20}c} {{ \cos }\left( {\theta_{0} } \right)} & {jZ_{0} { \sin }\left( {\theta_{0} } \right)} \\ {jY_{0} { \sin }\left( {\theta_{0} } \right)} & {{ \cos }\left( {\theta_{0} } \right)} \\ \end{array} } \right] $$
(2)
$$ \begin{aligned} M_{\text{c}} = & \left[ {\begin{array}{*{20}c} {\cos \left( {\theta_{{{\text{c}}1}} } \right)} & {jZ_{{{\text{c}}1}} { \sin }\left( {\theta_{{{\text{c}}1}} } \right)} \\ {jY_{{{\text{c}}1}} { \sin }\left( {\theta_{{{\text{c}}1}} } \right)} & {\cos \left( {\theta_{{{\text{c}}1}} } \right)} \\ \end{array} } \right] * \left[ {\begin{array}{*{20}c} 1 & 0 \\ {jY_{c3} { \tan }\left( {\theta_{{{\text{c}}3}} } \right)} & 1 \\ \end{array} } \right] \\ & \quad * \left[ {\begin{array}{*{20}c} 1 & 0 \\ {jY_{{{\text{c}}4}} { \tan }\left( {\theta_{{{\text{c}}4}} } \right)} & 1 \\ \end{array} } \right] * \left[ {\begin{array}{*{20}c} {{ \cos }\left( {\theta_{{{\text{c}}2}} } \right)} & {jZ_{{{\text{c}}2}} { \sin }\left( {\theta_{{{\text{c}}2}} } \right)} \\ {jY_{{{\text{c}}2}} { \sin }\left( {\theta_{{{\text{c}}2}} } \right)} & {{ \cos }\left( {\theta_{{{\text{c}}2}} } \right)} \\ \end{array} } \right] \\ \end{aligned} $$
(3)
$$ M_{\text{t}} = \left[ {\begin{array}{*{20}c} {\cos \left( {\theta_{{{\text{t}}1}} } \right)} & {jZ_{{{\text{t}}1}} { \sin }\left( {\theta_{{{\text{t}}1}} } \right)} \\ {jY_{{{\text{t}}1}} { \sin }\left( {\theta_{{{\text{c}}1}} } \right)} & {\cos \left( {\theta_{{{\text{t}}1}} } \right)} \\ \end{array} } \right]*\left[ {\begin{array}{*{20}c} 1 & 0 \\ {jY_{t3} { \tan }\left( {\theta_{{{\text{t}}3}} } \right)} & 1 \\ \end{array} } \right]* \left[ {\begin{array}{*{20}c} {{ \cos }\left( {\theta_{{{\text{t}}2}} } \right)} & {jZ_{{{\text{t}}2}} { \sin }\left( {\theta_{{{\text{t}}2}} } \right)} \\ {jY_{{{\text{t}}2}} { \sin }\left( {\theta_{{{\text{t}}2}} } \right)} & {{ \cos }\left( {\theta_{{{\text{t}}2}} } \right)} \\ \end{array} } \right] $$
(4)

Wu et al. [11] sets the parameters of the T-shaped TL, as shown in as Eqs. (5a, b) and (6).

$$ Z_{t1} = Z_{t2} = Z_{0} { \tan }\left( {\theta_{0} /2} \right){ \cot }\left( {\theta_{t1} } \right) $$
(5a)
$$ Z_{t3} = Z_{0} {\text{tan}}\left( {\theta_{0} /2} \right){ \tan }\left( {\theta_{t3} } \right)\frac{{\cos^{2} \left( {\theta_{t1} } \right)}}{{\cos \left( {2\theta_{t1} } \right) - \cos \left( {\theta_{0} } \right)}} $$
(5b)

In order to get the parameters of the equivalent cross-shaped TL, we make M c = M t, which means that Z c1 = Z c2 = Z t1, θ c1 = θ c2 = θ t1, and the two open stubs in the cross-shaped TL equal to the one open stub in the T-shaped TL @f 0. Then we will get Eq. (6) as below:

$$ Y_{c3} { \tan }\left( {\theta_{{{\text{c}}3}} } \right) + Y_{{{\text{c}}4}} { \tan }\left( {\theta_{{{\text{c}}4}} } \right) = Y_{t3} { \tan }\left( {\theta_{{{\text{t}}3}} } \right) = Y_{0} \frac{{\cos \left( {2\theta_{c1} } \right) - \cos \left( {\theta_{0} } \right)}}{{ { \tan }\left( {\theta_{0} /2} \right)\cos^{2} \left( {\theta_{c1} } \right)}} $$
(6)

To suppress 2nd and 3rd harmonics, we define θ c3 = 30° and θ c4 = 45°. We define the limit range of Z ci (general microstrip manufacture 25–135 Ω) and θ ci (0° < θ ci ≤ 45°). From Eq. (6), we can get that the values of Z c1, c2, Z c3 and Z c4 depend on Z 0, θ c1 and θ c0. The original TLs in the Gysel PDC which need to be replaced are all 90°. Then, we will get that

$$ Z_{c1} = Z_{c2} = Z_{0} { \cot }\left( {\theta_{c1} } \right) $$
(7a)
$$ \frac{\sqrt 3 }{ 3}Y_{c3} + Y_{c4} = Y_{0} \frac{{\cos \left( {2\theta_{c1} } \right)}}{{\cos^{2} \left( {\theta_{c1} } \right)}} $$
(7b)

Figure 2 shows that the values of Z c1, c2, Z c3 and Z c4 depend on θ c1 when Z 0 = 50 \( \varOmega \), θ 0 = 90°, θ c3 = 30° and θ c4 = 45°. From the Fig. 2, we can see that the higher θ c1, the lower Z c1, c2. It also shows that the higher is the value of θ c1, the higher is the value of Z c4 when making Z c3 be a fixed value. So we should choose suitable values to fabricate TLs. Table 1 gives an example of the equivalent cross-shaped TL with ideal parameter values. The simulation result in Fig. 3 shows that the cross-shaped TL not only has similar S-parameter with the original TL at around fundamental frequency, but also the bandstop filter character at the harmonic frequencies.

Fig. 2
figure 2

The value of Z c1, c2, Z c3 and Z c4 depend on θ c1

Full size image
Table 1 Ideal parameter values of the equivalent cross-shaped TL
Full size table
Fig. 3
figure 3

Simulated results of the original TL and equivalent cross-shaped TL (f 0 = 1 GHz, Z 0 = 50 \( \varOmega \) , θ 0  = 90°)

Full size image

3 Design Procedure of Proposed PDC

In this section, we introduce the design procedure of the proposed Gysel PDC. Generally, the impedances of TLs are Z 1 = 70.7 \( {\Omega} \), Z 2 = 50 \( {\Omega} \), Z 3 = 35 \( {\Omega} \), and Z L  = R L  = 50 \( {\Omega} \), [1–4]. Then we calculate and choose the suitable parameters of the equivalent cross-shaped TL depending on Eq. (7a, b) and Fig. 2.

By replacing the TLs in the GyselPDC with the equivalent cross-shaped TL cells, the modified Gysel PDC does not change the S-parameter characters nor other characters at the fundamental frequency f 0. The modified Gysel PDC provides transmission zeros at higher frequency. To make the design simple, the design procedure of the proposed PDC sets as follows:

  1. 1.

    Design a conventional Gysel PDC with the parameters of Zi, θ i , Z L and R L.

  2. 2.

    Calculate and choose the suitable parameters of the equivalent cross-shaped TL by formula (7a, b) and Fig. 3.

  3. 3.

    And then use the equivalent TL cells to replace the Zi TL in the Gysel PDC.

4 Simulation and Measurement

In order to verify the proposed structure, a proposed Gysel PDC (f 0 = 1 GHz) has been fabricated using microstrip TL, which is shown in Fig. 4.

Fig. 4
figure 4

The proposed Gysel PDC

Full size image

The measurement results are collected by a network analyzer. The simulated and measured S-parameter performance shows in Fig. 5. Inside the fundamental band, the PDC exhibits an insertion loss lower than 3.4 dB, a minimum input return loss and ports isolation higher than 15 dB covering a fractional bandwidth of about 30 %. From the simulation and measurement results, the proposed Gysel PDC shows good suppression at harmonic frequencies and good matching at fundamental frequency. It is also shown in Table 1 that Z0 with θ0 = 90° is substituted by equivalent TL structures which have smaller electrical length.

Fig. 5
figure 5

The simulated and the measured S-parameter performance of Gysel PDC

Full size image

5 Conclusion

In this paper, the design, fabrication and measurements of modified two-way Gysel PDC with equivalent cross-shaped TL cells are reported. Measurement results of the proposed PDC conform to the theoretical predictions. This presented PDC features suppression at the hoped harmonic frequencies with area miniaturization. This presented Gysel PDC could be applied to microwave circuits and systems which need PDC with not only harmonic suppression performance but also high power handling capability.