15.1 Introduction

The Fabry-Pérot resonator which was invented in 1899 [1] has proven very useful as a high-finesse interferometer in uncountable spectroscopic applications. Since 1960, it has also formed the fundamental basis for a large class of open resonators that have enabled laser oscillation. The Fabry-Pérot resonator has been extensively investigated, experimentally as well as theoretically. However, when the losses become high, discrepancies between the theoretical approaches surface, common approximations turn invalid, and even the definitions of typical parameters break down or prove inappropriate.

We analyze the performance and relevant parameters of the Fabry-Pérot resonator, with reference to the book on the Fabry-Pérot resonator by Vaughan [2] and the standard text books by Siegman [3], Svelto [4, 5], and Saleh and Teich [6,7,8]. We demonstrate that the sum of the mode profiles of all longitudinal modes, which are Lorentzian-shaped in case of frequency-independent losses, is the fundamental spectral function that characterizes the Fabry-Pérot resonator. It physically generates the Airy distribution of the Fabry-Pérot resonator. The resonator losses are quantified by the linewidths of the underlying Lorentzian lines. We define the Lorentzian finesse which provides the resolution of the Lorentzian lines, whereas the usually considered Airy finesse describes the performance of the Fabry-Pérot resonator as a scanning spectrometer.

15.2 Resonator Losses and Outcoupled Light

Throughout this paper, we assume a two-mirror Fabry-Pérot resonator of geometrical length ℓ, homogeneously filled with a medium of refractive index n r. Both, ℓ and n r are assumed to vary insignificantly over the frequency range of interest. The round-trip time t RT of light travelling in the resonator with speed c = c 0/n r, where c 0 is the speed of light in vacuum, is given by

$$ {t}_{RT}=\frac{2\mathrm{\ell}}{c}. $$
(15.1)

Outcoupling losses occur due to non-perfect reflectivity of the two mirrors,

$$ {\displaystyle \begin{array}{c}{r}_i^2={R}_i=1-{t}_{out,i}^2=1-{T}_{out,i}={e}^{-{t}_{RT}/{\tau}_{out,i}}\kern0.75em \iff \\ {}\frac{1}{\tau_{out,i}}=\frac{-\ln \left({R}_i\right)}{t_{RT}}=\frac{-\ln \left(1-{T}_{out,i}\right)}{t_{RT}}.\end{array}} $$
(15.2)

Here, r i(ν) and R i(ν) are the electric-field and intensity reflectivities, respectively, t out,i(ν) and T out,i(ν) are the electric-field and intensity transmissions, respectively, and τ out,i(ν) is the exponential decay time resulting from the outcoupling loss at mirror i. All other losses shall be neglected. The photon-decay time τ c(ν) of the resonator is then given by

$$ \frac{1}{\tau_c}=\sum \limits_i\frac{1}{\tau_{out,i}}=\frac{\sum \limits_i{\delta}_{out,i}}{t_{RT}}=\frac{\sum \limits_i-\ln \left({R}_i\right)}{t_{RT}}. $$
(15.3)

The number φ(t) of photons at frequency ν, present inside the resonator at time t, is described via the photon-decay time τ c(ν) by the differential rate equation

$$ \frac{d}{dt}\varphi (t)=-{R}_{decay}(t)=-\frac{1}{\tau_c}\varphi (t). $$
(15.4)

R decay(t) is the photon-decay rate per unit time. With a number φ s of photons present at the starting time t = 0, integration delivers

$$ \varphi (t)={\varphi}_s{e}^{-t/{\tau}_c}. $$
(15.5)

With ϕ(ν) quantifying the single-pass phase shift between the mirrors, the round-trip phase shift at frequency ν accumulates to

$$ 2\phi \left(\nu \right)=2\pi \nu {t}_{RT}=2\pi \nu \frac{2\mathrm{\ell}}{c}. $$
(15.6)

We have assumed above that the refractive index n r of the medium and, thus, the speed of light c are independent of frequency. Consequently, also the round-trip time t RT becomes independent of frequency. Resonances occur at frequencies at which light exhibits constructive interference after one round trip. The difference in phase shift per round trip between adjacent resonance frequencies amounts to 2π, from which the free spectral range Δν FSR then derives as [2].

$$ \frac{d}{d\nu}\left(2\phi \right)=\frac{d}{d\nu}\left(2\pi \nu {t}_{RT}\right)=2\pi {t}_{RT}\kern0.75em \Rightarrow \kern0.75em \frac{2\pi }{\Delta {\nu}_{FSR}}=2\pi {t}_{RT}\kern0.75em \Rightarrow \kern0.75em \Delta {\nu}_{FSR}\!=\!\frac{1}{t_{RT}}.\\[5pt] $$
(15.7)

Each resonator mode with its mode index q, where q is an integer number in the interval [−∞, …, −1, 0, 1, …, ∞], is associated with a resonance frequency ν q and wavenumber k q,

$$ {\nu}_q=q\Delta {\nu}_{FSR}=q/{t}_{RT}\kern0.75em \Rightarrow \kern0.75em {k}_q=\frac{2\pi q\Delta {\nu}_{FSR}}{c}. $$
(15.8)

Two modes with opposite values ±q and ±k of modal index and wavenumber, respectively, physically representing opposite propagation directions, occur at the same absolute value |ν q| of frequency.

According to Eq. (15.5), light at frequency ν oscillating inside the resonator decays out of the resonator with a time constant of τ c(ν). If the resonator losses are independent of frequency, the photon-decay time τ c(ν) is the same at all frequencies. The decaying electric field at frequency ν q is represented by a damped harmonic oscillation with an initial amplitude of E q,s and a decay-time constant of 2τ c. In phasor notation, it can be expressed as

$$ {E}_q(t)=\left\{\begin{array}{cc}{E}_{q,s}{e}^{i2{\pi \nu}_qt}{e}^{-t/\left(2{\tau}_c\right)}& t\ge 0\\ {}0& t<0\end{array}\right.. $$
(15.9)

Fourier transformation of the electric field in time provides the electric field per unit frequency interval,

$$ {\displaystyle \begin{array}{c}{\tilde{E}}_q\left(\nu \right)=\underset{-\infty }{\overset{+\infty }{\int }}{E}_q(t){e}^{-i2\pi \nu t} dt={E}_{q,s}\underset{0}{\overset{+\infty }{\int }}{e}^{-\left[1/\left(2{\tau}_c\right)+i2\pi \left(\nu -{\nu}_q\right)\right]t} dt\\ {}={E}_{q,s}\frac{1}{{\left(2{\tau}_c\right)}^{-1}+i2\pi \left(\nu -{\nu}_q\right)}.\end{array}} $$
(15.10)

Each mode has a normalized spectral line shape per unit frequency interval given by [9].

$$ {\displaystyle \begin{array}{c}{\tilde{\gamma}}_q\left(\nu \right)=\frac{1}{\tau_c}{\left|\frac{{\tilde{E}}_q\left(\nu \right)}{E_{q,s}}\right|}^2\\ {}=\frac{1}{\tau_c}{\left|\frac{1}{{\left(2{\tau}_c\right)}^{-1}+i2\pi \left(\nu -{\nu}_q\right)}\right|}^2=\frac{1}{\tau_c}\frac{1}{{\left(2{\tau}_c\right)}^{-2}+4{\pi}^2{\left(\nu -{\nu}_q\right)}^2}\\ {}=\frac{1}{\pi}\frac{1/\left(4{\pi \tau}_c\right)}{1/{\left(4{\pi \tau}_c\right)}^2+{\left(\nu -{\nu}_q\right)}^2}\kern1em \mathrm{with}\kern1em \int {\tilde{\gamma}}_q\left(\nu \right) d\nu =1,\end{array}} $$
(15.11)

in units of (1/Hz). Introducing the full-width-at-half-maximum (FWHM) linewidth Δν c of the Lorentzian spectral line shape, we obtain

$$ \Delta {\nu}_c=\frac{1}{2{\pi \tau}_c}\kern0.5em \Rightarrow \kern0.5em {\tilde{\gamma}}_q\left(\nu \right)=\frac{1}{\pi}\frac{\Delta {\nu}_c/2}{{\left(\Delta {\nu}_c/2\right)}^2+{\left(\nu -{\nu}_q\right)}^2}\kern1em \mathrm{with}\kern1em \int {\tilde{\gamma}}_q\left(\nu \right) d\nu =1. $$
(15.12)

Calibrated to a peak height of unity, we obtain the Lorentzian lines, in units of (1):

$$ {\gamma}_{q,L}\left(\nu \right)=\frac{\pi }{2}\Delta {\nu}_c{\tilde{\gamma}}_q\left(\nu \right)=\frac{{\left(\Delta {\nu}_c\right)}^2}{{\left(\Delta {\nu}_c\right)}^2+4{\left(\nu -{\nu}_q\right)}^2}\kern1em \mathrm{with}\kern1em {\gamma}_{q,L}\left({\nu}_q\right)=1. $$
(15.13)

When repeating the above Fourier transformation for all the modes with mode index q in the resonator, one obtains the full mode spectrum of the resonator.

15.3 Airy Distributions of the Fabry–Pérot Resonator

In this Section, we derive the generic Airy distribution, show that it represents the spectral dependence of the internal resonant enhancement factor, and demonstrate that all other Airy distributions describing the circulating, back-circulating, transmitted, and back-transmitted intensity (Fig. 15.1) only include simple scaling factors, depending on whether the light incident upon mirror 1 or its fraction launched into the resonator is considered as a reference. We verify that the physical origin of the Airy distribution is the sum of mode profiles of the longitudinal resonator modes.

Fig. 15.1
figure 1

Fabry-Pérot resonator with electric-field mirror reflectivities r 1 and r 2. Indicated are the characteristic electric fields produced by an electric field E inc incident upon mirror 1: E refl,1 initially reflected at mirror 1, E laun launched through mirror 1, E circ and E b-circ circulating inside the resonator in forward and backward propagation direction, respectively, E RT propagating inside the resonator after one round trip, E trans transmitted through mirror 2, E back transmitted through mirror 1, and the total field E refl propagating backward. Interference occurs at the left- and right-hand sides of mirror 1 between E refl,1 and E back, resulting in E refl, and between E laun and E RT, resulting in E circ, respectively. (Figure taken from Ref. [10])

Full size image

15.3.1 Generic Airy Distribution: The Internal Resonance Enhancement Factor

The response of the Fabry-Pérot resonator is most easily derived by use of the circulating-field approach [3], as displayed in Fig. 15.1. This approach assumes a steady state and derives the Airy distributions via the electric field E circ circulating inside the resonator. In fact, E circ is the field propagating in the forward direction from mirror 1 to mirror 2 after interference between the field E RT that is circulating after one round trip, i.e., after having suffered outcoupling losses at both mirrors, and the field E laun launched through the first mirror.

With the phase shift 2ϕ of Eq. (15.6) accumulated in one round trip, the field E circ can be related to the field E laun that is launched into the resonator in the situation of Fig. 15.1a by

$$ {E}_{circ}={E}_{laun}+{E}_{RT}={E}_{laun}+{r}_1{r}_2{e}^{-i2\phi }{E}_{circ}\kern0.75em \Rightarrow \kern0.75em \frac{E_{circ}}{E_{laun}}=\frac{1}{1-{r}_1{r}_2{e}^{-i2\phi }}.\\[4pt]\vspace*{-3pt} $$
(15.14)

Exploiting the identities

$$ {\displaystyle \begin{array}{c}{\left|{e}^{- i\phi}\right|}^2={\left|\cos \left(\phi \right)-i\sin \left(\phi \right)\right|}^2={\cos}^2\left(\phi \right)+{\sin}^2\left(\phi \right)=1\\ {}\cos \left(2\phi \right)=1-2{\sin}^2\left(\phi \right)\end{array}}\vspace*{-3pt} $$
(15.15)

yields

$$ {\displaystyle \begin{array}{c}{\left|1-{r}_1{r}_2{e}^{-i2\phi}\right|}^2={\left|1-{r}_1{r}_2\cos \left(2\phi \right)+{ir}_1{r}_2\sin \left(2\phi \right)\right|}^2\\ {}={\left[1-{r}_1{r}_2\cos \left(2\phi \right)\right]}^2+{r}_1^2{r}_2^2{\sin}^2\left(2\phi \right)\\ {}=1+{R}_1{R}_2-2\sqrt{R_1{R}_2}\cos \left(2\phi \right)={\left(1-\sqrt{R_1{R}_2}\right)}^2+4\sqrt{R_1{R}_2}{\sin}^2\left(\phi \right),\end{array}} $$
(15.16)
$$ {\displaystyle \begin{array}{c}{\left|{r}_1-{r}_2{e}^{-i2\phi}\right|}^2={\left|{r}_1-{r}_2\cos \left(2\phi \right)+{ir}_2\sin \left(2\phi \right)\right|}^2\\ {}={\left[{r}_1-{r}_2\cos \left(2\phi \right)\right]}^2+{\left[{r}_2\sin \left(2\phi \right)\right]}^2\\ {}={R}_1+{R}_2-2\sqrt{R_1{R}_2}\cos \left(2\phi \right)\\ {}={R}_1+{R}_2-2\sqrt{R_1{R}_2}\left[1-2{\sin}^2\left(\phi \right)\right]\\ {}={\left(\sqrt{R_1}-\sqrt{R_2}\right)}^2+4\sqrt{R_1{R}_2}{\sin}^2\left(\phi \right).\end{array}} $$
(15.17)

The generic Airy distribution, which considers solely the physical processes exhibited by light inside the resonator, then derives as the intensity circulating in the resonator relative to the intensity launched, which by use of Eqs. (15.15) and (15.16) yields

$$ {\displaystyle \begin{array}{c}{A}_{circ}=\frac{I_{circ}}{I_{laun}}=\frac{{\left|{E}_{circ}\right|}^2}{{\left|{E}_{laun}\right|}^2}=\frac{1}{{\left|1-{r}_1{r}_2{e}^{-i2\phi}\right|}^2}\\ {}=\frac{1}{{\left(1-\sqrt{R_1{R}_2}\right)}^2+4\sqrt{R_1{R}_2}{\sin}^2\left(\phi \right)}.\end{array}} $$
(15.18)

Physically, A circ represents the spectrally dependent internal resonance enhancement which the resonator provides to the light launched into it. It is displayed for different mirror reflectivities in Fig. 15.2. At the resonance frequencies ν q, where sin(ϕ) equals zero, the internal resonance enhancement factor is

$$ {A}_{circ}\left({\nu}_q\right)=\frac{1}{{\left(1-\sqrt{R_1{R}_2}\right)}^2}.\vspace*{-12pt} $$
(15.19)
Fig. 15.2
figure 2

Generic Airy distribution A circ, equaling the spectrally dependent internal resonance enhancement which the resonator provides to light that is launched into it. For the curve with R 1 = R 2 = 0.9, the peak value is at A circ(ν q) = 100, outside the scale of the ordinate. (Figure taken from Ref. [10])

Full size image

15.3.2 Other Airy Distributions

Once generic Airy distribution of Eq. (15.18), is established, all other Airy distributions, i.e., the observed light intensities relative to the launched or initial intensity from the light source (Fig. 15.1) can then be straight-forwardly deduced by simple scaling factors. Since the intensity launched into the resonator equals the transmitted fraction of the intensity incident upon mirror 1,

$$ {I}_{laun}=\left(1-{R}_1\right){I}_{inc}, $$
(15.20)

and the intensities transmitted through mirror 2, reflected at mirror 2, and transmitted through mirror 1 are the transmitted and reflected/transmitted fractions of the intensity circulating inside the resonator,

$$ {I}_{trans}=\left(1-{R}_2\right){I}_{circ},{I}_{b- circ}={R}_2{I}_{circ},{I}_{back}=\left(1-{R}_1\right){I}_{b- circ} $$
(15.21)

respectively, one obtains the following Airy distributions:

$$ {A}_{b\hbox{-} circ}=\frac{I_{b\hbox{-} circ}}{I_{laun}}={R}_2{A}_{circ}, $$
(15.22)
$$ {A}_{trans}=\frac{I_{trans}}{I_{laun}}=\left(1-{R}_2\right){A}_{circ}, $$
(15.23)
$$ {A}_{back}=\frac{I_{back}}{I_{laun}}=\left(1-{R}_1\right){R}_2{A}_{circ}, $$
(15.24)
$$ {A}_{emit}={A}_{trans}+{A}_{back}=\frac{I_{trans}+{I}_{back}}{I_{laun}}=\left(1-{R}_1{R}_2\right){A}_{circ}, $$
(15.25)
$$ {A}_{circ}^{\prime }=\frac{I_{circ}}{I_{inc}}=\left(1-{R}_1\right){A}_{circ},\vspace*{-6pt} $$
(15.26)
$$ {A}_{b\hbox{-} circ}^{\prime }=\frac{I_{b\hbox{-} circ}}{I_{inc}}=\left(1-{R}_1\right){R}_2{A}_{circ}, $$
(15.27)
$$ {A}_{trans}^{\prime }=\frac{I_{trans}}{I_{inc}}=\left(1-{R}_1\right)\left(1-{R}_2\right){A}_{circ}, $$
(15.28)
$$ {A}_{back}^{\prime }=\frac{I_{back}}{I_{inc}}={\left(1-{R}_1\right)}^2{R}_2{A}_{circ}, $$
(15.29)
$$ {\displaystyle \begin{array}{c}{A}_{emit}^{\prime }={A}_{trans}^{\prime }+{A}_{back}^{\prime }=\frac{I_{trans}+{I}_{back}}{I_{inc}}\\ {}=\left(1-{R}_1\right)\left(1-{R}_1{R}_2\right){A}_{circ}.\end{array}} $$
(15.30)

The index “emit” denotes Airy distributions that consider the sum of intensities emitted on both sides of the resonator. The prime denotes Airy distributions with respect to the incident intensity I inc.

The back-transmitted intensity I back cannot be measured, because also the initially back-reflected light adds to the backward-propagating signal. The measurable case of the intensity resulting from the interference of both backward-propagating electric fields is derived as follows. The back-transmitted electric field is

$$ {E}_{back}={it}_1{r}_2{E}_{circ}{e}^{-i2\phi}\kern0.75em \Rightarrow \kern0.75em \frac{E_{back}}{E_{inc}}=\frac{-{t}_1^2{r}_2{e}^{-i2\phi }}{1-{r}_1{r}_2{e}^{-i2\phi }}. $$
(15.31)

Including the initially back-reflected electric field, E refl,1 = r 1E inc, the total electric field propagating backward from mirror 1 is

$$ \frac{E_{refl}}{E_{inc}}=\frac{E_{refl,1}+{E}_{back}}{E_{inc}}={r}_1+\frac{-{t}_1^2{r}_2{e}^{-i2\phi }}{1-{r}_1{r}_2{e}^{-i2\phi }}=\frac{r_1-{r}_2{e}^{-i2\phi }}{1-{r}_1{r}_2{e}^{-i2\phi }}. $$
(15.32)

Exploiting Eqs. (15.15, 15.16, and 15.17), the total relative intensity propagating backward from mirror 1 amounts to

$$ {\displaystyle \begin{array}{l}{A}_{refl}^{\prime }=\frac{I_{refl}}{I_{inc}}=\frac{{\left|{E}_{refl}\right|}^2}{{\left|{E}_{inc}\right|}^2}=\frac{{\left|{r}_1-{r}_2{e}^{-i2\phi}\right|}^2}{{\left|1-{r}_1{r}_2{e}^{-i2\phi}\right|}^2}=\frac{{\left(\sqrt{R_1}-\sqrt{R_2}\right)}^2+4\sqrt{R_1{R}_2}{\sin}^2\left(\phi \right)}{{\left(1-\sqrt{R_1{R}_2}\right)}^2+4\sqrt{R_1{R}_2}{\sin}^2\left(\phi \right)}\\ {}\Rightarrow \kern0.75em {A}_{trans}^{\prime }+{A}_{refl}^{\prime }=\frac{I_{trans}+{I}_{refl}}{I_{inc}}=1,\end{array}} $$
(15.33)

as expected for a resonator that exhibits only outcoupling losses. At the resonance frequencies, the back-emitted electric field E back destructively interferes with the electric field E refl,1 initially back-reflected.

\( {A}_{circ}^{\prime } \) of Eq. (15.26) represents the external resonance enhancement factor with respect to I inc. The external resonance enhancement factor at the resonance frequencies is

$$ {A}_{circ}^{\prime}\left({\nu}_q\right)=\frac{\left(1-{R}_1\right)}{{\left(1-\sqrt{R_1{R}_2}\right)}^2}=\left(1-{R}_1\right){A}_{circ}\left({\nu}_q\right). $$
(15.34)

In experimental situations, often light is transmitted through a Fabry-Pérot resonator in order to characterize the resonator or to use it as a scanning interferometer (see later in Sect. 15.4). Therefore, an often applied Airy distribution is \( {A}_{trans}^{\prime } \) of Eq. (15.28). It describes the fraction I trans of the intensity I inc of a light source incident upon mirror 1 that is transmitted through mirror 2, see Fig. 15.1. \( {A}_{trans}^{\prime } \) is displayed in Fig. 15.3 (solid lines) for different values of the reflectivities R 1 = R 2. Its peak value at the resonance frequencies ν q is

$$ {A}_{trans}^{\prime}\left({\nu}_q\right)=\frac{\left(1-{R}_1\right)\left(1-{R}_2\right)}{{\left(1-\sqrt{R_1{R}_2}\right)}^2}\ \overset{R_1={R}_2}{=}\ 1. $$
(15.35)
Fig. 15.3
figure 3

Airy distribution \( {A}_{trans}^{\prime } \) (solid lines), corresponding to light transmitted through a Fabry-Pérot resonator, calculated from Eq. (15.28) for different values of the reflectivities R 1 = R 2, and comparison with a single Lorentzian line (dashed lines) calculated from Eq. (15.13) for the same R 1 = R 2. At half maximum (black line), with decreasing reflectivities the FWHM linewidth Δν Airy of the Airy distribution broadens compared to the FWHM linewidth Δν c of its corresponding Lorentzian line: R 1 = R 2 = 0.9, 0.6, 0.32, 0.172 results in Δν Airy/Δν c = 1.001, 1.022, 1.132, 1.717, respectively. (Figure taken from Ref. [10])

Full size image

15.3.3 Airy Distribution As a Sum of Mode Profiles

In Fig. 15.3 one observes that, at high reflectivity, there is almost perfect agreement between the spectral shape of the Airy distribution (solid purple line) and its underlying Lorentzian lines (dashed purple line), i.e., the former is rather well represented by the latter. This fact has prompted Saleh and Teich [6] to propose that in this case the Airy linewidth Δν Airy of a Fabry-Pérot resonator is similar to the linewidth Δν c = 1/(2πτ c) of its underlying Lorentzian lines, both defined as FWHM (black line). However, as is generally well known, with decreasing reflectivity the linewidth of the Airy distribution (solid lines) broadens faster than that of the underlying Lorentzian lines (dashed lines).

Svelto [5] attributes this discrepancy to Eq. (15.5) being only an approximation, thereby implicating that also Eq. (15.11) is only an approximation, such that the Airy linewidth Δν Airy of a Fabry-Pérot resonator can only at high reflectivity be approximated by the linewidth Δν c of its underlying Lorentzian lines. We will demonstrate that the discrepancy has a different reason.

According to Koppelmann [11], Bayer-Helms [12] “showed that the Airy distribution can be represented exactly” by the sum of Lorentzian spectral line shapes times a calibration factor. Firstly, while being literally correct, this statement is physically misleading, secondly, the calibration factor used in [11] remains unexplained, thirdly, the equivalence is shown only for equal reflectivities, R 1 = R 2, and finally, the equivalence is not investigated for non-Lorentzian spectral line shapes.

Here we verify that the Airy distribution is nothing else but the sum of the mode profiles of the longitudinal resonator modes, thereby revealing the physical origin of the Airy distribution. Our approach starts from the electric field E circ circulating inside the resonator, considers the exponential decay in time of this field through both mirrors of the resonator, see Fig. 15.1, Fourier transforms it to frequency space according to Eq. (15.10) to obtain the normalized spectral line shapes \( {\tilde{\gamma}}_q\left(\nu \right) \) of Eq. (15.11), divides it by the round-trip time t RT to account for how the total circulating electric-field intensity is longitudinally distributed in the resonator and coupled out per unit time, resulting in the emitted mode profiles,

$$ {\gamma}_{q, emit}\left(\nu \right)=\frac{1}{t_{RT}}{\tilde{\gamma}}_q\left(\nu \right), $$
(15.36)

in units of (1), and then sums over the emitted mode profiles of all longitudinal modes at positive, zero, and negative frequencies. Consequently, the sum of emitted mode profiles describes an experiment that must result in the Airy distribution A emit of Eq. (15.25). Exploiting the derivation given in Appendix C of [10], the sum of emitted mode profiles of Eq. (15.36) yields

$$ \sum \limits_{q=-\infty}^{\infty }{\gamma}_{q, emit}\left(\nu \right)=\frac{1-{R}_1{R}_2}{{\left(1-\sqrt{R_1{R}_2}\right)}^2+4\sqrt{R_1{R}_2}{\sin}^2\left(\phi \right)}={A}_{emit}, $$
(15.37)

which is indeed equal to Eq. (15.25), with Eq. (15.18) inserted. Each spectral line shape \( {\tilde{\gamma}}_q\left(\nu \right) \) of Eq. (15.11) and mode profile γ q, emit(ν) of Eq. (15.36) is extended over the infinite frequency range, consequently light at a specific frequency ν inside the resonator excites all longitudinal modes of the resonator. However, the contributions from different longitudinal modes to the light at frequency ν do not interfere with each other, because all optical modes are orthogonal with each other. For this reason, the sum in Eq. (15.37) is over the intensity mode profiles γ q, emit(ν) rather than over the electric fields. Because of resonant enhancement of the launched light the peak value of A emit at the resonance frequencies ν q,

$$ {A}_{emit}\left({\nu}_q\right)=\frac{1-{R}_1{R}_2}{{\left(1-\sqrt{R_1{R}_2}\right)}^2}=\frac{1+\sqrt{R_1{R}_2}}{1-\sqrt{R_1{R}_2}}>1, $$
(15.38)

becomes larger than unity. Nevertheless, because of Eqs. (15.20) and (15.33) the energy of the system is conserved.

The observation that with decreasing R 1 and R 2 the linewidth of the resulting Airy distribution in Fig. 15.3 is increasingly broader than the linewidth of the underlying Lorentzian lines simply arises from the fact that one sums up mode profiles (with the same linewidth as the Lorentzian lines) that resonate at different frequencies. It does not constitute a discrepancy, as has often been proposed.

The derivation shown here demonstrates that―from a physical point of view―the spectral line shapes and mode profiles are the fundamental spectral functions that characterize the Fabry-Pérot resonator and their sum quantifies its spectral response. As we will see in Sect. 15.4, this fundamental understanding has direct consequences for the definitions of linewidth and finesse.

The same simple scaling factors of Eqs. (15.20) and (15.21) that provide the relations between the individual Airy distributions, see Eqs. (15.18) and (15.22, 15.23, 15.24, 15.25, 15.26, 15.27, 15.28, 15.29, 15.30), also provide the relations among γ q, emit(ν) and the other mode profiles:

$$ {\displaystyle \begin{array}{l}{\gamma}_{q, circ}=\frac{1}{R_2}{\gamma}_{q,b\hbox{-} circ}=\frac{1}{1-{R}_2}{\gamma}_{q, trans}=\frac{1}{1-{R}_1}{\gamma}_{q, back}=\frac{1}{1-{R}_1{R}_2}{\gamma}_{q, emit}\\[8pt] {}{\gamma}_{q, circ}^{\prime }=\frac{1}{R_2}{\gamma}_{q,b\hbox{-} circ}^{\prime }=\frac{1}{1-{R}_2}{\gamma}_{q, trans}^{\prime }=\frac{1}{1-{R}_1}{\gamma}_{q, back}^{\prime }=\frac{1}{1-{R}_1{R}_2}{\gamma}_{q, emit}^{\prime}\\[8pt] {}\kern2em =\left(1-{R}_1\right){\gamma}_{q, circ}.\end{array}} $$
(15.39)

The various mode profiles γ q(ν) and \( {\gamma}_q^{\prime}\left(\nu \right) \) are calibrated with respect to the launched and the incident intensity, respectively, and the sum over one of these mode profiles at all resonance frequencies generates the corresponding Airy distribution.

15.4 Lorentzian Linewidth and Finesse Versus Airy Linewidth and Finesse

A commonly accepted definition of spectral resolution the Taylor criterion [13]. It proposes that two spectral lines can be resolved if the individual lines cross at half intensity. In the case of two identical, symmetric spectral lines their peaks would then be separated by their FWHM. The Taylor criterion is utilized in the following.

15.4.1 Characterizing the Fabry–Pérot Resonator: Lorentzian Linewidth and Finesse

When launching light into the Fabry-Pérot resonator in a non-scanning experiment, i.e., at fixed resonator length (and fixed angle of incidence), the Fabry-Pérot resonator becomes the object of investigation. The spectral line shapes, Lorentzian lines, and mode profiles are the fundamental functions. By measuring the sum of mode profiles, the Airy distribution, one can derive the total loss of the Fabry-Pérot resonator via recalculating the Lorentzian linewidth Δν c of Eq. (15.12), displayed (blue line) relative to the free spectral range in Fig. 15.4a, c.

Fig. 15.4
figure 4

(a) Relative Lorentzian linewidth Δν c/Δν FSR, with Δν c from Eq. (15.12) (blue curve), relative Airy linewidth Δν Airy/Δν FSR, with Δν Airy from Eq. (15.43) (green curve), and its approximation of Eq. (15.46) (red curve), and (b) Lorentzian finesse F c of Eq. (15.40) (blue curve), Airy finesse F Airy of Eq. (15.45) (green curve), and its approximation of Eq. (15.47) (red curve) as a function of reflectivity value R 1R 2. (c and d) Zoom into the low-reflectivity region. The exact solutions of the Airy linewidth and finesse (green lines) correctly break down at Δν Airy = Δν FSR, equivalent to F Airy = 1, whereas their approximations (red lines) incorrectly do not break down. (e) Ratio between the Airy linewidth Δν Airy of Eq. (15.43) and the Lorentzian linewidth Δν c of Eq. (15.12), equaling the ratio between the Lorentzian finesse F c of Eq. (15.40) and the Airy finesse F Airy of Eq. (15.45), as a function of reflectivity value R 1R 2. (Figure taken from Ref. [10])

Full size image

The underlying Lorentzian lines can be resolved as long as the Taylor criterion is obeyed (Fig. 15.5). Consequently, one can define a parameter which we call the Lorentzian finesse of a Fabry-Pérot resonator:

$$ {F}_c:= \frac{\Delta {\nu}_{FSR}}{\Delta {\nu}_c}=\frac{2\pi }{-\ln \left({R}_1{R}_2\right)}. $$
(15.40)
Fig. 15.5
figure 5

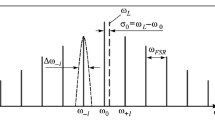
Illustration of the physical meaning of the Lorentzian finesse F c of a Fabry-Pérot resonator. Displayed is the situation for R 1 = R 2 ≈ 4.32%, at which Δν c = Δν FSR and F c = 1, i.e., two adjacent Lorentzian lines (dashed colored lines, only 5 lines are shown for clarity) cross at half maximum (solid black line) and the Taylor criterion for spectrally resolving two peaks in the resulting Airy distribution (solid purple line) is reached. (Figure taken from Ref. [10])

Full size image

It is displayed as the blue line in Fig. 15.4b, d. The Lorentzian finesse F c has a fundamental physical meaning: it describes how well the Lorentzian lines underlying the Airy distribution can be resolved when measuring the Airy distribution. A Fabry-Pérot resonator generating single-longitudinal-mode laser light is characterized by its Lorentzian linewidth and finesse.

Since Δν c exists for any mirror reflectivity, the definition of the Lorentzian finesse does not break down at a critical value. However, at the point where

$$ \Delta {\nu}_c=\Delta {\nu}_{FSR}\kern0.75em \Rightarrow \kern0.75em {R}_1{R}_2={e}^{-2\pi}\approx 0.001867, $$
(15.41)

equivalent to F c = 1, the Taylor criterion for the spectral resolution of a single Airy distribution is reached. For equal mirror reflectivities, this point occurs when R 1 = R 2 ≈ 4.32%. Therefore, the linewidth of the Lorentzian lines underlying the Airy distribution of a Fabry-Pérot resonator can be resolved by measuring the Airy distribution, hence its resonator losses can be spectroscopically determined, until this point. Obviously, the Lorentzian finesse according to the definition of Eq.~(15.40) plays an essential role in the characterization of low-reflectivity or otherwise high-loss Fabry-Pérot resonators.

15.4.2 Scanning the Fabry-Pérot Resonator: Airy Linewidth and Finesse

A different situation occurs when the Fabry-Pérot resonator is used as a scanning interferometer, i.e., at varying resonator length (or angle of incidence), to spectroscopically distinguish spectral lines at different frequencies within one free spectral range. In this case several Airy distributions, each one created by an individual spectral line, must be resolved. Therefore, now the Airy distribution becomes the underlying fundamental function and the measurement delivers a sum of Airy distributions. The parameters that properly quantify this situation are the Airy linewidth Δν Airy and the Airy finesse F Airy.

On either side of the peak of Eq. (15.35) located at ν q, the transmitted intensity decreases to \( {A}_{trans}^{\prime}\left({\nu}_q\right)/2 \) when the phase shift ϕ changes by the amount Δϕ and, accordingly, sin2(ϕ) changes from 0, such that in the denominator of A circ of Eq. (15.18)

$$ 4\sqrt{R_1{R}_2}{\sin}^2\left(\Delta \phi \right)={\left(1-\sqrt{R_1{R}_2}\right)}^2\kern0.75em \Rightarrow \kern0.75em \Delta \phi =\arcsin \left(\frac{1-\sqrt{R_1{R}_2}}{2\sqrt[4]{R_1{R}_2}}\right).\\[6pt] $$
(15.42)

Exploiting Eqs. (15.6) and (15.7) to calculate ϕ = πν/Δν FSR, resulting in Δϕ = π(Δν Airy/2)/Δν FSR, then provides the FWHM linewidth Δν Airy of the Airy distribution [3],

$$ \Delta {\nu}_{Airy}=\Delta {\nu}_{FSR}\frac{2}{\pi}\mathrm{arc}\sin \left(\frac{1-\sqrt{R_1{R}_2}}{2\sqrt[4]{R_1{R}_2}}\right). $$
(15.43)

The Airy linewidth Δν Airy is displayed as the green curve in Fig. 15.4a, c in direct comparison with the Lorentzian linewidth Δν c. The ratio between Δν Airy of Eq. (15.43) and Δν c of Eq. (15.12) is displayed in Fig. 15.4e.

The concept of defining the linewidth of the Airy peaks as FWHM breaks down at Δν Airy = Δν FSR (solid red line in Fig. 15.3), because at this point the Airy linewidth instantaneously jumps to an infinite value. For lower reflectivity values R 1R 2, the FWHM linewidth of the Airy peaks is undefined and other definitions or concepts would have to be utilized to describe the situation. The limiting case occurs at

$$ \Delta {\nu}_{Airy}=\Delta {\nu}_{FSR}\kern0.75em \Rightarrow \kern0.75em \frac{1-\sqrt{R_1{R}_2}}{2\sqrt[4]{R_1{R}_2}}=1\kern0.75em \Rightarrow \kern0.75em {R}_1{R}_2=17-12\sqrt{2}\approx 0.02944. $$
(15.44)

For equal mirror reflectivities, this point is reached when R 1 = R 2 ≈ 17.2% (solid red line in Fig. 15.3).

The finesse of the Airy distribution of a Fabry-Pérot resonator, which is displayed as the green curve in Fig. 15.4b, d in direct comparison with the Lorentzian finesse F c, is properly defined as

$$ {F}_{Airy}\overset{!}{:=}\frac{\Delta {\nu}_{FSR}}{\Delta {\nu}_{Airy}}=\frac{\pi }{2}{\left[\mathrm{arc}\sin \left(\frac{1-\sqrt{R_1{R}_2}}{2\sqrt[4]{R_1{R}_2}}\right)\right]}^{-1}. $$
(15.45)

When scanning the length of the Fabry-Pérot resonator (or alternatively the angle of incident light), the Airy finesse lucidly quantifies the maximum number of Airy distributions created by light at individual frequencies ν m within the free spectral range of the Fabry-Pérot resonator, whose adjacent peaks can be unambiguously distinguished spectroscopically, i.e., they do not overlap at their FWHM (Fig. 15.6). Consequently, this definition of the Airy finesse is consistent with the Taylor criterion of the resolution of a spectrometer and is, therefore, denoted by an exclamation mark in Eq. (15.45). Since the concept of the FWHM linewidth breaks down at Δν Airy = Δν FSR, consequently the Airy finesse is defined only until F Airy = 1, see Fig. 15.4d, because the arcsin function in Eq. (15.45) cannot produce values above π/2.

Fig. 15.6
figure 6

Illustration of the physical meaning of the Airy finesse F Airy of a Fabry-Pérot resonator. When scanning the Fabry-Pérot length (or alternatively the angle of incident light), Airy distributions (solid lines) are created by signals at individual frequencies. If the signals occur at frequencies ν m = ν q + mΔν Airy, where m is an integer starting at q, the Airy distributions at adjacent frequencies are separated from each other by the linewidth Δν Airy, thereby fulfilling the Taylor criterion for the spectroscopic resolution of two adjacent peaks. The maximum number of signals that can be resolved is F Airy. Since in this specific example the reflectivities R 1 = R 2 = 0.59928 have been chosen such that F Airy = 6 is an integer, the signal for m = F Airy at the frequency ν q + F AiryΔν Airy = ν q + Δν FSR coincides with the signal for m = q at ν q. In this example, a maximum of F Airy = 6 peaks can be resolved when applying the Taylor criterion. However, the sum of two adjacent “resolvable” peaks (dashed gray line) exhibits a deeper dip between the adjacent peaks to be resolved, i.e., a better resolution, than the sum of all “resolvable” peaks (dashed black line), see the difference highlighted in the red circle. (Figure taken from Ref. [10])

Full size image

Generally, one can argue that the Taylor criterion leaves some ambiguity to the definition of the limit of spectral resolution, because it does not state whether it requires the absence or allows for the presence of additional resolvable spectral lines. In the example of Fig. 15.6, the sum of two adjacent “resolvable” Airy distributions (dashed gray line) is better resolvable than the sum of all “resolvable” Airy distributions (dashed black line), because in the latter case additional Airy distributions contribute, see the dashed lines within the red circle in Fig. 15.6. If either of the two options defines the limit of spectral resolution, the other cannot.

Questionable Approximations and Definitions

Often the unnecessary approximation sin(ϕ) ≈ ϕ is made when deriving from \( {A}_{trans}^{\prime } \) of Eq. (15.28) the Airy linewidth [2, 4]. In contrast to the exact Eqs. (15.42) and (15.43), it leads to

$$ {\displaystyle \begin{array}{l}4\sqrt{R_1{R}_2}{\left(\Delta \phi \right)}^2\approx {\left(1-\sqrt{R_1{R}_2}\right)}^2\kern0.75em \Rightarrow \\ {}\Delta {\nu}_{Airy}\approx \Delta {\nu}_{FSR}\frac{2}{\pi}\Delta \phi =\Delta {\nu}_{FSR}\frac{1}{\pi}\frac{1-\sqrt{R_1{R}_2}}{\sqrt[4]{R_1{R}_2}}.\end{array}} $$
(15.46)

This approximation of the Airy linewidth, displayed as the red curve in Fig. 15.4a, c, deviates from the correct curve at low reflectivities and incorrectly does not break down when Δν Airy > Δν FSR. This approximation is then typically also inserted into Eq. (15.45) to calculate the Airy finesse [4], resulting in

$$ {F}_{Airy}\overset{!}{:=}\frac{\Delta {\nu}_{FSR}}{\Delta {\nu}_{Airy}}\approx \pi \frac{\sqrt[4]{R_1{R}_2}}{1-\sqrt{R_1{R}_2}}. $$
(15.47)

Vaughan [2] and Siegman [3] even defined the Airy finesse by its approximation of Eq. (15.47),

$$ {\overset{\frown }{F}}_{Airy}\overset{?}{:=}\pi \frac{\sqrt[4]{R_1{R}_2}}{1-\sqrt{R_1{R}_2}}\approx \frac{\Delta {\nu}_{FSR}}{\Delta {\nu}_{Airy}}, $$
(15.48)

thereby depriving this parameter of its lucid meaning. Since the definition of Eq. (15.48) does not comply with the Taylor criterion, it is denoted by a question mark. Saleh and Teich [7, 8] also proposed Eq. (15.48) for the Airy finesse, but from their derivation it remains unclear whether they consider it as a definition or as an approximation of Eq. (15.45).

15.4.4 Response to Frequency-Dependent Reflectivity

In the previous Sections we described a Fabry-Pérot resonator whose mirror reflectivities are independent of frequency. We showed that the Airy distribution is nothing else but the sum of its underlying mode profiles. Now we consider the mirror reflectivities as general functions of frequency, R i(ν), such that the photon-decay time τ c(ν) of Eq. (15.3) becomes a function of frequency. As a result, the spectral line shapes \( {\tilde{\gamma}}_q\left(\nu \right) \) of Eq. (15.11), the mode profiles γ q, emit(ν) of Eq. (15.36) and all other mode profiles, as well as the Airy distribution A emit(ν) of Eq. (15.37) and all other Airy distributions, are spectrally modified. In Eqs. (15.12) and (15.13), Δν c turns into a local function of frequency, thereby losing its meaning as the FWHM linewidth. Nevertheless, all Airy distributions fundamentally remain the sums of their corresponding mode profiles. Consequently, even for frequency-dependent reflectivities R i(ν) we can calculate the spectral line shape \( {\tilde{\gamma}}_q\left(\nu \right) \) and mode profile γ q, emit(ν) of each mode directly from Eqs. (15.11) and (15.36), respectively, and obtain all other mode profiles via the simple scaling factors of Eq. (15.39).

15.5 Summary

The understanding that the Airy distribution describing the spectral transmission of a Fabry-Pérot resonator physically originates in the sum of mode profiles of the longitudinal resonator modes has fundamental consequences. The resonator losses are related to the linewidth of the Lorentzian lines rather than the linewidth of the Airy distribution. Hence, a new parameter, the Lorentzian finesse, becomes important. Once the internal resonance enhancement, equaling the generic Airy distribution that characterizes the light intensity that is forward circulating inside the resonator, is known, all other Airy distributions of back-circulating, transmitted, back-transmitted, and total emitted light intensity can be derived by simple scaling factors. Furthermore, in the case of frequency-dependent mirror reflectivities, the deformed spectral line shapes and mode profiles of the underlying modes can be derived from the same simple equations. Also in this generalized situation, each sum of mode profiles generates the corresponding Airy distribution.