Keywords

1 Introduction

Employment of flexible link manipulator is recommended in the space and industrial applications in order to accomplish high performance requirements such as high-speed besides safe operation, increasing of positioning accuracy and lower energy consumption, namely less weight. However, it is not usually easy to control a flexible manipulator because of its inheriting flexibility. Deformation of the flexible manipulator when it is operated must be considered by any control. Its controller system should be dealt with not only its motion but also vibration due to the flexibility of the link.

In the past few decades, a number of modeling methods and control strategies using piezoelectric actuators to deal with the vibration problem have been investigated by researchers [1–3]. Nishidome and Kajiwara [1] investigated a way to enhance performances of motion and vibration of a flexible-link mechanism. They used a modeling method based on modal analysis using the finite-element method. The model was described as a state space form. Their control system was constructed with a designed dynamic compensator based on the mixed of H 2/H ∞ . They recommended separating the motion and vibration controls of the system. Zhang et al. [2] has studied a flexible piezoelectric cantilever beam. The model of the beam using finite-elements was built by ANSYS application. Based on the Linear Quadratic Gauss (LQG) control method, they introduced a procedure to suppress the vibration of the beam with the piezoelectric sensors and actuators were symmetrically collocated on both sides of the beam. Their simulation results showed the effectiveness of the method. Gurses et al. [3] investigated vibration control of a flexible single-link manipulator using three piezoelectric actuators. The dynamic modeling of the link had been presented using Euler-Bernoulli beam theory. Composite linear and angular velocity feedback controls were introduced to suppress the vibration. Their simulation and experimental results showed the effectiveness of the controllers.

Furthermore, applications of the AF control strategy to suppress vibration of a flexible system were done by some researchers [4–6]. Hewit et al. [4] used the AF control for deformation and disturbance attenuation of a flexible manipulator. Then, a PD control was used for trajectory tracking of the flexible manipulator. They used a motor as an actuator. Modeling of the manipulator was done using virtual link coordinate system (VLCS). Their simulation results had shown that the proposed control could cancel the disturbance satisfactorily. Tavakolvour et al. [5] investigated the AF control application for a flexible thin plate. Modeling of their system was done using finite-difference method. Their calculated results showed the effectiveness of the proposed controller to reduce vibration of the plate. Tavakolvour and Mailah [6] studied the AF control application for a flexible beam with an electromagnetic actuator. Modeling of the beam was done using finite-difference method. The effectiveness of the proposed controller was confirmed through simulation and experiment.

The purposes of this research are to derive the equations of motion of a flexible single-link system by a finite-element method, to develop the computational codes in order to perform dynamics simulations with vibration control, to propose an effective control scheme of a flexible single-link manipulator using three control strategies namely active-force (AF), proportional (P) and proportional-derivative (PD) controls and to confirm the calculated results by experiments of the flexible single-link manipulator.

The flexible manipulator used in this paper consists of an aluminum beam as a flexible link, a clamp-part, a servo motor to rotate the link and a piezoelectric actuator to control vibration. Computational codes on time history responses, Fast Fourier Transform (FFT) processing and eigenvalues–eigenvectors analysis were developed to calculate the dynamic behavior of the link and validated by the experimental one. Furthermore, the AF, P, and PD controls strategies were designed to suppress the vibration. It was done by adding bending moments generated by the piezoelectric actuator to the single-link. Finally, their performances were compared through calculations and experiments.

2 Formulation by Finite-Element Method

The link has been discretized by finite-elements [7, 8]. The finite-element has two degrees of freedom, namely the lateral deformation v(x, t), and the rotational angle ψ(x, t). The length, the cross-sectional area and the area moment of inertia around z-axis of every element are denoted by l i , S i and I zi respectively. Mechanical properties of every element are denoted as Young’s modulus E i and mass density ρ i .

2.1 Kinematics

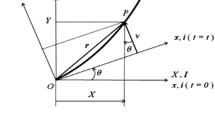
Figure 1 shows the position vector of an arbitrary point P in the link in the global and rotating coordinate frames. Let the link as a flexible beam has a motion that is confined in the horizontal plane as shown in Fig. 1. The O–XY frame is the global coordinate frame while O–xy is the rotating coordinate frame fixed to the root of the link. A motor is installed on the root of the link. The rotational angle of the motor when the link rotates is denoted by θ(t).

Fig. 1
figure 1

Position vector of an arbitrary point P in the link in the global and rotating coordinate frames. O–XY Global coordinate frame. O–xy Rotating coordinate frame

Full size image

The position vector r (x, t) of the arbitrary point P in the link at time t = t, measured in the O–XY frame shown in Fig. 1 is expressed by

$$ \varvec{r}(x,t) = X(x,t)\varvec{I} + Y(x,t)\varvec{J} $$
(1)

where

$$ X(x,t) = x\cos \theta (t) - v(x,t)\sin \theta (t) $$
(2)
$$ Y(x,t) = x\sin \theta (t) + v(x,t) \cos \theta (t) $$
(3)

The velocity of P is given by

$$ \dot{\varvec{r}}(x,t) = \dot{X}(x,t)\varvec{I} + \dot{Y}(x,t)\varvec{J} $$
(4)

2.2 Finite-Element Method

Figure 2 shows the rotating coordinate frame and the link divided by one-dimensional and two-node elements. Then, Fig. 3 shows the element coordinate frame of the i-th element. Here, there are four boundary conditions together at nodes i and (i + 1) when the one-dimensional and two-node element is used. The four boundary conditions are expressed as nodal vector as follow

$$ {\varvec{\delta}}_{i} = \left\{ {\begin{array}{*{20}c} {v_{i} } & {\psi_{i} } & {v_{i + 1} } & {\psi_{i + 1} } \\ \end{array} } \right\}^{T} $$
(5)
Fig. 2
figure 2

Rotating coordinate frame and the link divided by the one-dimensional and two-node elements. o–xy Rotating coordinate frame

Full size image
Fig. 3
figure 3

Element coordinate frame of the i-th element. o i –x i y i Element coordinate frame of the i-th element

Full size image

Then, the hypothesized deformation has four constants as follows [9]

$$ v_{i} = a_{1} + a_{2} x_{i} + a_{3} x_{i}^{2} + a_{4} x_{i}^{3} $$
(6)

The relation between the lateral deformation v i and the rotational angle ψ i of the node i is given by

$$ \psi_{i} = \frac{{\partial v_{i} }}{{\partial x_{i} }}. $$
(7)

Furthermore, from mechanics of materials, the strain of node i can be defined by

$$ \varepsilon_{i} = \varepsilon_{{x_{i} }} = - y_{i} \frac{{\partial^{2} v_{i} }}{{\partial x_{i}^{2} }} $$
(8)

2.3 Equations of Motion

Equation of motion of the i-th element is given by

$$ \varvec{M}_{i} \ddot{\varvec{\delta}}_{i} + \varvec{C}_{i} \dot{\varvec{\delta }}_{i} + \left[ {\varvec{K}_{i} - \dot{\theta }^{2} (t)\varvec{M}_{i} } \right]\,\varvec{\delta}_{i} = \ddot{\theta }(t)\varvec{f}_{i} $$
(9)

where M i , C i , K i , \( \mathop \theta \limits^{..} (t){\user2{f}}_{i} \) are the mass matrix, damping matrix, stiffness matrix and the excitation force generated by the rotation of the motor respectively. The representation of the matrices and vector in Eq. (9) can be found in [7]. Finally, the equation of motion of the system with n elements considering the boundary conditions is given by

$$ \varvec{M}_{n} \ddot{\varvec{\delta}}_{n} + \varvec{C}_{n} \dot{\varvec{\delta }}_{n} + \left[ {\varvec{K}_{n} - \dot{\theta }^{2} (t)\varvec{M}_{n} } \right]\,\varvec{\delta}_{n} = \ddot{\theta }(t)\varvec{f}_{n} $$
(10)

3 Modeling

Figure 4 shows a model of the single-link manipulator, the clamp-part and the piezoelectric actuator. The link including the clamp-part and actuator were discretized by 35 elements. The clamp-part is more rigid than the link. Therefore Young’s modulus of the clamp-part was set in 1,000 times of the link’s. The piezoelectric actuator was bonded to a one-side surface of Element 4. A schematic representation on modeling of the piezoelectric actuator is shown in Fig. 5. Furthermore, a strain gage was bonded to the position of Node 6 of the single-link (0.11 m from the origin). Physical parameters of the single-link model and the piezoelectric actuator are shown in Table 1 [8].

Fig. 4
figure 4

Computational model of the flexible single-link manipulator

Full size image
Fig. 5
figure 5

Modeling of the piezoelectric actuator

Full size image
Table 1 Physical parameters of the flexible link and the piezoelectric actuator [10]
Full size table

The piezoelectric actuator suppressed the vibration of the flexible link manipulator by adding bending moments at Nodes 3 and 6, M 3 and M 6 to the flexible link. The bending moments are generated by applying voltages +E to the piezoelectric actuator as shown in Fig. 5. The relation between the bending moments and the voltages are related by

$$ M_{3} = -M_{6} = d_{1} E $$
(11)

here d 1 is a constant quantity.

Furthermore, the voltage to generate the bending moments is proportional to the strain ε of the single-link due to the vibration. The relation can be expressed as follows

$$ E = \pm \frac{1}{{d_{2} }}\varepsilon $$
(12)

here d 2 is a constant quantity. Then, d 1 and d 2 will be determined by comparing the calculated results and experimental ones.

Computational codes were developed to perform dynamics simulation of the system based on the formulation that explained above. The validation was done using time history responses analysis of free vibration, natural frequencies using Fast Fourier Transform (FFT) processing, vibration modes and natural frequencies using eigenvalues–eigenvectors analysis and time history responses analysis due to the base excitation [8].

4 Control Scheme and Strategies

A control scheme to suppress the vibration of the single-link was designed using the piezoelectric actuator. It was done by adding bending moments generated by the piezoelectric actuator to the single-link. Therefore, the equation of motion of the system become

$$ \varvec{M}_{n} \ddot{\varvec{\delta}}_{n} + \varvec{C}_{n} \dot{\varvec{\delta }}_{n} + \left[ \varvec{K}_{n} - \dot{\theta }^{2} (t) \varvec{M}_{n} \right]\,\varvec{\delta}_{n} = \ddot{\theta }(t)\varvec{f}_{n} + \varvec{u}_{n} (t) $$
(13)

where the vector u n (t) containing M 3 and M 6 is the control force generated by the actuator to the single-link.

To drive the actuator, three different control strategies namely AF, P and PD controls have been designed and examined. Their performances were compared through calculations and experiments.

4.1 Active-Force Control

Figure 6 shows the block diagram of the AF control that is proposed in this research. In this strategy, vibration of the system is controlled by canceling bending moments acting at Nodes 3 and 6 due to the base excitation (excitation bending moments). The following steps are the way to estimate and cancel the excitation bending moments.

Fig. 6
figure 6

Block diagram of active-force control of the flexible link manipulator. ε d Desired strain. ε i Measured strains at Node i. θ Rotation angle of the motor. M ii Component of mass matrix. A Conversion from ε i to v i . d Position vector. U nd Desired bending moments. U n Applied bending moments. U ne Excitation bending moments. U nt Bending moments

Full size image

Firstly, the strain, ε 6 at Node 6 is measured to estimate the lateral deformation, v 6 at the Node 6. Substituting Eq. (6) to Eq. (8) considering the boundary conditions then the relation between the strain and the lateral deformation can be defined as follows

$$ \frac{{v_{6} }}{{\varepsilon_{6} }} = - \frac{{x^{2} \left( {x - 3l} \right)}}{{6y\left( {x - l} \right)}} = A $$
(14)

where l, x and y are the length of the link, the position of Node 6 in x and y directions, respectively.

Secondly, the actual force in the s-domain acting at Node 6 can be defined in the form of the Newton’s equation of motion as follows

$$ F_{6} (s) = M_{ii(i = 11)} \,s^{2} \,v_{6} $$
(15)

where M ii(i = 11) is the component of the mass matrix corresponding to v 6.

Thirdly, the bending moments acting at Nodes 3 and 6 are estimated using the following equation

$$ \varvec{U}_{nt} (s) = \pm F_{6} (s)\,\varvec{d} $$
(16)

The vector d that represents the position vector from the reference point to the position where the excitation force acting can be written as follows

$$ \varvec{d} = \left\{ {{\kern 1pt} \begin{array}{*{20}c} {{\kern 1pt} 0} & 0 & 0 & {l_{2} } & 0 & {l_{2} } & 0 & \ldots & 0 \\ \end{array} } \right\}{\kern 1pt}^{T} $$
(17)

Fourthly, based on Fig. 6, the excitation bending moments can be calculated as

$$ \varvec{U}_{ne} (s) = K_{pa} \,\left\{ {\varvec{U}_{nt} (s) - \varvec{U}_{n} (s)} \right\} $$
(18)

where K pa is the non-dimensional proportional gain of the proposed AF control.

Finally, the bending moments applying as a control force to control the vibration of the system can be calculated as follows

$$ \varvec{U}_{n} (s) = - \varvec{U}_{ne} (s) + \varvec{U}_{nd\,} (s) $$
(19)

where U nd (s) is the desired bending moments which is zero. The negative of U ne (s) indicates that the bending moments used to cancel the vibration of the system.

4.2 Proportional and Proportional-Derivative Controls

Substituting Eq. (12) to Eq. (11) gives

$$ M_{3,6} = \pm \frac{{d_{1} }}{{d_{2} }}\varepsilon $$
(20)

Based on Eq. (20), the bending moments for P and PD controllers can be defined in s-domain as follows

$$ \varvec{U}_{n} (s) = \varvec{G}_{C1,2} (s)\left( {\varepsilon_{d} (s) - \varepsilon_{6} (s)} \right) $$
(21)

where ε d and ε 6 denote the desired and measured strains at Node 6, respectively. The gain of P and PD controllers can be written by a vector in s-domain respectively as follows

$$ \varvec{G}_{C1} (s) = \left\{ {{\kern 1pt} \begin{array}{*{20}c} {{\kern 1pt} 0} & 0 & 0 & {K_{p} } & 0 & { - K_{p} } & 0 & \ldots & 0 \\ \end{array} } \right\}{\kern 1pt}^{T} $$
(22)

and

$$ \varvec{G}_{C2} (s) = \left\{ {{\kern 1pt} \begin{array}{*{20}c} {{\kern 1pt} 0} & 0 & 0 & {K_{p} + K_{d} s} & 0 & { - \left( {K_{p} + K_{d} s} \right)} & 0 & \ldots & 0 \\ \end{array}} \right\}{\kern 1pt}^{T} $$
(23)

A block diagram of the proportional and proportional-derivative controls strategies for the single-link system is shown in Fig. 7.

Fig. 7
figure 7

Block diagram of P and PD controls of the flexible link manipulator. ε d Desired strain. ε i Measured strains at Node i. θ Rotation angle of the motor. U n Applied bending moments

Full size image

5 Experiment

5.1 Experimental Set-up

In order to investigate the validity of the proposed control strategies, an experimental set-up was designed. The set-up is shown in Fig. 8. The flexible link manipulator consists of the flexible aluminum beam, the clamp-part, the servo motor and the base. The flexible link was attached to the motor through the clamp-part. In the experiments, the motor was operated by an independent motion controller. A strain gage was bonded to the position of 0.11 [m] from the origin of the link.

Fig. 8
figure 8

Schematics of measurement and control system [8]. Dashed arrow Measurement of strains. Thick arrow Vibration control. Thin arrow Motion control

Full size image

The piezoelectric actuator was attached on one side of the flexible manipulator to provide the blocking force against vibrations. A Wheatstone bridge circuit was developed to measure the changes in resistance of the strain gage in the form of voltages. An amplifier circuit was designed to amplify the small output signal of the Wheatstone bridge.

Furthermore, a data acquisition board and a computer that have functionality of analog to digital (A/D) conversion, signal processing, control process and digital to analog (D/A) conversion were used. The data acquisition board connected to the computer through USB port. Finally, the controlled signals sent to a piezo driver to drive the piezoelectric actuator in its voltage range.

5.2 Experimental Method

The rotation of the motor was set from 0 to π/2 radians (90°) within 0.68 [s]. The outputs of strain gage were converted to voltages by the Wheatstone bridge and magnified by the amplifier. The noises that occur in the experiment were reduced by a 100 [µF] capacitor attached to the amplifier. The output voltages of the amplifier sent to the data acquisition board and the computer for control process.

The control strategies were implemented in the computer using the visual C++ program. The analog output voltages of the data acquisition board sent to the input channel of the piezo driver to generate the actuated signals for the piezoelectric actuator.

6 Calculated and Experimental Results

6.1 Calculated Results

Time history responses of strains on the uncontrolled and controlled systems were calculated when the motor rotated by the angle of π/2 radians (90°) within 0.68 [s]. Time history responses of strains on the controlled system were calculated for the model under three control strategies as shown in Figs. 6 and 7.

Examining several gains of the AF, P and PD controllers leaded to K pa  = 0.83 [−], K p  = 30 [Nm], K d  = 0.02 [Nms] as the better ones. Figure 9 shows the uncontrolled and controlled time history responses of strains at Node 6. The maximum and minimum strains of uncontrolled system in positive and negative sides were 387.00 × 10−6 and −435.00 × 10−6, as shown in Fig. 9a. By using AF-controller they became 66.50 × 10−6 and \( - 8 8. 60 \times 10^{{{-} 6}} \), as shown in Fig. 9b. Moreover, by using P-controller they became 127.00 × 10−6 and −145.00 × 10−6, as shown in Fig. 9c. By adding D-gain they became −124.00 × 10−6 and −143.00 × 10−6, as shown in Fig. 9d.

Fig. 9
figure 9

Calculated time history responses of strains at Node 6 for uncontrolled and controlled systems due to the base excitation. a Uncontrolled system. b Controlled by AF-controller, K pa  = 0.4 [−]. c Controlled by P-controller, K p  = 30 [Nm]. d Controlled by PD-controller, K p  = 30 [Nm], K d  = 0.02 [Nms]

Full size image

Based on the calculated results, the effect of D-controller was very small compare to P-controller, therefore using a P-controller will be sufficient for experiment [7].

6.2 Experimental Results

Experimental time history responses of the strains on the uncontrolled and controlled systems were measured when the motor rotated by the angle of π/2 radians (90°) within 0.68 [s]. Experimental time history responses on the controlled system were measured under the control strategies as shown in Figs. 6 and 7.

Furthermore, the experimental active-force and proportional gains that are non-dimensional gains, K pa and K p ′ were examined. The examination of gains leaded to K p ′ = 600 [−] and K pa ′ = 125 [−], as the better ones. Figure 10 shows the experimental uncontrolled and controlled time history responses of strains at the same position in the calculations. The maximum and minimum strains of uncontrolled system in positive and negative sides were 359.40 × 10−6 and −440.40 × 10−6, as shown in Fig. 10a. By using AF-controller they became 175.50 × 10−6 and −303.50 × 10−6, as shown in Fig. 10b. Moreover, by using P-controller they became 262.40 × 10−6 and −373.40 × 10−6, as shown in Fig. 10c.

Fig. 10
figure 10

Experimental time history responses of strains at 0.11 (m) from the link’s origin for uncontrolled and controlled systems due to the base excitation. a Uncontrolled system. b Controlled by AF-controller, K pa ′ = 125 [−]. c Controlled by P-controller, K p ′ = 600 [−]

Full size image

It was verified from these results that the vibration of the flexible link manipulator can be more effectively suppressed using the proposed AF-control compared to the P and PD ones.

7 Conclusion and Future Work

The equations of motion for the flexible link manipulator had been derived using the finite-element method. Computational codes had been developed in order to perform dynamic simulations of the system. Experimental and calculated results on time history responses, natural frequencies and vibration modes show the validities of the formulation, computational codes and modeling of the system. The active-force (AF), proportional (P) and proportional-derivative (PD) controls strategies were designed to suppress the vibration of the system. Their performances were compared through the calculations and experiments. The calculated and experimental results show the superiority of the proposed AF control compared to the P and PD ones to suppress the vibration of the flexible single-link manipulator.

A flexible two-link manipulator is being prepared. The control scheme and strategies presented in this paper will be applied to the flexible two-link system.