Abstract
In this chapter bi-intuitionism is interpreted as an intensional logic which is about the justification conditions of assertions and hypotheses, extending C. Dalla Pozza and C. Garola’s pragmatic interpretation [18] of intuitionism, seen as a logic of assertions according to a suggestion by M. Dummett. Revising our previous work on this matter [5], we consider two additional illocutionary forces, \((i)\) conjecturing, seen as making the hypothesis that a proposition is epistemically necessary, and \((ii)\) expecting, regarded as asserting that a propostion is epistemically possible; we show that a logic of expectations justifies the double negation law. We formalize our logic in a calculus of sequents and study bimodal Kripke semantics of bi-intuitionism based on translations in S4. We look at rough set semantics following P. Pagliani’s analysis of “intrinsic co-Heyting boundaries” [40] (after Lawvere). A Natural Deduction system for co-intuitionistic logic is given where proofs are represented as upside down Prawitz trees. We give a computational interpretation of co-intuitionism, based on T. Crolard’s notion of coroutine [16] as the programming construction corresponding to subtraction introduction. Our typed calculus of co-routines is dual to the simply typed lambda calculus and shows features of concurrent and distributed computations.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
This chapter aims at developing an intensional logic of the justification conditions of some illocutionary acts, namely, asserting, making hypotheses, conjecturing and expressing an epistemic expectation, where the intended interpretation of the logical connectives and of the forms of inference are those of intuitionistic logicFootnote 1 \(^{,}\) Footnote 2. Our work belongs to the project of a Logic for Pragmatics, initiated by the philosopher Carlo Dalla Pozza and by the physicist Claudio Garola [18] and later continued by Dalla Pozza and Bellin [7] and others, in particular Bellin and Biasi [5]. Characteristic of our approach with respect to similar ones, e.g., S. Artemov’s justification logic, is the focus on illocutionary forces in the elementary expressions of our language, where propositions in the classical sense are never presented without an illocutionary force and thus an “illocutionary mood” (e.g., assertive or hypothetical) is inherited also by composite expressions of the language. This fact is essential in our case study here, bi-intuitionistic logic, where intuitionstic and its dual co-intuitionistic logic are joined together. In natural language the acts of asserting, on one hand, and of making hypotheses and expressing a doubt, on the other, may in some sense be regarded as dual. Thus we have an interpretation of bi-intuitionism as an intensional logic of assertions and of hypotheses, where the dual intuitionistic and co-intuitionistic parts are “polarised” and kept separate. In this framework it is perfectly appropriate and unproblematic that the law of non-contradiction and the disjunction property hold for the assertive notions of intuitionistic negation, conjunction, and disjunction, while the law of excluded middle and para-consistency hold for the hypothetical notions of co-intuitionistic negation, conjunction, and disjunction.
In this chapter we revised and sharped the discussion of the logical properties of assertions and conjectures in Bellin and Biasi [5], by distinguishing between conjectures and hypotheses. In a nutshell, the justification of an assertion requires epistemic necessity of the truth of the propositional content p, which is given, e.g., by a proof of p; making a hypothesis is justified by the epistemic possibility of the truth of the propositional content; similarly, expressing a doubt about a statement is justified by the epistemic possibility that the statement may be unjustified. But for the justification of a conjecture we need the possibility of the epistemic necessity of the truth of its propositional content, not just epistemic possibility. Dually, we are led to the distinction between assertions and epistemic expectations: for the justification of an expectation, it suffices to have the necessity of epistemic possibility, which we regard as the assertion that in all situations it will be possible for the propositional content to be true. It turns out that a logic of expectations satisfies the law of double negation, a feature of classical logic.
There is a philosophical question about the nature of the epistemic modal notions used here. Every expression of our logic for pragmatics has an interpretation in classical S4, the assertion  and hypothesis
and hypothesis  of a proposition \(p\) are interpreted as \(\Box p\) and \(\Diamond p\), respectively; similarly, the conjecture \(\mathcal {C}p\) and the expectation \(\mathcal {E}p\) become \(\Diamond \Box p\) and \(\Box \Diamond p\). Thus we have an intensional counterpart of all modalities of S4; but we do not regard such correspondence with classical S4 as a definition of the new “illocutionary forces” of conjecture and expectation. Indeed, we intend the pragmatic interpretations of intuitionistic and bi-intuitionistic logic as bona fide representations of such logics from the viewpoint of an intuitionistic philosopher; moreover, we intend our “logic for pragmatics” to be compatible with the rich proof-theory of intuitionistic logic, including the Curry–Howard correspondence and categorical interpretations. Thus, we are inclined to regard conjectures and expectations as examples of how a theory of intuitionistic modalities can be developed starting from the illocutionary forces of assertions and hypotheses as basic. However, this investigation is left for another occasion.
of a proposition \(p\) are interpreted as \(\Box p\) and \(\Diamond p\), respectively; similarly, the conjecture \(\mathcal {C}p\) and the expectation \(\mathcal {E}p\) become \(\Diamond \Box p\) and \(\Box \Diamond p\). Thus we have an intensional counterpart of all modalities of S4; but we do not regard such correspondence with classical S4 as a definition of the new “illocutionary forces” of conjecture and expectation. Indeed, we intend the pragmatic interpretations of intuitionistic and bi-intuitionistic logic as bona fide representations of such logics from the viewpoint of an intuitionistic philosopher; moreover, we intend our “logic for pragmatics” to be compatible with the rich proof-theory of intuitionistic logic, including the Curry–Howard correspondence and categorical interpretations. Thus, we are inclined to regard conjectures and expectations as examples of how a theory of intuitionistic modalities can be developed starting from the illocutionary forces of assertions and hypotheses as basic. However, this investigation is left for another occasion.
1.1 Logic for Pragmatics: Dalla Pozza and Garola’s Approach
The aim of Dalla Pozza and Garola’s “logic for pragmatics” is to capture the logical properties of what are called illocutionary acts—asserting, conjecturing, commanding, promising, and so on. Consider assertions. In their framework there is a logic of propositions and a logic of assertions. Propositions can be either true or false, according to classical semantics, assertions are acts that can be justified or unjustified, felicitous or infelicitous. They propose a two-layer theory with a distinctive informal interpretation, according to which propositions have truth conditions, i.e., a semantics, whereas assertions have justification conditions, belonging to pragmatics. As a consequence, we can form logical combinations of propositions, which are given a classical semantics as usual, but we can also form logical combinations of assertions, and interpret these combinations along the familiar lines of Heyting’s interpretation of intuitionistic connectives. This is Dalla Pozza and Garola’s pragmatic interpretation of intuitionistic logic: if \(\alpha \) denotes a proposition, the elementary expression
 stands for an assertion and
stands for an assertion and  is justified just in case we have conclusive evidence that \(\alpha \) is true; in the case of a mathematical statement \(\alpha \), “conclusive evidence” is a proof of \(\alpha \). Moreover, an assertive expression of conditional type \(A \supset B\) is justified by providing a method that transforms a justification of an assertive type \(A\) into a justification of an assertive type \(B\).Footnote 3
\(^{,}\)
Footnote 4
is justified just in case we have conclusive evidence that \(\alpha \) is true; in the case of a mathematical statement \(\alpha \), “conclusive evidence” is a proof of \(\alpha \). Moreover, an assertive expression of conditional type \(A \supset B\) is justified by providing a method that transforms a justification of an assertive type \(A\) into a justification of an assertive type \(B\).Footnote 3
\(^{,}\)
Footnote 4
It should be noticed that intuitionistic logic is represented in Dalla Pozza and Garola’s framework as a theory of pragmatic validity only if the justification of elementary expressions  does not depend on the logical structure of the radical expression
\(\alpha \) as a classical proposition—e.g., we shall not allow \(\alpha \) to be \(p\vee \lnot p\). Thus in every investigation of intuitionistic theories within the framework of Dalla Pozza and Garola [18] it is assumed that elementary expressions have atomic radicals, i.e., \(\alpha = p\). This convention is essential also for the present investigation of our co-intuitionistic and bi-intuitionistic logic.
does not depend on the logical structure of the radical expression
\(\alpha \) as a classical proposition—e.g., we shall not allow \(\alpha \) to be \(p\vee \lnot p\). Thus in every investigation of intuitionistic theories within the framework of Dalla Pozza and Garola [18] it is assumed that elementary expressions have atomic radicals, i.e., \(\alpha = p\). This convention is essential also for the present investigation of our co-intuitionistic and bi-intuitionistic logic.
The novelty of Dalla Pozza and Garola’s work is that Heyting’s semantics is applied to illocutionary types of acts, not to propositions; if the justification of an assertion of atomic type  is related to the semantics of the propositional content \(\alpha \), a complex type has only a pragmatic justification value, not a semantic one. To recover propositions and semantic values one considers semantic projections given by the Gödel, McKinsey, Tarski and Kripke’s translation:
is related to the semantics of the propositional content \(\alpha \), a complex type has only a pragmatic justification value, not a semantic one. To recover propositions and semantic values one considers semantic projections given by the Gödel, McKinsey, Tarski and Kripke’s translation:

This modal formalism can be given the usual interpretation through an epistemic view of Kripke S4 semantics. Thus in a Kripke model \((W, R, \Vdash )\) for S4 every \(w\in W\) is seen as a stage of human knowledge and the accessibility relation expresses ways in which our knowledge may evolve; at each stage atomic propositions are locally true or false according to \(\Vdash \); reflexivity of \(R\) means that what we know must be true also locally and transitivity of \(R\) expresses the fact that human knowledge cannot be forgotten or falsified, and so on.Footnote 5
The basic approach of Dalla Pozza and Garola seems to stand as a helpful conceptual clarification, following Quine saying that a change of logic reflects a change of the subject matter of the logic. The remarkable technical developments of the proof-theory of classical logic in the last decades suggest the possibility of a pragmatic interpretation of classical methods of inference; despite some hints in [5], Sect. 5, and the result in Sect. 2.5, this remains an essentially unfinished business.
Justification and Felicity Conditions
Going back to the basic texts of modern pragmatics, such as Austin [2] and Levinson [31], every speech act has a propositional content, an illocutionary force (or pragmatic mood) and perlocutionary effects. Now it seems that the felicity or infelicity conditions of a speech act essentially depend on the actual circumstances of its performance and on its intended or unintended perlocutionary effects. Thus a formalization of the felicity or infelicity conditions of a statement would be based on a formal theory of actions including a representation of the agent and the addressees of a speech act and also its preconditions and postconditions (for a first formulation of such a theory, see [60]).
On the contrary, the contribution of the illocutionary mood to the pragmatics of speech acts can be characterized by abstracting away from the actual agents and addressees and from their specific context, effects, and goals. Thus an impersonal illocutionary operator of an intensional logic may suffice to express illocutionary force, if the justification of the illocutionary mood of such type of acts makes reference to a relatively stable and uniform context (e.g., scientific knowledge in a given time, obligations within an established legal system, unambiguous linguistic acts within a linguistic community, and so on).
In this framework, several works have explored the “logic for pragmatics” of obligations [19] and then the logic of assertions, obligations with causal reasoning [6, 7, 48, 49]. In general, the development of such logics requires an identification of the appropriate modal operators or non-classical connectives used in the modal projection and their Kripke semantics; then one proceeds to a more abstract treatment of the proof theory, as in Ranalter’s work.
2 PART I. Conceptual Analysis: Assertions, Hypotheses, and Conjectures
In extending Dalla Pozza and Garola’s framework to a logic of hypothetical and conjectural moods, we encounter a variety of moods with different linguistic and logical properties.Footnote 6 It is familiar the distinction in Latin between three kinds of if clauses, the first one using the indicative to express the condition as a matter of fact, the second the present subjunctive to express possibility of the condition and, finally, the third one using the past subjunctive for counterfactuals. Also consider the theory of argumentation. Here six proof-standards have been identified from an analysis of legal practice: no evidence, scintilla of evidence, preponderance of evidence, clear and convincing evidence, beyond reasonable doubt, and dialectical validity, in a linear order of strength [24].Footnote 7
It is essential to remember that “legal reasoning is not primarily deductive, but rather a modelling process of shaping an understanding of the facts, based on evidence, and an interpretation of the legal sources, to construct a theory for some legal conclusion” ([12] cited in [24]). More precisely, in order to decide whether to accept or reject each element of a given set of “claims,” one constructs a consistent “theory of the generalizations of the domain and the facts of the particular case,” together with “a proof justifying the decision of each issue, showing how the decision is supported by the theory” [24].
Thus in Argumentation Theory one starts with an inconsistent knowledge base and a set of claims and proceeds to build a consistent theory from them; later, when deriving the claims from such a theory one uses (some fragment of) classical logic. But in this stage it might be desirable to use a logic that retains essential pragmatic information such as the standards of evidence of the premises, rather than classical logic that omits it. Thus some refinement of our logic may have applications to Argumentation Theory to establish a closer correspondence between “theory searching” and deductive reasoning. Here we use the notion of “standards of proof” in an informal way and regard the possibility of developing a theory of positive evidence for hypotheses in our framework as a suggestion for future work.
2.1 First Attempt: Assertive and Hypothetical Types
In Bellin and Biasi [5] we have given a logic of hypothetical types parallel to Dalla Pozza and Garola’s logic of assertions. We start with elementary illocutionary acts of hypothesis, denoted by  : here \(\alpha \) is a proposition which is presented as possibly true; such an act is justified if there are grounds for believing that \(\alpha \) may be true in some circumstances. Next we consider connectives building up complex hypothetical types from elementary ones. For instance, through the connective of subtraction we build the hypothetical expression possibly
\(C\)
but not
\(D\) (written \(C \backslash D\)); such an expression is justified if it is justified to believe the truth of the hypothetical expression \(C\) while also believing that the hypothesis \(D\) may never be true; the disjunction \(C\curlyvee D\) of the hypothetical expressions \(C\) and \(D\) is also a hypothetical expression, and so on.
: here \(\alpha \) is a proposition which is presented as possibly true; such an act is justified if there are grounds for believing that \(\alpha \) may be true in some circumstances. Next we consider connectives building up complex hypothetical types from elementary ones. For instance, through the connective of subtraction we build the hypothetical expression possibly
\(C\)
but not
\(D\) (written \(C \backslash D\)); such an expression is justified if it is justified to believe the truth of the hypothetical expression \(C\) while also believing that the hypothesis \(D\) may never be true; the disjunction \(C\curlyvee D\) of the hypothetical expressions \(C\) and \(D\) is also a hypothetical expression, and so on.
The modal projection of hypothetical expressions is also in classical S4:

Namely, the modal translations of assertions \(A^M\) and hypotheses \(C^M\) are both interpreted in models \((W,R,\Vdash )\) where \(R\) is transitive and reflexive. This choice is crucial for the approach of [5]: other modal candidates are possible as discussed in [5] and in more detail below.
In natural language, illocutionary acts of hypothesis may be embedded into a context consisting of illocutionary act of assertion, for instance,
Arturo is the best pianist of his generation and will not refuse to play in this town, although the audience may be slightly noisy;
an assertive conjunction of two assertions and a hypothetical statement; conversely, assertions may be embedded in a hypothetical context:
We may not hear Arturo playing, because he has very high standards and if the audience is slightly noisy then he may refuse to play.
containing a hypothetical implication with an assertive antecedent and hypothetical consequent. Taking this idea seriously, one obtains a rather unmanageable family of mixed connectives [5]; in this chapter we shall consider only the role of mixed negations turning assertive expressions into hypothetical ones and conversely.
Three Methodological Principles
Our logical treatment of assertions and hypotheses is based on the notion of a duality between these two illocutionary moods: informally it is a familiar idea, since a proof of a proposition may be obtained as a refutation of the conjecture that its dual is true. In a formal treatment, there are many aspects to this duality, which are certainly satisfied by the modal translation in S4. In [5], Sect 1.1, three methodological principles are stated for a logic expressing the duality between assertive and hypothetical types:
-
1.
The grounds that justify asserting a proposition \(\alpha \) certainly suffice also for conjecturing it, whatever these grounds may be;
-
2.
in any situation, the grounds that justify the assertion of \(\alpha \) are also necessary and sufficient to regard the conjecture that \(\lnot \alpha \) as unjustified;
-
3.
the justification of non-elementary assertive or hypothetical types, built up from elementary types using pragmatic connectives, depends on the justification of the component types, possibly using intensional operations.
The third principle requires a sort of compositionality of justification: this is certainly satisfied by the intended informal interpretation of the connectives.
As it stands, the second principle is inadequate. On one hand, it is indisputable that the grounds allowing one to regard the assertion of \(\alpha \) as justified must override any ground in favor of the conjecture of \(\lnot \alpha \); on the other hand, it is wrong and contrary to common sense to say that if the conjecture of \(\lnot \alpha \) is unjustified then the assertion of \(\alpha \) is justified: the grounds we may have to dismiss the conjecture that \(\lnot \alpha \) may be the case may not be strong enough to justify the assertion that \(\alpha \) is true. There are at least two issues here.
First, we must distinguish between the illocutionary force of a mere hypothesis and that of a conjecture, a distinction we shall develop later in this chapter. Let us split the second principle into two parts, replacing “hypothesis” for “conjecture”:
-
2.i
If the assertion of \(\alpha \) is justified, then the hypothesis that \(\lnot \alpha \) is true cannot be justified.
-
2.ii
If the hypothesis that \(\lnot \alpha \) is true is unjustified, then the assertion of \(\alpha \) is justified.
Except for the case of counterfactuals, which are not our concern here, (\(2.i\)) is still correct; as for \((2.ii)\), it becomes plausible if we assume that a hypothesis  may be justified by a mere cognitive possibility of a situation, no matter how unlikely it may be, in which \(\lnot \alpha \) is true. The epistemic interpretation of the modal interpretation in S4 validates this reading of \((2.ii)\).
may be justified by a mere cognitive possibility of a situation, no matter how unlikely it may be, in which \(\lnot \alpha \) is true. The epistemic interpretation of the modal interpretation in S4 validates this reading of \((2.ii)\).
This raises a second issue: in our framework there is no theory of positive evidence; nevertheless we must be able to distinguish illocutionary forces whose justification depends on different strengths of evidence. Thus the logic of hypothetical reasoning in [5] reduces to a refutation calculus; although pure refutation does correspond to common-sense reasoning—indeed it seems to be very close to the medieval practice of disputation [1]Footnote 8—it may not suffice for applications, e.g., to a theory of laws and to legal reasoning.
Finally, the first principle is true for any reading of  , e.g., as hypothesis or conjecture. Also it is true in argumentation theory: the assertion
, e.g., as hypothesis or conjecture. Also it is true in argumentation theory: the assertion  must be justified by “standards of proof” at least as strong as those justifying the hypothesis
must be justified by “standards of proof” at least as strong as those justifying the hypothesis  . Notice that this principle shows a basic asymmetry between assertions and hypotheses.
. Notice that this principle shows a basic asymmetry between assertions and hypotheses.
A Logic of Assertions and Hypotheses: The Language \(\mathcal {L}^{{{\varvec{A}}H}}\)
The core fragment of the logic of assertions and hypotheses in [5] is a propositional language built from a countable set of atomic formulas \(p\), \(p_1\), \(p_2\), \(\ldots \) and symbols of illocutionary force yielding elementary formulas  (certainly
\(p\)) and
(certainly
\(p\)) and  (perhaps
\(p\)). It consists of two dual parts:
(perhaps
\(p\)). It consists of two dual parts:
-
an assertive part \(\mathcal {L}^A\) built from elementary assertions
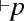 , a sentential constant for validity (\(\curlyvee \)), using assertive conjunction (\(\cap \)) and assertive implication (\(\supset \)) and
, a sentential constant for validity (\(\curlyvee \)), using assertive conjunction (\(\cap \)) and assertive implication (\(\supset \)) and -
a hypothetical part \(\mathcal {L}^H\) built from elementary hypotheses
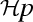 and a constant for absurdity (\(\curlywedge \)), using hypothetical disjunction (\(\curlyvee \)), and hypothetical subtraction (\(\backslash \)).
and a constant for absurdity (\(\curlywedge \)), using hypothetical disjunction (\(\curlyvee \)), and hypothetical subtraction (\(\backslash \)).
Thus \(\mathcal {L}^A\) and \(\mathcal {L}^H\) are negation-free fragments of the language of intuitionistic and co-intuitionistic logic. Let abs be an absurd statement in \(\mathcal {L}^A\) and val is a valid statement in \(\mathcal {L}^H\). Then \(\sim X =_{def} X \supset \mathbf {abs}\) expresses assertively the existence of a method to turn a justification of \(X\) into a justification of an absurdity. Similarly \(\smallfrown Y =_{def} \mathbf {val}\backslash Y\) expresses the doubt that \(Y\) may be true, namely, the hypothesis that a valid statement val may be compatible with the negation of \(Y\). Thus we have four negations:
-
1.
if \(X\) is an assertive expression, then \(\sim X\) is the usual intuitionistic negation;
-
2.
if \(Y\) is a hypothetical expression, \(\smallfrown Y\) is co-intuitionistic supplement;
-
3.
if \(X\) is a hypothetical, then the mixed expression \(X \supset \mathbf {abs}\) is an assertive type;
-
4.
if \(Y\) is assertive, then \(\mathbf {val}\backslash Y\) is a hypothetical type.Footnote 9
Our logic is therefore bi-intuitionistic, in the sense that it has intuitionistic and co-intuitionistic connectives, but it is polarized, as elementary formulas are either intuitionistic  or co-intuitionistic
or co-intuitionistic  , but not both, and connectives, with the possble exception of negations, preserve the polarity. Thus we have the following grammar of the language of polarized bi-intuitionistic logic for the pragmatics of assertions and hypotheses \(\mathcal {L}^{AH}{:}\)
, but not both, and connectives, with the possble exception of negations, preserve the polarity. Thus we have the following grammar of the language of polarized bi-intuitionistic logic for the pragmatics of assertions and hypotheses \(\mathcal {L}^{AH}{:}\)
\(A, B\) | := |
| \(\quad \curlyvee \quad \) | \(\quad A\supset B\quad \) | \(\quad A\cap B\quad \) | \(\quad \sim C\quad \) |
\(C, D\) | := |
| \(\quad \curlywedge \quad \) | \(\quad C\backslash D\quad \) | \(\quad C\curlyvee D\quad \) | \(\quad \smallfrown A\quad \) |
2.2 Second Attempt: More General Modal Translations
In order to approximate alternative treatments of a logic of assertions, hypotheses and conjectures, we consider more general modal translations in bimodal S4.
Translations in Bimodal S4
Definition 1
(i) Let \(p\) range over a denumerable set of propositional variables Var = \(\{p_1, p_1, \ldots \}\). The bimodal language  is defined by the following grammar.
is defined by the following grammar.

Define \(\Diamond \alpha =_{df} \lnot \Box \lnot \alpha \) and  .
.
(ii) Let \(\mathcal {F} = (W, R, S)\) be a multimodal frame, where \(W\) is a set, \(R\) and \(S\) are preorders on \(W\). Given a valuation function \(V : \mathbf {Var} \rightarrow \wp (W)\), the forcing relations are defined as follows:
-
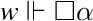 iff \(\forall w'. wRw' \Rightarrow w'\Vdash \alpha \),
iff \(\forall w'. wRw' \Rightarrow w'\Vdash \alpha \), -
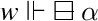 iff \(\forall w'. wSw' \Rightarrow w'\Vdash \alpha \).
iff \(\forall w'. wSw' \Rightarrow w'\Vdash \alpha \).
(iii) We say that a formula \(A\) in the language  is valid in bimodal
S4 if \(A\) is valid in all bimodal frames \(\mathcal {F} = (W, R, S)\) where \(R\) and \(S\) are preorders.
is valid in bimodal
S4 if \(A\) is valid in all bimodal frames \(\mathcal {F} = (W, R, S)\) where \(R\) and \(S\) are preorders.
Lemma 1
Let \(\mathcal {F} = (W, R, S)\) be a multimodal frame, where \(R\) and \(S\) are preorders.
\((i)\) The following are valid in \(\mathcal {F}\)

\((ii)(a)\) The following are equivalent:
-
1.a:
\(S\subseteq R\);
-
2.a:
the following scheme is valid in \(\mathcal {F}\):
-
.
(Ax.a)
 ;
; -
3.a:
the following rule is valid in \(\mathcal {F}\):
-
.
(R.a)
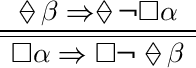
\((ii)(b)\) The following are equivalent
-
1.b:
\(R\subseteq S\);
-
2.b:
the following scheme is valid in \(\mathcal {F}\):
-
.
(Ax.b)

-
3.b:
the following rule is valid in \(\mathcal {F}\):
-
.
(R.b)
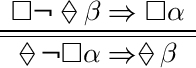
Proof of
\((ii)(a)\). (1.a \(\Rightarrow \) 2.a) is obvious. (2.a \(\Rightarrow \) 1.a): If \(S\) is not a subset of \(R\), then given \(wSv\) and not \(wRv\) define a model on \(\mathcal {F}\) where \(w'\Vdash p\) for all \(w'\) such that \(wRw'\) but \(v\not \Vdash p\); thus  is false at \(w\). (2.a \(\Rightarrow \) 3.a): If
is false at \(w\). (2.a \(\Rightarrow \) 3.a): If  is valid in \(\mathcal {F}\) then so is
is valid in \(\mathcal {F}\) then so is  and the conclusion of \((R.a)\) is valid because of \((Ax.a)\). From the conclusion of \((R.a)\) the premise follows using part (i). (3.a \(\Rightarrow \) 2.a): \((Ax.a)\) is obtained by applying \((R.a)\) downwards to
and the conclusion of \((R.a)\) is valid because of \((Ax.a)\). From the conclusion of \((R.a)\) the premise follows using part (i). (3.a \(\Rightarrow \) 2.a): \((Ax.a)\) is obtained by applying \((R.a)\) downwards to  . The other parts are similar.
. The other parts are similar.
2.3 Bimodal Interpretations of \(\mathcal {L}^{AH}\)
Definition 2
The interpretation \((\ )^M\) of \(\mathcal {L}^{AH}\) into  is defined inductively thus:
is defined inductively thus:
\((\curlywedge )^{M}\ \) | \(=_{df}\) | \(\ \bot \) | \((\curlyvee )^{M}\ \) | \(=_{df}\) | \(\ \top \) | |
| \(=_{df}\) | \(\ \Box p\) |
| \(=_{df}\) |
| |
\((A\supset B)^{M}\ \) | \(=_{df}\) | \(\ \Box (A^{M}\rightarrow B^{M})\) | \((C\backslash D)^{M}\ \) | \(=_{df}\) |
| |
\((A_1\cap A_2)^{M}\ \) | \(=_{df}\) | \(\ A_1^{M}\wedge A_2^{M}\) | \((C_1\curlyvee C_2)^{M}\ \) | \(=_{df}\) | \( C_1^{M}\vee C_2^{M}\) | |
\((\sim C)^{M}\ \) | \(=_{df}\) | \(\ \Box \lnot C^M\) | \((\smallfrown A)^{M}\ \) | \(=_{df}\) |
|
It is easy to prove that \(A^M \iff \Box A^M\) and  in the semantics of (bimodal) S4.
in the semantics of (bimodal) S4.
(i) The propositional theory PBL (polarized bi-intuitionistic logic) is the set of all formulas \(\delta \) in the language \(\mathcal {L}^{AH}\) such that \(\delta ^M\) is valid in every preordered bimodal frame (i.e, in any frame \((W, R, S)\) where \(R\) and \(S\) are arbitrary preorders).
(ii) The propositional theory APBL (asymmetric polarized bi-intuitionistic logic) is the set of all formulas \(\delta \) in the language \(\mathcal {L}^{AH}\) such that \(\delta ^M\) is valid in every preordered bi-modal frame \((W, R, S)\) where \(S\subseteq R\).
(iii) The propositional theory AHL (bi-intuitionistic logic of assertions and hypotheses) is the set of all formulas \(\delta \) in the language \(\mathcal {L}^{AH}\) such that \(\delta ^M\) is valid in every preordered bi-modal frame \((W, R, S)\)
where
\(R = S\). In other words, in the modal translation let  ; then \(\delta \) is in AHL if and only if \(\delta ^M\) is valid in S4.
; then \(\delta \) is in AHL if and only if \(\delta ^M\) is valid in S4.
Remark 1
(i) PBL is the most abstract theory of bi-intuitionistic logic where all formulas are polarized as assertive or hypothetical. PBL is not a suitable candidate for our logic of assertions and hypotheses, since the pair  ,
,  is consistent in bi-modal S4, contrary to the accepted principle \((2.i)\). We will not speculate about the possibility of interpreting
is consistent in bi-modal S4, contrary to the accepted principle \((2.i)\). We will not speculate about the possibility of interpreting  as a counterfactual.
as a counterfactual.
(ii) On the contrary, the asymmetric logic APBL satisfies \((2.i)\), but not \((2.ii)\).Footnote 10 Thus APBL may be the right context for studying assertive and hypothetical reasoning where hypothetical statements have different degrees of positive evidence and thus are not representable in a pure refutation calculus.
(iii) Finally, our canonical system is the bi-intuitionistic logic of assertions and hypotheses AHL—poorly named intuitionistic logic for pragmatics ILP in [5]—satisfying both conditions \((2.i)\) and \((2.ii)\). It is motivated by the epistemic interpretation of (uni-modal) S4, where hypotheses are seen as mere epistemic possibilities and assertions as epistemic necessities.
Dualities
Definition 3
Let \((\ )^{\bot } : \mathbf {Atoms}\rightarrow \mathbf{Atoms}\) be an involution without fixed points on the atomic formulas \(p_i\). Intuitively, we may think of \(p_i^{\bot }\) as \(\lnot p_i\), but intuitionistic dualites are defined best without any reference to the classical part. We extend \((\ )^{\bot }\) to maps \(F: \mathcal {L}^A\rightarrow \mathcal {L}^H\) and \(G: \mathcal {L}^H\rightarrow \mathcal {L}^A\) letting
\((a)\) |
|
|
\((b)\) | \(F(A\cap B) = F(A)\curlyvee F(B)\) | \(G(C\curlyvee D) = G(C)\cap G(D)\) |
\((c)\) | \(F(A\supset B) = F(B)\backslash F(A)\) | \(G(C\backslash D) = G(D)\supset G(C)\) |
Lemma 2
In AHL let \(F(A) =\, \smallfrown A\) and \(G(C) =\, \sim C\). Then
-
1.
if we interpret \((p^{\bot })^M\) as \(\lnot p\), then the modal translations of conditions (a)–(c) are valid equivalences in S4;
-
2.
\(GF(A) \equiv A\) and \(FG(C)\equiv C\);
-
3.
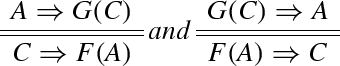
Proof
By definition of the modal translation we have
(1)(a): |
|
|
(1)(b): | \(\bigl (\smallfrown (A\cap B)\bigr )^M = \Diamond \lnot (A^M\wedge B^M)\equiv (\Diamond \lnot A^M)\vee (\Diamond \lnot B^M) = \bigl ((\smallfrown A)\curlyvee (\smallfrown B)\bigr )^M\) |
\(\bigl (\sim (C\curlyvee D)\bigr )^M = \Box \lnot (C^M\vee D^M) \equiv (\Box \lnot C^M)\wedge (\Box \lnot D^M) = \bigl ((\sim C)\cap (\sim D)\bigr )^M\) | |
(1)(c): | \(\bigl (\smallfrown (A\supset B)\bigr )^M = \Diamond \lnot \Box (A^M\rightarrow B^M)\equiv \Diamond (\Diamond \lnot B^M\wedge \lnot \Diamond \lnot A^M) = \bigl ((\smallfrown B)\backslash (\smallfrown A)\bigr )^M\) |
\(\bigl (\sim (C\backslash D)\bigr )^M = \Box \lnot \Diamond (C^M\wedge \lnot D^M) \equiv \Box (\Box \lnot D^M\rightarrow \Box \lnot C^M) = \bigl ((\sim D)\supset (\sim C)\bigr )^M\) |
(2): The conditions
follow from Lemma 1 \(.(i)\) and \((ii)\). The conditions in (3) follow from rules (R.a) and (R.b) in Lemma 1 \(.(ii)\).
Remark 2
(i) Lemma 2 fails for PBL and APBL.
(ii) As the only mixed formulas in \(\mathcal {L}^{AH}\) are negations, Lemma 2 gives us a (meta-theoretic) “method for eliminating mixed formulas in AHL” modulo the atomic involution
\((\ )^{\bot }\), (interpreted in the modal translation as classical negation \(\lnot p\)). e.g., the mixed expression  is equivalent in the S4 semantics to the purely assertive expression
is equivalent in the S4 semantics to the purely assertive expression  .
.
(iii) Sometimes we shall write \(A^{\bot }\) and \(C^{\bot }\) for \(F(A)\) and \(G(C)\), respectively.
Proposition 1
(restricted substitution) Let \(\sigma \) be a map

sending a vector \(\overline{\eta _a}\) of assertive elementary formulas to a vector \(\overline{A}\) of assertive formulas and a vector \(\overline{\eta _h}\) of hypothetical elementary formulas to a vector \(\overline{C}\) of hypothetical formulas. Then \(X(\overline{\eta _a}, \overline{\eta _h})\) is a theorem of AHL [ PBL , APBL ] if and only if \(X(\sigma (\overline{\eta _a}), \sigma (\overline{\eta _h}))\) is a theorem of AHL [ PBL , APBL ].
On the other hand, the theories AHL, PBL and APBL are not closed under substitution of hypothetical formulas for assertive elementary formulas (and symmetrically). An example is the following:
| is valid, but |
| is not. | |
Indeed | \(\Box \Diamond \Box \Diamond \lnot p\Rightarrow \Box \Diamond \lnot p\) | is valid, but | \(\Box \Diamond \Box \lnot p\Rightarrow \Box \lnot p\) | is invalid in S4. |
2.4 Sequent Calculi for PBL, APBL, AHL
The logics PBL, APBL, AHL can be formalized in G3-style sequent calculi [59], where the rules of Weakening and Contraction are implicit, as in [5]. One then proves that the rules of Weakening and Contraction are admissible preserving the depth of the derivation.
Definition 4
All the sequents \(S\) are of the form
where
-
\(\Theta \) is a sequence of assertive formulas \(A_1\), \(\ldots \), \(A_m\);
-
\(\Upsilon \) is a sequence of hypothetical formulas \(C_1\), \(\ldots \), \(C_n\);
-
\(\epsilon \) is hypothetical and \(\epsilon '\) is assertive and exactly one of \(\epsilon \), \(\epsilon '\) occurs.
The bi-intuitionistic logic of assertions and conjectures AHL is formalized in the sequent calculus given by the axioms and rules in the Table 1.Footnote 11 Let us call this fragment standard AH-G3.
The polarized bi-intuitionistic logic PBL and the asymmetric polarized bi-intuitionistic logic APBL are formalized by restricting the rules of canonical AH-G3 as indicated below: the restrictions only modify the rules \(\supset \)-right, \(\sim \)-right, \(\backslash \,\)-left and \(\smallfrown \,\)-left. Let us call the resulting sequent calculi abstract PB-G3 and asymmetric APB-G3, respectively.
AH-G3: | ||
|
| |
|
| |
|
|
To see why in the asymmetric APB-G3 and in the canonical AH-G3 systems the formulas in \(\Theta \) are allowed in the antecedent of the sequent-premise of \(\backslash \)-left and of \(\smallfrown \)-left, notice that by the valid scheme \((Ax.a)\) of Lemma 1 \(.(ii)(a)\)

Thus the unrestricted rule \(\smallfrown \)-left of AP-G3 and AH-G3 becomes derivable in PB-G3 using cut with scheme (1) taken as axiom:

Similarly, using the fact that

we show that in AH-G3 \(\Upsilon \) is allowed in the succedent of the sequent premise of \(\supset \)-right and of \(\sim \)-right.
Using the methods of [5] one may prove the following result:
Theorem 1
The sequent calculi PB-G3 [ APB-G3 , AH-G3 ] without the rules of cut are sound and complete with respect to the interpretation of PBL [ APBL , AHL , respectively] in bimodal S4.
2.5 First Conclusions: Assertions and Conjectures
Although our approach to the logic for pragmatics does not provide a theory of positive evidence, the epistemic reading of the modal interpretation in S4 does suggest a way to characterize different degrees of evidence, through the essential distinction between hypotheses and conjectures. While “epistemic possibility,” namely the mere knowledge of a situation in which \(\alpha \) happens to be true, does provide enough evidence to justify the hypothesis of \(\alpha \), conjecturing the truth of \(\alpha \) requires knowing conditions in which \(\alpha \) would be “epistemically necessary.” We write \(\mathcal {C}\alpha \) to express the conjecture that \(\alpha \) is true.
Moreover, consider circumstances in which it is unjustified to conjecture the truth of \(\alpha \). This is certainly the case when no matter how our present knowledge evolves, it always reaches a state in which \(\alpha \) fails to be true: we may call this epistemic condition safe expectation that \(\lnot \alpha \) eventually becomes true. We write \(\mathcal {E}\alpha \) to express the safe expectation of \(\alpha \).
Setting \((\mathcal {C}\alpha )^M\) = \(\Diamond \Box \alpha \) and \((\mathcal {E}\alpha )^M\) = \(\Box \Diamond \alpha \), we have a modal interpretation in S4 that fits nicely in the above informal interpretation. In Table 2 we find the map of all distinct modalities in S4; arrows indicate valid implications between non-equivalent modalities.
Table 3 presents all pragmatic expressions corresponding to modalities of S4 and the valid implications between them.
We shall not develop a full theory of assertions, hypotheses, conjectures and expectation with four corresponding types of pragmatic connectives. We are interested in theories obtained by extending the polarized language \(\mathcal {L}^{AH}\) of assertions and hypotheses with new elementary expressions \({\mathcal {C}\! p}\) for conjectures and dually, expressions \({\mathcal {E}\! p}\) for expectations. Let us write \({\mathcal {L}^{AHC}}\) [\({\mathcal {L}^{AHCE}}\)] for the extension of \({\mathcal {L}^{AH}}\) with elementary expressions \({\mathcal {C}\!p}\) for conjectures [and \({\mathcal {E}\!p}\) for expectations].
Let AHCE be the set of all expressions in \(\mathcal {L}^{AHCE}\) that are valid in the S4 modal translation. We conjecture in order to axiomatize AHCE in a cut-free sequent calculus it suffices to extend AH-G3 with the following rules:
| |
| |
Duality Between Safe Expectations and Conjectures
Clearly the S4 translations of conjectures and of assertions are not dual from the viewpoint of modal logic, but the modal translations of conjectures and safe expectations certainly are; if in Definition 3 and in Lemma 2 we replace the illocutionary operators “\(\mathcal {C}\)” (conjectures) and “\(\mathcal {E}\)” (safe expectations) for the operators “ ” (hypotheses) and “
” (hypotheses) and “ ” (assertions), respectively, then clearly the conditions of duality are expressible through negations within a logic AHCEL of assertions, hypotheses, conjectures and safe expectations. For instance, the base case becomes:
” (assertions), respectively, then clearly the conditions of duality are expressible through negations within a logic AHCEL of assertions, hypotheses, conjectures and safe expectations. For instance, the base case becomes:
\((a)\qquad \) | setting | \(F(\mathcal {E} p) = \mathcal {C} p^{\bot }\) | and | \(G(\mathcal {C} p) = {\mathcal E} p^{\bot }\) |
we have | \(\smallfrown \mathcal {E} p \equiv \mathcal {C} p^{\bot }\) | and | \(\sim \mathcal {C} p \equiv \mathcal {E} p^{\bot }\) | |
since | \(\Diamond \lnot \Box \Diamond p \equiv \Diamond \Box \lnot p\qquad \) | and | \(\Box \lnot \Diamond \Box p \equiv \Box \Diamond \lnot p\). |
The Logic of Safe Expectations is Classical
Let \(\mathcal {L}^{E}\) be the language defined by the grammar
and let bf EL be the set of all formulas \(\delta \) in the language \(\mathcal {L}^E\) such that the modal translation \(\delta ^{M}\) is valid in S4.
Proposition 2
The theory EL (logic of safe expectations) is closed under the double negation rule, i.e., \(\sim \sim E \Rightarrow E\) is a valid axiom of EL.
The proof shows by induction on the logical complexity that the double negation rule for molecular formulas can be reduced to applications of the double negation rule for elementary formulas (essentially, as in [46]). The base case is then given by the following equivalence:
On the other hand, if we extend \(\mathcal {L}^E\) with intuitionistic disjunction \((\cup )\), then \(E \cup \sim E\) is not a theorem of the logic of safe expectations extended in this way. Indeed
is not valid in S4.
Historical Note
In Appendix B of [46] Prawitz considers an extension of the language of intuitionistic logic with an involutory negation \(\lnot \) and then extends intuitionistic natural deduction \(\mathbf {NJ}^{\supset \cap }\) with rules \(\lnot \!\!\supset \)-I, \(\lnot \!\!\supset \)-E, \(\lnot \cap \)-I and \(\lnot \cap \)-E; these new rules are presented as an axiomatization of Nelson’s logic of constructible falsity [38].Footnote 12 Thomason [58] provides a Kripke semantics for Nelson’s logic of constructible falsity, where \(w\Vdash \lnot p\) if and only if \(w'\Vdash \lnot p\) for all \(w'\) with \(wRw'\); this implies that the evaluation function must be partial. Miglioli et al. [37] introduce an operator \(\mathbf {T}\) which represents classical truth within the context of Nelson’s logic of constructive negation: in particular we have \(A\) is classically valid if and only if \(\sim \sim A\) is intuitionistically valid (by Gödel’s translation) if and only if \(\mathbf {T} A\) is valid in the constructive extended system. In [37] a Kripke semantics for the constructive logic with \(\mathbf {T}\) operator is presented, where Thomason’s semantics is restricted to frames satisfying the additional condition that from each world \(w\) a terminal world \(w'\) is reached where all atoms and negations of atoms are evaluated. Then the forcing conditions for \(\mathbf {T} p\) by Miglioli et al. are expressible as \(w \Vdash \mathbf {T} p\) if and only if \(w\Vdash \Box \Diamond p\) and \(w \Vdash \lnot \mathbf {T} p\) if and only if in all \(w'\) with \(wRw'\) we have that \(p\) is either not evaluated or false in \(w'\). Comparing the operator \(\mathbf {T}\) to our operator \(\mathcal {E}\) of safe expectation, when applied to atomic formulas, we can say that their properties are similar, but in the context of a polarized bi-intuitionistic system they can be expressed in a simpler way. We cannot discuss the intriguing work by Miglioli and his co-workers in more detail here; a recent discussion of their approach is in Pagliani’s book [39].
3 PART II. Rough-Set Semantics
Proofs and Refutations
The idea that a characterization of constructive logic must include a definition not only of what proofs of a formula \(A\) are but also of refutations of \(A\) goes back at least to Nelson [38] and comes up in various contexts related to game semantics and in particular the construction of Chu spaces. Thus we may say that a proof of \(A\supset B\) is a method transforming a proof of \(A\) into a proof of \(B\) and that a refutation of \(A\supset B\) is a pair consisting of a proof of \(A\) together with a refutation of \(B\); in some contexts instead of proofs and refutations we may speak of evidence for and against \(A\). To study bi-intuitionistic logic and its dualities one may say that a proof of \(C\backslash D\) is a pair consisting of a proof of \(C\) and of a refutation of \(D\) and that a refutation of \(C\backslash D\) is a method transforming a proof of \(C\) into a proof of \(D\). But we will not go very far if the spaces of proofs and of refutations of \(A\) coincide with the spaces of refutations and of proofs of \(A^{\bot }\), respectively. This is certainly not the case if we consider the semantics of assertions, hypotheses, and conjectures rather than that of assertions and hypotheses, as discussed informally in Sect. 2.1. Moreover, it turns out that Rough-Set semantics applied to our canonical polarized system AHCB does provide new insight and also a bridge to geometric models [57].
3.1 Rough Sets
As pointed out in [5], any topological space provides a mathematical model of bi-intuitionistic logic, thus also of our canonical system AHL, if we interpret the assertive expressions by open sets and the hypothetical ones by closed sets. A more interesting suggestion comes from the interpretation in terms of Rough Sets, following Piero Pagliani’s work (in particular, see [40, 41] and Lech Polkowski’s book [45], Chap. 12).
Definition 5
Given an indiscernibility space \((U,E)\), where \(U\) is a finite set and \(E \subseteq U\times U\) an equivalence relation, identifying objects that may be indiscernible from some point of view, let \(\mathbf {AS}(U)\) be the atomic Boolean algebras having the set of equivalence classes \(U\slash E\) as atoms; then \((U, \mathbf {AS}(U))\) is a topological space, called the Approximation Space of \((U,E)\), which induces an interior operator and a closure operator \(\mathcal {I}, \mathcal {C}: \wp (U)\rightarrow \mathbf {AS}(U)\). If two subsets \(G', G'' \subseteq U\) have the same interior and the same closure, then they are roughly equal, i.e., indistinguishable either by the coarsest classification given by \(\mathcal {C}\), or by the finest classification \(\mathcal {I}\); thus each subset \(G\) is a representative of a class of subsets identified by the pair \((\mathcal {I}(G), \mathcal {C}(G))\); only a clopen \(G\) for which \(\mathcal {I}(G)=\mathcal {C}(G)\) is fully characterized in \((U,E)\).
For our purpose it is more convenient the disjoint representation \((\mathcal {I}(G), -\mathcal {C}(G))\) using the complement of the closure of \(G\), the set of object different from \(G\) even for the coarser classification, instead of \(\mathcal {C}(G)\). Thus we may regard the two clopen sets \((\mathcal {I}(G)\) and \(-\mathcal {C}(G))\) as representing the space of proofs and of refutations of an intuitionisitc formula.
Following Pagliani, we can define the following data and operations on pairs
-
1
\(1 = (U,\emptyset )\), \(0 = (\emptyset , U)\);
-
2
\((X^+,X^-) \wedge (Y^+, Y^-)\) \(=\) \((X^+\cap Y^+, X^-\cup Y^-)\) (conjunction);
-
3
\((X^+,X^-) \vee (Y^+, Y^-)\) \(=\) \((X^+\cup Y^+, X^-\cap Y^-)\) (disjunction);
-
4
\((X^+, X^-) \rightarrow (Y^+,Y^-)\) \(=\) \((-X^+\cup Y^+, X^+\cap Y^-)\); (Nelson’s implication)
-
5
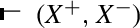 \(=\)
\((-X^+, X^+)\) (weak negation or supplement);
\(=\)
\((-X^+, X^+)\) (weak negation or supplement); -
6
\((X^+, X^-)^{\bot }\) \(=\) \((X^-, X^+)\) (orthogonality);
-
7
\((X^+, X^-) \Rightarrow (Y^+, Y^-)\) \(=\) \(((-X^+\cup Y^+) \cap (-Y^-\cup X^-), -X^- \cap Y^-)\) (Heyting’s implication);
-
8
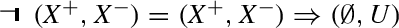 \(=\)
\((X^-, -X^-)\) (intuitionistic negation);
\(=\)
\((X^-, -X^-)\) (intuitionistic negation); -
9
\((X^+, X^-) \backslash (Y^+, Y^-)\) \(=\) \((X^+\cap -Y^+), (-X^+ \cup Y^+) \cap (-Y^-\cup X^-)\) (co-intuitionistic subtraction).
(see Pagliani [41], Polkowski [45], p. 363—with an equivalent definition of Heyting implication).Footnote 13
Of course one will not obtain a complete semantics for intuitionistic logic starting from a finite base of clopen sets. Thus we need to look at general topological spaces. Since the language of our logic of assertions, hypotheses, and conjectures AHCL is polarized, in order to turn Pagliani’s operations into a topological model of AHCL we need to make sure that the interpretation of an assertive expression is an open set and a hypothetical expression is assigned a closed set; this is not always the case for Pagliani’s operations, in particular implications and negations, which have to be modified as follows.
Definition 6
Let \((U, O)\) be a topological space, where \(O\) is the collection of open sets on \(U\), and \(\mathcal {I}(X)\) and \(\mathcal {C}(X)\) are the interior and the closure of \(X\),Footnote 14 respectively. We write \((A^+_o, A^-_c)\) and \((C^+_c, C^-_o)\) for pairs of disjoint sets of the types (open, closed) and (closed, open), respectively. We define the rough set interpretation \((\ )^R\) of the language of assertions, hypotheses, and conjectures \(\mathcal {L}^{AC}\) (in the disjoint representation) as follows.
Fix an assignment \(R\) :  and
and  to the elementary expressions of \(\mathcal {L}^{AH}\). Then
to the elementary expressions of \(\mathcal {L}^{AH}\). Then
-
1
\(\curlyvee ^R = (U, \emptyset )\) and \(\curlywedge ^M = (\emptyset , U)\) (clopen, clopen);
-
2
\((A\cap B)^R = (A_o^+, A_c^-)\wedge (B_o^+, B_c^-)\) \(=\) \((A_o^+ \cap B_o^+, A_c^- \cup B_c^-)\) ;
-
3
\((C\curlyvee D)^R = (C_c^+, C_o^-)\vee (D_c^+, D_O^-)\) \(=\) \((C_c^+\cup D_c^+, C_o^-\cap D_o^-)\);
-
4
\((A_o^+, A_c^-)\rightarrow (B_o^+, B_c^-)\) \(=\) \(\bigl (\mathcal {I}(-A_o^+\cup B_o^+), \mathcal {C}(A_o^+ \cap B_c^-)\bigr )\) Footnote 15;
-
5
\((\smallfrown C)^R\) \(=\)
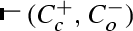 \(=\)
\(\bigl (\mathcal {C}(-C_c^+), \mathcal {I}(C_c^+)\bigr )\) and
\(=\)
\(\bigl (\mathcal {C}(-C_c^+), \mathcal {I}(C_c^+)\bigr )\) and -
.
\((\smallfrown A)^R\) \(=\)
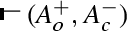 \(=\)
\((-A_o^+, A_o^+)\);
\(=\)
\((-A_o^+, A_o^+)\); -
6
\((A_o^+, A_c^-)^{\bot }\) \(=\) \((A_c^-, A_o^+)\) and \((C_c^+, C_o^-)^{\bot }\) \(=\) \((C_o^-, C_c^+)\) Footnote 16;
-
7
\((A\supset B)^R\) \(=\) \((A_o^+, A_c^-)\Rightarrow (B_o^+, B_c^-)\) \(=\)
-
.
\(=\) \(\bigl (\mathcal {I}(-A_o^+ \cup B_o^+)\cap \mathcal {I}(-B_c^-\cup A_c^-), \mathcal {C}(-A_c^- \cap B_c^-)\bigr )\);
-
8
\((\sim A)^R\) \(=\)
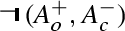 \(=\)
\(\bigl (\mathcal {I}(A_c^-), \mathcal {C}(-A_c^-)\bigr )\) and
\(=\)
\(\bigl (\mathcal {I}(A_c^-), \mathcal {C}(-A_c^-)\bigr )\) and -
.
\((\sim C)^R\) \(=\)
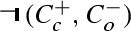 \(=\)
\((C_o^-, -C_o^-)\);
\(=\)
\((C_o^-, -C_o^-)\); -
9
\((C\backslash D)^R\) \(=\) \((C_c^+, C_o^-) \backslash (D_c^+, D_c^-)\) \(=\)
-
.
\(=\) \(\bigl (\mathcal {C}(C_c^+\cap -D_c^+), \mathcal {I}(-C_c^+\cup D_c^-)\cap \mathcal {I}(-D_o^-\cup C_o^-)\bigr )\).
Let \(\mathcal {L}^{AHC}\) a language of assertions, hypotheses, and conjectures built from a set of propositional atoms \(p_0\), \(p_1\), \(\ldots \) and let \((\ )^{\bot }\) be an involution without fixed points on the atoms. A rough set interpretation \(\mathcal {M} = (U, O, R)\) of the language \(\mathcal {L}^{AHC}\) (with an involution \((\ )^{\bot }\) on the atoms) is a topological space \((U, O)\) together with an assignment \(R\) to the elementary expressions of disjoint pairs of the following forms:
| \((A_o^+, A_c^-)\); | |
| \((C_c^+, C_o^-)\); | |
\((\mathcal {C} p_i)^R\) = | \(\bigl (\mathcal {C}(X^+), \mathcal {I}(X^-)\bigr ),\) | where |
Lemma 3
Let \(\mathcal {M} = (U, O, R)\) be an interpretation of \(\mathcal {L}^{AHC}\), with an involution \((\ )^{\bot }\) on the atoms. Then \(\mathcal {M}\) is a model of AHCL if and only if the assignment \(R\) to elementary expressions of \(\mathcal {L}^{AHC}\) satisfies the following duality conditions:
| where |
|
| where |
|
and moreover for every \((A_o^+, A_c^-)\) and \((C_c^+, C_o^-)\) in \(R\) we have
Proof
Concerning conditions \(\sim \smallfrown A \equiv A\) and \(\smallfrown \sim C\equiv C\) of Lemma 2, notice that

if and only if \(A_c^- = -A_o^+\) and similarly

where the last equality holds if and only if \(C_c^+ = -C_o^-\). Moreover, the conditions \((b) - (c)\) in the definition of duality between \(\mathcal {L}^A\) and \(\mathcal {L}^H\) (Definition 3) are clearly satisfied by the standard Rough Set definition. As for condition (a), given the involution \((\ )^{\bot }\) on the atoms, we have

where the third equality holds by condition (5) and the fourth by the condition of duality in a model. Similarly,

as required.
Remark 3
In a model \(\mathcal {M} = (U, O, R)\) for AHCL intuitionistic negation and Nelson’s negation coincide:
Thus to exploit Rough-Set semantics in full, we may want to consider notions of duality where condition (5) does not hold.
3.2 Algebra of Regions
A main reason of interest in bi-intuitionistic logic are its topos-theoretic models studied by Lawvere [32] Reyes and Zolfaghari [52], recently reconsidered by Stell and Worboys [57] in their “algebra of regions.” It is clearly impossible here to compare Reyes and Zolfaghari’s modal logic to our polarized bi-intuitionistic systems, but we must say something about Stell and Worboys’ geometric examples.
The first one is Reyes and Zolfaghari’s motivating example [52]: it provides a model of bi-intuitionistic logic based on the subgraphs of arbitrary undirected graphs. It ought to be possible to define graphic models of AHL and PBL, but we shall not attempt this here. On the other hand, “two stages sets” in the second example are just a geometric representation of the basic notion of “rough equality”: in an approximation space each subset \(G\) of the universe is identified only by the pair \((\mathcal {I}(G), \mathcal {C}(G))\)—or with \((\mathcal {I}(G), -\mathcal {C}(G))\) in the disjoint representation—where the interior and closure operator result from two stages of process of classification.
Now it is evident that condition (5) on models of AHL restricts the interpretation to sets \(G\) that are fully characterized in \((U,E)\), i.e., such that \(\mathcal {I}(G)=\mathcal {C}(G)\). We illustrate more interesting semantics applications with an example. Consider the Kripke model \(K\) for S4 obtained from the reflexive and transitive closure of the graph in Fig. 1.
Writing \(\alpha _K\) for the set of possible worlds satisfying \(\alpha \), we have  , \(({\mathcal {C}\! p})_K = \{w_0, w_1\}\) and
, \(({\mathcal {C}\! p})_K = \{w_0, w_1\}\) and  . We are satisfied with the Rough Set interpretation of assertions in the disjoint representation as
. We are satisfied with the Rough Set interpretation of assertions in the disjoint representation as  : after all, the grounds for an assertion ought to be a “stable” state of knowledge; by duality the representation of hypotheses as
: after all, the grounds for an assertion ought to be a “stable” state of knowledge; by duality the representation of hypotheses as  = \((K\setminus \{w_2\}, \{w_2\})\) is appropriate. On the other hand, the state of knowledge justifying conjectures is “unstable”; thus there seems to be a meaningful “two-stage set” representation of conjectures of the form \(({\mathcal {C}\! p})^R\) = \((\{w_1\}, K\setminus \{w_0, w_1\})\), of type (open, open). We notice that such an interpretation is possible for the logic AHCL of assertions, conjectures, and hypotheses, as it does not interfere with the basic symmetry between assertions and hypotheses. It remains an open problem whether these very conjectural remarks can be developed into an interesting rough-set semantics of a logic of assertions, hypotheses, conjectures, and expectations.
= \((K\setminus \{w_2\}, \{w_2\})\) is appropriate. On the other hand, the state of knowledge justifying conjectures is “unstable”; thus there seems to be a meaningful “two-stage set” representation of conjectures of the form \(({\mathcal {C}\! p})^R\) = \((\{w_1\}, K\setminus \{w_0, w_1\})\), of type (open, open). We notice that such an interpretation is possible for the logic AHCL of assertions, conjectures, and hypotheses, as it does not interfere with the basic symmetry between assertions and hypotheses. It remains an open problem whether these very conjectural remarks can be developed into an interesting rough-set semantics of a logic of assertions, hypotheses, conjectures, and expectations.
4 PART III. Proof Theory
We shall start with the definition of a sequent-style single-assumption multiple-conclusions natural deduction system for the subtractive-disjunctive fragment \(\mathbf {NJ}^{\backslash \curlyvee }\) of co-intuitionistic logic. We have sequents of the form
where \(A\) indicates the only open assumption in a derivation with the multiset \(C_1\), \(\ldots \), \(C_m\) of open conclusions. The rules of inference are in Table 4.
Definition 7
We say that \(C_1, \ldots , C_m\) is derivable from \(A\) if there is a natural deduction derivation of the sequent \(A\vdash \Gamma \) where all formulas in the multiset \(\Gamma \) are among \(C_1, \ldots , C_m\).
Remark 4
(i) Looking at the deduction rules in Table 4, notice that \(\backslash \)-introductions, \(\curlyvee \)-eliminations and \(\backslash \)-eliminations discharge the open assumption(s) of the sequent-premise(s) to the right, but a \(\backslash \)-elimination discharges also a multiset of open conclusions. As a consequence, \(\backslash \)-eliminations are the only inferences that cannot be permuted freely with other inferences. From another point of view, here we have a limit to the “parallelization of the syntax,” a box in the sense of Girard. To remove such a box, a device is needed to discharge open conclusions preserving as much as possible the geometry of proofs. In this section we recover Prawitz trees as an appropriate representation of proofs in \(\mathbf {NJ}^{\backslash \curlyvee }\).
(ii) As in Prawitz’s natural deduction weakening is not explicitly represented in proof-trees and contraction appears only in the discharging of conclusions in a \(\backslash \)-E inference.
Definition 8
(i) (active and passive formula-occurrences) In assumptions and in rules of inference the indicated formula-occurrences in the succedent of a sequent are active and all occurrences in the multisets \(\Gamma \), \(\Gamma _i\), \(\Delta \) are passive. Also the discharged assumptions in a \(\backslash \)-I, \(\curlyvee \)-E and \(\backslash \)-E are active, all other assumptions are passive. An active formula in the sequent-conclusion of an inference is also called the conclusion of the inference.
(ii) (segments) If \(\Upsilon \) occurs in the premise and in the conclusion of an inference then an occurrence \(D_i\in \Upsilon \) in the premise is the immediate ancestor of the occurrence \(D_i\) in the conclusion. Then as in Prawitz [46] we define a segment as a sequence \(D_1\), \(\ldots \), \(D_m\) of occurrences of the same formula where \(D_1\) and \(D_m\) are active, and \(D_i\) is the immediate ancestor of \(D_{i+1}\), for \(i < m\).
(iii) Thus we may speak of a segment as the conclusion or the premise of some inference.
(iv) A maximal segment is the conclusion of an introduction rule which is premise of an elimination. A derivation is normal if it does not have maximal segments.
4.1 Structure of Normal Proofs
The structure of normal deductions in co-intuitionistic logic \(\mathbf {NJ}^{\backslash ,\!\curlyvee }\) mirrors that of normal deductions in intuitionistic logic \(\mathbf {NJ}^{\supset ,\cap }\).
Definition 9
(i) A Prawitz path in a normal deduction is a sequence \(C_1\), \(\ldots \), \(C_i\), \(\ldots \), \(C_n\) of segments such that
-
\(C_1\) is an assumption, either open or discharged by a \(\backslash \)-introduction;
-
for \(j\) with \(1\le j <i\), \(C_j = C\backslash D\) is a premise of a \(\curlyvee \)- or \(\backslash \)-elimination and \(C_{j+1} = C\) is an assumption discharged by the inference;
-
for \(j\) with \(i\le j < n\), \(C_j\) is a premise of a \(\curlyvee \)- or \(\backslash \)-introduction with conclusion \(C_{j+1}\);
-
\(C_n\) is a conclusion of the derivation, either open or discharged by a \(\backslash \)-E.
(ii) The collection of all Prawitz paths in a derivation is a graph, called the tree of Prawitz paths \(\tau \). If we collapse segments to their formulas, the resulting tree yields a graphical representation of proofs which we shall call Prawitz tree for \(\mathbf {NJ}^{\backslash \curlyvee }\). Such trees are similar to those in Prawitz-style Natural Deduction derivation for \(\mathbf {NJ}^{\supset \cap }\), but in \(\mathbf {NJ}^{\backslash \curlyvee }\) the logical flow goes from the root to the leaves, rather than from the leaves to the root as in \(\mathbf {NJ}^{\supset \cap }\).
(iii) The definition of the depth of a path \(\pi \) in a tree \(\tau \) is familiar: the depth of \(\pi \) is 0 if its first formula \(C_1\) is open; the depth of \(\pi \) is \(n+1\) if \(C_1\) is discharged by a \(\backslash \)-introduction with conclusion in a path of depth \(n\).
From this analysis we derive as usual the subformula property for normal deductions:
Proposition 3
Every formula occurring in a normal deduction of \(A\vdash C_1, \ldots , C_m\) is a subformula either of \(A\) or of \(C_i\) for some \(i\).
Example
We constuct a derivation \(d\) in \(\mathbf {NJ}^{\backslash \curlyvee }\) of
It may be helpful to think of the dual derivation in \(\mathbf {NJ}^{\supset \cap }\) of
We write \(\mathbf {F}\) for \((B \backslash A)\curlyvee (D\backslash A)\) and \(\mathbf {G}\) for \(C\backslash (B\curlyvee D)\).
|
|
In Fig. 2 we find the tree-structure of “Prawitz’ paths” of the derivation \(d\).
4.2 Sequents with Tail Formula
A very perspicuous representation of derivations in co-intuitionistic logic is through sequent calculus with tail formula q-\(\mathbf {LJ}^{\backslash \curlyvee }\), the exact dual of the well-known sequent calculus with head formula t-\(\mathbf {LJ}^{\supset \cap }\).Footnote 17 Here sequents have the form
with one formula in the antecedent, a multiset in the ordinary area, and at most one formula in the linear area (stoup) of the succedent. The principal formulas of the right-rules are in the stoup and left-rules require empty stoup in the sequent-premies.Footnote 18 The rules of q-\(\mathbf {LJ}^{\backslash \curlyvee }\) are given in Table 5.
The following fact is the dual of a well-known correspondence between Natural Deduction derivations in \(\mathbf {NJ}^{\supset \cap }\) and Sequent Calculus derivations in t-\(\mathbf {LJ}^{\supset \cap }\). For sequent calculi with head formulas or tail formulas see, for instance, [20].
Proposition 4
There is a bijection between trees of Prawitz paths of normal derivations in \(\mathbf {NJ}^{\backslash \curlyvee }\) and cut-free derivations in q-\(\mathbf {LJ}^{\backslash \curlyvee }\) (modulo the order of structural inferences).
Proof
Given a Prawitz tree \(\tau \), by induction on \(\tau \) we construct a q-\(\mathbf {LJ}^{\backslash \curlyvee }\) derivation with the property that the formula in the stoup (tail formula), if any, is the conclusion of a path of depth 0 (main path) of \(\tau \). If \(\tau \) begins with an elimination rule, the result is immediate by the inductive hypothesis applied to the immediate subtree(s) from the top, since we may assume that the corresponding cut-free derivations have conclusions with empty stoup. If \(\tau \) begins with an introduction rule, then there is only one main path and we remove the last inference of it: if the conclusion was a formula \(C\backslash D\), the inductive hypothesis yields two q-\(\mathbf {LJ}^{\backslash \curlyvee }\) derivations; in one the endsequent must have \(C\) in the stoup, since \(C\) belongs to the main path; in the other the endsequent has \(D\) in the antecedent and we may assume that it has no formula in the stoup, by applying dereliction if necessary. Therefore we may apply \(\backslash \)-R to obtain the desired derivation. The other cases are obvious.
The fact that two derivations \(d'\) and \(d''\) corresponding to the same tree \(\tau \) can only differ for the order of structural inferences is due to the fact that in q-\(\mathbf {LJ}^{\backslash \curlyvee }\) logical inferences cannot be permuted with each other. Indeed, the principal formulas of all inferences occur either in the antecedent or in the stoup, and the rule of dereliction is irreversible.
Example
(cont.) The following sequent derivation \(d_q\) corresponds to the natural deduction derivation \(d\):

5 PART IV.Term Assignment for Co-intuitionistic Logic
In a tantalising pair of papers [42, 44] Michel Parigot introduced Free Deduction, a formalism consisting of elimination rules only, with the property that both Natural Deduction and the Sequent Calculus could be represented in it simply by restricting the order of deduction, e.g., by permutations of inferences. Free Deduction was conceived to study the computational properties of classical logic, but it can be adapted to intuitionistic and co-intuitionistic logic through the analog of Gentzen’s restrictions on sequents.
For instance, although they do not appear in this form in [42], the rules for multiplicative implication and subtraction can be formulated as follows:
multiplicative implication |
|
|
multiplicative subtraction |
|
|
The intuitionistic restriction ¶\((\Sigma ^{})\), namely that \(\Sigma \) is empty, applies to the secondary premise of the \(\rightarrow \)-left elimination rule, and the dual restriction holds for \(\backslash \)-right elimination. The sequent calculus rules are obtained by killing the main premise (i.e., keeping it only as an axiom). Here are the rules for subtraction:
subtraction rules, as in the sequent calculus |
|
|
Natural Deduction, on the other hand, is given by keeping all inputs on the left. Namely: for left elimination rules, we kill the main premise; for right elimination rules, we kill the secondary premises which have only a left active formula. Thus no premise is killed in subtraction elimination right.
subtraction rules, as in natural deduction |
|
|
Since Free Deduction yields a multiple conclusion natural deduction system in a very straightforward way, one would expect that a term assignment to Free Deduction might be distributed to all formula in the succedent of sequents. On the contrary in 1992 Michel Parigot introduced the \(\lambda \)-\(\mu \) calculus as “an algorithmic interpretation of classical Natural Deduction,” which is based on a notion of “central control.” In the last part of this chapter we propose a distributed term assignment to co-intuitionistic logic.
5.1 Term Assignment to the Subtraction Rules in the \(\varvec{\lambda }\)-\(\mu \) Calculus
Recently the proof theory of bi-intuitionistic (subtractive) logic has been studied by Crolard [15, 16]: in [16] a Natural Deduction system is presented with a calculus of coroutines as term assignment.Footnote 19 Crolard works in the framework of Parigot’s \(\lambda \mu \)-calculus: sequents may be written in the formFootnote 20 \(\Gamma \vdash t: A\ |\ \Delta \), with contexts \(\Gamma \) = \(x_1:C_1, \ldots , x_m:C_m\) and \(\Delta \) = \(\alpha _1:D_1, \ldots , \alpha _n:D_n\), where the \(x_i\) are variables and the \(\alpha _j\) are \(\mu \)-variables. In addition to the rules of the simply typed lambda calculus, there are naming rules
It is well-known that the \(\lambda \mu \)-calculus provides a computational interpretation of classical logic and a typing system for functional programs with continuations (see, e.g., [17, 54]).
Crolard extends the \(\lambda \mu \) calculus with introduction and elimination rules for subtractionFootnote 21:
|
|
The reduction of a redex of the form  yields \(\mu \gamma .[\beta ]u[t/x]\), where the \(\mu \)-variables are typed as \(\beta :B\) and \(\gamma : C\). Namely
yields \(\mu \gamma .[\beta ]u[t/x]\), where the \(\mu \)-variables are typed as \(\beta :B\) and \(\gamma : C\). Namely

reduces to

Working with the full power of classical logic, if a constructive system of bi-intuitionistic logic is required, then the implication right and subtraction left rules must be restricted by considering relevant dependencies.Footnote 22 Crolard is able to show that the term assignment for such a restricted logic is a calculus of safe coroutines, namely terms in which no coroutine can access the local environment of another coroutine.
5.2 A Distributed Term Assignment for the Subtractive Fragment
When we consider a term assignment for the Natural Deduction system \(\mathbf {NJ}^{\backslash \curlyvee }\) of dual intuitionistic logic only, we are led to ask what Crolard’s calculus becomes when separated from its \(\lambda \mu \) context. Indeed the naming rules of the \(\lambda \mu \) calculus allow us to represent the action of an operating system jumping from one thread of computation to another: when a name \(\beta \) for a coroutine has been created by make-coroutine, it can be later accessed by the system and the coroutine executed.
On the contrary in our proposal different terms are simultaneously assigned to the multiple conclusions of a sequent in a sequent-style Natural Deduction, (or in the Sequent Calculus with tail formula). There is no mechanism to simulate the passage of control from one “thread” to another. A process is stopped by the operator assigned to subtraction elimination (called here postpone rather than Crolard’s resume) and becomes active only in the normalization process. Thus in the presence of different processes running in parallel, one wonders whether our system can still be regarded as a calculus of coroutines: it is perhaps closer to an abstract representation of a multiprocessing system.
Before giving formal definitions, let us survey the most distinctive features of our calculus for the terms assignment to the subtractive fragment only. Most characteristic is the treatment of variables: there is no operator for explicitly binding variables or delimiting the scope of an implicitly binding operation. We may say that a computational context is characterized by exactly one free variable and that a free variable \(a\) becomes bound when its computational context \(\mathcal {S}_a\) is plunged into the computational context \(\mathcal {S}_b\) associated with another variable \(b\). In this case, the variable \(a\) is replaced everywhere by \(\mathtt {a}(t)\) for some term \(t\) containing \(b\); here the function \(\mathtt {a}\) is vaguely reminiscent of a Herbrand function. In the normalization process the term \(\mathtt {a}(t)\) may later be replaced by another term \(u\) throughout the new computational context; thus we assume that a mechanism is in place for broadcasting substitutions throughout an environment.
We have the following operators:
-
the term \(\mathtt {mkc}(t, \mathtt {y})\), which is assigned to the conclusion of a \(\backslash \)-introduction, connects two disjoint computational contexts, say, \(\mathcal {S}_x\) and \(\mathcal {S}_y\). Every term in \(\mathcal {S}_x\) contains exactly one free variable \(x\), and we assume that the term \(t\) represents a thread starting from \(x\).Footnote 23 The computational context \(\mathcal {S}_y\) contains the free variable \(y\) and all threads starting from \(y\). When the term \(\mathtt {mkc}(t, \mathtt {y})\) is introduced, the substitution \(y := \mathtt {y}(t)\) must be performed throughout the environment \(\mathcal {S}_y\). Thus the term \(\mathtt {mkc}(t, \mathtt {y})\) represents a jump extending the thread \(t\) to all threads in \(\mathcal {S}_y\{y := \mathtt {y}(t)\}\); the substitution of \(\mathtt {y}(t)\) for \(y\) throughout \(\mathcal {S}_y\) has the effect that the extended computational context contains only the free variable \(x\). Here we retain Crolard’s name make-coroutine for historic reasons; a more precise but more redundant description would be the following:
$$ \mathtt {mkc}(t, {\mathtt {y}})\qquad \hbox {stands for}\qquad \mathtt {extend\ thread}\ t\ \mathtt{from }\ \mathtt {y}(t). $$ -
The term \(\mathtt {postp}(\mathtt {z}\mapsto \ell , t)\), which is assigned to the conclusion of a \(\backslash \)-elimination, takes a computational context \(\mathcal {S}_z\) containing the only free variable \(z\), and plunges it into another context \(\mathcal {S}_x\) where the only free variable is \(x\); this is done by selecting the list \(\ell \) of threads starting from \(z\) and the term \(t\) with free variable \(x\), replacing \(z\) with \(\mathtt {z}(t)\) throughout \(\mathcal {S}_z\) and freezing \( \ell \{z:= \mathtt {z}(t)\}\) until through normalization the term \(t\) is transformed to a term of the form \(\mathtt {extend\ thread}\). A fuller description is therefore the following:
$$ \mathtt {postp}(\mathtt {z}\mapsto \ell , w)\ \hbox {stands for}\ \mathtt {postpone\ subthreads}\ \ell \{z:= \mathtt {z}(w)\}\ \mathtt{u ntil}\ w. $$
Let \(\mathbf {M}\) be \(\mathtt {mkc}(t, \mathtt {y})\) and let \(\mathbf {P}(v)\) be \(\mathtt {postp}(\mathtt {z}\mapsto \ell , v)\). Then
is a redex. The main idea of a reduction is to replace the jump from \(t\) to \(\mathtt {y}(t)\) with each one of the subthreads in \(\ell \). But such an operation has important side effects. A redex \(\mathbf {P(M)}\) occurs in a computational context \(\mathcal {S}_x\) of the form
where \(\overline{\zeta }_{\mathtt {y}}\) is a sequence of terms containing \(\mathtt {y}(t)\), \(\overline{\xi }_{\mathtt {z}}\) a sequence of terms containing \(\mathtt {z}(\mathtt {mkc}(t,\mathtt {y}))\) and \(\overline{\kappa }\) a sequence containing neither \(\mathtt {y}(t)\) nor \(\mathtt {z}(\mathtt {mkc}(t,\mathtt {y}))\). Thus the side effects consist in the replacement of \(\mathtt {z}(\mathtt {mkc}(t,\mathtt {y}))\) with \(t\) in \(\overline{\xi }_{\mathtt {z}}\) and in each subthread \(s_k\) of \(\ell \); let \(\ell ' = s'_1, \ldots , s'_n\) be the resulting sequence. Finally, we replace \(\mathtt {y}(t)\) in \(\overline{\zeta }_{\mathtt {y}}\) with each one of the subthreads \(s'_k\), thus expanding the sequence \(\overline{\zeta }_{\mathtt {y}}\) in a sense to be made precise below. To indicate such a rewriting process we shall use the notation
where \(z = \mathtt {z}(\mathtt {mkc}(t,\mathtt {y}))\) and \(y = \mathtt {y}(t)\).
In an enterprise where notation is in danger of growing out of control, readability is essential. The notations \(\mathtt {mkc}(t, \mathtt {y})\) and \(\mathtt {postp}(\mathtt {z}\mapsto \ell , w)\) are already effective abbreviations, as from them we can recover the terms \(\mathtt {y}(t)\) and \(\mathtt {z}(w)\) present in the context. Further simplification is given by Corrado Biasi’s elegant notations:

If we consider the typed version of the above rewriting we have the following reduction. Let us writeFootnote 24
\(\mathcal {S}_{x}\ : \Delta \) | for | \( \pi _0 : \bullet \ |\ \overline{\kappa } : \Delta \) |
\(\mathcal {S}_{y}\ : \Upsilon \) | for | \( \pi _1 : \bullet \ |\ \overline{\zeta } : \Upsilon \) |
\(\mathcal {S}_{z}\ : \Xi \) | for | \( \pi _2 : \bullet \ |\ \overline{\xi } : \Xi \) |
and also | ||
\(\mathcal {S}_{x}\ : \Delta , \mathcal {S}_{y}\ : \Upsilon , \mathcal {S}_{z}\ : \Xi \) | for | \( \pi _0, \pi _1, \pi _2 : \bullet \ |\ \overline{\kappa } : \Delta , \overline{\zeta } : \Upsilon , \overline{\xi } : \Xi \). |
Next | ||
let \(\mathcal {S}_{\mathtt {y}}\ : \Upsilon \) | be | \(\mathcal {S}_{y}\{y := \mathtt {y}(t) \} : \Upsilon \), |
let \(\mathcal {S}_{\mathtt {z}}\ : \Xi \) | be | \(\mathcal {S}_{z}\{z := \mathtt {z}((\mathtt {mkc}(t, \mathtt {y})) \}:\Xi \). |
Then we have:

6 A Distributed Term Assignment for Co-intuitionistic Logic \(\mathbf {NJ}^{\backslash \curlyvee }\)
We present the grammar and the basic definitions of our distributed calculus for the fragment of co-intuitionistic logic with subtraction and disjunction.
Definition 10
We are given a countable set of free variables (denoted by \(x\), \(y\), \(z\) \(\ldots \)), and a countable set of unary functions (denoted by \(\mathtt {x}, \mathtt {y}, \mathtt {z}, \ldots \)).
(i) Terms and lists of terms are defined by the following grammar:
\(t\ :=\) | \( x\ |\ \mathtt {x}(t) \ |\ \mathtt {inl}(t)\ |\ \mathtt {inr}(t)\ |\ \mathtt {casel}(t)\ |\ \mathtt {caser}(t)\ |\ \hbox \mathtt{mkc}(t, \mathtt {x})\) |
\(\ell \ :=\) | \(()\ |\ t\cdot \ell \) |
(ii) Let \(t_1\), \(t_2\), \(\ldots \) an enumeration in a given order of all the terms freely generated by the above grammar starting with a special symbol \(*\) and no variables (a selected variable \(a\) would also do the job). Thus we have a fixed bijection \(t_i \mapsto x_i\) between terms and free variables.
(iii) Moreover, if \(t\) is a term and \(\ell \) is a list such that for each term \(u\in \ell \), \(y\) occurs in \(u\), then \(\mathtt {postp}(\mathtt {y}\mapsto \ell \{y:= \mathtt {y}(t)\}, t)\) is a p-term.
We use the abbreviations \((t\rightarrow \mathtt {y})\) for \(\mathtt {mkc}(t, \mathtt {y})\) and  for \(\mathtt {postp}(\mathtt {z}\mapsto \ell , w).\)
for \(\mathtt {postp}(\mathtt {z}\mapsto \ell , w).\)
Thus a p-term cannot be a subterm of other terms. In the official definition above lists appear only as arguments of postp,Footnote 25 It is notationally convenient to extend the above definition so that our operators apply to lists in addition to terms:
Definition 11
Let \(\mathtt {op}(\ )\) be one of \(\mathtt {x}(\ )\), \(\mathtt {inl}(\ )\), \(\mathtt {inr}(\ )\), \(\mathtt {casel}(\ )\), \(\mathtt {caser}(\ )\),  , \(\mathtt {postp}(\mathtt {x}\mapsto \ell , (\ ))\).
, \(\mathtt {postp}(\mathtt {x}\mapsto \ell , (\ ))\).
Then the term expansion \(\mathtt {op}(\ell )\) is the list of terms defined inductively thus:

Remark 5
By term expansion, a term consisting of an operator applied to a list of terms is turned into a list of terms; thus terms may always be transformed into an expanded form where operators are applied only to terms, except for expressions \(\ell \) occurring in terms of the form \(\mathtt {postp}(\mathtt {y}\mapsto \ell , u)\).
Definition 12
(i) The free variables \(FV(\ell )\) in a list of terms \(\ell \) are defined as follows:

(ii) A computational context \(\mathcal {S}_x\) is a set of terms and p-terms containing the free variable \(x\) and no other free variable.
Definition 13
Substitution of a term \(t\) for a free variable \(x\) in a term \(u\) is defined as follows:
We define substitution of a list of terms \(\ell \) for a variable \(x\) in a list of terms \(\kappa \):
If \(\overline{\zeta }\) is a vector of lists \(\ell _1, \ldots , \ell _m\), then \(\overline{\zeta }\{x:=\ell \} = \ell _1\{x:=\ell \}, \ldots , \ell _m\{x:= \ell \}\).
Definition 14
\(\beta \)-reduction of a redex \(\mathcal {R}ed\) in a computational context \(\mathcal {S}_x\) is defined as follows.
(i) If \(\mathcal {R}ed\) is a term \(u\) of the following form, then the reduction is local and consists of the rewriting \(u\rightsquigarrow _{\beta }u'\) in \(\mathcal {S}_x\) as follows:
(ii) If \(\mathcal {R}ed\) has the form  , i.e., \(\mathtt {postp}(\mathtt {z}\mapsto \ell , \mathtt {mkc}(t, \mathtt {y})),\) then \(\mathcal {S}_x\) has the form
, i.e., \(\mathtt {postp}(\mathtt {z}\mapsto \ell , \mathtt {mkc}(t, \mathtt {y})),\) then \(\mathcal {S}_x\) has the form
where \(\mathtt {y}(t)\) occurs in \(\overline{\zeta }_{\mathtt {y}}\) and \(\mathtt {z}((t\rightarrow \mathtt {y}))\) occurs in \(\overline{\xi }_{\mathtt {z}}\) and neither \(\mathtt {y}(t)\) nor \(\mathtt {z}((t\rightarrow \mathtt {y}))\) occurs in \(\overline{\kappa }\). Writing \(y = \mathtt {y}(t)\) and \(z = \mathtt {z}((t\rightarrow \mathtt {y}))\), a reduction of \(\mathcal {R}ed\) transforms the computational context as follows:
Thus for \(\overline{\zeta } = u_1, \ldots , u_k\), for \(\overline{\xi } = r_1, \ldots , r_m\) and for \(\ell = s_1,\ldots , s_n\) we have:
Given the correspondence between Prawitz style Natural Deduction derivations in \(\mathbf {NJ}^{\supset \cap }\) and sequent derivations in t-\(\mathbf {LJ}^{\supset \cap }\), and the dual correspondence between Prawitz trees for \(\mathbf {co-NJ}^{\backslash \curlyvee }\) and sequent derivations in q-\(\mathbf {LJ}^{\backslash \curlyvee }\), we find it convenient to define the term assignment directly to sequent calculus in q-\(\mathbf {LJ}^{\backslash \curlyvee }\), given in Appendix III, Table 7.
Definition 15
( term assignment ) The assignment of terms of the distributed calculus to sequent calculus derivation in q-\(\mathbf {LJ}^{\backslash \curlyvee }\) is given in Appendix III, Table 7. In Table 8 we give the familiar assignment of \(\lambda \)-terms to sequent calculus with head formulas t-\(\mathbf {LJ}^{\supset \cap }\).
Remark on free variables and \(\varvec{\alpha }\) conversion. Since in our calculus the binding of a free variable \(x\) is expressed through its substitution with a term \(\mathtt {x}(t)\), the so-called “capture of free variables” takes a different form. Suppose a free variable \(y\) has been replaced by \(\mathtt {y}(t)\) in the construction of a term \(M = \mathtt {mkc}(t, \mathtt {y})\) or \(P(t) = \mathtt {postp}(\mathtt {y}, \ell \{y:= \mathtt {y}(t)\}, t)\): all other occurrences of \(y\) in the previous context have been replaced with \(\mathtt {y}(t)\) in the current context, represented, say, by a vector \(\overline{\ell }\), and we may say that \(M\) or \(P(t)\) is a binder of \(\mathtt {y}(t)\) in \(\overline{\ell }\).
In the process of normalization such a “bound” term \(\mathtt {y}(t)\) may be replaced by another term \(u\). It would be natural to think of such a replacement as a two-step process, first recovering the free variable \(y\) and then applying a substitution \(\{y:= u\}\) to the current computational context. However, it may also happen that in the process of normalization different occurrences of the term \(\mathtt {y}(t)\) evolve to \(\mathtt {y}(t')\) and to \(\mathtt {y}(t'')\) so that distinct variables \(y'\) and \(y''\) are needed for distinct substitutions. For this reason we have established a bijection between freely generated terms and free variables.
This may not solve all problems: indeed in the untyped formulation of our calculus it might happen that the same free variable \(y\) has been replaced with \(\mathtt {y}(t)\) in the construction of two distinct terms of \(\overline{\ell }\): our syntax may not have tools to disambiguate the “scope” of the bindings and some further restrictions may be needed to block such pathologies. However, if the calculus is used for assigning term to derivations in \(\mathbf {NJ}^{\backslash \curlyvee }\), then to avoid “capture of free variables” it is enough to set the following condition.
Convention. We assume that
-
Derivations have the pure parameter property, i.e., that in a derivation free variables assigned to distinct open assumptions are distinct;
Since to distinct free variables \(x\), \(y\) there correspond distinct unary functions \(\mathtt {x}\), \(\mathtt {y}\), then it is clear that in the term assignment to derivations with the pure parameter property the above indicated ambiguity cannot occur. Moreover, a derivation resulting by normalization from a derivation with the pure parameter property can be transformed again into a derivation with the pure parameter property. Indeed, the set of terms assigned to a \(\mathbf {NJ}^{\backslash \curlyvee }\) derivation encode a tree-structure, and it is easy to see that if different occurrences of the term \(\mathtt {y}(t)\) evolve to \(\mathtt {y}(t')\) and to \(\mathtt {y}(t'')\) in a tree, then the terms \(t'\) and \(t''\) are distinct as they encode distinct threads. Thus once again applying the bijection between terms and free variables can be used to produce a derivation with the pure parameter property.
Example
(i) Assigning terms to the derivation \(d_q\) in Sect. 4.2 we obtain the following assignment to the endsequent:

where we have
(ii) Applying cut-elimination to the derivation
|
|
we obtain the following rewritings: \(t_1 = \mathtt {casel}(\mathtt {inl}(a)) \rightsquigarrow a\);
and the term assignment
6.1 Duality Between the Distributed Calculus and the Simply Typed \(\lambda \) Calculus
Consider the term assignment in Appendix III, Tables 7 and 8. In this setting the following facts are clear:
-
given a sequent \(S\) in q-\(\mathbf {LJ}^{\backslash \curlyvee }\), there is a dual sequent \(S^{\bot }\) in h-\(\mathbf {LJ}^{\supset \cap }\), and conversely;
-
given a derivation \(d\) of \(S\) in q-\(\mathbf {LJ}^{\backslash \curlyvee }\), there is a dual derivation \(d^{\bot }\) of \(S^{\bot }\) in h-\(\mathbf {LJ}^{\supset \cap }\), and conversely.
Therefore any cut-elimination procedure in h-\(\mathbf {LJ}^{\supset \cap }\) induces a cut-elimination procedure for q-\(\mathbf {LJ}^{\backslash \curlyvee }\); clearly the steps of such reduction procedure for q-\(\mathbf {LJ}^{\backslash \curlyvee }\) must be seen as “macro” instructions for several steps of rewriting, which may nevertheless be seen as a unit. Thus we have the following fact:
Theorem 2
There is a correspondence between reduction sequences starting from a derivation \(d\) of \(S\) in q-\(\mathbf {LJ}^{\backslash \curlyvee }\) and reduction sequences from a derivation \(d^{\bot }\) of \(S^{\bot }\), and conversely.
In the present setting this result seems obvious and its proof straightforward. Going through the details of the construction, as done in [8], does give an insight into the structure of terminating computations in our distributed calculus. Assigning terms to derivations in q-\(\mathbf {LJ}^{\backslash \curlyvee }\) as in in Appendix III, Table 7 makes the structure of the calculus clearer and provides a bridge to the representation of computations in the graphical notation of Prawitz trees as in Appendix II.
7 Conclusions
In this chapter we have given an account of research in the logic for pragmatics of assertions and conjectures, following the paper Bellin and Biasi [5] and also of work in the proof-theory of co-intuitionistic logic aiming at defining natural deduction system and a distributed term-assignment for it.
A conceptual clarification of the distinction between hypotheses and conjectures with respect to their interpretation in epistemic S4, where hypotheses are justified by mere epistemic possibility of the truth of their propositional content and conjectures require possible necessity, has shown connections with other areas of logic and semantics. On one hand, within our framework we can make distinctions which may be relevant to work on standards of evidence in the theory of argumentation [13, 24]. On the other hand, the semantics of rough sets and the notion of an approximation space provide another semantics to a theory of assertions, hypotheses, conjectures, and expectations, in addition to Kripke models through the translation in epistemic S4 and in bimodal S4, as in [5]. Rough sets point at promising connections with research by Pagliani [40, 41].
Abstract relations between functional programming and concurrent programming have been studied extensively, e.g., through translations of the \(\lambda \) calculus into R. Milner’s \(\pi \)-calculus. Abstract forms of the continuation-passing style, e.g., as in Thielecke’s work, have been typed in classical logic, suggesting an interpretation of these relations as a logical duality between classical and intuitionistic logic. In this way, the \(\lambda \mu \) calculus is naturally invoked here. In [8] and this chapter we propose the duality between intuitionistic and co-intuitionistic logic as the most basic type theoretic setting for studying the relations between distributed and functional programming calculi. Our calculus distributed displays exactly the programming features that are required in order to implement such a logical duality. In this way this chapter and other still unpublished work by Corrado Biasi give a type-theoretic framework for studying the relations between safe and unsafe coroutines in the sense of Crolard: typically, safe coroutines are those which can be represented as constructs of a distributed calculus without making essential use of the \(\lambda \mu \) calculus and can be typed in co-intuitionistic logic. Thus the term assignment to proofs in co-intuitionistic logic can be seen as a contribution to a challenging problem, namely providing a logical foundation to distributed calculi by means of a typing system, in the Curry-Howard approach. Clearly solving such a problem has a clear interest in computer science, if only to ensure properties of such systems such as termination and confluence.
All the paths followed in this research are open and point at possible directions of work, as already suggested. Other projects could explore the proof-net representation of co-intuitionistic logic and the construction of a term model for co-Cartesian Closed Categories. The proof theory of classical logic is the framework of Crolard’s investigations [15, 16] and the concern of Bellin, Hyland, Robinson, and Urban [9]: it is expected that eventually research in bi-intuitionistic logic may improve our understanding of classical logic. But this is now a good point to take a rest.
Notes
- 1.
We wish to thank Prof Andrew Pitts and Dr Valeria de Paiva for their comments on various aspects of this research and Dr Piero Pagliani for his expert support in the Rough Sets semantics. We are indebted with Prof Tristan Crolard for his intriguing work on bi-intuitionistic and classical logic and with Dr Hugo Herbelin for suggestions about our calculus of coroutines for co-intuitionistic logic. Thanks to Dr Carlo Dalla Pozza, Dr Kurt Ranalter, Dr Corrado Biasi, and Dr Graham White for their cooperation in the “logic for pragmatics” enterprise. I am grateful to Prof Dag Prawitz, my first marvellous supervisor in Stockholm 1978 and to Dr Luiz Carlos Pereira, a fellow student then and a supportive colleague now.
- 2.
Since April 2011 when significant revisions were made to this chapter, categorical models of bi-intuitionism have been studied based on monoidal categories. In particular, if the term assignment to a Gentzen system for co-intuitionistic logic is used in building a categorical model, then disjunction is best given multiplicative rules rather than additive ones, as it is done in this chapter. Further work on the mathematical structure and the philosophical interpretation of “polarized bi-intuitionism” is in G. Bellin, M. Carrara, D. Chiffi, and A. Menti, A pragmatic dialogic interpretation of bi-intuitionism, submitted to Logic and Logical Philosophy, 2013.
- 3.
We wish to thank Prof Andrew Pitts and Dr Valeria de Paiva for their advice on various aspects of this research and Dr Piero Pagliani for his expert support in the Rough Sets semantics. We are much indebted to Tristan Crolard for his intriguing work on bi-intuitionistic and classical logic and to Hugo Herbelin for important suggestions about the distributed calculus for co-intuitionistic logic. Thanks to Carlo Dalla Pozza, Kurt Ranalter, Corrado Biasi, and Graham White for their cooperation in the “logic for pragmatics” enterprise and thanks to Ugo Solitro for useful discussions. I am grateful to Dag Prawitz, my first marvellous supervisor in Stockholm 1978 and to Luiz Carlos Pereira, a fellow student and a supportive colleague.
- 4.
Since April 2011 when revisions were made to this chapter, categorical models of bi-intuitionism have been studied based on monoidal categories. In particular, if the term assignment to a Gentzen system for co-intuitionistic logic is used in building a categorical model, then disjunction is best given multiplicative rules rather than additive ones, as it is done in this chapter. For the conceptual significance of such a choice, see G. Bellin, M. Carrara, D. Chiffi and A. Menti. A pragmatic dialogic interpretation of bi-intuitionism, submitted to Logic and Logical Philosophy, 2013.
- 5.
The interpretation of intuitionistic logic as a logic of assertions appears already in Dummett’s work. Martin-Löf regards his intuitionistic theory of types as expressing judgements about the truth of propositions; in his system well-formed complex types are propositions and the terms inhabiting them are witnesses of their truth, intuitionistically understood. This view is disputed by Dalla Pozza: for him only atomic types assert the truth of propositions, but complex types neither are propositions nor assert propositions. To recover a proposition corresponding to the complex type

we need a semantic projection, i.e., \(\Box (\Box \alpha \rightarrow \Box (\Box \beta \rightarrow \Box \alpha ))\); but justification of the assertion type
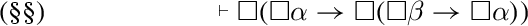
is a semantic argument for a sentence of classical S4 while (§) is justified by something like a program \(\lambda x.\lambda y.x\), where
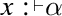 and
and 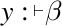 are variable ranging over proofs of the truth of \(\alpha \) and of \(\beta \).
are variable ranging over proofs of the truth of \(\alpha \) and of \(\beta \). - 6.
The conceptual development traced results from cooperation with other researchers, in particular with Corrado Biasi, whose doctoral dissertation at Queen Mary University of London is still unfinished.
- 7.
In the formal treatment of Carneades model of argumentation, proof-standards occur in the definition of what it means for an argument with conclusion \(c\) from premises \(P\) and exceptions \(E\) to be applicable in a Carneades argument evaluation structure \(\mathcal {S}\) = \(\langle \text { arguments, assumptions, weights, standard}\rangle \). The definition relies on a non-logical real-valued function weights ranging over arguments. The notion of applicability is recursive, as it depends on the notion of a proposition \(p\) being acceptable in an argument evaluation structure \(\mathcal {S}\). Here a proposition \(p\) is acceptable with a scintilla of evidence if there is at least one applicable argument for \(p\) and \(p\) is acceptable as dialectically valid if there is an applicable argument for \(p\) and no applicable argument against \(p\). All other proof standards require comparing the weights of arguments for and against \(p\). See [13, 24].
- 8.
We are grateful to an anonymous referee to [5] for making the point clear and for indicating the reference. The same referee, acknowledging that our “refutation calculus” is dual to intuitionistic logic, questioned whether a calculus based on a theory of positive evidence could be co-intuitionistic: we come back to this issue below.
- 9.
As in [5], to these pragmatic negations one should add classical negation in the radical part \(\lnot \alpha \); but no logical property of the radical part can be used in the treatment of intuitionistic pragmatics. To avoid confusions with the “polarized classical logic” in [5], Sect. 5, in the treatment of dualities we shall assume that the atoms occurring in the radical part are either positive \(p_i^+\) or negative \(p_i^-\), i.e., that there is an involution without fixed point on atoms exchanging \(p^+_i\) and \(p^-_i\).
- 10.
Condition \(S\subseteq R\) guarantees that if \(w \Vdash \Box p\) then
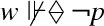 . To see that \(w\Vdash \Box p\) is not a valid consequence of
. To see that \(w\Vdash \Box p\) is not a valid consequence of 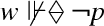 , consider a model \(\mathcal {M}= (W, R, S, \Vdash )\) with \(W = \{w, w'\}\), \(R\) and \(S\) reflexive and transitive and such that \(w R w'\) but not \(w S w'\), and \(w\Vdash p\) but \(w'\Vdash \lnot p\). Notice that
, consider a model \(\mathcal {M}= (W, R, S, \Vdash )\) with \(W = \{w, w'\}\), \(R\) and \(S\) reflexive and transitive and such that \(w R w'\) but not \(w S w'\), and \(w\Vdash p\) but \(w'\Vdash \lnot p\). Notice that 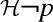 is not an expression of the language \(\mathcal {L}^{AH}\), but the same remark applies to
is not an expression of the language \(\mathcal {L}^{AH}\), but the same remark applies to 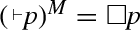 and
and 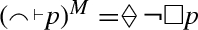 .
. - 11.
This calculus is essentially the system Intuitionistic Logic for Pragmatics ILP presented and studied in [5], Sect. 3, restricted to the language \(\mathcal {L}^{AH}\) - namely a sequent calculus with axioms and rules for assertive validity, implication and conjunction, hypothetical absurdity, subtraction and disjunction and two mixed negations.
- 12.
The negation “\(\lnot \)” corresponds to the orthogonality \((\ )^{\bot }\), as in Remark 2.
- 13.
Notational decisions are nightmarish if we try to match the uses in the literature of Rough Sets, in Rauszer’s bi-intuitionistic logic and our own. In our polarized bi-intuitionistic logic [5] we used \(\sim A\) for intuitionistic negation and \(\smallfrown C\) for co-intuitionistic supplement, leaving \(\lnot \alpha \) for classical negation, as required in Dalla Pozza and Garola’s framework and following the meaning originally given to the symbol “\(\lnot \)” by Frege. C.Rauszer uses
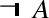 for intuitionistic negation and
for intuitionistic negation and 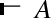 for co-intuitionistic supplement; but in the later literature on bi-intuitionistic logic \(\sim \! A\) is used for co-intuitionistic supplement. In the literature on Rough Sets, weak-negation is sometimes written \(\lnot C\); intuitionistic negation is written in various ways (Pagliani uses \(\div A\), in Polkowski’s book there is \(\dag A\)), while the symbol \(\sim A\) is used exactly in the sense of orthogonality
\(A^{\bot }\). However, it is unnecessary to make notations uniform across three areas, where similar connectives have different meanings: e.g., in Rough Sets negations are defined in a more general algebraic setting than Heyting algebras. Hence it seems reasonable for us to retain the notation of [5] for our polarized logic, while using “
for co-intuitionistic supplement; but in the later literature on bi-intuitionistic logic \(\sim \! A\) is used for co-intuitionistic supplement. In the literature on Rough Sets, weak-negation is sometimes written \(\lnot C\); intuitionistic negation is written in various ways (Pagliani uses \(\div A\), in Polkowski’s book there is \(\dag A\)), while the symbol \(\sim A\) is used exactly in the sense of orthogonality
\(A^{\bot }\). However, it is unnecessary to make notations uniform across three areas, where similar connectives have different meanings: e.g., in Rough Sets negations are defined in a more general algebraic setting than Heyting algebras. Hence it seems reasonable for us to retain the notation of [5] for our polarized logic, while using “ ,” “
,” “  ,” and “\((\ )^{\bot }\)” for intuitionistic negation, co-intuitionistic supplement and orthogonality in Rough Sets.
,” and “\((\ )^{\bot }\)” for intuitionistic negation, co-intuitionistic supplement and orthogonality in Rough Sets. - 14.
The notation \(\mathcal {C} X\) is overloaded, for the illocutionary operator of conjecture in the syntax of the language of pragmatics and for the closure operator in a topological space. No confusion is possible, given the difference in context.
- 15.
There is no connective to represent Nelson’s implication as distinct from intuitionistic implication in \(\mathcal {L}^{AH}\).
- 16.
There is no specific connective for orthogonality in \(\mathcal {L}^{AH}\).
- 17.
The “q” in q-\(\mathbf {LJ}^{\backslash \curlyvee }\) stands for queue, tail, as the “t” in t-\(\mathbf {LJ}^{\supset \cap }\) stands for tête, head.
- 18.
It ought to be clear that the use of focalization in the sequent calculus q-\(\mathbf {LJ}^{\backslash \curlyvee }\) and in the dual t-\(\mathbf {LJ}^{\supset \cap }\) (see Table 8, Appendix III), is unrelated to the use of the “stoup” in our sequent calculi AH-G3, PB-G3, and APB-G3 for bi-intuitionistic logic, where it is used simply to highlight the restrictions of intuitionistic systems.
- 19.
This part is joint work with Corrado Biasi and incorporates important contributions from his still unfinished doctoral dissertation at Queen Mary, University of London.
- 20.
Parigot and Crolard actually write sequents in the form \(t: \Gamma \vdash \Delta ; A\), where the term \(t\) is given the type of the formula \(A\) in the stoup, if such a formula exists. If the stoup is empty, the notation allows one to think of \(t\) as being assigned to the entire sequent or to a formula \(\bot \) implicitly present in the stoup.
- 21.
In Crolard [16] the introduction rule corresponds to the more general form \(\backslash \)-I given above, and more general continuation contexts occur in place of \(\beta \); the above formulation suffices for our purpose here.
- 22.
For instance, in the derivation of the right premise of a subtraction elimination (\(\backslash E\)), there should be no relevant dependency between the formula \(B\) and the assumptions in \(\Gamma \), but only between \(B\) and \(A\).
- 23.
Here we use the term “thread” in the sense of Prawitz [46], p. 25; namely, a thread is a branch in the proof-tree from the a leaf to the root. The equivalent notion here is that of a branch in Prawitz’ tree \(\tau \) from the root to the leaf. No claim is made here about the computer science usage of the term “thread.”
- 24.
The expression \(\bullet \) is not a formula, but a non-logical expression, which cannot be part of other formulas; its meaning could be though of as an absurdity.
- 25.
In our definition we use lists of terms where multisets are intended. A multiset can be represented as a list \(\ell = (t_1, \ldots , t_n)\) with the action of the group of permutations \(\sigma : n \rightarrow n\) given by \(\ell _{\sigma }\) = \((t_{\sigma (1)}, \ldots , t_{\sigma (n)})\).
References
Angelelli, I. (1970). The techniques of disputation in the history of logic. The Journal of Philosophy, 67(20), 800–815.
Austin, J. L. (1970). Philosophical papers (2nd ed.). USA: Oxford University Press.
Bellin, G., & Scott, P. J. (1994). On the Pi-calculus and linear logic. Theoretical Computer Science, 135, 11–65.
Bellin, G. (2003). Chu’s Construction: A Proof-theoretic Approach. In Ruy J.G.B. de Queiroz (Ed.), Logic for Concurrency and Synchronisation (Vol. 18, pp. 93–114). Dordrecht: Kluwer Trends in Logic.
Bellin, G., & Biasi, C. (2004). Towards a logic for pragmatics. Assertions and conjectures. Journal of Logic and Computation, 14(4), 473–506. Special Issue with the Proceedings of the Workshop on Intuitionistic Modal Logic and Application (IMLA-FLOC 2002), V. de Paiva, R. Goré & M. Mendler (Eds.).
Bellin, G., & Ranalter, K. (2003). A Kripke-style semantics for the intuitionistic logic of pragmatics ILP. Journal of Logic and Computation, 13(5), 755–775. Special Issue with the Proceedings of the Dagstuhl Seminar on Semantic Foundations of Proof-search, Schloss Dagstuhl.
Bellin, G., & Dalla Pozza, C. (2002). A pragmatic interpretation of substructural logics. Reflection on the Foundations of Mathematics (Stanford, CA, 1998), Essays in honor of Solomon Feferman, W. Sieg, R. Sommer and C. Talcott (Eds.), Association for Symbolic Logic, Urbana, IL, Lecture Notes in Logic, (Vol. 15, pp. 139–163).
Bellin, G. (2005). A Term Assignment for Dual Intuitionistic Logic. Conference paper presented at the LICS’05-IMLA’05 Workshop, Chicago, IL, June 30.
Bellin, G., Hyland, M., Robinson, E., & Urban, C. (2006). Categorical proof theory of classical propositional calculus. Theoretical Computer Science, 364(2), 146–165.
Biasi, C. (2003). Verso una logica degli operatori prammatici asserzioni e congetture. Tesi di Laurea: Facoltà di Scienze, Università di Verona.
Biasi, C., & Aschieri, F. (2008). A term assignment for polarized bi-intuitionistic logic and its strong normalization. Fundamenta Informaticae, 84(2), 185–205. Special issue on Logic for Pragmatics.
Bing, J. (1982). Uncertainty, decisions and information systems. In C. Ciampi (Ed.), Artificial Intelligence and Legal Information Systems. Amsterdam: North-Holland.
Brewka, G. & Gordon, T. (2010). Carneades and Abstract Dialectical Frameworks: A Reconstruction. In: P. Baroni, M. Giacomin & G. Simari (Ed.), Computational Models of Argument, Proceedings of COMMA 2010, IOS Press.
Crolard, T. (1996). Extension de l’isomorphisme de Curry-Howard au traitement des exceptions (application d’une ètude de la dualité en logique intuitionniste) (p. 7). Thèse de Doctorat: Université de Paris.
Crolard, T. (2001). Subtractive logic. Theoretical Computer Science, 254(1–2), 151–185.
Crolard, T. (2004). A formulae-as-types interpretation of subtractive logic. Journal of Logic and Computation, 14(4), 529–570. Special Issue with the Proceedings of the Workshop on Intuitionistic Modal Logic and Application (IMLA-FLOC 2002), V. de Paiva, R. Goré and M. Mendler (Eds.).
Curien, P. L. (2002). Abstract Machines, Control, and Sequents. In G. Barthe, P. Dybjer, L. Pinto, J. Saraiva (Eds.), Applied Semantics, International Summer School, APPSEM 2000, Caminha, Portugal, September 9–15, Advanced Lectures. Lecture Notes in Computer Science, Vol. 2395, Springer.
Dalla Pozza, C., & Garola, C. (1995). A pragmatic interpretation of intuitionistic propositional logic. Erkenntnis, 43(1995), 81–109.
Dalla Pozza, C. (1997). Una logica prammatica per la concezione “espressiva” delle norme. In A. Martino (Ed.), Logica delle Norme. Pisa: Servizio Editoriale Universitario.
Danos, V., Joinet, J.-B., & Schellinx, H. (1995). LKQ and LKT: Sequent calculi for second order logic based upon dual linear decompositions of classical implication. In Proceedings of the workshop on Advances in linear logic (pp. 211–224). New York: Cambridge University Press.
Dummett, M. (1991). The Logical Basis of Metaphysics. Cambridge: Cambridge University Press.
Girard, J.-Y. (1993). On the unity of logic. Annals of Pure and Applied Logic, 59, 201–217.
Gödel, K. (1933). Eine Interpretation des Intuitionistischen Aussagenkalküls. Ergebnisse eines Mathematischen Kolloquiums IV, pp. 39–40.
Gordon, T. F., & Walton, D. (2009). Proof burdens and standards In: I. Rahwan & G. Simari (Eds.), Argumentations in Artificial Intelligence (pp. 239–258). New York: Springer.
Goré, R. (2000). Dual intuitionistic logic revisited. In TABLEAUX00: Automated reasoning with analytic tableaux and related methods, LNAI (Vol. 1847, pp. 252–267). Berlin: Springer.
Hyland, J. M., & De Paiva, V. C. V. (1993). Full intuitionistic linear logic. Annals of Pure and Applied Logic, 64, 273–291.
Kripke, S. A. (1963). Semantical analysis of modal logic I: Normal modal propostional calculi. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, 9.
Kripke, S. A. (1965). Semantical analysis of intuitionistic logic I. Formal Systems and Recursive Functions. In J. N. Crossley & M. A. E. Dummett (Eds.), Studies in logic and the foundations of mathematics (pp. 92–130). Amsterdam: North-Holland.
Krivine, J. L. (1990). Lambda-calcul, types et modèles. Paris: Masson.
Lambek, J., & Scott, P. J. (1986). Introduction to higher order categorical logic. Cambridge: Cambridge University Press.
Levinson, S. C. (1983). Pragmatics. Cambridge: Cambridge University Press.
Lawvere, F. W. (1991). Intrinsic co-Heyting boundaries and the Leibniz rule in certain toposes. In A. Carboni, M. C. Pedicchio, & G. Rosolini (Eds.), Category Theory (Como 1990), Lecture Notes in Mantehmatics (Vol. 1488, pp. 279–297). Verlag: Springer.
Makkai, M., & Reyes, G. E. (1995). Completeness results for intuitionistic and modal logic in a categorical setting. Annals od Pure and Applied Logic, 72, 25–101.
Martin-Löf, P. (1985). On the meaning and justification of logical laws. In Bernardi & Pagli (Eds.) Atti degli Incontri di Logica Matematica, vol. II, Universita‘ di Siena.
Martin-Löf, P. (1987). Truth of a proposition, evidence of a judgement, validity of a proof. Synthese, 73, 407–420.
McKinsey, J. C. C., & Tarski, A. (1948). Some theorems about the sentential calculi of Lewis and Heyting. Journal of Symbolic Logic, 13, 1–15.
Miglioli, P., Moscato, U., Ornaghi, M., & Usberti, U. (1989). A constructivism based on classical truth. Notre Dame Journal of Formal Logic, 30, 67–90.
Nelson, D. (1949). Constructible falsity. The Journal of Symbolic Logic, 14, 16–26.
Pagliani, P., & Chakraborty, M. (2008). A geometry of approximation rough set theory: Logic algebra and topology of conceptual patterns. Verlag: Springer.
Pagliani, P. (2009). Intrinsic co-Heyting boundaries and information incompleteness in Rough Set Analysis. In L. Polkowski & A. Skowron (Eds.), RSCTC 1998. Lecture Notes in Computer Science (Vol. 1424, pp. 123–130). Heidelberg: Springer.
Pagliani, P. (1997). Information gaps as communication needs: A new semantic foundation for some non-classical logics. Journal of Logic, Language and Information, 6(1), 63–99.
Parigot, M. (1991). Free Deduction: An Analysis of “Computations” in Classical Logic. In A. Voronkov (Ed.), Logic Programming, Proceedings of the First Russian Conference on Logic Programming, Irkutsk, Russia, September 14–18, 1990–Second Russian Conference on Logic Programming, St. Petersburg, Russia, September 11–16, Springer Lecture Notes in Computer Science, ISBN 3-540-55460-2, London: Springer, pp. 361-380.
Parigot, M. (1992). Lambda-My-Calculus: An Algorithmic Interpretation of Classical Natural Deduction. In A. Voronkov (Ed.), Logic Programming and Automated Reasoning, Proceedings of the International Conference LPAR’92, St. Petersburg, Russia. Springer Lecture Notes in Computer Science 624, 1992, ISBN 3-540-55727-X, pp. 190-201.
Parigot, M., (1993). Strong Normalization for Second Order Classical Natural Deduction. In LICS,. (1993). Proceedings (pp. 39–46). Canada: Eighth Annual IEEE Symposium on Logic in Computer Science Montreal.
Polkowski, L. (2002). Rough Sets. Physical-Verlag: Mathematical Foundations. Advances in Soft Computing. Heidelberg.
Prawitz, D. (1965). Natural deduction. A proof-theoretic study. Stockholm: Almquist and Wikksell.
Prawitz, D. (1987). Dummett on a theory of meaning and its impact on logic. In B. Taylor (Ed.), Michael Dummett: Contributions to philosophy (pp. 117–165). The Hague: Nijhoff.
Ranalter, K. (2008). A semantic analysis of a logic for pragmatics with assertions, obligations, and causal implication. Fundamenta Informaticae, 84(3–4), 443–470.
Ranalter, K. (2008). Reasoning about assertions, obligations and causality: on a categorical semantics for a logics for pragmatics. PhD Thesis, Queen Mary, University of London and University of Verona.
Rauszer, C. (1974). Semi-Boolean algebras and their applications to intuitionistic logic with dual operations. Fundamenta Mathematicae, 83, 219–249.
Rauszer, C. (1977). Applications of Kripke models to Heyting-Brouwer logic. Studia Logica, 36, 61–71.
Reyes, G., & Zolfaghari, H. (1996). Bi-Heyting algebras, toposes and modalities. Journal of Philosophical Logic, 25, 25–43.
Ryan, M., & Schobbens, P.-Y. (1997). Counterfactuals and updates as inverse modalities. Journal of Logic, Language and Information, 6(2), 123–146.
Selinger, P. (2001). Control categories and duality: On the categorical semantics of the lambda-mu calculus. Mathematical Structures in Computer Science, 11, 207–260.
Shapiro, S. (1985). Epistemic and Intuitionistic Arithmetic. In S. Shapiro (Ed.), Intensional mathematics (pp. 11–46). Amsterdam: North-Holland.
Shapiro, S. (1997). Philosophy of mathematics : structure and ontology. New York: Oxford University Press.
Stell, J., & Worboys, M. (1997). The Algebraic Structure of Sets of Regions. In S. Hirtle & A. Frank (Eds.), Spatial Information Theory, COSIT’97 Proceedings Lecture Notes in Computer Science (Vol. 1329, pp. 163–174). Verlag: Springer.
Thomason, R. (1969). A semantical study of constructible falsity. Zeitschrift fur mathematische Logik und Grundlagen der Mathematik, 15, 247–257.
Troelstra, A. S. & Schwichtenberg, H. (1996). Basic proof theory. Cambridge tracts in theoretical computer science (Vol. 43). Cambridge: Cambridge University Press.
White, G. (2008). Davidson and Reiter on actions. Fundamenta Informaticae, 84(2), 259–289.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix I. Polarized Rauszer’s Logic
The main stream of bi-intuitionistic logic follows the tradition of Cecylia Rauszer, who created the theory of bi-Heyting algebras [50, 51], and defined its Kripke semantics, later studied with categorical methods by Lawvere [32], Makkai, Reyes and Zolfaghari [33, 52]; more recently, proof theoretic treatments of subtractive or bi-intuitionistic logic have been given by Rajeev Gore [25], Tristan Crolard [14, 15] and others.
In Rauszer’s possible-world semantics the forcing conditions for implication refer to up-sets of possible worlds with respect to the accessibility relation, while the forcing conditions for subtraction refer to down-sets. Namely, \((A\supset B)^M\) = \(\Box (A^M\rightarrow B^M)\) is true in a world \(w\) if for all \(w'\) such that \(wRw'\)
\(A^M\rightarrow B^M\) is true in \(w'\); on the other hand, \((C\backslash D)^M\) =  is true in a world \(w\) if for some \(w'\) such that \(w'Rw\) we have \(C^M\wedge \lnot D^M\) is true in \(w'\); in other words, modal translations are interpreted in models \(\mathcal {M}\) = \((W, R, S, \Vdash )\) where \(R\) and \(S\) are pre-orders such that \(S = R^{-1}\). This suggests a temporal dimension in the bi-modal translation: the forcing condition for the operator \(\Box \) may be seen as referring to “future knowledge” and those for
is true in a world \(w\) if for some \(w'\) such that \(w'Rw\) we have \(C^M\wedge \lnot D^M\) is true in \(w'\); in other words, modal translations are interpreted in models \(\mathcal {M}\) = \((W, R, S, \Vdash )\) where \(R\) and \(S\) are pre-orders such that \(S = R^{-1}\). This suggests a temporal dimension in the bi-modal translation: the forcing condition for the operator \(\Box \) may be seen as referring to “future knowledge” and those for  to “past knowledge.”
to “past knowledge.”
We see at once that Rauzer’s bi-intuitionistic logic is as inadequate for a representation of assertions and hypotheses as PBL: letting  and
and  , it is consistent to assert \(p\) (with respect to “the future”) and also to conjecture \(\lnot p\) (in the past). Although the issue is beyond the range of the present chapter, it may be interesting to catch a glimpse of what polarized Rauszer’s logic looks like in our framework.
, it is consistent to assert \(p\) (with respect to “the future”) and also to conjecture \(\lnot p\) (in the past). Although the issue is beyond the range of the present chapter, it may be interesting to catch a glimpse of what polarized Rauszer’s logic looks like in our framework.
Tense-Sensitive Polarization
Is there a pragmatic interpretation of dual intuitionistic logic which retains such a temporal element and is thus closer to Rauszer’s tradition? The question does make sense. Clearly, the justification conditions for assertions and conjectures concerning the future and the past are different in several important ways: for instance, direct observations of some future events will be possible, but never of past events. Thus it would be plausible to introduce tense-sensitive illocutionary operators, giving assertive force to statements about the future ( ) and about the past (
) and about the past ( ) and, similarly, conjectural force to statements about the future (
) and, similarly, conjectural force to statements about the future ( ) and about the past (
) and about the past ( ). Moreover, we would have strong negation about the future (\(\sim ^{_{\bullet }}\)) and about the past (\(\,^{_{\bullet }}\!\!\sim \)) and weak negation about the future (\({\smallfrown ^{_{\bullet }}}\)) and about the past (\({^{_{\bullet }}\!\!\!\smallfrown }\)). More generally, all pragmatic formulas would become tense-sensitive and could polarized in four ways:
). Moreover, we would have strong negation about the future (\(\sim ^{_{\bullet }}\)) and about the past (\(\,^{_{\bullet }}\!\!\sim \)) and weak negation about the future (\({\smallfrown ^{_{\bullet }}}\)) and about the past (\({^{_{\bullet }}\!\!\!\smallfrown }\)). More generally, all pragmatic formulas would become tense-sensitive and could polarized in four ways:
We define a language \(\mathcal {L}^{PB}_t\) according to the grammar in Table 6.
This would lead to the development of a tense-sensitive polarized bi-intuitionistic logic (\(\mathbf {PBL}_t\)). The “semantic reflection” of \(\mathcal {L}^{PB}_t\) is in temporal
S4, where formulas of  are interpreted in bimodal frames \(\mathcal {F} = (W, R, S)\) with \(R\) a preorder and \(S = R^{-1}\).
are interpreted in bimodal frames \(\mathcal {F} = (W, R, S)\) with \(R\) a preorder and \(S = R^{-1}\).
The following fact is standard (see, e.g., Ryan and Shobbens [53]):
Proposition 5
Given a bimodal frame \(\mathcal {F}\), the following are equivalent:
-
1.
\(S = R^{-1}\);
-
2.
 and
and 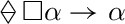 are valid in every Kripke model over \(\mathcal {F}\);
are valid in every Kripke model over \(\mathcal {F}\); -
3.
the following rule is valid and semantically invertible in \(\mathcal {F}\)

Therefore the following are equivalent:
-
1.
the modal interpretation \((\ )^M\) of the language \(\mathcal {L}^{PB}_t\) is in temporal S4;
-
2.
for any formula \(\delta ^{_{\bullet }}\) and \(\,^{_{\bullet }}\delta \), the sequents \(\delta ^{_{\bullet }}\Rightarrow \sim ^{_{\bullet }}\!\,^{_{\bullet }}\!\!\sim \delta ^{_{\bullet }}\) and \({^{_{\bullet }}\!\!\!\smallfrown }{\smallfrown ^{_{\bullet }}}{\,^{_{\bullet }}\delta } \Rightarrow \,^{_{\bullet }}\delta \) are valid axioms of \(\mathbf {PBL_t}\).
We leave the task of finding a suitable formalization of \(\mathbf {PBL}_t\) as an open problem.
Appendix II. Example of Computation
In this section we consider an example of computation that is dual to a familiar reduction sequence for Church’s numerals.
Two Times Zero
We consider the dual of a computation of the term representing \(\mathbf {2\times 0}\) :
We follow a call by value strategy:
1.1 Labelled Prawitz’ Trees
As trees in Prawitz style Natural Deduction \(\mathbf {NJ}^{\supset }\) can be decorated with \(\lambda \) terms, so we can assign terms of our dual calculus to Prawitz trees of subformulas for \(\mathbf {co-NJ}^{\backslash }\) derivations. For convenience, we still draw trees with the root at the bottom, keeping in mind that here derivations are built from bottom up. We shall use Biasi’s notation \((t\rightarrow \mathtt {a})\) for \(\mathtt {mkc}(t,a)\) and  for \(\mathbf {postp}(e\mapsto \ell , t)\).
for \(\mathbf {postp}(e\mapsto \ell , t)\).


Appendix III. Term Assignment to q-\(\mathbf {LJ}^{\backslash \curlyvee }\)
Rights and permissions
Copyright information
© 2014 Springer Science+Business Media Dordrecht
About this chapter
Cite this chapter
Bellin, G. (2014). Assertions, Hypotheses, Conjectures, Expectations: Rough-Sets Semantics and Proof Theory. In: Pereira, L., Haeusler, E., de Paiva, V. (eds) Advances in Natural Deduction. Trends in Logic, vol 39. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-7548-0_10
Download citation
DOI: https://doi.org/10.1007/978-94-007-7548-0_10
Published:
Publisher Name: Springer, Dordrecht
Print ISBN: 978-94-007-7547-3
Online ISBN: 978-94-007-7548-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)





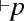 , a sentential constant for validity (
, a sentential constant for validity ( and a constant for absurdity (
and a constant for absurdity (

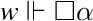 iff
iff 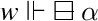 iff
iff  ;
;

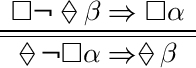







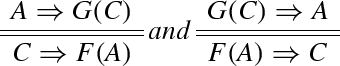














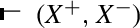
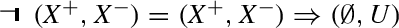
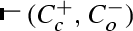
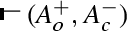
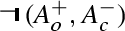
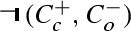
 =
= =
= .
.




















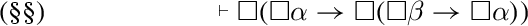
 and
and  are variable ranging over proofs of the truth of
are variable ranging over proofs of the truth of 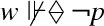 . To see that
. To see that 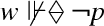 , consider a model
, consider a model 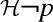 is not an expression of the language
is not an expression of the language 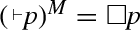 and
and 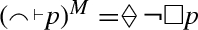 .
.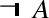 for intuitionistic negation and
for intuitionistic negation and 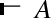 for co-intuitionistic supplement; but in the later literature on bi-intuitionistic logic
for co-intuitionistic supplement; but in the later literature on bi-intuitionistic logic  ,” “
,” “  ,” and “
,” and “ and
and 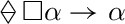 are valid in every Kripke model over
are valid in every Kripke model over