On Revocable and Irrevocable Belief Revision

Abstract

Krister Segerberg proposed irrevocable belief revision, to be contrasted with ‘standard’ belief revision, in a setting wherein belief of propositional formulas is modelled explicitly. In standard belief revision one can unmake (‘revoke’) belief in any formula, given yet further information that contradicts it. But irrevocable formulas remain believed forever. We compare traditional AGM belief revision with Segerberg’s dynamic doxastic logic, and with dynamic epistemic logical approaches to belief revision. Our work falls in the latter category. In that context with explicit belief operators and dynamic modal operators $[* \varphi ]$ for belief revision with $\varphi$, we define revocable belief revision as belief revision satisfying that $\psi \leftrightarrow [* \varphi ] [* \lnot \varphi ] \psi$ is valid; such that irrevocable means not revocable. Segerberg’s irrevocable belief revision is indeed irrevocable in that sense. We give semantic constraints (on multi-agent Kripke models) for revocable belief revision. In order for belief revision to be revocable: (i) the agents should consider the same states possible before and after revision, (ii) states that are non-bisimilar before revision may not be bisimilar after revision (if states are non-bisimilar, they can be distinguished from one another in the logical language), and (iii) it should be possible that states that are not equally plausible before revision become equally plausible after revision. We reformulate four well-known belief revision operators (hard update, soft update, conservative revision, severe revision) as qualitative dynamic belief revision operators. They are irrevocable in the (strong) sense above, because they violate one or more of these three requirements. However, single-agent severe revision is revocable in a weaker sense that following a revision $*\varphi$ there is a sequence of further revisions recovering the initial state of belief. The work may be relevant for restricted-memory or other bounded rationality approaches to belief revision, e.g., when only a finite number of plausibility distinctions may be stored in memory. Therefore, it may be relevant for the study of logic and cognition.

I had the pleasure to be introduced by Greg Restall to Krister Segerberg at the Logic, Methodology and Philosophy of Science conference in 2003 in Oviedo, Spain. This was not entirely coincidental. I presented at that LMPS my first steps in modelling belief revision in dynamic epistemic logic, joint work with my Otago colleague Willem Labuschagne, rather an abstract than a formal publication: [47]. But from that initial study I had become acquainted with Segerberg’s work, and I was therefore eager to meet him. Our relationship has developed since. With great pleasure I recall the event organized at the University of Amsterdam by Olivier Roy where we met again in 2006. This was the 4th Paris-Amsterdam Logic Meeting of Young Researchers (PALMYR-4): Logics for Belief Dynamics. In 2008 we both became editors of the Journal of Philosophical Logic. In 2012 I still am, this a position I cherish, and I tend to feel that I owe it to Krister. The hospitality offered by Krister and Anita Segerberg, whereever they reside, is legendary. It need hardly be mentioned. But one should, on occasion.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

1.1 Belief Revision and Dynamic Epistemic Logic

Both belief revision and dynamic epistemic logic have been on the research agenda for quite a while [1, 22, 30, 39].

Belief revision has been studied from the perspective of structural properties of reasoning about changing beliefs [15], from the perspective of changing, growing and shrinking knowledge bases, and from the perspective of models and other structures of belief change wherein such knowledge bases may be interpreted, or that satisfy assumed properties of reasoning about beliefs. A typical approach involves preferential orders to express increasing or decreasing degrees of belief [14, 22, 26, 27] (such works provided a basis for [45]), where these works refer to the ‘systems of spheres’ in [19, 24]. Within this tradition multi-agent belief revision has also been investigated, e.g., belief merging [20]. Belief operators are normally not explicit in the logical language, so that higher-order beliefs (I know that you are ignorant) cannot be formalized. Iterated belief revision may be also be problematic.

Dynamic epistemic logic has developed more or less since the late 1980s, with seminal publications by [6, 17, 30, 43, 44]. Precursors with dynamic but without epistemic operators are [12, 38]. Such logics have epistemic operators (or any other base modality, e.g. a doxastic operator) to formalize knowledge or belief, and dynamic modal operators to formalize change of knowledge or belief. They are typically multi-agent logics. Initially, e.g. in all the seminal publications mentioned above, change of knowledge always meant some kind of growth of knowledge or strengthening of belief, and not belief revision in the sense of incorporating otherwise inconsistent novel beliefs. Research in dynamic epistemic logic was mainly driven by the attempt to model higher-order phenomena of belief change, and was initially motivated by the attempt to model so-called ‘unsuccessful updates’, as in the well-known muddy children problem [28]: from a public update with ‘nobody knows whether he/she is muddy’, the muddy children may learn that they are muddy.

Dynamic doxastic logic was proposed and investigated by Krister Segerberg and collaborators in works such as [25, 34–36]. From the biased viewpoint of dynamic epistemic logic these works are seen as its direct forerunners; as such, they are distinct from yet (many) other approaches to belief revision in modal logics but without dynamic modal operators, such as [2, 9, 10, 23], that also influenced the development of dynamic logics combining knowledge and belief change. In dynamic doxastic logics belief operators are in the logical language, and belief revision operators are dynamic modalities. Higher-order belief change, i.e., to revise one’s beliefs about one’s own or other agent’s beliefs and ignorance, are considered problematic in dynamic doxastic logic, see [25]. In [34, 36] belief revision is restricted to propositional formulas (factual revision). There are dynamic doxastic logics wherein $[*\varphi ]$ merely means belief revision with $\varphi$ according to some externally defined strategy, as in AGM style (this is the general setup in [36], not unlike the non-epistemic/doxastic modal setup in [38]), but there are also dynamic doxastic logics, such as the irrevocable belief revision that is the topic of this investigation [34], wherein $[*\varphi ]$ is a recipe operating on a semantic structure and outputting a novel structure, the standard approach in dynamic epistemic logic.

Belief revision in dynamic epistemic logic (in short: dynamic belief revision) was initiated by a group of researchers all more or less in contact with one another and in various and changing relations of collaborator, student, and supervisor, active all over the globe. The initial publications are [4, 7, 40, 45] (where we should note that [4] is based on Aucher’s Master of Logic thesis [3], that was written under the supervision of van Benthem and van Ditmarsch). From these, [4, 45] propose a treatment involving degrees of belief and based on degrees of plausibility among states in structures interpreting such logics, so-called quantitative dynamic belief revision; whereas [7, 40] propose a treatment involving comparative statements about plausibilities (a binary relation between states denoting more/less plausible), so-called qualitative dynamic belief revision. The latter is clearly more suitable for logics of belief revision, and for notions such as conditional belief. Given the usual prewellorders for plausibility, qualitative and quantitative approaches are interdefinable (see [46] for details)—but that amounts to saying that propositional logic might as well be written with Sheffer strokes. Qualitative approaches are much more succinct. Quantitative approaches may have special uses in artificial intelligence. The analogue of the AGM postulate of ‘success’ must be given up when one incorporates higher-order belief change as in dynamic epistemic logic, where again a prime mover are Moore-sentences of the form ‘proposition $p$ is true but you don’t know it’, which cannot after acceptance be believed by you. Many more works and whole PhD theses [5, 13, 18] on dynamic belief revision have appeared since, and the work has greatly developed towards philosophical logic and formal epistemology [8], that we do not wish to give a comprehensive overview of. For that we refer to [41].

1.2 Irrevocable Belief Revision in Dynamic Doxastic Logic

In [34] Krister Segerberg coined the term irrevocable belief revision.

Ordinary theories of belief change do not seem suited to handle the sort of hypothetical belief change that goes on, for example, in debates where the participants agree, “for the sake of argument,” on a certain common ground on which possibilities can be explored and disagreements can be aired. One need not actually believe what one accepts in this way. Nevertheless such acceptance amounts to what may be called a doxastic commitment, one that cannot be given up within the perimeter of the debate.

He then proceeds to explain that for such belief change one does not expect a further revision with another formula to be executable. That would merely be a different common ground for debate. It is not puzzling, nor required that argument assumed for the sake of argument are consistent. He then proceeds to call this irrevocable belief revision, and proposes a logic, in the setting with dynamic modalmodal logic operators for revision and explicit belief and knowledge (conviction) operators. For that, we have to explain how Segerberg’s setting relates to the standard AGM setting.

In AGM belief revision, a given set of formulas incorporated in a deductive closed theory $\mathcal {K}$ is revised with a formula $\varphi$ resulting in a revised theory $\mathcal {K}*\varphi$. Typically, $\lnot \varphi$ is in $\mathcal {K}$, one has to give up belief in $\lnot \varphi$ by a process of retraction, and $\varphi$ is in $\mathcal {K}*\varphi$. In the setting of dynamic doxastic logic, formulas $B \varphi$ or $K \varphi$ with explicit modal belief or knowledge operators, and where $\varphi$ is a propositional formula, are interpreted on systems of algebras that are so-called hypertheories. For our purposes it is sufficient to think of them as ‘systems of spheres’ $M$ with certain additional properties, and where truth is defined relative to a point $s$ in the system. Instead of writing $\lnot \varphi \in \mathcal {K}$ for ‘the agent believes $\lnot \varphi$, we have that $M,s \models B \lnot \varphi$ for the $\lnot \varphi \in \mathcal {K}$ as above (and, indeed, $M,s$ should be such that $\psi \in \mathcal {K}$ iff $M,s\models \psi$). ‘Revision with $\varphi$’ is now a program $*\varphi$ that transforms the structure $(M,s)$ into another structure $(M', s')$. The transformation is described in the logical language by a dynamic modal operator $[*\varphi ]$, that is interpreted as a binary relation between structures. In irrevocable belief revision (but not in all other dynamic doxastic logics), $M^{*\varphi }$ is computed from $M$ by standard restriction of the model to the $\varphi$-states, and $s' = s$. So in that sense, the semantic operation is like ‘hard update’, ‘public announcement’, etc. The crucial aspect of this update is that the most plausible states in $M$ may no longer be ‘believable’ (namely because they did not satisfy $\varphi$), but the construction makes the most plausible $\varphi$-states now the overall most plausible states. (Examples are given in the following sections. For dynamic epistemic logic the procedure is quite similar.) We now have that $\psi \in \mathcal {K} *\varphi$ iff for all $M,s$, if $M,s \models B \chi$ for all $\chi \in \mathcal {K}$, then $M^{*\varphi },s \models B \varphi$. In this framework, knowledge or convinced belief plays the role of background knowledge. Unlike standard AGM, iterated belief revision is quite natural in this setting. Expansion and revision are combined in this update. If the revision formula $\varphi$ is consistent with the current beliefs, we have expansion, otherwise revision.

1.3 Overview

We have already reviewed the literature in the area: AGM belief revision, dynamic epistemic logic, dynamic doxastic logic, and more recent approaches to belief revision in dynamic epistemic logic. We also recalled Segerberg’s irrevocable belief revision in dynamic doxastic logic. In the next section we compare revocable to irrevocable belief revision, and illustrate the dynamic epistemic logic approach to belief revision in a number of extended examples. Section 3 contains the more technical part of our contribution. First, we define structures with plausibility relations, and a logical language for belief, knowledge, and belief change (i.e, nearly exactly as in Segerberg’s original proposal). Then, we demonstrate that various well-known kinds of belief revision are irrevocable in a strict sense, and only one is revocable in a limited sense. The conclusion outlines why our study is relevant for modelling bounded rationality and the area of logic and cognition.

2 An Example of Revocable Belief Revision

I have this electric water heater, to make cups of tea and such. It has a heating element that is a metal coil, and also a light to indicate when the heater is turned on. Normally, they work in tandem, the light is on exactly when the element heats the water. But the following malfunctions are known to happen: the element still heats the water but the light is off, because it’s blown; and dually, the light may still be on indicating that the element is heating the water up, but in fact it doesn’t due to malfunction. Then, very rarely when there it’s turned on while there is a current, both might be gone. Let $p$ stand for ‘the coil is heating’ and let $q$ stand for ‘the light is on’. The default is that both are true when I turn on the heater: $p \wedge q$. It seems somewhat less likely, but very possible, that at least one is OK: $p \vee q$. And least plausible is that they are both malfunctioning: $\lnot p \vee \lnot q$. That is depicted in Fig. 1. Observing that the coil does not work, more or less (I am impatient, and the typical sizzling noise accompanying the water heating up may not yet have started) makes us want to revise the belief in $p \wedge q$ with $*\lnot p$ into belief in $\lnot p \wedge q$. Such a transition is depicted in Fig. 2. And so on... With a fair stretch of the imagination for the wilder transitions we can thus accommodate the belief revision examples provided in this section.

Fig. 1

Knowledge, belief and plausibility about two propositions $p$ and $q$. The agent believes that $p$ and $q$ are true

Fig. 2

The agent changes hes belief in $p$ and $q$ by revising with $\lnot p$. After the revision, the agent believes $\lnot p$ instead. She still believes $q$

Consider one agent and two factual propositions $p$ and $q$ that the agent is uncertain about. The state of uncertainty is represented in Fig. 1. There are four states of the world, $\{ 00, 01, 10, 11 \}$. Atom $p$ is only true in $\{10,11\}$, and atom $q$ is only true in $\{01,11\}$. The agent has preferences among these states. He considers it most plausible that 11 is the actual state, i.e., that both $p$ and $q$ are true, slightly less plausible that 01 or 10 are the actual state, and least plausible that 00 is the actual state. (We assume that this perspective on plausibilities is the same in all states.) We write

$$\begin{aligned} 11 < 01 = 10 < 00 \end{aligned}$$

The agent believes propositions when they hold in the most plausible states. For example, she believes that $p$ and $q$ are true. This is formalized as

$$\begin{aligned} B (p \wedge q) \end{aligned}$$

As usual we write $B$ for belief, and honouring Segerberg-style we will write $B$ for its dual. E.g., the truth of both propositions is also believable: $b (p \wedge q)$. Her belief in the slightly weaker proposition $p \vee q$ is slightly stronger than his belief in $p \wedge q$. Note that $p$ or $q$ are true in all three of $11, 01$, and $10$, i.e., including state 11.

Her strongest beliefs, or knowledge, involve in this case only tautologies such as $p \vee \lnot p$ and $q \vee \lnot q$. This is described as

$$\begin{aligned} K (p \vee \lnot p) \end{aligned}$$

As usual $K$ stands for knowledge. We will also, less usual, let it stand for conviction, or, as Segerberg playfully and appropriately writes: Konviction. Also as in Segerberg we write $k$ for the dual of knowledge. For example, we have that the state of affairs where $p$ and $q$ are both false is considered possible: $k (\lnot p \wedge \lnot q)$, but also the state of affairs where they are both true $k (p \wedge q)$. The last already follows from the fact that this was believable $b (p \wedge q)$. Her strong beliefs are also about her plausibilities. For example, she knows that she believes $p$ and $q$

$$\begin{aligned} K B (p \wedge q) \end{aligned}$$

This is, because whatever the actual state of the world is, $B (p \wedge q)$ is true.

Now imagine that the agent wants to revise her current beliefs. She believed that $p$ and $q$ are both true, but has been given sufficient reason to be willing to revise her beliefs with $\lnot p$ instead. We can accomplish that when we allow a model transformation. On the right in Fig. 2 the agent believes that $p$ is false and that $q$ is true. So in particular, in modal terms, $B \lnot p$ is true. Therefore, the revision was successful. This can already be expressed in the model on the left, by using a dynamic modal operator $[* \lnot p]$ for the relation induced by the program “belief revision with $\lnot p$”, followed by what should hold after that program is executed. On the left, it is true that the agent believes $p$ and that after belief revision with $\lnot p$ the agent believes that $\lnot p$. In a dynamic modal setting this is described as $B p \wedge [* \lnot p] B \lnot p$.

To prolong the comparison with standard belief revision of sets of formulas, we observe that the plausibility order $11 < 01 = 10 < 00$ on the states in this model reflects the order $\{p,q\} < \{ p \vee q \} < \{ \top \}$ on belief bases, or the order $Cl(\{p,q\}) < Cl(\{ p \vee q \}) < Cl(\{ \top \})$ on theories, i.e., deductively closed sets of formulas that are believed by the agent. In dynamic epistemic logic, beyond the original Segerberg setting, beliefs and knowledge can also be about modal formulas. For example, we not only have that $B (p \wedge q)$, because $p \wedge q \in Cl(\{p,q\})$, but we also have that $B \lnot B (\lnot p \wedge \lnot q)$: $\lnot p \wedge \lnot q \not \in Cl(\{p,q\})$ means that $\lnot B (\lnot p \wedge \lnot q)$ is valid on the model, which by introspection delivers $B \lnot B (\lnot p \wedge \lnot q)$; so that $\lnot B (\lnot p \wedge \lnot q)$ is in the set of formulas believed by the agent. As another example we already mentioned that $K B (p \wedge q)$.

The revision above is obtained as follows—we prefer an informal description as we will not further develop this line of quantitative belief revision. Given the belief revision formula, $\lnot p$, (i) increase the plausibility of the states satisfying it sufficiently so that the most plausible $\lnot p$ states becomes the overall most plausible state, and (ii) simultaneously decrease the plausibility of the $p$ states sufficiently so that the most plausible $p$ states are no longer the overall most plausible states. The order $11 < 01 = 10 < 00$ defines degrees of plausibility $0, 1, 2$. In order to make a $\lnot p$ state the most plausible, we increase the plausibility of those states by 1: 01 then gets degree of plausibility 0 and 00 gets degree of plausibility 1. In order to undo that a $p$ state is the most plausible, we decrease the plausibility of those states by 1: 11 then gets degree of plausibility 1 and 10 gets degree of plausibility 2. In the revision process, states 00 and 11 have become equally plausible, and the new order is therefore $01 < 00 = 11 < 10$. This proposal was named successful minimal belief revision in [45], it is a particular case of the proposal in [4], and like that it is inspired by the ordinal conditional functions in [37]. It comes close to what is known in the AGM community as conservative revision, see e.g. [32]. It defies an elegant qualitative formulation. But it serves our purpose wonderfully: it is revocable.

Subsequently to the revision $* \lnot p$ we perform a revision $* p$. Now, we increase the degree of plausibility of the $p$ states 10 and 11 from 2 and 1 to 1 and 0, and decrease the degree of plausibility of the $\lnot p$ states 10 and 11 from 1 and 0 to 2 and 1. The original model, encoding the original beliefs, reappears. See Fig. 3.

Fig. 3

Subsequent to revision $*\lnot p$, the agent revises with $*p$. The original state of belief is recovered

It is clear that the depicted model satisfies

$$\begin{aligned} B (p \wedge q) \rightarrow [*\lnot p] [* p] B (p \wedge q). \end{aligned}$$

As the two revision operations return the original model we also have that, for any $\psi$,

$$\begin{aligned} \psi \rightarrow [*\lnot p] [* p] \psi . \end{aligned}$$

It will be obvious that this works for any form of plausibility change on this model, so that

$$\begin{aligned} \psi \rightarrow [* \varphi ] [* \lnot \varphi ] \psi \end{aligned}$$

is valid on the model for all formulas $\varphi$. This seems an interesting principle, formalizing that belief revision $* \varphi$ is ‘revocable’, undone, by the additional belief revision $*\lnot \varphi$. Let us investigate this principle a bit further.

Segerberg irrevocable belief revision is indeed not revocable. Figure 4 shows the effect of Segerberg irrevocable belief revision with $* \lnot p$. All $p$-states are eliminated. Before the revision, both $B p$ and $B q$ hold, afterwards, $B \lnot p$ and $B q$, but also that $K \lnot p$: prior belief in $p$ is irrecoverable indeed. This form of belief revision is called maximal belief revision in [45], hard update in [40], and is clearly based on the semantics of truthful public announcement [6, 30]. Subsequent belief revision $* p$ is not even executable, as there are no $p$-states left that are considered possible by the agent. Diagnosing the illness, the crucial feature making the belief revision irrevocable is that in the process of the revision some states are eliminated, or, putting it in even more general terms also compatible with arrow-eliminating update: some states have become inaccessible (unbelievable) from the actual state.

Fig. 4

Segerberg irrevocable belief revision

We have demonstrated that Segerberg irrevocable belief revision does not satisfy the principle $\psi \rightarrow [* \varphi ] [* \lnot \varphi ] \psi$. Does successful minimal belief revision satisfy this principle? We worked our way towards suggesting that it does, but in fact it does not. The beliefs that the agents have, are not merely about factual propositions but also about each others’ beliefs. It is then perfectly conceivable that an agent finds one state more plausible than another one even though they have the same valuations. They simply differ in their belief properties.

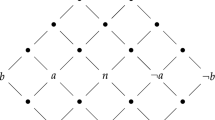
Consider two agents Anne ($a$) and Bill ($b$), say, that have different access to the state of a light. Proposition $p$ stands for ‘the light is on’. Bill knows whether the light is on, but he is uncertain if Anne believe that the light is on, or that she believes that the light is off. This situation is depicted in Fig. 5. Access for $a$ is solid and access for $b$ is dashed. We distinguish the plain 0 and 1 states from the bold 0 and 1 states. Proposition $p$ is true in 1 and in 1.

Again, we can now evaluate various statements about knowledge and belief, where we now label the $K$ and $B$ operators with the agents ($a$ for Anne, and $b$ for Bill) whose modalities they represent. In state 0 the light is off but Anne (incorrectly) believes that it is on:

$$\begin{aligned} \lnot p \wedge B_a p, \end{aligned}$$

whereas Bill does not know that, knows that the light is off, and also considers it possible that Anne correctly believes that:

$$\begin{aligned} \lnot K_b (\lnot p \wedge B_a p) \wedge K_b \lnot p \wedge k_b B_a \lnot p \end{aligned}$$

We now execute belief revision with $* p$ according to the successful minimal belief revision policy explained above. This does not affect Bill’s knowledge or beliefs. If the actual states are 1 or 1 he is already convinced of $p$, and otherwise he is already convinced of $\lnot p$. (And no evidence to the contrary will make him change his mind—according to the procedure for belief revision described above, the 0 and 0 states will get degree of plausibility 1 for agent $b$, but given the absence of states with degree of plausibility 0 in that $b$-equivalence class, they still remain the most plausible states.) But it affects the plausibilities for agent $a$. Proceeding as above, state $1$ will become more plausible than state 0 for agent $a$. The transition is as follows.

Fig. 5

Bill knows the value of $p$ but does not know what Anne believes about $p$

However, the states 1 and 1 can no longer be distinguished in the logical language from each other: they share the same value of the proposition $p$ and are also both more plausible than a $\lnot p$ state. We can therefore identify them. Similarly, for states 0 and 0. (We will see that 1 and 1, and 0 and 0, respectively, are bisimilar.) The following structure results.

A further revision with $* \lnot p$ will now not return the original state of information, but instead a model wherein, in state 0: Bill knows that $\lnot p$, and Anne believes that $\lnot p$, and Bill knows that Anne believes that $\lnot p$. The transitions in sequence are as follows.

However, single-agent successful minimal belief revision is revocable. Our $B$ and $K$ operators satisfy the standard KD45 properties for belief, and (at least) those properties for conviction/knowledge. For single-agent KD45 and stronger it cannot be that different states in the same equivalence class have the same valuation but satisfy different modal properties. It follows that states that are not equally plausible must have a different valuation.

Again diagnosing the illness here, this time the crucial feature making the two-agent successful minimal belief revision irrevocable is that in the process of the revision some states that could be distinguished by a formula in the logical language (that were not bisimilar) have become indistinguishable after the revision (are now bisimilar). Then, the original distinction cannot be recovered by subsequent belief revision with the negation of the revision formula (or by any other formula).

We now continue with the formal presentation of such results, for a number of well-known qualitatively defined forms of belief revision.

3 A Language and Logic for Dynamic Belief Revision

We present a fairly standard multi-agent dynamic doxastic logic. The language is presented Segerberg-style [34], the structures are presented as in our [45], and the dynamic belief revision operators are presented Baltag/Smets qualitative style [7]. The four belief revision operators presented in that style are: soft update / lexicographic belief revision [7, 40], hard update / public announcement / irrevocable revision / radical revision [30, 34], conservative revision [11, 31], and severe revision [32] (based on various severe belief contraction proposals).

Definition 1

(Doxastic model) Given are countable sets of agents $A$ and propositional variables $P$. A doxastic model is a triple $(S, \le , V)$. The set $S$ is a domain of factual states, and valuation $V$ is a function $V: P \rightarrow {\mathcal P}(S)$ such the subset $V(p)$ denotes the states where $p$ is true. The plausibility function $\le : A \rightarrow S \rightarrow {\mathcal P}(S \times S)$ defines a plausibility relation $\le ^s_{a}$ for each agent $a \in A$ and for each $s \in S$, that is a prewellorder.¹ We require that $t \le ^s_{a} t'$ implies ${\le ^s_{a}} = {\le ^t_{a}} = {\le ^{t'}_{a}}$. If $t \le ^s t'$ we say that $t$ is more plausible than $t'$ given / from the perspective of $s$. The set $Plaus_{a}(s) := \{ t \mid t' \le ^s t\,\text { or } t \le ^s t' \}$ defines the plausible states for agent $a$ given $s$. The set $\min _{a}(s) := \{ t \mid t' \le ^s t\,\text { implies } t \le ^s t' \}$ are the most plausible states for agent $a$ given $s$. If $s \in Plaus_{a}(s)$ for all states $s$, $(S, \le , V)$ is a doxastic epistemic model.$\dashv$

For “$t' \le ^s t$ or $t \le ^s t'$” we write $t \sim ^s_{a} t'$. For $t \sim ^s_{a} t'$ and $t \le ^s_{a} t'$ we can respectively write $t \sim _{a} t'$ and $t \le _{a} t'$ without ambiguity, because ${\le ^s_{a}} = {\le ^t_{a}} = {\le ^{t'}_{a}}$. For $t \le _{a} t'$ and not ($t' \le _{a} t$) we write $t <_{a} t'$ (strictly more plausible), and for $t \le _{a} t'$ and $t' \le _{a} t$ we write $t \equiv _{a} t'$ (equally plausible).

The relation $\sim _{a}$ ‘almost’ defines an equivalence relation for agent $a$. The domain can be partitioned in $\sim _{a}$ equivalence classes, that constitute disjoint sets of plausible states, plus some isolated states. From an isolated state only the states in one such class are considered plausible. (It is a multi-agent KD45 structure, partitioned into, for each agent, ‘KD45 balloons’: a balloon is a prewellorder.)

Definition 2

(Bisimulation) Let doxastic models $M = (S, \le , V)$ and $M'= (S', \le ', V')$ be given, $u \in S$ and $u'\in S'$. A relation $\mathfrak {R}\subseteq S \times S'$ is a bisimulation iff for all $(s,s') \in \mathfrak {R}$:

• [atoms] for all $p \in P$, $s \in V(p)$ iff $s' \in V'(p)$;

• [forth] for all $a \in A$, if $t,u \in S$ and $t \le ^s_{a} u$ then there are $t',u'\in S'$ such that $t' \le ^{s'}_{a} u'$ and $(t,t'), (u,u') \in \mathfrak {R}$;

• [back] for all $a \in A$, if $t',u' \in S'$ and $t' \le ^{s'}_{a} u'$ then there are $t,u\in S$ such that $t \le ^s_{a} u$ and $(t,t'), (u,u') \in \mathfrak {R}$.

A total bisimulation between $M$ and $M'$ is a bisimulation with domain $S$ and codomain $S'$ (all states are related). For a bisimulation between doxastic states $(M,s)$ and $(M',s')$ it is required that $(u,u')\in \mathfrak {R}$.$\dashv$

For doxastic epistemic models, back and forth reduce to the more intuitive (for all $a \in A$):

• [forth] if $s \le _{a} u$ then there is a $u'\in S'$ such that $s' \le _{a} u'$ and $(u,u') \in \mathfrak {R}$;

• [back] if $s' \le _{a} u'$ then there is a $u\in S$ such that $s \le _{a} u$ and $(u,u') \in \mathfrak {R}$.

Definition 3

(Language of doxastic logic) Given are countable sets of agents $A$ and propositional variables $P$. The language $\mathcal {L}$ of doxastic logic is defined as

$$\begin{aligned} \varphi \;{::=} p \ | \ \lnot \varphi \ | \ \varphi \wedge \psi \ | \ B_{a} \varphi \ | \ K_{a} \varphi \ | \ [*\varphi ] \varphi \end{aligned}$$

where $a \in A$ and $p \in P$.$\dashv$

We allow for the usual abbreviations of proposotional connectives and also define $b_{a} \varphi \leftrightarrow \lnot B_{a} \lnot \varphi$ and $k_{a} \varphi \leftrightarrow \lnot K_{a} \lnot \varphi$.

Definition 4

(Semantics of doxastic logic) Let $(S, \le , V)$ be a doxastic model, $s \in S$, and $\varphi \in \mathcal {L}$.

$$\begin{aligned}&M, s \models B_{a} \varphi&\text {iff}\;&\text {for all } t,t'\,\text { such that } t \le ^s_{a} t'\,\text {and}\;t\,\text {is minimal}: M, t \models \varphi \\&M, s \models K_{a} \varphi&\text {iff}\;&\text {for all } t,t'\,\text { such that } t \le ^s_{a} t'\,\text { or } t' \le ^s_{a} t: M, t \models \varphi \\&M, s \models [*\psi ]\varphi&\text {iff}\;&M^{*\psi }, s \models \varphi \quad \text {where}\; M^{*\psi }\;\text {is defined below} \end{aligned}$$

We denote $[\![{\psi }]\!]_M = \{ s \in S \mid M,s \models \psi \}$. $\dashv$

Definition 5

(Belief revision) Let $M = (S, \le , V)$ be a doxastic model and $\psi \in \mathcal {L}$. We give four different constructions for $M^{*\psi } = (S, \le ^*, V)$, defining four belief revision policies. For convenience of presentation we write $t \le t'$ for $t \le _{a}^s t'$ and $t \le ^* t'$ for $t {\le ^*}_{a}^s t'$ (all the below are for arbitrary states $s$ and agents $a$), and we write $s \models \varphi$ for $M,s \models \varphi$, and $s,s' \models \varphi$ for $s \models \varphi$ and $s' \models \varphi$.

$$\begin{aligned} \begin{array}{llll} \text {hard revision} &{} t \le ^* t' &{} \text { iff } &{} t \le t'\,\text {and}\;s, t' \models \psi \\ &{}&{}&{} \\ \text {soft revision} &{} t \le ^* t' &{} \text { iff } &{} t \le t'\,\text {and}\;t,t' \models \psi \\ &{}&{}&{} \text {or} \\ &{}&{}&{} t \models \psi \text { and } t' \not \models \varphi \\ &{}&{}&{} \text {or } \\ &{}&{}&{} t \le t'\,\text { and } t,t' \not \models \psi \\ &{}&{}&{} \\ \text {conservative revision} &{} t \le ^* t' &{} \text { iff } &{} t \models \varphi \,\text { and for all } t'' < t: t'' \not \models \varphi \\ &{}&{}&{} \text {or} \\ &{}&{}&{} t \le t'\,\text { otherwise} \\ &{}&{}&{} \\ \text {severe revision} &{} t \le ^* t' &{} \text { iff } &{} t \le t'\,\text { and } t,t' \models \varphi \\ &{}&{}&{} \text {or} \\ &{}&{}&{} t \models \varphi \,\text { and } t' \not \models \varphi \\ &{}&{}&{} \text {or} \\ &{}&{}&{} (t \le t'\,\text { or } t' \le t)\,\text { and } t,t' \not \models \varphi \qquad \qquad \qquad \dashv \end{array} \end{aligned}$$

Examples of the different effects of these belief revision strategies are shown in Fig. 9.

Hard revision is also known under the names: public announcement [30] (although without the aspect of plausibility), hard update [40], and (Segerberg) irrevocable revision [34]. In this contribution, we will merely see the latter as one kind of irrevocable belief revision. We presented hard revision in the version of the semantics known as ‘believed public announcement’ [16, 21], not in the more standard version ‘truthful public announcement’ [6, 30]. This why in the example the 01 and 00 states remain there after revision. If these were the actual states, the agent would now incorrectly believe that $p$ is false: $01 \models Bp$. She would also be convinced (konvinced) that $p$ is true: $01 \models Kp$. A further revision with $*\lnot p$ would ‘drive her mad’: her accessibility relation would become empty. Soft revision also goes under the name of lexicographic update (a proposal with many old roots), or Spohn-maximal revision. Conservative revision [11] is also known as Spohn-minimal revision (see [46] for the exact relation to Spohn’s [37]). Severe revision is taken from [32] that also lists other forms of severe revision. Their unifying trait is that unequally plausible states become equally plausible. It therefore carries stronger aspects of contraction in it than other belief revision operators. As we will see, merging of plausibilities while retaining (the conceivability of) all states is a requirement for revocable belief revision.

In the standard AGM sense, hard revision, i.e., Segerberg irrevocable belief revision, can be revision but also expansion. In the dynamic epistemic logic setting (that is more semantic than syntactic) it is a mere change of perspective whether something counts as revision or expansion, and not a radically different method. Consider yet another Segerberg style irrevocable update, now with $*p$ instead of $*\lnot p$, on a similar model. Before the revision, the agent believes $p \vee q$, the new information $p$ is consistent with those beliefs. As a consequence of the expansion with $*p$ the agent now believes $p$ ($Bp$ is true in any state of the model). This is an example of expansion.

Definition 6

(Revocable belief revision) A belief revision operator is revocable iff $\psi \rightarrow [*\varphi ][*\lnot \varphi ]\psi$ is valid for all $\varphi ,\psi \in \mathcal {L}$. A belief revision operator is irrevocable iff it is not revocable.

We observe that from the validity of $\psi \rightarrow [*\varphi ][*\lnot \varphi ]\psi$ also follows the validity of $B_{a} \psi \rightarrow [*\varphi ][*\lnot \varphi ]B_{a} \psi$ that spells out the belief change for an individual agent. Therefore the principle formalizes exactly that the beliefs of the agent do not change. For this to hold in the dynamic epistemic logic setting wherein also higher-order beliefs are relevant, we also need the additional principle that $K_{a} \psi \rightarrow [*\varphi ][*\lnot \varphi ]K_{a} \psi$. Obviously that is valid as well.

Definition 7

(Restrictive) A belief revision operator is restrictive iff there is a doxastic model $M$, a state $s$ in $M$ and an agent $a$ such that the plausible states after revision are strictly contained in the plausible states before the revision: $Plaus^*_{a}(s) \subset Plaus_{a}(s)$.$\dashv$

The next proposition needs no proof.

Proposition 8

Hard update is restrictive. The other three belief revision operators are not restrictive.$\dashv$

Proposition 9

A restrictive belief revision operator is irrevocable.$\dashv$

Corollary 10

Hard update is irrevocable.$\dashv$

Definition 11

(Merging) A belief revision operator is merging iff it does not preserve non-bisimilarity of states.$\dashv$

Proposition 12

A merging belief revision operator is irrevocable.$\dashv$

Proof

If belief revision is merging, non-bisimilar states may become bisimilar, and can then no longer be distinguished from one another in the logical language.$\square$

If a revision operator preserves non-bisimilarity, one might say that it preserves structural complexity. The revision operator may jumble plausibilities around as it pleases, but not to the extent that two states with the same valuation become equally plausible for all agents. We recall Definition 2 of bisimilarity: two states are bisimilar if they have the same valuation and the same ‘relation to plausible states’, i.e., for doxastic epistemic models, the same valuation and equal plausibility.

Proposition 13

All four belief revision operators are merging.$\dashv$

Proof

The revision executed in Fig. 6, on page xx would also be the result for soft, conservative, and severe revision. For hard revision, only the 1 and 1 states remain plausible, but the structures are again bisimilar. In all four cases, the total bisimulation is: $\mathfrak {R}= \{ (0,\mathbf {0}), (1, \mathbf {1}) \}$).$\square$

Corollary 14

All four belief revision operators are irrevocable.$\dashv$

Fig. 6

A revision with $*p$

Given this result, surely ‘merging’ is a trivial notion. Not really. The multi-agent versions of the logics are pathological in the sense that bisimilarity resulting from revision is (always) a consequence of identification of equivalence classes (or KD45 balloons). Within a given equivalence class we cannot have such merging. Non-bisimilar states in a KD45 (or S5) equivalence class must have a different valuation, because all states in the class satisfy the same modal formulas (formulas of form $B \psi$ or $K \psi$).

Proposition 15

In the single-agent case, all four belief revision operators are not merging. $\dashv$

Proof

We show that all four belief operators preserve non-bisimilarity. We check the clauses on the right-hand side of the four belief revision operators in Definition 5. We recall that there are two reasons for non-bisimilarity: different valuation, or different degree of plausibility. Or else, combining one or the other, satisfying different formulas of the logic (bisimilarity implies logical equivalence, so logical difference implies non-bisimilarity).

Fig. 7

Identification of bisimilar states

Fig. 8

An example of irrevocable belief revision

Fig. 9

Belief revision with $*\lnot p$ according to the four different revision strategies

Fig. 10

Segerberg irrevocable belief revision can be expansion or revision. This is an example of expansion: belief in $p \vee q$ is strengthened to belief in $p$

Hard revision: $t \le ^* t'$ on the left follows from $t \le t'$ on the right. If there was a different degree of plausibility, it will remain so.

Soft revision: $t \le ^* t'$ follows from one of three clauses on the right. In the first clause it follows from $t \le t'$, which preserves non-bisimilarity. In the second clause non-bisimilarity is preserved because the states $t$ and $t'$ satisfy $\psi$ and $\lnot \psi$, respectively: states satsifying different formulas are non-bisimilar. The third clause is as the first.

Conservative revision: In the first clause, first assume that $t$ and $t'$ are both minimal. They both satisfy $\psi$. If $t$ and $t'$ are not bisimilar (in $M$), they must have a different valuation (see the explanation prior to the proposition), so in $M^{*\psi }$ they still have that different valuation: the two states remain non-bisimilar. Or else, the equally plausible and minimal $t$ and $t'$ already were bisimilar. If $t$ and $t'$ are both minimal but not equally plausible, they remain so. The second clause is also as before.

Severe revision: The first two clauses are as before. In the third clause, states $t$ and $t'$ may become equally plausible. They both satisfy $\lnot \psi$. Either they already were bisimilar, or they have a different valuation (as for conservative revision), so they still carry that valuation in $M^{*\psi }$ and despite being now equally plausible they still remain non-bisimilar.$\square$

We have shown that all four belief operators preserve non-bisimilarity in the single-agent case, but do not preserve it in the multi-agent case. Note that they all preserve bisimilarity, single-agent or multi-agent. This is a standard requirement for such dynamic modal operators. We have not yet shown that they are revocable.

Definition 16

(Plausibility Merging) A belief revision operator is plausibility merging iff states with unequal plausibility before revision may become equally plausible after revision. $\dashv$

Proposition 17

A revocable belief revision operator must be plausibility merging.

$\dashv$

Proof

If a belief revision operator is not plausibility merging, it preserves unequal plausibility. Now, maybe somewhat obviously, no belief revision operator that is not restrictive preserves equal plausibility. For any form of belief revision $*\varphi$, the effect of a revision is not merely change of belief or knowledge but also that ‘$\varphi$ has become an issue’: a refinement of, or different treatment in the model, of the $\varphi$-states and $\lnot \varphi$-states. So belief revision $*\varphi$ may make two equally plausible states unequally plausible after revision. In order for a belief revision operator to be revocable, it should be able that these states become equally plausible again.$\square$

Proposition 18

Single-agent severe revision is plausibility merging. Single-agent hard, soft and conservative revision are not plausibility merging.$\dashv$

Proof

Single-agent severe revision is plausibility merging because two states $t,t'$ not satisfying the revision formula $\varphi$ become equally plausible after revision. In the third clause of Definition 5 of severe revision, we get both $t \le ^* t'$ and $t \le ^* t'$ from the given ‘$(t \le t'$ or $t' \le t')$’.

It is trivial that the other three belief revision operators are not plausibility merging. (A proof would be similar to that of Proposition 15.)$\square$

Corollary 19

Single-agent soft and conservative revision are irrevocable.$\dashv$

Hard revision was already shown to be irrevocable because it is restrictive. We are not left with a small window of opportunity. The only remaining candidate for revocable belief revision is single-agent severe belief revision. In order to be revocable, a belief revision operator must not be merging, but on the other hand it must be plausibility merging. Merging implies plausibility merging, but plausibility merging does not imply merging, as we have seen in the case of severe revision. Unfortunately also single-agent severe revision is irrevocable (see next proposition) but we can still obtain that severe revision is irrevocable in a slightly weaker sense.

Definition 20

(Weakly revocable) A belief revision operator is weakly revocable iff for all $\psi ,\varphi$, there are $\varphi _1,\,\ldots ,\,\varphi _n$ such that $\psi \rightarrow [*\varphi ][*\varphi _1],\,\ldots ,\,[*\varphi _n] \psi$ is valid.

$\dashv$

Proposition 21

Single-agent severe revision is irrevocable, but it is weakly revocable on models with a finite number of degrees of plausibility.$\dashv$

Proof

Single-agent severe revision is irrevocable. For a counterexample see Fig. 11, upper part.

Single-agent severe revision is weakly revocable if there is only a finite number of degrees of plausibility. After the initial revision $*\varphi$, we can recover the original model by successively revising with the formulas characterizing the ‘onions’ from the inside out—and for the finite-degree single-agent model these characterizations are simply the disjunctions of the valuations of the states in these onion bits. An example of this general procedure is given in Fig. 11, lower part.$\square$

Fig. 11

Severe revision is weakly revocable

The successful minimal belief revision that guided us through Sect. 2 is revocable (in the single agent case). It is plausibility merging, but not merging, and the recipe to increase/decrease levels of plausibility is simply reversed by having the revision $*\varphi$ followed by a revision $*\lnot \varphi$. However, as we already observed, it does not allow an elegant reformulation as a qualitatively defined belief revision operator.

4 Conclusion and Further Research

Guided by a proposal by Krister Segerberg on irrevocable belief revision, we defined four belief revision operators, hard/soft/conservative/severe revision, in the setting of dynamic epistemic logic, and investigated whether they are revocable. Belief revision that is restrictive (arrow or state eliminating) and belief revision that is merging (non-bisimilar states become similar) is irrevocable. However, a requirement for revocable belief revision is that it is plausibility merging. Single-agent severe belief revision is revocable on models with a finite number of plausibility distinctions.

It is unclear to us if there are common belief revision operators that are revocable. Is a revocable belief revision operator desirable? It seems a very intuitive concept to us. An undo-button, so to speak. But maybe we have not looked in the proper direction. Instead of looking forward—given a model that is the result of belief revision, what further belief revision restores the original state of information—we should maybe be looking backward: the real undo. In a dynamic epistemic logic with history-based structures [29, 42] and history-operators [33] undoing belief revision $[*\varphi ]$ should not be much else then going back one step in the temporal tree-unfolding, a real sort of $[*\varphi ]^{-1}$ operator.

We think that our work may be relevant for restricted-memory or other bounded rationality approaches to belief revision, e.g., when only a finite number of plausibility distinctions may be stored in memory. A real disadvantage of an otherwise elegant framework like soft update (soft belief revision) is that in the course of iterated revision, the number of belief distinctions only increases and never decreases. For a closer correspondence between logic and cognition, one would like to stick to structures with seven non-bisimilar states, say, corresponding to what the average human can juggle in his or her mind at the same time. Another way to reduced complexity than the plausibility merging that we investigated here, would be awareness/unawareness changing logics, e.g., abstraction as vocabulary restriction (propositional variable restriction). Logics for knowledge, plausibility and awareness have been proposed in [48].