Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

El universo (que otros llaman la Biblioteca)

se compone de un numero indefinido,

y tal vez infinito, de galerías hexagonales… Footnote 1

(Jorge Luis Borges, Ficciones, 1941)

4.1 Introduction

There are atomic surfaces which have no underlying bulk and are free-standing thanks to their covalent bonding architecture. Their vibrational structure reflects, in its general features, their topological constitution, thus playing a relevant role in the growth mechanisms and spectroscopic characterization. The recognition to the studies on graphene (Novoselov et al. 2004, 2005a, b; Geim and Novoselov 2007; Castro Neto et al. 2009) has, by extension, revived the interest in the vast zoo of curved surfaces of carbon which are made possible by sp 2 hybridization. Besides the well-known forms like fullerenes (Kroto et al. 1985), single-walled and multi-walled nanotubes (Iijima 1991), worth mentioning are the three-dimensional forms of sp 2 carbon, random schwarzites. Figure 4.1a, c shows a transmission electron microscope (TEM) image of a random carbon schwarzite obtained by supersonic cluster beam deposition with a deposition energy of 0.1 eV/atom (Barborini et al. 2002; Donadio et al. 1999; Benedek et al. 2003). Raman and near-edge x-ray absorption fine structure (NEXAFS) spectra indicate a pure sp 2-bonding structure, suggesting a single, highly connected graphene sheet with an average pore diameter in the range of 100 nm. Although carbon schwarzites have been first synthesized and characterized more than a decade ago (Barborini et al. 2002; Donadio et al. 1999; Benedek et al. 2003), they did not meet the glamour of the ordered sp 2 carbon forms. Nevertheless, random schwarzites, otherwise termed spongy carbon (Donadio et al. 1999), qualify for their unique properties, such as unconventional magnetism (Rode et al. 2004; Arčon et al. 2006), and applications in efficient super-capacitors (Diederich et al. 1999), field emitters (Boscolo et al. 2000; Benedek et al. 2001; Ferrari et al. 1999), and carbon-based composites (Bongiorno et al. 2005) up to the recent demonstration of interfacing live cells with nano-carbon substrates (Agarwal et al. 2010).

Fig. 4.1
figure 00041

Two transmission electron microscope (TEM) pictures (a, b) of a random carbon schwarzite as grown by supersonic cluster beam deposition (Reprinted from Benedek et al. 2003, Copyright (2003), with permission from Elsevier) and two simulations (c, d, respectively) of the TEM images obtained from analytical approximations of three-periodic minimal surfaces (gyroids) with a self-affine distortion (Reprinted with permission from Barborini et al. 2002. Copyright (2002), American Institute of Physics)

Full size image

Triply periodic minimal surfaces as possible sp 2 carbon structures have been theoretically suggested already in the mid-1980s (McKay 1985) then with more momentum in the early 1990s, following the nanotube vogue (McKay and Terrones 1991; Terrones and McKay 1993; O’Keeffe et al. 1992; Lenosky et al. 1992; Townsend et al. 1992; Vanderbilt and Tersoff 1992).

They have since termed schwarzites after the name of the mathematician Hermann Schwarz (Schwarz 1990) who first investigated that class of surfaces. The synthesis of random schwarzites was obtained by means of supersonic cluster beam deposition (SCBD) (Barborini et al. 2002). SCBD experiments demonstrated that spongy carbon grows in the presence of finely dispersed Mo nano-catalysts, with porous size decreasing with increasing deposition energy and no tendency to form triply periodic structures. These aspects, as well as the growth in the form of a self-affine minimal random surface, have been theoretical elucidated on the basis of pure topological arguments (Benedek et al. 2003, 2005; Bogana et al. 2001). Many relevant properties of schwarzites can actually be derived in a first approximation from a topological analysis. For a thorough discussion of these aspects, the reader is referred to the previously published chapter (Benedek et al. 2011) in this series of book. In this chapter, it is shown that also the vibrational spectra of schwarzitic structures can be estimated from topology, more precisely from the adjacency matrices. After assessing the method on standard cases as the fullerene C60 and the simplest three-periodic schwarzite fcc-(C28)2, for which the vibrational spectra are well established, the novel class of two-periodic schwarzites (Fig. 4.2) shall be introduced and their vibrational spectra as derived with the adjacency matrix method discussed. The interest for two-periodic schwarzites, here discussed for the first time, is related to the possibility of growing them by means of near-to-come planar technologies through the direct joining of nanotubes. We will also present the main result of the first ab initio study about the most interesting planar schwarzite. This study gives us the opportunity to make a comparison between the stability of atoms obtained from ab initio calculation and topological arguments involving the Wiener index. Finally, a quantum-mechanical argument will be exposed and discussed which justifies the success and outlines the applicability range of the Wiener index in determining the stability scale of isomeric carbon structures.

Fig 4.2
figure 00042

The tiling with 6 (light gray) and 7 (dark gray) rings of the unit cell of a P-type (a) and D-type (b) schwarzite, both having 216 atoms per unit cell. The 7 rings are 24 per unit cell in both cases. The unit cell of the D-type schwarzite is made of two identical but nonequivalent elements, containing twelve 7 rings each, joined in the staggered position as atoms are in the diamond lattice (Reprinted from Spagnolatti et al. 2003. Copyright (2003) with kind permission from Springer Science and Business Media)

Full size image

4.2 Adjacency Matrix

For a mono-atomic network of N nodes labeled by an index i = 1,2,…,N, the simplest topological characterization is provided by its adjacency matrix (AM) A whose elements are defined by

$$ {A_{ij }}=\left\{ {\begin{array}{*{20}{l}} 1 & {\mathrm{if}\,\mathrm{nodes}\;\;i,j\,\,\mathrm{a}\mathrm{re}\,\,\mathrm{linked}\,\,\mathrm{by}\,\,\mathrm{a}\;\mathrm{bond}} \\ 0 & {\mathrm{otherwise},\,\,\mathrm{including}\;i=j} \\ \end{array}} \right.. $$
(4.1)

There are elementary structural and physical properties of atomic networks which can be qualitatively understood in terms of the AM. For example, the eigenvectors of A lead to the definition of topological coordinates of three-coordinated carbon structures like fullerenes (Manolopoulos and Fowler 1992) and nanotubes (Làszlò et al. 2001). The topological coordinates may be defined as the set of atomic positions having the highest point symmetry compatible with the adjacencies. The topological coordinates can be defined also for D-type schwarzites, either referring to a single element (genus 2) or to a unit cell (genus 3), and provide a straightforward method to construct a structure with all the same adjacency matrix and point symmetries of the real structure, which may serve as the starting configuration for a molecular dynamics minimization procedure.

As shown in more detail elsewhere (D’Alessio, Master thesis, 2007, Unpublished), isomers of a D-type schwarzite element can be enumerated with the spiraling procedure similar to that introduced for fullerenes (Manolopoulos and Fowler 1992). As an example, Tables 4.1, 4.2, 4.3, and 4.4 list the isomers of the smallest D-type elements C2h+28 with h = 0,2–6. For h = 2–6 only schwarzites within the restricted class with hexagonal necks joining adjacent elements are considered. In this class the isolated elements have therefore a 6-membered ring also at each of the four terminations. The spiral sequences of the 6- and 7-membered rings and the four terminations (0) are listed for each isomer in the second column of Tables 4.1, 4.2, 4.3, and 4.4. For each isomer the point group of the element is also indicated. The smallest D-type schwarzite with h = 0 only contains 7-membered rings and exists in two isomers, one with hexagonal necks (Fig. 4.3) and one with dodecagonal necks. Both isomers are chiral and have their own enantiomer. Examples of topologically equivalent structures constructed by means of the topological coordinates are illustrated in Figs. 4.3 and 4.4 for the elements of the D-type schwarzite (C28)2 and of the three isomers of (C34)2, respectively.

Table 4.1 Isomers of the D-type schwarzite (C32)2 element classified according the sequence of 7- and 6-membered rings determined with the spiraling procedure
Full size table
Table 4.2 Same as Table 4.1 for the isomers of the D-type schwarzite (C34)2 element
Full size table
Table 4.3 Same as Table 4.1 for the isomers of the D-type schwarzite (C36)2 element. Note that the spiraling procedure to enumerate isomers is unable to find the highest symmetry isomer of T d symmetry
Full size table
Table 4.4 Same as Table 4.1 for the isomers of the D-type schwarzite (C38)2 element
Full size table
Fig. 4.3
figure 00043

The element of the (C28)2 isomer with hexagonal necks (a) and its topological coordinate model (b). There are three inequivalent bond lengths labeled by a, b, and c (D’Alessio, Master thesis, 2007, Unpublished)

Full size image
Fig. 4.4
figure 00044

Front and side views of the three topological coordinate models of (C34)2 isomers classified according to their point symmetry groups (see Table 4.2) (D’Alessio, Master thesis, 2007, Unpublished)

Full size image

As seen in Table 4.3, the isomer of highest (T d) symmetry (#19) is not the most stable according to the ranking based on the Wiener index W and topological efficiency index ρ. In any case the stability ranking based on the global topological indices, accounting for the conjugation long-range effects, is in clear conflict with the ranking based on the transferability of fixed bonding energies assigned to the three geometrically inequivalent bonds (D’Alessio, Master thesis, 2007, Unpublished). The former proved to account quite well for the theoretical isomer ranking of some fullerenes (Vukicevic et al. 2011), and it is suggested that it should work equally well for schwarzites. However, both approaches agree in explaining why more compact, though less symmetric isomers are more stable, which favors the growth of random rather than periodic schwarzites in SCBD experiments (Barborini et al. 2002).

4.3 Topological Electronic States

A straightforward application of the AM is the calculation of the electronic energies of a mono-atomic network in the tight-binding (TB) approximation for a band originated from a single atomic state, for example, the p z band in an sp 2 carbon network. By assuming the same diagonal matrix element α of the Hamiltonian for all atomic orbitals, the same overlap integral s, and the same Hamiltonian matrix element (resonance integral) β between the atomic orbitals for all nearest-neighbor pairs, the energy eigenvalues \( E={E_j} \) and the eigenvectors c = c j providing the coefficients of atomic orbital combinations are obtained by solving the TB equation:

$$ {{(\operatorname{I}-s\operatorname{A})}^{-1 }}(\beta \operatorname{A}+\alpha \operatorname{I})\,\mathbf{c}=E\kern-3pt\operatorname{I}\,\mathbf{c} $$
(4.2)

where I is the unitary matrix. The extension of this equation to the periodic schwarzite lattice would provide the valence band structure. In this way a qualitative information about the size of the gap between the highest occupied (HOMO) and the lowest unoccupied (LUMO) molecular orbitals can be obtained as a function of the topology, here represented by the adjacency matrix, and to infer whether the periodic schwarzite will be an insulator or a metal.

As previously shown for tetrahedral D-type schwarzites with 6-membered necks (Gaito et al. 1998; Benedek et al. 2011), the smallest members of the series are alternatively metallic and insulating. The link of the HOMO and LUMO states to basic chemical properties such as site reactivity, electronegativity, and chemical hardness in polyaromatic hydrocarbons (PAH’s) is exploited in the formulation of the so-called colored molecular topology (Putz et al., Chap. 9). In this way these properties, though intrinsically dependent on the electronic structure, may receive a first estimation on purely topological grounds. Figure 4.5 displays a simple application to the icosahedral C60 molecule, where the energy levels of the 60 π-electrons calculated by solving Eq. (4.2) with α = −2.60 eV, β = 3.01 eV, s = 0 are compared with the Hückel energy levels reported by Bühl and Hirsch in units of β (Bühl and Hirsch 2001). In the approximation where β is the same for all bonds, the Hückel energy levels scale exactly as the topological eigenvalues.

Fig. 4.5
figure 00045

The topological energy levels (in eV) of icosahedral C60 from the diagonalization of the adjacency matrix (α = −2.60 eV, β = 3.01 eV, s = 0) compared with Hückel energy levels (in units of β) (Reprinted with permission from Bühl and Hirsch 2001. Copyright (2001) the American Chemical Society). Shadowed peaks correspond to occupied states

Full size image

4.4 Topological Phonon Structure

With the same formalism, though slightly complicated by the vector nature of the atomic displacements, one can investigate the vibrational spectra at zero wavevector of these periodic structures, at least for the part which depends on topology. It is indeed expected that in systems where atoms are all alike and approximately bonded in the same way the gross features of the vibrational spectrum are first of all determined by topology.

It is noted that the vibrational spectra extracted from the adjacency matrix of a P-type element or a D-type schwarzite unit cell, with each of their six terminations closed on the opposite one so as to form a three-handle torus, are topologically equivalent to the spectra at zero wavevector (q = 0) of the corresponding three-periodic solid with periodic boundary conditions. For a flat surface (graphene), the vector nature of the phonon displacement field at q = 0 is factorized into a transverse out-of-plane component, corresponding to a transverse optical mode normal to the surface (TO⊥ mode) having a frequency ω ⊥ = 16.3 rad/s, and two orthogonal in-plane components corresponding to the parallel optical (TO||) and longitudinal optical (LO) modes, having the same frequency of ω ||  = 29.8 rad/s. The degeneracy of TO|| and LO modes at q = 0 is intrinsically due to the symmetry of the three sp 2 bonds forming three angles in plane of 120° and is only approximately fulfilled for a heterocyclic nonplanar structure. In general, on curved surfaces the three angles are distorted and no longer in plane, a fact which is however irrelevant at the topological level. This level of approximation may be referred to as topological dynamics and the eigensolutions as topological phonons.

The assumption that each of the orthogonal components of each atomic displacement only couples with the same component of the three adjacent atoms reduces the dynamical problem to the diagonalization of three independent combinations of the adjacent matrix. In a simplified nearest-neighbor interaction picture, only two nearest-neighbor force constants f ⊥ and f || are needed. The eigenvalue equation providing the angular frequencies \( \omega ={\omega_{{\alpha \nu }}} \) and the components u i  = u iα,ν of the atomic displacements for each phonon ν and each polarization α = ⊥,|| can be expressed in terms of the adjacency matrix as

$$ -M{\omega^2}{\,}{u_i}={f_{\alpha }}\sum\limits_j {\left( {{A_{ij }}-3{\delta_{ij }}} \right)\,} {u_j},\quad \alpha =\bot, \parallel $$
(4.3)

where M is the carbon atom mass, and the term with the Kronecker delta is implied by the translational invariance of the system Hamiltonian. The force constants f α are fitted to the respective angular frequencies ω ⊥ and ω || for graphene given above and considered to be transferable to other sp 2 carbon structures. The angular frequencies are directly obtained from the eigenvalues λ αν of the adjacency matrix and are given by

$$ {\omega_{{\alpha \nu }}}={{\left[ {\frac{{{f_{\alpha }}}}{M}\left( {3-{\lambda_{{\alpha \nu }}}} \right)} \right]}^{\,1/2 }}. $$
(4.4)

4.4.1 Topological Phonons of Fullerenes and Schwarzites

An example of topological phonon spectrum derived from Eq. (4.3) is shown in Fig. 4.6 for the icosahedral isomer of the fullerene C60. There is a good correspondence between the calculated topological phonon spectrum and the experimental spectrum derived by inelastic neutron scattering (NIS) (Cappelletti et al. 1991; Pintschovius 1996). This indicates that the gross features of the C60 vibrational spectrum are accounted for by its topology, that is, by its bonding network.

Fig. 4.6
figure 00046

Comparison between the vibrational spectrum of the icosahedral fullerene C60 measured with neutron inelastic scattering (NIS) (Cappelletti et al. 1991) (a) and the topological phonon spectrum calculated from the adjacency matrix (b). In the latter spectrum, a finite line width is attributed to each phonon peak in order to obtain a smooth spectrum with a resolution comparable to that of experiment (Image reproduced from De Corato and Benedek 2012. Copyright @ 2012 World Scientific, New York)

Full size image

A similar calculation has been done for the D-type schwarzite (C28)2 for which a comparison is possible between ab initio and topological phonon spectra (De Corato et al. 2012) (Fig. 4.7). While the ab-initio spectrum in Fig. 4.7c carries the information about the detailed equilibrium structure of the schwarzite element as depicted in Fig. 4.7a, the topological spectrum only depends on the structure of the graph shown in Fig. 4.7b. Nevertheless, the comparison of the ab initio eigenvectors to those of topological phonons permits to associate four spectral regions of the ab initio spectrum (Fig. 4.7c) to corresponding regions (marked by segments in Fig. 4.7d) of the topological spectrum.

Fig. 4.7
figure 00047

The element C28 of the smallest D-type schwarzite with 6-membered necks (a), the corresponding planar graph (b) with its topological constants (gray regions represent the four necks), and the zero-wavevector ab initio vibrational spectrum of its fcc lattice (C28)2 (c) (Reprinted from Spagnolatti et al. 2003. Copyright (2003) with kind permission from Springer Science and Business Media). The topological phonon spectrum is shown in (d) for comparison. The analysis of the eigenvectors allows to associate four spectral regions of the ab initio spectrum (c) to the marked topological spectral regions in (d). The three modes of zero frequency corresponding to the free translations are not shown

Full size image

The topological phonon spectrum may be conveniently used in the calculation of integral properties such as the vibrational part of thermodynamic functions. As an example, it is perfectly sufficient to use the topological phonon frequencies for the calculation of the mean-square atomic displacement relative to the interatomic distance d, given with the equation

$$ {f_{\mathrm{c}}}\equiv \frac{1}{d}\left\langle {{u^2}} \right\rangle_T^{1/2 }=\frac{1}{d}{{\left[ {\sum\limits_{\lambda } {\frac{\hbar }{{2NM{\omega_{\lambda }}}}} \left( {\frac{1}{{{{\mathrm{e}}^{{\hbar {\omega_{\lambda }}/kT}}}-1}}+\frac{1}{2}} \right)} \right]}^{1/2 }} $$
(4.5)

where T is the absolute temperature. It is possible to estimate the temperature at which the bonds start breaking, leading to melting by means of the Lindemann criterion: For carbon materials, this occurs at f c = 0.084 (Gersten and Smith 2001). A semi-empirical tight-binding molecular dynamics simulation of the topological connectivity as a function of temperature for the D-type schwarzite (C36)2 (Fig. 4.8a) (Rosato et al. 1999) shows that a graphitization transition, consequent to a rapid break of prevalently single bonds, is predicted to occur around 4,000 K. At this temperature, the ratio f c derived from Eq. (4.5), with the topological phonon spectrum (Fig. 4.8b) and the graphite interatomic distance d = 1.42 Å, is equal to 0.077. Raising the temperature beyond graphitization, melting of graphite sheets occurs. A simulation for graphene by Zakharchenko et al. (2011) gives a melting temperature of 4,900 K, which would correspond, on the basis of Eq. (4.5), to f c = 0.085, in good agreement with the Lindemann criterion for carbon materials. In view of such a good correspondence for melting, this analysis provides therefore a criterion for the graphitization transition of schwarzite structures, which can be confidently fixed at f c = 0.077.

Fig. 4.8
figure 00048

(a) The three-dimensional fcc lattice generated by the schwarzite (C36)2 (Image reproduced from Rosato et al. 1999, Copyright (1999) by the American Physical Society). (b) The predicted topological phonon distribution at zero wavevector for a single element of the schwarzite (C36)2 using adjacency matrix diagonalization

Full size image

4.4.2 Topological Phonon Spectrum Versus Genus

It is interesting to compare the topological phonon spectrum for three isomeric structures mapped on closed surfaces of different genus g, for example, a sphere (g = 0), a one-handle torus (g = 1), and a two-handle torus (g = 2). A very simple structure is a hypothetical fourfold coordinated molecule X20 with a single nearest-neighbor force constant (Fig. 4.9). The topological phonon spectra for shear displacements normal to the surface are shown in Fig. 4.10 for the three surfaces. The observed trend is a compactification of the spectrum towards the higher frequencies with increasing genus. Note that the three surfaces represent, in the case of threefold coordination, the topology of fullerene, nanotubes, and the unit cell of a squared planar schwarzite, respectively, the latter two with cyclic boundary conditions.

Fig. 4.9
figure 00049

Isomeric structures of a hypothetical fourfold coordinated molecule X20 mapped on closed surfaces of different genus g: a sphere (g = 0), a one-handle torus (g = 1), and a two-handle torus (g = 2)

Full size image
Fig. 4.10
figure 000410

The topological phonon spectra for shear displacements normal to the surface for the fourfold coordinated isomers shown in Fig. 4.9. The increasing genus of the tessellated surface leads to a compactification of the spectrum towards higher frequencies with increasing genus

Full size image

4.5 Planar Schwarzites

After the discovery of nanotubes (Iijima 1991), the prediction (Fig. 4.11, Spadoni et al. 1997) and the experimental realization of X- and Y-shaped nanotube junctions (Fig. 4.12b, Barborini et al. 2002; Fig. 4.12c, Satishkumar et al. 2000; Deepak et al. 2001) have been the object of an extensive investigation over a decade, with the aim of fabricating electronic devices on the nanoscale (Bandaru et al. 2005).

Fig. 4.11
figure 000411

(a) Illustration of formation of Y-shaped nanojunctions through the welding of a nanotube at the knee of another nanotube and the replacement of two 5-membered rings (yellow) with four (two per corner) 7-membered rings (Reproduced by Spadoni et al. 1997 doi:10.1209/epl/i1997-00346-7. Copyright (1997) by IOP Publishing). Y-shaped nanotubes have been observed in both experiments (b) SCBD (Adapted with permission from Barborini et al. 2002. Copyright (2002), American Institute of Physics) and (c) pyrolysis; see also Satishkumar et al. (2000) and Deepak et al. (2001)

Full size image
Fig. 4.12
figure 000412

The plumber art of connecting elbow-shaped nanotubes (a) and T- (b) and Y-shaped (c) nanotube junctions allows for the fabrication of complex 0-D (d), 1-D (b, e), and 2-D networks (c) of potential use in nanoelectronics; 4-branched schwarzite elements (f) may be used for the construction of either planar or D-type 3-D networks (Adapted from Chernozatonskii 1993. Copyright (1993), with permission from Elsevier)

Full size image

A more ambitious goal is the construction of complex structures of potential interest in nanoelectronics in one (linear schwarzites) and two dimensions (planar schwarzites) through the connection of nanotube segments, as envisaged in the early works by Chernozatonskii (1993) and Spadoni et al. (1997) and following experimental achievements by Terrones et al. (2002) and Romo-Herrera et al. (2007) (Fig. 4.13).

Fig. 4.13
figure 000413

The welding of nanotubes (a) (Adapted with permission from Romo-Herrera et al. 2007. Copyright (2007) American Chemical Society) (From Terrones et al. 2002. © 2002 The American Physical Society) allows in principle to engineer periodic 2-D schwarzitic networks (b) suitable for nanoelectronics

Full size image

On pure geometrical grounds, these architectures could in principle be obtained also through a transformation of a graphene bilayer, where covalent bonds between the two graphene sheets are formed so as to join them through a periodic array of throats, in the manner illustrated in Fig. 4.14. The toll to be paid to topology is the formation of a suitable number of 7-membered rings – 12 per throat. The smallest unit cell of this kind of planar graphite-like (G-type) schwarzites contains just 12 heptagons with no hexagonal ring and has the formula (C14)2 (Fig. 4.15). The threefold symmetric C14 elements can be connected in various ways by nano-tubular throats as, for example, in the planar schwarzites (C18)2 and (C26)2 depicted in Fig. 4.16.

Fig. 4.14
figure 000414

The transformation of a graphene bilayer into a planar schwarzite (C38)2: A ring of six hexagons in the lower graphene sheet is transformed into a ring of six heptagons by inserting six new (red) bonds. In this way a throat is formed with six new (red) hexagons and dangling bonds to be saturated by the equivalent bonds of the specular upper portion. The smallest hexagonal array of such connections has a unit cell (gray area) made of 19 × 2 atoms (green dots) (Reproduced from De Corato et al. 2012, (https://www.novapublishers.com/catalog/product_info.php?products_id=33851. Copyright (2012) by Nova Science Publishers))

Full size image
Fig. 4.15
figure 000415

Elements of the smallest G-type planar schwarzite (C14)2 exclusively made of 7-membered rings. Two elements (A + B) form the unit cell of the periodic graphite-like lattice (Reproduced from De Corato and Benedek 2012. Copyright @ 2012 World Scientific, New York)

Full size image
Fig. 4.16
figure 000416

Graphs representing the planar schwarzites (C18)2 with one tubular neck per element and (C26)2 with three necks per element. A similar planar schwarzite with two such necks per element (not shown) has the formula (C22)2 (Reproduced from De Corato and Benedek 2012. Copyright @ 2012 World Scientific, New York)

Full size image

It should be noted that planar G-type schwarzites are all topologically equivalent, independently of the length of the nanotube connectors, with the same number (12) of 7-membered rings per unit cell. Due to the potential interest of planar schwarzites in devices, the characterization of possible defective structures by means of vibrational spectroscopies is rather important. The defect-induced modification of the vibrational spectrum represents another convenient example of the application of the topological phonon concept.

4.5.1 Vibrational Characterization of Perfect and Defective Planar Schwarzites

Since infrared absorption and Raman vibrational spectroscopies only involve long-wave phonons, the calculation of the zero-wavevector (Q = 0) topological phonons for ideal and defective planar schwarzites should be sufficient for the characterization of their general features. As regards the defects, the following configurations have been considered: (a) the ideal planar schwarzite, (b) a single bond broken, (c) a single bond stiffened, (c) the stiffening of all the three bonds of an atom, (d) a mass defect, and (e) a vacancy. The calculated topological phonon spectra are shown in Figs. 4.17, 4.18, and 4.19 for (C14)2, (C18)2, and (C26)2 and the five above defect configurations.

Fig. 4.17
figure 000417

The topological vibrational spectra at zero wavevector of the smallest G-type planar schwarzite (C14)2: (a) pure lattice, (b) one bond broken at a central atom, (c) one of the three force constants connecting a central atom is doubled, (d) all three force constants of a central atom are doubled, (e) the mass of a central atom is multiplied by 4, and (f) a vacancy at a central atom site (Reproduced from De Corato and Benedek 2012. Copyright @ 2012 World Scientific, New York)

Full size image
Fig. 4.18
figure 000418

Same as in Fig. 4.17 for (C18)2 (Reproduced from De Corato and Benedek 2012. Copyright @ 2012 World Scientific, New York)

Full size image
Fig. 4.19
figure 000419

Same as in Fig. 4.17 for (C26)2 (Reproduced from De Corato and Benedek 2012. Copyright @ 2012 World Scientific, New York)

Full size image

The main vibrational spectral features of schwarzite surfaces depend on the topological structure more than on their two-dimensional nature. In this respect the calculation of the defect perturbation of the phonon density of states (DOS) based on adjacency matrix approximation is sufficiently reliable as long as the general features are concerned. A reason for this prevalence of the topological effects is that the spectral perturbation mostly depends on the Hilbert transform of the bulk densities projected onto the defect sites, that is, on the real parts of the projected Green’s functions: They are integral functions and essentially depend on the gross features of the unperturbed spectra. In detail it appears that the stiffening of the force constants leads to localized modes above the maximum frequency of the unperturbed spectrum (black triangles in Figs. 4.17, 4.18, and 4.19c, d), whereas the break of bonds and the mass increase produce a general phonon softening, with the emergence of resonances in the lower part of the spectrum (black triangles in Figs. 4.17, 4.18e). In all structures there is a narrow gap around 32 THz, separating the lower phonon band of shear vertical (ZO) modes from the upper longitudinal (LO) and shear horizontal (SH) phonon bands. In some cases the local perturbation causes the appearance of a gap mode, as, for example, for a vacancy in (C14)2 (Fig. 4.17f) or a mass increase perturbation in (C18)2 (Fig. 4.18e).

These few examples illustrate the optical vibrational spectra expected for this class of graphene-like carbon nanostructures and the spectral modifications induced by defects, or in general by any local structure which may occur, for example, in functionalized sp 2 carbon samples.

4.5.2 The Planar Schwarzite (C38)2

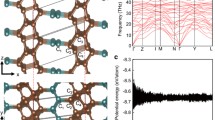
In addition to the proposed structure, we have fully investigated another type of planar carbon schwarzite which has the standard nanotube connection and so is the best candidate for experimental growth. Ab initio calculations have been performed for this particular junction in order to investigate the geometry, the electronic structure, and its phonon frequency distribution at gamma. The carbon planar schwarzite like (C38)2 contains 12 hexagons and the canonical 12 heptagons per element. As argued from the top view of the structure obtained from ab initio calculations and of its unit cell (Fig. 4.20), there are short nanotubes made of six hexagons connected by islands made of six heptagons each. These features reflect in the band structure. The 2-D lattice is hexagonal within the layer group P6/mmm (80); only five atoms are found to be independent by symmetry.

Fig. 4.20
figure 000420

(C38)2 planar schwarzite: a top view of the lattice (a) and unit cell (b) (Reproduced from De Corato et al. 2012, (https://www.novapublishers.com/catalog/productinfo.php?productsid=33851. Copyright (2012) by Nova Science Publishers))

Full size image

The calculations are based on Quantum ESPRESSO codes (Giannozzi et al. 2009) within the density functional theory, with a Perdew-Burke-Ernzerhof exchange-correlation functional (Perdew et al. 1996), a ultrasoft pseudopotential (Vanderbilt 1990), a plane-wave expansion of Kohn-Sham orbitals up to the kinetic cutoff of 30 Ry, and a charge-density cutoff up to 240 Ry. The integration over the Brillouin Zone (BZ) has been performed over a 2 × 2 × 1 Monkhorst-Pack mesh (Monkhorst and Pack 1976) corresponding to 2 k-points in the irreducible two-dimensional wedge. The structure has been optimized by computing its equation of state at zero temperature (energy per unit area) keeping a vacuum distance of 15 Å within the replicas in order to avoid their interaction. The optimized lattice parameter turns out to be a = 10.82 Å. The calculated cohesive energy with respect to that of diamond (Table 4.5) is consistent with previous calculations for three-dimensional schwarzites (Gaito et al. 1998; Spagnolatti et al. 2003).

Table 4.5 Ab initio cohesive energy per atom of the planar schwarzite (C38)2 with respect to other three-dimensional D-type schwarzites and diamond
Full size table

The planar schwarzite (C38)2, as appears from the calculated band structure along high symmetry directions (Fig. 4.21a), is metallic. The band structure shows a large number of flat bands due to the presence of heptagonal rings which break conjugation. This peculiarity, similar to that of 3-D schwarzites (Spagnolatti et al. 2003), yields sharp peaks in the electronic density of states (Fig. 4.21b).

Fig. 4.21
figure 000421

Electronic band structure (a) and density of states (DOS) (b) of the planar schwarzite (C38)2. The zero energy corresponds to the Fermi level (E F)

Full size image

Topology, in particular graph theory, also allows predicting the relative stability of isomers and single atoms. As explained in the next section, for sp 2-bonded structures, this goal can be achieved by using the Wiener index (Wiener 1947). This topological index provides a stability hierarchy of various isomers in the sense that, to a good approximation, the minimum value of the Wiener indices for various isomeric structures indicates the most stable one. This topological approach has been proven successful in the prediction, for example, of the most stable isomers of the fullerene C66 (Vukicevic et al. 2011).

Also the stability hierarchy of single atoms can be established by the ordering of local Wiener indices. Each independent atom has its particular local Wiener index according to its topological position in the graph, and the best connected atom is shown to give the minimum local Wiener index. On the contrary, the least connected atom will provide the maximum local Wiener index. Due to symmetry, only a limited number of independent atoms have different local Wiener indices. In the case of (C38)2, there are only five independent atoms in the unit cell, indicated by the letters A to E in Fig. 4.20b. The corresponding local Wiener indices are reported in Table 4.6 and compared with the medium bond length obtained from DFT calculations.

Table 4.6 The five local (first-order) Wiener indices \( w_i^{(1) } \) of (C38)2 compared with the respective bond lengths from an ab initio calculation
Full size table

It appears from Table 4.6 that the most stable atom (A), having the shortest average bond length, also has the minimum local Wiener index. Similarly the least stable (E) atom with the longest bond lengths has the maximum local Wiener index. The correspondence is however not so precise for the intermediate values. As seen in the next section, the Wiener index is the simplest among various topological indices. Better performances with respect to stability can be obtained with other indices like higher-order Wiener and efficiency. In practice, the stability of single atoms is also related to their chemical reactivity.

4.6 A Physical Basis for the Wiener Index

The physical meaning of the Wiener index for a conjugated sp 2 carbon network and its role in providing a stability hierarchy of isomers can be derived from a tight-binding model for the π electron band structure. Although in the tight-binding picture only nearest-neighbor (nn) matrix elements of the Hamiltonian and overlap integrals between p z atomic orbitals are considered, conjugation effects are felt at large topological distances and contribute a long-range potential energy term which depends on the isomer topology. The wavefunctions of the π electronic band are written as linear combination of atomic orbitals:

$$ {\psi_k}(\mathbf{r})=\mathcal{N}_k^{-1/2}\sum\limits_m {{e_{km }}\varphi (\mathbf{r}-{{\mathbf{r}}_m})}, $$
(4.6)

where k labels the electronic states, m the atoms of the network at positions r m , and e km are the projections of the wavefunctions ψ k on the atomic orbitals \( \varphi (\mathbf{r}-{{\mathbf{r}}_m}) \). Normalization requires that

$$ {{\mathcal{N}}_k}\equiv \sum\limits_{{l{l}^{\prime}}} {e_{kl}^{{_{*}}}{e_{{k{l}^{\prime}}}}{s_{{l{l}^{\prime}}}}} =1+{\sum\limits_{{l{n_l}}}\left( {e_{kl}^{{_{*}}}{e_{{k{n_l}}}}{s_{{l{n_l}}}}+e_{{k{n_l}}}^{{_{*}}}{e_{kl }}{s_{{{n_l}l}}}} \right)}, $$
(4.7)

where

$$ {s_{{m{m}^{\prime}}}}\equiv \int {{d^3}r\,{\varphi^*}(\mathbf{r}-{{\mathbf{r}}_m})\varphi (\mathbf{r}-{{\mathbf{r}}_{{m^{\prime}}}})} =\left\{ {\begin{array}{*{20}{l}} 1 \hfill & {m^{\prime}=m} \hfill \\ {{s_{{m{n_m}}}}} \hfill & {m^{\prime}=nn\;\mathrm{of}\;m\equiv {n_m}} \hfill \\ 0 \hfill & {m^{\prime}\ne m,{n_m}} \hfill \\ \end{array}}\right.\;\;; $$
(4.8)

index n m labels the three closest atoms of atom m. The contribution of the electron in the state k to the expectation value of the energy U m (r) of an atom at a conventional origin (m = 0) is written as

$$ {{\left\langle {{U_0}} \right\rangle}_k}=\mathcal{N}_k^{-1}\sum\limits_{{m{m}^{\prime}}} {e_{km}^{{_{*}}}{e_{{k{m}^{\prime}}}}\int {{d^3}r\,{\varphi^*}(\mathbf{r}-{{\mathbf{r}}_m})\,{U_0}(\mathbf{r})}}\,\varphi (\mathbf{r}-{{\mathbf{r}}_{{m^{\prime}}}}). $$
(4.9)

Although the matrix element in Eq. (4.9) is nonvanishing only for m′, m = 0, n 0, the above expression is a function of the atom positions at any distance r m from the origin via the normalization factor. Its derivative with respect to r m for m ≠ 0, n 0, after some algebraic manipulation, is found to be

$$ \begin{array}{lll}[b] \frac{{\partial {{{\left\langle {{U_0}} \right\rangle}}_k}}}{{\partial {{\mathbf{r}}_m}}}= & -\mathcal{N}_k^{-1 }{{\left\langle {{U_0}} \right\rangle}_k}\sum\limits_{{l{l}^{\prime}}} {e_{kl}^{{_{*}}}{e_{{k{l}^{\prime}}}}({\delta_{{l^{\prime}m}}}-{\delta_{lm }}){{\boldsymbol{\upgamma}}_{{l{l}^{\prime}}}}} \\ & +2\mathcal{N}_k^{-1}\operatorname{Re}\sum\limits_l {e_{km}^{*}{e_{kl }}} \int {{d^3}r\;{U_0}\left( \mathbf{r} \right)\phi \left( {\mathbf{r}-{{\mathbf{r}}_l}} \right)\frac{\partial }{{\partial \mathbf{r}}}\,{\phi^{*}}\left( {\mathbf{r}-{{\mathbf{r}}_m}} \right)} \\ & \equiv {{\mathbf{F}}_{k,m0 }}. \end{array} $$
(4.10)

where

$$ {{\boldsymbol{\upgamma}}_{{{\it ll}^{\prime}}}}=-\boldsymbol{\upgamma}_{{l^{\prime}l}}^{{_{*}}}=\left\{ {\begin{array}{*{20}{l}} {\int {{d^3}r\dfrac{{\partial {\varphi^*}(\mathbf{r}-{{\mathbf{r}}_l})}}{{\partial \mathbf{r}}}\,\varphi (\mathbf{r}-{{\mathbf{r}}_{{l^{\prime}}}}),\quad {l}^{\prime}={n_l},} } \\ {0,\quad\;{l}^{\prime}\neq {n_l},} \hfill \\ \end{array}} \right. $$
(4.11)

The vectors \( {{\boldsymbol{\upgamma}}_{{l^{\prime}l}}} \) are nonvanishing only when l and l′ are nearest neighbor and are directed along the ll′ bond. Consistently with the tight-binding approximation, the integral term in Eq. (4.10) is hereafter neglected, since m ≠ 0,n 0. Equation (4.10) defines a nonvanishing long-range force F k,m0 between atoms 0 and m acting due to an electron in the k-th state of the π-band. The sum over all band states, Σ k F k,m0, is null due to the completeness of coefficients e kl , but the sum restricted to the occupied states of an unfilled band, like that required by conjugation, generally yields a nonvanishing force, which we call conjugation force. On the other hand, it is easily seen that the sum over the conjugation forces exerted by all atoms m on atom 0 vanishes, Σ m F k,m0 = 0, as required by equilibrium.

We now search a potential for the conjugation forces. After neglecting the integral term in Eq. (4.10), the latter can be rewritten as

$$ \begin{array}{lll}[b] \frac{\partial }{{\partial {{\mathbf{r}}_m}}}\ln {{\left\langle {{U_0}} \right\rangle}_k}= & -2\mathcal{N}_k^{-1}\operatorname{Re}\sum\limits_l {e_{kl}^{{_{*}}}\,} {e_{km }}\,{{\boldsymbol{\upgamma}}_{lm }} \\ {} = & -2\mathcal{N}_k^{-1}\operatorname{Re}\left[ {e_{km}^{{_{*}}}\sum\limits_{{{n_m}}} {e_{{k{n_m}}}\,} {{\boldsymbol{\upgamma}}_{{m{n_m}}}}} \right]\equiv -{{\boldsymbol{\upalpha}}_{k;m }}. \end{array} $$
(4.12)

For \( {{\left\langle {{U_0}} \right\rangle}_k} \) a central potential, vector α k;m , expressing the inverse of the conjugation potential range, points in the same direction as r m , as one can argue from a careful inspection of Eqs. (4.10) and (4.11) when the wavefunctions φ(r) refer to p z states. However, it does not depend explicitly on the position of the atom m but on the phase changes of the k-th wavefunction, associated to the products \( e_{km}^{{_{*}}}e_{{k{n_m}}} \), between atom site m and its nearest neighbors n m . For a double bond between m and one of its neighbors, \( e_{km}^{{_{*}}}e_{{k{n_m}}} \) is positive, whereas the other two single bonds starting from m give a negative \( e_{km}^{{_{*}}}e_{{k{n_m}}} \). Thus, the inverse-range vector α k;m is in general nonvanishing; it is however of order N −1, with N the number of atoms, due to the normalization to unity of the coefficients e km . It should be noted, however, that these arguments are valid for threefold coordination and could fail, for example, for atoms on the contour of the network. We assume that the contour effects are either removed by periodic boundary conditions or neglected by considering a large number N of atoms.

It is now convenient to consider the network of N atoms as made of s atomic shells, each shell including the s j atoms which have the same topological distance j from the origin atom (j = 0). Since the maximum topological distance normally depends on the choice of the origin atom, s is defined as the maximum topological distance in the given network. With these definitions, a sum over the atom index m from 0 to N − 1 is replaced by a sum over the s j atoms belonging to the j-th shell times the sum over the s + 1 shells (including the origin, j = 0, s 0 = 1), that is, by a sum over the indices (i,j):

$$ \sum\limits_{l=0}^{N-1 } {\to \sum\limits_{j=0}^s {\sum\limits_{i=1}^{{{s_j}}} {} } } . $$
(4.13)

With the prescription of a constant \( {{\mathcal{N}}_k} \) referred to the equilibrium configuration, the conjugation force F k,m0 can be derived from the potential energy:

$$ \begin{aligned}[b] U_k^{(c) }({r_{i,j }})= & {U_k}\exp \left[ {-{{\boldsymbol{\upalpha}}_{k;i,j }}\cdot ({{\mathbf{r}}_{i,j }}-{{\mathbf{r}}_{i,j-1 }})-(j-1){\beta_{k;i,j }}a} \right] \\ = & {U_k}\exp \left( {-j{\beta_{k;i,j }}a} \right), \end{aligned} $$
(4.14)

where index i has been conventionally used for the atom on each shell belonging to the shortest topological path from atom 0 to atom m = (i,j). We have defined a as the average interatomic distance and

$$ {\beta_{{k;{\,}i,j}}}\equiv {{\boldsymbol{\upalpha}}_{{k;{\,}i,j}}}\cdot \frac{{{{\mathbf{r}}_{i,j }}-{{\mathbf{r}}_{i,j-1 }}}}{a} $$
(4.15)

as the projections of the inverse-range vectors onto the bonds connecting atom (i,j − 1) to atom (i,j). U k is an integration constant which eventually needs to be derived from ad hoc ab initio calculations and is expected to be negative (attractive), similarly to tight-binding resonance integrals between nearest neighbors. A dimensional argument requires U k  = o(N −2).

The total conjugation potential energy U 0,N of atom 0 in an sp 2 network of N atoms is calculated by summing over all occupied electron states of the π-band and all atoms m = (i,j):

$$ \begin{array}{lll}[b] U_{0,N }= & \sum\limits_k^{{(\mathrm{occ})}} {\sum\limits_{j=0}^s {\sum\limits_{i=1}^{{{s_j}}} {{U_k}} } \exp (-j{\beta_{k;i,j }}a)} \\ = & \sum\limits_k^{{(\mathrm{occ})}} {\sum\limits_{j=0}^s {\sum\limits_{i=1}^{{{s_j}}} {{U_k}} \left[ {1-j{\beta_{{k;\,i,j\,}}}a+o\left( {\beta_{{k;{\,}{\,}i,j}}^2} \right)} \right]} } \\ \equiv & \sum\limits_k^{{(\mathrm{occ})}} {{U_k}\sum\limits_{j=0}^s {{s_j}\left[ {1-j{{\bar{\beta}}_{{k\,}}}a+o\left( {\bar{\beta}_k^2} \right)} \right]} } \\ = & {U_{\infty }}-w_0^{(1)}\left( {a\sum\limits_k^{{(\mathrm{occ})}} {U_k{{\bar{\beta}}_k}} } \right)+w_0^{(2)}\left( {{a^2}\sum\limits_k^{{(\mathrm{occ})}} {U_k\bar{\beta}_k^2} } \right)-\cdots, \end{array} $$
(4.16)

where in the third row of Eq. (4.16), the inverse-range constants have been substituted by their average \( {{\bar{\beta}}_k} \). It is this important approximation which allows expressing the conjugation potential energy in terms of the local Wiener index of order 1 for site 0

$$ w_0^{(1)}\equiv \sum\limits_{j=0}^s{j{s_j}}, $$
(4.17)

of the local Wiener index of order 2 for site 0,

$$ w_0^{(2)}\equiv \frac{1}{2}\sum\limits_{j=0}^s {{j^2}{s_j}}, $$
(4.18)

etc. Actually, the expansion to all orders of the exponent in Eq. (4.10) involves the local Wiener index of order n for site 0

$$ w_0^{(n)}\equiv \frac{1}{n!}\sum\limits_{j=0}^s {{j^n}{s_j}} . $$
(4.19)

One may also consider the exponential local Wiener index for site 0

$$ w_0^{{(\exp )}}\equiv \sum\limits_n {{(-1)^n}w_0^{(n) }=\sum\limits_{{j = 0}}^s {{s_j}{e^{-j }}} } . $$
(4.20)

As regards the dependence on the network size, that is, on atom number N, the sum \( \sum\nolimits_k^{{(\mathrm{occ})}} {{U_k}} \) over the occupied states k is of order N −1 and the first term in Eq. (4.16) tends to a constant \( {U_{\infty }} \) for N → ∞ which is independent of the site. The Wiener index \( w_0^{(1) } \) for a single site grows with the number of atoms as N 3/2, so that the term in Eq. (4.10) proportional to \( w_0^{(1) } \) is of order N −1/2. Similarly \( {{w_0^{(n)}\sim o\left( {{N^{1+n/2 }}/n!} \right)}} \) and therefore the corresponding term in the expansion of Eq. (4.16) is of order N −n/2/n!

Since U k  < 0 and \( {{\bar{\beta}}_k} \) > 0, Eq. (4.10) tells that, for a sufficiently large N so that only the Wiener index of order 1 is retained in the expansion, the network site 0 which gives a minimum of the conjugation potential energy corresponds to a minimum in the local Wiener index \( w_0^{(1) } \). For small atom numbers N the local higher-order Wiener indices may not be negligible and deviations from the minimum-\( w_0^{(1) } \) rule may occur. The sum over all sites gives the total conjugation potential energy:

$$ U_N^{\mathrm{tot}}=N{U_{\infty }}-{W^{(1) }}\left( {a\sum\limits_k^{{(\mathrm{occ})}} {U_k{{\bar{\beta}}_k}} } \right)+{W^{(2) }}\left( {{a^2}\sum\limits_k^{{(\mathrm{occ})}} {U_k\bar{\beta}_k^2} } \right)-\cdots $$
(4.21)

where

$$ {W^{(1) }}=\frac{1}{2}\sum\limits_{h=0}^{N-1 } {w_h^{(1) }}, \quad {W^{(2) }}=\frac{1}{2}\sum\limits_{h=0}^{N-1 } {w_h^{(2) },\ldots .} $$
(4.22)

are the Wiener indices of order 1, 2, … of the network. The factor ½ is needed to avoid double counting of the interaction terms. In the first-order approximation, the minimum of the Wiener index of order 1 indicates the most stable isomer. Moreover, it is convenient to define the topological efficiency index ρ as follows (Ori et al. 2009):

$$ \rho =\frac{{{W^{(1) }}}}{{Nw_{\min}^{(1) }}}, $$
(4.23)

where \( w_{\min}^{(1) } \) is the minimum of the local Wiener indices \( w_h^{(1) } \). In case all sites are equivalent (as, e.g., for the icosahedral isomer of C60) so as to give the same local Wiener index, it is ρ = 1. In any other isomer with inequivalent sites, that is, with a lower symmetry, it is ρ > 1, its departure from unity being a measure of a lower topological efficiency.

Within this approach also physical properties directly related to the energy U 0,N can in principle be expanded with the respect to the Wiener indices of increasing order, similarly to Eq. (4.16). Among these properties of fundamental importance are the electronegativity χ and chemical hardness η, which are its first- and second-order functional derivatives of the total energy with respect to the electron density, respectively (see Chap. 9). Actually the present approach leads with a novel way in re-defining the so called intrinsic framework electronegativity (Genechten et al. 1987) and chemical hardness, which can be written as

$$ \chi^{W}=\Sigma_{k}X_{k}W^{(k)}, $$
(4.24)
$$ \eta^{W}=\Sigma_{k}H_{k}W^{(k)}, $$
(4.25)

where X k and H k are suitable coefficients to be determined from the functional derivation of the conjugation energy expressed by Eq. (4.16). Similar expressions can be obtained for the respective local quantities in terms of the local Wiener indices of increasing order, thus providing an analytical route to the coloring procedure (see Chap. 9). The minimal properties, illustrated for the Wiener indices and topological indicators like the topological efficiency index ρ, reflect also on the derived properties, providing fruitful routes for assessing stability (e.g., minimum topological electronegativity \( \chi^{W} \) and maximum topological chemical hardness \( \eta^{W} \)) or reactivity (max \( \chi^{W} \), min \( \eta^{W} \)). They work as abstract chemical reactivity principles (Putz 2010, 2011) among various nano-isomers based on topo-chemical reactivity.

4.7 Conclusions

It has been shown that sp 2-bonded extended systems host an infinite-range interaction associated with conjugation. This global property dominates in many respects over local features so as to make the general topological characteristics of the structure, such as the genus of the supporting surface, the eigenvalues and eigenvectors of the adjacency matrix, the total and local Wiener indices, and the topological efficiency of the corresponding graph, sufficient to estimate many general physical properties such as global and local stability. It is shown elsewhere in this book (Putz et al., Chap. 9) that also local chemical properties such as the chemical potential, chemical hardness, and reactivity can be referred to local topological properties. Topological intrinsic defects in sp 2-carbon structures can as well be characterized by topological indices as far as their stability and thermodynamic probability are concerned. Besides establishing a stability hierarchy of isomers, which is relevant to the configurational entropy of the structure, the topological approach also allows to approximately determine the vibrational contribution to the thermodynamic functions through the diagonalization of the adjacency matrix. The discussion presented in Sect. 4.5 on physical meaning of the stability criteria based on topological indices also warns about the limitations of these indices when applied to small systems. Higher-order Wiener indices may be necessary for a more precise and predictive analysis of isomer stability. Neither this convergence issue nor the effectiveness of the local exponential Wiener index has been so far investigated in comparison with first-principle calculation of the electronic structure. In view of the enormous potential of the topological approach and its numerical applications in disentangling relevant physical properties of complex structures, it is hoped that this chapter will stimulate further studies in this direction.