Worst Case Response Time Analysis of Sporadic Tasks with Precedence Constrained Subtasks Using Non-preemptive EDF Scheduling

Abstract

In this paper, we address the problem of Worst Case Response Time (WCRT) analysis of hard real-time systems composed of sporadic tasks scheduled under non-preemptive Earliest Deadline First (EDF) scheduler. WCRT of each subtask is examined based on the constructed Directed Acyclic Graph of each task. Previous work, does not consider arbitrary timing requirements of subtasks; authors investigate simultaneous arrival time of subtasks only where arbitrary deadlines is not concerned. In contrast to previous work that provides guarantee for a task set that in fact is not schedulable in the worst case, our results show accurate WCRTs.

1 Introduction

In this paper, we consider the problem of schedulability of a set of independent sporadic tasks, where each sporadic task consists of a set of precedence constrained subtasks with arbitrary timing requirements. Subtasks are scheduled using non-preemptive EDF scheduler such that; subtasks with precedence constraints are scheduled according to their precedence relations, subtasks with no precedence relations are scheduled according to non-preemptive EDF algorithm.

Spuri et al. [1] models Worst Case Response Time (WCRT) for sporadically periodic tasks with arbitrary deadlines. However, [1] does not cover subtask dependencies. One approach to consider precedence constraints between subtasks of a sporadic task is to represent the sporadic task by a graph [2, 3]. In order to find WCRT of a subtask, those approaches adopt a technique to convert the sporadic graph of the task under analysis to a canonical chain. This technique is still somehow an approximation to the response times, because in some particular cases, transformation of graph to chain is not able to exploit sufficiently the priorities among subtasks. Moreover, authors covered simultaneous arrival time of subtasks only. In this paper, to acquire accurate WCRTs, no deadline modification is allowed and the analysis is performed on the sporadic graph. In the study of task model defined in [3] (simultaneous arrival of subtasks), our contribution is shown to be effective with an extensive set of simulations in Sect. 5.

This paper starts by introducing related works in Sect. 2, the computational model in Sect. 3. The proposed WCRT analysis is described in Sect. 4. A case study is presented in Sect. 5. Finally, our conclusions are stated in Sect. 6.

2 Related Works

A well-known result for periodic tasks is that the preemptive EDF algorithm is optimal in the sense that it will successfully generate a processor schedule for any periodic task system that can be scheduled [4]. In contrast to periodic tasks, a sporadic task is invoked at arbitrary times but with a specified minimum time interval between invocations. Spuri in [1] proposed WCRT analysis of sporadically periodic task sets with arbitrary timing requirements scheduled under preemptive EDF. However, [1] does not cover dependency among subtasks of a sporadic task. The approaches proposed by Zhao in [2, 3], concerns WCRT analysis for a set of sporadic tasks, scheduled under non-preemptive EDF and fixed priority, respectively. The main idea in [3] is to transform the sporadic graph of analyzed task to a canonical chain so that each subtask in the obtained canonical chain has a priority strictly higher than its predecessors. However, authors in [2, 3] cover simultaneous arrival of subtasks only. Since our approach allows arbitrary arrival time of subtasks within a task, our WCRT analysis includes the computational model presented by [3] as a special case. In the study of task level precedence constraints, [5] generalizes the concept of precedence constraint between tasks to allow tasks to have different rates. [6] partitions the graph of tasks into a set of parallel flows, to meet the specified timing constraints.

As for distributed hard real-time systems, Spuri in [7] adapted the Holistic Analysis technique to the systems that scheduled under EDF. Later [8–11] improved the estimations of WCRTs by developing the offset based technique. The fundamental principle behind is that, given the offset information of tasks at a communication resource one can compute (in a worst-case manner) the jitter and offset for tasks leaving that communication resource, which in turn becomes the arrival pattern for tasks to the subsequent communication resource [12]. Another extension is proposed by [13], which allows each task to have one or more immediate successors.

3 System Model and Notations

Definition Sporadic Task (τ _i )

sporadic task τ_i consists of n _i number of subtasks τ_i = {τ_i,1, …, τ_i,ni} with precedence constraints and arbitrary timing requirements. Inter-arrival time of each task is separated by a minimum time T _i . Each task activation at time t results in activation of all subtasks, each one at time t _i,j  = t + O _i,j , where O _i,j denotes the arrival time relative to the activation of the task, Fig. 1. Each subtask has an execution time C _i,j , and relative deadline D _i,j . The absolute deadline d _i,j of subtask τ_i,j requested at time t _i,j equals $d_{i,j} = t_{i,j} + D_{i,j}$ Relative deadline of task τ_i is denoted by $D_{i};$ where $D_{i}$ equals $D_{i} = \max_{j} \left({O_{i,j} + D_{i,j}} \right)$. The precedence relations in each sporadic task are represented by a Directed Acyclic Graph (DAG) as shown in Fig. 1.

Fig. 1

Computational model of a sporadic task

Definition Busy Period

the time interval delimited by two successive idle times, during which the CPU is not idle. Let us denote the length of the longest busy period by L and the starting instance of the longest busy period by t _B .

Definition Deadline- $d$ Busy Period

A processor busy period in which only the subtasks with absolute deadline smaller than or equal to $d$ execute.

Definition Worst Case Response Time (WCRT) $\left({R_{i,j}} \right)$

maximum possible delay between arrival time and completion time of subtask τ_i,j on each activation time of the subtask τ_i,j inside the longest busy period:

$$ R_{i,j} = max \left\{{R_{i,j} \left(r \right)} \right\};\forall r t_{B} \le r < t_{B} + L $$

(1)

Procedure 1 determines the order of scheduling of subtasks:

Procedure 1

// τk,l denotes the subtask that is released inside the busy period

Set t = 0

Do

Among subtasks with no predecessors select subtasks that arrived in the interval $\left[{t_{B},t_{B} + t} \right]$; Execute a  subtask τk,l with minimum deadline; $t = t + c_{k,l}$;  Remove the executed subtask, τk,l , from its associated task graph;

Until processor becomes idle

4 Response Time Analysis of Sporadic Tasks

To find the WCRT of analyzed subtask, we must build the critical instant, leading to the calculation of the worst case execution interference. Since in our model each task consists of subtasks with arbitrary release times, we must take into account that the critical instance may not be obtained by occurrence of all tasks at the starting instance of the busy period, as was considered as the worst case in [1, 3]. Let us consider coincidence of which subtasks of a task τ_k to $t_{B}$ would result in the critical instance. To do so, first we shall categorize subtasks of the task τ_k in two sets: Set ^H_k : composed of subtasks with $D_{k,l} \le d,$ Set ^L_k : composed of subtasks with $D_{k,l} > d$. According to the definition of deadline$- d$ busy period, only the subtasks of task τ_k, $k \ne a$, included in Set ^H_k would be considered to delay the execution of the subtask τ_a,b, by arriving inside a deadline—d busy period. Therefore, a deadline—d busy period could be constructed by releasing one subtask of each task with $D_{k,l} \le d$ at $t_{B}$. However, we don’t know which subtask coincidence to $t_{B}$ corresponds to the critical instant for the analysis of the subtask τ_a,b. So in the procedure of considering critical instance of subtask τ_a,b, we must study all possible deadline—d busy periods created by choosing one higher priority subtask in each task to occur at time $t = t_{B}$. Notice that, from [14] we have, the computation of the invocation of subtasks released before $t_{B}$ can be ignored provided that an additional deadline—d busy period could be examined, which starts at the release of that invocations.

Let us consider possible blocking times due to non-preemptability. Suppose that a subtask τ_p,q with $D_{p,q} > d$ starts its execution one unit time before releasing higher priority subtasks at $t_{B}$. Due to non-preemtability, the subtask τ_p,q has to be executed completely before starting of the execution of higher priority subtasks. Consequently, execution of subtask τ_p,q will allow the successors of τ_p,q, denoted by τ_p,j, with $d_{p,j} \le d$ to possibly be executed in the considered deadline$- d$ busy period. Furthermore, since each τ_p,q could be followed by different amount of computation time of higher priority subtasks, we tend to consider all possible deadline$- d$ busy periods by further incurring all possible priority inversions. Notice that, in this case, to take care of definition of the busy period, we move $t_{B}$ to starting instance of execution of τ_p,q. Consequently, all higher priority subtasks will be released at time $t = t_{B}+1$.

Theorem 1

The WCRT of subtask τ _a,b with release time at $t_{B} \le r < t_{B} + L$ and absolute deadline $d$ , is found in one of the following cases:

• 1. In a deadline—d busy period of subtask τ _a,b where the first activation of some subtask τ _k,l , of task τ _k , k$\ne\, a, with$$D_{k,l} \le d$coincides with$t = t_{B}$and task activations of τ _k occur periodically with their maximum rate inside the busy period.

• 2. In a deadline —d busy period of subtask τ _a,b where the first activation of some subtask τ _k,l , of task τ _k , k$\ne a, with$$D_{k,l} \le d$coincides with$t = t_{B} + 1$and task activations of τ _k occur periodically with their maximum rate inside the busy period, also a priority inversion occurs at time$t = t_{B} + 1$, where one subtask τ _p,q , p$\ne$ a with$D_{p,q} > d$activates at time$t = t_{B}$.

Proof consider the first case: let $t_{1} > t_{B}$ be the instant at which a subtask τ_k,l , $k \ne a$ with absolute deadline $d_{k,l}$ is activated the first time inside the busy period, and let $d_{k,l} \le d$. Suppose that we move $t_{1}$ to coincide with $t = t_{B}$ in this circumstance, it is possible that an activation of successor subtasks of subtask τ_k,l , denoted by τ_k,j, with an absolute deadline after instant $d$ may have been moved earlier to have a deadline before or at $d$, thus it would possibly increase the response time of analyzed subtask. The proof of second case, is similar to above discussions. □

Based on Theorem 1, in the procedure of finding the critical instance of subtask τ_a,b released at time $t_{B} \le r < t_{B} + L$, we must study all possible deadline$- d$ busy periods created by choosing one higher priority subtask in each task to occur at time $t = t_{B}$. Further we must study all possible deadline$- d$ busy periods created by choosing one higher priority subtask in each task to occur at time $t = t_{B} + 1$ where one lower priority subtask in one task occurs at time $= t_{B}$ and consequently incurs priority inversion at time $t = t_{B} + 1$. Given all possible deadline$- d$ busy periods, the largest response time of subtask τ _a,b is accounted for its WCRT, denote by $R_{i,j}$. Without loss of generality, in the rest of this paper, we shall denote the time $t = t_{B} + 1$, in the second condition of Theorem 1, by $t = t_{B}$. Further the coincided subtask of task τ_k to $t_{B}$ is denoted by τ _k,l . Through analysis expressed in Eqs. 2–10 we shall assume that task τ _a consists of one subtask, τ_a,b, only. In the latter part of this section we will extend the analysis to consider response time of τ_a,b where the task τ _a includes a sporadic graph with precedence constraints.

Let us first consider a complete activation of task τ_k that occurs in the time interval $\left[{t_{B},t} \right]$ where $t > t_{B}$. This activation occurs before $t$ so that $t - {^{\prime}}{activation\;time}^\prime \ge T_{k}$ and $^{\prime}activation\;time^{\prime} - t_{B} \ge 0$. We denote the total number of complete activations of task τ_k that occur in the time interval $\left[{t_{B},t} \right]$, by $N_{k,l} (t)$. Remember that in our analysis we assume that the subtask τ_k,l has been released at $t_{B}$. From Fig. 2, it is easy to see that $N_{k,l} (t)$ could be obtained by: $N_{k,l} (t) = \frac{{t - \rho_{k,l}}}{{T_{k}}},$ where $\rho_{k,l}$ represents the phase between $t_{B}$ and the first activation of task τ_k inside the busy period. Hence we have $\rho_{k,l} = T - O_{k,l}$ if $O_{k,l} > 0$ and $\rho_{k,l} = 0$ otherwise. The total time required to schedule activations of task τ_k occurred completely in the time interval $\left[{t_{B},t} \right]$ quals:

Fig. 2

A scenario to obtain complete activations of task τ_k up to time t

$$ {\text{C}}_{k,l} \left(t \right) = \left\lfloor{ \frac{{t - \rho_{k,l}}}{{T_{k}}}} \right\rfloor \cdot \mathop \sum \limits_{{{\text{i}} = 1}}^{{{\text{n}}_{\text{k}}}} {\text{c}}_{{{\text{k}},{\text{i}}}} $$

(2)

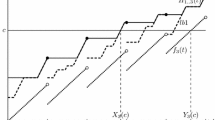
Figure 3 represents a scenario for the alignment of task τ_k arrival pattern after $t_{B}$. Upper part of this figure corresponds to the activation and deadline of subtask τ_a,b, and the lower part represents the activation of subtasks of task τ_k. In this figure, $N_{k,2} \left({t^{\prime}} \right) = 0$, because $t^{\prime} - t_{2} < T_{k}$. Further, since $t^{\prime\prime} - t_{2} > T_{k}$, $t_{2} - t_{B} > 0$ also $t^{\prime\prime} - t_{3} > T_{k}$, $t_{3} - t_{B} > 0$, we have $N_{k,2} \left({t^{\prime\prime}} \right) = 2$.

Fig. 3

An example for calculating required time to schedule task τ_k up to time $t$

Notice that in above discussion we only find the time required to execute $N_{k,l} (t)$ activations of task τ_k. However, among those, activations of task τ_k released after $d - D_{k}$ would not contribute to the response time of analyzed subtask. Thus at each given time interval $\left[{t_{B},t} \right]$, only activations of task τ_k with deadlines before or at $d$, can contribute to the response time of analyzed subtask. That is at each given time interval $\left[{t_{B},t} \right]$, ${\text{C}}_{k,l} (t)$ is bounded by:

$$ G_{k,l} \left(d \right) = \left({1 +\left\lfloor {{\frac{{d - (D_{k} + \varphi_{k,l})}}{{T_{k}}}}}\right\rfloor}\right) \cdot \mathop \sum \limits_{i = 1}^{{{\text{n}}_{\text{k}}}} c_{k,i} $$

(3)

Therefore, the contribution of ${\text{N}}_{k,l} \left(t \right)$ complete activations of task τ_k to the response time of analyzed subtask, at each given time interval $\left[{t_{B},t} \right]$, is given by:

$$ W_{k,l} \left({t,d} \right) = { \hbox{min} }( {\text{C}}_{k,l} \left(t \right),G_{k,l} \left(d \right)) $$

(4)

To see this, redo example in Fig. 3, let us assume that $D_{k,1} = D_{k,3} = T_{k},$ $D_{k,2} = 3 \cdot T_{k} - O_{k,2}$ and hence $D_{k} = 3 \cdot T_{k}$. In this case, we have ${\text{C}}_{k,2} \left({t^\prime{^\prime}} \right) = 2.\mathop \sum \limits_{{{\text{i}} = 1}}^{3} {\text{c}}_{{{\text{k}},{\text{i}}}}$, $G_{k,2} \left(d \right) = 0$ and consequently $W_{k,l} \left({t^\prime{^\prime,d}} \right) = 0$.

Equation 4 only obtains contribution of complete activations of task τ_k that occur inside the time interval $\left[{t_{B},t} \right]$. The problem that remains is to obtain contribution of activations that do not interfere to the response time of subtask under analysis, completely. We shall categorize those contributions of task τ_k in two sets. Set A: Activations included in this set occur completely inside the time interval $\left[{t_{B},t} \right]$ but they have deadline greater than $d$. Thus those activations do not interfere to the response time of τ_a,b, completely. For example in Fig. 3; consider $D_{k,1} = D_{k,3} = T_{k}$, $D_{k,2} = 3 \cdot T_{k} - O_{k,2}$. In this case, we have $W_{k,2} \left({t^\prime{^\prime},d} \right) = 0$, but activations of task τ_k occurred at times $t_{2}$, $t_{3}$ consist of some subtasks that would delay the response time of τ_a,b; subtasks τ ²_k,1 , τ ³_k,1 . We shall define $\delta_{k,l}^{A} \left({t,d} \right)$ to obtain total computation time of subtasks of activations of task τ_k in Set A by:

$$ \delta_{k,l}^{A} \left({t,d} \right) = \hbox{max} \left({E_{k}} \right) $$

(5)

where $\hbox{max} (E_{k})$ represents summation of computation time of subtasks of activations in Set A that have an absolute deadline less than or equal to $d$ and activation time before or at $t$, so that all their predecessors also have an absolute deadline less than or equal to $d$ and activation time before or at $t$. In Fig. 3, consider $D_{k,1} = D_{k,3} = T_{k}$, $D_{k,2} = 3 \cdot T_{k} - O_{k,2}$, we have $\delta_{k,l}^{A} \left({t,d} \right) = 2 \cdot c_{k,1}$. Set B: Activations included in this set do not occur inside the time interval $\left[{t_{B},t} \right]$, completely. This set may consists of two members only. The first one is the first activation that occurs immediately before $t_{B}$, where $O_{k,l} \ne 0$; e.g. activation of task τ_k occurred at time $t_{1}$, in Fig. 3. The second member of Set B is the last activation, where $t - ^{\prime}\, {\rm activationtime} ^\prime < T_{k}.$ Consider time interval $\left[{t_{B},t} \right]$ in Fig. 3, activation of task τ_k occurs at time $t_{2}$, corresponds to this element. We shall define $\delta_{k,l}^{B} \left({t,d} \right)$ to account for total computation time of subtasks of activations of task τ_k in Set B by:

$$ \delta_{k,l}^{B} (t,d) = \hbox{max} (E_{k}) $$

(6)

where $\hbox{max} (E_{k})$ is defined as for Eq. 5. Finally, we shall define $\delta_{k,l} \left({t,d} \right)$ to obtain total computation time of subtasks of activations of task τ_k in Set A and Set B by:

$$ \delta_{k,l} \left({t,d} \right) = \delta_{k,l}^{A} \left({t,d} \right) + \delta_{k,l}^{B} (t,d) $$

(7)

So far, we have studied the contribution of task τ_k to the response time of τ_a,b that has been released until time $t$. In general the study of response time of a subtask τ_a,b with deadline d is an iterative procedure. The basic idea is that in each step the obtained busy period, must be the end of execution of all instances of all tasks with deadlines less than or equal to d, that have been released in previous steps. Toward this we shall define $LN_{a,b} (t,d)^{(k)}$ to represent the length of the resulting busy period in the k’th iteration of response time analysis of subtask τ_a,b with deadline d, where $t$ is substituted with the length of obtained busy period in previous step. $LN_{a,b} (t,d)^{(k)}$ is obtained by the iterative equation Eq. 9. This equation represents the iterative procedure where at each step the length of busy period is given by summation of execution times obtained in Eqs. 4, 7. We shall initiate this iterative procedure by Eq. 8. In Eq. 8, $c_{k,l}$ represents the execution time of coincided subtask of each task to $t_{B}$. The upper part of Eq. 8 indicates the initial value of $LN_{a,b} (t,d)$ in a scenario constructed based on first term of Theorem 1. The lower part of Eq. 8 indicates a scenario constructed based on second condition of Theorem 1. The iteration is halted where the computations converge.

$$ LN_{a,b} (t,d)^{(0)} = \left\{{\begin{array}{ll} {\sum_{{\forall k}} c_{k,l}} & {first\;scenario\;in\;Theorem.\;1} \\ {\sum_{{\forall k}} c_{k,l}} - 1 & {second\;scenario\;in\;Theorem.\;1} \\ \end{array}} \right. $$

(8)

$$ LN_{a,b} \left({t,d} \right)^{{\left({m + 1} \right)}} = \mathop \sum \limits_{k} W_{k,l} (LN_{a,b} (t,d)^{(m)},d) + \mathop \sum \limits_{k} \delta_{k,l} (LN_{a,b} \left({t,d} \right)^{\left(m \right)},d) $$

(9)

The response time of subtask τ_a,b where it occurs at time $t_{B} \le {\text{r}} < t_{B} + L$ is:

$$ R_{a,b} \left(r \right) = LN_{a,b} \left({t,d} \right) + c_{a,b} - r $$

(10)

Then the worst case response time of subtask τ _a,b can be obtained by Eq. 1.

The problem that remains to be solved is to determine the response time of subtask τ_a,b where task τ _a includes a sporadic graph with precedence constraints. Consider a scenario where τ _a,b is released at $r$. In this case, the response time of τ _a,b is influenced by the order of execution of all subtasks of task τ _a that must be scheduled before τ _a,b . Further, this sequence of subtasks of task τ _a may not be the same as sequence of subtasks in another scenario where τ _a,b is released at $r^\prime$. Therefore, it is of great importance to determine the order of subtasks of task τ _a that must be scheduled before τ _a,b for each release time of τ _a,b .

Let us denote the current subtask of task τ _a that its response time has been considered by τ_a,q and the next chosen subtask by τ_a,p. Consider a scenario where τ _a,b is released at $r$. In order to find the correct response time of subtask τ _a,b , we shall use Procedure 1, to determine the correct sequence of subtasks of task τ _a that must be scheduled before τ _a,b . This procedure would let us to consider the correct sequence of subtasks of task τ _a that must be scheduled before τ _a,b and consequently the correct response time of subtask τ _a,b . Because τ_a,q and all the subtask of task τ _a that has been considered by Eqs. 8 or 9 will be dropped from the sporadic graph of task τ _a . Finally, τ_a,p would be a subtask with minimum deadline among subtasks of task τ _a with no predecessor and arrival time at or before completion of execution of τ_a,q.

5 Comparison with Existing Techniques

We have compared the results of our proposed analysis, with the results obtained by [3], the only bibliography of our work. Reference [3] defines sporadic task model with a major constraint; simultaneous arrival time of all subtasks of a task after the arrival of the external event. Due to space constraint we refer reader to [3] for more details. We have conducted a set of simulations with a set of tasks represented in Table 1.

Table 1 Tasks parameters

Figure 4 compares the WCRT of tasks τ1, τ2 with WCRT obtained by Zhao’s technique and the response times obtained using our approach. The X axis represents processor utilization and the Y axis represents WCRT. The processor utilization is raised by changing the period of task under analysis in the interval [9,300], where at 9 the system no longer meets its deadlines and at 300 the utilization is close to zero. It can be seen that for utilization values of 50 % and lower, our approach and the algorithm in [3] obtain same results. However, for utilization values of 50 % and higher, increasing the utilization of the task cannot increase the obtained WCRT by Zhao’s approach but we can get an increase of response time over two times greater than Zhao’s algorithm. This result is due to graph to canonical chain transformation in Zhao’s approach where it incurs deadlines of predecessor subtasks of the subtask under analysis to be increased. Specifically, in a case where the analyzed subtask has a larger deadline than its successors and the associated task has a tight period, Zhao analysis would imply that the system is still schedulable but in fact tasks will miss their deadlines in the worst case.

Fig. 4

Response time comparison

6 Conclusion

In this paper we studied WCRT analysis of sporadic tasks scheduled under non-preemptive EDF scheduling. The objective is to obtain precise WCRTs of a task with arbitrary timing requirements that is not considered in previous works. A nice feature of our work is that it exploits precedence constraints between subtasks in an accurate way while taking advantage of deadline of subtasks. We find via simulation results that our methodology provides accurate results compare with existing work in [3].