Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In the current educational climate, tracking students’ academic growth in subjects (i.e. mathematics, reading, etc.) over time is of great interest to educators, as well as to the public. An implicit requirement of tracking is that performance and test items across grades can be compared using an established framework. It is obvious that the scores across grades obtained in achievement tests routinely used by schools or large-scale assessment programs cannot be compared directly because the difficulty of such tests and programs differs between grades. Suppose students A and B got the same score, for example, 80 points, in Primary 1 mathematics test and Primary 4 test, respectively. Although they have the same score, student B certainly has higher mathematical ability than student A because the test for Primary 4 level is more difficult than the test for the Primary 1 level. Such scores obtained from the different tests must be placed on a common scale before they can be compared and interpreted under the same framework.

Vertical scaling places the scores obtained from tests with different difficulty levels and measures the same construct on a common scale. The scale developed through vertical scaling is called a vertical scale (also referred to as a developmental scale) (Briggs and Weeks 2009; Harris 2007; Tong and Kolen 2007).

Vertical scaling is usually derived from a set of tests that are developed to assess the same domain across a range of grades. These tests are linked through common items (or linking items) that are shared by adjacent grades. A statistical procedure, usually using unidimensional item response theory (IRT), is then applied to the set of tests, and all of the items in those tests are calibrated on the same latent scale. The resulting vertical scale consists of an item pool, with each item having a fixed difficulty estimate.

2 Importance of Vertical Scaling

Vertical scales facilitate monitoring of students’ academic growth over time. This has proved challenging for traditional grade-by-grade assessment approaches due to the incomparability of scores obtained on different tests, which are comprised of different items with various difficulty levels. Vertical scales overcame this problem by calibrating all of the items in different tests on a common scale. It provides a stable framework for comparison and interpretation of students’ abilities estimated from different tests. Once an item is calibrated on the vertical scale, it has a unique estimate of difficulty on the scale, and this estimate remains invariant for all students and all test situations. Teachers, parents or anyone who wishes to measure students’ achievement levels can formulate a test by drawing items from the item pool provided by the vertical scales according to different criteria or different situations. It is just like selecting different “rulers” with different minimum and maximum values, while using the same unit of length from a ruler pool to measure the length of objects with different sizes. A “0–200 cm” ruler can be used to measure adults’ heights, and a “0–100 cm” ruler can be used to measure babies’ heights. In a similar way, a test can be formulated for grade 4 students by selecting items with a particular range of difficulty levels; a specific item with a lower difficulty level can also be utilised to assess the ability levels of grade 2 students. What is more important and exciting is that students’ ability levels measured by the different tests—they are calibrated on the same vertical scale—can be interpreted in the same framework and compared along the same scale. Another important feature of vertical scales developed using unidimensional IRT models is that the scores obtained in the vertical scales are linear and equal-interval measures. The same scores reflect the same amount of the construct measured, irrespective of the source test; moreover, adding one more unit results in equal-size increments. For example, a score of 60 in the grade 2 test represents the same level of ability as that of a 60 in the grade 4 test as long as both tests are vertically scaled. The growth from 60 to 70 (10 points) is the same as the growth from 70 to 80 (10 points) on a vertical scale. Therefore, as long as the item pool covers a corresponding range of difficulty, vertical scales make it feasible to track students’ academic growth across a range of grades.

3 Challenges in Vertical Scaling

Although vertical scaling is a promising approach for monitoring students’ development over time, there are concerns about the utility of these scales in a practical educational context. The most important concern probably relates to doubts about the validity of the unidimensionality assumption of the construct being measured across several grades (e.g. Camilli 1999; Lissitz and Huynh 2003; Yon 2006). As vertical scales are usually developed using unidimensional IRT models, the tests across grades are assumed to measure the same trait, just at different difficulty levels. Violation of the unidimensionality assumption would influence the vertical scaling results. If the assessments are designed to measure several distinct dimensions of the content that explains performance differences, then a vertical scale is not expected to produce usable data (Yen 2009). Therefore, test developers need to ensure that the items in the tests across different grades measure the same dimension of the construct to satisfy the unidimensionality assumption for vertical scaling. However, in practice, this assumption may not hold in many situations. As pointed out by Yen (2007), educational achievement tests are usually multidimensional, although they tend to have a strong principal domain. Not all of the links between different grade tests are strong enough to maintain a robust connection between those grades.

Furthermore, vertical scaling is a complex procedure. Previous research (e.g. Camilli et al. 1993; Petersen et al. 1983; Custer et al. 2006; Hanson and Béguin 2002; Hendrickson et al. 2006; Ito et al. 2008; Kim and Cohen 1998; Pomplun et al. 2004; Tong and Kolen 2007; Wingersky et al. 1987) has shown that vertical scaling results depend on many factors, such as the linking method and the IRT model used, the ability/difficulty estimation method employed and the design of the data collection used in the construction of the scale. A number of important decisions need to be made during the construction of the scale, and the combinations of these decisions probably result in somewhat different vertical scales.

Ito et al. (2008) used real data from a national standardisation assessment study and compared two vertical scaling approaches—concurrent and separate grade-groups linking—for grades kindergarten through 9 for reading and mathematics. They found that reading is more likely than mathematics to have a single prevalent trait across grades because similar results were generated at more grades in reading than in mathematics. The two approaches produced similar results in terms of item difficulties, discriminations and ability estimates. However, the separate grade-groups scaling had better control in terms of scale expansion than did concurrent scaling. Thus, an increase in the score variance at the highest and lowest grades is more salient for concurrent scaling than for separate grade-groups scaling. Kim and Cohen (1998) also found that similar results were generated by concurrent and separate methods except that the separate method provided more accurate estimates when the number of common items was small. In contrast, some research (e.g. Petersen et al. 1983; Wingersky et al. 1987) found that concurrent estimation was better than separate estimation. Hanson and Béguin (2002) also found that concurrent estimation outperformed separate estimation by generating a lower error in most conditions.

Pomplun et al. (2004) compared scaling results from WINSTEPS (Linacre 2011) and BILOG-MG (Zimowski et al. 1996) with both real and simulated data. WINSTEPS and BILOG-MG differ in two respects: WINSTEPS uses joint maximum likelihood estimation (JMLE) as the estimation method, whereas BILOG-MG uses marginal maximum likelihood estimation (MMLE). BILOG-MG also has a group option during estimation, whereas WINSTEPS has not. The findings of concurrent calibration showed that WINSTEPS generated more accurate individual and mean estimates, whereas BILOG-MG produced more accurate standard deviations. In another similar study, Custer et al. (2006) further compared results generated with WINSTEPS and BILOG-MG. Based on simulated vocabulary tests, they conducted vertical scaling with the Rasch model for grades kindergarten through 10. They used a common item block design and concurrent calibrations for scaling. Their results suggested that the convergence setting in the program was an important factor that influenced the parameter estimation. BILOG-MG generated more accurate individual and mean estimates than did WINSTEPS under default convergence settings. Tightened convergence settings enabled both programs to produce more accurate estimates than did default convergence settings. Furthermore, under tightened convergence settings, WINSTEPS and BILOG-MG produced similar scaling results. They recommended using MMLE with the direct group option of BILOG-MG to estimate group parameters in concurrent vertical scaling.

Tong and Kolen (2007) employed two data collection designs: the scaling test (SC) design and the common-item (CI) design. Under the SC design, the scaling test was calibrated concurrently while the tests for different levels were separately calibrated, and then these calibrations for the different levels were placed on the common scale. In the CI design, grade 3 was chosen as the base grade, and the other grades were separately calibrated to the grade scale. The results, in line with Hendrickson et al.’s (2006) research, found that the base grade chosen for vertical scaling under the common-item design had no substantial impact on the scaling results. In other words, choosing the lowest grade or the highest grade or the middle grade had little impact on the final scale results. However, Tong and Kolen (2007) noted that using as few links as possible might reduce the extent of scale shrinkage, which is common in vertical scaling with IRT models. Therefore, using a middle grade instead of the lowest or highest level as the base grade might be a better choice. The results also showed that the choice of scaling design has an important impact on the scaling result. Estimated student growth under the CI design was greater than that under the SC design. The parameter estimates generated by the SC design were more accurate. The multiple linking involved in the CI design possibly introduced more linking errors. The results also indicated that the real data were sensitive to the scaling procedure because many assumptions imposed by scaling methods were not met in the real data. The different scaling methods generated different scaling results for real data. However, the simulated data showed great tolerance to variation in the scaling methods. The different scaling methods produced very similar scaling results for simulated data.

In sum, vertical scaling is a complex procedure, which is influenced by many factors. Researchers usually determine the vertical scaling procedure according to their own situations and purposes. There is no agreement in the literature with regard to which approach generates the “best” vertical scales. Scale developers should make their own decisions based on their conception of estimated student growth and the nature of the scale to be developed.

4 Mathematics Competency Vertical Scale

In spite of the complexity of scale construction and the lack of consensus on the optimal approach, vertical scales are still attractive to researchers and test publishers. The Mathematics Competency Vertical Scale (MCVS) was created to measure the development of competency of Hong Kong students in mathe­matics; the scale utilises real data from 9,531 students between Primary 2 (P2 or grade 2) and Secondary 3 (S3 or grade 10). The MCVS was built using a new approach, the concurrent-separate approach, under the Rasch model. Both concurrent and separate calibrations were used at different stages of the vertical scaling procedure.

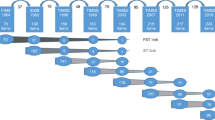
The MCVS covers a wide range of mathematical developmental competencies from P2 to S3. Two assessment booklets were designed for each grade to measure the mathematical competencies of students who had just completed their first semester (e.g. P2_1, P3_1.) and the competencies of those who had completed the second semester (e.g. P2_2, P3_2). The MCVS comprises 16 measurement booklets, with each pair of adjacent booklets (e.g. P2_1 and P2_2, P2_2 and P3_1, P3_1 and P3_2) having several common items through which all of the papers are interlinked. Figure 10.1 depicts the assessment design for the scale.

Fig. 10.1
figure 1

Assessment design for the scale

Full size image

The number of items in each measurement booklets ranges from 29 to 42. As indicated by the overlap between the blocks in Fig. 10.1, there is a set of common items in the adjacent booklets. The number of common items for each booklet ranges from 4 to 14. All of the items in the booklets were developed according to the Mathematics Curriculum Guide (P1–P6) (Hong Kong Education Bureau 2000) and the Syllabuses for Secondary Schools–Mathematics (Secondary 1–5) (Hong Kong Education Bureau 1999). There are three types of items: multiple-choice questions, short questions requiring a brief answer and open-ended questions requiring steps and reasons for the answer. All items in the booklets for the primary students are grouped into five content strata: numbers, measures, shapes and spaces, data handling and algebra. All of the items in the booklets for the secondary ­students are grouped into three content strata: number and algebra, measure, and shape and space.

In the common-item design, the quality of the common items is important, and they should be considered carefully from both content and statistics perspectives. Lack of examination of the quality of the common items probably leads to unsatisfactory scaling results. In the design of MCVS, all of the common items were designed according to the suggestions provided by previous research (e.g. Kolen and Brennan 2004; Patz and Yao 2007). They argued that the common items should (1) be appropriate in difficulty for the adjacent grades linked through the common items; (2) be representative of the whole test in terms of the representation of standards, the range of difficulty and the item’s format; and (3) be in a similar position with the same appearance across test papers.

All of the data were collected in the academic year 2006–2007. The tests for the first semester (i.e. P2_1, P3_1, etc.) were administered in December 2006 or January 2007, and the tests for the second semester (i.e. P2_2, P3_2, etc.) were administered in May or June 2007. The study sample comprised 5,755 primary students enrolled in grades P2 through P6 from 24 schools and 3,776 secondary students enrolled in grades S1 through S3 from 11 schools in Hong Kong. The sample size for each booklet varied with a range from 177 to 1,405. According to Kolen and Brennan (2004), most of the booklets have a sufficient number of examinees (more than 400) for vertical scaling with the Rasch model. The number of items for each booklet and the number of participants who completed each booklet are presented in Table 10.1.

Table 10.1 The item and participant distribution for booklets
Full size table

As discussed earlier in this chapter, both concurrent and separate linking methods have advantages and disadvantages. The separate method calibrates the parameters for items and individuals grade by grade and, thus, suffers from measurement error. Since for the calibration at each grade, there is estimation error and the error might be cumulative across the calibrations for different grades, more rounds of calibrations might imply greater cumulated error. This may explain why some research (e.g. Ito et al. 2008) has reported that as the grade deviates from the base grade, the best-fit linear line through the pairs of item discriminations start to rotate away from the identity line. In contrast, the concurrent method calibrates all of the parameters simultaneously in one analysis and, therefore, minimises the errors associated with calibrations. However, Hanson and Béguin (2002) noted that concurrent calibration imposes more constraints on item parameter estimates than the separate method, especially when calibrating many forms of tests at the same time, and that this might contaminate the resulting scale. Kolen and Brennan (2004) further pointed out that although, in theory, concurrent calibration that makes full use of all available information might be preferable, additional considerations, including violation of the unidimensionality assumption, might favour separate calibration.

Considering the inherent defects of using the single method, either concurrent or separate, to create a vertical scale, we adopted a combination of the two approaches, i.e. concurrent-separate. The concurrent and separate methods were carried out at different stages. This approach was partially inspired by that proposed by Wright (1996) and elaborated on by Wolfe and Chiu (1999) who measured the changes in person or item estimates across different times. To disentangle changes in persons (or items) from changes in items (or persons) in the measurement context, Wolfe and Chiu (1999) stacked the data collected from different time occasions together and obtained a set of category threshold calibrations of a rating scale that were shared by all time occasions. These threshold calibrations provided a unique and stable framework in which person and item estimates for each time occasion were calibrated. In addition, in the same framework, all person and item estimates could be compared and the development in individual abilities or changes in item difficulty could be interpreted.

The procedure for constructing MCVS consists of three steps which are illustrated in the following section.

4.1 Step 1: Identify Qualified Linking Items

The main purpose of this step was to identify quality linking items that are invariant in item difficulty across adjacent grades. For each grade, two rounds of analyses were undertaken. The first round of analysis was to identify the underfit persons whose OUTFIT or INFIT MNSQ were larger than 2.0 because they have a negative impact on the construction of the scale (Linacre 2011). The second round of the analysis was conducted by excluding all underfit persons identified in the first round of the analysis. Each linking item has two estimates of difficulty, one for each of the two adjacent grades. Two criteria were used to examine the quality of the lining items: the goodness of fit to the Rasch model and the invariance across adjacent grades. The linking items were disqualified and treated as different items in sub­sequent steps if any of the criteria below was satisfied.

(1) The item’s OUTFIT or INFIT MNSQ was less than 0.5 or larger than 1.5; and

(2) The standardised difference of the item difficulties for adjacent grades was larger than 2.0, and the actual difference of the item difficulties was larger than 0.5 logits.

Any overfit (OUTFIT or INFIT MNSQ was less than 0.5) or underfit (OUTFIT or INFIT MNSQ was larger than 1.5) items were disqualified as linking items because of their misfit to the Rasch model. The items identified by the second criterion were also disqualified as linking items because they are not invariant in terms of item difficulty across grades.

As a result, 37 linking items were identified as quality linking items and used in the following steps.

4.2 Step 2: (Concurrent Analysis) Obtain the Item Measures for the Quality Linking Items

The main purpose of this step was to obtain the difficulty estimates for the quality linking items identified in step 1. All of the data from different grades were stacked together. The data for the quality linking items were placed in the same column, and the disqualified linking items were treated as different items. Rasch analysis of the stacked data was conducted. Similar to step 1, two rounds of analyses were undertaken. The first round of the analysis identified the underfit persons whose OUTFIT or INFIT MNSQ were larger than 2.0, and the second round of the analysis without the underfit persons identified in the first round of the analysis calibrated the difficulty estimates for all the quality linking items. As the quality linking items were calibrated based on the whole data set, the results yielded a shared framework for the following separate calibrations.

4.3 Step 3: (Separate Analysis) Obtain the Item Measures for All Items and Construct the Scale

In this step, separate analyses for each grade were conducted with the quality linking items anchored at the value that had been calibrated in step 2 to generate item measures for all of the items. Similar to the previous steps, the first round of the analysis was undertaken to identify the underfit persons whose OUTFIT or INFIT MNSQ were larger than 2.0, and the second round of the analysis without the underfit persons identified in the first round of the analysis was used to calibrate the difficulty estimates for all of the items. Any items showing misfit to the Rasch model, i.e. the OUTFIT or INFIT MNSQ was larger than 2.0, were removed from the scale. Eight items were identified by this criterion and removed. Furthermore, any items with extremely high or low difficulty were investigated by experts specialised in mathematics to determine whether they were appropriate for inclusion in the scale. Consequently, four items were removed because their difficulties were not appropriate for the corresponding grades. The remaining items comprised the MCVS.

The final version of the MCVS consists of 510 unique items. The details of each final booklet and the whole scale are presented in Table 10.2.

Table 10.2 The details of the MCVS
Full size table

It can be seen that the mean item measures for each booklet ranged from 27.5 (P2_1) to 68.4 (S3_2). These values for the item measures (the second column in Table 10.2) are neither students’ raw scores on assessment booklets nor the Rasch calibration in logits: they are units in the Rasch analysis, and the meaning of the units depends on the settings in the Rasch analysis. In this case, the mean of item difficulty across all items was set to 50, and one logit was divided into 10 units in the concurrent analysis conducted in step 2. Therefore, one unit of item measured in this method stands for 0.1 logit. Consequently, the mean test difficulty for the booklet ranged from 2.75 logits (27.5/10) for P2_1 to 6.84 logits (68.4/10) for S3_2. In other words, the whole scale covered a difficulty range of 4.09 logits for 7.5 schooling years of development (from the first semester of P2 to the second semester of S3), resulting in 0.55 logits per year. This amount of advancement in difficulty level of items from year to year is consistent with children’s development because many studies of their development have shown that it is typical for a child to gain 0.5 logits growth within 1 year.

It can also be seen from Table 10.2 that each booklet had quite good Rasch reliability, ranging from 0.97 to 1.00. The separation index of the booklets ranged from 5.88 to 18.43. The statistical data provide strong confidence in the practical application of the MCVS scale. Figure 10.1 presents the item distribution by grades for the MCVS.

Each dot in Fig. 10.2 stands for a single item. The items are grouped by their grades and placed along the x axis from the left to the right. The y axis represents item difficulty. It can be seen that, in general, the item difficulty advanced gradually from the lower grades to higher grades. The red solid line is a regression line that indicates that the item difficulty could be predicted, to some extent, by the grade where the item is placed. The R square was equal to 0.456, which is far from perfect prediction, but still substantial.

Fig. 10.2
figure 2

Item distribution of the MCVS

Full size image

As the item difficulties are on the same scale as person ability, teachers, parents or anyone who wishes to measure students’ achievement levels in mathematics could use items from the scale according to the students’ mathematics abilities or their grades to form a test, administer the test to the students and analyse the test results under the Rasch model with the items anchored at the values provided by the scale. Thus, the students’ mathematics competencies can be calibrated along the scale. More importantly, the competency estimates of the students from different grades could be compared directly, even though they were assessed by totally different sets of items because the items had been calibrated along the same scale, which provides a stable framework for the comparison. Consequently, students’ growth in mathematics competencies could be tracked from P2 to S3 with the MCVS.

As noted earlier, all of the items in the MCVS are grouped into five content strata for the primary levels and three content strata for the secondary levels (all of the strata belong to the same dimension, i.e. overall mathematics competency). It can be seen from Figs. 10.2 and 10.3, which illustrate the item distribution by strata for the primary levels and the secondary levels, respectively, that the items in each content strata cover quite a wide range of difficulties. The item difficulty advances gradually with grades for each stratum. Such a trend is especially salient for strata at primary levels.

Fig. 10.3
figure 3

Items by strata of the MCVS (primary)

Full size image

The results presented in Figs. 10.3 and 10.4 indicate that the MCVS could be divided into sub-scales according to the content strata. The items belonging to the same strata could be selected and used to measure students’ competencies in a particular mathematical domain, i.e. numbers, measures, shapes and spaces, data handling and algebra for primary levels and number and algebra, measure, and shape and space for the secondary levels. Thus, tracking the students’ development in mathematics could be done in a more detailed way.

Fig. 10.4
figure 4

Items by strata of the MCVS (secondary)

Full size image

In sum, the MCVS was built under the Rasch model with a concurrent-separate approach, which incorporates the strength of both concurrent and separate methods. First of all, a separate analysis was conducted to investigate the quality of all of the linking items and identify those items that could be fitted to the Rasch model and invariant in terms of difficulty. The concurrent analysis was then utilised to calibrate the difficulty estimates of the quality linking items and to provide a stable and unambiguous framework for the construction of the scale. With those quality linking items anchored at the values obtained in the concurrent calibration, a separate analysis was undertaken for each booklet to calibrate the difficulty estimates of all of the items and, thus, form the whole scale. Furthermore, the impact of underfit persons was taken into account during the scale construction, and all persons with too large INFIT or OUTFIT MNSQ were excluded from each round of the analysis, and the “best sample” was used to construct the scale. The resulting scale comprised 16 booklets with a total of 510 items, encompassing P2 to S3 grades. The mean test difficulty for the booklet ranged from 2.75 logits for the first semester of P2 to 6.84 logits for the second semester of S3. Each booklet showed quite good Rasch reliability (ranging from 0.97 to 1.00) and separation index (ranging from 5.88 to 18.43). The properties of the MCVS make it a suitable vertical scale for tracking Hong Kong students’ development in mathematics, or in particular domains of mathematics, over time.

Of course, this scale has some limitations in common with all other vertical scales. Previous research (e.g. Harris 2007; Kolen and Brennan 2004; Patz and Yao 2007) emphasised that the common items determine the quality of the constructed scale because all item parameters are estimated based on common items. The pilot study of the current research also showed that a minor change in the linking items (e.g. adding/deleting/changing even only one linking item) has quite a large impact on the calibration of the other items, especially when the number of linking item is small. Thus, this research examined the quality of the linking items from both content and statistics perspectives. Only those linking items that met several prior requirements, such as sufficient goodness of fit to the Rasch model, invariant in terms of item difficulty across grades and appropriate in terms of content were retained. As a result, there were too few qualified linking items for some grades, especially for P2_1 and P2_2. Most of the linking items had to be disqualified because they were not invariant across adjacent grades in terms of difficulty. This research highlights the fact that the linking items should be trait-related but not curriculum-related. Thus, students’ performance on linking items should be determined by the trait measured but not by whether they have learned the content in the classroom. If the linking items are overly linked with the curriculum, the linking items will be easy for students who studied with a curriculum that includes knowledge required to solve the items and difficult for students who studied with another curriculum that does not include such knowledge. The difference in curriculum coverage will in turn lead to a large standardised difference in item difficulty. Further studies are needed on the characteristics of quality linking items to shed light on how researchers should select linking items in the construction of vertical scales.