Abstract
This chapter illustrates the use of algebraic flux correction in the context of finite element methods for the incompressible Navier-Stokes equations and related models. In the convection-dominated flow regime, nonlinear stability is enforced using algebraic flux correction. The numerical treatment of the incompressibility constraint is based on the ‘Multilevel Pressure Schur Complement’ (MPSC) approach. This class of iterative methods for discrete saddle-point problems unites fractional-step/operator-splitting methods and strongly coupled solution techniques. The implementation of implicit high-resolution schemes for incompressible flow problems requires the use of efficient Newton-like methods and optimized multigrid solvers for linear systems. The coupling of the Navier-Stokes system with scalar conservation laws is also discussed in this chapter. The applications to be considered include the Boussinesq model of natural convection, the k–ε turbulence model, population balance equations for disperse two-phase flows, and level set methods for free interfaces. A brief description of the numerical algorithm is given for each problem.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Computational Fluid Dynamics
- Discontinuous Galerkin
- Computational Fluid Dynamics Code
- Direct Numerical Simulation Result
- Population Balance Equation
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
One of the most fundamental models in fluid mechanics is the incompressible Navier-Stokes equations for the velocity u and pressure p of a Newtonian fluid
where ν is the kinematic viscosity of the fluid and f is a given external force. In contrast to compressible flow models, there is no equation of state. The constant density ρ is “hidden” in the modified pressure p which adjusts itself instantaneously so as to render the velocity field u divergence-free. The solution to (1) is sought in a bounded domain Ω⊂ℝd, d=2,3 on a finite time interval (0,T]. The choice of initial and boundary conditions depends on the particular application.
The Navier-Stokes equations (NSE) describe an amazing variety of fluid flows and represent a ‘grand challenge’ problem of profound importance to mathematicians, physicists, and engineers. It is not surprising that the NSE were among the seven Millennium Problems selected by the Clay Mathematics Institute in 2000. The associated $1,000,000 prize is to be awarded for “substantial progress toward a mathematical theory which will unlock the secrets hidden in the Navier-Stokes equations.” During the first decade of the XXI century, no major breakthrough was achieved on the theoretical side of this enterprise. However, a lot of progress has been made in the development of numerical methods for the Navier-Stokes equations and their applications in Computational Fluid Dynamics (CFD).
Models based on the incompressible Navier-Stokes equations are widely used in applied mathematics and engineering sciences. The nonlinearity of the convective term, the incompressibility constraint, and the possible coupling of (1) with other equations make the numerical implementation of such models rather challenging. Numerical instabilities may be caused not only by the dominance of convective terms at high Reynolds numbers but also by the velocity-pressure coupling or by the numerical treatment of sources/sinks. In many applications, the flow is turbulent and takes place in a domain of complex geometrical shape. Additional difficulties are associated with the presence of moving boundaries, free interfaces, or unresolvable small-scale features. All peculiarities of a given model must be taken into account when it comes to the design of reliable and efficient numerical methods.
The performance of CFD software depends not only on the accuracy of the underlying discretization techniques but also on the choice of iterative solvers, data structures, and programming concepts. Explicit schemes are easy to implement and parallelize but give rise to severe time step restrictions. In the case of an implicit scheme, one has to solve sparse nonlinear systems for millions of unknowns at each time step. The computational cost can be reduced by using optimal preconditioners, multigrid solvers, local mesh refinement, and adaptive time step control. Last but not least, parallelization of the code is a must for many real-life applications.
The development of improved numerical algorithms for the incompressible Navier-Stokes equations has been actively pursued for more than 50 years. The number of publications on this topic is overwhelming. For a comprehensive overview, the reader is referred to the book by Gresho et al. [22]. In many cases, numerical solutions to the NSE are accurate enough to look realistic. The result of a 2D simulation for the laminar flow around a cylinder is shown in Fig. 1(a). The snapshot exhibits a remarkably good agreement with the experimental data in Fig. 1(b). However, a quantitative comparison of drag and lift coefficients produced by different codes reveals significant differences in their accuracy and efficiency [63].
A current trend in CFD is to combine the ‘basic’ Navier-Stokes equations (1) with more or less sophisticated engineering models for industrial applications. Additional equations are included to describe turbulence, nonlinear fluids, combustion, detonation, multiphase flow, free and moving boundaries, fluid-structure interaction, weak compressibility, and other effects. Some of these extensions will be discussed in the present chapter. All of them require a very careful choice of numerical approximations and iterative solution techniques. In summary, the main ingredients of a ‘perfect’ CFD code for a generalized Navier-Stokes model are as follows:
-
Discretization: adaptive high-resolution schemes, discrete maximum principles;
-
Solvers: robust and efficient iterative methods for linear and nonlinear systems;
-
Implementation: optimal data structures, hardware-specific code, parallelization.
The availability and compatibility of these components would make it possible to attain high accuracy with a relatively small number of unknowns. Alternatively, discrete problems of the same size could be solved more efficiently. The marriage of accurate numerical methods and fast iterative solvers would make it possible to exploit the potential of modern computers to the full extent and improve the MFLOP/s rates of incompressible flow solvers by orders of magnitude. Hence, algorithmic aspects play an increasingly important role in contemporary CFD research.
This chapter begins with a brief review of the Multilevel Pressure Schur Complement (MPSC) approach to solving the incompressible Navier-Stokes equations at high and low Reynolds numbers. Next, the coupling of the basic flow model with additional transport equations is discussed in the context of the Boussinesq approximation for natural convection problems. Algebraic flux correction is shown to be a useful tool for enforcing positivity on unstructured meshes in 3D. In particular, a positivity-preserving implementation of the standard k–ε turbulence model is described. The application of the proposed algorithms to multiphase flow models is illustrated by a case study for population balance equations and free surface flows.
2 Discretization of the Navier-Stokes Equations
The incompressible Navier-Stokes equations are an integral part of all mathematical models to be considered in this chapter. First of all, we discretize (1) in space and time. For our purposes, it is convenient to begin with the time discretization. As a time-stepping method, we will use an implicit two-level θ-scheme (backward Euler or Crank-Nicolson) or the fractional-step θ-scheme proposed by Glowinski.
Let Δt denote the time step for advancing the solution from the time level t n to the time level t n+1:=t n+Δt. The value of Δt may be chosen adaptively. The semi-discrete version of (1) can be written in the following generic form [78]:
Given u(t n) find u=u(t n+1) and p=p(t n+1) such that
where
The values of the parameters θ and θ i , i=1,2,3 depend on the time-stepping scheme. For example, θ=θ 2=1, θ 1=θ 3=0 for the backward Euler method.
Next, let us discretize the above problem in space using the finite element method (FEM). The algorithms to be presented in this chapter are also applicable to finite difference and finite volume approximations since the structure of the discrete problems is the same. We favor the finite element approach because the applications we have in mind require the use of high-order discretizations on unstructured meshes. Moreover, the FEM is backed by a solid mathematical theory that makes it possible to obtain rigorous a posteriori error estimates for adaptation in space and time.
The Galerkin finite element approximation to (2) is derived from a variational form of the semi-discretized Navier-Stokes equations. The discretization in space begins with the generation of a computational mesh  for the domain Ω. As usual, the subscript h refers to the local size of mesh cells (triangles or quadrilaterals in 2D, tetrahedra or hexahedra in 3D). Inside each cell, the numerical solution is defined in terms of polynomial basis functions. Let V
h
and Q
h
denote the finite-dimensional spaces for the velocity and pressure approximations, respectively. The discretization of (2) is stable if V
h
and Q
h
satisfy the Babuška–Brezzi (BB) condition [20]
for the domain Ω. As usual, the subscript h refers to the local size of mesh cells (triangles or quadrilaterals in 2D, tetrahedra or hexahedra in 3D). Inside each cell, the numerical solution is defined in terms of polynomial basis functions. Let V
h
and Q
h
denote the finite-dimensional spaces for the velocity and pressure approximations, respectively. The discretization of (2) is stable if V
h
and Q
h
satisfy the Babuška–Brezzi (BB) condition [20]
with a mesh–independent constant γ. If the use of equal-order interpolations is desired, additional stabilization terms must be included (see, e.g., [28]).
The lowest-order finite element approximations satisfying the above inf-sup condition are the nonconforming Crouzeix-Raviart (\(\tilde{P}_{1}/P_{0}\)) and Rannacher-Turek (\(\tilde{Q}_{1}/Q_{0}\)) elements [11, 62]. In either case, the degrees of freedom for the velocity are associated with edge/face mean values, whereas the pressure is approximated in terms of cell mean values. A sketch of the nodal points for a quadrilateral \(\tilde{Q}_{1}/Q_{0}\) element is shown in Fig. 2. The benefits of using low-order nonconforming approximations include a relatively small number of unknowns and the availability of efficient multigrid solvers which are sufficiently robust in the whole range of Reynolds numbers, even on nonuniform and highly anisotropic meshes [64, 78]. Last but not least, algebraic flux correction is readily applicable to \(\tilde{P}_{1}\) and \(\tilde{Q}_{1}\) elements [41].
The most popular inf-sup stable approximation of higher order is the Taylor-Hood (P 2/P 1 or Q 2/Q 1) element. In our experience, the Q 2/P 1 element is a better choice for non-simplex meshes [12]. Since no algebraic flux correction schemes are currently available for higher-order finite elements, the Q 2/P 1 version of our Navier-Stokes solver is stabilized using continuous interior penalty techniques [56, 86].
The vectors of discrete nodal values for the velocity and pressure will also be denoted by u and p. The nonlinear discrete problem is formulated as follows:
Given u n find u=u n+1 and p=p n+1 such that
where
Here M is the (consistent or lumped) mass matrix, B is the discrete gradient operator, and −B T is the discrete divergence operator. The matrix A is given by
where
K(u) is the discrete transport operator and L is the viscous part of the stiffness matrix. The nonlinear operator N(u) may also include artificial diffusion due to algebraic flux correction or other stabilization/shock-capturing techniques.
The discretization of the stationary Navier-Stokes equations also leads to a nonlinear system of the form (5). To use the same notation for steady and time-dependent flow problems, we replace (7) with the more general definition
The discrete evolution operator given by (7) corresponds to α=1. The steady-state approximation is defined by the parameter settings α=0, θ=1, Δt=1.
The design of efficient iterative methods for the above discrete problem involves a linearization of N(u) or iterative solution of the nonlinear system using fixed-point defect correction or Newton-like methods. Special techniques (explicit or implicit underrelaxation, line search, Anderson acceleration) may be implemented to achieve and speed up convergence. When it comes to the numerical treatment of the incompressibility constraint, one has a choice between a strongly coupled approach (simultaneous computation of u and p) and fractional-step algorithms (projection schemes [8, 91], pressure correction methods [16, 58]). The abundance of choices has generated a great variety of incompressible flow solvers that exhibit considerable differences in terms of their complexity, robustness, and efficiency.
The Multilevel Pressure Schur Complement (MPSC) formulation to be presented below makes it possible to put many existing solution algorithms into a common framework and combine their advantages. In particular, the iterative solver may be configured in an adaptive manner so as to achieve the best run-time characteristics for a given problem. For a more detailed presentation of the MPSC paradigm and additional numerical examples, we refer to the monograph by Turek [78].
3 Pressure Schur Complement Solvers
The linearized form of the fully discrete problem (5), as well as the linear systems to be solved at each iteration of a nonlinear scheme, can be written as
This is a typical saddle point problem in which the pressure p acts as the Lagrange multiplier for the discretized incompressibility constraint.
The Schur complement equation for the pressure can be derived using a formal elimination of the velocity unknowns. The discrete form of ∇⋅u=0 is
where u is the solution to the discretized momentum equation, that is,
Thus, an equivalent formulation of the discrete saddle-point problem (9) reads:


Since the right-hand side of (12) depends on the solution to (13), the two subproblems should actually be solved in the reverse order:
-
1.
Solve the pressure Schur complement (PSC) equation (13) for p.
-
2.
Substitute p into the momentum equation (12) and compute u.
In the fully nonlinear version, the Schur complement operator S:=B T A −1 B depends on the solution to (12), so a number of outer iterations are performed.
The practical implementation of the two-step algorithm also requires a number of inner iterations. Since the matrix A −1 is full, the assembly and storage of S would be prohibitively expensive in terms of CPU time and memory requirements. Thus, it is imperative to solve the PSC equation in an iterative way. For instance, consider a preconditioned Richardson’s method based on the following basic iteration
where l=1,2,…,L is the iteration counter, C −1 is a suitable approximation to S −1, and the expression in the brackets is the residual of the PSC equation.
By definition of S, an equivalent form of the pressure correction equation (15) is
In practice, the matrices A and C are “inverted” by solving a linear system. Thus, the implementation of (15) can be split into the following basic tasks:
-
1.
Given the pressure p (l−1), solve the discrete momentum equation
$$A\mathbf {u}^{(l)}=\mathbf{g}-\varDelta t Bp^{(l-1)}. $$(16) -
2.
Given the velocity u (l), solve the pressure correction equation
$$Cq^{(l)}=\frac{1}{\varDelta t}B^T\mathbf {u}^{(l)}. $$(17) -
3.
Add the pressure increment q (l) to the current approximation
$$p^{(l)}=p^{(l-1)} + q^{(l)}. $$(18)
The number of pressure correction cycles L can be fixed or variable. The iterative process may be terminated when the increments and residuals become small enough. Using C:=S, one obtains the solution to (9) in one step (L=1). The assembly of C can be avoided using a GMRES-like iterative solver that operates with matrix-vector products. The evaluation of Cy=B T A −1 By would involve an iterative solution of the linear system Ax=By followed by the matrix-vector multiplication Cy:=B T y. This procedure must be repeated as many times as necessary to reach the prescribed tolerance for the residual of the PSC equation. Hence, the computational cost per time step is likely to be very high even if multigrid acceleration is employed.
In many cases, the matrix-free ‘inversion’ of C:=S is impractical. In particular, the cost per time step is always the same, although a good initial guess is available when the time steps are small. In this case, the discrete evolution operator

represents a well-conditioned perturbation of the symmetric positive-definite mass matrix M. Hence, the discrete momentum equation can be solved efficiently for small Δt. However, the condition number of the PSC operator is given by

and does not improve when the time step is refined. The invariably high cost of solving the “elliptic” pressure Schur complement equation makes C:=S a poor choice when it comes to simulation of unsteady flows with small time steps.
A computationally efficient Schur complement preconditioner for time-dependent flow problems can be designed using approximations of the form
where \(\tilde{A}\approx A\) is a matrix that can be ‘inverted’ in an efficient way. By (20), the condition number of the PSC operator is dominated by the elliptic part. Thus, the preconditioner can be defined using the symmetric positive definite matrix
By (19), a usable preconditioner for high Reynolds number flows is given by
Replacing M with a lumped mass matrix M L , one obtains a sparse approximation to the Schur complement operator. Another simple choice is the diagonal matrix
In general, the formula for \(\tilde{A}\) should be as simple as possible but not simpler. Sparse approximations like \(C := B^{T}{M}^{-1}_{L} B\) or C:=B Tdiag(A)−1 B rely on the diagonal dominance of A. The total number of iterations increases at large time steps, and convergence may fail if the off-diagonal part of A can no longer be neglected.
The preconditioning of (15) by a global matrix of the form (21) is called the global pressure Schur complement approach [78]. A typical implementation is based on the fractional-step algorithm (16)–(18). The well-known representatives of such segregated incompressible flow solvers include discrete projection schemes [15, 23, 60, 77], various modifications of the SIMPLE method, and Uzawa-like algorithms. For an overview of segregated methods, we refer to [16] and references therein.
An alternative to the sequential update of the velocity and pressure unknowns is the solution of small coupled subproblems. This solution strategy is recommended for steady-state computations and low Reynolds number flows. It should also be considered if the Navier-Stokes system is coupled with a RANS turbulence model or another set of convection-diffusion equations. If the variables are updated in a segregated manner, strong two-way coupling may result in slow convergence. In this case, it is worthwhile to replace (21) with a sum of local preconditioners
where \(S_{i}:=B^{T}_{i} A_{i}^{-1} B_{i}\) is the Schur complement matrix for a local subproblem that corresponds to a small subdomain (a single element or a patch of elements) Ω i . The multiplication by the transformation matrix P i picks out the degrees of freedom associated with Ω i , whereas the multiplication by \(P_{i}^{T}\) locates the global degrees of freedom to be updated after solving a local subproblem of the form S i x i =P i y.
The basic iteration (15) preconditioned by (25) is called the local pressure Schur complement method [78]. The embedding of “local solvers” into an outer iteration loop of Jacobi or Gauss–Seidel type has a lot in common with domain decomposition methods but multilevel PSC preconditioners of the form (25) do not require a special treatment of interface conditions. A typical representative of such schemes is the Vanka smoother [90] which is widely used in the multigrid community.
As a matter of fact, it is possible to combine global PSC (“operator splitting”) and local PSC (“domain decomposition”) methods in a general-purpose CFD code. This can be accomplished by using additive preconditioners of the form
In what follows, we briefly discuss the design of such preconditioners and present the resulting algorithms. The convergence of these basic iteration schemes can be accelerated by using them as preconditioners for Krylov subspace methods (CG, BiCGStab, GMRES) or smoothers for a multigrid solver. The latter approach leads to a family of Multilevel pressure Schur complement (MPSC) methods that prove robust and efficient, as demonstrated by the benchmark computations in [63].
4 Global MPSC Approach
The construction of globally defined additive preconditioners for the Schur complement operator S=B T A −1 B is motivated by the following algebraic splitting
where β=−θΔt and γ=νβ. Consider \(C:=B^{T} \tilde{A}^{-1} B\), where \(\tilde{A}\) is an approximation to A. The above decomposition of A into the reactive (M), convective (K), and viscous (L) part suggests the use of a similar splitting for C −1. Let
-
C M be an approximation to the reactive part B T M −1 B,
-
C K be an approximation to the convective part B T K −1 B,
-
C L be an approximation to the viscous part B T L −1 B.
The preconditioner C M is well-suited for computations with small time steps. C K is optimal for steady flows at high Reynolds numbers, and C L is optimal for steady flows at low Reynolds numbers. Hence, a general-purpose PSC preconditioner can be defined as a suitable combination of the above. In particular, we consider
where α′∈[0,α], β′∈[0,β], γ′∈[0,γ] are parameters that can be used to activate, deactivate, and blend partial preconditioners depending on the flow regime.
To achieve the best overall performance, the meaning of ‘optimality’ has to be defined more precisely. Clearly, the most accurate preconditioner for each subproblem is the one that does not involve any approximations. In principle, even a full matrix of the form \(B^{T} \tilde{A}^{-1} B\) can be “inverted” using a matrix-free iterative solver (see above). However, simpler partial preconditioners are likely be more efficient smoothers in the context of a multigrid method. The MPSC solver is well-designed if each subproblem can be solved efficiently and the convergence rates are not sensitive to the parameter settings and geometric properties of the mesh. Optimal preconditioners satisfying these criteria are introduced and analyzed in [78].
At high Reynolds numbers, the use of small time steps is dictated by the physical scales of flow motion. Thus, the lumped mass matrix M L is a reasonable approximation to A, and the sparse matrix \(C:=B^{T}M_{L}^{-1}B\) may be used as a preconditioner for the basic iteration (15). The practical implementation of the PSC cycle
is based on the fractional-step algorithm (16)–(18) and can be interpreted as a discrete projection scheme [15, 23, 60, 77]. An additional step is included to enforce the incompressibility constraint after the last iteration. The algorithm becomes:
-
1.
Given the pressure p (l−1), solve the “viscous Burgers” equation
$$A\mathbf {u}^{(l)}=\mathbf{g}-\varDelta t Bp^{(l-1)}. $$(29) -
2.
Given the velocity u (l), solve the “pressure Poisson” equation
$$B^TM_L^{-1}Bq^{(l)}=\frac{1}{\varDelta t}B^T\mathbf {u}^{(l)}. $$(30) -
3.
Add the pressure increment q (l) to the current approximation
$$p^{(l)}=p^{(l-1)} + q^{(l)}. $$(31)To enforce B T u=0, perform the divergence-free L 2 projection
$$\mathbf{u}=\mathbf{u}^{(l)}-\varDelta tM_L^{-1}Bq^{(l)}. $$(32)
The projection step is included because the intermediate velocity u (l) is calculated using an approximate pressure p (l−1) and is generally not (discretely) divergence-free. Multiplying (32) by B T and using (30), we obtain
It can be shown that \(B^{T} M_{L}^{-1} B\) corresponds to a mixed discretization of the Laplacian operator [23]. If just one basic iteration is performed, algorithm (29)–(32) has the structure of a classical projection scheme for the time-dependent incompressible Navier-Stokes equations. In particular, a discrete counterpart of Chorin’s method [8] is obtained with the trivial initial guess p (0)=0. The choice p (0)=p(t n) leads to the discrete version of the second-order accurate van Kan scheme [91].
The derivation of continuous projection methods involves the use of operator splitting and the Helmholtz decomposition of the intermediate velocity [21, 60]. Replacing differential operators with matrices, one obtains a discrete projection scheme of the form (29)–(32). The advantages of the algebraic approach include
-
applicability to discontinuous pressure approximations,
-
consistent treatment of boundary conditions (no splitting),
-
alleviation of spurious boundary layers for the pressure,
-
convergence to the fully coupled solution as l increases,
-
possibility of using other global PSC preconditioners.
On the negative side, discrete projection schemes lack inherent stabilization mechanisms, whereas the continuous Chorin and van Kan methods may be used with equal-order (P 1/P 1) interpolations if the time step is not too small [59].
The vectorizable global MPSC schemes are more efficient than coupled solvers in the high Reynolds number regime. If the discrete evolution operator A is dominated by the reactive part, it is sufficient to perform just one pressure Schur complement iteration per time step. The number of inner iterations for the viscous Burgers equation (29) can also be as small as 1 since u(t n) is a good initial guess.
If an optimized multigrid method is used to solve the pressure Poisson problem (29), the total cost per time step is just a small fraction of that for a coupled solver. However, the sparse matrix \(B^{T}M_{L}^{-1}B\) may become a poor approximation to B T A −1 B at large time steps. Therefore, the local MPSC approach presented in the next section is a better choice for low Reynolds number flows and steady-state computations.
5 Local MPSC Approach
In contrast to the global MPSC approach, local Schur complement preconditioners make it possible to update the velocity and pressure in a strongly coupled fashion. In this section, we explain the underlying design philosophy and practical implementation. As already mentioned, the basic idea is to solve small coupled subproblems associated with patches of degrees of freedom. We define a patch as a small subset of the vector of unknowns. The solutions to the local subproblems are used to correct the corresponding subsets of the global solution vector. The so-defined block-Jacobi or block-Gauß-Seidel iteration provides a very robust smoother for a multilevel solution strategy [13]. The local MPSC algorithm is amenable to a parallel implementation that exploits the fast cache of modern processors.
The coefficients of local subproblems for the multilevel “domain decomposition” method are extracted from the global matrices using a restriction matrix P i that picks out the degrees of freedom associated with the i-th patch. We define
Thus, the ‘boundary conditions’ for subdomains are also taken from the global matrices. The local Schur complement matrix for the i-th subproblem is given by
The block-Jacobi version of the local PSC method can be formulated as follows:
Given u (l−1) and p (l−1), assemble the defect of the discrete problem (9)
and perform one basic iteration with the additive PSC preconditioner
The local stiffness matrix \(\tilde{A}_{i}\) matrix is chosen to be an approximation to A i . The default is \(\tilde{A}_{i}:=A_{i}\). The relaxation parameter ω (l) can be fixed or chosen adaptively.
The practical implementation of (37) begins with the solution of local problems
Next, the calculated local increments are inserted into the global vectors
Finally, the velocity and pressure approximations are updated thus:
If some degrees of freedom are shared by two or more patches, a weighted average of the corresponding local increments is inserted into the global vector. The simplest strategy is to overwrite the contributions of previously processed patches or to calculate the arithmetic mean over all patch contributions.
The local subproblems (38) are so small that they can be solved using Gaussian elimination. A further reduction in the size of the linear system is offered by the Schur complement formulation of the local subproblem. The preconditioner
is a full matrix but its size depends on the number of pressure unknowns only. If the patch Ω i contains just a moderate number of degrees of freedom, then the small matrix C i is likely to fit into the processor cache. The local PSC problem can be solved very efficiently making use of hardware–optimized BLAS libraries. The corresponding velocity increment can be recovered as explained in Sect. 3.
In a sequential code, the block-Jacobi form of the basic iteration may be replaced with a block-Gauß-Seidel relaxation that calculates the local residuals using the latest solution values. Both versions are likely to perform well as long as there are no strong mesh anisotropies. However, severe convergence problems may occur on meshes with sharp angles and/or large aspect ratios. The local MPSC approach makes it possible to avoid the potential troubles by “hiding” the anisotropic mesh cells inside macroelements that have a regular shape. Several adaptive blocking strategies for generation of such macromeshes are described in [64, 78].
6 Multilevel Solution Strategy
The presented PSC schemes are particularly efficient if a multilevel solution strategy is adopted. To begin with, consider an abstract linear system of the form
The subscript N refers to the number of approximation levels. In geometric multigrid methods, these levels are characterized by the mesh size h. Let A k and f k denote the matrix and the right-hand side for the level number k=1,…,N−1. The convergence of a basic iteration scheme on finer levels can be significantly accelerated by a few iterations on coarser levels. The multilevel solution algorithm can be interpreted as a hierarchical preconditioner for the slowly converging basic solver.
The main ingredients of a (geometric) multigrid method for solving (42) are:
-
matrix–vector multiplication routines for the operators A k , k=1,…,N,
-
an inexpensive smoother (basic iteration scheme) and a coarse grid solver,
-
prolongation \(I_{k-1}^{k}\) and restriction \(I^{k-1}_{k}\) operators for grid transfer.
Let \(u_{k}^{0}\) denote the initial guess for the k-level iteration \(\mathit{MPSC}(k,u_{k}^{0},f_{k})\). The so-defined multigrid cycle yields an approximate solution to the linear system
On the coarsest level, the number of unknowns is typically so small that the discrete problem A 1 u 1=f 1 can be solved directly. The result is
For all other levels of approximation (k>1), the following algorithm is used [78]:
-
1.
Presmoothing
Given \(u_{k}^{0}\), perform m basic iterations (smoothing steps) to obtain \(u_{k}^{m}\).
-
2.
Coarse grid correction
Restrict the residual of the discrete problem to the coarse grid
$$f_{k-1} = I^{k-1}_k \bigl(f_k -A_k u_k^m\bigr).$$Set \(u_{k-1}^{0} = 0\) and calculate \(u_{k-1}^{i}\) recursively for i=1,…,p
$$u_{k-1}^i = \mathit{MPSC}\bigl(k-1,u_{k-1}^{i-1},f_{k-1}\bigr).$$ -
3.
Relaxation and update
Correct \(u_{k}^{m}\) using a prolongation of the coarse grid solution
$$u_k^{m+1} = u_k^m +\alpha_k I_{k-1}^k u_{k-1}^p.$$ -
4.
Postsmoothing
Given \(u_{k}^{m+1}\), perform m smoothing steps to obtain \(u_{k}^{m+1+n}\).
The relaxation parameter α k may be fixed or chosen adaptively so as to minimize the error in a certain norm. Using the discrete energy norm, one obtains
After sufficiently many cycles on level N, the above multigrid algorithm yields the converged solution to (42). An extension to the discrete saddle point problem (9) can be performed using a global or local pressure Schur complement approach.
The global MPSC approach corresponds to solving the generic system (42) with
The basic iteration is given by (15). After solving the Schur complement equation for the pressure p, the velocity u is updated. The bulk of CPU time is spent on matrix-vector multiplications for smoothing, defect calculation, and adaptive coarse grid correction. The multiplication by \(C=B^{T} \tilde{A}^{-1} B\) requires an iterative solution of a linear system, unless \(\tilde{A}\) is a diagonal matrix. The choice \(C=B^{T} M_{L}^{-1} B\) leads to a discrete projection scheme (16)–(18) that requires solving a viscous Burgers equation and a Poisson-like equation. Both subproblems can be solved efficiently using linear multigrid methods. For the reasons explained in Sect. 4, the global MPSC approach is recommended for unsteady flows at high Reynolds numbers.
The local MPSC approach corresponds to solving the generic system (42) with
The basic iteration is the block-Jacobi method given by (37) or the block-Gauß-Seidel version of the local PSC method. The cost-intensive part is the smoothing step, as in the case of standard multigrid techniques for elliptic problems. Local MPSC schemes lead to very robust solvers for coupled problems. This solution strategy is recommended for flows at low and intermediate Reynolds numbers.
The presented MPSC solvers have been implemented in the open-source software package featflow [79]. The source code and documentation are available at http://www.featflow.de. Further algorithmic details (adaptive coarse grid correction, grid transfer operators, nonlinear iteration techniques, time step control, implementation of boundary conditions) can be found in the monograph by the first author [78]. Some programming strategies, data structures, and guidelines for the development of a hardware-oriented code are presented in [80–82, 84].
7 Coupling with Scalar Equations
In many practical applications, the Navier-Stokes equations are coupled with a system of conservation laws for scalar quantities transported with the flow. In the context of turbulence modeling, the additional variables may represent the turbulent kinetic energy k, its dissipation rate ε, or the components of the Reynolds stress tensor. The evolution of temperatures, concentrations, and volume fractions is also governed by convection-dominated transport equations with coefficients that depend on the solution to the basic flow model. The discrete maximum principle for these additional equations can be enforced using algebraic flux correction [38].
To explain the ramifications of a two-way coupling with scalar equations, we consider the Boussinesq model of natural convection. The weakly compressible flow induced by temperature gradients is described by the Navier-Stokes system
where T is the temperature, and e g stands for the unit vector directed opposite to the gravitational acceleration g. The temperature equation is given by
In the nondimensional form of this model, the viscosity and diffusion coefficient
depend on the Rayleigh number Ra and Prandtl number Pr. A detailed description of the Boussinesq model and the parameter settings for the MIT benchmark problem (natural convection in a differentially heated enclosure) can be found in [9].
7.1 Finite Element Discretization
Adding the buoyancy force and the temperature equation to the discretized Navier-Stokes equations, one obtains a nonlinear algebraic system of the form



The subscripts u and T are used to distinguish between the evolution operators and right-hand sides of the momentum and temperature equations. As before, the matrices A u and A T can be decomposed into a reactive, convective, and diffusive part


The finite element spaces and discretization techniques for u and T may be chosen independently. For example, the temperature may be discretized with linear finite elements even if \(\tilde{Q}_{1}/Q_{0}\) or Q 2/P 1 elements are employed for the Navier-Stokes part. Moreover, different stabilization techniques may be used for K u and K T .
The generic matrix form of the discretized Boussinesq model (45)–(47) reads
This generalization of (9) can be solved using a global or local MPSC algorithm.
7.2 Global MPSC Algorithm
In the case of unsteady buoyancy-driven flows, the equations of the Boussinesq model (50) can be solved in a segregated manner. A discrete projection method for the Navier-Stokes equations can be combined with an algebraic flux correction scheme for the temperature equation using outer iterations to update the unknown coefficients. The decoupled solution of the two subproblems makes it possible to develop software in a modular way making use of optimized multigrid solvers. Moreover, the time step can be chosen individually for each subproblem.
In the simplest implementation, one outer iteration per time step is performed. Given the velocity u n, temperature T n, and pressure p n at the time level t n, the following fractional-step algorithm is used to advance the solution in time [87]:
-
1.
Solve the viscous Burgers equation
$$A_u(\tilde{\mathbf{u}}) \tilde{\mathbf{u}}= \mathbf{f}_u-\varDelta t M_T T^{n}- \varDelta tB p^n.$$ -
2.
Solve the Pressure-Poisson equation
$$B^TM_L^{-1}Bq = \frac{1}{\varDelta t}B^T\tilde{\mathbf{u}}.$$ -
3.
Correct the velocity and pressure
$$\mathbf{u}^{n+1}=\tilde{\mathbf{u}}-\varDelta tM_L^{-1}Bq,$$$$p^{n+1}=p^n+q.$$ -
4.
Solve the temperature equation
$$A_T\bigl(\mathbf {u}^{n+1},T^{n+1}\bigr) T^{n+1}= {f}_T.$$
Since the matrix \(A_{u}(\tilde{\mathbf{u}})\) depends on the unknown solution \(\tilde{\mathbf{u}}\) to the discrete momentum equation, the system is nonlinear. We solve it using iterative defect correction or a Newton-like method. The discrete problem associated with the temperature equation is also nonlinear if algebraic flux correction is performed. Nonlinear solvers and convergence acceleration techniques for such systems are discussed in [38].
7.3 Local MPSC Algorithm
A generalization of the local MPSC approach can be used in situations when the above fractional-step algorithm proves insufficiently robust. The local problems are formulated using a restriction of the approximate Jacobian matrix associated with the nonlinear system (50). The structure of this matrix is as follows [64, 78]:
The nonlinearity of the convective term gives rise to the ‘reactive’ part R which represents a solution-dependent mass matrix and may cause severe convergence problems. For this reason, we multiply R by an adjustable parameter σ. The choice σ=1 corresponds to Newton’s method. Setting σ=0, one obtains the fixed-point defect correction scheme. In either case, the linearized problem is solved using a fully coupled multigrid solver equipped with a local MPSC smoother of ‘Vanka’ type [64]. The global matrix J(σ,u (l)) is decomposed into small blocks
associated with patches of regular shape. The smoothing of the global defect vector is performed patchwise by solving the corresponding local subproblems.
The size of the local matrices can be further reduced by using the Schur complement approach. For simplicity, consider the case σ=0 (an extension to σ>0 is straightforward). Using (47) to eliminate the temperature in (45), we obtain
Next, we use (52) to eliminate the velocity in the discretized continuity equation
Thus, the pressure Schur complement equation associated with (50) reads
At the local subproblem level, the matrix J i is replaced with the Schur complement preconditioner C i that has the same size as in the case of the basic Navier-Stokes system. After solving the local PSC equation and updating the pressure, the velocity and temperature increments are calculated and added to the global vectors.
The local MPSC algorithm is more difficult to implement than the fractional-step method presented in Sect. 7.2. However, the coupled solution strategy has a number of attractive features. Above all, steady-state solutions can be obtained without resorting to pseudo-time stepping. In the case of unsteady flows at low Reynolds numbers, the strongly coupled treatment of local subproblems makes it possible to use large time steps without any loss of robustness. On the other hand, the convergence behavior of multigrid solvers with Newton-type linearization may turn out to be unsatisfactory, and the computational cost per outer iteration is rather high compared to the global MPSC algorithm. The performance of both solution techniques is illustrated by the numerical study for the MIT benchmark problem [87].
8 Case Study: Turbulent Flows
Turbulence plays an important role in many incompressible flow problems. Since direct numerical simulation (DNS) of turbulent flows is unaffordable for Reynolds numbers of practical interest, eddy viscosity models based on the Reynolds Averaged Navier-Stokes (RANS) equations are commonly employed in CFD codes.
This section describes a numerical implementation of the k–ε model that has been in use since the 1970s. To model the effect of unresolved velocity fluctuations, the viscous part of the Navier-Stokes equations is replaced with
where ν T is the turbulent eddy viscosity. In the standard k–ε model [50], ν T depends on the turbulent kinetic energy k and its dissipation rate ε as follows:
The evolution of k and ε is governed by the convection-diffusion-reaction equations


where \(P_{k}=\frac{\nu_{T}}{2}|\nabla\mathbf{u}+\nabla\mathbf {u}^{T}|^{2}\) is responsible for the production of k. The involved empirical constants are given by C 1=1.44, C 2=1.92, σ k =1.0, σ ε =1.3.
The above equations are nonlinear and strongly coupled, which makes them very sensitive to the choice of numerical algorithms. In particular, the discretization procedure must be positivity-preserving because negative values of the eddy viscosity would produce numerical instabilities and eventually result in a crash of the code.
8.1 Positivity-Preserving Linearization
In our implementation of k–ε model, the incompressible Navier-Stokes equations are discretized using the nonconforming \(\tilde{Q}_{1}/Q_{0}\) element pair. Standard Q 1 elements are employed for k and ε. The discretization of (59)–(60) yields [41, 42]


The use of algebraic flux correction for the convective terms is not sufficient for positivity preservation. Indeed, nonphysical negative values can also be produced by the right-hand sides f k and f ε . As shown by Patankar [58], a negative slope linearization of sink terms is required to maintain positivity.
To write the equations of the k–ε model in the desired form, we introduce
The negative slope linearization of (59)–(60) is based on the representation [47]


where ν T and γ are evaluated using the solution from the last outer iteration [42].
After solving the linearized equations (59) and (60), the new values k (l) and ε (l) are used to calculate the linearization parameter γ (l) for the next outer iteration, if any. The associated eddy viscosity ν T is bounded below by a certain fraction of the laminar viscosity 0<ν min≤ν and above by \(\nu_{\max}=l_{\max}\sqrt{k}\), where l max is the maximum admissible mixing length (the size of the largest eddies, e.g., the width of the domain). In our implementation, the limited mixing length
is used to calculate the turbulent eddy viscosity by the formula
The corresponding linearization parameter γ is given by
The above representation makes it possible to avoid division by zero and obtain bounded nonnegative coefficients without manipulating the values of k and ε.
8.2 Initial Conditions
It is not always easy to find reasonable initial values for the k–ε model. If the velocity is initialized by zero, it takes the flow some time to become turbulent. Therefore, we use a constant eddy viscosity ν 0 during a startup phase that ends at a certain time t ∗>0. The values to be assigned to k and ε at t=t ∗ depend on the choice of ν 0 and on the mixing length l 0∈[l min,l max], where the threshold parameter l min is related to the size of the smallest admissible eddies. Given ν 0 and l 0, we define
Alternatively, the initial values of k and ε can be estimated with a zero-equation turbulence model or defined using an extension of the boundary conditions.
8.3 Boundary Conditions
The k–ε model is very sensitive to the choice and numerical implementation of boundary conditions. In particular, an improper near-wall treatment can render the algorithm useless. The right choice of inflow values is also important. For this reason, we discuss the imposition of boundary conditions in some detail.
At the inflow boundary Γ in , the values of all variables are commonly prescribed:
where c ∞∈[0.003,0.01] and |u| stands for the magnitude of the velocity vector.
At the outlet Γ out, the normal derivatives of all variables are set equal to zero
In the context of finite element methods, the normal derivatives appear in the surface integrals that result from integration by parts in the variational form of the governing equations. These integrals do not need to be assembled if homogeneous Neumann (“do-nothing”) boundary conditions of the form (66) are prescribed.
On a fixed solid wall Γ w , the velocity must satisfy the no-penetration condition
In laminar flow models, the tangential velocity is also set equal to zero, so that the no-slip condition u=0 holds on Γ w . To avoid the need for resolving the viscous boundary layer in turbulent flow simulations, the boundary condition for the tangential direction is frequently given in terms of the wall shear stress
If t w is prescribed on Γ w , then (67) is called the free slip condition because the tangential velocity is defined implicitly and its value is generally unknown.
The practical implementation of the free-slip condition is nontrivial, unless the boundary of the domain is aligned with the axes of the Cartesian coordinate system. In contrast to the no-slip condition, (67) constrains a linear combination of several velocity components whose boundary values are unknown. Therefore, standard implementation techniques do not work. The free-slip condition can be implemented using element-by-element transformations to a local coordinate system aligned with the wall [17]. However, this strategy requires substantial modifications of the code. In our current implementation, we drive the normal velocities to zero in an iterative way using projections of the form u:=u−(n⋅u)n [41]. Other implementation techniques are discussed in [40] in the context of compressible flow problems.
8.4 Wall Functions
To complete the problem statement, we still have to prescribe the tangential stress t w , as well as the boundary conditions for k and ε on the wall Γ w . Note that the equations of the standard k–ε model are invalid in the near-wall region, where the Reynolds number is rather low and viscous effects are dominant. To bridge the gap between the no-slip boundaries and the region of turbulent flow, analytical solutions to the boundary layer equations are frequently used to determine the values of t w , k, and ε near the wall. The use of logarithmic wall laws leads to the following set of boundary conditions to be prescribed at a small distance y from the wall Γ w
where κ=0.41 is the von Kármán constant. The friction velocity u τ is given by
The value of the parameter β depends on the wall roughness (β=5.2 for smooth walls). The above logarithmic relationship is valid for 11.06≤y +≤300.
The use of wall functions implies that a thin boundary layer of width y is removed, and the equations of the k–ε model should be solved in the reduced domain. Since the local Reynolds number y + is proportional to y, the wall distance should be chosen carefully. It is common to apply the wall laws (69) at the first internal node or integration point. However, the so-defined y depends on the mesh size and may fall into the viscous sublayer where (70) is invalid.
Another possibility is to adapt the mesh so that the location of boundary nodes always corresponds to a fixed value of y + which should be as small as possible for accuracy reasons. Taking the smallest value for which the logarithmic law still holds, one can neglect the width of the removed boundary layer and avoid mesh adaptation [25, 47]. In this case, the nodes located on the wall Γ w should be treated as if they were shifted by the distance \(y=\frac{y^{+}\nu}{u_{\tau}}\) in the normal direction.
As explained in [25], the smallest wall distance for the definition of y + corresponds to the point where the logarithmic layer meets the viscous sublayer. At this point, the linear relation \(y^{+}=\frac{|\mathbf{u}|}{u_{\tau}}\) and the logarithmic law (70) must hold, whence
This nonlinear equation can be solved iteratively. The resulting value of the parameter y + (for the default settings κ=0.41, β=5.2) is given by \(y^{+}_{*}\approx11.06\).
The relationship between \(y^{+}_{*}\) and the friction velocity u τ becomes very simple:
On the other hand, the wall boundary condition for k implies that
Following Grotjans and Menter [25], we use a combination of the above to define
This definition of t w is consistent with (69) and prevents the momentum flux from going to zero at separation/stagnation points [25]. The natural boundary condition for the wall shear stress is used to evaluate the surface integral
where w is the test function for the Galerkin weak form of the momentum equation.
By (69), the wall function for the turbulent eddy viscosity ν T is given by
This relation is satisfied automatically if the wall functions for k and ε are implemented in the strong sense. However, the use of Dirichlet boundary conditions implies that the values of k and ε depend on u via the friction velocity \(u_{\tau}=\frac{|\mathbf{u}|}{y^{+}_{*}}\) but there is no feedback. The result is an unrealistic one-way coupling.
To release the boundary values of k and ε and let them influence the tangential velocity via (74)–(75), the wall functions must be implemented in a weak sense. Differentiating (69), one obtains the Neumann boundary conditions [25]

The unknown wall distance y can be expressed in terms of the turbulent eddy viscosity ν T =κu τ y, which yields a natural boundary condition of Robin type
The surface integrals associated with the Neumann boundary condition are given by


Alternatively, the strong form of the wall law \(\varepsilon=\frac{u_{\tau}^{3}}{\kappa y}=\frac{u_{\tau}^{4}}{\kappa y_{*}^{+}\nu}\) can be used to prescribe a Dirichlet boundary condition for ε or evaluate the right-hand side of (80).
If the wall functions for ε and/or k are prescribed in a weak sense, it is essential to calculate ν T and P k using the strong form of the wall law. That is, the correct value of the turbulent eddy viscosity is given by (76), while the production term
is in equilibrium with the dissipation rate. The friction velocity u τ is defined by (74).
8.5 Chien’s Low-Re k–ε Model
Logarithmic laws provide a reasonably accurate description model of the flow in the near-wall region avoiding the need for costly integration to the wall. The derivation is only valid for flat-plate boundary layers and developed flow conditions but wall functions of the form (69) are frequently used in more general settings with considerable success. An obvious drawback to this approach is the assumption that the viscous sublayer is very thin. Clearly, it is no longer safe to apply the wall functions on Γ w if the wall distance associated with the constant \(y_{*}^{+}\) becomes too large.
A robust, albeit costly, alternative to wall laws is the use of damping functions that provide a smooth transition from laminar to turbulent flow. In Chien’s low-Reynolds number k–ε model [7], the turbulent eddy viscosity is redefined thus:


This popular model is supported by the DNS results which indicate that the ratio \(f_{\mu}=\frac{\nu_{T}\tilde{\varepsilon}}{C_{\mu}k^{2}}\) is not a constant but a function approaching zero at the wall.
The following modification of (59)–(60) is used in Chien’s model [7]


where the coefficients and damping functions are given by

In contrast to wall functions, the boundary conditions on Γ w are very simple:
Note that the sink terms in (84) and (85) have positive coefficients, as required by Patankar’s rule [58]. The value of y + is a function of the friction velocity:
The wall shear stress t w is calculated using (68). Note that the computation of y + requires knowing the wall distance y. In the current implementation, we calculate it using a brute-force approach. More efficient techniques for computing distance functions can be found in the literature on level set methods (see Sect. 10).
8.6 Numerical Examples
To verify the above implementation the k–ε model, we perform a numerical study for two test problems. The first one is used to validate the code for Chien’s low-Reynolds number k–ε (LRKE) model. In the second example, we use the LRKE solution to evaluate the results obtained with logarithmic wall functions implemented as Dirichlet (DIRBC) and Neumann (NEUBC) boundary conditions.
8.6.1 Channel Flow Problem
In the first example, we simulate the turbulent channel flow at Re τ =395 based on the friction velocity u τ , half of the channel width d, and kinematic viscosity ν. The reference data for this well-known benchmark problem are provided by the DNS results of Kim et al. [36]. In order to obtain the developed flow conditions required for validation, the inflow and outflow boundary conditions for the reduced domain were swapped repeatedly so as to emulate periodic boundary conditions.
The equations of the LRKE model are solved with the 3D code on a hexahedral mesh of 50,000 elements. Due to the need for high resolution, local mesh refinement is performed in the near-wall region, as shown in Fig. 3. The distance from the wall boundary to the nearest interior point corresponds to y +≈2. The numerical results for this test are presented in Fig. 4. The profiles of the nondimensional quantities
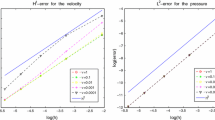
are in a good agreement with the DNS results [36] for this benchmark. The calculated profiles of u + and ε + are particularly close to the reference data.
8.7 Backward Facing Step
In the second example, we simulate the turbulent flow past a backward facing step in 3D. The definition of the Reynolds number Re=47,625 is based on the step height H, mean inflow velocity u mean, and kinematic viscosity ν. The objective is to evaluate the performance of the k–ε model with three different kinds of near-wall treatment: LRKE vs. DIRBC and NEUBC implementation of wall functions.
All simulations are performed on the same mesh that consists of approximately 260,000 hexahedral elements. Local mesh refinement is performed in the near-wall region and behind the step (see Fig. 5). A comparison of the steady-state solutions for the turbulent kinetic energy k and eddy viscosity ν T with the reference solution from [33] is presented in Figs. 6 and 7. Significant differences between the solutions computed using the strong and weak form of logarithmic wall functions are observed even in the “eyeball norm.” DIRBC was found to produce disappointing results, whereas the accuracy of the NEUBC solution is similar to LRKE.
Backward facing step: steady-state distribution of k for Re=47,625. (a) reference solution [33], (b) DIRBC solution, (c) NEUBC solution, (d) LRKE solution
Backward facing step: steady-state distribution of ν T for Re=47,625. (a) reference solution [33], (b) DIRBC solution, (c) NEUBC solution, (d) LRKE solution
An important evaluation criterion for this popular test problem is the recirculation length defined as L R =x r /H. For the implementation based on wall functions implemented as Dirichlet boundary conditions, this integral quantity can be readily inferred from the distribution of the skin friction coefficient
on the bottom wall (see Fig. 8). The recirculation length predicted by LRKE and NEUBC is underestimated (L R ≈5.4). The computational results published in the literature exhibit the same trend (5.0<L R <6.5, see [25, 33, 74]). On the other hand, the implementation of wall functions in the strong sense yields L R ≈7.1, which matches the experimentally measured recirculation length (L R ≈7.1, see [35]). Unfortunately, this perfect agreement turns out to be a pure coincidence.
In Fig. 9, the calculated velocity profiles for 6 different distances from the step are compared to one another and to the experimental data from Kim’s thesis [35]. The corresponding profiles of k and ε are displayed in Fig. 10 and Fig. 11, respectively. This comparative study indicates that NEUBC yields essentially the same results as Chien’s low-Reynolds number model, whereas the use of DIRBC leads to a significant discrepancy, especially at small distances from the step. It is also worth mentioning that the presented profiles of ε do not suffer from spurious undershoots which are frequently observed in other computations. This can be attributed to the positivity-preserving treatment of the convective terms and sinks in our algorithm.
9 Case Study: Population Balances
The hydrodynamic behavior of a polydisperse two-phase flow can be described by a RANS model for the continuous phase coupled with a population balance model for the size distribution of the disperse phase (bubbles, drops, or particles). Population balance equations (PBEs) describe crystallization processes, liquid-liquid extraction, gas-liquid dispersions, and polymerization, to name just a few important applications. The implementation of PBE models in CFD software adds an extra dimension to the problem, which increases the complexity of the code and incurs exorbitant computational costs. For this reason, examples of RANS-PBE multiphase flow models have been rare. In addition to our own work [3] to be presented here, we mention the Multiple Size Group (MUSIG) model [48] implemented in the commercial code ANSYS CFX and the recent publications by John et al. [26, 34] who used algebraic flux correction of FCT type to enforce positivity preservation.
9.1 Mathematical Model
The PBE for gas-liquid or liquid-liquid flows is an integro-differential transport equation for a probability density function f that depends on certain internal properties of the disperse phase. In the case of polydisperse bubbly flows, the internal coordinate of primary interest is the volume υ of the bubble, and f(x,t,υ) is the probability that a bubble of volume υ will occupy location x at time t. The number density N ab and volume fraction α ab of bubbles with υ∈[υ a ,υ b ] are given by


The changes in the bubble size distribution are caused by convection in the physical space and by bubble-bubble interactions (breakage and coalescence) that change the profile of f along the internal coordinate. Let u g (x,t,υ) denote the average velocity of bubbles that may be defined by adding an empirical slip velocity u slip(m) to the solution u(x,t) of the RANS model for the continuous phase. For simplicity, we assume that the slip velocity is constant, i.e., bubbles of all sizes are moving with the same velocity u g . The general form of population balance equation reads
where ν T is the turbulent eddy viscosity and σ T is the turbulent Schmidt number.
The terms in the right-hand side of (91) describe the changes of f due to breakage (B) and coalescence (C) phenomena. The superscripts “+” and “−” are used to distinguish between sources and sinks. In this study, we use the models developed by Lehr et al. [44, 45] with some modifications proposed in [5]. Let r B and r C denote the kernel functions that describe the rates of breakage and coalescence, respectively. The modeling of B ± and C ± is based on the assumption that
-
the probability that a parent bubble of volume υ will break up to form two daughter bubbles of volumes \(\tilde{\upsilon}\) and \(\upsilon-\tilde{\upsilon}\) is given by \(r^{B}(\upsilon,\tilde{\upsilon})f(\upsilon)\),
-
the probability that two bubbles of volumes \(\tilde{\upsilon}\) and \(\upsilon-\tilde{\upsilon}\) will coalesce to form a bubble of volume υ is given by \(r^{C}(\upsilon-\tilde{\upsilon},\tilde{\upsilon})f(\tilde{\upsilon}) f(\upsilon-\tilde{\upsilon})\).
Integrating the breakage and coalescence rates over all bubble sizes, one obtains

The model is closed by the choice of the kernel functions r B and r C, see [5, 44, 45].
9.2 Discretization of PBEs
In our algorithm [3], the population balance equation (92) is discretized using the method of classes which corresponds to a piecewise-constant approximation along the υ-coordinate. In the case of n classes, the pivot volumes are defined by
where υ min is the volume of the smallest “resolved” class and q is a scaling factor.
The class width Δυ i is defined as the length of the interval \([\upsilon_{i}^{L},\upsilon_{i}^{U}]\), where [3]
The method of classes transforms the integro-differential equation (92) into a system of n coupled transport equations for the class probability densities f i

The number density and volume fraction of bubbles in the i-th class are given by
Multiplying (95) by υ i Δυ i , one obtains a system of transport equations for the class holdups α i . This transformation leads to a conservative scheme such that the discretized source terms are balanced by the discretized sink terms, and the total holdup of the disperse phase is not affected by breakage or coalescence. We tacitly assume that the bubbles are incompressible so that the conservation of volume is equivalent to the conservation of mass. The number density is generally not conserved but the results of Buwa and Ranade [5] indicate that this inconsistency has hardly any influence on the specific interfacial area and the average bubble size.
The discretization of the bubble size distribution is conservative if a source in the equation for one class appears as a sink in the equation for another class. To verify this, consider a bubble of class i that breaks up into bubbles of classes j and k such that υ i =υ j +υ j . The increments to the three right-hand sides sum to zero:
Next, suppose that bubbles of the j-th and k-th class coalesce to form a bubble of class i. The gains and losses in the three classes are as follows:
Suppose that all classes have the same width, that is, Δυ i =Δυ j =Δυ k . Using the fact that υ i =υ j +υ k , we obtain the following relationship
which proves that the source and sink terms due to coalescence are also balanced.
In our implementation, the discretization of the internal coordinate is performed using nonuniform grids. To maintain the conservation of volume under coalescence, we calculate the sinks for every possible pair of classes and add their absolute values to the equation for the class that contains the emerging bubble. By this definition, the sources and sinks sum to zero, so that the total volume remains unchanged.
9.3 Integration of PBE in CFD Codes
The implementation of PBE in an existing CFD code calls for a block-iterative solution strategy. The diagram in Fig. 12 illustrates the coupling effects that arise when a PBE model is combined with the algorithm described in Sect. 8. In addition to the internal couplings within the Navier-Stokes system (C1 and C2), the k–ε model (C3), and the PBE transport equations (C4), the two-way couplings between these blocks must be taken into account (C5-C7). To reduce the computational cost, we currently neglect the influence of the disperse phase on the continuous phase and make a number of other simplifying assumptions (see below). The one-way coupling is a good approximation for flows driven by pressure and/or shear-induced turbulence. The numerical treatment of buoyancy-driven bubbly flows was addressed in [43] in the context of a drift-flux model with a two-way interphase coupling.
9.4 Numerical Examples
To our knowledge, there is no standard benchmark problem for population balance models coupled with the fluid dynamics of turbulent two-phase flows. In this section, we study the influence of turbulence on the bubble size distribution in a turbulent 3D pipe flow. The main quantity of interest is the Sauter mean diameter d 32 defined as the diameter of the sphere that has the same volume/surface area ratio as the entire ensemble. To show the potential of the CFD-PBE model in the context of an industrial application, we simulate the flow through a Sulzer static mixer SMVTM. The results are compared to experimental data provided by Sulzer Chemtech Ltd.
9.4.1 Turbulent Pipe Flow
Turbulent pipe flow is well suited for testing population balance models with one spatial and one internal coordinate [27]. The preliminary validation of our algorithm was performed on a 3D version of this problem [3]. The continuous phase is water flowing through a 1 m long pipe of diameter d=3.8 cm. The incompressible fluid that constitutes the droplets of the disperse phase has similar physical properties (density and viscosity). Due to this assumption, the interphase slip and buoyancy effects are neglected. That is, both phases are assumed to move with the mixture velocity which is calculated using the k–ε turbulence model. The Reynolds number for this simulation is \(\mathit{Re}=\frac{dw}{\nu}=114{,}000\), where w stands for the bulk velocity. The computational mesh is generated using a 2D to 3D extrusion of the mesh for the circular cross section. Each layer consists of 1,344 hexahedral elements.
The calculated radial profiles of the axial velocity, turbulent dissipation rate, and eddy viscosity for the developed flow pattern are presented in Fig. 13. The results of the turbulent flow simulation determine the velocity and the breakage/coalescence rates for the population balance model. The CFD-PBE simulations are performed for 30 classes with nonuniform spacing that corresponds to the discretization factor q=1.7. The feed stream is generated by a circular sparger of diameter 2.82 cm that produces droplets of diameter d in =1.19 mm. At the inlet, the volume fraction of droplets equals α in =0.55. In the region of fully developed flow, the total holdup of the disperse phase has the constant value α tot =0.30. Moreover, the droplet size distribution reaches an equilibrium under the developed flow conditions.
Figure 14 displays the distribution of the Sauter mean diameter d 32 in five cross sections. For better visualization, the axis scaling x:y:z=10:1:1 is employed in this diagram. Note that the equilibrium is attained at a short distance from the inlet. The distributions of the droplet size distribution and the radial profiles of the Sauter mean diameter for x={0,0.06,0.18} are presented in Fig. 15. The diagrams in Fig. 16 show the size distribution at the outlet and Sauter mean diameter along the x-axis for radii r={0,R/3,2R/3}. As expected, a high concentration of larger droplets is observed in the middle of the pipe, where the flow is fully turbulent and ε is relatively small. The concentration of smaller droplets is higher in the near-wall region, where ε is relatively large. The holdup distributions for three representative droplet classes (small, medium, and large) are presented in Fig. 17. The corresponding droplet diameters are given by 0.49 mm, 1.70 mm, and 4.90 mm.
9.4.2 Static Mixer SMVTM
Static mixers are used in industry to disperse immiscible liquids as they flow around mixer elements rigidly installed in a tubular housing. The mechanical simplicity of static mixers makes them an attractive alternative to rotating impellers. Moreover, the dissipation of frictional energy in the packing is more uniform, and so is the resultant drop size distribution [61]. This homogeneity can be attributed to the stable flow pattern that depends on the geometry of the internal parts. The Sulzer SMVTM mixing elements consist of intersecting corrugated plates and channels. This design leads to fast and efficient dispersive mixing in the turbulent flow regime.
Many experimental and computational studies of laminar and turbulent static mixers can be found in the literature. For a detailed review, we refer to Thakur et al. [73]. Our interest in this industrial application is driven by the desire to explore the capabilities of the developed simulation tools. The complex geometry of the static mixer SMVTM, as shown in Fig. 18 justifies the combination of a multidimensional flow model with PBEs. The inlet condition is that of a water-oil mixture with oil holdup α ij =0.1, Sauter mean diameter d 32=10−3 m, and inflow speed v in =1 m/s. The physical properties of the two phases are listed in Table 1. The mixture is treated as a single fluid with density and viscosity defined as a weighted average of those for oil and water. The weights are given by the corresponding volume fractions.
Computations are performed on a mesh that consists of approximately 50,000 hexahedral elements. Due to the high computational cost, a one-way coupling between the flow and the PBEs is assumed. The simulation run begins with the computation of a steady-state solution for the turbulent flow field, see Fig. 19. The converged velocity and turbulent dissipation rate are used to solve the PBEs for 45 classes. The discretization constant equals q=1.4 and the smallest droplets have the diameter of 0.5 mm. The distributions of the Sauter mean diameter d 32 and droplet ensembles with d 32∈[0.62,0.63] mm are displayed in Fig. 20.
For comparison purposes, we also present the experimental data provided by Sulzer Chemtech Ltd. The measurements are performed in the cross section right after the mixer element, and the detected droplets are assigned to the corresponding discrete classes. Since the number of classes for the numerical simulation is too large to obtain a representative number of droplets for each class, both numerical solutions and the measured data are mapped onto a size distribution with 15 classes, see Fig. 21. The results indicate that the CFD-PBE model provides a fairly good description of the population dynamics in turbulent mixtures. However, further effort is required to improve the accuracy of the model and of the numerical algorithms. This research will be continued in collaboration with Sulzer Chemtech Ltd.
10 Case Study: Interfacial Dynamics
Population balance models yield just a rough statistical estimate of the size distribution in gas-liquid and liquid-liquid dispersions. The position, shape, and size of individual drops or bubbles cannot be determined using such a model. To resolve the microscopic scales, the incompressible Navier-Stokes equations for the two immiscible fluids must be solved on subdomains separated by a moving boundary. The position of the interface is generally unknown and must be determined as a part of the problem. In this section, we describe level set methods that provide an implicit description of the interface and make it possible to solve a wide range of free boundary problems (deformation of drops/bubbles, breaking surface waves, slug flow, capillary microreactors, dendritic crystal growth) on fixed meshes.
10.1 The Level Set Method
The idea behind modern level set methods, as described in [55, 66, 67], is an implicit representation of the interface Γ(t) in terms of a scalar variable φ(x,t) such that
For practical purposes it is worthwhile to define φ as the signed distance function
As a useful byproduct, one obtains the globally defined normal and curvature
Since |φ(x,t)| is the (shortest) distance from x to Γ(t), it may serve as an indicator of interface proximity for adaptive mesh refinement techniques [2, 37].
It can be shown that the evolution of φ is governed by the transport equation
The velocity field u is obtained by solving the generalized Navier-Stokes system


where f| Γ is an interfacial force. The density ρ and viscosity μ are assumed to be constant in the interior of each phase and have a jump across Γ. We have


The value of the discontinuous Heaviside function H depends on the sign of φ
In numerical implementations, regularized approximations to H are employed.
In most existing level set codes, equations (99)–(101) are discretized using finite difference or finite volume approximations on structured meshes. However, the last decade has witnessed a lot of progress in the development of FEM-based level set algorithms [32, 46, 52, 57, 68, 75, 93]. In particular, discontinuous Galerkin methods have become popular in recent years [14, 24, 49]. The advantages of the finite element approach include the ease of mesh adaptation and the availability of a robust variational method for the numerical treatment of surface tension [1, 29].
10.2 Reinitialization
Even if the level set function φ is initialized using definition (97), it may cease to be a distance function as time evolves. In many situations, this is undesirable or unacceptable. First, nonphysical displacements of the interface and large conservation errors are likely to arise. Second, the lack of the distance function property has an adverse effect on the accuracy of numerical approximations to normals and curvatures. Third, if the gradients of φ become too steep, approximate solutions to (99) may be corrupted by spurious oscillations or excessive numerical diffusion.
The usual way to prevent a deterioration of the level set function is a postprocessing step known as ‘reinitialization’ or ‘redistancing.’ The purpose of this correction is to restore the distance function property of φ without changing its zero level set. Of course, it is possible to recalculate the distance from each mesh point to the interface. Such a ‘direct’ reinitialization is straightforward but computationally expensive, even if restricted to a narrow band around Γ. Alternatively, the distance function property can be enforced by solving the Eikonal equation
subject to φ=0 on \(\varGamma(t)=\{\mathbf{x}\,|\, \tilde{\varphi}(\mathbf {x},t)=0\}\), where \(\tilde{\varphi}\) is the level set function before reinitialization. The most popular techniques for solving (105) are fast sweeping methods [76], fast marching methods [65, 66], and the hyperbolic PDE approach [72]. In the latter method, equation (105) is treated as the steady-state limit of
The solution to this nonlinear equation is initialized by \(\tilde{\varphi}\) and marched to the steady state. In practice, it is enough to restore the distance function property in a narrow band around the interface. Hence, a few pseudo-time steps are sufficient.
For stability reasons, the discontinuous sign function is typically replaced with a smooth approximation. This practice may result in a loss of accuracy and displacements of Γ. In the interface local projection method of Parolini [57], finite element techniques are employed to perform direct reinitialization in the interface region. The corrected values of φ provide the boundary conditions for the subsequent solution of (106) in a reduced domain, where \(\mathrm{sign}(\tilde{\varphi})\) has no jumps.
To avoid the need for postprocessing, Ville et al. [93] replace (99) and (106) with a single transport equation. The so-defined ‘convected’ level set method leads to an elegant and efficient algorithm. We also subscribe to the viewpoint that convection and reinitialization should be combined as long as there is no fail-safe way to fix φ when the damage is already done. This has led us to develop a variational level set method in which the Eikonal equation (105) is treated as a constraint for the level set transport equation [39]. The nonlinear Lagrange multiplier term
added to the weak form of (99) corrects the gradients by adding artificial diffusion (λ>0) or antidiffusion (λ<0) whenever |∇φ|>1 or |∇φ|<1, respectively. In our experience, no flux limiting is required since φ remains smooth. A detailed description of the Lagrange multiplier approach will be presented elsewhere [39].
10.3 Mass Conservation
A major drawback of level set algorithms is the lack of mass conservation. Indeed, ρ(φ) given by (102) may fail to satisfy the nonlinear continuity equation
As an alarming consequence, the volume of incompressible fluids may change in an unpredictable manner. In particular, this is likely to happen when evolving interfaces undergo topological changes such as coalescence or breakup.
Both transport and redistancing may be responsible for mass conservation errors in level set algorithms. To some extent, these errors can be reduced by using more accurate numerical schemes and adaptive mesh refinement techniques [53]. Many tricks for improving the conservation properties of level set algorithms have been proposed in recent years [14, 46, 68, 71, 88]. Again, the usual approach relies on the use of postprocessing techniques designed to preserve the total volume
where H is the Heaviside function defined by (104). Smolianski [71] enforces this constraint by adding a constant c φ to the nonconservative approximation
This level correction ensures global mass conservation but there is a danger that the lost mass will reappear in a wrong place. If one fluid consists of multiple disconnected components, global conservation does not ensure that the mass/volume of each component is conserved. Clearly, manipulations of the form (110) are inappropriate in such situations. In our opinion, an incorrect distribution of mass is more harmful than (readily identifiable) mass conservation errors.
Lesage and Dervieux [46] proposed a localized mass corrector in which the constant c φ is multiplied by the nodal residual of a dual level set equation. If the mass is conserved in a control volume around node i, then the value of φ i remains unchanged. However, the corrections to other nodes depend on the global constant c φ , which implies that the distribution of the lost mass may still be incorrect.
In the conservative level set method of Olsson and Kreiss [54], φ is replaced with a regularized Heaviside function. This definition makes the algorithm akin to the phase field (diffuse interface) method. Due to the presence of a steep front and the absence of Cahn-Hilliard terms, the use of flux limiting is a must. A finite difference TVD scheme is used to solve the transport equation in the original publication [54]. In the context of a finite element approximation, the conservative level set method can be implemented using algebraic flux correction of FCT or TVD type.
10.4 Surface Tension
The overall accuracy of level set algorithms depends not only on the computation of φ but also on the numerical treatment of the surface tension force
where σ is a surface tension coefficient and δ is the Dirac delta function localizing the effect of f| Γ to Γ. The normal n and curvature κ are given by (98).
In a finite element code, the values of n and κ can be obtained using variational recovery techniques [30]. A better approach to the numerical treatment of surface tension effects is based on the following fact from differential geometry:
where id Γ is the identity mapping on Γ and \(\underline{\varDelta}\) is the Laplace-Beltrami operator
The contribution of (111) to the weak form of the momentum equation (100) is calculated using the definition of δ(x,t) and integration by parts [1, 29, 30]
Since a fully explicit treatment of this term leads to a capillary time step restriction, we follow the semi-implicit approach proposed by Bänsch [1] in the context of a front-tracking method. Plugging x n+1=x n+Δt u n+1 into (112), we obtain
Note that the second term is linear in u n+1 and has the structure of a discrete diffusion operator. In contrast to the fully explicit approach, the discretization becomes more stable for large values of σ, as shown by the numerical study in [29, 30].
Following Hysing [29, 30], we evaluate f σ using the continuum surface force (CSF) approximation [4]. By definition of the Dirac delta function, we have
Since δ is singular, numerical integration is performed using a regularized delta function. Given an approximate distance function φ, we define
where ε is a small parameter. Note that there is no need to know the position of Γ that would be difficult to determine for bilinear and higher-order elements.
Sussman and Ohta [70] have recently found another promising way to achieve unconditional stability in a numerical implementation of stiff surface tension terms. Their algorithm is based on the concept of volume preserving motion by mean curvature. Reportedly, it offers a speed-up by a factor 3–5 for a given accuracy.
10.5 Putting It All Together
The above presentation of the level set method reveals that its practical implementation involves many choices and tradeoffs. The most important components are the solver for the Navier-Stokes equations with discontinuous coefficients, the numerical approximation of the level set transport equation, mechanisms for maintaining the distance function property and mass conservation, the method for computation of normals and curvatures, and the numerical treatment of surface tension.
In the parallel 3D code developed by our group at the TU Dortmund, the incompressible Navier-Stokes equations are solved using a generalization of the discrete projection scheme described in Sect. 4. The velocity and pressure are discretized using \(\tilde{Q}_{1}/Q_{0}\) or Q 2/P 1 elements. The level set equation is solved with a FEM-TVD scheme for continuous Q 1 elements [30, 32] or an upwind-biased P 1 discontinuous Galerkin (DG) method without any extra stabilization [85]. A variety of methods have been implemented to solve the Eikonal equation at the reinitialization step for the Q 1 version [31]. The DG approach makes it possible to reinitialize φ without displacing the free interface. The gradient of the piecewise-linear solution is constant inside each cell. To enforce |∇φ|=1, we correct the slopes in elements crossed by the interface and solve (106) elsewhere, see [85] for details. The implementation of the surface tension force is based on the semi-implicit algorithm presented in Sect. 10.4. The option of solving contact angle problems is also provided.
10.6 Numerical Examples
In the absence of analytical solutions (which are very difficult to derive for interfacial two-phase flows) benchmarking is the only way to verify the developed method. Pure numerical benchmarks are of little help if no quantitative comparisons can be made. A visual inspection alone is rarely, if ever, sufficient for validation purposes. To illustrate this, consider the bubble shapes shown in Fig. 22. These shapes were calculated by six different codes with identical problem formulations. Ideally, the six solutions should be identical on fine meshes. Unfortunately, this is not the case. The shapes are quite similar but it is impossible to tell which solutions, if any, are really correct. In order to identify the good ones, one must replace the “eyeball norm” with some quantitative criteria for measuring the accuracy of simulation results.
10.6.1 Two-Dimensional Rising Bubble
In a recent paper [32], we proposed a new benchmark for interfacial two-phase flows. In collaboration with two other groups, we simulated a two-dimensional bubble rising in a liquid column. Two parameter constellations were considered. In the first test, the densities and viscosities of the two phases differ by a factor of 10, and the surface tension coefficient is chosen large enough to hold the bubble together. At the final time, the bubble assumes a typical ellipsoidal shape that was predicted very well by all codes under investigation, see Fig. 23(a). In the second test, the density and viscosity ratios are as large as 1000 and 100, respectively. Moreover, the value of the surface tension coefficient is reduced. The bubble shape falls into the skirted/dimpled ellipsoidal-cap regime, and a breakup occurs before the final time, see Fig. 23(b). The topological changes of the interface make this test rather challenging. All computational details (geometry, initial and boundary conditions, parameter values) and the reference data for both cases are available online [6].
Since the publication of rising bubble benchmark, several other groups have contributed their results. It turned out that many different interface capturing techniques (level set, volume of fluid, phase field) produce very similar results. We remark that the rationale for developing a 2D test configuration was not an accurate prediction of physical reality (2D bubbles do not exist in nature) but the computation of reference solutions for evaluation of CFD software and underlying numerical methods.
10.6.2 Three-Dimensional Rising Bubble
The 3D version of our level set code has also been tested on a rising bubble problem [85]. The settings for this simulation correspond to test cases B, C, and D defined in the paper by van Sint Annaland et al. [92]. The proportions of the bubble diameter d and domain dimensions a x ×a y ×a z are (d b :a x :a y :a z )=(3:10:10:20). The bubble undergoes significant deformations but does not break up. The densities and viscosities of the two immiscible fluids differ by a factor of 100. The values of the surface tension coefficient σ gl and gravitational acceleration g z are given in terms of the dimensionless Eötvös and Morton numbers defined as in [10]
The Reynolds number associated with the terminal rise v ∞ velocity is defined by
In order to assess the dependence of the bubble shape and v ∞ on the mesh size, simulations were performed with two different meshes and two levels of refinements for each mesh (2, 3 for mesh A and 3, 4 for mesh B). The equilibrium bubble shapes shown in Fig. 24 indicate that the employed mesh resolution is sufficient, especially in the cases B and D. The measured and calculated values of the Reynolds number for all cases are listed in Table 2. The empirical data of Clift et al. [10] and simulation results of van Sint Annaland [92] are shown in the columns labeled Re E and Re S , respectively. The last 4 columns show our results obtained on meshes A and B for refinement levels 2–4. Although these results are essentially mesh-independent, Re S exhibits a better correlation with Re E . Since no grid convergence studies were performed in [92], it is unclear if the values of Re S have also converged. This state of affairs illustrates the urgent need for a collaborative research effort aimed at the development of a new 3D benchmark for interfacial two-phase flows.
10.6.3 Droplet Dripping
In the last numerical example, we simulate the process of droplet dripping in a liquid stream [85]. In the corresponding experimental setup, the continuous phase is a glucose-water mixture and the disperse phase is silicon oil. The dripping mode is characterized by relatively low volumetric flow rates and by the fact that the droplets are generated in the near vicinity of the capillary, so that the stream length is comparable to the size of the generated droplets. Since the temperature is kept at a constant value during the whole experiment, the densities and viscosities of the two phases are also constant. The experimental studies performed by the group of Prof. Walzel (BCI, TU Dortmund) provide the average values of target quantities like the droplet size, droplet generation frequency, and the stream length. These experimental data make it possible to validate the 3D simulation results to be presented below.
The geometry of the domain around the capillary is sketched in Fig. 25. The problem dimensions measured in decimeters (dm) are as follows:
domain dimensions | 0.3×0.3×1.2 |
inner capillary radius | R 1=0.015 |
outer capillary radius | R 2=0.030 |
primary phase inlet radius | R 3=0.15 |
The physical properties of the continuous (C) and disperse (D) phase are given by

The inflow boundary conditions are given in terms of the volumetric flow rates

and
The parabolic velocity profile at the inflow boundary is defined by the formula
The parameter values a 1=10.14 dm−1 s−1, a 2=763.7 dm−1 s−1 correspond to

The above operating conditions lead to a pseudo-steady dripping mode. The measured frequency of droplet formation is \(f=0.60~\mathrm{Hz}\;(\mathrm{cca}~0.58~\mathrm{Hz}^{\exp})\), the diameter of the generated droplets is \(d=0.058~\mathrm{dm}\;(\mathrm{cca}\;0.062~\mathrm{dm}^{\exp})\), and the maximum stream length is \(L=0.102~\mathrm{dm}\;(\mathrm{cca}\;0.122~\mathrm{dm}^{\exp})\). The process of droplet dripping is illustrated by the diagrams and photographs in Fig. 26. The agreement between the simulation results and physical reality is remarkably good. In this study, we used the Q 2/P 1/P 1 version of the 3D code. The total holdup of the disperse phase evolves as shown in Fig. 27. The slope of the lines that correspond to the experimental data is given by q=6.07⋅10−5 dm3 s−1. The measured and simulated holdups follow the same trend, although the optional mass correction step was deactivated.
11 Conclusions
In this chapter, we presented a family of multilevel pressure Schur complement methods for the incompressible Navier-Stokes equations. The coupling of the basic flow model with (systems of) scalar transport equations was illustrated by the case studies for the k–ε turbulence model, population balance equations, and level set algorithms. This survey covers a small but representative selection of incompressible problems that can be solved efficiently using the proposed tools. The current research activities of our groups cover a wide range of other applications such as particulate and granular flows [51, 56], viscoelastic fluids [12], computational hemodynamics [18], benchmarking for fluid-structure interaction [83], chemotaxis problems [69], and GPU computing [19, 82], to name just a few.
The design of professional CFD software for grand-challenge industrial problems requires an optimal interaction of discretization methods, iterative solvers, and software engineering aspects. The overall performance of the code depends on all of these components. Obtaining quantitatively accurate results in a computationally efficient manner is still an issue even for scalar convection-dominated transport problems and laminar flow models. The mathematical challenges of today include the extension of algebraic flux correction schemes to higher-order finite elements and tensor-valued transport operators, hp-adaptivity in space and time, rigorous a posteriori error estimation, and model-dependent improvements.
The optimization of iterative solvers for linear and nonlinear systems requires a further analysis of Newton-like methods, convergence acceleration techniques, monolithic multigrid solvers, and domain decomposition methods for parallel computing. Furthermore, the importance of benchmark computations and grid convergence studies cannot be overemphasized. We invite the reader to visit our CFD benchmarking site [6], get familiar with the test cases and propose new ones.
In addition to the above mathematical challenges, the growing demands of the CFD industry require a further investment in the development of hardware-oriented implementation techniques for modern computer architectures. The main bottleneck to high performance is not the actual data processing but slow memory access (see [80] for a critical discussion). For this reason, the actual MFLOP/s rates are typically very low compared to the theoretical peak performance. A major gain of efficiency can be achieved, for example, by using cache-based implementation techniques and exploiting the tensor product structure of stencils for block-structured grids. Such a hardware-oriented approach may yield an overall speedup factor of up to 1000 even on a single processor. On top of that, the use of optimal parallelization strategies may boost the performance of the code by further orders of magnitude.
In light of the above, the key to achieving optimal performance in the context of implicit finite element flow solvers lies in shifting the distribution of CPU times from costly memory access tasks (assembly of matrices/right-hand sides/residuals, adaptive mesh refinement/coarsening) toward more arithmetic-intensive work (solution of sparse linear systems). High-performance computing techniques based on this philosophy are already available and prove remarkably efficient [81].
In recent years, graphics processing units (GPUs) have become a popular tool for scientific computing. The contributions of our group include a GPU- and multicore-oriented implementation technique for geometric multigrid solvers [19]. Sparse matrix-vector multiplications are utilized throughout the multigrid pipeline: in the coarse-grid solver, in smoothers, and even in grid transfer operators. The current implementation can handle several low- and high-order finite element spaces in 2D and 3D. On a single GPU, we achieve speedups by nearly an order of magnitude compared to a multithreaded CPU code. We conclude that the practical implementation of a numerical algorithm may be as important as the choice of its mathematical components. This means that the methods of scientific computing will continue to evolve following the technological trends in computer architecture.
References
Bänsch, E.: Finite element discretization of the Navier-Stokes equations with a free capillary surface. Numer. Math. 88, 203–235 (2001)
Barth, T.J., Sethian, A.: Numerical schemes for the Hamilton-Jacobi and level set equations on triangulated domains. J. Comput. Phys. 145, 1–40 (1998)
Bayraktar, E., Mierka, O., Platte, F., Kuzmin, D., Turek, S.: Numerical aspects and implementation of population balance equations coupled with turbulent fluid dynamics. Comput. Chem. Eng. (2011). doi:10.1016/j.compchemeng.2011.04.001
Brackbill, J.U., Kothe, D.B., Zemach, C.: A continuum method for modeling surface tension. J. Comput. Phys. 100, 335–354 (1992)
Buwa, V.V., Ranade, V.V.: Dynamics of gas-liquid flow in a rectangular bubble column: experiments and single/multi-group CFD simulations. Chem. Eng. Sci. 57, 4715–4736 (2002)
CFD benchmarking site. http://www.featflow.de/en/benchmarks/cfdbenchmarking
Chien, K.-Y.: Predictions of channel and boundary-layer flows with a low-Reynolds number turbulence model. AIAA J. 20, 33–38 (1982)
Chorin, A.J.: Numerical solution of the Navier–Stokes equations. Math. Comput. 22, 745–762 (1968)
Christon, M.A., Gresho, P.M., Sutton, S.B.: Computational predictability of natural convection flows in enclosures. In: Bathe, K.J. (ed.) Proc. First MIT Conference on Computational Fluid and Solid Mechanics, pp. 1465–1468. Elsevier, Amsterdam (2001)
Clift, R., Grace, J.R., Weber, M.E.: Bubbles, Drops and Particles. Dover, New York (2005)
Crouzeix, M., Raviart, P.A.: Conforming and non-conforming finite element methods for solving the stationary Stokes equations. RAIRO R–3, 77–104 (1973)
Damanik, H.: Monolithic FEM techniques for viscoelastic fluids. PhD thesis, TU Dortmund (2011)
Damanik, H., Hron, J., Ouazzi, A., Turek, S.: Monolithic Newton-multigrid solution techniques for incompressible nonlinear flow models. Int. J. Numer. Methods Fluids (2012). doi:10.1002/fld.3656
Di Pietro, D.A., Lo Forte, S., Parolini, N.: Mass preserving finite element implementations of the level set method. Appl. Numer. Math. 56, 1179–1195 (2006)
Donea, J., Giuliani, S., Laval, H., Quartapelle, L.: Finite element solution of the unsteady Navier-Stokes equations by a fractional step method. Comput. Methods Appl. Mech. Eng. 30, 53–73 (1982)
Engelman, M.S., Haroutunian, V., Hasbani, I.: Segregated finite element algorithms for the numerical solution of large–scale incompressible flow problems. Int. J. Numer. Methods Fluids 17, 323–348 (1993)
Engelman, M.S., Sani, R.L., Gresho, P.M.: The implementation of normal and/or tangential boundary conditions in finite element codes for incompressible fluid flow. Int. J. Numer. Methods Fluids 2, 225–238 (1982)
Galdi, G., Rannacher, R., Robertson, A., Turek, S.: Hemodynamical Flows: Modelling, Analysis and Simulation. WS-Oberwolfach Seminars. Birkhäuser, Basel (2008). ISBN: 978-3-7643-7805-9
Geveler, M., Ribbrock, D., Göddeke, D., Zajac, P., Turek, S.: Towards a complete FEM-based simulation toolkit on GPUs: unstructured grid finite element geometric multigrid solvers with strong smoothers based on sparse approximated inverses. Comp. Fluids (2012). doi:10.1016/j.compfluid.2012.01.025. Special issue ParCFD’11
Girault, V., Raviart, P.A.: Finite Element Methods for Navier–Stokes Equations. Springer, Berlin (1986)
Glowinski, R.: Finite element methods for incompressible viscous flow. In: Ciarlet, P.G., Lions, J.L. (eds.) Numerical Methods for Fluids (Part 3). Handbook of Numerical Analysis, vol. IX, pp. 3–1176. North-Holland, Amsterdam (2003)
Gresho, P.M., Sani, R.L., Engelman, M.S.: Incompressible Flow and the Finite Element Method: Advection-Diffusion and Isothermal Laminar Flow. Wiley, New York (1998)
Gresho, P.M.: On the theory of semi–implicit projection methods for viscous incompressible flow and its implementation via a finite element method that also introduces a nearly consistent mass matrix, Part 1: Theory, Part 2: Implementation. Int. J. Numer. Methods Fluids 11, 587–659 (1990)
Grooss, J., Hesthaven, J.S.: A level set discontinuous Galerkin method for free surface flows. Comput. Methods Appl. Mech. Eng. 195, 3406–3429 (2006)
Grotjans, H., Menter, F.: Wall functions for general application CFD codes. In: ECCOMAS 98, Proceedings of the 4th Computational Fluid Dynamics Conference, pp. 1112–1117. Wiley, New York (1998)
Hackbusch, W., John, V., Khachatryan, A., Suciu, C.: A numerical method for the simulation of an aggregation-driven population balance system. Int. J. Numer. Methods Fluids (2011). doi:10.1002/fld.2656
Hu, B., Matar, O.K., Hewitt, G.F., Angeli, P.: Population balance modelling of phase inversion in liquid-liquid pipeline flows. Chem. Eng. Sci. 61, 4994–4997 (2006)
Hughes, T.J.R., Franca, L.P., Balestra, M.: A new finite element formulation for computational fluid mechanics: V. Circumventing the Babuska–Brezzi condition: A stable Petrov–Galerkin formulation of the Stokes problem accommodating equal order interpolation. Comput. Methods Appl. Mech. Eng. 59, 85–99 (1986)
Hysing, S.: A new implicit surface tension implementation for interfacial flows. Int. J. Numer. Methods Fluids 51, 659–672 (2006)
Hysing, S.: Numerical simulation of immiscible fluids with FEM level set techniques. PhD thesis, TU Dortmund (2007)
Hysing, S., Turek, S.: The Eikonal equation: numerical efficiency vs. algorithmic complexity on quadrilateral grids. In: Proceedings of Algoritmy, pp. 22–31 (2005)
Hysing, S., Turek, S., Kuzmin, D., Parolini, N., Burman, E., Ganesan, S., Tobiska, L.: Quantitative benchmark computations of two-dimensional bubble dynamics. Int. J. Numer. Methods Fluids 60, 1259–1288 (2009)
Ilinca, F., Hétu, J.-F., Pelletier, D.: A unified finite element algorithm for two-equation models of turbulence. Comput. Fluids 27, 291–310 (1998)
John, V., Roland, M.: On the impact of the scheme for solving the higher-dimensional equation in coupled population balance systems. Int. J. Numer. Methods Eng. 82, 1450–1474 (2010)
Kim, J.: Investigation of separation and reattachment of a turbulent shear layer: flow over a backward facing step. PhD thesis, Stanford University (1978)
Kim, J., Moin, P., Moser, R.D.: Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166 (1987)
Kohno, H., Tanahashi, T.: Numerical analysis of moving interfaces using a level set method coupled with adaptive mesh refinement. Int. J. Numer. Methods Fluids 45, 921–944 (2004)
Kuzmin, D.: Algebraic flux correction I. Scalar conservation laws. Chap. 6 in this book. doi:10.1007/978-94-007-4038-9_6
Kuzmin, D., Basting, C., Bänsch, E.: The Lagrange multiplier approach to maintaining the distance function property in level set algorithms. In preparation
Kuzmin, D., Möller, M., Gurris, M.: Algebraic flux correction II. Compressible Flow Problems. Chap. 7 in this book. doi:10.1007/978-94-007-4038-9_7
Kuzmin, D., Mierka, O., Turek, S.: On the implementation of the k–ε turbulence model in incompressible flow solvers based on a finite element discretization. Int. J. Comput. Sci. Math. 1, 193–206 (2007)
Kuzmin, D., Turek, S.: Multidimensional FEM-TVD paradigm for convection-dominated flows. In: Proceedings of the IV European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2004), vol. II (2004). ISBN:951-39-1869-6
Kuzmin, D., Turek, S.: Numerical simulation of turbulent bubbly flows. In: Proceedings of the 3rd International Symposium on Two-Phase Flow Modelling and Experimentation, Pisa, September 22–24, 2004
Lehr, F., Mewes, D.: A transport equation for interfacial area density applied to bubble columns. Chem. Eng. Sci. 56, 1159–1166 (2001)
Lehr, F., Millies, M., Mewes, D.: Bubble size distribution and flow fields in bubble columns. AIChE J. 48, 2426–2442 (2002)
Lesage, A.-C., Dervieux, A.: Conservation correction by dual level set. INRIA Report 7089 (November 2009)
Lew, A.J., Buscaglia, G.C., Carrica, P.M.: A note on the numerical treatment of the k-epsilon turbulence model. Int. J. Comput. Fluid Dyn. 14, 201–209 (2001)
Lo, S.: Application of the MUSIG model to bubbly flows. AEAT-1096, AEA Technology (1996)
Marchandise, E., Geuzaine, P., Chevaugeon, N., Remacle, J.-F.: A stabilized finite element method using a discontinuous level set approach for solving two phase incompressible flows. J. Comput. Phys. 225, 949–974 (2007)
Mohammadi, B., Pironneau, O.: Analysis of the k–Epsilon Turbulence Model. Wiley, New York (1994)
Münster, R., Mierka, O., Turek, S.: Finite element-fictitious boundary methods (FEM-FBM) for 3D particulate flow. Int. J. Numer. Methods Fluids (2011). doi:10.1002/fld.2558
Nagrath, S.: Adaptive stabilized finite element analysis of multi-phase flows using level set approach. PhD Thesis, Rensselaer Polytechnic Institute, New York (2004)
Nourgaliev, R.R., Wiri, S., Dinh, N.T., Theofanous, T.G.: On improving mass conservation of level set by reducing spatial discretization errors. Int. J. Multiph. Flow 31, 1329–1336 (2005)
Olsson, E., Kreiss, G.: A conservative level set method for two phase flow. J. Comput. Phys. 210, 225–246 (2005)
Osher, S., Fedkiw, R.: Level Set Methods and Dynamic Implicit Surfaces. Springer, New York (2003)
Ouazzi, A.: Finite element simulation of nonlinear fluids with application to granular material and powder. PhD thesis, TU Dortmund (2005)
Parolini, N.: Computational fluid dynamics for naval engineering problems. PhD thesis, EPFL Lausanne (2004)
Patankar, S.V.: Numerical Heat Transfer and Fluid Flow. McGraw-Hill, New York (1980)
Prohl, A.: Projection and Quasi-Compressibility Methods for Solving the Incompressible Navier-Stokes Equations. Advances in Numerical Mathematics. Teubner, Stuttgart (1997)
Quartapelle, L.: Numerical Solution of the Incompressible Navier-Stokes Equations. Birkhäuser, Basel (1993)
Rama Rao, N.V., Baird, M.H.I., Hrymak, A.N., Wood, P.E.: Dispersion of high-viscosity liquid-liquid systems by flow through SMX static mixer elements. Chem. Eng. Sci. 62, 6885–6896 (2007)
Rannacher, R., Turek, S.: A simple nonconforming quadrilateral Stokes element. Numer. Methods Partial Differ. Equ. 8, 97–111 (1992)
Schäfer, M., Turek, S. (with support of F. Durst, E. Krause, R. Rannacher): Benchmark computations of laminar flow around cylinder. In: Hirschel, E.H. (ed.) Flow Simulation with High-Performance Computers II. Notes on Numerical Fluid Mechanics, vol. 52, pp. 547–566. Vieweg, Wiesbaden (1996)
Schmachtel, R.: Robuste lineare und nichtlineare Lösungsverfahren für die inkompressiblen Navier-Stokes-Gleichungen. PhD thesis, University of Dortmund (2003)
Sethian, J.A.: A fast marching level set method for monotonically advancing fronts. Proc. Natl. Acad. Sci. USA 93(4), 1591–1595 (1996)
Sethian, J.A.: Level Set Methods and Fast Marching Methods: Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science. Cambridge University Press, Cambridge (1999)
Sethian, J.A., Smereka, P.: Level set methods for fluid interfaces. Annu. Rev. Fluid Mech. 35, 341–372 (2003)
Smolianski, A.: Numerical modeling of two-fluid interfacial flows. PhD thesis, University of Jyväskylä (2001)
Strehl, R., Sokolov, A., Kuzmin, D., Horstmann, D., Turek, S.: A positivity-preserving finite element method for chemotaxis problems in 3D. Ergebnisber. Angew. Math. 417, TU Dortmund (2010)
Sussman, M., Ohta, P.M.: A stable and efficient method for treating surface tension in incompressible two-phase flow. SIAM J. Sci. Comput. 31, 2447–2471 (2009)
Sussman, M., Puckett, E.G.: A coupled level set and volume of fluid method for computing 3D and axisymmetric incompressible two-phase flows. J. Comput. Phys. 162, 301–337 (2000)
Sussman, M., Smereka, P., Osher, S.: A level set approach for computing solutions to incompressible two-phase flow. J. Comput. Phys. 114, 146–159 (1994)
Thakur, R.K., Vial, Ch., Nigam, K.D.P., Nauman, E.B., Djelveh, G.: Static mixers in the process industries—A review. Trans. IChemE 81, 787–826 (2003)
Thangam, S., Speziale, C.G.: Turbulent flow past a backward-facing step: a critical evaluation of two-equation models. AIAA J. 30, 1314–1320 (1992)
Tornberg, A.-K.: Interface tracking methods with applications to multiphase flows. PhD thesis, Royal Institute of Technology, Stockholm (2000)
Tsai, Y.R., Cheng, L.-T., Osher, S., Zhao, H.-K.: Fast sweeping algorithms for a class of Hamilton-Jacobi equations. SIAM J. Numer. Anal. 41(2), 673–694 (2003)
Turek, S.: On discrete projection methods for the incompressible Navier-Stokes equations: An algorithmical approach. Comput. Methods Appl. Mech. Eng. 143, 271–288 (1997)
Turek, S.: Efficient Solvers for Incompressible Flow Problems: An Algorithmic and Computational Approach. Lecture Notes in Computational Science and Engineering, vol. 6. Springer, Berlin (1999)
Turek, S., et al.: FEATFLOW: finite element software for the incompressible Navier-Stokes equations. User manual, University of Dortmund (2000). http://www.featflow.de
Turek, S., Becker, C., Kilian, S.: Hardware-oriented numerics and concepts for PDE software. Future 1095, 1–23 (2003)
Turek, S., Becker, C., Kilian, S.: Some concepts of the software package FEAST. In: Palma, J.M., Dongarra, J., Hernandes, V. (eds.) VECPAR’98—Third International Conference for Vector and Parallel Processing. Lecture Notes in Computer Science. Springer, Berlin (1999)
Turek, S., Göddeke, D., Buijssen, S., Wobker, H.: Hardware-oriented multigrid finite element solvers on (GPU)-accelerated clusters. In: Kurzak, J., Bader, D.A., Dongarra, J. (eds.) Scientific Computing with Multicore and Accelerators, pp. 113–130. CRC Press, Boca Raton (2010). Chap. 6
Turek, S., Hron, J., Razzaq, M., Wobker, H., Schäfer, M.: Numerical Benchmarking of Fluid-Structure Interaction: A Comparison of Different Discretization and Solution Approaches. In: Bungartz, H.-J., Mehl, M., Schäfer, M. (eds.) Fluid Structure Interaction II: Modelling, Simulation, Optimization. Lecture Notes in Computational Science and Engineering, vol. 73, pp. 413–424. Springer, Berlin (2010)
Turek, S., Kilian, S.: An example for parallel ScaRC and its application to the incompressible Navier-Stokes equations. In: Proc. ENUMATH’97. World Scientific, Singapore (1998)
Turek, S., Mierka, O., Hysing, S., Kuzmin, D.: Numerical study of a high order 3D FEM-level set approach for immiscible flow simulation. Submitted to Proceedings of the ECCOMAS Thematic Conference on Computational Analysis and Optimization (June 9–11, 2011, Jyväskylä, Finland)
Turek, S., Ouazzi, A.: Unified edge-oriented stabilization of nonconforming FEM for incompressible flow problems: Numerical investigations. J. Numer. Math. 15, 299–322 (2007)
Turek, S., Schmachtel, R.: Fully coupled and operator-splitting approaches for natural convection. Int. J. Numer. Methods Fluids 40, 1109–1119 (2002)
van der Pijl, S.P., Segal, A., Vuik, C.: A mass-conserving level-set method for modelling of multi-phase flows. Int. J. Numer. Methods Fluids 47, 339–361 (2005)
Van Dyke, M.: An Album of Fluid Motion. The Parabolic Press, Stanford (1982)
Vanka, S.P.: Implicit multigrid solutions of Navier–Stokes equations in primitive variables. J. Comput. Phys. 65, 138–158 (1985)
Van Kan, J.: A second-order accurate pressure–correction scheme for viscous incompressible flow. SIAM J. Sci. Stat. Comput. 7, 870–891 (1986)
Van Sint Annaland, M.S., Deen, N.G., Kuipers, J.A.M.: Numerical simulation of gas bubbles behaviour using a three-dimensional volume of fluid method. Chem. Eng. Sci. 60, 2999–3011 (2005)
Ville, L., Silva, L., Coupez, T.: Convected level set method for the numerical simulation of fluid buckling. Int. J. Numer. Methods Fluids 66, 324–344 (2011)
Acknowledgements
The authors would like to thank Shu-Ren Hysing, Otto Mierka, and Evren Bayraktar (TU Dortmund) for contributing their results. The collaboration with Prof. Peter Walzel (TU Dortmund) and Sulzer Chemtech Ltd is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2012 Springer Science+Business Media Dordrecht
About this chapter
Cite this chapter
Turek, S., Kuzmin, D. (2012). Algebraic Flux Correction III. In: Kuzmin, D., Löhner, R., Turek, S. (eds) Flux-Corrected Transport. Scientific Computation. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-4038-9_8
Download citation
DOI: https://doi.org/10.1007/978-94-007-4038-9_8
Publisher Name: Springer, Dordrecht
Print ISBN: 978-94-007-4037-2
Online ISBN: 978-94-007-4038-9
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)