Keywords

Introduction

In this chapter, we seek to develop a specific account of scientific reasoning, its role, and its value in science education. One of the defining characteristics of science (and scientists) is the critical spirit that is central to science as a practice. Such reasoning is essential for the construction of claims to knowledge which are based on data and warrants which are then used to justify a claim. Typically, arguments may be either deductions about the world from a set of a priori premises such as those used in the development of kinetic theory; inductive generalizations about what patterns may exist typified by laws such as the law of conservation of energy; or inferences to the best explanation such as those used by Darwin in developing his argument for evolutionary theory. As important as the use of reasoning for the construction of knowledge is its use for critical review and evaluation for, as Ford (2008) argues, it is “critique which motivates authentic construction of scientific knowledge.” Claims must be defended against arguments that question either the validity or reliability of the data, the warrant that justifies the significance of the data to the claim, or the background theoretical assumptions. The formal embodiment of this process is peer review and it is through this practice of discourse and argument that science maintains its objectivity (Longino, 1990).

However, whilst all might concur that such discursive practices are characterized by the use of reasoning, what are the salient features that distinguish scientific reasoning? Some conceptual clarity is needed if we are to distinguish good reasoning from that which is weak, wanting, or simply erroneous. In this chapter, therefore, we seek to explore briefly what are the some common characterizations of scientific reasoning. Our goal here is to suggest that all of these fail to capture an account of scientific reasoning which captures how individuals really reason. Instead, our main argument is that it is a form of Bayesian reasoning that offers the most comprehensive articulation of reasoning in a scientific context. As we will show, not only does it explain existing controversies that exist within the body of empirical research but it also offers an explanatory account of why critique is an essential element of scientific practice and effective pedagogy in science.

Scientific Reasoning

Historically, there have been three fundamental perspectives on the nature of scientific reasoning—the psychological, the philosophical, and the sociological. The psychological perspective is probably most strongly associated with the work of Jean Piaget (Inhelder & Piaget, 1958; Piaget, 1929, 1953) who saw reasoning in science as a practice dominated by a set of logico-mathematical operations such as compensation, seriation, classification, and logical reasoning typified by hypothetico-deductive arguments of the form “if…then…therefore.” Such reasoning required the ability to identify and control variables and manipulate abstract representations. Children were seen as progressing through a set of stages of mental development, attaining the highest level, formal reasoning, in adolescence. The apotheosis of the influence of this perspective on the classroom was Shayer & Adey’s curriculum intervention for middle school science—Thinking Science (Michael Shayer, 1999; Michael Shayer & Adey, 1992). This was a two-year course consisting of interventions once every two weeks that were designed to cognitively accelerate children’s ability to undertake these operations. Much of the research has focused specifically on developing children’s capability to identify and control variables as this is seen as a cognitive operation which is core to the process of inquiry. Zimmerman offers a good summary of much of this work (Zimmerman, 1999, 2007). Clearly, this form of reasoning is an essential feature of experimental design as experiments where all the relevant variables are not identified, or where there is more than one dependent variable produce results which are confounded and cannot make claims to knowledge. The use of this reasoning strategy is very much at the core of double-blind trials of new pharmaceutical products.

There are many well-known objections to the Piagetian account—most notably those summarized by Metz (1995). However, the substance of the critique is that while such reasoning is required by science, the common interpretation of an implied deterministic developmental pathway is simply flawed and not supported by the evidence. Children, it is argued, are much more capable than the Piagetian account would suggest. Our critique, however, is somewhat different. Essentially, a focus on a specific set of logico-mathematical operations as the principal forms of reasoning in science offers only a narrow and incomplete vision of scientific reasoning. In short, reasoning is always situated in a context and only makes sense when judged within that context. Judgments about what constitute good data depend critically on well-established “concepts of evidence” (Gott & Duggan, 1996) such as whether the data are valid, are subject to random or systematic error, how reliable they are, and what the degree of error might be. Further, reasoning is also context dependent in that judgments about the validity of any scientific argument are reliant on the construction of meaning from scientific texts or discourse (Norris & Phillips, 2003). Only an individual who has an appropriate level of scientific knowledge is able to construct the meaning necessary to reason with. Scientific reasoning, therefore, does not take place in some contextual vacuum. This is the essence of the critique mounted by Koslowski and her co-workers that individual performance varies significantly when subjects have credible theoretical justifications for why two variables might co-vary (Koslowski, 1996; Koslowski, Marasia, Chelenza, & Dublin, 2008). Finally, research in psychology has focused overwhelmingly on student’s capability to achieve an agreed performance. Little of the work has examined student’s capability to detect erroneous reasoning and justify why it is flawed. Given that the ability to engage in critique is a major element of scientific reasoning, this omission is surprising. Thus, our view of this perspective on scientific reasoning is not so much that it is wrong or flawed but rather it offers a partial or incomplete view of the edifice.

A somewhat different perspective is offered by philosophical accounts of scientific reasoning. These have ranged through Baconian descriptions of science as a process of generalizations emerging from empirical enquiry; Popperian notions of science as a process of conjecture and refutation; Kuhn’s view that science was a community of practice governed by internal norms that framed the paradigm in which scientists work; and to the more radical views of Feyerabend that there was no common, identifiable method that could characterize science (Chalmers, 1999). All of these have attempted to describe the normative criteria used by science in its search for knowledge which would help distinguish science from other forms of cultural activity. To date, most would agree that this has been a failed project. Rather, each of these descriptions captures some but not all elements of scientific practice and each have been individually questioned and found incomplete (Fuller, 1997; Nowotny & Scott, 2001; Taylor, 1996). Siegel, for instance, in response to some of the common criticisms has attempted to argue that a central commitment of science is to evidence as the basis of belief (Siegel, 1989). Whilst that is generally unquestioned, it is also the basis of belief, at least to some extent in the social sciences and history. Donnelly, for instance, takes a different tack arguing that it is not the epistemic but the ontic nature of science which is its distinguishing feature (Donnelly, 2005). The best that the philosophy of science can offer for an account of scientific reasoning is the distinction between the three forms of argument that are commonly used in science—abductive, deductive, and inductive. Whilst school science arguably overemphasizes the inductive and deductive form of argument, philosophical analysis of this form has little substantive to offer science education in helping to identify the forms of detailed practice that would help students to develop their skill and aptitude with such forms of reasoning. Rather, it offers a meta-language for describing the broadest features of the argument and a rationale for the importance of certain activities such as modeling (Nercessian, 2008). But whereas the teacher of science needs a detailed picture of the scientific landscape and how it is mapped, the philosophy of science offers a picture sketched only in the broadest of brush strokes.

One philosopher who has been influential in this field is Toulmin. His attempt to capture the nature of informal argument as used in everyday life, as opposed to the strict requirements of logic, has helped the field to recognize that argumentation is a form of reasoning which is central to all forms of human activity (Toulmin, 1958). His field-independent notion that the essential elements of argument consist of a claim, albeit qualified, supported by data and a warrant where the warrant justifies the relevance of the data to the claim has led to an enhanced emphasis for this form of reasoning in science education (Driver, Newton, & Osborne, 2000; Duschl & Osborne, 2002; Kuhn, 1993). Its importance has been lent additional significance by work conducted in the field of science studies which has portrayed science as a practice where scientists marshal resources gathered from “inscription devices” that transform data to commonly recognized forms. This evidence is then used as a resource in developing arguments to persuade other scientists of the validity of a range of differing ontological entities and causal mechanisms (Latour & Woolgar, 1986; Traweek, 1988). Such an analysis of the practice of science has offered education a rationale for the significance of argument as a form of reasoning and its study. In addition, it provides a meta-language for describing its essential features. In that sense, the analysis of the detail of discursive practice has been useful in foregrounding the essential elements that are necessary to any account of scientific reasoning. Conjoined with the analysis offered by psychology of particular forms of argument/reasoning used within science such as the control of variables, it might be said to offer a good account of the major elements of scientific reasoning.

However, we would contend that there is still an essential element missing in all of these descriptions of scientific reasoning. This is that such accounts fail to account for the importance of criticism in the practice of science and why it is so central to scientific reasoning. Essentially, constructing an argument for the validity of a scientific claim depends as much on knowing why the wrong answers are wrong as much as it does knowing why the right answer is right. Such a position, we will show, has clear implications both for our conception of the nature of scientific reasoning and for pedagogy within science education. The substance of our argument is drawn from Bayesian accounts that see reasoning as a process not of constructing an infallible argument but rather one of drawing inferences based on the assessment of relative probabilities.

A Bayesian Perspective on Scientific Reasoning

The distinguishing feature of Bayesian inference is that it is a system of describing the certainty of knowledge. The degree of this certainty is reflected in probabilities assigned to a given hypothesis or event. As new evidence emerges, these probabilities are updated. Sometimes, the new evidence strongly favors the target hypothesis over rival hypothesis and sometimes it does not. Bayes’ theorem describes mathematically how this balance of evidence changes the assigned probabilities. In other words, Bayes’ theorem describes how the certainty of knowledge is updated given the new data. In this regard, Bayesian inference shares many aspects with scientific reasoning and argumentation. Both involve evaluating uncertain hypotheses and both involve weighing new evidence against target and alternative theories. In certain ways, the very process of science can be viewed as the repeated application of Bayes’ theorem as data and evidence gradually change the probabilities in the minds of scientists, “convincing” them of the truth or falsity of a given hypothesis.

Bayesian inference offers a means of characterizing an individual’s assessment of a hypothesis. Its tenets are derived from Bayesian probability, which is typically used to describe random, well-defined systems. Examples of such systems include gambling outcomes, gene assortment, and many quantum phenomena. However, whereas Bayesian inference is still developing as a model for scientific reasoning (Howson & Urbach, 2006), Bayesian probability is widely accepted as an interpretation for probabilistic systems.

Origins and an Intuitive Explanation

Bayesian probability was named after Thomas Bayes (1702–1761), an English clergyman and mathematician. Pierre-Simon Laplace (1749–1827) subsequently elaborated and popularized the field into what is known today as Bayesian probability theory (Stigler, 1986). The logic of Bayesian probabilities can be justified directly from certain requirements of rationality and internal consistency (see Cox’s theorem in Cox, 1961).

An Intuitive Explainer

One of the problems confronting the wider adoption of Bayesian reasoning as a model for scientific reasoning is its expression in a mathematical formalism which is somewhat opaque. In its original mathematical form, Bayes’ theorem appears as follows:

$${\textrm{P}}\left( {h|e} \right) = \frac{{{\textrm{P}}\left( {e|h} \right){\textrm{P}}\left( h \right)}}{{{\textrm{P}}\left( e \right)}}$$

In this formula, P (h|e) is the probability of a hypothesis h given that some evidence e is true. This is referred to as the posterior probability as it is the new, updated probability assessment given the evidence e. P (e|h) is the probability of the evidence e occurring given that hypothesis h is true. This is referred to as the likelihood of h on e because it reflects how determinate h is to explaining e. P(h) is the probability of hypothesis h being true by itself. This is called the prior probability since it reflects the probability of h independent of the new evidence e. Finally, P(e) is the probability of evidence e being true by itself.

This abstract formulation is the typical presentation for Bayes’ theorem and while it has the advantage of being mathematically concise, the heavy use of logical symbolism does not facilitate an intuitive grasp of the meaning of the theorem. Without this, it is difficult to judge its implications or utility as a conceptual framework. It is this lack of transparency that has hindered the acceptance of Bayesian inference as a framework for science educators. To address this, we turn instead to a more intuitive example to explain how Bayesian probabilities work: the likelihood of breast cancer and mammogram tests. Both events have some associated randomness. Importantly though, the two systems are inter-related: when a woman receives a positive mammogram, her likelihood of breast cancer increases. Bayes’ theorem describes how much that likelihood changes. Put differently, it explains how knowledge of the probabilities in one system changes the probabilities of a system which is related, yet distinct.

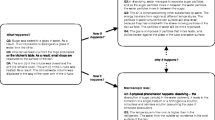
The updated probability of breast cancer (called the posterior probability) can be determined from three pieces of information. The first is that 1% of women, say in their 50 s, have breast cancer (the prior probability, labeled “Info A” in Fig. 4.1). The second is that for women who definitively have breast cancer, mammograms are positive 80% of the time (the true positives, labeled “Info B”). The third is that for women without cancer, mammograms are still positive 10% of the time (the false positives, labeled “Info C”). Before continuing, we recommend the reader to estimate an answer: given a positive mammogram, what is the likelihood of cancer?

Fig. 4.1
figure 4_1_210703_1_En

Graphical representation of probabilityupdate calculation with Bayes’ Theorem

Full size image

When phrased in this way, an alarming six out of seven doctors arrive at the wrong answer (Casscells, Schoenberger, & Graboys, 1978; Eddy, 1982). Most vastly overestimate the likelihood. The most typical error is to assume that a positive test implies that the individual has an 80% chance of cancer. However, this is mistaken because it neglects the large number of false positives that happen for normal individuals without cancer who are routinely tested. The correct calculation begins with the prior probability: since 1% of women have breast cancer, when testing a 1000 people, 990 will not have cancer. Of those 990, 99 will have a positive result and do not actually have cancer. Of this sample of 1000, only 10 individuals actually do have cancer and only 8 of them will be detected by the test. Therefore, given a positive test, the actual chance of having cancer is only 8 out of the 107 (99 + 8) positive results, that is, 7.5%. Whilst the answer might seem surprising, it is a common error of logic that neglects the fact that most cases of positive mammograms actually occur when there is no cancer, that is, the false positives. A graphical demonstration of how this probability is calculated is offered in Fig. 4.1.

Bayes’ theorem can be further simplified into its key conceptual components. Figure 4.2 captures the essence of what Bayes’ theorem postulates: new evidence is used to update prior probabilities to what are now posterior probabilities, a change in the degree of certainty that depends on the likelihood ratio (how strongly the evidence pertains to true versus false positives). In Bayesian epistemology, this is referred to as the Simple Principle of Conditionalization (Adams, 1965).

Fig. 4.2
figure 4_2_210703_1_En

Simplified Bayesian probability update model

Full size image

What these examples mean is that all decisions have to be weighed not solely in terms of what information or evidence there is that they are correct but also in terms of what the likelihood is that they might be wrong. To do otherwise is to engage in faulty reasoning and logic and to misinterpret the inferences that can be drawn from the evidence. A patient might still opt for aggressive cancer treatment given a positive mammogram, but this is because their likelihood of a cancer has increased a little over sevenfold, and not to the commonly mistaken 80%. In reality, the unreliability of the test requires a more reliable test—a biopsy. However, it is because of the large number of false positives in women under 50 and the associated emotional turmoil that the United States Preventive Task Force recommended in its new guidelines that most women start regular screening at age 50 and not age 40 which has been the practice until now (US Dept of Health and Human Services, 2009).

Applications to the Reasoning Process

This Bayesian probability model is a widely accepted interpretation for external, objectively probabilistic systems. What is less established is using this model to describe the assessments of hypotheses by individuals. This is the key leap that characterizes the debate about the value of Bayesian inference as a model of scientific reasoning. In other words, can a probabilistic model that characterizes external, random systems be used to describe the cognitive process of belief assessment?

This application of Bayesian notions to personal degrees of belief is sometimes called the subjectivist view (De Finetti, 1974) and has been developed by certain authors such as Howson & Urbach (2006). The subjectivist use of Bayesian ideas shares the same fundamental concepts and calculus with the example above of breast cancers and mammograms. However, instead of the likelihood of cancer, Bayesian inference replaces this with an individual’s likelihood assessment that a given hypothesis is correct. Such a hypothesis could be scientific such as the likelihood that the theory of dark matter is correct, or something more mundane such as the likelihood that some car mechanic is trustworthy. The subjectivist view therefore acknowledges the subjective beliefs of the individual while also claiming that updating those beliefs should follow certain elements of logic and reason.

As a model of informal reasoning, Bayesian inference provides a useful analog. When we are considering a theory, we tend to have some preconceived notions (i.e., prior probabilities). Using the car mechanic example above, we may feel that a car mechanic is trustworthy for any number of preconceived reasons. When new evidence arises, such as a friend recommending the mechanic, we are apt to update our assessment (i.e., posterior probability). That new probability, however, depends on both true and false positive considerations. If our friend is reliable and is mechanically knowledgeable, then that increases the strength of our certainty. However, if our friend is shifty and owns a stake in the mechanic’s shop, it has the opposite effect enhancing the evidence of false positives. In Bayesian inference, the degree that the new data supports our target hypothesis versus alternative hypothesis is the likelihood ratio.

Bayesian inference does not explain all aspects of human thinking. Instead, it is meant as a model for rational thinking, namely an attempt at one’s best objective assessment in contrast to a stubbornly prejudiced or capricious one. Degrees of belief are clearly individual and subjective. Nonetheless, Bayesian inference suggests that these beliefs must be updated according to the axioms of probability in order to be optimal (Maher, 1993). Support for this claim comes from the Dutch Book theorem, developed in the 1920s and 1930s by Frank Ramsey and Bruno de Finetti. They showed that violating the axioms of probability resulted in belief probabilities that were incoherent, meaning the beliefs are demonstrably irrational (De Finetti, 1937). A simple example of this theorem is a belief held that there is 70% expectation of rain which is also held conjointly with a 40% expectation of no-rain. These beliefs are incoherent when taken together because the probabilities add to 110%. If a bookie took both bets together, the combined odds would guarantee a loss of 10%. This situation, where a set of odds guarantees a loss regardless of the outcome, is known as a “Dutch Book.” To prevent getting swindled by Dutch Books, wiser bookmakers are trained to build and update their odds using the rules of Bayesian calculus. These examples simply highlight the damage that irrational beliefs can have. Put another way, judging whether you will be right without judging the probability of whether you will be wrong will lead to poor assessments which are incoherent and pragmatically self-defeating: that is actions that, based on logical inconsistency alone, are guaranteed to make things worse than they otherwise would have been (Talbott, 2008).

The appeal then of Bayesian inference is that, in two different ways, it juxtaposes a mathematical model with intuitive experience. In one sense, it combines subjective likelihood assessments (i.e., prior probabilities) with an objective set of procedures and formula for updating those assessments (Bayes’ formula). In another sense, it offers a kind of “independent opinion” about scientific reasoning since its notions are derived logically from the axioms of probability mathematics. If corroborated by empirical evidence then, Bayesian inference offers a take on scientific reasoning that arises from an independent, non-empirical source. We turn now to that empirical evidence.

Empirical Findings

In this section, we examine empirical findings about scientific reasoning from the areas of science education and psychology. Our objective is to see if the key conceptual components of Bayesian inference fit with the findings of these fields. We consider three groups of empirical results: (1) misconceptions research on students’ alternative explanations; (2) findings on argumentation in classrooms; and (3) studies on coordination of theory and evidence.

Misconception Research on Students’ Alternative Explanations

Numerous findings in science education have shown that providing students with correct explanations alone is inferior to also explaining why misconceptions are incorrect. For instance, Hynd & Alvermann (1986) found that physics texts that contained “refutation text” addressing common misconceptions resulted in significantly better conceptual gains. Likewise, Ames & Murray (1982) found greater learning gains among discussion groups with differing preconceptions versus those with more similar ones, even if those differences were based on incorrect premises. In short, providing information about both negative and positive cases significantly improves conceptual learning in the sciences.

These findings are consistent with Bayesian conceptions of probability updates, namely that it is not possible to develop a posterior probability without a consideration of competing alternative hypotheses. According to this view, correct explanations only provide half of the picture. They explain why the target hypothesis is right, increasing the likelihood of the true positives. However, they provide no information about why other alternative hypotheses are incorrect. This is critical because in the Bayesian model, the strength of the true positive information does not stand alone; it is always relative to strength of the false positive alternatives (Royall, 1997). As such, students need both target and competing explanations to construct assessments of the presented material. Good teachers of science recognize this need intuitively, attempting to contrast the scientific explanation with the common intuitive notions addressing why they are wrong as much as why the scientific idea is correct (Ogborn, Kress, Martins, & McGillicuddy, 1996). Likewise, the French philosopher Bachelard understood this concept when he argued that “two people must first contradict each other if they really wish to understand each other. Truth is the child of argument, not of fond affinity” (Bachelard, 1968). What both are pointing to is that it is difference which enables conceptual understanding because, as we would argue, from a Bayesian perspective it provides the individual with evidence both for the proposition and the false positives.

Argumentation in Classrooms

Whereas explanations presume truth, arguments establish it by a process of claims, counterarguments, and rebuttals (Toulmin, 1958). When utilized in the classroom, this process has been shown to result in greater conceptual learning gains (Asterhan & Schwarz, 2007; Zohar & Nemet 2001). However, the use of argument in classrooms is still not a common pedagogical practice in science education (Newton, Driver, & Osborne, 1999).

The benefits observed from argumentation for learning are also consistent with Bayesian notions of scientific reasoning. With Bayesian inference, evaluating the likelihood ratio lies at the heart of assessing a posterior probability. Therefore, evaluating a hypothesis rests critically on weighing true positive and false positive perspectives that are both consistent with the new evidence. Yet, studies have shown that individual scientists have difficulty generating alternative inductions (i.e., false positives) from data; in comparison, groups of scientists engaged in collaborative discussion are more able to do so (Dunbar, 1997). Group discussion may, therefore, enhance scientific reasoning by facilitating the otherwise difficult process of generating and evaluating false positives individually. Similar evidence comes from the work of Johnson on the history of the development of one specific engineering product—ABS braking (Johnson, 2009). In her historical account of the development of this technology, Johnson shows how knowledge sharing was essential to the process. Those who did not contribute any knowledge to the community, predominantly American engineers (regardless of whether it was right or wrong), simply did not have the information necessary to make a good judgment about the Bayesian likelihood ratio, which resulted in a loss to their European counterparts. Similar arguments can be made about Crick and Watson’s development of their model for DNA. The critical pieces of information were as much the evidence why certain of their proposed structures were wrong, as it was the evidence from Rosalind Franklin’s X-ray crystallography suggesting that the structure was a helix.

Coordination of Theory and Evidence

Several studies have evaluated the capability of individuals to coordinate theory and evidence (Kanari & Millar, 2004; Koslowski, 1996; Kuhn, 1991, 1993). A particularly interesting finding in this field was a study by Koslowski (Koslowski, 1996; Koslowski, Marasia, Chelenza & Dublin 2008). Koslowski and her colleagues found that information was more likely to be considered as evidence when a causal explanation was provided. In this study, subjects were provided two plausible explanations for some phenomenon. Data were presented that supported one explanation over the other. The authors observed that subjects were more likely to consider the data as evidence when given a causal framework that permitted its incorporation. Without this explanatory framework, subjects were more likely to disregard the data and did not change their evaluation of which hypothesis was better.

The results of this study can be interpreted with a Bayesian notion of likelihood ratios. By pointing out explicitly a possible explanatory framework, the likelihood of the data supporting the target hypothesis over the rival hypothesis increases. From this perspective, the data that subjects considered irrelevant may have had an evidentiary basis. However, without an explanatory framework which identifies why the data are salient to the hypothesis, the evidence is not so much discounted as simply not counted. Thus, it is not just data that matters for updating probabilities. Providing an explanatory framework which helps the individual see why the data supports the positive hypothesis enables the individual to reassess the likelihood ratio from one where the probabilities may be evenly balanced toward the target hypothesis. Such an interpretation would predict a greater change to the posterior probabilities in the subjects who were provided explanations versus those that were not, an effect that was indeed observed in the study.

Framework Comparison

In addition to empirical congruence, Bayesian inference can also be used to address problems with existing models of scientific reasoning. In this section, we compare Bayesian inference to Popper’s model of falsification as well as the model of hypothesis testing known as the Frequentist probabilities.

Popperian Falsification

Falsification is a well-known concept in science and scientific reasoning developed by Karl Popper (1959). The theory of falsification states that theories can never be confirmed. Instead, confirming data merely allows a given theory to survive disconfirmation. In contrast, disconfirming data negates the theory and new theories must subsequently be developed that encompass the disconfirming case. In this way, science progressively accumulates theories of greater explanatory power. However, even theories that have survived multiple disconfirmations are never decisively proven as true.

Several aspects of Popper’s model are in conflict with actual experience. The first is that falsification classifies all current theories as only having survived disconfirmation. However, scientists clearly have different certainties about different theories. No reasonable scientist would consider the theory of dark matter to be as certain as the atomic theory of matter. Popper attempts to address this by introducing the notion of “corroborated” theories. However, this effectively adds gradations in certainty, an interpretation that begins to look more like one associated with Bayesian probabilities. In fact, the very notion of degrees of corroboration is what Bayesian inference formalizes as belief probabilities (Sokal & Bricmont, 1998).

The falsification model has the additional problem of making a fundamental distinction between confirming and disconfirming evidence. With falsification, confirming evidence is not utilized in any meaningful way while disconfirming evidence has the effect of negating the theory. In actual experience, however, confirming evidence does increase the strength of a theory and multiple disconfirmations are typically needed before discarding a theory, particularly if the theory was well established (Collins & Pinch, 1993). The Bayesian model reflects both of these realities more accurately. Confirming evidence raises posterior probabilities and disconfirming evidence decreases it, reflecting the changes in certainty produced by new evidence. In addition, with Bayesian inference, no single disconfirmation is ever likely to reduce a posterior probability to zero. Instead, multiple disconfirmations are typically needed, a pattern that is more consistent with actual scientific practice.

Finally, the Bayesian model reflects a key observation of Popperian falsification, namely that disconfirmation has a more profound effect than confirmation. However, it does so under a broader explanatory framework that does not resort to fundamental distinctions between the two. In Bayesian calculus, the strength of evidence is reflected in the likelihood ratio. The numerator of this ratio is the probability that the evidence would be observed if the target theory was correct (i.e., true positives). The denominator is the probability that the evidence would be observed if some alternative theory was correct (i.e., false positives). However, in the sciences, there is almost always some alternative theory consistent with the evidence. For instance, even though Newton’s theory of gravity had been confirmed by vast amounts of evidence, this evidence was also consistent with an alternative theory: general relativity, which ultimately subsumed it. As a result, the denominator for any given likelihood ratio in the sciences will always be sizeable. This limits the effect of confirming evidence: the target theory may have predicted the observed evidence, but so would various alternative theories. As a result, scientists often must address competing hypotheses when making their case.

Disconfirming evidence, however, has the opposite outcome. If a theory predicts some evidence, but that evidence is not observed, this results in a very small numerator. The sizeable denominator then results in a tiny likelihood ratio, amplifying the effect of disconfirming evidence. In this way, the Bayesian model reflects the Popperian observation that disconfirmation is stronger than confirmation. However, it does so by treating both of them probabilistically in contrast to the Popperian model, which treats each of them fundamentally in a different way (Yudkowsky, 2010).

Frequentist Inference

For probability mathematics, the Frequentist perspective is the other major competing notion to Bayesian probabilities. Mathematicians and statisticians consider both methods as having strong merits. However, the Frequentist approach has become the dominant approach to inferring results from data containing variability (Hacking, 1965). The Frequentist perspective presumes that multiple sampling of some phenomenon results in a distribution of possible values. The spread of these values can be estimated and compared to a null hypothesis. If the distribution of values within some confidence interval (typically 95%) does not contain the null value, the null hypothesis is said to be rejected at a certain significance level.

Proponents of Bayesian inference—as a model for reasoning—have sometimes tried to support their positions by attacking the Frequentist perspective (Howson & Urbach, 1991). This turns out to be unnecessary. The Frequentist approach to probabilities is generally used to characterize well-defined random experiments only (Hacking, 1965). It is not typically used to characterize assessment of hypothesis by individuals. The distinction lies in the Bayesian interpretation of probabilities as “a measure of a state of knowledge” (Jaynes & Bretthorst, 2003). This allows probabilities to be assigned to any statement, even one that does not involve a random process. Frequentists, on the other hand, make no such claims. The statement “I trust this car mechanic” can therefore be assigned a Bayesian probability. However, since it involves no random sampling, it cannot be assigned a Frequentist probability. An active debate may exist between Frequentist and Bayesians over probabilities for external random systems, but not over applications to individual assessments of hypothesis.

Discussion

Bayesian inference, we believe, offers a promising putative framework for scientific reasoning. It provides an alternative lens for explaining many of the empirical findings in science education and educational psychology. Yet, it arises independently from mathematical derivations that are neither empirical nor normative. Bayesian inference also addresses the shortcomings of alternative frameworks for scientific reasoning such as Popperian falsification.

Given these findings, what implications does Bayesian inference have for the practice of science education and instruction? From a curricular perspective, one immediate implication is that if individuals are to behave rationally, they need to see judgments about data and evidence being an assessment not only of the probability of the hypothesis being correct but also of it being wrong. Such evidence is essential to making an assessment of the Bayesian likelihood ratio. Within the field of argumentation, Nussbaum (2010) has proposed that Bayesian inference could be used to provide a mathematical structure to Toulmin’s model for argument. For instance, he suggests that when evaluating a social issue—such as hunger—students could conduct on-line research to complete actual probability trees such as those provided in Fig. 4.1. This sort of instruction is likely to be particularly useful for students entering scientific research and practice. As mentioned earlier, most doctors are unable to make the correct assessment of risks in the breast cancer example. More generally, Bayesian inference can also be taught as a model for the reasoning process of science. Highlighting the importance of false negatives, for instance, can improve awareness of common pitfalls to rational reasoning. In this way, Bayesian inference can help bring increased use of statistical reasoning into real-world applications. For instance, Goldacre showed the fallacy of engaging in data mining as a means of identifying terrorists simply because of the large number of false negatives identified (Goldacre, 2009).

Bayesian inference also has several potential implications for classroom pedagogy. First, it adds further emphasis to the significance of findings that alternative misconceptions must be addressed if students are to gain secure understandings of scientific concepts. Teachers need to be aware that lowering the likelihood of false positives (i.e., alternative “wrong” ideas) is as instructionally powerful as raising the likelihoods of true positives (the “correct” idea). Second, if learning does indeed occur though a Bayes-like process of data weighing and integration, this reinforces constructivist notions of knowledge acquisition. From this perspective, simply providing the correct answer is not sufficient. Students must be given evidence and allowed to grapple with assessing likelihoods in order to properly update their belief assessments (i.e., posterior probabilities). Specifically, acceptance of new concepts is a function not only of how well the teacher presents the case for a new idea (i.e., strength of the likelihood ratios), but also the extent to which they address the strength of the student’s misconceptions (i.e., strength of individual prior probabilities). For students with strongly held prior misconceptions, it may take multiple exposures to evidence to change these beliefs. The Bayesian model suggests this is normal, even when the learner is evaluating the evidence rationally. Therefore, even if a student does not initially accept a new concept, instruction can still be considered a success as long as the learner is more open to the idea than they were before.

Perhaps most fundamentally, this account of scientific reasoning from a Bayesian perspective offers a rationale for why argument and critique are central and core to scientific activity. If, as we have suggested, beliefs are transformed not solely by confirming evidence but by negating alternative hypotheses, it suggests a central role for critique to the construction of knowledge both for the scientist and the learner of science. It also suggests why the few merchants of doubt who wish to cast aspersions on the scientific evidence for climate change have been so successful. In their absence, the likelihood ratio is virtually unitary. In their presence, particularly when they have scientific credibility, the existence of an alternative hypothesis which seems plausible substantially diminishes the likelihood ratio and therefore the certainty of individuals in the main hypothesis. A Bayesian perspective would suggest that the case for climate change would be made much more successfully not by asserting the validity of the scientific evidence but rather by undermining the validity of the naysayer’s case. Or to put it another way, knowing why the wrong answer is wrong matters as much as knowing why the right answer is right.