A Risk-Based Decision Analytic Approach to Assessing Multi-stakeholder Policy Problems

Abstract

The design of a public-private flood insurance system is a multi-stakeholder policy problem. The stakeholders include, among others, the public in the high-risk and low-risk areas, the insurance companies and the government. With an understanding of the preferences of the stakeholder groups, decision analysis can be a useful tool in establishing and ranking different policy alternatives. However, the design of a nation-wide insurance system involves handling imprecise information, including estimates of the stakeholders’ utilities, outcome probabilities and importance weightings. This chapter describes a general approach to analysing decision situations under risk involving multiple stakeholders. The approach was employed to assess options for designing a public-private flood insurance and reinsurance system in Hungary with a focus on the Tisza river basin. It complements the actual stakeholder process for this same purpose described in previous chapters of this book. The general method of probabilistic, multi-stakeholder analysis extends the use of utility functions for supporting evaluation of imprecise and uncertain information.

1 Introduction

The primary purpose of this chapter is to demonstrate a methodological approach able to cope with multi-stakeholder decision problems in disaster risk management. The methodology was applied to the Tisza river case study described in Chaps. 12 and 13. The upper Tisza river is subject to annual floods, and extreme floods are expected every 10–12%;years (Vári 1999). Financial losses from floods are severe in this region, and costs for compensation to victims and mitigation strategies are increasing. At the time of this study, the government was seeking alternative flood management strategies, where part of the economic responsibility would be transferred from the public to the private sector. This meant finding a balance between social solidarity and private responsibility. Most Hungarians, however, viewed the government as primarily responsible, meaning it should both protect them from flooding and compensate them for flood losses. The government considered this policy as no longer affordable. Moreover, a flood risk management policy would need to consider other views, including those of residents in high – and low-risk areas, insurers, the tourist and other industries, farmers, environmental groups and other NGOs, (non-governmental organizations). Consequently, there was a strong need for reaching a consensus on loss sharing policies that would include stakeholders.

As discussed in Chaps. 12 and 13, the design of a public-private flood insurance system for Hungary presents a significant multi-stakeholder policy problem, and this article focuses on its decision analytical component. In particular we apply a decision tree evaluation method integrated with a common framework for analysing multi-stakeholder decision situations under risk. The background data for the analysis was provided by the Hungarian Academy of Sciences and complemented by stakeholder interviews and a simulation model for investigating the effects of selected policy options for a flood risk management program in the region (see also Brouwers et al. 2004).

Since standard decision analytical methods are not suitable for this multistakeholder problem, we used an interval-based method. Stakeholders rank the relevant attributes of the policy option, such as whether it includes subsidies to low-income households or presents low or high risks to the private insurers. Furthermore, the design of a nation-wide insurance system involves imprecise information, including estimates of the stakeholders’ utilities, outcome probabilities, and weights.

Based upon statistical data and interviews (Brouwers and Riabacke 2012, Chap. 13 this book), we demonstrate how implementation of a simulation and decision analytical model can provide insights on the desirability of the selected general policy options for a flood risk management program in the region. The emphasis is on the multi-criteria and multi-stakeholder issues as well as on the high degree of uncertainty in the background data.

2 A Decision Theoretical Approach

The advantages and disadvantages of approaches for evaluating imprecisely stated decision problems are discussed elsewhere (see Ekenberg 2000; Ekenberg and Thorbiörnson 2001; Ekenberg et al. 2005; Danielson and Ekenberg 2007). Our selected decision analytic approach as it is applied to the Tisza multi-stakeholder policy problem, i.e., the design of a Hungarian flood insurance system that maximizes stakeholder utilities, is discussed below.

2.1 Decision Analysis

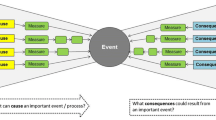
Decisions under risk are often represented by decision trees as shown in Fig. 14.1.

Fig. 14.1

A decision tree for decisions under risk

The decision tree consists of (1) a root, representing the decision, (2) a set of intermediary (event) nodes, representing uncertain events, and (3) consequence nodes, representing possible final outcomes. Usually, probability distributions are assigned as weights in the event nodes as measures of the uncertainties involved. For an alternative A_i, there is a probability p_ij that the accompanying event occurs. This event can have a consequence with a value v_ijk assigned to it or a subsequent event. Commonly, the maximization of the expected value is used as an evaluation rule. For instance, in Fig. 14.1, the expected value of alternative A_i is

$$ E({{A}_i}) = \sum\limits_{{j = 1}}^2 {{{p}_{{ij}}}} \sum\limits_{{k = 1}}^2 {{{p}_{{ijk}}}} {{v}_{{ijk1}}} $$

(14.1)

There are several methodologies for analysing multi-criteria, multi-stakeholder problems. However, these methodologies typically do not take adequate account of uncertainty in the decision process. Precise decision information is generally not available in public decision support situations.

The Tisza policy context is characterized by severe uncertain information, which makes it suitable for our structured decision analytic method (Danielson 2004; Danielson and Ekenberg 2007). There are some approaches that are also interesting candidates for this analysis, such as the generic multi-attribute analysis (GMAA) system (Jiménez et al. 2006) that takes account of uncertainty by allowing value intervals to represent incomplete information about the alternative consequences as well as the decision-maker’s preferences. Salo and Hämäläinen (1995) have also developed a set of tools that have been discussed e.g. in (Danielson et al. 2008). An important criterion in choosing the appropriate methodology for the Tisza case is its acceptance by stakeholders.

The method used for evaluating the policy decision problem in the pilot basin was developed for use in large decision problems similar to this case, with several stakeholders and requirements of transparency. It is a multi-stakeholder extension of a method for analyzing decisions containing imprecise information represented as intervals and as qualitative estimates (Danielson and Ekenberg 2007; Ekenberg et al. 2001; Danielson 2004).

In an interval decision analytic method, problem statements are explicitly given, but as intervals or comparisons instead of fixed numbers, and only with the precision the decision makers feel they have evidence for at that moment, e.g., the utility of a consequence is greater or less than the utility of another consequence, or that the probability of an event is within an interval between 30 and 40%. This has a number of advantages. First, the underlying information must be made explicit, and second, the statements can be discussed with (and criticized by) other participants in the decision process. Third, the requisite precision for a decision becomes clearer, including needs for more information. Fourth, arguments for (and against) a specific decision can be derived from the analysis material. Fifth, the decision can be better documented, and the underlying information as well as the reasoning leading up to a decision can be traced afterwards. The decision can even be changed in a controlled way should new information become available at a later stage.

3 The Policy Problem Formulation

As described in Chap. 13, two stochastic variables are used to represent flood uncertainties, and the decision problem is based on various scenarios given the stated sets of financial indicators.

Based on this, we have four prototypical scenarios. The first scenario is a private insurance alternative with government subsidies for the poor, and the government acts as reinsurer. This is option B1 in Brouwers and Riabacke (2012).

• No post-disaster government compensation to private flood victims

• Private insurance system characterized by

  • non-mandatory policies,

  • cover for flood, standing water, and all hazards (not modeled),

  • insurance purchased separately or bundled with property insurance policies,

  • up to 100% cover for damage without deductibles, and

  • risk-based premiums;

• Government subsidies for poor households up to 100% of premium;

• Government re-insurance fund financed by tax revenues.

In the second scenario, the government compensates flood failure victims. Private insurance with government subsidies for the poor are used and the government re-insure. The assumptions are the following:

• Government compensation to private flood victims for 50% of their damages

• Private insurance system

  • Private, non-mandatory policies

  • Natural disaster (flood, standing water, earthquake, etc.) insurance can be purchased separately or bundled with property insurance policies

  • Can reach 50% of the damage

  • No risk-based pricing for natural disasters (cross subsidies within system)

• Government subsidies for poor persons to purchase natural disaster insurance (can reach 100%)

• Government acts as re-insurer of last resort. Government re-insurance fund financed by tax revenues

• Contribution to prevention fund by insurance companies.

The third scenario is a variant of the second, where the government compensates flood failure victims, but does not re-insure. The assumptions are the following:

• Government compensation to private flood victims for 50% of their damages – contingent upon the purchase of natural disaster insurance;

• Private insurance system

  • Private, non-mandatory policies;

  • Natural disaster (flood, standing water, earthquake, etc.) insurance can be purchased separately or bundled with property insurance policies;

  • Covers 50% of the damage;

  • No risk-based pricing for natural disasters (cross subsidies within system);

• Government subsidies for poor persons to purchase natural disaster insurance (100%);

• No government reinsurance fund;

• Contribution to prevention fund by insurance companies.

In the fourth scenario, the responsibility is partly shifted from the government to the individual property owner. It includes mandatory public insurance for natural disasters with government subsidies for the poor. The assumptions are the following:

• Public insurance system administered by private insurance companies

  • Public, mandatory policies;

  • Only for natural disasters (flood, standing water, earthquake, etc.);

  • Can reach 100% of the damage;

  • No risk-based pricing (cross subsidies within system);

• Government subsidies for poor persons to purchase natural disaster insurance (can reach 100%);

• Government establishes catastrophe fund to compensate natural disaster victims and to assume all risks (risk of diverting catastrophe fund).

4 Analysing the Policy Scenarios

The computer tool DecideIT was employed (Danielson et al. 2003) for the evaluations. The tool enables handling the information and making evaluations in an automated way. The values from the Tisza investigations were entered into the tool from the simulations similar to Brouwers and Riabacke (2012).

4.1 Representation of the Decision Problem

The decision tree is generated from the four policy scenarios, which are represented as alternative branches. The final outcomes are divided into the three stakeholder categories: Government, Insurance companies, and Pilot basin (i.e. municipalities). Figure 14.2 shows a simplified tree used for option analyses. Figure 14.3 shows a part of the actual expansion of one of the final nodes in Fig. 14.2.

Fig. 14.2

The simplified decision tree

Fig. 14.3

Small part of the decision tree as viewed in the tool

In the absence of an actual and precise uncertainty measure, the simulations serve as a basis for a more elaborate sensitivity analysis that will consider both probabilities for floods and estimates of losses. The frequency of floods and levee failures used in the background simulations is based on historical data. In general, simulations of this type are dependent on a large number of input data, are, as such, are sensitive to various types of errors. For instance, the simulations do not reflect the flood frequency and magnitude (peak) increase during recent years. This may be a result of the changes in forestation, urbanization, asphalting, and other land uses or climate change (IPCC 2001). In the analyses below, ranges of values have been used instead of the precise values from the simulations. The ranges are intervals centred on the simulation values as mid-points.

Furthermore, since no structural mitigation measures are taken into account, the decision problem is a zero-sum game, i.e., the problem is to find how the relative importance of the stakeholders should be taken into account. This can be done by assigning their preferences different weights. Naturally, there are severe difficulties in assigning precise numbers for these importance weights, and it is more natural to study the effects from weaker qualitative statements such as “the importance of stakeholder 1 is greater than the importance of stakeholder 2”, etc. The effects of altering the feasible space of the importance weights are then easily analysed in the tool.

4.2 Evaluation of the Policy Options

Using the simulation results from Brouwers and Riabacke (2012) in Chap. 13 of this book, the analyses incorporate the stakeholder preferences, costs of the different mitigation measures as well as costs for damages and property losses, and probabilities of the different flood scenarios. In the Tisza case, three stakeholder categories were modelled and the evaluation procedure is described below.

The primary evaluation rule for the decision trees is based on the generalized expected values of the scenarios, taking all probabilities, values and (in the final analysis) criteria weights into account. Since neither probabilities nor values are fixed numbers, the calculation of the expected value yields multi-linear objective functions as in Eq. 14.1 above. Maximization of such non-linear expressions are computationally demanding problems to solve for an interactive tool in the general case, using techniques from the area of non-linear programming. In, e.g., Danielson and Ekenberg (2007) there are discussions about computational procedures to reduce non-linear problems to systems with linear objective functions, solvable with ordinary linear programming methods. Equation 14.1 is then evaluated with respect to the outcomes of the stakeholders and a total value range for the alternatives is then obtained by weighting these results with respect to the stakeholders’ assigned relative importance. Since it is practically impossible to assert a meaningful quantitative (numeric) stakeholder weight (e.g. w₁ = 0.427), qualitative weights are used instead in the analysis (e.g. w₁ > w₂). This is easier to understand for the participants in the process.

How is it now possible to compare the scenarios? For a regular decision tree with decision nodes, event nodes, and consequence nodes, there is one probability constraint, P, and one value constraint, V. For a multi-criteria model, as in the case here, there is also a weight constraint. When the probabilistic decision trees are evaluated under some stakeholder preferences, the probability variables, value variables and related constraints are assigned to the alternatives of the model. For a decision tree, variables and constraints are assigned to the consequence nodes.

To further aid in the modelling of the problem, the orthogonal hull concept indicates to the decision-maker which parts of the statements are consistent with the available information given. The decision information can be considered as constraints in the space formed by all decision variables. The (orthogonal) hull is then the projection of the constrained spaces onto each variable axis, and can thus be seen as the meaningful interval boundaries (Danielson and Ekenberg 2007). The same type of input is used for values, probabilities, and weights, although the normalization constraints Σ p _i = 1 (for probabilities) and Σ w _j = 1 (for weights) must not be violated. All input into the model is subject to consistency checks performed by the tool.

For each variable, there is also a focal point, which may be viewed as the ‘most likely’ or ‘best representative’ value for that variable. Hence, a focal point is a unique solution vector whose components for each dimension (variable) lies within the orthogonal hull. Given this, we calculate the strength of alternatives as a means for further discriminating the alternatives. The strength δ _ij simply denotes the difference in expected value between two scenarios (alternatives) A _i and A _j, i.e. the expression E(A _i)– E(A _m). For multi-criteria models, the expected value for each criterion is aggregated into a weighted sum of expected values for the entire decision problem. By denoting the expected value of an alternative A _i with respect to the k ^th stakeholder with ^k E(A _i), this leads to an expression for the weighted strength

$$ \sum\nolimits_k {{{w}_k}\left( {{}^k\mathrm{E}({{A}_i}) - {}^k\mathrm{E}({{A}_j})} \right)} $$

In its most basic form (one-level decision tree), ^k E(A _i) is reduced to

$$ \sum\nolimits_k {{{p}_{{ik}}}\cdot {{v}_{{ik}}}} - \sum\nolimits_l {{{p}_{{jl}}}\cdot {{v}_{{jl}}}} $$

over all consequences belonging to alternative A _i and A _j respectively, such that p _il denotes the probability of the l ^th consequence, possibly occurring when choosing scenario A _i. Details on how this is computationally handled in the evaluation are found in (Larsson et al. 2005; Danielson and Ekenberg 2007). Hence, in the tool, probabilistic decision trees may be used alone for single-objective decision problems and can also be “connected” at any time to a criterion leaf-node in the criteria tree as long as the initial alternatives in the probabilistic decision trees map one-to-one onto the alternative set in the multi-criteria tree.

In the evaluation, the alternatives are pair-wise compared and a ranking is induced. The strengths of each alternative compared to all the others can then be compared using the tool. This results in graphs showing the maximum strengths of the alternatives.

Figure 14.4 shows the result of asserting government as the most important stakeholder. The importance weights were set accordingly (i.e. w(Gov) > w(Mun) and w(Mun) > w(Ins) for a weight function w(·) that sums to one) and the probabilities and costs were provided from the simulations. Note that no explicit numerical weights had to be supplied. The x-axis shows the base cut, which is a sensitivity analysis zooming in on central parts of the intervals. See below for a more detailed discussion on the concept. The y-axis shows the difference in strength.¹ Figure 14.4 shows graphs, representing the strengths of the alternatives. at various base cuts. Thus, the upper graph represents the most preferred alternative. Thus, in Fig. 14.4, the ranking of the alternatives is (from most to least preferred): Alt. 3 (Refined Alt. 2), Alt. 2 (Mixed Insurance), Alt. 1 (Individualistic), and Alt. 4 (Public). It should be emphasized that this does not mean that it is impossible for, e.g., Alt. 2 to be more favourable than Alt. 3. As long as the graph of Alt. 2 is above the x-axis, there is such a possibility. However, the likelihood that Alt. 3 is the alternative to prefer is much higher, so this should be chosen if no other information is available. A natural way to handle the inherent imprecision is to consider values near the boundaries of the intervals as being less reliable than more central ones. If the strength is evaluated on a sequence of ever-smaller sub-bases, a good appreciation of the strength’s dependency on boundary values can be obtained. This is taken into account by cutting off the dominated regions indirectly. This is called cutting the bases, and the amount of cutting is indicated as a percentage, which can range from 0 to 100%.

Fig. 14.4

Government is considered to be the most important category

This can be seen as the x-axis in Fig. 14.4, which shows progressively larger cuts. For a 100% cut, the bases are transformed into single points (focal points), and the evaluation becomes the calculation of the ordinary expected value. It is possible to regard the hull cut as an automated kind of sensitivity analysis. Since the belief in peripheral values is somewhat less, the interpretation of the cut is to zoom in on more believable values that are more centrally located. Or conversely, to zoom out from the focal points, adding uncertainty as the zooming out progresses (leftwards in the figures). Thus, this kind of contraction along the x-axis is a sensitivity analysis procedure, in which all intervals are compressed in a controlled way towards the focal point of the multi-dimensional space that all consequences span. Using cut levels as in Fig. 14.4, it can be seen that δ_23, δ₁₂ and δ₄₁ are strictly less that 0 at cut levels 80, 85, and 95%, respectively. This means that in a quite substantial volume around the focal point, Alt. 3 is definitely better than Alt. 2, etc., and consequently, that there is no possibility for the converse to hold. Thus, the above ranking is fairly stable under this kind of sensitivity analyses.

More formally, for comparing alternatives A_i and A_j, the upper line is max(δ _ij) and the lower is – min(δ _ij), i.e. the lower line is reversed to facilitate an easier comparison. Thus, one can see from which cut level an alternative dominates another. As the cut progresses, one of the alternatives eventually dominates strongly, i.e. there are no variable assignments yielding max(δ _ij) > 0. The interpretation of the figures will be further described below.

Figure 14.5 shows the analysis when the difference of the weight of the government is greater than the weight of the municipalities plus a constant of 0.3, i.e., the government is perceived to be of even greater importance. As in the previous analysis, both these weights are greater than the weight of the insurance companies. It can be seen from the figure that the preference order is still the same as above, but that the relative difference between these have increased. The x-axis shows the cut in per cent ranging from 0 to 100. The y-axis is the expected value difference δ _ij for the pairs. Using the same kind of analysis as above, it can be seen from Fig. 14.5 that the ranking of the alternatives this time is the same.

Fig. 14.5

Weight of government much greater than municipalities

Figure 14.6 shows the result of asserting the municipalities as being the most important stakeholders (i.e. w(Mun) > w(Ins) and w(Mun) > w(Gov)). The ranking of the alternatives is (from most to least preferred): Alt. 3, Alt. 4, Alt. 2, and Alt. 1.

Fig. 14.6

Municipalities is considered to be the most important category

We will here refrain from any recommendations concerning the best overall choice, but note that during the discussions with the stakeholders, it seemed to be a common view that at least the insurance companies should not be considered the most important. If also it is assumed that the government and the municipalities are considered as more important than the insurance companies (i.e. w(Mun) > w(Ins) and w(Gov) > w(Ins)), we receive the result that the final alternative from the stakeholder workshop is the preferred one. Now, one might argue that Alt. 4 ought to be slightly modified to better fit also the perspective of the insurance companies. In this way, information from the analyses can be fed back into the decision process, yielding modified alternatives that in the end would be more acceptable to a majority of the stakeholders. Such feedback loops are typical when working with a method allowing imprecise data.

In conclusion, this brief analysis shows the stability of the results. Importantly, it is not necessary to assign explicit weights to the stakeholders (which could be difficult or even controversial) to obtain this result. It is sufficient to give general and comparatively weak preferences and still obtain confidence in the result.

It should be emphasized that the figures above are intended to explain the basics of the method and do not present conclusive analyses of the Tisza case. The analysis can (and should) be extended by, at least, further sensitivity analysis, analysis of critical factors, and settings of security levels (Ekenberg 2000).

5 Summary and Concluding Remarks

We have discussed a decision analytical method for investigating the effects of different policy options for a flood risk management program in the Tisza region. This multi-stakeholder problem could not be solved using standard approaches, and we have used an interval approach, called EDM, for the decision analytical part.

We have focused on the analysis of four alternative flood management policy strategies, and used computational decision analysis to investigate the strategies. We have explored the effects of imposing the strategies for the purpose of illuminating significant effects of adopting different insurance policies. The main focus has been on insurance schemes in combination with the level of government compensation.

The analyses of the different policy strategies have been based on a simulation model where expected flood failures as well as geographical, hydrological, social, and institutional data have been taken into account. The generated results were thereafter transposed to decision trees under three stakeholder perspectives. Taking the simulation results into account, the scenarios have been analysed with the decision tool DecideIT for evaluating the policy options under the various costs, importance weights, and probabilities involved. No explicit importance weights for the stakeholders were necessary, but only an ordering among them.

Note that we do not present all analyses performed, since the primary purpose is to demonstrate a methodological approach to the multi-stakeholder decision problem. It is important to note that the end result of the analysis is a thorough understanding of the problem and recommendations relative to the input material and preferences. Varying the importance weights of the stakeholders produced, as expected, differing results. Needless to say, the issues involve several non-mathematical aspects, not least political and it is up to the political process to make the final decision with information based on results from the method proposed in this article.