Keywords

1 Introduction

Nowadays, full-wave electromagnetic methods [9, 11, 17] are widely used to simulate a variety of complex electromagnetic systems and are considered to be essential for efficient design. The use of these methods usually results in the computation of a huge number of field (E,H) or circuit (i,v) unknowns, in the frequency-domain or time-domain, although users are usually only interested in a few of them at the input and output ports. These methods provide high accuracy, often at a significant cost in terms of memory storage and computing time. Therefore, Model Order Reduction (MOR) techniques are crucial to reduce the complexity of the model defined by the full-wave numerical method and the computational cost required by simulations, while retaining the important physical features of the original system [3, 7].

Efficient real-time design space exploration, design optimization and sensitivity analysis require the development of accurate parametric broadband macromodels that approximate the dynamic behavior of a system characterized by several design parameters, such as geometrical layout or substrate characteristics, in addition to time or frequency. These applications call for Parameterized Model Order Reduction (PMOR) techniques.

A frequency-domain technique called Multivariate Orthonormal Vector Fitting (MOVF) was presented in [4], to compute accurate rational parametric macromodels, based on parameterized frequency responses with a highly dynamic behavior. This technique can be seen as a data-driven PMOR method. Instead of reducing the size of the matrices of a parameterized state-space model directly (model-based PMOR), MOVF builds rational parametric macromodels with a reduced model complexity based on a set of input-output data samples. The goal of the macromodeling algorithm is to find a multivariate rational function which approximates a large set of K + 1 data samples \(\left\{(s,\mathbf{g})_{k},\;H(s,\mathbf{g})_{k}\right\}_{k=0}^{K}\) in a least-squares sense. These data samples depend on the complex frequency s = jω and several additional parameters \(\mathbf{g}=(g^{(n)})_{n=1}^{N}\) as design variables which describe e.g. the metallizations in an EM circuit (lengths, widths, \(\ldots\)) or the substrate features (thickness, dielectric constant, losses, \(\ldots\)). The proposed approach results in accurate and compact rational parametric macromodels of complex electromagnetic systems. A generalization of MOVF to include parameter derivatives in the modeling process was proposed in [6]. Parameter derivatives provide additional information about the underlying system and can often be simulated at a significantly lower computational cost than additional samples [5, 13, 15, 20]. The inclusion of derivatives can be useful to reduce the required amount of data samples, while preserving the accuracy of the results. In this chapter a new technique, the z-domain Multivariate Orthonormal Vector Fitting (ZD-MOVF) is described, representing the z-domain counterpart of [4]. It is a robust multivariate extension of the z-domain Orthonormal Vector Fitting technique (ZD-OVF) proposed in [14, 16, 21]. A microstrip example confirms the ability of the new algorithm to build parametric macromodels of dynamic systems with a good accuracy.

2 Background

In this section we explain the generation of z-domain data starting from frequency-domain or time-domain data and the choice of the λ parameter of the Tustin transform.

2.1 Generation of z-Domain Data

Microwave circuits and components can be characterized in frequency-domain or time-domain by numerical electromagnetic simulations or measurements. To obtain the corresponding parameterized z-domain response, H d (z, g), where z is the complex discrete frequency variable and g is a real design variable, a Tustin (bilinear) transform:

$$ s \longrightarrow z={\frac{\lambda + s}{\lambda - s}},\quad \lambda \in \mathbb R^{+} $$
(7.1)

can be used starting from frequency-domain data H c (s, g):

$$ H_{c}(s,g) \longrightarrow H_{d}\left(z={\frac{\lambda + s}{\lambda - s}},g \right)$$
(7.2)

where c stands for continuous and d for discrete. If time-domain data is available, under the hypothesis of a negligible or absent aliasing in the sampling process, the frequency response of a continuous-time system can be computed by applying standard techniques, such as Fast Fourier Transform (FFT) algorithms on the data samples:

$$ h_{d}(\left[n\right],g) = h_{c}(nT_{s},g) $$
(7.3)

where the real sequence h d ([n], g) is equal to the signal in the time domain h c (t, g) at the equally spaced time samples nT s and T s is the sampling period. Once the parameterized frequency response is computed, the Tustin transform (7.1) is used as before. The obtained z-domain data can be normalized by discrete frequency z [14]. Once the parametric macromodel is computed in the z-domain, it can be converted back to the s-domain by using inverse Tustin transform.

2.2 Choice of λ of the Tustin Transform

The λ parameter of the Tustin transform can be freely chosen [19] under the constraint that it is not a real pole of the continuous-time system [1]. The numerical example in this letter shows that the algorithm is robust with respect to an arbitrary choice of λ, since its value does not affect the accuracy of the results over a wide range. To avoid harmful numerical conditions, extreme values of λ have to be discarded, such as very low (near zero) or very high (near infinity).

3 Parametric Macromodeling

To simplify the notation, the algorithm is only described for bivariate systems. The extension to the full multivariate formulation is straightforward. As in [4], the ZD-MOVF algorithm proposes to represent the parametric macromodel as the ratio of a bivariate numerator and denominator

$$ R(z,g)={\frac{N(z,g)}{D(z,g)}}={\frac{\sum_{p=0}^{P}\sum_{v=0}^{V}c_{pv}\chi _{p}(z)\psi_{v}(g)}{\sum_{p=0}^{P}\sum_{v=0}^{V}\tilde{c}_{pv}\chi _{p}(z)\psi_{v}(g)}} $$
(7.4)

where P and V represent the maximum order of the corresponding basis functions χ p (z) and ψ v (g) in the complex discrete frequency variable z and the real design variable g, respectively. To establish the coefficients c pv and \(\tilde{c}_{pv}\) of numerator and denominator in (7.4), the ZD-MOVF algorithm minimizes the Sanathanan–Koerner (SK) cost function [18] on a set of K + 1 data samples \(\left\{(z,g)_{k},H_{d}(z,g)_{k}\right\} _{k=0}^{K}\). SK is an iterative procedure, in the first iteration step of the algorithm (t = 0) Levi’s cost function [12] is minimized to obtain an initial estimate of the coefficients c pv and \(\tilde{c}_{pv}\). In the following steps (\(t=1,\ldots,T\)) of the SK iteration, the inverse of the previously estimated denominator D (t-1)(z,g) is used as an explicit least-squares weighting factor. A relaxed non-triviality constraint is added as an additional row in the system matrix [8], to avoid the trivial null solution and improve the convergence of the algorithm. Each equation is split in its real and imaginary parts, to ensure that the model coefficients c (t) pv , \(\tilde{c}_{pv}^{(t)}\) are real. Scaling each column to unity length [7] is suitable to improve the numerical accuracy of the results.

4 Choice of Basis Functions

In this section we describe the choice of the basis functions for the discrete frequency and other parameters.

4.1 Discrete Frequency-Dependent Basis Functions

Based on a prescribed set of stable poles \(\mathbf{a}=\{-a_{p}\}_{p=1}^{P}\), a set of partial fractions \(\chi_{p}(z,\mathbf{a})\) is chosen, with χ0(z) = 1. To select the poles two steps are followed: first, they are chosen in the s-domain as complex conjugate pairs with small real parts and the imaginary parts linearly spaced over the frequency range of interest [7] and after that, the Tustin transform (7.1) is applied to map them from s- to z-domain. A linear combination of two fractions is chosen to ensure that the residues of \(\chi_{p}(z,\mathbf{a})\) and \(\chi_{p+1}(z,\mathbf{a})\) come in perfect conjugate pairs leading to real-valued time domain responses, i.e.:

$$ \chi_{p}(z,\mathbf{a})=z(z+a_{p})^{-1}+z(z+a_{p+1})^{-1} $$
(7.5)
$$ \chi_{p+1}(z,\mathbf{a})=jz(z+a_{p})^{-1}- jz(z+a_{p+1})^{-1} $$
(7.6)

To improve the numerical stability of the modeling algorithm, the Takenaka–Malmquist basis functions [10] can be used, as shown in [16]:

$$ \chi_{p}(z,\mathbf{a})=k_{p} \left(\prod\limits_{i=1}^{p-1}{\frac{1+a_{i}^{\ast}z} {z+a_{i}}}\right){\frac{(1-z)|1-a_{p}|}{(z+a_{p})(z+a_{p+1})}} $$
(7.7)
$$ \chi_{p+1}(z,\mathbf{a})=k_{p+1} \left( \prod\limits_{i=1}^{p-1}{\frac{1+a_{i}^{\ast}z}{z+a_{i}}}\right) {\frac{(1+z)|1+a_{p}|}{(z+a_{p})(z+a_{p+1})}} $$
(7.8)

where

$$ k_{p}=k_{p+1}={\frac{\sqrt{2}}{2}} \sqrt{1-|a_{p}|^{2}} $$
(7.9)

The orthonormal basis functions can improve the conditioning of the system equations and are less sensitive to the choice of the initial poles. Their use ensures a more numerically robust macromodeling procedure [3].

4.2 Parameter-Dependent Basis Functions

The parameter-dependent basis functions \(\psi_{v}(g,\mathbf{b})\) are also chosen in partial fraction form as a function of jg, hence in rational form. The set of starting poles \(\mathbf{b}=\{-b_{v}\}_{v=1}^{V}\) is composed by complex pairs with small real parts of opposite sign and imaginary parts linearly spaced over the parameter range of interest, provided that ψ0(g) = 1. A linear combination of two fractions is used to ensure that \(\psi_{v}(g,\mathbf{b})\) and \(\psi_{v+1}(g,\mathbf{b})\) are real functions [4]:

$$ \psi_{v}(g,\mathbf{b})=(jg+b_{v})^{-1}-(jg-(b_{v})^{\ast})^{-1} $$
(7.10)
$$ \psi_{v+1}(g,\mathbf{b})=j(jg+b_{v})^{-1}+j(jg-(b_{v})^{\ast})^{-1} $$
(7.11)

5 Example: Double Folded Stub Microstrip Bandstop Filter

The double folded stub microstrip bandstop filter [2] under study is shown in Fig. 7.1. The substrate is \(0.1270\,\hbox {mm}\) thick with a relative dielectric constant ε r equal to 9.9. The scattering parameters of the system are simulated by ADS-Momentum [1] Footnote 1 in the s-domain and subjected to (7.2), to obtain the corresponding parametrized z-domain response.

Fig. 7.1
figure 1

Geometry of the double folded stub microstrip bandstop filter [2]

Full size image

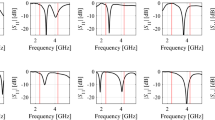
The parametric macromodels of scattering parameters S 11 and S 21 are built as functions of the varying length of each folded segment \(L\in\lbrack 1.98-2.40\,{\hbox{mm}}]\) and varying spacing between a folded stub and the main line \(S\in\lbrack 0.061\)–0.243 mm] over the frequency range (5–20 GHz). The desired model accuracy is set to −60 dB, which corresponds to three significant digits. The initial data grid for S 11 and S 21 is of size 14 × 10 × 22 samples (L, S, freq). The corresponding number of poles is chosen 6, 4 and 10 for both scattering parameters. Figures 7.2 and 7.3 show the magnitude of the trivariate macromodels of S 11 and S 21 for the minimum and maximum values of the spacing variable S.

Fig. 7.2
figure 2

Magnitude of the trivariate macromodels of S 11 (light grey surface) and S 21 (dark grey surface) for \(S = 0.061\,\hbox{mm}\)

Full size image
Fig. 7.3
figure 3

Magnitude of the trivariate macromodels of S 11 (light grey surface) and S 21 (dark grey surface) for \(S = 0.243\,\hbox{mm}\)

Full size image

To compute the macromodels only 4 and 3 iterations of SK method discussed in Sect. 7.3 are needed and the maximum absolute error in the initial data grid corresponds to −62.84 and −67.54 dB, respectively. To confirm the quality of built macromodels a set of validation data samples is computed on a very dense grid of size 50 × 30 × 151 samples. The histogram in Fig. 7.4 shows the number of validation samples that corresponds to a certain absolute error for both trivariate macromodels. Figure 7.4 shows that they have a good overall accuracy and the maximum absolute error over all the validation samples is bounded by −60.17 and −61.06 dB for S 11 and S 21 respectively. The choice of the λ parameter in the Tustin transform (7.1) does not influence the model accuracy over a broad range of values [10−3−1023]. It confirms that λ is free to choose and illustrates the robustness of the algorithm.

Fig. 7.4
figure 4

Histogram: error distributions of the trivariate macromodels of S 11 (light grey) and S 21 (dark grey) over 226,500 validation samples

Full size image

6 Conclusions

This chapter presents a robust multivariate extension of the z-domain Vector Fitting technique [14, 16, 21] for the calculation of accurate and compact parametric macromodels of high-speed components. By combining rational basis functions and the Sanathanan–Koerner least-squares estimator, the robustness of the method is ensured. An example illustrates the capability of the algorithm to model dynamic parameterized frequency responses with a good accuracy. Once the multivariate macromodeling process is completed, the resulting scalable behavior model can efficiently be employed in real-time design space exploration, fast optimization and sensitivity analysis.